STAIR 2.0: A Generic and Automatic Algorithm to Fuse Modis, Landsat, and Sentinel-2 to Generate 10 m, Daily, and Cloud-/Gap-Free Surface Reflectance Product
Abstract
1. Introduction
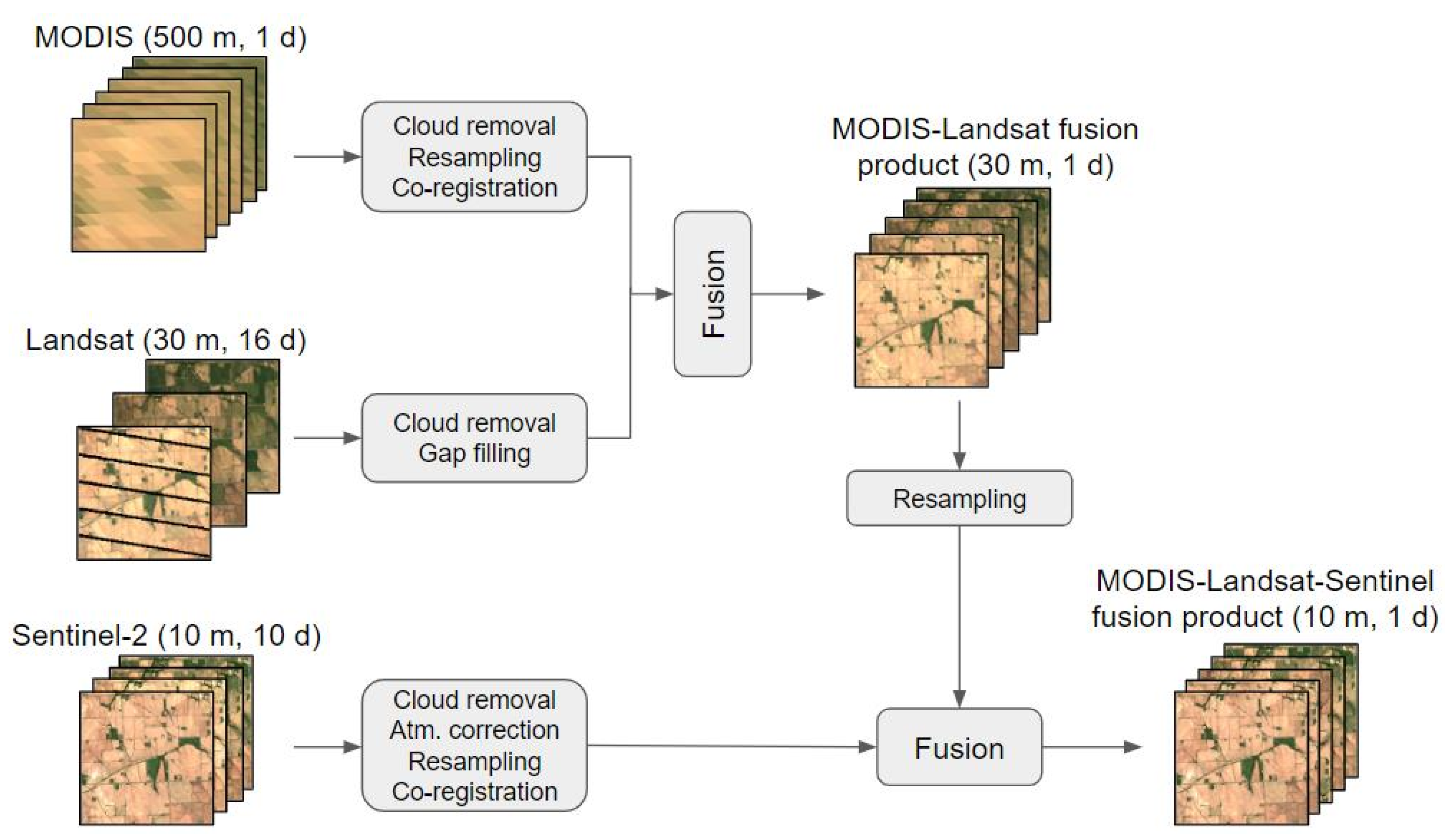
2. Materials and Methods
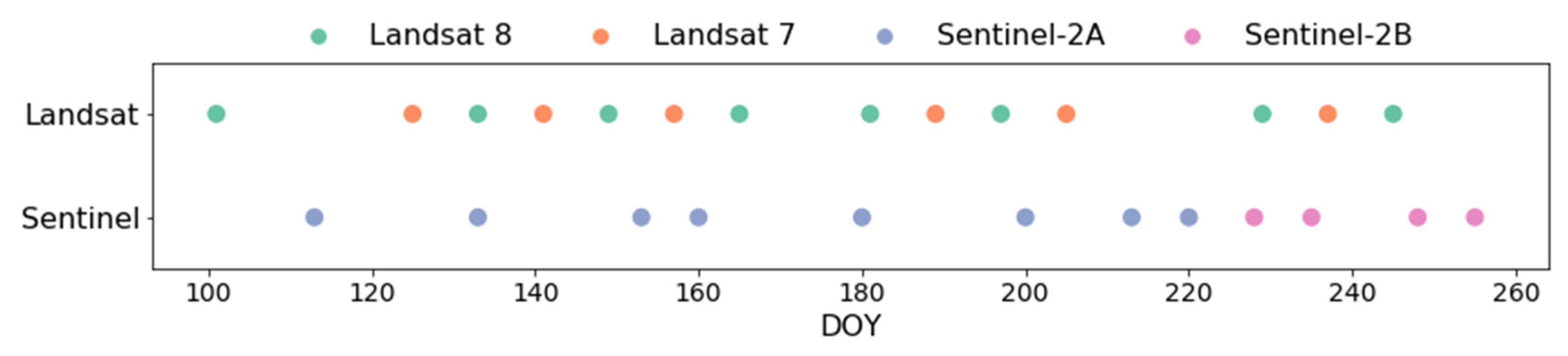
2.1. Dataset
2.2. Data Preprocessing
2.2.1. Spatial Co-Registration
2.2.2. Spectral Adjustment
2.3. Imputation of Missing Pixels
2.3.1. Step 1: Segmentation of Land Covers
2.3.2. Step 2: Temporal Interpolation through a Linear Regression
2.3.3. Step 3: Adaptive-Average Correction with Similar Neighborhood Pixels
2.3.4. Step 4: Searching Similar Neighborhood Pixels
2.3.5. Step 5: Iterative Imputation Using Multiple Reference Images
2.4. Fusion of Multiple Sources of Optical Satellite Data
2.4.1. Fusion of MODIS and Landsat Data
2.4.2. Fusion of Sentinel-2 and Synthetic MODIS–Landsat Data
2.5. Assessments of Fusion Results
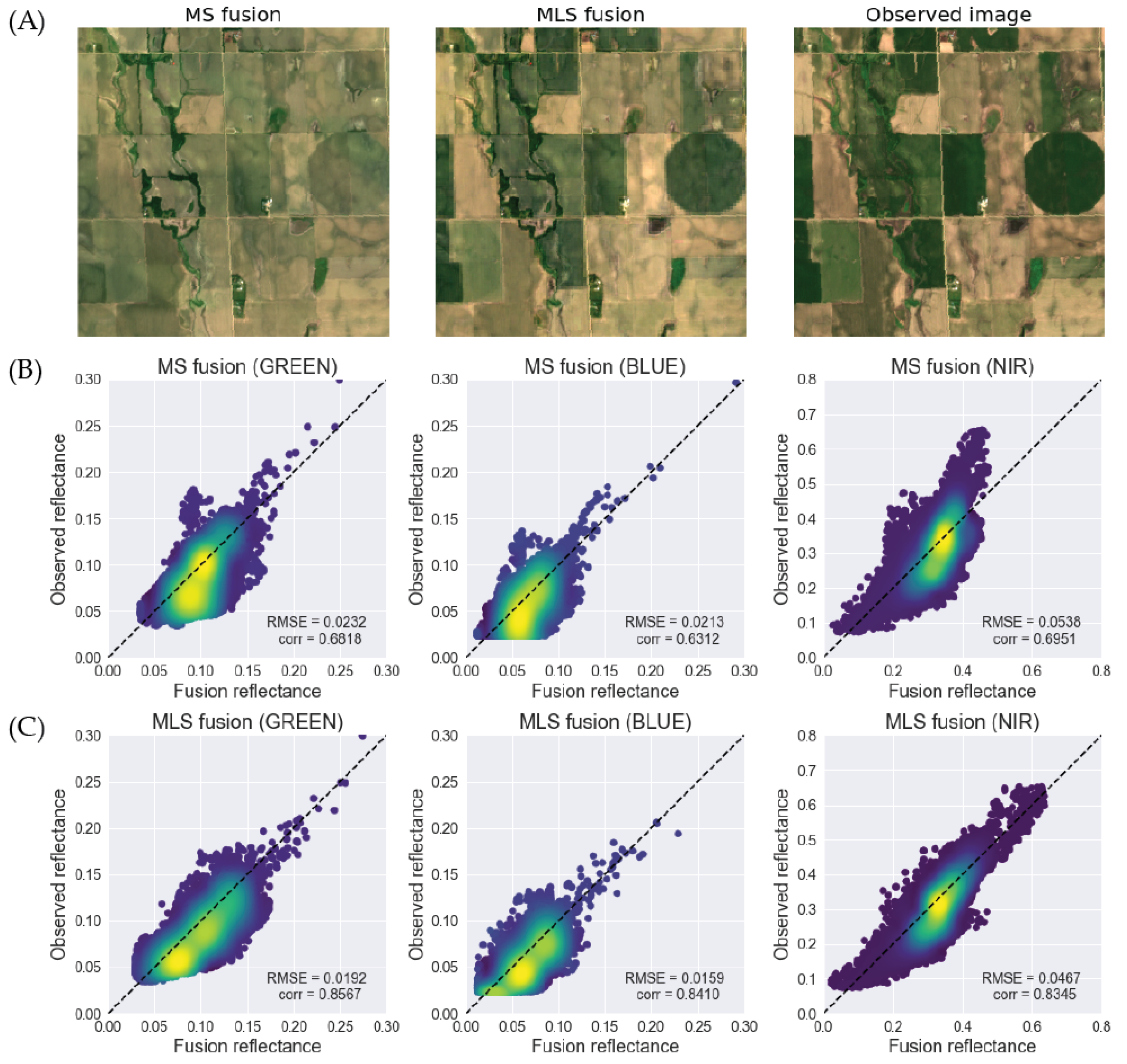
3. Results
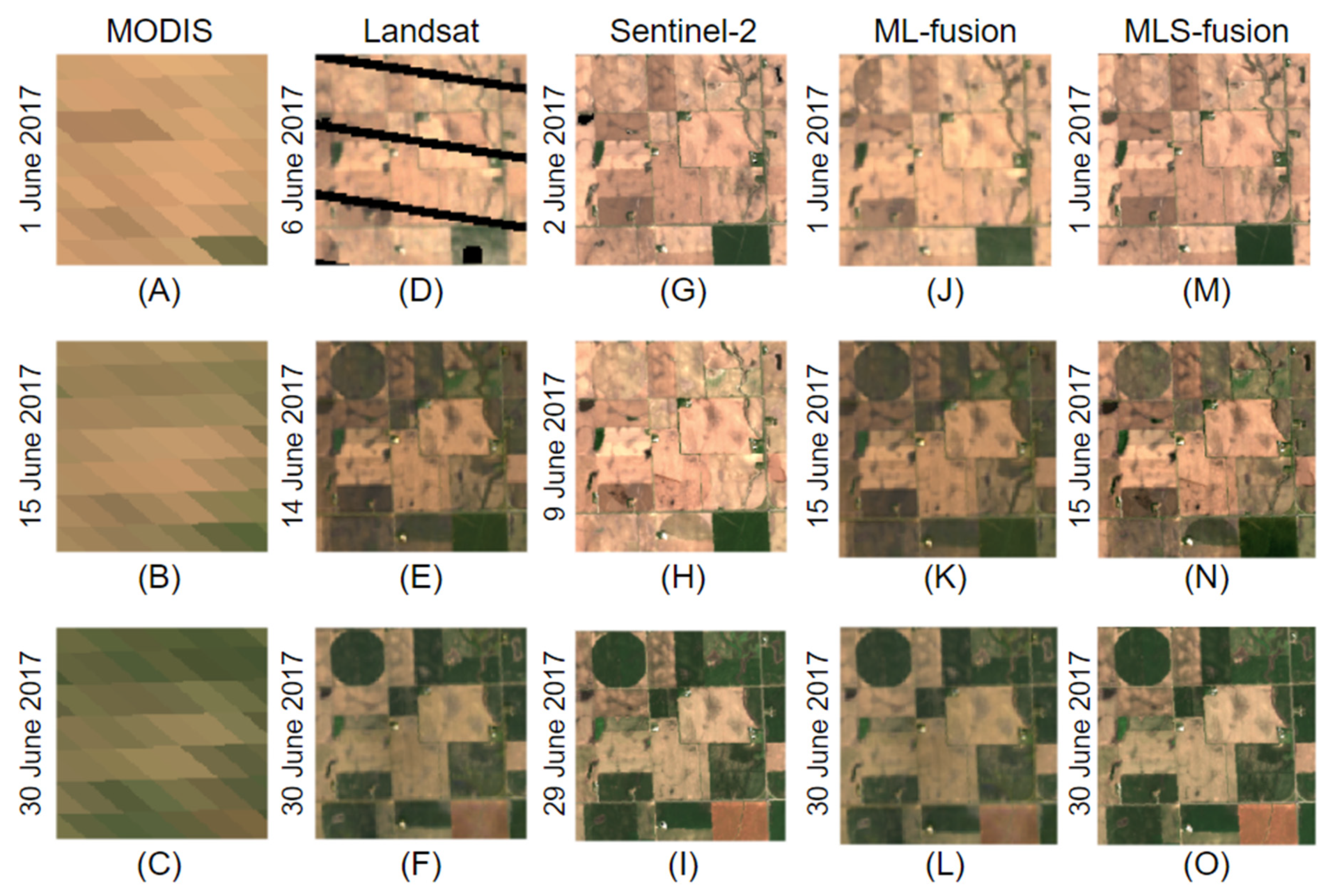
3.1. STAIR 2.0 Generates Daily, 10-m Time Series of Surface Reflectance
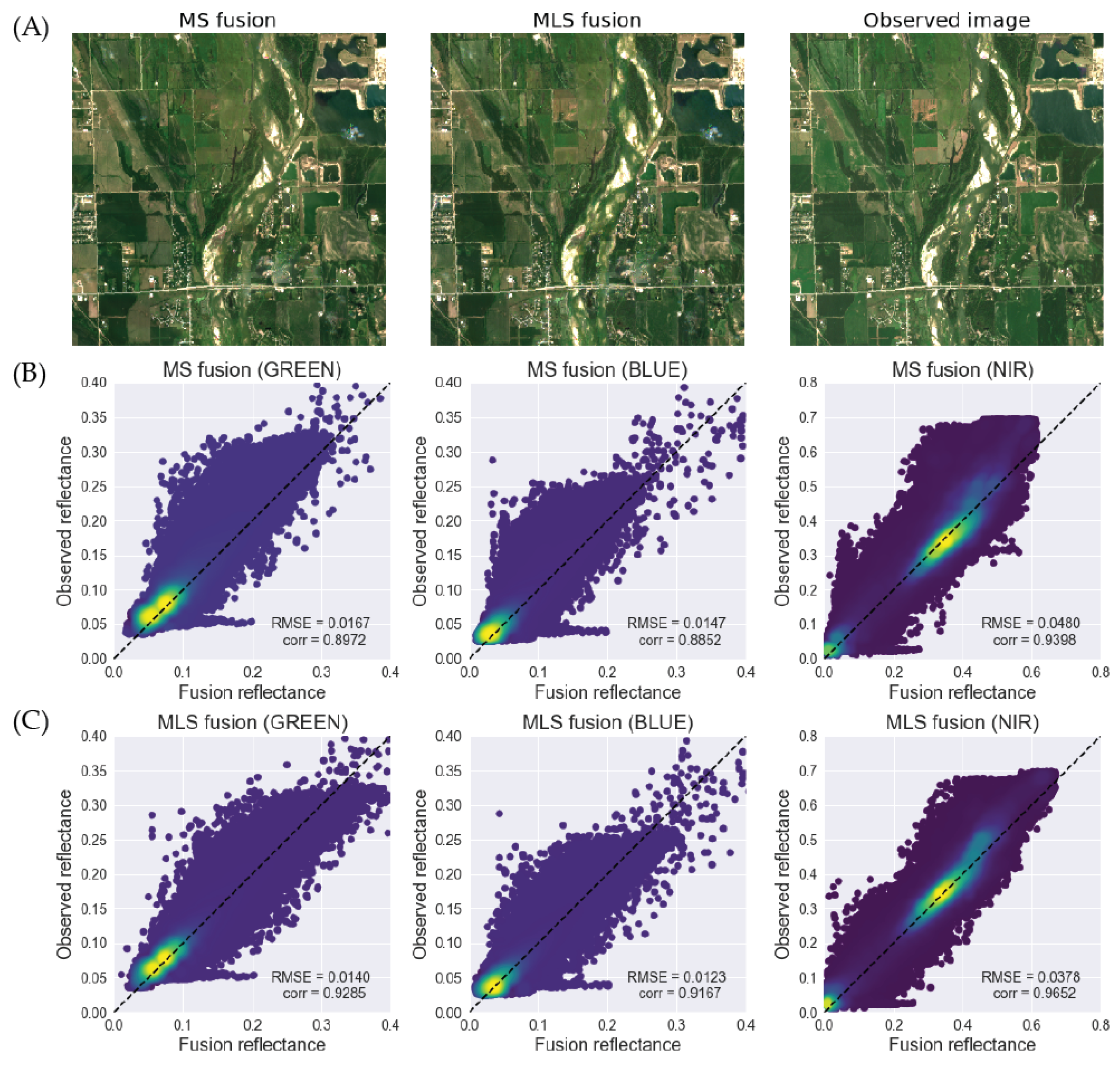
3.2. Quantitative Assessments
3.3. Values of Integrating Three Satellite Sources
4. Discussion
4.1. Advancements of STAIR 2.0
4.2. Spectral Correction and Spatial Alignments of Multiple Satellite Sources
4.3. Fusion Strategy of Multiple Satellite Sources
4.4. Computational Efficiency and Scalability
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Data Availability Statement
References
- Schneider, A. Monitoring land cover change in urban and peri-urban areas using dense time stacks of Landsat satellite data and a data mining approach. Remote Sens. Environ. 2012, 124, 689–704. [Google Scholar] [CrossRef]
- Cai, Y.; Guan, K.; Peng, J.; Wang, S.; Seifert, C.; Wardlow, B.; Li, Z. A high-performance and in-season classification system of field-level crop types using time-series Landsat data and a machine learning approach. Remote Sens. Environ. 2018, 210, 35–47. [Google Scholar] [CrossRef]
- Gao, F.; Anderson, M.C.; Zhang, X.; Yang, Z.; Alfieri, J.G.; Kustas, W.P.; Mueller, R.; Johnson, D.M.; Prueger, J.H. Toward mapping crop progress at field scales through fusion of Landsat and MODIS imagery. Remote Sens. Environ. 2017, 188, 9–25. [Google Scholar] [CrossRef]
- Johnson, M.D.; Hsieh, W.W.; Cannon, A.J.; Davidson, A.; Bédard, F. Crop yield forecasting on the Canadian Prairies by remotely sensed vegetation indices and machine learning methods. Agric. For. Meteorol. 2016, 218, 74–84. [Google Scholar] [CrossRef]
- Guan, K.; Wu, J.; Kimball, J.S.; Anderson, M.C.; Frolking, S.; Li, B.; Hain, C.R.; Lobell, D.B. The shared and unique values of optical, fluorescence, thermal and microwave satellite data for estimating large-scale crop yields. Remote Sens. Environ. 2017, 199, 333–349. [Google Scholar] [CrossRef]
- Guan, K.; Li, Z.; Rao, L.N.; Gao, F.; Xie, D.; Hien, N.T.; Zeng, Z. Mapping Paddy Rice Area and Yields Over Thai Binh Province in Viet Nam from MODIS, Landsat, and ALOS-2/PALSAR-2. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2238–2252. [Google Scholar] [CrossRef]
- Jamshidi, S.; Zand-Parsa, S.; Naghdyzadegan Jahromi, M.; Niyogi, D. Application of a simple Landsat-MODIS fusion model to estimate evapotranspiration over a heterogeneous sparse vegetation region. Remote Sens. 2019, 11, 741. [Google Scholar] [CrossRef]
- Jamshidi, S.; Zand-parsa, S.; Pakparvar, M.; Niyogi, D. Evaluation of evapotranspiration over a semiarid region using multiresolution data sources. J. Hydrometeorol. 2019, 20, 947–964. [Google Scholar] [CrossRef]
- Stone, B., Jr.; Rodgers, M.O. Urban form and thermal efficiency: How the design of cities influences the urban heat island effect. Am. Plan. Assoc. J. Am. Plan. Assoc. 2001, 67, 186. [Google Scholar] [CrossRef]
- Imhoff, M.L.; Zhang, P.; Wolfe, R.E.; Bounoua, L. Remote sensing of the urban heat island effect across biomes in the continental USA. Remote Sens. Environ. 2010, 114, 504–513. [Google Scholar] [CrossRef]
- Streets, D.G.; Canty, T.; Carmichael, G.R.; De Foy, B.; Dickerson, R.R.; Duncan, B.N.; Edwards, D.P.; Haynes, J.A.; Henze, D.K.; Houyoux, M.R.; et al. Emissions estimation from satellite retrievals: A review of current capability. Atmos. Environ. 2013, 77, 1011–1042. [Google Scholar] [CrossRef]
- Arvidson, T.; Goward, S.; Gasch, J.; Williams, D. Landsat-7 long-term acquisition plan. Photogramm. Eng. Remote Sens. 2006, 72, 1137–1146. [Google Scholar] [CrossRef]
- Budaev, D.; Lada, A.; Simonova, E.; Skobelev, P.; Travin, V.; Yalovenko, O. Conceptual design of smart farming solution for precise agriculture. Manag. App. Complex Syst. 2019, 13, 309–316. [Google Scholar]
- Dong, T.; Shang, J.; Liu, J.; Qian, B.; Jing, Q.; Ma, B.; Huffman, T.; Geng, X.; Sow, A.; Shi, Y.; et al. Using RapidEye imagery to identify within-field variability of crop growth and yield in Ontario, Canada. Precis. Agric. 2019, 20, 1231–1250. [Google Scholar] [CrossRef]
- Cammalleri, C.; Anderson, M.C.; Gao, F.; Hain, C.R.; Kustas, W.P. A data fusion approach for mapping daily evapotranspiration at field scale. Water Resour. Res. 2013, 49, 4672–4686. [Google Scholar] [CrossRef]
- Wu, M.; Wu, C.; Huang, W.; Niu, Z.; Wang, C.; Li, W.; Hao, P. An improved high spatial and temporal data fusion approach for combining Landsat and MODIS data to generate daily synthetic Landsat imagery. Inf. Fusion 2016, 31, 14–25. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar]
- Zhu, X.; Chen, J.; Gao, F.; Chen, X.; Masek, J.G. An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions. Remote Sens. Environ. 2010, 114, 2610–2623. [Google Scholar] [CrossRef]
- Zhu, X.; Cai, F.; Tian, J.; Williams, T. Spatiotemporal fusion of multisource remote sensing data: Literature survey, taxonomy, principles, applications, and future directions. Remote Sens. 2018, 10, 527. [Google Scholar]
- Luo, Y.; Guan, K.; Peng, J. STAIR: A generic and fully-automated method to fuse multiple sources of optical satellite data to generate a high-resolution, daily and cloud-/gap-free surface reflectance product. Remote Sens. Environ. 2018, 214, 87–99. [Google Scholar] [CrossRef]
- Claverie, M.; Ju, J.; Masek, J.G.; Dungan, J.L.; Vermote, E.F.; Roger, J.-C.; Skakun, S.; Justice, C. The Harmonized Landsat and Sentinel-2 surface reflectance data set. Remote Sens. Environ. 2018, 219, 145–161. [Google Scholar] [CrossRef]
- Houborg, R.; McCabe, M.F. A CubeSat enabled spatio-temporal enhancement method (CESTEM) utilizing Planet, Landsat and MODIS data. Remote Sens. Environ. 2018, 209, 211–226. [Google Scholar] [CrossRef]
- Schaaf, C.; Gao, F.; Strahler, A.H.; Lucht, W.; Li, X.; Tsang, T.; Strugnell, N.C.; Zhang, X.; Jin, Y.; Muller, J.-P.; et al. First operational BRDF, albedo nadir reflectance products from MODIS. Remote Sens. Environ. 2002, 83, 135–148. [Google Scholar] [CrossRef]
- Wang, Z.; Schaaf, C.; Strahler, A.H.; Chopping, M.J.; Román, M.O.; Shuai, Y.; Woodcock, C.E.; Hollinger, D.Y.; Fitzjarrald, D.R. Evaluation of MODIS albedo product (MCD43A) over grassland, agriculture and forest surface types during dormant and snow-covered periods. Remote Sens. Environ. 2014, 140, 60–77. [Google Scholar] [CrossRef]
- Masek, J.; Vermote, E.; Saleous, N.; Wolfe, R.; Hall, F.; Huemmrich, K.; Lim, T. A Landsat Surface Reflectance Dataset for North America, 1990–2000. IEEE Geosci. Remote Sens. Lett. 2006, 3, 68–72. [Google Scholar] [CrossRef]
- Roy, D.; Wulder, M.A.; Loveland, T.; Woodcock, C.E.; Allen, R.; Anderson, M.C.; Helder, D.; Irons, J.; Johnson, D.; Kennedy, R.; et al. Landsat-8: Science and product vision for terrestrial global change research. Remote Sens. Environ. 2014, 145, 154–172. [Google Scholar] [CrossRef]
- Louis, J.; Debaecker, V.; Pflug, B.; Main-Knorn, M.; Bieniarz, J.; Mueller-Wilm, U.; Cadau, E.; Gascon, F. Sentinel-2 Sen2Cor: L2A Processor for Users. In Proceedings of the Living Planet Symposium 2016, Prague, Czech Republic, 9–13 May 2016; Volume 740, p. 91. [Google Scholar]
- Lowe, D. Object Recognition from Local Scale-Invariant Features. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Corfu, Greece, 20–27 September 1999. [Google Scholar]
- Roy, D.P.; Kovalskyy, V.; Zhang, H.K.; Vermote, E.F.; Yan, L.; Kumar, S.S.; Egorov, A. Characterization of Landsat-7 to Landsat-8 reflective wavelength and normalized difference vegetation index continuity. Remote Sens. Environ. 2016, 185, 57–70. [Google Scholar] [CrossRef]
- Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Tibshirani, R.; Walther, G.; Hastie, T. Estimating the number of clusters in a data set via the gap statistic. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2001, 63, 411–423. [Google Scholar] [CrossRef]
- Zhu, X.; Helmer, E.H.; Gao, F.; Liu, D.; Chen, J.; Lefsky, M.A. A flexible spatiotemporal method for fusing satellite images with different resolutions. Remote Sens. Environ. 2016, 172, 165–177. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, X.; Vogelmann, J.E.; Gao, F.; Jin, S. A simple and effective method for filling gaps in Landsat ETM+ SLC-off images. Remote Sens. Environ. 2011, 115, 1053–1064. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, D.; Chen, J. A new geostatistical approach for filling gaps in Landsat ETM+ SLC-off images. Remote Sens. Environ. 2012, 124, 49–60. [Google Scholar] [CrossRef]
- Yan, L.; Roy, D.; Zhang, H.; Li, J.; Huang, H. An automated approach for sub-pixel registration of Landsat-8 Operational Land Imager (OLI) and Sentinel-2 Multi Spectral Instrument (MSI) imagery. Remote Sens. 2016, 8, 520. [Google Scholar] [CrossRef]


| Band | MODIS | Landsat 5/7 | Landsat 8 | Sentinel-2 |
|---|---|---|---|---|
| Blue | 459–479 | 441–514 | 452–512 | 458–523 |
| Green | 545–565 | 519–601 | 533–590 | 543–578 |
| Red | 620–670 | 631–692 | 636–673 | 650–680 |
| NIR | 841–876 | 772–898 | 851–879 | 785–900 |
| SWIR1 | 1628–1652 | 1547–1749 | 1566–1651 | 1565–1655 |
| SWIR2 | 2105–2155 | 2064–2345 | 2107–2294 | 2100–2280 |
| Test Date | Band | RMSE | Pearson correlation | SSIM | |||
|---|---|---|---|---|---|---|---|
| MS Fusion | MLS Fusion | MS Fusion | MLS Fusion | MS Fusion | MLS Fusion | ||
| 29 June 2017 (area 1) | Red | 0.0354 | 0.0222 | 0.7409 | 0.9117 | 0.8667 | 0.9349 |
| NIR | 0.0656 | 0.0620 | 0.5570 | 0.7509 | 0.8767 | 0.9002 | |
| SWIR2 | 0.0558 | 0.0455 | 0.7863 | 0.9341 | 0.8836 | 0.9232 | |
| 29 June 2017 (area 2) | Red | 0.0334 | 0.0236 | 0.7023 | 0.9042 | 0.884 | 0.9342 |
| NIR | 0.0538 | 0.0467 | 0.6951 | 0.8345 | 0.898 | 0.9222 | |
| SWIR2 | 0.0563 | 0.0693 | 0.7669 | 0.8800 | 0.8903 | 0.9002 | |
| 19 July 2017 (area 1) | Red | 0.0195 | 0.0165 | 0.6770 | 0.7675 | 0.9328 | 0.9522 |
| NIR | 0.0529 | 0.0458 | 0.7656 | 0.8617 | 0.9108 | 0.9249 | |
| SWIR2 | 0.0315 | 0.0336 | 0.8123 | 0.8184 | 0.9513 | 0.9490 | |
| 19 July 2017 (area 2) | Red | 0.0216 | 0.0181 | 0.9035 | 0.9344 | 0.949 | 0.9595 |
| NIR | 0.0515 | 0.0380 | 0.9376 | 0.9669 | 0.9131 | 0.9142 | |
| SWIR2 | 0.0339 | 0.0248 | 0.9060 | 0.9494 | 0.9467 | 0.9539 | |
| 8 August 2017 (area 1) | Red | 0.0103 | 0.0100 | 0.8328 | 0.8508 | 0.9785 | 0.9813 |
| NIR | 0.0497 | 0.0432 | 0.9059 | 0.9300 | 0.9274 | 0.9344 | |
| SWIR2 | 0.0185 | 0.0180 | 0.8701 | 0.8762 | 0.9771 | 0.9782 | |
| 8 August 2017 (area 2) | Red | 0.0109 | 0.0096 | 0.8485 | 0.8877 | 0.9745 | 0.9797 |
| NIR | 0.0417 | 0.0347 | 0.9427 | 0.9564 | 0.9288 | 0.9361 | |
| SWIR2 | 0.0144 | 0.0134 | 0.9337 | 0.9422 | 0.9817 | 0.9818 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Y.; Guan, K.; Peng, J.; Wang, S.; Huang, Y. STAIR 2.0: A Generic and Automatic Algorithm to Fuse Modis, Landsat, and Sentinel-2 to Generate 10 m, Daily, and Cloud-/Gap-Free Surface Reflectance Product. Remote Sens. 2020, 12, 3209. https://doi.org/10.3390/rs12193209
Luo Y, Guan K, Peng J, Wang S, Huang Y. STAIR 2.0: A Generic and Automatic Algorithm to Fuse Modis, Landsat, and Sentinel-2 to Generate 10 m, Daily, and Cloud-/Gap-Free Surface Reflectance Product. Remote Sensing. 2020; 12(19):3209. https://doi.org/10.3390/rs12193209
Chicago/Turabian StyleLuo, Yunan, Kaiyu Guan, Jian Peng, Sibo Wang, and Yizhi Huang. 2020. "STAIR 2.0: A Generic and Automatic Algorithm to Fuse Modis, Landsat, and Sentinel-2 to Generate 10 m, Daily, and Cloud-/Gap-Free Surface Reflectance Product" Remote Sensing 12, no. 19: 3209. https://doi.org/10.3390/rs12193209
APA StyleLuo, Y., Guan, K., Peng, J., Wang, S., & Huang, Y. (2020). STAIR 2.0: A Generic and Automatic Algorithm to Fuse Modis, Landsat, and Sentinel-2 to Generate 10 m, Daily, and Cloud-/Gap-Free Surface Reflectance Product. Remote Sensing, 12(19), 3209. https://doi.org/10.3390/rs12193209






