Abstract
Our work’s primary goal is to reveal the problematic issues related to estimates of the colored organic matter absorption coefficient in the northern seas from data of the Ocean and Land Color Instrument (OLCI) installed on the Sentinel-3 satellites, e.g., a comparison of the OLCI standard error assessment ADG443_NN_err relating to the measurement and the retrieval of the geophysical products and the uncertainties in the northern seas’ real situation. The natural conditions are incredibly unfavorable there, mainly due to frequent cloudiness and low sun heights. We conducted a comprehensive multi-sensor study of the uncertainties using various approaches. We directly compared the data from satellites (OLCI Sentinel-3 and four other ocean color sensors) and field measurements in five sea expeditions (2016–2019) using the different processing algorithms. Our analysis has shown that the final product’s real uncertainties are significantly (≥100%) higher than the calculated errors of the ADG443_NN_err (~10%). The main reason is the unsatisfactory atmospheric correction. We present the analysis of the various influential factors (satellite sensors, processing algorithms, and other parameters) and formulate future work goals.
1. Introduction
The content of our study is an analysis of problematic issues related to estimates of the absorption coefficient of colored dissolved organic matter (CDOM) in the northern seas from data of the Ocean and Land Color Instrument (OLCI) on the Sentinel-3 satellites. Three factors determine the importance of the problem: firstly, a subject of our research, the CDOM absorption coefficient, which is usually the essential part of the seawater absorption of solar radiation in the visible range; secondly, the area of our study, the Arctic Basin, the region where global warming is most pronounced; third, OLCI, a new generation of ocean color scanners designed to replace well-known devices such as MEdium Resolution Imaging Spectrometer (MERIS) and Moderate Resolution Imaging Spectroradiometer (MODIS).
Our possibilities for carrying out such a study are based on many field measurements carried out in the northern seas in expeditions by the Shirshov Institute of Oceanology Russian Academy of Science (SIO RAS) on R/V Akademik Mstislav Keldysh in 2016–2019.
The absorption of solar radiation in the surface layer affects an increase in water temperature and a decrease in the ice cover area in the Arctic seas (see, for example, [1,2]). The absorption coefficient determines the seawater’s ability to absorb solar radiation, and the colored organic matter (also called yellow substance or gelbstoff) is one of the main absorbing components of seawater.
Direct determinations of the concentration of CDOM are quite difficult; therefore, its content is usually estimated through the spectral absorption coefficient ag(λ), which can be obtained with acceptable accuracy using optical methods, both contact and remote [3,4]. We have to consider the CDOM absorption when calculating the visible solar radiation entering the water column in a wavelength range of 400–700 nm, called photosynthetically available radiation (PAR), a fundamental factor for ocean primary bio-productivity. The visible radiation entering the water column contributes to the ocean heat budget [5], determines underwater visibility, and practical use of various equipment for activity, studying, and monitoring of the marine environment.
The colored organic matter plays a role in many biogeochemical processes occurring in the ocean: this fraction is included in the ocean organic carbon cycle [6]; affects the photochemical formation of biologically labile photoproducts [7]; can help to identify the different biogeochemical regimes in a surveyed area [8]; and correlates with bacterial activity [9]. CDOM absorption allows one to register the effect of river runoff [10,11,12], to study the dynamics of water masses [13], to assess water quality [14,15,16], and to more accurately estimate the chlorophyll concentration [17].
The conditions for obtaining satellite data in the Arctic Basin are incredibly unfavorable, primarily due to frequent cloud cover, an insurmountable obstacle for optical radiation in visible and infrared ranges. Even under conditions of variable cloudiness, when ocean color data are available in the gaps between the clouds, the data can be distorted by the influence of nearby clouds.
The Ob and Yenisei river runoff brings a large amount of dissolved organic matter into the Kara Sea, which significantly affects its bio-optical characteristics [18,19,20,21], especially in the shortwave bands, the visible range of satellite color scanners. Due to errors in atmospheric correction, the radiance reflectance of the water column in these spectral channels can even take negative values. That leads to difficulties in using some algorithms, for example, the Quasi-Analytical Algorithm [22]. For taking into account this feature, Vazyulya et al. [23] developed a regional algorithm for the Kara Sea that does not use the remote sensing reflectance values Rrs in the shortwave bands (the wavelengths <488 nm). This algorithm gives good results in the Kara Sea but can be applied to other seas as well. In the Barents Sea, coccolithophore blooms may interfere with standard algorithms for determining the ag values. The blooms occur in July–September and lead to a significant change in the spectral water-leaving radiance [3,4]. Not all algorithms cope with these changes. The solution to the atmospheric correction problem is beyond this work; our task is to assess the results of its application.
The regional SIO RAS algorithms were derived using the data from SeaWiFS and MODIS color scanners [3,4]. SeaWiFS completed work in December 2010, MODIS-Aqua and MODIS-Terra scanners are still working, even though the duration of their activity (about 20 years already) has far exceeded the planned period of their operation. OLCI color scanners should provide satellite data in the next decade. The Sentinel-3A (S3-A) satellite was launched in February 2016 and has been in the routine phase since October 2017; the Sentinel-3B (S3-B) was launched in April 2018. During the commissioning period, the two satellites were positioned in tandem configuration, separated by 30 s; Sentinel-3B flew in the same orbit of Sentinel-3A, but 140° ahead.
Each satellite carries three primary sensors, specifically an SAR radar altimeter, SST radiometer, and OLCI, revisiting the same place every two days. The launch of the next OLCI is expected aboard the satellite Sentinel 3C in 2023.
The authors [24] made the first attempt to assess the OLCI sensor’s capability to monitor the bio-optical characteristics even before the S3-A launch [24]. The authors reconstructed 16 OLCI bands using in situ data measured by the TRIOS spectroradiometer in Fram Strait and the Nordic seas during field studies conducted in July 2013–2015. They estimated the uncertainties in chlorophyll concentration and the total and particle absorption coefficients retrieved with the locally adjusted algorithm.
A unique ability to estimate the uncertainties in Level 1 data of OLCI on S3-A and S3-B was provided in the tandem phase mentioned above [25,26,27]. The developed methodology allowed one to adjust one sensor based on the other, although without absolute calibration [25]. Calibration with ground-truth measurements could solve the problem. The benefit of retrieving the Level 2 data products from the Sentinel-3 Tandem Phase was also considered [26,27].
Our article highlights the use of the Sentinel-3 OLCI data with the existing regional algorithms. The absorption coefficient of colored organic matter is in a list of Essential Climate Variables (ECV) necessary for systematic observations to estimate climate change in the atmosphere, ocean, and land, according to the program of the Global Climate Observing System (GCOS). The obtained results will help improve quality and consistency of applications with respect to inter-annual and climate scale variability. For example, they will be useful for the future issues of the Atlas of the Russian seas bio-optical characteristics [4].
Our approach to the uncertainties assessment is based on using the available in situ data obtained during our field studies in the Arctic seas. Such an approach was used before addressing the atmospheric correction problem in two bio-optical contrasted French coastal waters [28] and also for bio-optical parameters, including the CDOM absorption, in the Baltic Sea [29]. We will discuss all the available data in Section 4.
2. Materials and Methods
2.1. Study Area
We analyzed the ship measurements performed on five expedition cruises of the R/V Akademik Mstislav Keldysh (AMK), carried out in 2016–2019. Table 1 presents information on these cruises. In total, we collected data from 341 stations with in situ measurements of the absorption spectra required to validate satellite data. However, due to frequent cloudiness, it was impossible to compare many of these stations with satellite data.

Table 1.
The Arctic and Atlantic R/V AMK voyages with measured data.
We focused on the Arctic seas, so for our analysis, we used data only for stations located north of the Arctic Circle; Figure 1 shows their location. The selection of stations for various types of research is elucidated in Section 3.
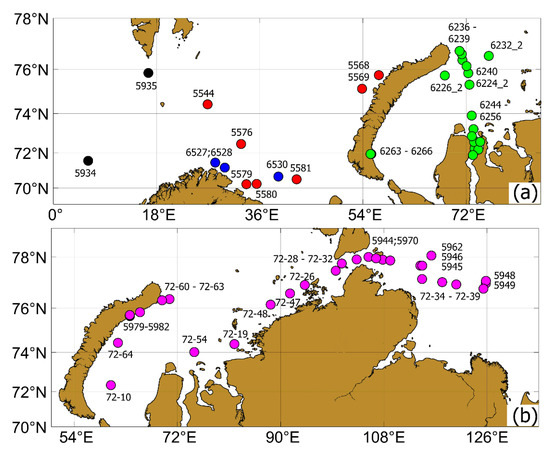
Figure 1.
Location of the selected stations: (a)—AMK-65 (blue), AMK-68 (red), AMK-71 (black), AMK-76 (green), (b)—AMK-72 (magenta).
The weather conditions in the seas under consideration are almost constant cloud cover; this is an insurmountable obstacle for visible and infrared radiation. Frequent cloudiness impedes data acquisition from simultaneous shipborne and satellite measurements; substantial horizontal heterogeneity and temporal variability of the cloudiness and bio-optical parameters make the error estimates in satellite algorithms a rather tricky problem in the Arctic seas. Therefore, when using satellite data in the visible range, it becomes necessary to average them over several days or weeks.
Figure 2 shows maps of distributions of the number of days with data for each bin and the cloud coverage maps, according to the OLCI_CLOUD flags, averaged over the voyages. The longer the averaging period on the cloud coverage maps, the higher proportion of cloudy days.
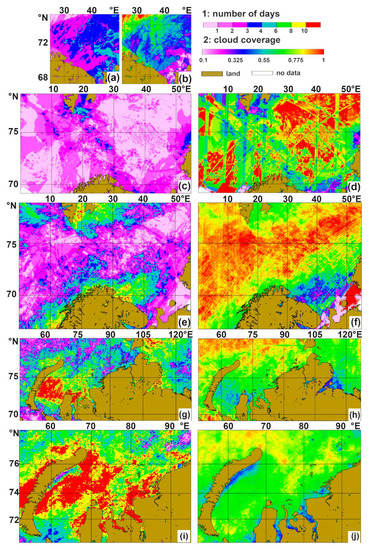
Figure 2.
Distributions of the number of days with data per bin (a,c,e; scale 1) and cloud coverage according to OLCI_CLOUD flag data (b,d,f; scale 2). AMK-65: (a,b); AMK-68: (c,d); AMK-71: (e,f), AMK-72: (g,h), AMK-76: (i,j).
2.2. Field Measurements
At all selected stations, we determined the absorption coefficients of seawater and its components. At some stations, a floating (on the AMK 68th, 72nd, and 76th voyages) or a deck (on the AMK-65 and AMK-71) spectroradiometer measured the spectral values of the upwelling radiance just beneath the sea surface (a floating device) or above the sea surface (a deck instrument). A floating device was used on the AMK 68th, 72nd, and 76th voyages, a deck one on the AMK-65 and AMK-71. Two irradiance meters, BIC and RAMSES, measured the spectral underwater irradiances, downward and upward. A transparency meter PUM-A measured the seawater beam attenuation coefficient.
2.2.1. Measurements of the Spectral Absorption Coefficients
A portable spectrophotometer in the ICAM (Integrated Cavity Absorption Meter) configuration measured the spectral seawater absorption coefficients. The device was built by specialists from the Department of Biophysics, Biological Faculty, Moscow State University, Moscow, Russia [30]; the ICAM technology allows us to eliminate the influence of light scattering. For each 330 mL water sample, we measured three absorption spectra (seawater, filtrate, and pure water).
Knowledge of the effective path length of photons, taking into account their multiple scattering, is necessary to determine the absolute values of the absorption coefficient. The calculations by the Monte Carlo method revealed the absence of absorption dependence on the scattering properties of seawater. The scattering coefficient in the calculations varied from 0 to 5 m−1 [31].
We determined the CDOM spectra ag(λ) as the difference between the filtrate and pure water [32]. A more detailed description of the measurement and calculation procedure is available in [31,33].
2.2.2. Floating and Deck Spectroradiometers
For measurements of the spectral upwelling radiance just beneath the sea surface, we used a PRO-1 floating spectroradiometer developed at the SIO RAS [34]. It also measures the spectral surface irradiance, making it possible to calculate the spectral remote sensing reflectance Rrs. During the measurements at drift stations, the device floats off the ship at a distance of 0–50 m to avoid shading and reflection. Depending on weather conditions, 20–50 spectral scans are averaged during processing, using a specially developed algorithm. The subsurface radiance reflectance ρ(λ) is calculated as ρ(λ) = πLu(λ)/Ed(λ), where Lu(λ) and Ed(λ) are the upwelling radiance and the downwelling irradiance just beneath the sea surface, respectively. A particular deck sensor, installed on the open deck in a place free from shading, performs the continuous monitoring of changes in surface irradiance during measurements.
A deck spectroradiometer was built by specialists from the Marine Hydrophysical Institute (MHI) [35] to measure the spectral remote sensing reflectance in the range of 390–720 nm with a resolution of 5 nm. The device uses a prism monochromator and an optical receiving system installed on its entrance slit. A cosine collector is used for the sea surface irradiance, the radiance channel lens for the water-leaving radiance.
This device measures the ratio of water radiance to the surface irradiance; the calibration is performed with a reference screen. We took the measurements at a 45° zenith angle from the ship and the azimuthal angles where the sun’s glints were minimal. After measuring the sea surface radiance reflectance, the spectrophotometer measures the radiance reflectance of a black cuvette filled with water. Under the constant observation conditions, using a black cuvette with an absorbing interior makes it possible to take into account the reflected component. The average of several sequential measured values allowed us to eliminate random errors.
2.2.3. Measurements of the Diffuse Attenuation Coefficient Kd
We used data on underwater spectral irradiance Ed(z, λ) measured by two irradiance meters BIC and RAMSES to calculate the diffuse attenuation coefficient.
A spectral underwater irradiation meter RAMSES ACC-VIS (TRIOS, Rastede, Germany) has 190 spectral channels in the spectral range of 320–950 nm (spectral resolution is 3 nm) and an accuracy of ±5%. We used a particular protective frame to conduct measurements in the sounding mode. The data were transmitted to the ship laboratory via a cable. TRIOS provided calibration of the instrument according to the National Institute of Standard and Technology (NIST) standards.
The other irradiance meter BIC 2100 has two measuring modules for the surface and underwater irradiance; both can simultaneously measure the irradiance in four spectral bands 443, 490, 555, and 625 nm. The SIO RAS specialists modernized the device to perform measurements in an autonomous regime without a cable. We calibrated the instrument at the SIO RAS before each expedition, according to the working standard of the spectral irradiance density.
The measured Ed(z, λ) values allow us to compute the diffuse attenuation coefficients Kd(λ) for underwater irradiance, assuming the exponential law Ed(z) = Ed(0−) exp[–Kd × z], and omitting wavelength λ for simplicity. In this work, we used Kd(λ) values for the upper uniform layer, the thickness of which varied from 10 to 30 m.
The maximum available satellite observation depth Z* is assumed to be equal to the depth where the contribution of the radiance, coming from depths greater than Z*, is less than 10% of the total radiance, and then Z* approximately equals 1/Kd [36]. From our field measurements, Kd(490) varied from 0.03 to 0.34 m−1 for the Norwegian and Barents seas and within 0.06–0.36 m−1 for the Kara Sea. Hence, the informative satellite depth Z* was within 2.8–16 m in the Kara Sea and 3.0–33 m in the Norwegian and Barents seas. Usually, the thickness of the layer, where the Kd values were measured, exceeded the Z* value; only in the clear waters of the Barents Sea (stations 5557 and 5560 of AMK-68),the Z* value was higher.
2.2.4. The Beam Attenuation Coefficient Measurements
We used these measurements to compare the particle backscattering coefficient values bbp calculated from in situ measured Rrs and the satellite color scanner data (see Section 3.3). The values of the beam attenuation coefficient were measured by a PUM-A transparency meter in the laboratory mode—on water samples or as a part of a shipboard flow-through system [37]. The device measures the beam attenuation coefficient at 530 nm in a range of 0.050–1.0 m−1 with an error of 0.005 m−1.
For checking the stability of measurements, the cuvette was filled with type 1 ultrapure water prepared on a “Simplicity 185” device by “Millipore” at the SIO RAS. The measured value of the beam attenuation coefficient was c = 0.057 m−1. To verify the results, we also carried out the inter-calibration of the laboratory PUM-A device with a submersible PUM transparency meter. The beam attenuation coefficient values of the water sample from the bottle, measured by PUM-A in a cuvette, were compared with the PUM data at the same depth. The difference did not exceed 0.01 m−1.
2.3. Satellite Data and Algorithms
2.3.1. Satellite Data and Software
We ordered Level 1 and Level 2 data of the OLCI-A and OLCI-B sensors at (https://archive.eumetsat.int, https://codarep.eumetsat.int and https://coda.eumetsat.int), and the data from MODIS-Aqua, MODIS-Terra, VIIRS NPP and VIIRS NOAA on the website https://oceancolor.gsfc.nasa.gov/.
Level 2 satellite data were processed using software developed by the Ocean Optics Laboratory of the SIO RAS [38], designed to batch process large datasets of ocean color scanners. The set of programs includes the modules to calculate new products, record results in HDF and/or NetCDF format, average data, export maps in a given projection, match in situ and satellite observation data, etc. The essential feature of this software is the dynamic loading of libraries that can be developed and implemented by users without having to recompile programs. For the convenience of using programs designed for working with data in the NASA format, we prepared a converter transforming OLCI data to the above-mentioned SeaWiFS-like format. We applied this software for converting the OLCI Level 2 data. The following standard products were used: OLCI water-leaving reflectance (16 bands), absorption coefficient, Total Suspended Matter (TSM) concentration, and the diffuse attenuation coefficient Kd. When processing, the following data flags were used: OLCI_LAND, OLCI_CLOUD, OLCI_CLOUD_AMBIGUOUS, OLCI_CLOUD_MARGIN. For map building, we binned the data on a 3 × 3 km grid.
The software [38] allows us to process the Level 2 data from MODIS-Aqua, MODIS-Terra, VIIRS SNP, and VIIRS NOAA sensors. These data include the remote sensing reflectance Rrs and the diffuse attenuation coefficients Kd(490). Using the values of Rrs, the absorption coefficients of yellow substance ag and the particle backscattering coefficients [4] were calculated for the field stations where the time difference between satellite and field measurements was no more 24 h. Since the algorithms for these products were developed for MODIS color scanners, we interpolated the VIIRS Rrs to MODIS wavelengths. When calculating the parameters, the pixels flagged with LAND, CLDICE, SEAICE, and STRAYLIGHT were filtered out.
The Sentinel Application Platform (SNAP) software, developed by Brockmann Consult, allowed us to work with the OLCI Level 1 data and derive the water-leaving radiance from the Top of Atmosphere (TOA) radiances. The neural network Case 2 Regional Coast Colour (C2RCC) processor, developed by Doerffer and Schiller [39], provided us the opportunity to derive the seawater inherent optical properties, including the seawater absorption of detritus and yellow substances as well as the particle backscattering coefficient.
2.3.2. Algorithms
To calculate the inherent optical properties (IOP) from remote sensing data, primarily for the absorption coefficients, and also the particle backscattering coefficient bbp and the TSM concentration, we used the algorithms listed below.
OLCI NN
The IMT (Inverse Modeling Technique) neural networks derive the standard OLCI product ADG_443_NN (colored Detrital and Dissolved Material absorption coefficient) in OLCI Level 2 files. The neural network atmospheric correction provides the input spectral remote sensing reflectance Rrs. The standard atmospheric correction also derives the Rrs spectral values.
The SNAP program, developed by ESA (European Space Agency, Paris, France), can also provide other IOP data (pigment absorption, two components for detritus and gelbstoff absorption as well as white and typical sediment particle scattering) as a result of the C2RCC neural network processor operation [40].
GIOP
The GIOP (Generalized Inherent Optical Property) model of the optical properties of seawater was presented in [41,42]. The algorithm applies various analytical models, parameterized for the surface layer in different seasons. It uses Rrs(λ) in the visible range of the spectrum and can derive the absorption coefficients of colored dissolved organic matter ag(λ) and of phytoplankton pigments aph(λ), as well as the particle backscattering coefficient bbp(λ). Based on the obtained data on the remote sensing reflectance Rrs(λ), the model performs an inversion to find the optimal set of the bio-optical characteristics of the water column, which minimizes the difference between the simulated and the measured values. The model provides the possibility of adjusting input parameters (such as chlorophyll concentration, the spectral slope for yellow substance absorption).
The Quasi-Analytical Algorithm (QAA)
This algorithm was evolved by Lee et al. [22] to determine the backscattering and absorption coefficients from the spectral remote-sensing reflectance Rrs(λ) as a result of analysis of several empirical, analytical, and semi-analytical models, in particular, Gordon et al. [43] and Lee et al. [44]. The generally utilized expression [45,46] presents the spectral bb(λ) values.
Along with the bb(λ), the QAA algorithm can derive the seawater absorption coefficient and estimate the values of the detrit-gelbstoff and the phytoplankton pigment absorption coefficients. The ESA Ocean Colour Climate Change Initiative selected the QAA algorithm to derive bbp for creating a long-term series of satellite ocean color products.
Regional Semi-Analytical Algorithm (RSA)
The regional semi-analytical algorithm was developed to estimate the yellow substance absorption coefficient ag, particle backscattering coefficient bbp, and diffuse attenuation coefficient Kd(λ) in four spectral channels 443, 490, 555, and 625 nm in the Kara and White seas using MODIS satellite data [23]. It uses the Rrs data for the wavelength range ≥488 nm. The above-surface remote-sensing reflectances Rrs(412) and Rrs(443) are not used due to the high probability of the atmospheric correction errors. In the present work, we modified the RSA algorithm to the OLCI spectral channels, and now it uses the Rrs data for the wavelength range greater than or equal to 490 nm.
The inverse problem of finding seawater absorption a(λ) and backscattering bb(λ) is solved using the low-parametric models representing the seawater coefficients as a superposition of the contributions of the main components. The absorption coefficient a(λ) is defined as the sum of the absorption of pure sea water, yellow substance or CDOM, and the phytoplankton pigments, while bb(λ) is defined as the superposition of the backscattering by pure seawater and the suspended particles. The contribution of chlorophyll is accounted for using a regional algorithm for the Kara Sea [47]. An iterative approach was used to improve the accuracy while estimating the slope of the absorption spectrum. As a result of solving the inverse problem, two parameters are defined: ag(443) and bbp(555). These parameters also allow to calculate the Kd(λ) value using Gordon’s formula [48]. The RSA algorithm was validated using the shipboard data, measured with a floating spectroradiometer [34] and free from errors of atmospheric correction. The algorithm was also tested on satellite data and showed acceptable results [23].
Algorithm for Determining bbp and TSM
The algorithm [49] was developed for cases where the semi-analytical algorithm cannot work properly due to large errors in atmospheric correction. This situation is characteristic of the Barents and White seas. The modified algorithm uses only two SeaWiFS wavelengths, 510 and 555 nm, where the errors in atmospheric correction are much lower than at 412, 443, and 490 nm. To determine the particle backscattering coefficient bbp = bbp(555), the diffuse attenuation coefficient Kd(555) and the parameter X(555) = bb(555)/[a(555) + bb(555)] are calculated. The value of X(555) is determined through the value of the normalized water-leaving radiances Lwn(555), Kd(555) using the ratio Lwn(510)/Lwn(555). The value [a(555) + bb(555)] can be obtained from Kd(555) using Gordon’s formula [48]; the backscattering coefficient bbp as the difference between the seawater bb and the known pure water backscattering coefficient bbw. We adapted this algorithm to the MODIS, OLCI, and VIIRS spectral channels.
A regional algorithm to determine TSM concentration from satellite data was derived using the ship measurements on the R/V Akademik Sergey Vavilov voyages 13 and 14 (August–September 1998). The data on quasi-simultaneous measurements of the upwelling radiance Lwn by a floating spectroradiometer and TSM were used to derive the regression equation TSM vs. bbp: TSM = 73.5 bbp + 0.016, where bbp, m−1 and TSM, mg/L. The average error in determining the concentration of suspended matter is about 30%.
2.3.3. Error Estimates
To estimate the accuracy of performed calculations, we used the root mean square error (RMSE) and the average relative error (RE), determined as:
where N is the number of points and <estimate> is the mean of the estimated value.
To evaluate the derived regression equation usefulness, we used the correlation coefficient, the coefficient of determination, and the regression error:
where <x> and <y> are the mean x and y values, fi indicates fit values, and is the standard deviation.
3. Results
The absorption coefficients of the colored organic matter are available on the OLCI website as a Level 2 standard product ADG_443_NN. In this section, we compare them with the data of direct measurements of the absorption coefficient by the ICAM device ag_icam (Section 2.2). To verify the results, we also calculated the ag_olci_C2RCC values using the SNAP program C2RCC processor with default parameters [40].
The difference between the satellite and in situ measured values is affected by the atmospheric correction errors; the significant losses in satellite data due to cloudiness affect the obtained results in some aspects of our statistical analysis.
In our work, we try to redeem the lack of a sufficient amount of data to obtain reliable statistical estimates by multiparameter comparison. For that, we used data from other field measurements to confirm the results obtained. These data included the remote sensing reflectance Rrs(λ) measured by floating or deck spectroradiometers, the spectral diffuse attenuation coefficient of the underwater irradiance Kd(λ), the beam attenuation coefficient c, as well as data from other satellite ocean color scanners and results of calculations by various algorithms (see Section 2.2 and Section 2.3).
3.1. Validation and Analysis of the ADG_443_NN Values Derived from OLCI Data
The absorption coefficient of the colored organic matter ADG_443_NN (from now on ag_olci_std) is available as a Level 2 standard product of the OLCI instrument on the Sentinel 3A, B satellites (see Section 2.2). Figure 3 presents the results of comparing ag_olci_std with the data of direct absorption measurements by the ICAM technique (ag_icam).
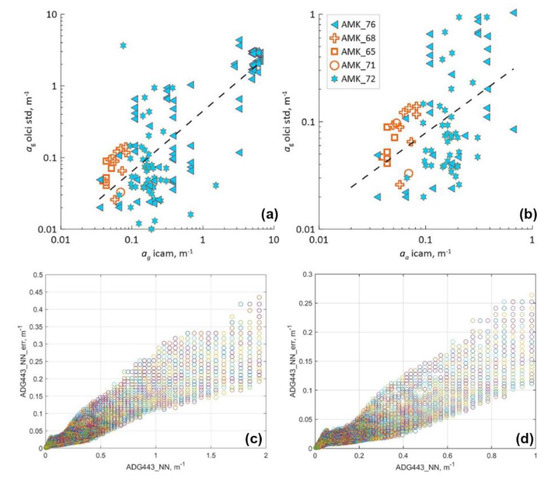
Figure 3.
Top: scatter plots of the in situ measured and satellite derived ag(443) values: (a)—complete dataset; (b)—river estuary data excluded. The Barents Sea points are shown in orange, the Kara and Laptev seas are shown in turquoise. Various cruises are represented by symbols. The dotted line is the correlation across all data. Bottom: the standard product errors ADG_443_NN_err in comparison with the ADG_443_NN values for OLCI Level 2 file S3A_OL_2_WFR_20170814T091713; (c) complete dataset; (d) the same in the enlarged scale. The Barents Sea, 14 August 2017.
Figure 3a shows the complete dataset (151 points), including the Ob and Yenisei river estuaries (stations 6244–6256 and 72–54, 72–19 in Figure 1). Figure 3b (89 points) excludes river mouths, as well as stations with large zenith angles of the sun (more than 75°) and other factors that impede obtaining quality data (see Section 3.2).
As we see in Figure 3b, even after excluding the above stations, the scatter of points is enormous. It is especially characteristic of the Kara Sea, where the difference between the ag_olci_std and ag_icam values can be more than 30-fold. Comparing Figure 3b,d, one can see that the real uncertainties are significantly (≥100%) higher than the calculated errors of the ADG443_NN_err (~10%).
The main reasons for such discrepancy are the errors of atmospheric correction since the results for the absorption values calculated from the Rrs data measured by the floating (or deck) spectroradiometer are incomparably better (see below).
An analysis of atmospheric correction errors in Section 3.2 allowed us to select 15 stations with acceptable atmospheric correction. We excluded Station 6240 in the Kara Sea due to the high spatial variability around this station (see Section 3.2), and Station 5704 located to the south of the polar front. Therefore, we have 13 selected stations. However, several passes of Sentinel 3A,B satellites were available at some stations, and the total number of OLCI data points used was 19 (10 for the Barents Sea, 9 for the Kara Sea).
Figure 4 shows the results of comparing the absorption values at 13 aforecited stations calculated from the Rrs measurements by the floating (or deck) spectroradiometer and the values measured by the ICAM device; we use different algorithms for calculations. The values of the determination coefficients R2 turned out to be large enough for all the algorithms used: 0.656 for RSA, 0.922 for QAA, 0.960 for GIOP.
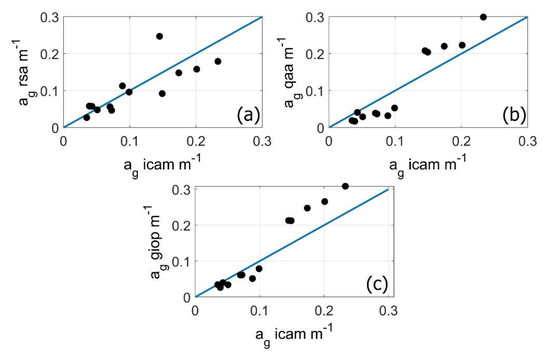
Figure 4.
Comparison of the absorption values calculated from the Rrs measurements by the floating (or deck) spectroradiometer using different algorithms with the values measured by the ICAM device for 13 stations. The solid line is 1:1 dependency. (a)—RSA algorithm (RMSE = 0.042, RE = 40%); (b) QAA (RMSE = 0.04, RE = 38%); (c)—GIOP (RMSE = 0.045, RE = 36%) (see Section 2.3).
We also calculated the absorption coefficients from satellite data of four other satellite sensors—MODIS-Aqua, MODIS-Terra, VIIRS SNPP, and VIIRS NOAA-20, using the above algorithms. Along with the standard ADG_443_NN, the ag_olci_C2RCC values were calculated from the L1 level OLCI data by the C2RCC processor [40]. All algorithms, except for neural networks, gave negative values in the calculations for some individual flybys, which caused the difference in the number of data pairs (Table 2). We consider the atmospheric correction errors in more detail in Section 3.2.

Table 2.
Regression parameters between the absorption values derived from satellite and in situ data for various algorithms and neural networks (NN) OLCI. N is the number of pairs to calculate the regression, R2 is the coefficient of determination.
Figure 5 shows the regressions of the calculated values of ag_olci_std and ag_olci_C2RCC versus the measured values of ag_icam; Table 3 presents the regression parameters.
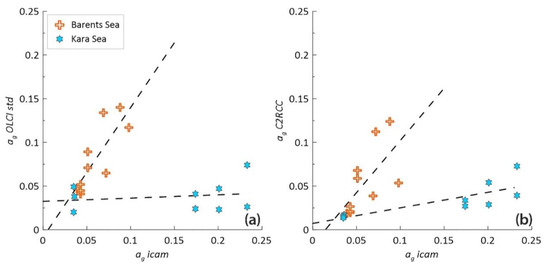
Figure 5.
Regressions of satellite values ag_olci_std (a) and ag_olci_C2RCC (b) vs. measured values ag_icam. The dotted lines represent the correlations for the corresponding seas.

As can be seen from Table 3, for the Barents Sea OLCI standard product, we have an acceptable correlation; the relationship for the Kara Sea is insignificant. For the ag_olci_C2RCC values, a significant relationship is observed for both seas, and even better for the Kara Sea.
We need the equations for practical use, allowing us to obtain the absorption coefficient values close to the measured ones, from satellite data. For that, it is necessary to derive the inverse regression equations; Table 4 presents such equations. The correlation is insignificant for the standard ag_olci_std values, and the retrieval of the absorption coefficient values is practically possible only with the C2RCC processor data.

Table 4.
Regression equations for calculation of the absorption coefficient from OLCI data.
As can be seen from Table 4, the coefficient of determination for the Kara Sea turns out to be even higher than that for the Barents Sea, and the regression errors are also quite acceptable. As noted above, the statistical support of the obtained equations is insufficient, and it is too early to recommend them for practical use. In Section 3.4, we will test the obtained equations with the diffuse attenuation coefficient values.
At the end of this section, we will give an example of correcting the ag spatial distributions using the derived equation for the Barents Sea. Figure 6 shows the ADG_443_NN spatial distributions in the Barents and partly in the Norwegian seas built with standard ag_olci_std and corrected ag_corr data for AMK-65 and AMK-68 cruises. Adjusted distributions look more plausible; the vast white area between 30° and 50° E in Figure 6B is due to a lack of satellite data due to cloudiness.
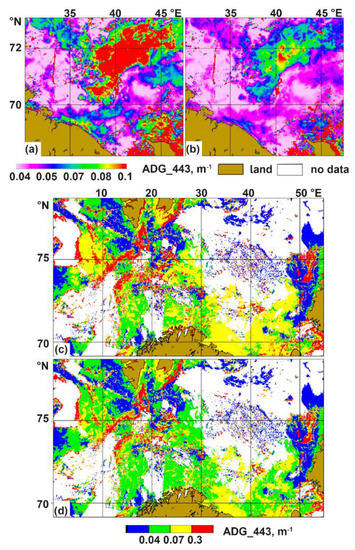
Figure 6.
The ADG_443_NN distributions based on standard OLCI data ag_olci_std (a,c) and corrected ag_corr data (b,d) for the AMK-65 (a,b) and AMK-68 (c,d) cruises.
3.2. Results of Atmospheric Correction
As shown in the previous section, the quality of the atmospheric correction is critical for obtaining reliable absorption coefficient values. Unfortunately, in the Arctic seas, ensuring a high-grade atmospheric correction is a most challenging task due to extremely unfavorable natural conditions. Frequent cloudiness and low sun angles lead to a significant loss of data. In this section, we estimate the atmospheric correction errors as a function of various factors, using Rrs as a reference to compare the values of the spectral radiance reflectance directly above the sea surface.
We selected 189 data pairs based on the requirement that a time difference between the in situ measurement and the satellite overpass should not exceed 24 h. Figure 7 shows the dependencies of the average (for all bands) root mean square error of Rrs on the above difference (Figure 7A) and the solar zenith angle (SZA) (Figure 7B). Spectral Rrs standard errors are significantly wavelength-dependent; they increase in the shortwave region of the visible spectrum [28].
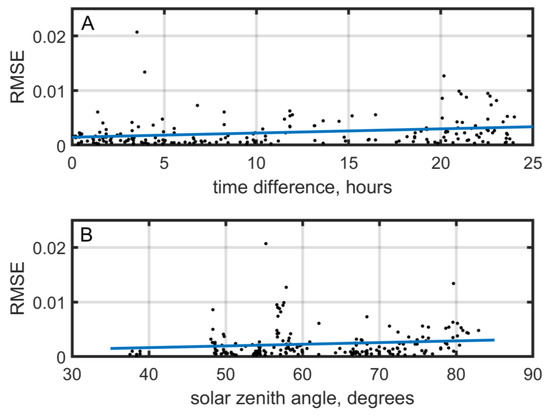
Figure 7.
Dependences of the average RMSE of the Rrs values on the absolute difference between the time of the in situ and the satellite measurements (A) and on the zenith angle of the sun (B). The blue lines show the trend assessment.
Both figures show a large scatter of points. A weak trend is observed—the errors increase with increasing time difference between the field and satellite measurements and the solar zenith angle. Still, one can see the RMSE values of about 0.001 even with a time difference of more than 20 h and solar zenith angles more 70°. Conversely, errors exceeding 0.004 can be detected with a time difference of fewer than 5 h and angles less than 50°. Next, we will consider the influence of various factors in more detail, and we will start with the errors of atmospheric correction not associated with the atmosphere and observation conditions, but with the optical characteristics and processes occurring in the surface water layer.
The errors increase at angles >75°. For the entire dataset (N = 189), there are no significant dependencies: the coefficient of determination R2 = 0.043 for the module of the time interval at a significance level of p = 0.004, compared with R2 = 0.016, p = 0.083 for the solar zenith angle. The independence of the error value from the time interval between shipboard and satellite data points out the stability of the measurement conditions determined by the hydrometeorological factors and oceanological processes prevailing in the period under consideration. Nevertheless, at intervals exceeding 20 h, the errors increase by a factor of 1.5 (RMSE for time difference >20 h equals 0.0036 while the mean RMSE = 0.0024, N = 48). That may relate to the surface water dynamics [50].
For further analysis, we chose only satellite spectra with RMSE ≤ 0.001.
In the Kara and Laptev seas, the strong influence of river runoff leads to a decrease in the water-leaving radiance in the short-wavelength part of the spectrum due to absorption by dissolved organic matter. That increases the errors in the determination of the absorption coefficient ADG_443_NN. As an example, Figure 8 shows all the Rrs spectra measured at Station 6240 in the Kara Sea on 14 July 2019. For this station, we collected the most significant amount of satellite data—23 files. The colors show the various sensors; black line—the result of direct determinations; gray lines—the spectra with RMSE > 0.001.
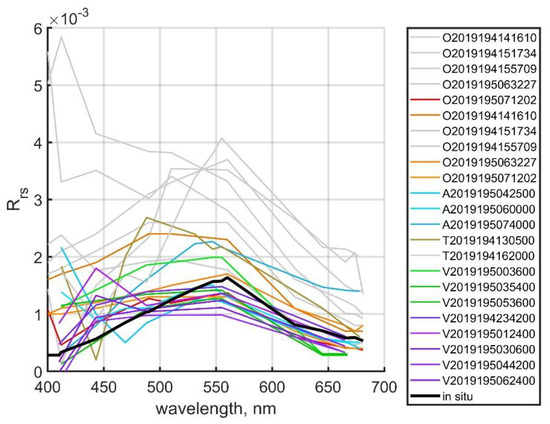
Figure 8.
Rrs(λ) values obtained from the shipboard (black line) and satellite measurements (colored lines: red—OLCI BAC, orange—OLCI AAC, blue—MODIS Aqua, brown—MODIS Terra, green—VIIRS SNPP, purple—VIIRS NOAA-20). The grey color shows data for which the RMSE values obtained by comparing shipboard and satellite data were greater than 0.001. Station 6240, Kara Sea, 14 July 2019.
Figure 9 demonstrates the variability of errors depending on the solar zenith angle and the time interval between field measurements and the satellite overpass time for station 6240.
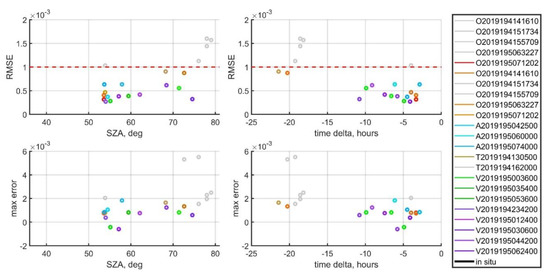
Figure 9.
RMSE (top row) and maximum error (bottom row) values obtained when comparing shipboard and satellite data depending on the sun zenith angle (left column) and the time interval between data (right column). The colors of the circles correspond to the colors of the lines in Figure 1. The gray circles show the data for which the RMSE values exceed 0.001. The red dotted line on the right side of the figure corresponds to RMSE = 0.001. Station 6240, Kara Sea, 14 July 2019.
Figure 10 shows the spatial distribution of the beam attenuation coefficient c in the Kara Sea on the day for station 6240 (14 July 2019) using the flow-through measuring complex.
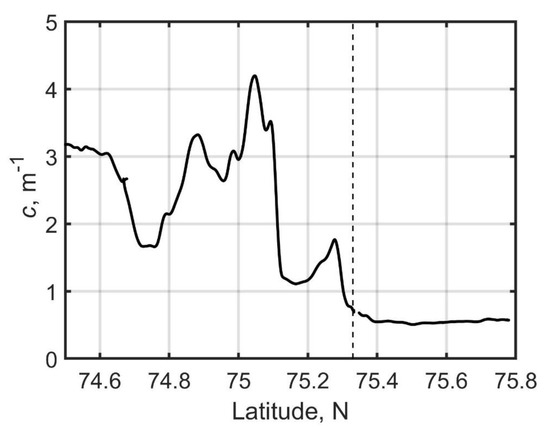
Figure 10.
Spatial distribution of the beam attenuation coefficient c measured in the Kara Sea on 14 July 2019. The dotted line shows the position of station 6240.
The values of c(530) exceeding 1 m−1 correspond to the waters of the surface desalinated layer formed in the summer season by the Ob and Yenisei river runoff [51]. The lower salinity and a high content of colored dissolved organic matter are typical for this water compared to waters outside the influence of river runoff [50]. Station 6240 is located in the area where waters with different optical characteristics come into contact, which causes the observed differences in the values of the absorption coefficient, calculated with different algorithms and dates.
Table 5 shows the total number of satellite data points for the stations with the shipboard reflectance measurements, and their number with RMSE < 0.001. One can see that the results of the OLCI Alternative Atmospheric Correction (AAC) better match shipboard data (13 spectra out of 27) than the results of Baseline Atmospheric Correction (BAC) correction (3 spectra out of 27).

Table 5.
The total number of satellite data points for 15 stations with shipboard reflectance measurements and their number with RMSE ≤ 0.001. AAC—Alternative Atmospheric Correction, BAC—Baseline Atmospheric Correction.
Figure 11 shows the RMSE values for all 27 OLCI spectra obtained using the alternative atmospheric correction. This figure presents three dependencies of RMSE: on the solar and observation zenith angles (SZA and OZA correspondingly), and the difference in the azimuthal angles (OAA—observation azimuthal angle, SAA—solar azimuthal angle). The symbols point out the flags; there is a small number of data points without flags—only six spectra. That indicates unfavorable conditions for satellite observations in the studied seas. The most frequent flag is the ‘cloud risk’ (12 points), the ‘sun glint risk’ flag at four locations, and all other flags at five. The errors increase at solar azimuthal angles more 75° and viewing angles greater than 15°. It should be noted that the risk of cloudiness or glint does not always lead to errors.
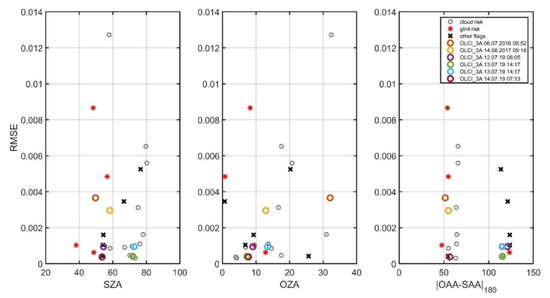
Figure 11.
Average RMSE values obtained by comparing shipboard and satellite data for 15 ship stations and 27 OLCI spectra calculated using the C2RCC processor, depending on the solar zenith angle (left), observation zenith angle (center), and the absolute values of azimuth angle differences (right). Gray circles indicate the cloud risk flag, red asterisks—glint risk, black crosses—any other flag, colored circles—data without flags.
3.3. OLCI Estimates of the Particle Backscattering Coefficient
3.3.1. In Situ Measurements in the Barents Sea
In this section, we consider the measured data from the AMK-65 and AMK-68 voyages. We did not directly measure the particle backscattering coefficient bbp values in our field studies. These values were calculated using the Rrs values, measured by floating (AMK-65) and deck (AMK-68) spectroradiometers. We calculated the bbp(555) for a wavelength of 555 nm using the different algorithms described in Section 2.2.2: the simplified regression algorithm (SRA) [23], a quasi-analytical algorithm QAA [22], and the GIOP model [41,42].
We compared the obtained bbp(555) values for the selected stations with the beam attenuation coefficient c(530) for the subsurface layer (5 m) measured by the PUM-A device (Section 2). Such a comparison makes clear physical sense because TSM mainly determines both the beam attenuation and backscattering coefficients. Figure 12 shows the comparison results.
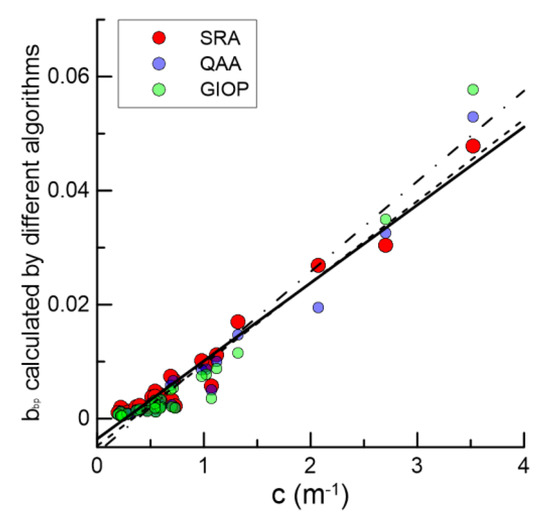
Figure 12.
Comparison of the particle backscattering coefficient bbp(555) with the beam attenuation coefficient c(530) for the Barents Sea. Red circles—SRA algorithm, blue—QAA algorithm, green—GIOP algorithm. The black line is a correlation based on SRA, black dotted line—correlation based on QAA data, dash-dotted line – based on GIOP data.
Table 6 presents the statistical parameters of the regression bbp(555) vs. c(530) with different algorithms.

Table 6.
The statistical parameters of the regression bbp(555) (Y) vs. c(530) (X) with different algorithms.
3.3.2. Comparison between the Particle Backscattering Coefficient Values Derived from Field and OLCI Satellite Data
We selected some stations in the Barents and Kara seas from the AMK-65, 68, 72, and 76 voyages to compare the bbp data derived from field and OLCI satellite data. The selected stations included the data from a floating or a deck spectroradiometer, satellite data from OLCI, MODIS, and VIIRS, and absorption data measured by ICAM. For OLCI data, the calculation was performed using the Rrs values available as a result of the BAC (standard) and AAC (NN) atmospheric correction. In the last case, the Rrs Level 2 data were derived from the TOA Level 1 radiance data, using the C2RCC processor [40]. For the calculations in the Kara Sea, we used the regional semi-analytical RSA. Figure 13 shows the regression lines for the Barents, Kara, and Laptev seas. Table 7 presents the regression parameters for different regions, algorithms, and satellites.
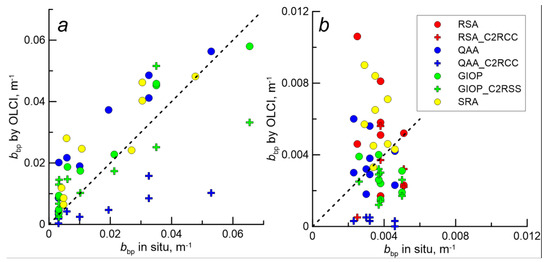
Figure 13.
Scatterplots of in situ bbp(555) data and data from satellite calculations for the Barents Sea (a), the Kara Sea, and the Laptev Sea (b). Red circles—RSA algorithm for the Level 2 data, red crosses—RSA_C2RCC algorithm; blue circles—QAA algorithm for the Level 2 data, blue crosses—QAA_C2RCC algorithm; green circles—GIOP algorithm for the Level 2 data, green crosses—GIOP _C2RCC algorithm; yellow circles—SRA. Dashed lines—1: 1 match.

Table 7.
Regression parameters between bbp(555) from satellite (Y) and in situ (X) data for different algorithms (only cases where the values of the coefficient of determination exceed 0.3).
In the Kara Sea, a correlation with R2 > 0.3 is observed only in the case of the C2RCC processor, the QAA algorithm. That may be due to the strong influence of river runoff in this region. A better correlation is obtained for stations in the Barents Sea. For example, for standard OLCI Level 2 data using the GIOP algorithm, R2 = 0.92.
3.4. Diffuse Attenuation Coefficient
3.4.1. Comparison of ag and Kd Measured In Situ
Figure 14 shows the results of the comparison between the values of ag(443) and Kd(443) measured in situ, separately for the Barents and Norwegian seas (AMK 68—Figure 14A) and the Kara Sea (AMK 72 and 76—Figure 14B). The ag coefficient was measured using ICAM, Kd calculated from the data of the underwater irradiance measured by two instruments (BIC and Ramses) in the upper homogeneous layer. We determined the Kd coefficient as the average between the measurements if they were made with both devices.
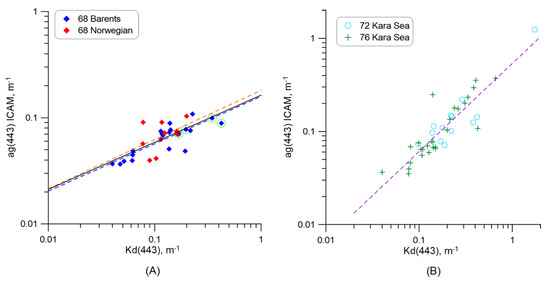
Figure 14.
Comparison of the yellow substance absorption coefficient ag(443) and the diffuse attenuation coefficient Kd(443) measured in situ: (A) for the Barents and Norwegian seas (AMK 68); (B) the Kara Sea (AMK 72 and 76). The solid black line is the regression line for all AMK 68 data; blue dotted line—the Barents Sea, AMK 68; red dotted line—the Norwegian Sea, AMK 68; purple dotted line—the Kara Sea, AMK 72 and 76. Green circles show the stations with coccolithophore blooms.
Table 8 presents the parameters of the regression between the values ag(443) and Kd(443). One can see a reasonably good correlation for the Kara Sea, with data from the AMK 72 and AMK 76 voyages: the coefficient of determination R2 = 0.73. We also obtained a high correlation (R2 = 0.72) for the Barents Sea, but the regression equations in these two seas differ significantly. The stations with coccolithophore blooms (see Figure 14A) fit well into the obtained regression. For the waters of the Norwegian Sea, there is no stable relationship between ag(443) and Kd(443): R2 = 0.21, but the resulting regression equation does not differ much from that obtained for the Barents Sea. The results obtained indicate the consistency of measurements of ag and Kd.

Table 8.
Regression parameters between values of ag and Kd measured in situ at a wavelength of 443 nm.
3.4.2. Consistency between the Data Derived from Field Measurements
For checking the consistency of the field measurements, we calculated Kd using a simple formula: Kd = (1 + 0.005 θ0) a + 3.47 bb, where a and bb—the seawater absorption and backscattering coefficients, θ0—the solar zenith angle [52]. This formula provides reasonable accuracy for waters with coccolithophore blooms and no bloom [53].
We used the spectral values of the absorption coefficient a(λ), measured by ICAM, and the backscattering coefficient determined as the sum of the scattering by the particles and pure water; the particle backscattering bbp was calculated from the in situ measured spectra Rrs(λ) using algorithm [49].
Figure 15 shows the correspondence of the Kd values for two wavelengths, 443 and 490 nm, calculated by formula [52], and from in situ measurements of underwater irradiance at 18 stations in the Barents Sea (AMK 68). It is seen an excellent agreement of the Kd estimates obtained for both spectral channels: the coefficient of determination is R2 = 0.98; the RMSE equals 0.028 and 0.035 m−1 for 443 and 490 nm, respectively. The stations with coccolithophore blooms do not worsen the obtained correspondence. That proves a good agreement between the data of our field measurements of the absorption coefficient a(λ), remote sensing reflectance spectra Rrs(λ), and the diffuse attenuation coefficient Kd(λ).
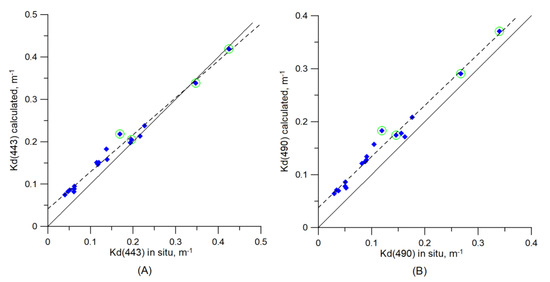
Figure 15.
Scatterplot of the diffuse attenuation coefficient Kd for the wavelengths 443 (A) and 490 (B) nm calculated by formula [52], and from in situ measurements of underwater irradiance at 18 stations in the Barents Sea (AMK 68). Solid black line—perfect correspondence 1:1; dotted black line—linear regression. Green circles show the stations with coccolithophore blooms.
3.4.3. Comparison of Kd(490) Values from Satellite and Field Data (Standard Algorithms)
Figure 16A shows the comparison between the values of the diffuse attenuation coefficient Kd(490) calculated from the data of field measurements and the OLCI Level 2 standard product. We used the Kd(490) value for the nearest pixel, but only for those satellite overpasses with the number of valid pixels being at least 17 out of the 25 closest. Some stations have more overpasses than others; the maximum number equal to 9 was for station 6239 in the Kara Sea (AMK 76, Kd(490) = 0.32 m−1 according to in situ data). As seen, almost all OLCI flights resulted in underestimated Kd(490) values (0.10–0.15 m−1); only the OLCI flight, closest by the time of the field measurements (less than four hours), gave Kd(490) = 0.39 m−1.
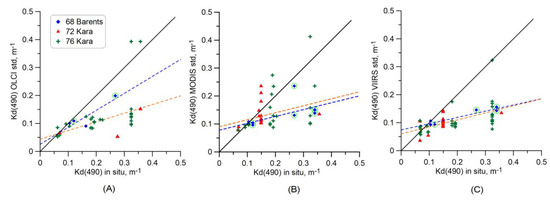
Figure 16.
Scatterplot of the diffuse attenuation coefficient Kd(490) values calculated from field measurements and satellite data (standard algorithm, nearest pixel): (A) OLCI; (B) MODIS; (C) VIIRS. Solid black line—perfect correspondence 1:1; dotted blue line—the regression line for the Barents Sea, AMK 68; dotted red line—the Kara Sea, AMK 72, and 76. Green circles show the stations with coccolithophore blooms.
Figure 16B,C show the correspondence between the values of the diffuse attenuation coefficient Kd(490) calculated from field measurements and satellite MODIS and VIIRS data. As in the OLCI case, we took the Kd(490) values from Level 2 files in the nearest pixel, so they were the standard product of these scanners. Since the overpass of the considered satellites differs, the set of presented data for each scanner is different. For MODIS and VIIRS scanners, we managed to obtain data for station 5580 in the Barents Sea with an intense coccolithophore bloom; the directly measured coccolithophore plated cell concentration was approximately 5 × 106 cell/L, the detached coccoliths 1.5 × 108 cell/L, and Kd(490) = 0.34 m−1.
Table 9 shows the parameters of the correspondence between the Kd(490) values calculated from satellite and field data (the nearest pixel). As seen from Figure 16A and Table 9, a good agreement between OLCI and field data is observed for the Barents Sea (AMK 68): coefficient of determination R2 = 0.80, standard error RMSE = 0.05 m−1, relative error RE = 20%. However, these calculations were only for four stations. The stations with coccolithophore blooms did not show much difference from other stations in this region. In the Kara Sea (AMK 72 and 76), the OLCI estimates of Kd(490), in general, are approximately two times lower than Kd(490) from in situ measurements: the ratio of the mean values is 0.51, RE = 45%, but for stations in clear waters with Kd(490) < 0.1 m−1, satellite data errors do not exceed 15%.

Table 9.
Correspondence parameters between the Kd(490) values obtained from field measurements (X) and satellite data (Y). Satellite data for the nearest pixel.
The calculated parameters are almost the same for MODIS and VIIRS scanners and depend little on the region: the regression equations and the errors are practically the same. For all three scanners, we observed a good agreement between the Kd(490) estimates from satellite and the field data in clear waters (Kd(490) < 0.2 m−1). In more turbid waters, the satellite Kd(490) values were underestimated by about a factor of 2. The intense coccolithophore bloom in the Barents Sea and the river runoff in the Kara Sea cause such turbid waters.
4. Discussion
Specialists in various scientific and engineering directions, using satellite data, need to know the uncertainties in the end product, not only the errors in measurement and retrieval of the geophysical parameter used. We hope our study allows the users to assess the real possibilities of evaluating seawater absorption and colored organic matter with OLCI satellite scanner data in the Barents Sea (partly Norwegian Sea) and the Kara Sea (partly Laptev Sea), our considered regions.
The conditions for satellite observation in the Arctic Basin are incredibly unfavorable; our work gives the estimates of the real uncertainties, which may significantly differ from the errors of the instrumental measurements and the parameter retrieval by the developed algorithms.
We mentioned in the Introduction several works dealing with the uncertainties in OLCI data [24,25,26,27,28,29]. The study [24] is closest to ours regarding approach, research content, and geographically, which combined broad field measurements in the eastern part of the Fram Strait and a transect between northern Norway and southern Spitsbergen in July 2013–2015 with MODIS-Aqua satellite observations, modeling OLCI spectral values using the obtained in situ data. They measured the vertical CTD profiles, including chlorophyll-a fluorescence, performed laboratory determinations of chlorophyll-a concentration, CDOM, and particulate absorption using the collected water samples. However, they focused mainly on the particle absorption coefficients ap at 443 and 670 nm as a proxy of chlorophyll concentration; they presented almost no results on the CDOM absorption. The authors mentioned the factors limiting ocean color remote sensing capability in the Nordic Seas (low sun zenith angle, persistent cloudiness, and fog) without focusing on them.
The work [29] is thematically close to our studies but was carried out in the north-western Baltic Sea. The authors focused mainly on improving Total Suspended Matter (TSM) retrieval. They used the C2RCC processor to derive several remote sensing products, including the remote sensing reflectance, the diffuse attenuation coefficient Kd(489), the particle scattering coefficient at 443 nm, and the product “iop_adg” (the sum of organic detritus and gelbstoff absorption at 443 nm). They statistically compared the satellite Level 2 products with the in situ data from several validation campaigns in 2016–2018. In particular, the authors presented estimates for “iop_adg”—a mean normalized bias 8%, root-mean-square error 56%, average absolute percentage 54%, N = 18.
The works [25,26,27,28] mainly focused on the Level 1 OLCI data and the atmospheric correction problem.
Summarizing our review of the current publications on the considered problem, we may conclude that our work is the first presenting the results of the real uncertainties in the OLCI CDOM absorption in the Arctic seas. We managed to demonstrate that the real uncertainties may significantly differ from the instrumental measurements errors and the parameter retrieval by the developed algorithms (see Figure 3 in Section 3).
We executed our study by applying the comprehensive approach based on multi-sensor and multi-variable data from satellite and in situ measurements. Our analysis included satellite data from OLCI Sentinel-3A and 3B, MODIS Aqua and MODIS-Terra, VIIRS SNPP, and VIIRS NOAA-20 from 2016 to 2019, and the field data on the spectral absorption coefficients of seawater and the colored organic matter, the spectral remote sensing reflectance above and beneath the sea surface, the spectral diffuse attenuation coefficient, and the beam attenuation coefficient. We used the different algorithms to calculate the IOP from remote sensing data, primarily for the absorption coefficients, the particle backscattering coefficient, and TSM concentration.
We compared the OLCI ADG443_NN values obtained as a standard Level 2 product and derived by the C2RCC neural network processor of the SNAP program [39,40]. We also performed a comparison of the spectral remote sensing reflectance values derived with the Baseline Atmospheric Correction algorithm and with the Alternative Atmospheric Correction algorithm based on a neural network procedure. To estimate the uncertainties and assess the real possibilities of evaluating the absorption of colored organic matter from OLCI data, we compared the OLCI ADG443_NN values with the directly measured values of the yellow substance absorption coefficient ag.
The poor observation conditions are the main factor determining a significant loss of data entirely or in their quality. In Section 2.1, Figure 2 shows that the number of days with at least one pixel per bin in most of the Barents Sea did not exceed 6; there are the bins with no pixels with data over the whole expedition period.
If we take the value of 0.02 m−1 as an absolute error for the ag_olci_std values, which is less than 0.1 m−1, and 20% as a relative error for the values exceeding 0.1 m−1, we must reject more than a half of the total number of pairs (Figure 3a). The main reason for the appearance of poor points is unsatisfactory atmospheric correction. In Section 3.2, we considered this problem in detail. As a parameter for analysis of the atmospheric correction errors, we used the values of the remote sensing reflectance Rrs. We built the dependences of the RMSE values on the time difference and from the solar zenith angle. Analysis of these dependencies allowed us to present the reasonable limitations of using the satellite Rrs spectra: RMSE ≤ 0.001. This value is not a strict requirement; at present, we consider it a reference point.
An essential advantage of the OLCI data product is that it provides the user the data files with the error estimates and the annotations data files comprising the classification, Water Quality and Science Flags (WQSF). The WQSF file provides information about the validity and suspicious quality; Level-1B products contain atmospheric and meteorological data, solar, and satellite angles. Combining these data with the uncertainties estimates will allow us to provide users with information about the quality of the data obtained, similar, as an example, to the meteorological data for atmospheric visibility.
5. Conclusions
We conducted a comprehensive multi-sensor study of the uncertainties in satellite OLCI data related to colored dissolved organic matter absorption under the Arctic Seas specific conditions. For that, we used various approaches, comparing data from satellites (Sentinel-3 and four others) and field measurements from five sea expeditions (2016–2019) and different data processing algorithms.
The critical problem of the satellite ocean color observations, particularly obtaining accurate data on the absorption coefficient, is the significant loss in satellite data due to cloudiness and the unreliable atmospheric correction under poor observation conditions. The comparison of the OLCI ADG443_NN standard products with the values of the yellow substance absorption coefficient ag, directly measured by the ICAM spectrophotometer, has shown that the real uncertainties are quite different from the calculated errors, ADG443_NN_err. The former can exceed 100%, while the latter, even for a single OLCI file, is ~10%. The main reason is the unsatisfactory atmospheric correction.
We have estimated the satellite atmospheric correction errors depending on various factors, using the spectral radiance reflectance Rrs directly measured above the sea surface as a reference. The standard error RMSE increases weakly with increasing time difference between the in situ measurement and the satellite overpass and the solar zenith angle. However, the RMSE values can be about 0.001 even with a time difference of more than 20 h and solar zenith angles greater than 70°. Conversely, errors exceeding 0.004 can be detected with a time difference of fewer than five hours and angles less than 50°. The other factors that affected RMSE are the azimuth angle difference and the surface water layer condition.
We have derived the regression equations, allowing us to obtain satellite absorption coefficient values closer to the measured ones. For the Barents Sea: the coefficient of determination R2 = 0.670, the regression error sregr = 0.010 m−1, and the relative error (variation coefficient) RE = 17%. For the Kara Sea, the absorption coefficient values were calculated with the C2RCC processor: R2 = 0.624, sreg = 0.045 m−1, RE = 30%. Statistical support for the derived equations is insufficient, and it is too early to present the derived equations for practical use.
Now we see as the main task of our future work, the development of a statistically reliable method for assessing the uncertainties in the retrieval of the bio-optical parameters from satellite data under the real conditions in the Arctic basin. We realize that such a problem requires the broader coverage of satellite data collection combined with field measurements; this can be solved only by joint efforts of international cooperation.
Absorption coefficient data are important in different essential problems, primarily climate change in the Arctic Basin, as well as in various technical applications.
Author Contributions
Conceptualization, O.K.; methodology, D.G., O.K.; software, S.S., D.G.; validation, D.G., A.Y., S.V., P.K., I.S.; formal analysis, D.G., A.Y., S.V., P.K.; investigation, D.G., A.Y., S.V., P.K.; data curation, S.S.; writing—D.G., O.K. and others; writing—review and editing, O.K.; visualization, D.G., A.Y., S.V., P.K., I.S. All authors have read and agreed to the published version of the manuscript.
Funding
The reported study was funded by RFBR according to the research project No. 19-55-45024.
Acknowledgments
The results were obtained in the framework of the state assignment of Minobrnauki RF (theme No.0149-2019-0003) and the RFBR research project No. 19-55-45024. We thank S.I. Pogosyan for the opportunity to use the ICAM absorption meter in our expedition research; V.A. Artemiev, A.V. Grigoriev and A.N. Khrapko for their help in the field studies; Juan Ignacio Gossn and Mohamed Mograne for their kind help in dealing with different C2RCC versions. We also thank three anonymous reviewers for their careful reading and useful comments.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Perovich, D.K.; Nghiem, S.V.; Markus, T.; Schweiger, A.J. Seasonal evolution and interannual variability of the local solar energy absorbed by the Arctic sea ice–ocean system. J. Geophys. Res. 2007, 112, C03005. [Google Scholar] [CrossRef]
- Perovich, D.K.; Jones, K.F.; Light, B.; Eicken, H.; Markus, T.; Stroeve, J.; Lindsay, R. Solar partitioning in a changing Arctic sea-ice cover. Ann. Glaciol. 2011, 52, 192–196. [Google Scholar] [CrossRef]
- Kopelevich, O.V.; Sahling, I.V.; Vazyulya, S.V.; Glukhovets, D.I.; Sheberstov, S.V.; Burenkov, V.I.; Karalli, P.G.; Yushmanova, A.V. Bio-Optical Characteristics of the Seas, Surrounding the Western Part of Russia, from Data of the Satellite Ocean Color Scanners of 1998–2017; VASh FORMAT, OOO: Moscow, Russia, 2018. [Google Scholar]
- Kopelevich, O.V.; Sahling, I.V.; Vazyulya, S.V.; Glukhovets, D.I.; Sheberstov, S.V.; Burenkov, V.I.; Karalli, P.G.; Yushmanova, A.V. Electronic Atlas. Bio-Optical Characteristics of the Seas, Surrounding the Western Part of Russia, from Data of the Satellite Ocean Color Scanners of 1998–2018. Available online: http://optics.ocean.ru/ (accessed on 31 July 2020).
- Kopelevich, O.V.; Sheberstov, S.V.; Burenkov, V.I.; Vazyulya, S.V.; Likhacheva, M.V. Assessment of underwater irradiance and absorption of solar radiation at water column from satellite data. In Remote Sensing, Laser Probing, and Imagery in Natural Waters, edited by Iosif M. Levin, Gary D. Gilbert, Charles C. Trees, Proceeding of SPIE Vol.6615; SPIE: Bellingham, WA, USA, 2007; p. 661507. [Google Scholar]
- Amon, R.M.W. The role of dissolved organic matter for the organic carbon cycle in the Arctic Ocean. In The Organic Carbon Cycle in the Arctic Ocean; Stein, R., MacDonald, R., Eds.; Springer: Berlin, Germany, 2003; pp. 83–99. [Google Scholar] [CrossRef]
- Miller, W.L.; Moran, M.; Sheldon, W.M.; Zepp, R.G.; Opsahl, S. Determination of apparent quantum yield spectra for the formation of biologically labile photoproducts. Limnol. Oceanogr. 2002, 47, 343–352. [Google Scholar] [CrossRef]
- Pugach, S.P.; Pipko, I.I.; Shakhova, N.E.; Shirshin, E.A.; Perminova, I.V.; Gustafsson, Ö.; Bondur, V.G.; Ruban, A.S.; Semiletov, I.P. Dissolved organic matter and its optical characteristics in the Laptev and East Siberian seas: Spatial distribution and interannual variability (2003–2011). Ocean Sci. 2018, 14, 87. [Google Scholar] [CrossRef]
- Matsuoka, A.; Ortega-Retuerta, E.; Bricaud, A.; Arrigo, K.R.; Babin, M. Characteristics of colored dissolved organic matter (CDOM) in the Western Arctic Ocean: Relationships with microbial activities. Deep Sea Res. Part II Top. Stud. Oceanogr. 2015, 118, 44–52. [Google Scholar] [CrossRef]
- Gonçalves-Araujo, R.; Stedmon, C.A.; Heim, B.; Dubinenkov, I.; Kraberg, A.; Moiseev, D.; Bracher, A. From fresh to marine waters: Characterization and fate of dissolved organic matter in the Lena River Delta region, Siberia. Front. Mar. Sci. 2015, 2, 108. [Google Scholar] [CrossRef]
- Matsuoka, A.; Boss, E.; Babin, M.; Karp-Boss, L.; Hafez, M.; Chekalyuk, A.; Proctor, C.W.; Werdell, P.J.; Bricaud, A. Pan-Arctic optical characteristics of colored dissolved organic matter: Tracing dissolved organic carbon in changing Arctic waters using satellite ocean color data. Remote Sens. Environ. 2017, 200, 89–101. [Google Scholar] [CrossRef]
- Fichot, C.G.; Kaiser, K.; Hooker, S.B.; Amon, R.M.W.; Babin, M.; Bélanger, S.; Walker, S.; Benner, R. Pan-Arctic distributions of continental runoff in the Arctic Ocean. Sci. Rep. 2013, 3, 1053. [Google Scholar] [CrossRef]
- Matsuoka, A.; Bricaud, A.; Benner, R.; Para, J.; Sempéré, R.; Prieur, L.; Bélanger, S.; Babin, M. Tracing the transport of colored dissolved organic matter in water masses of the Southern Beaufort Sea: Relationship with hydrographic characteristics. Biogeosciences 2012, 9, 925. [Google Scholar] [CrossRef]
- Brezonik, P.; Menken, K.D.; Bauer, M. Landsat-based remote sensing of lake water quality characteristics, including chlorophyll and colored dissolved organic matter (CDOM). Lake Reserv. Manag. 2005, 21, 373–382. [Google Scholar] [CrossRef]
- Aiken, G.R.; Gilmour, C.C.; Krabbenhoft, D.P.; Orem, W. Dissolved organic matter in the Florida Everglades: Implications for ecosystem restoration. Crit. Rev. Environ. Sci. Technol. 2011, 41, 217–248. [Google Scholar] [CrossRef]
- Kothawala, D. Dissolved Organic Matter in Inland Waters and Its Impacts on Drinking Water Quality. 2019. Available online: https://kalendarium.uu.se/event/?eventId=43238 (accessed on 30 July 2020).
- Kuznetsova, O.A.; Kopelevich, O.V.; Sheberstov, S.V.; Burenkov, V.I.; Mosharov, S.A.; Demidov, A.B. Assessment of chlorophyll concentration in the Kara Sea based on the data of satellite scanner MODIS–AQUA. Curr. Probl. Remote Sens. Earth Space 2013, 5, 21–31. [Google Scholar]
- Glukhovets, D.I.; Goldin, Y.A. Research of the relationship between salinity and yellow substance fluorescence in the Kara Sea. Fundamentalnaya i Prikladnaya Gidrofizika 2018, 11, 34–39. [Google Scholar] [CrossRef]
- Kubryakov, A.; Stanichny, S.; Zatsepin, A. River plume dynamics in the Kara Sea from altimetry-based lagrangian model, satellite salinity and chlorophyll data. Remote Sens. Environ. 2016, 176, 177–187. [Google Scholar] [CrossRef]
- Zavialov, P.O.; Izhitskiy, A.S.; Osadchiev, A.A.; Pelevin, V.V.; Grabovskiy, A.B. The structure of thermohaline and bio-optical fields in the surface layer of the Kara Sea in September 2011. Oceanology 2015, 55, 461–471. [Google Scholar] [CrossRef]
- Burenkov, V.I.; Goldin, Y.A.; Artem’ev, V.A.; Sheberstov, S.V. Optical characteristics of the Kara Sea derived from shipborne and satellite data. Oceanology 2010, 50, 675–687. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.; Arnone, R. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41, 5755–5772. [Google Scholar] [CrossRef]
- Vazyulya, S.V.; Kopelevich, O.V.; Sheberstov, S.V.; Artemiev, V.A. Satellite estimation of the coefficients of CDOM absorption and diffuse attenuation in the White and Kara seas. Curr. Probl. Remote Sens. Earth Space 2014, 11, 31–41. [Google Scholar]
- Konik, M.; Kowalczuk, P.; Zabłocka, M.; Makarewicz, A.; Meler, J.; Zdun, A.; Darecki, M. Empirical Relationships between Remote-Sensing Reflectance and Selected Inherent Optical Properties in Nordic Sea Surface Waters for the MODIS and OLCI Ocean Colour Sensors. Remote Sens. 2020, 12, 2774. [Google Scholar] [CrossRef]
- Lamquin, N.; Clerc, S.; Bourg, L.; Donlon, C. OLCI A/B Tandem Phase Analysis, Part 1: Level 1 Homogenisation and Harmonisation. Remote Sens. 2020, 12, 1804. [Google Scholar] [CrossRef]
- Lamquin, N.; Déru, A.; Clerc, S.; Bourg, L.; Donlon, C. OLCI A/B Tandem Phase Analysis, Part 2: Benefits of Sensors Harmonisation for Level 2 Products. Remote Sens. 2020, 12, 2702. [Google Scholar] [CrossRef]
- Clerc, S.; Donlon, C.; Borde, F.; Lamquin, N.; Hunt, S.E.; Smith, D.; McMillan, M.; Mittaz, J.; Woolliams, E.; Hammond, M.; et al. Benefits and Lessons Learned from the Sentinel-3 Tandem Phase. Remote Sens. 2020, 12, 2668. [Google Scholar] [CrossRef]
- Mograne, M.A.; Jamet, C.; Loisel, H.; Vantrepotte, V.; Mériaux, X.; Cauvin, A. Evaluation of Five Atmospheric Correction Algorithms over French Optically-Complex Waters for the Sentinel-3A OLCI Ocean Color Sensor. Remote Sens. 2019, 11, 668. [Google Scholar] [CrossRef]
- Kyryliuk, D.; Kratzer, S. Evaluation of Sentinel-3A OLCI Products Derived Using the Case-2 Regional CoastColour Processor over the Baltic Sea. Sensors 2019, 19, 3609. [Google Scholar] [CrossRef]
- Pogosyan, S.I.; Durgaryan, A.M.; Konyukhov, I.V.; Chivkunova, O.B.; Merzlyak, M.N. Absorption spectroscopy of microalgae, cyanobacteria, and dissolved organic matter: Measurements in an integrating sphere cavity. Oceanology 2009, 49, 866–871. [Google Scholar] [CrossRef]
- Glukhovets, D.I.; Sheberstov, S.V.; Kopelevich, O.V.; Zaytseva, A.F.; Pogosyan, S.I. Measuring the sea water absorption factor using integrating sphere. Light Eng. 2018, 26, 120–126. [Google Scholar] [CrossRef]
- Pope, R.M.; Fry, E.S. Absorption spectrum (380–700 nm) of pure water. I. Integrating cavity measurements. Appl. Opt. 1997, 36, 8710–8723. [Google Scholar] [CrossRef]
- Yushmanova, A.V.; Kopelevich, O.V.; Vazyulya, S.V.; Sahling, I.V. Inter-annual variability of the seawater light absorption in surface layer of the northeastern Black Sea in connection with hydrometeorological factors. J. Mar. Sci. Eng. 2019, 7, 326. [Google Scholar] [CrossRef]
- Artemiev, V.A.; Burenkov, V.I.; Vortman, M.I.; Grigoriev, A.V.; Kopelevich, O.V.; Khrapko, A.N. Sea-truth measurements of ocean color: A new floating spectroradiometer and its metrology. Oceanology 2000, 40, 139–145. [Google Scholar]
- Li, M.E.; Shibanov, E.B.; Martynov, O.V.; Korchemkina, E.N. Determination of the impurities concentration in the sea water on the range of the rising radiation brightness. Morskoi Gidrofizicheskii Zhurnal 2015, 186, 17–33. [Google Scholar]
- Gordon, H.R.; McCluney, W.R. Estimation of the depth of sunlight penetration in the sea for remote sensing. Appl. Opt. 1975, 14, 413–416. [Google Scholar] [CrossRef] [PubMed]
- Goldin, Y.A.; Glukhovets, D.I.; Gureev, B.A.; Grigoriev, A.V.; Artemiev, V.A. Shipboard flow-through complex for measuring bio-optical and hydrological seawater characteristics. Oceanology 2020, 60, 713–720. [Google Scholar]
- Sheberstov, S.V. A system of batch processing of oceanological satellite data. Curr. Probl. Remote Sens. Earth Space 2015, 12, 154–161. [Google Scholar]
- Doerffer, R.; Schiller, H. The MERIS case 2 water algorithm. Int. J. Remote Sens. 2007, 28, 517–535. [Google Scholar] [CrossRef]
- Brockmann, C.; Doerffer, R.; Peters, M.; Stelzer, K.; Embacher, S.; Ruescas, A. Evolution of the C2RCC neural network for Sentinel 2 and 3 for the retrieval of ocean colour products in normal and extreme optically complex waters. In Proceedings of the Living Planet Symposium, Prague, Czech Republic, 9–13 May 2016. ESA SP-740. [Google Scholar]
- Werdell, P.J.; Franz, B.A.; Bailey, S.W.; Feldman, G.C.; Boss, E.; Brando, V.E.; Mangin, A. Generalized ocean color inversion model for retrieving marine inherent optical properties. Appl. Opt. 2013, 52, 2019–2037. [Google Scholar] [CrossRef]
- Werdell, P.J.; McKinna, L.I.W.; Boss, E.; Ackleson, S.G.; Craig, S.E.; Gregg, W.W.; Lee, Z.; Maritorena, S.; Roesler, C.S.; Rousseaux, C.S.; et al. An overview of approaches and challenges for retrieving marine inherent optical properties from ocean color remote sensing. Prog. Oceanogr. 2018, 160, 186–212. [Google Scholar] [CrossRef]
- Gordon, H.R.; Brown, O.B.; Evans, R.H.; Brown, J.W.; Smith, R.C.; Baker, K.S.; Clark, D.K. A semianalytical radiance model of ocean color. J. Geophys. Res. 1988, 93, 10909–10924. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral remote sensing for shallow waters: 2. Deriving bottom depths and water properties by optimization. Appl. Opt. 1999, 38, 3831–3843. [Google Scholar] [CrossRef]
- Gordon, H.R.; Morel, A. Remote assessing of ocean color for interpretation of satellite visible imagery: A review. Lect. Notes Coast. Estuar. Stud. 1983, 4, 44. [Google Scholar]
- Smith, R.C.; Baker, K.S. Optical properties of the clearest natural waters. Appl. Opt. 1981, 20, 177–184. [Google Scholar] [CrossRef]
- Demidov, A.B.; Kopelevich, O.V.; Mosharov, S.A.; Sheberstov, S.V.; Vazyulya, S.V. Modelling Kara Sea phytoplankton primary production: Development and skill assessment of regional algorithms. J. Sea Res. 2017, 125, 1–17. [Google Scholar] [CrossRef]
- Gordon, H.R. Can the Lambert-Beer law be applied to the diffuse attenuation coefficient of ocean water? Limnol. Oceanogr. 1989, 34, 1389–1409. [Google Scholar] [CrossRef]
- Burenkov, V.I.; Ershova, S.V.; Kopelevich, O.V.; Sheberstov, S.V.; Shevchenko, V.P. An Estimate of the Distribution of Suspended Matter in the Barents Sea Waters on the Basis of the SeaWiFS Satellite Ocean Color Scanner. Oceanology 2001, 41, 622–628. [Google Scholar]
- Glukhovets, D.I.; Goldin, Y.A. Surface desalinated layer distribution in the Kara Sea determined by shipboard and satellite data. Oceanologia 2020, 62, 364–373. [Google Scholar] [CrossRef]
- Zatsepin, A.G.; Zavialov, P.O.; Kremenetskiy, V.V.; Poyarkov, S.G.; Soloviev, D.M. The upper desalinated layer in the Kara Sea. Oceanology 2010, 50, 657–667. [Google Scholar] [CrossRef]
- Lee, Z.-P.; Du, K.-P.; Arnone, R. A model for the diffuse attenuation coefficient of downwelling irradiance. J. Geophys. Res. 2005, 110, 02016. [Google Scholar] [CrossRef]
- Kopelevich, O.; Sheberstov, S.; Vazyulya, S. Effect of a Coccolithophore Bloom on the Underwater Light Field and the Albedo of the Water Column. J. Mar. Sci. Eng. 2020, 8, 456. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).