Introducing an Improved GRACE Global Point-Mass Solution—A Case Study in Antarctica
Abstract
1. Introduction
2. Material and Methods
2.1. Methodology
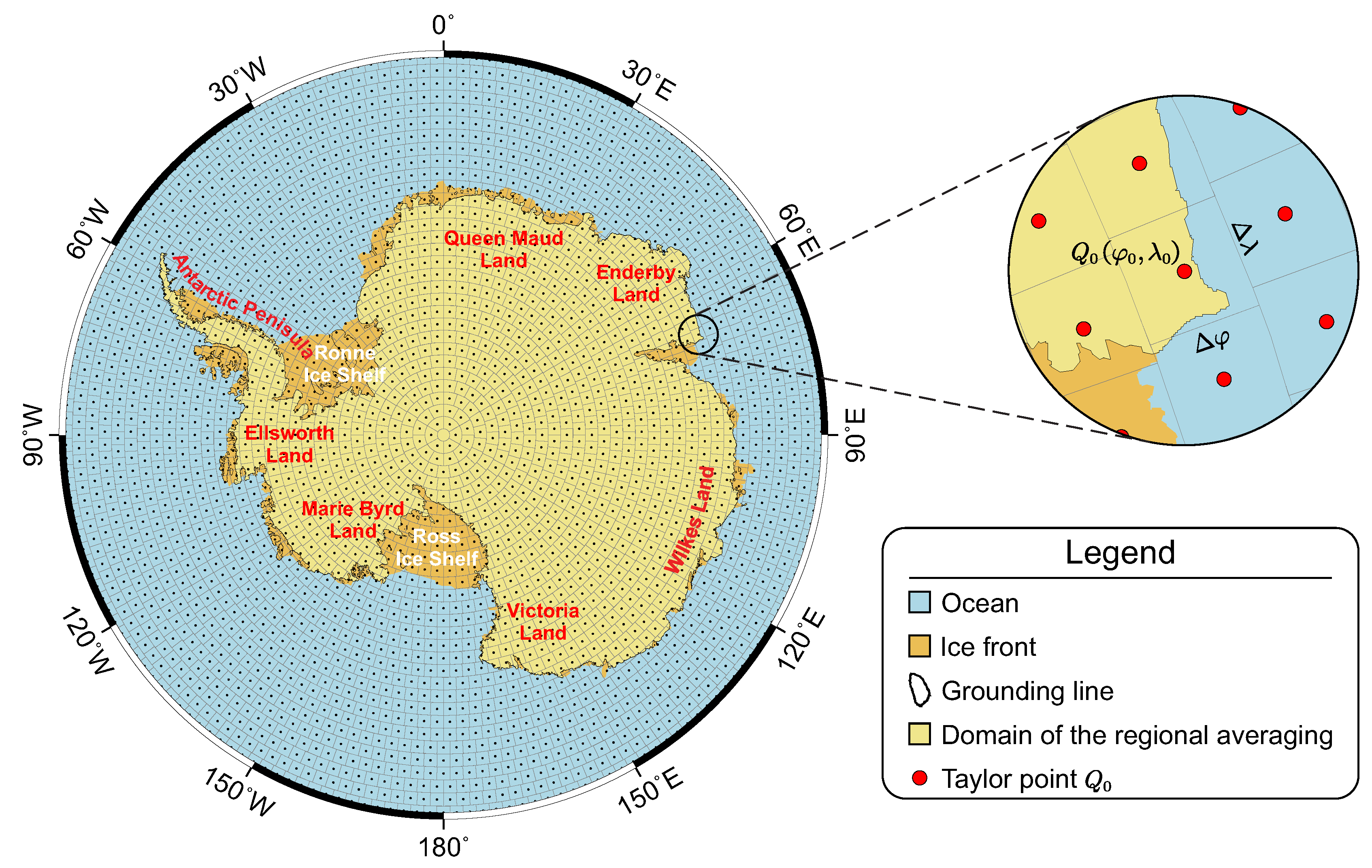
2.1.1. The Improved Point-Mass (IPM) Solution
2.1.2. The Surface Integral Considering the Exact Kernel
2.2. GRACE Products
2.2.1. GRACE Level-2 Data
2.2.2. GRACE Level-3 Data
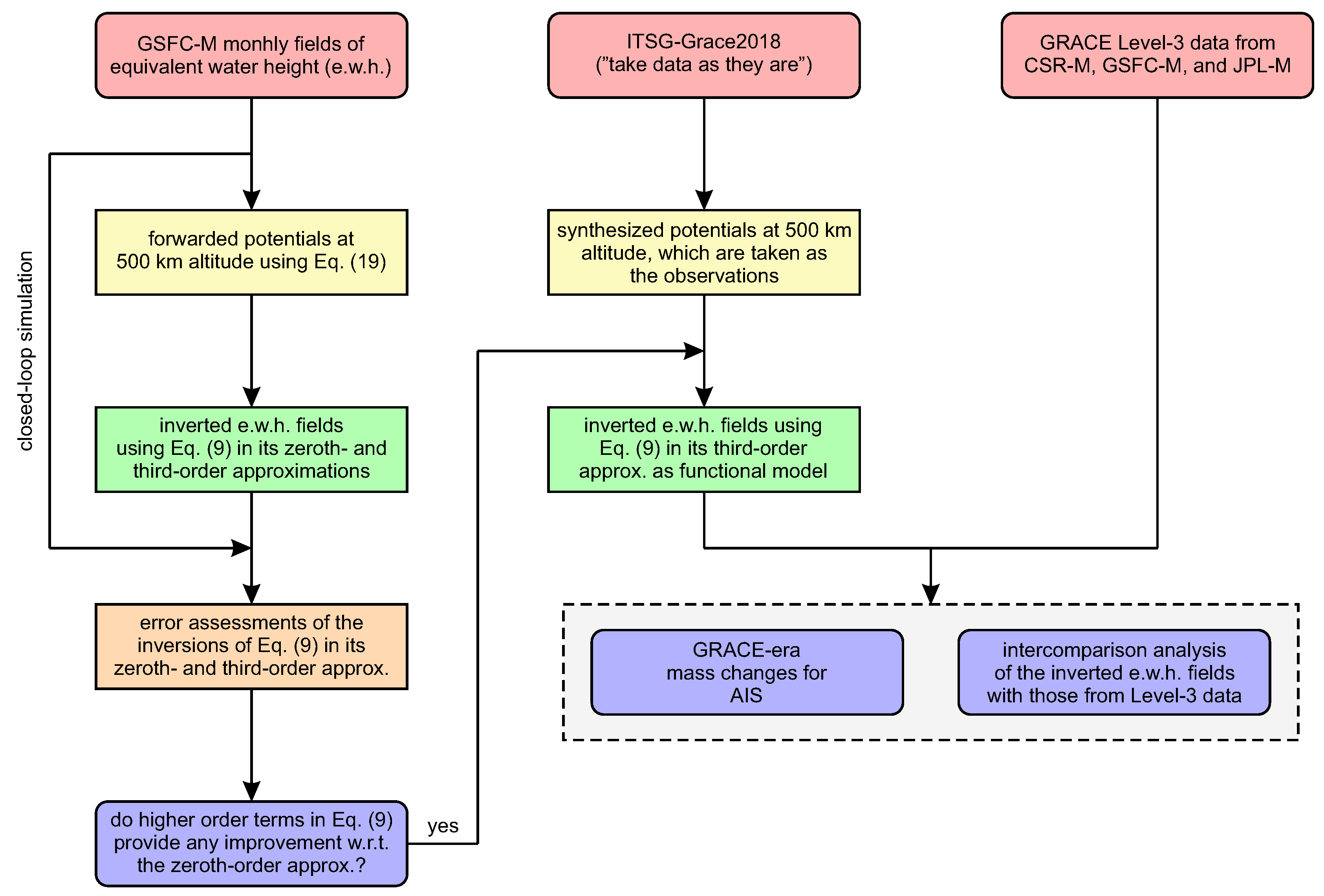
2.3. Experimental Design
3. Results
3.1. Assessment of OPM and IPM by Means of a Closed-Loop Simulation
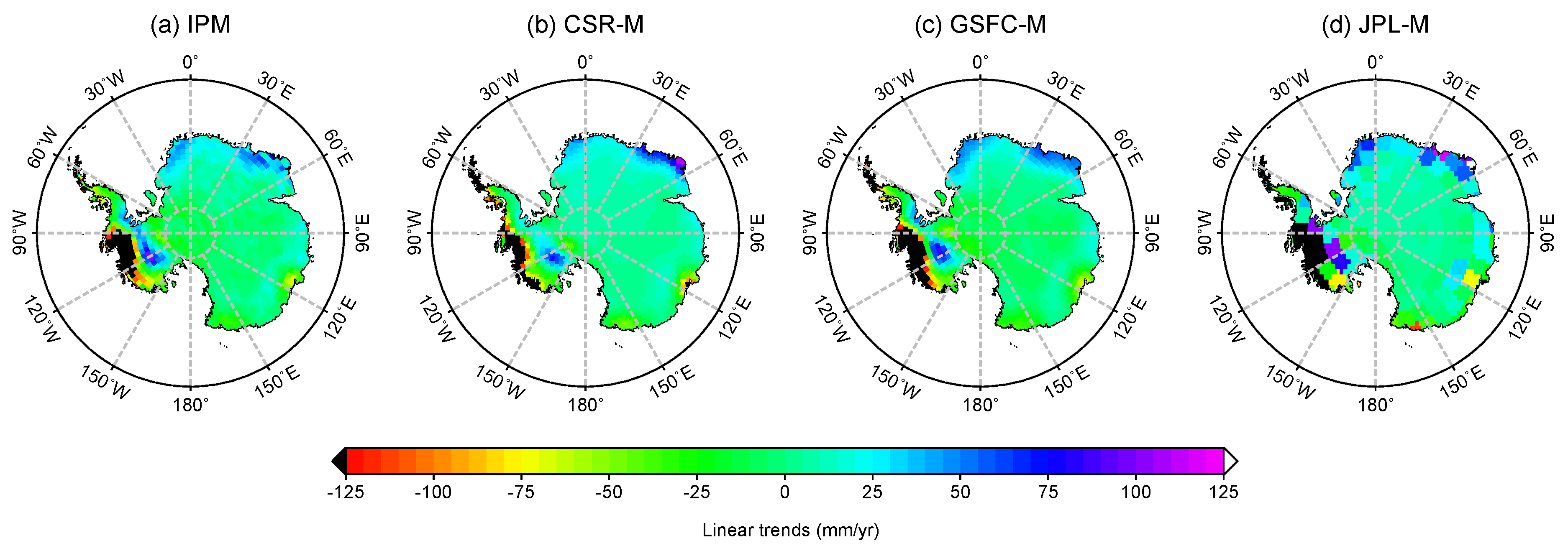
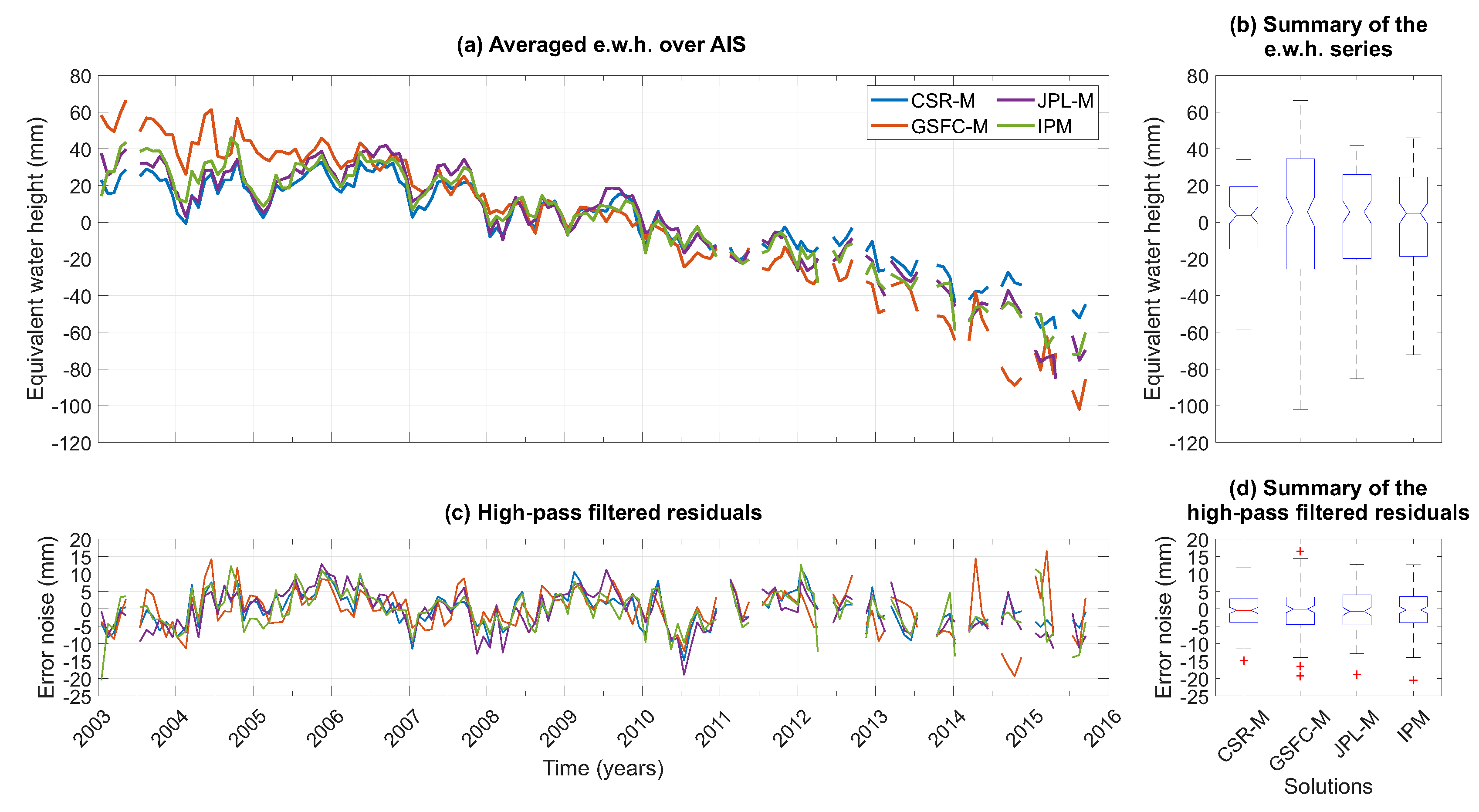
3.2. Inversion of GRACE Level-2 Data Using the IPM Modeling
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. The Surface Integral via Analytical Integration over the Radial Direction
Appendix B. The Expression for the Remainder
References
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE measurements of mass variability in the Earth system. Science 2004, 305, 503–505. [Google Scholar] [CrossRef]
- Tapley, B.D.; Watkins, M.M.; Flechtner, F.; Reigber, C.; Bettadpur, S.; Rodell, M.; Sasgen, I.; Famiglietti, J.S.; Landerer, F.W.; Chambers, D.P.; et al. Contributions of GRACE to understanding climate change. Nat. Clim. Chang. 2019, 9, 358–369. [Google Scholar] [CrossRef]
- Bettadpur, S. UTCSR Level-2 Processing Standards Document: For Level-2 Product Release 0006; Center for Space Research, The University of Texas at Austin: Austin, TX, USA, 2018. [Google Scholar]
- Watkins, M.M.; Yuan, D.N. JPL Level-2 Processing Standards Document for Level-2 Product Release 05.1; Jet Propulsion Laboratory–JPL, California Institute of Technology: Pasadena, CA, USA, 2014. [Google Scholar]
- Dahle, C.; Flechtner, F.; Murböck, M.; Michalak, G.; Neumayer, K.; Abrykosov, O.; Reinhold, A.; König, R. GRACE 327–743 (Gravity Recovery and Climate Experiment): GFZ Level-2 Processing Standards Document for Level-2 Product Release 06 (Rev. 1.0, 26 October 2018); Scientific Technical Report str—Data; GFZ German Research Centre for Geosciences: Potsdam, Germany, 2018. [Google Scholar] [CrossRef]
- Lemoine, J.; Bruinsma, S.; Gegout, P.; Biancale, R.; Bourgogne, S. Release 3 of the GRACE gravity solutions from CNES/GRGS. In Geophysical Research Abstracts; European Geoscience Union: Vienna, Austria, 2013; Volume 15, p. EGU2013-11123. [Google Scholar]
- Liu, X.; Ditmar, P.; Siemes, C.; Slobbe, D.C.; Revtova, E.; Klees, R.; Riva, R.; Zhao, Q. DEOS Mass Transport model (DMT-1) based on GRACE satellite data: Methodology and validation. Geophys. J. Int. 2010, 181, 769–788. [Google Scholar] [CrossRef]
- Kvas, A.; Behzadpour, S.; Ellmer, M.; Klinger, B.; Strasser, S.; Zehentner, N.; Mayer-Gürr, T. ITSG-Grace2018: Overview and Evaluation of a New GRACE-Only Gravity Field Time Series. J. Geophys. Res. Solid Earth 2019, 124, 9332–9344. [Google Scholar] [CrossRef]
- Meyer, U.; Jäggi, A.; Jean, Y.; Beutler, G. AIUB-RL02: An improved time-series of monthly gravity fields from GRACE data. Geophys. J. Int. 2016, 205, 1196–1207. [Google Scholar] [CrossRef]
- Chen, Q.; Shen, Y.; Zhang, X.; Hsu, H.; Chen, W.; Ju, X.; Lou, L. Monthly gravity field models derived from GRACE Level 1B data using a modified short-arc approach. J. Geophys. Res. Solid Earth 2015, 120, 1804–1819. [Google Scholar] [CrossRef]
- Naeimi, M.; Koch, I.; Khami, A.; Flury, J. IfE monthly gravity field solutions using the variational equations. In Geophysical Research Abstracts; European Geoscience Union: Vienna, Austria, 2018; Volume 20. [Google Scholar]
- Chen, W.; Luo, J.; Ray, J.; Yu, N.; Li, J.C. Multiple-data-based monthly geopotential model set LDCmgm90. Sci. Data 2019, 6, 228. [Google Scholar] [CrossRef]
- Jean, Y.; Meyer, U.; Jäggi, A. Combination of GRACE monthly gravity field solutions from different processing strategies. J. Geod. 2018, 92, 1313–1328. [Google Scholar] [CrossRef]
- Meyer, U.; Jean, Y.; Kvas, A.; Dahle, C.; Lemoine, J.M.; Jäggi, A. Combination of GRACE monthly gravity fields on the normal equation level. J. Geod. 2019, 93, 1645–1658. [Google Scholar] [CrossRef]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.N.; Boening, C.; Landerer, F.W. Improved methods for observing Earth’s time variable mass distribution with GRACE using spherical cap mascons. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006, 33, L08402. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Methods for inferring regional surface-mass anomalies from Gravity Recovery and Climate Experiment (GRACE) measurements of time-variable gravity. J. Geophys. Res. 2002, 107, 2193. [Google Scholar] [CrossRef]
- Kusche, J. Approximate decorrelation and non–isotropic smoothing of time-variable GRACE-type gravity field models. J. Geod. 2007, 81, 733–749. [Google Scholar] [CrossRef]
- Rowlands, D.D.; Luthcke, S.B.; Klosko, S.M.; Lemoine, F.G.R.; Chinn, D.S.; McCarthy, J.J.; Cox, C.M.; Anderson, O.B. Resolving mass flux at high spatial and temporal resolution using GRACE intersatellite measurements. Geophys. Res. Lett. 2005, 32, L04310. [Google Scholar] [CrossRef]
- Luthcke, S.B.; Zwally, H.J.; Abdalati, W.; Rowlands, D.D.; Ray, R.D.; Nerem, R.S.; Lemoine, F.G.; McCarthy, J.J.; Chinn, D.S. Recent Greenland ice mass loss by drainage system from satellite gravity observations. Science 2006, 314, 1286–1289. [Google Scholar] [CrossRef] [PubMed]
- Klees, R.; Liu, X.; Wittwer, T.; Gunter, B.C.; Revtova, E.A.; Tenzer, R.; Ditmar, P.; Winsemius, H.C.; Savenije, H.H.G. A Comparison of Global and Regional GRACE Models for Land Hydrology. Surv. Geophys. 2008, 29, 335–359. [Google Scholar] [CrossRef]
- Rowlands, D.D.; Luthcke, S.B.; McCarthy, J.J.; Klosko, S.M.; Chinn, D.S.; Lemoine, F.G.; Boy, J.P.; Sabaka, T.J. Global mass flux solutions from GRACE: A comparison of parameter estimation strategies—Mass concentrations versus Stokes coefficients. J. Geophys. Res. 2010, 115, B01403. [Google Scholar] [CrossRef]
- Sabaka, T.J.; Rowlands, D.D.; Luthcke, S.B.; Boy, J.P. Improving global mass flux solutions from Gravity Recovery and Climate Experiment (GRACE) through forward modeling and continuous time correlation. J. Geophys. Res. 2010, 115, 1–20. [Google Scholar] [CrossRef]
- Luthcke, S.B.; Sabaka, T.; Loomis, B.; Arendt, A.; McCarthy, J.; Camp, J. Antarctica, Greenland and Gulf of Alaska land-ice evolution from an iterated GRACE global mascon solution. J. Glaciol. 2013, 59, 613–631. [Google Scholar] [CrossRef]
- Save, H.; Bettadpur, S.; Tapley, B.D. High-resolution CSR GRACE RL05 mascons. J. Geophys. Res. Solid Earth 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Andrews, S.B.; Moore, P.; King, M.A. Mass change from GRACE: A simulated comparison of Level-1B analysis techniques. Geophys. J. Int. 2014, 200, 503–518. [Google Scholar] [CrossRef][Green Version]
- Scanlon, B.R.; Zhang, Z.; Save, H.; Wiese, D.N.; Landerer, F.W.; Long, D.; Longuevergne, L.; Chen, J. Global evaluation of new GRACE mascon products for hydrologic applications. Water Resour. Res. 2016, 52, 9412–9429. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. 1998, 103, 30205. [Google Scholar] [CrossRef]
- Klees, R.; Zapreeva, E.A.; Winsemius, H.C.; Savenije, H.H.G. The bias in GRACE estimates of continental water storage variations. Hydrol. Earth Syst. Sci. 2007, 11, 1227–1241. [Google Scholar] [CrossRef]
- Tiwari, V.M.; Wahr, J.; Swenson, S. Dwindling groundwater resources in northern India, from satellite gravity observations. Geophys. Res. Lett. 2009, 36, L18401. [Google Scholar] [CrossRef]
- Jacob, T.; Wahr, J.; Pfeffer, W.T.; Swenson, S. Recent contributions of glaciers and ice caps to sea level rise. Nature 2012, 482, 514–518. [Google Scholar] [CrossRef]
- Schrama, E.J.; Wouters, B.; Rietbroek, R. A mascon approach to assess ice sheet and glacier mass balances and their uncertainties from GRACE data. J. Geophys. Res. Solid Earth 2014, 119, 6048–6066. [Google Scholar] [CrossRef]
- Ran, J.; Ditmar, P.; Klees, R.; Farahani, H.H. Statistically optimal estimation of Greenland Ice Sheet mass variations from GRACE monthly solutions using an improved mascon approach. J. Geod. 2018, 92, 299–319. [Google Scholar] [CrossRef]
- Forsberg, R.; Reeh, N. Mass change of the Greenland Ice Sheet from GRACE. In Gravity Field of the Earth—1st Meeting of the International Gravity Field Service; Dergisi, H., Ed.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 1–5. [Google Scholar]
- Sørensen, L.S.; Forsberg, R. Greenland Ice Sheet Mass Loss from GRACE Monthly Models. In Gravity, Geoid and Earth Observation; Mertikas, S.P., Ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 527–532. [Google Scholar]
- Baur, O.; Sneeuw, N. Assessing Greenland ice mass loss by means of point-mass modeling: A viable methodology. J. Geod. 2011, 85, 607–615. [Google Scholar] [CrossRef]
- Barletta, V.R.; Sørensen, L.S.; Forsberg, R. Scatter of mass changes estimates at basin scale for Greenland and Antarctica. Cryosphere 2013, 7, 1411–1432. [Google Scholar] [CrossRef]
- Forsberg, R.; Sørensen, L.; Simonsen, S. Greenland and Antarctica Ice Sheet Mass Changes and Effects on Global Sea Level. Surv. Geophys. 2017, 38, 89–104. [Google Scholar] [CrossRef]
- Ferreira, V.; Yong, B.; Tourian, M.; Ndehedehe, C.; Shen, Z.; Seitz, K.; Dannouf, R. Characterization of the hydro-geological regime of Yangtze River basin using remotely-sensed and modeled products. Sci. Total Environ. 2020, 718, 137354. [Google Scholar] [CrossRef]
- Heck, B.; Seitz, K. A comparison of the tesseroid, prism and point-mass approaches for mass reductions in gravity field modelling. J. Geod. 2007, 81, 121–136. [Google Scholar] [CrossRef]
- Mohr, P.J.; Newell, D.B.; Taylor, B.N. CODATA Recommended Values of the Fundamental Physical Constants: 2014. J. Phys. Chem. Ref. Data 2016, 45, 043102. [Google Scholar] [CrossRef]
- Chao, B.F. Caveats on the equivalent water thickness and surface mascon solutions derived from the GRACE satellite-observed time-variable gravity. J. Geod. 2016, 90, 807–813. [Google Scholar] [CrossRef]
- Wild-Pfeiffer, F. A comparison of different mass elements for use in gravity gradiometry. J. Geod. 2008, 82, 637–653. [Google Scholar] [CrossRef]
- Grombein, T.; Seitz, K.; Heck, B. Optimized formulas for the gravitational field of a tesseroid. J. Geod. 2013, 87, 645–660. [Google Scholar] [CrossRef]
- Grombein, T.; Seitz, K.; Awange, J.L.; Heck, B. Detection of hydrological mass variations by means of an inverse tesseroid approach. In Geophysical Research Abstracts; European Geoscience Union: Vienna, Austria, 2012; Volume 14, p. EGU2012-7548. [Google Scholar]
- Mayer-Gürr, T.; Behzadpur, S.; Ellmer, M.; Kvas, A.; Klinger, B.; Strasser, S.; Zehentner, N. ITSG-Grace2018—Monthly, Daily and Static Gravity Field Solutions from GRACE. Available online: https://www.tugraz.at/institute/ifg/downloads/gravity-field-models/itsg-grace2018/ (accessed on 13 March 2020).
- Swenson, S.; Chambers, D.; Wahr, J. Estimating geocenter variations from a combination of GRACE and ocean model output. J. Geophys. Res. 2008, 113, 1–12. [Google Scholar] [CrossRef]
- Cheng, M.; Tapley, B.D. Variations in the Earth’s oblateness during the past 28 years. J. Geophys. Res. 2004, 109, B09402. [Google Scholar] [CrossRef]
- A, G.; Wahr, J.; Zhong, S. Computations of the viscoelastic response of a 3-D compressible Earth to surface loading: An application to Glacial Isostatic Adjustment in Antarctica and Canada. Geophys. J. Int. 2013, 192, 557–572. [Google Scholar] [CrossRef]
- Save, H. CSR GRACE RL06 Mascon Solutions. Texas Data Repository Dataverse, V1. Available online: https://disc.gsfc.nasa.gov/datasets/GLDAS_NOAH10_M_V2.1/summary (accessed on 23 October 2019).
- Wiese, D.N.; Landerer, F.W.; Watkins, M.M. Quantifying and reducing leakage errors in the JPL RL05M GRACE mascon solution. Water Resour. Res. 2016, 52, 7490–7502. [Google Scholar] [CrossRef]
- Wiese, D.N.; Yuan, D.N.; Boening, C.; Landerer, F.W.; Watkins, M.M. JPL GRACE Mascon Ocean, Ice, and Hydrology Equivalent Water Height Release 06 Coastal Resolution Improvement (CRI) Filtered Version 1.0. Ver. 1.0. Available online: https://grace.jpl.nasa.gov/data/get-data/jpl_global_mascons/ (accessed on 16 March 2019).
- Rignot, E.; Jacobs, S.; Mouginot, J.; Scheuchl, B. Ice-Shelf Melting Around Antarctica. Science 2013, 341, 266–270. [Google Scholar] [CrossRef]
- Mouginot, J.; Scheuchl, B.; Rignot, E. MEaSUREs Antarctic Boundaries for IPY 2007–2009 from Satellite Radar, Version 2. Available online: https://nsidc.org/data/nsidc-0709 (accessed on 12 July 2020).
- Hansen, P.C. The L-Curve and its Use in the Numerical Treatment of Inverse Problems. In Computational Inverse Problems in Electrocardiology, Advances in Computational Bioengineering; Johnston, P., Ed.; WIT Press: Southampton, UK, 2000; Volume 4, pp. 119–142. [Google Scholar]
- Moriasi, D.N.; Arnold, J.G.; Liew, M.W.V.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Hochberg, Y.; Tamhane, A.C. Multiple Comparison Procedures; Wiley Series in Probability and Statistics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1987. [Google Scholar] [CrossRef]
- Kruskal, W.H.; Wallis, W.A. Use of Ranks in One-Criterion Variance Analysis. J. Am. Stat. Assoc. 1952, 47, 583–621. [Google Scholar] [CrossRef]
- Groh, A.; Horwath, M.; Horvath, A.; Meister, R.; Sørensen, L.S.; Barletta, V.R.; Forsberg, R.; Wouters, B.; Ditmar, P.; Ran, J.; et al. Evaluating GRACE Mass Change Time Series for the Antarctic and Greenland Ice Sheet–Methods and Results. Geosciences 2019, 9, 415. [Google Scholar] [CrossRef]
- Sakumura, C.; Bettadpur, S.; Bruinsma, S. Ensemble prediction and intercomparison analysis of GRACE time-variable gravity field models. Geophys. Res. Lett. 2014, 41, 1389–1397. [Google Scholar] [CrossRef]
- Ferreira, V.G.; Montecino, H.D.C.; Yakubu, C.I.; Heck, B. Uncertainties of the Gravity Recovery and Climate Experiment time-variable gravity-field solutions based on three-cornered hat method. J. Appl. Remote. Sens. 2016, 10, 015015. [Google Scholar] [CrossRef]
- Paige, C.C.; Saunders, M.A. LSQR: An Algorithm for Sparse Linear Equations and Sparse Least Squares. ACM Trans. Math. Softw. 2002, 8, 43–71. [Google Scholar] [CrossRef]
- Bronstein, I.; Semendjajew, K.; Musiol, G.; Mühlig, H. Taschenbuch Der Mathematik, 4th ed.; Verlag Harri Deutsch: Frankfurt am Main, Germany, 1999. [Google Scholar]

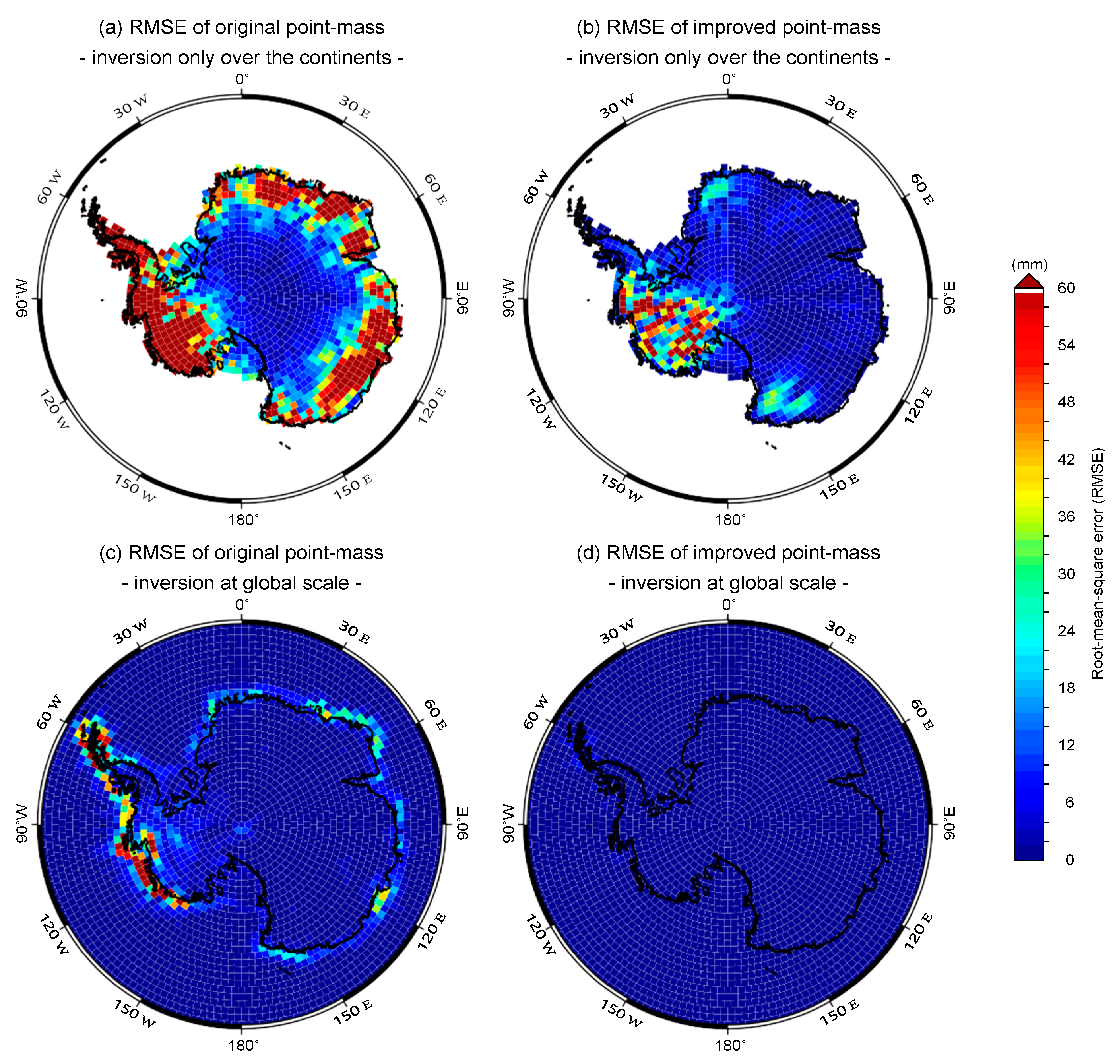
| Domain of the Inversion | Solution | Domain of the Evaluation | |||||
|---|---|---|---|---|---|---|---|
| Land | Global | Antarctica | |||||
| RMSE (mm) | RSR (Unitless) | RMSE (mm) | RSR (Unitless) | RMSE (mm) | RSR (Unitless) | ||
| Land | OPM | 23.82 | 0.29 | - | - | 58.94 | 0.52 |
| IPM | 2.90 | 0.03 | - | - | 9.46 | 0.08 | |
| Global | OPM | 2.41 | 0.03 | 1.68 | 0.04 | 3.83 | 0.03 |
| IPM | 0.16 | 0.00 | 0.13 | 0.00 | 0.21 | 0.00 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferreira, V.G.; Yong, B.; Seitz, K.; Heck, B.; Grombein, T. Introducing an Improved GRACE Global Point-Mass Solution—A Case Study in Antarctica. Remote Sens. 2020, 12, 3197. https://doi.org/10.3390/rs12193197
Ferreira VG, Yong B, Seitz K, Heck B, Grombein T. Introducing an Improved GRACE Global Point-Mass Solution—A Case Study in Antarctica. Remote Sensing. 2020; 12(19):3197. https://doi.org/10.3390/rs12193197
Chicago/Turabian StyleFerreira, Vagner G., Bin Yong, Kurt Seitz, Bernhard Heck, and Thomas Grombein. 2020. "Introducing an Improved GRACE Global Point-Mass Solution—A Case Study in Antarctica" Remote Sensing 12, no. 19: 3197. https://doi.org/10.3390/rs12193197
APA StyleFerreira, V. G., Yong, B., Seitz, K., Heck, B., & Grombein, T. (2020). Introducing an Improved GRACE Global Point-Mass Solution—A Case Study in Antarctica. Remote Sensing, 12(19), 3197. https://doi.org/10.3390/rs12193197







