An Image-Based Real-Time Georeferencing Scheme for a UAV Based on a New Angular Parametrization
Abstract
1. Introduction
1.1. Feature Extraction and Matching Review
1.2. Image-Based SLAM Approaches
1.3. Novel Aspects of this Article
2. Background
2.1. Coplanarity and Collinearity
2.2. Automatic Feature Extraction and Matching
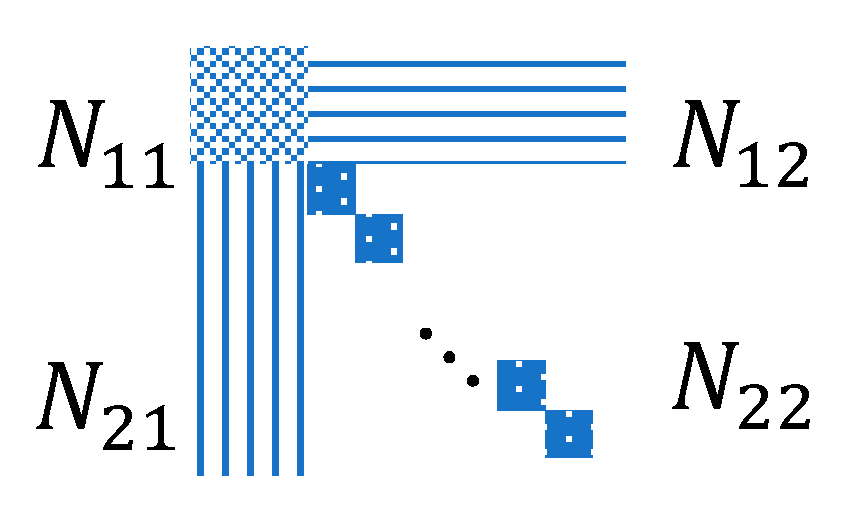
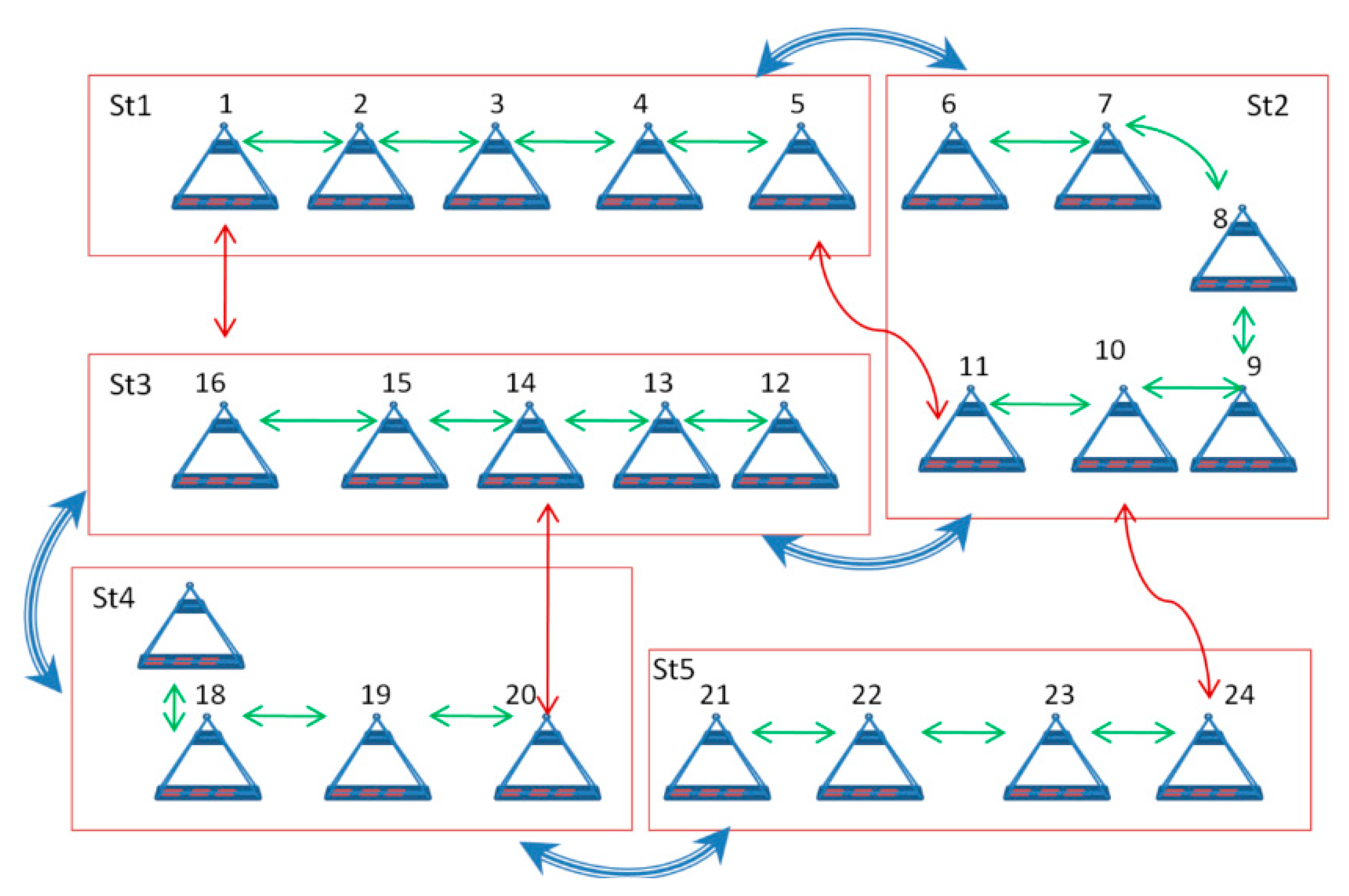
2.3. Network Creation Strategy
2.4. Euler Angles
2.5. Euler Angles from an Arbitrary Rotation Matrix
2.6. Quaternions
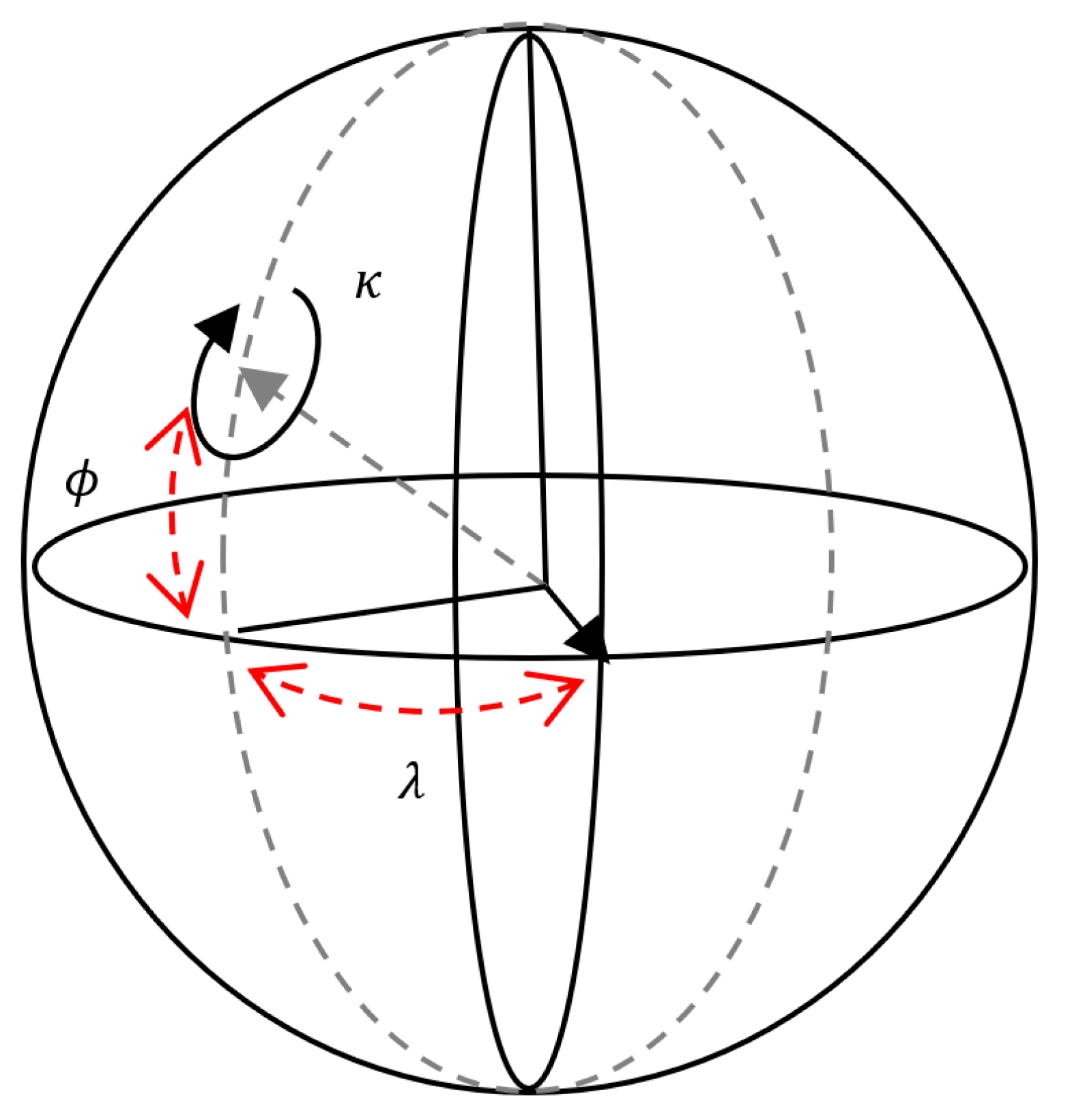
2.7. Rotation Axis-Angle, and Spherical Angles
2.8. Sparse Bundle Block Adjustment
3. Material and Methods
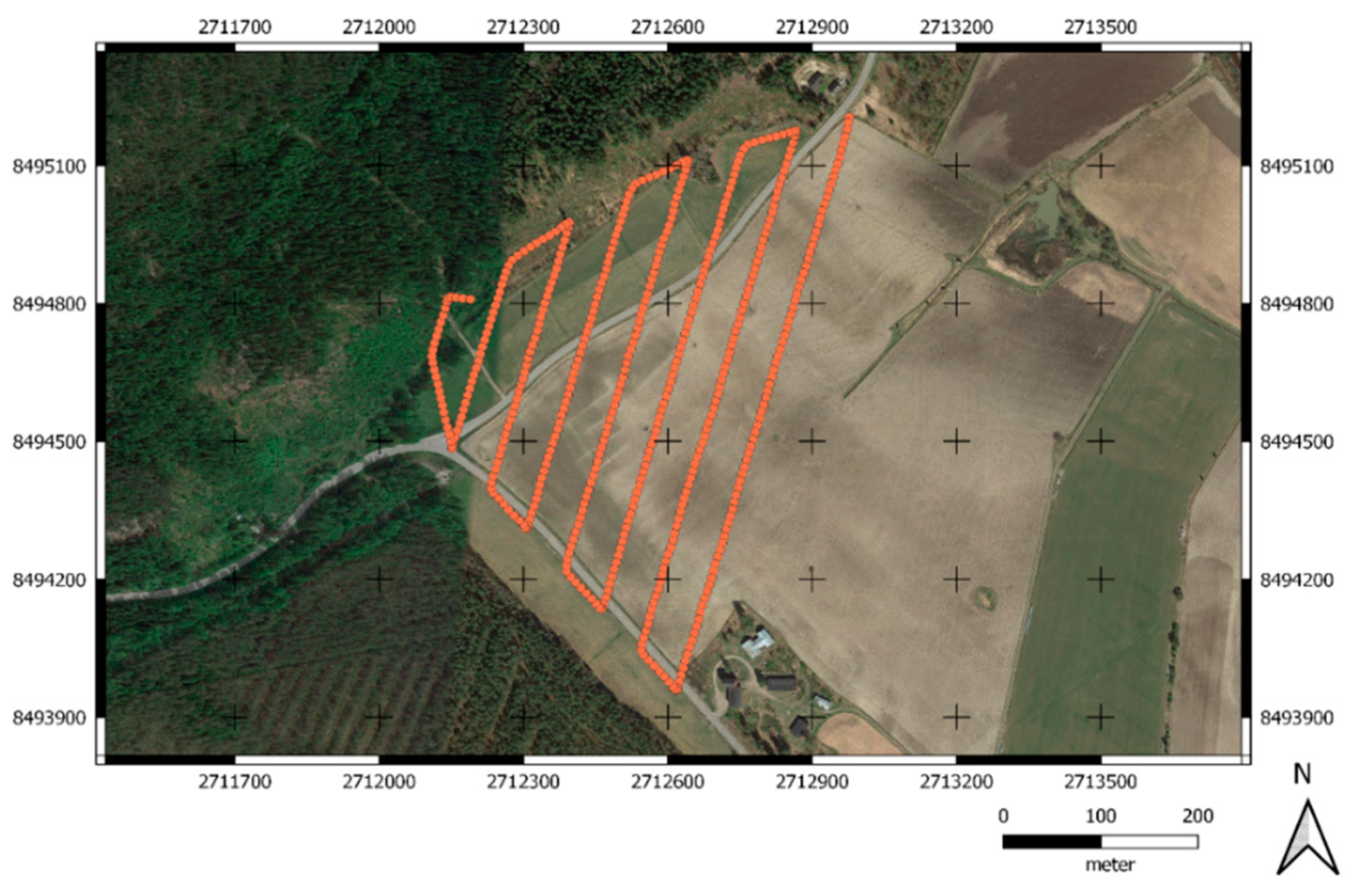
3.1. Datasets
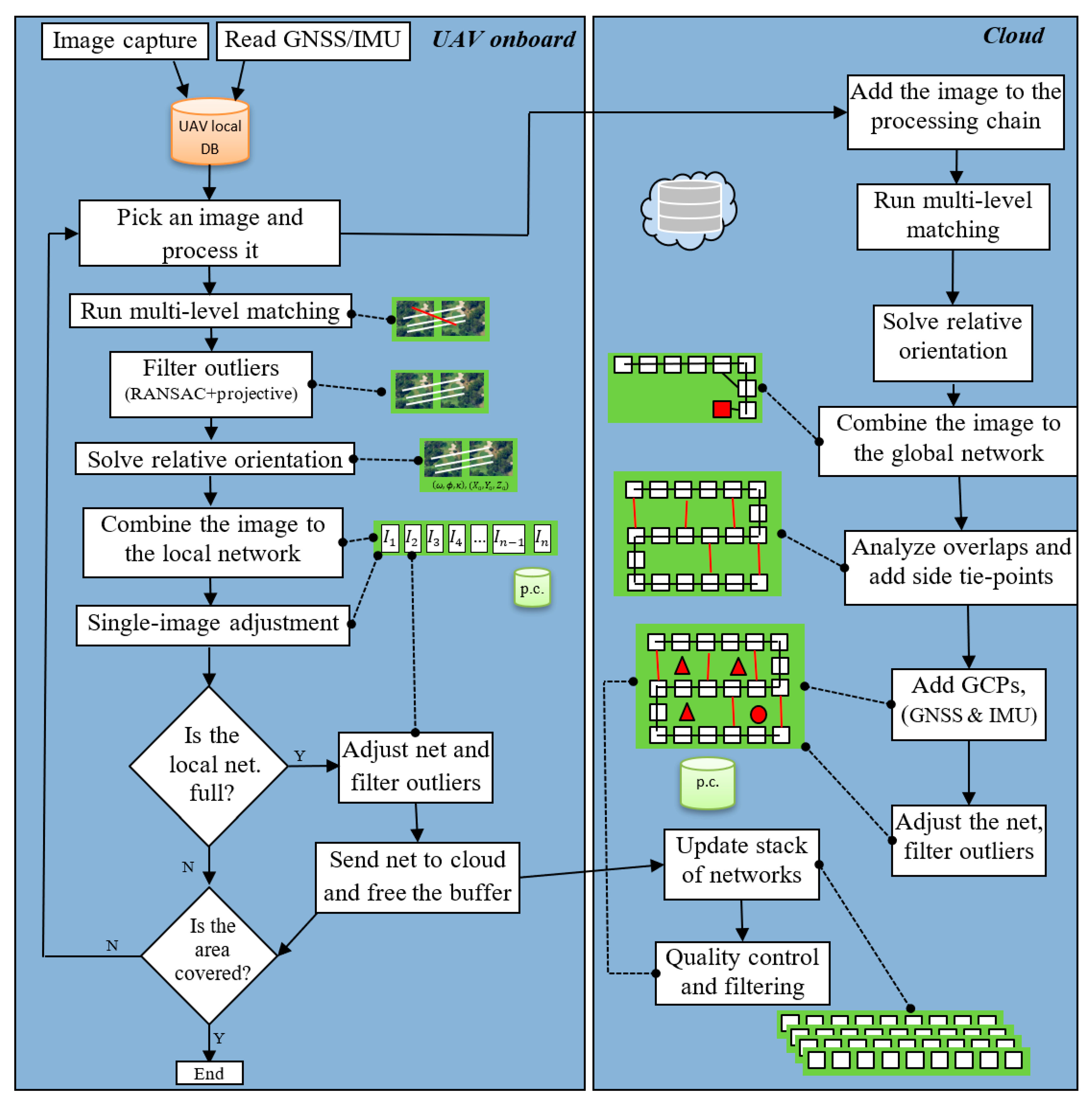
3.2. Real-Time Computing
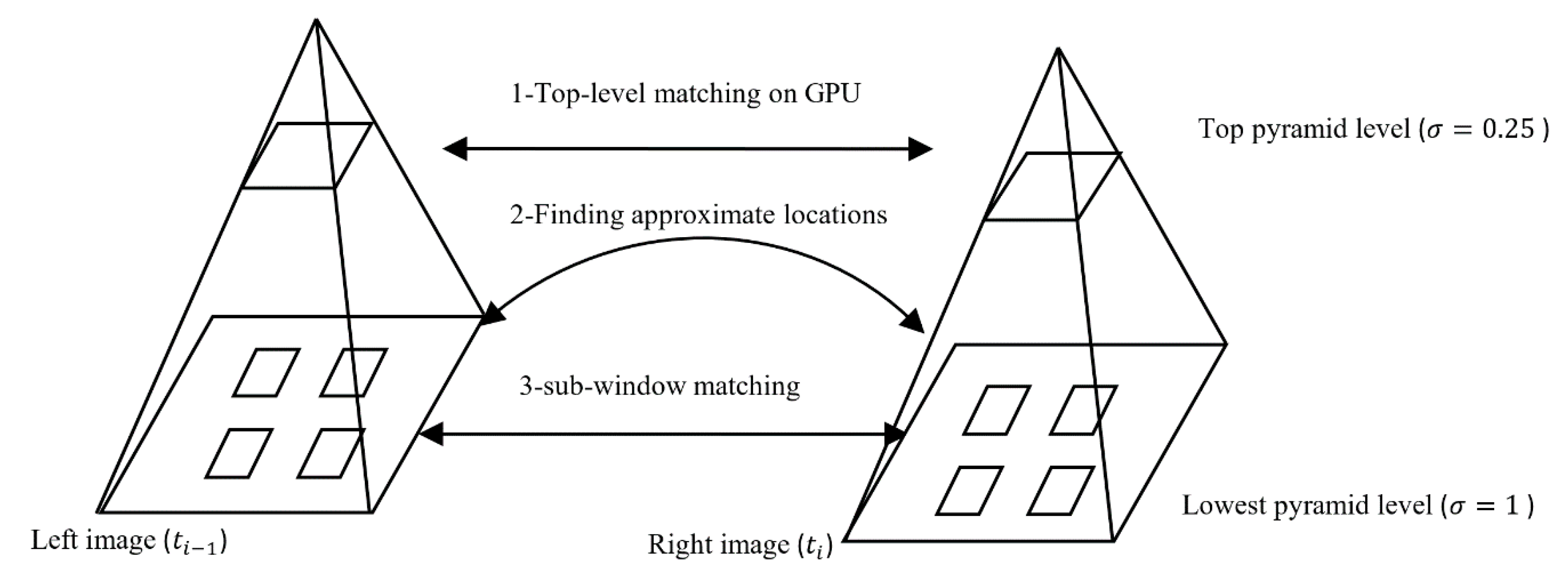
3.3. Multilevel Matching
3.4. Monocular SLAM
3.5. Performance Assessment
4. Results
4.1. Feature-Extraction Methods Comparison
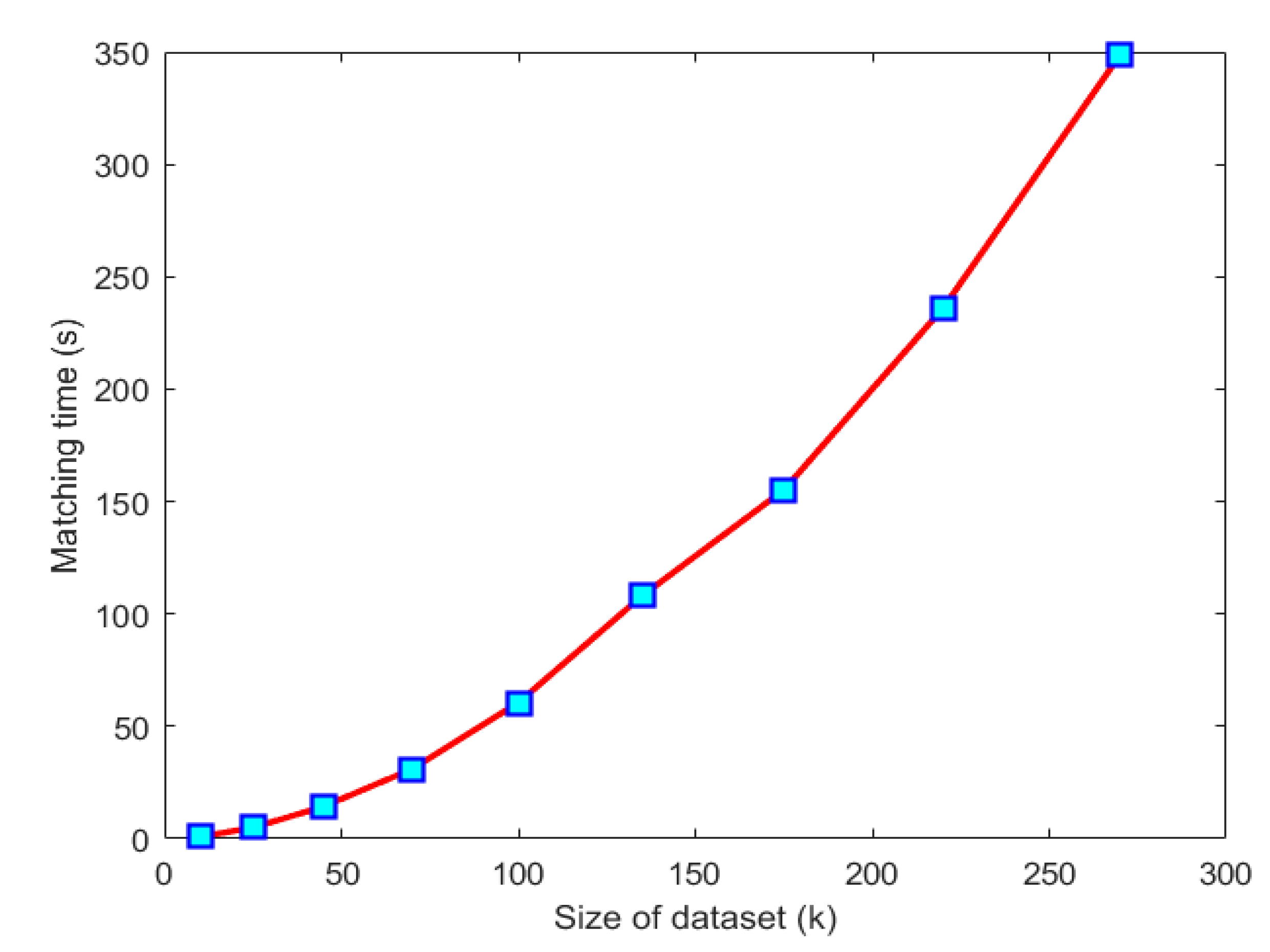
4.2. Multilevel Matching
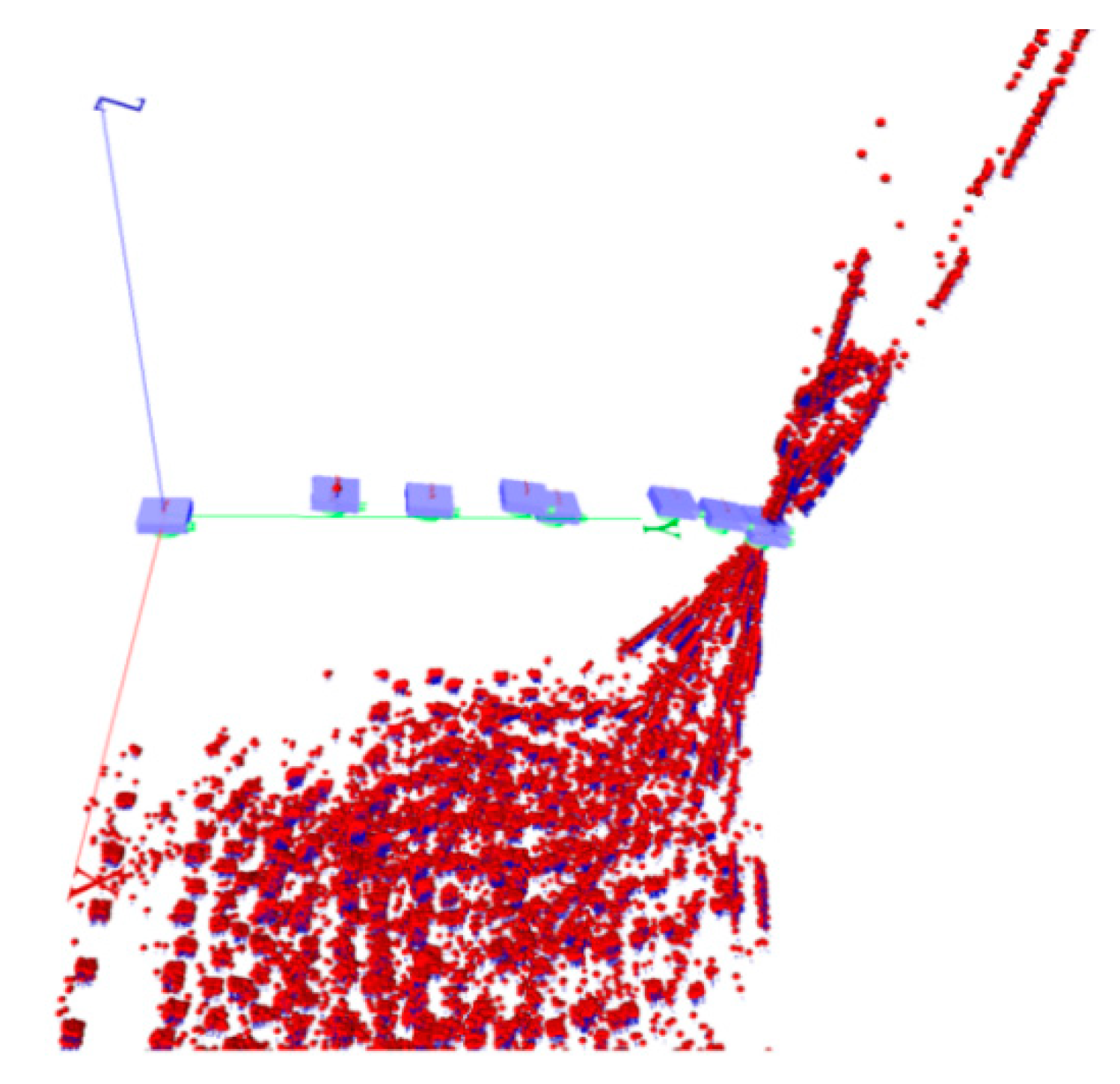
4.3. Image-Based SLAM
4.4. Postprocessing
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Honkavaara, E.; Saari, H.; Kaivosoja, J.; Pölönen, I.; Hakala, T.; Litkey, P.; Mäkynen, J.; Pesonen, L. Processing and assessment of spectrometric, stereoscopic imagery collected using a lightweight UAV spectral camera for precision agriculture. Remote Sens. 2013, 5, 5006–5039. [Google Scholar] [CrossRef]
- Suomalainen, J.; Anders, N.; Iqbal, S.; Roerink, G.; Franke, J.; Wenting, P.; Hünniger, D.; Bartholomeus, H.; Becker, R.; Kooistra, L. A lightweight hyperspectral mapping system and photogrammetric processing chain for unmanned aerial vehicles. Remote Sens. 2014, 6, 11013–11030. [Google Scholar] [CrossRef]
- Oliveira, R.A.; Khoramshahi, E.; Suomalainen, J.; Hakala, T.; Viljanen, N.; Honkavaara, E. Real-time and post-processed georeferencing for hyperpspectral drone remote sensing. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 42, 789–795. [Google Scholar] [CrossRef]
- Hu, Z.; Bai, Z.; Yang, Y.; Zheng, Z.; Bian, K.; Song, L. UAV aided aerial-ground IoT for air quality sensing in smart city: Architecture, technologies, and implementation. IEEE Netw. 2019, 33, 14–22. [Google Scholar] [CrossRef]
- Boccardo, P.; Chiabrando, F.; Dutto, F.; Tonolo, F.G.; Lingua, A. UAV deployment exercise for mapping purposes: Evaluation of emergency response applications. Sensors 2015, 15, 15717–15737. [Google Scholar]
- Casbeer, D.W.; Beard, R.W.; McLain, T.W.; Li, S.-M.; Mehra, R.K. Forest fire monitoring with multiple small UAVs. In Proceedings of the 2005, American Control Conference, Portland, OR, USA, 8–10 June 2005; pp. 3530–3535. [Google Scholar]
- Zhou, G. Near real-time orthorectification and mosaic of small UAV video flow for time-critical event response. IEEE Trans. Geosci. Remote Sens. 2009, 47, 739–747. [Google Scholar] [CrossRef]
- Puri, A.; Valavanis, K.; Kontitsis, M. Statistical profile generation for traffic monitoring using real-time UAV based video data. In Proceedings of the 2007 Mediterranean Conference on Control & Automation, Athens, Greece, 27–29 June 2007; pp. 1–6. [Google Scholar]
- Aguilar, W.G.; Luna, M.A.; Moya, J.F.; Abad, V.; Parra, H.; Ruiz, H. Pedestrian detection for UAVs using cascade classifiers with meanshift. In Proceedings of the 2017 IEEE 11th International Conference on Semantic Computing (ICSC), San Diego, CA, USA, 30 January 2016–1 Feburary 2017; pp. 509–514. [Google Scholar]
- Li, X.; Chuah, M.C.; Bhattacharya, S. Uav assisted smart parking solution. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; pp. 1006–1013. [Google Scholar]
- Ballari, D.; Orellana, D.; Acosta, E.; Espinoza, A.; Morocho, V. UAV monitoring for environmental management in Galapagos Islands. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41. [Google Scholar] [CrossRef]
- Giyenko, A.; Cho, Y.I. Intelligent UAV in smart cities using IoT. In Proceedings of the 2016 16th International Conference on Control, Automation and Systems (ICCAS), Gyeongju, Korea, 16–19 October 2016; pp. 207–210. [Google Scholar]
- Bendig, J.; Bolten, A.; Bennertz, S.; Broscheit, J.; Eichfuss, S.; Bareth, G. Estimating biomass of barley using crop surface models (CSMs) derived from UAV-based RGB imaging. Remote Sens. 2014, 6, 10395–10412. [Google Scholar] [CrossRef]
- Feng, Q.; Liu, J.; Gong, J. UAV remote sensing for urban vegetation mapping using random forest and texture analysis. Remote Sens. 2015, 7, 1074–1094. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Watson, C.; Turner, D. Development of a UAV-LiDAR system with application to forest inventory. Remote Sens. 2012, 4, 1519–1543. [Google Scholar] [CrossRef]
- Dash, J.P.; Watt, M.S.; Pearse, G.D.; Heaphy, M.; Dungey, H.S. Assessing very high resolution UAV imagery for monitoring forest health during a simulated disease outbreak. ISPRS J. Photogramm. Remote Sens. 2017, 131, 1–14. [Google Scholar] [CrossRef]
- Kang, B.-J.; Cho, H.-C. System of Agricultural Land Monitoring Using UAV. J. Korea Acad. Ind. Coop. Soc. 2016, 17, 372–378. [Google Scholar]
- Lottes, P.; Khanna, R.; Pfeifer, J.; Siegwart, R.; Stachniss, C. UAV-based crop and weed classification for smart farming. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 3024–3031. [Google Scholar]
- Ribeiro, L.R.; Oliveira, N.M.F. UAV autopilot controllers test platform using Matlab/Simulink and X-Plane. In Proceedings of the 2010 IEEE Frontiers in Education Conference (FIE), Arlington, VA, USA, 27–30 October 2010; p. S2H-1. [Google Scholar]
- Caballero, F.L.; Merino, L.; Ferruz, J.; Ollero, A. Vision-based odometry and SLAM for medium and high altitude flying UAVs. J. Intell. Robot. Syst. 2009, 54, 137–161. [Google Scholar] [CrossRef]
- Li, B.; Fei, Z.; Zhang, Y. UAV communications for 5G and beyond: Recent advances and future trends. IEEE Internet Things J. 2018, 6, 2241–2263. [Google Scholar] [CrossRef]
- Luo, C.; Nightingale, J.; Asemota, E.; Grecos, C. A UAV-cloud system for disaster sensing applications. In Proceedings of the 2015 IEEE 81st Vehicular Technology Conference (VTC Spring), Glasgow, Scotland, 11–14 May 2015; pp. 1–5. [Google Scholar]
- Mahmoud, S.Y.M.; Mohamed, N. Toward a cloud platform for UAV resources and services. In Proceedings of the 2015 IEEE Fourth Symposium on Network Cloud Computing and Applications (NCCA), Munich, Germany, 11–12 June 2015; pp. 23–30. [Google Scholar]
- Gruen, A.; Huang, T.S. Calibration and Orientation of Cameras in Computer Vision; Springer Science & Business Media: Heidelberg/Berlin, Germany, 2013; Volume 34. [Google Scholar]
- Hartley, R.I. In defence of the 8-point algorithm. In Proceedings of the IEEE International Conference on Computer Vision, Cambridge, MA, USA, 20–23 June 1995; pp. 1064–1070. [Google Scholar]
- Nistér, D. An efficient solution to the five-point relative pose problem. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 756–770. [Google Scholar] [CrossRef]
- Cramer, M.; Stallmann, D.; Haala, N. Direct Georeferencing Using GPS/Inertial Exterior Orientations for Photogrammetric Applications. Int. Arch. Photogramm. Remote Sens. 2000, 33, 198–205. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Ke, Y.; Sukthankar, R. PCA-SIFT: A more distinctive representation for local image descriptors. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 27 June–2 July 2004; Volume 2, p. II-II. [Google Scholar]
- Wu, C. A GPU Implementation of Scale Invariant Feature Transform (SIFT). 2007. Available online: https://github.com/pitzer/SiftGPU (accessed on 28 September 2020).
- Morel, J.-M.; Yu, G. ASIFT: A new framework for fully affine invariant image comparison. SIAM J. Imaging Sci. 2009, 2, 438–469. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; van Gool, L. Surf: Speeded up robust features. In Proceedings of the European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; pp. 404–417. [Google Scholar]
- Rosten, E.; Drummond, T. Machine learning for high-speed corner detection. In Proceedings of the European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; pp. 430–443. [Google Scholar]
- Calonder, M.; Lepetit, V.; Strecha, C.; Fua, P. Brief: Binary robust independent elementary features. In Proceedings of the European Conference on Computer Vision, Heraklion, Greece, 5–11 September 2010; pp. 778–792. [Google Scholar]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- Juan, L.; Gwon, L. A comparison of sift, pca-sift and surf. Int. J. Signal Process. Image Process. Pattern Recognit. 2007, 8, 169–176. [Google Scholar]
- Karami, E.; Prasad, S.; Shehata, M. Image Matching Using SIFT, SURF, BRIEF and ORB: Performance Comparison for Distorted Images. Available online: https://arxiv.org/ftp/arxiv/papers/1710/1710.02726.pdf (accessed on 28 September 2020).
- Wu, Y.; Tang, F.; Li, H. Image-based camera localization: An overview. Vis. Comput. Ind. Biomed. Art 2018, 1, 1–13. [Google Scholar] [CrossRef]
- Williams, B.; Cummins, M.; Neira, J.; Newman, P.; Reid, I.; Tardós, J. An image-to-map loop closing method for monocular SLAM. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 2053–2059. [Google Scholar]
- Forstner, W.; Steffen, R. On visual real time mapping for Unmanned Aerial Vehicles. In Proceedings of the 21st Congress of the International Society for Photogrammetry and Remote Sensing (ISPRS), Beijing, China, 3–11 July 2008. [Google Scholar]
- Gálvez-López, D.; Tardos, J.D. Bags of binary words for fast place recognition in image sequences. IEEE Trans. Robot. 2012, 28, 1188–1197. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM: A versatile and accurate monocular SLAM system. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Fink, G.; Franke, M.; Lynch, A.F.; Röbenack, K.; Godbolt, B. Visual inertial SLAM: Application to unmanned aerial vehicles. IFAC-Pap. 2017, 50, 1965–1970. [Google Scholar] [CrossRef]
- Jiang, S.; Jiang, W. Efficient sfm for oblique uav images: From match pair selection to geometrical verification. Remote Sens. 2018, 10, 1246. [Google Scholar] [CrossRef]
- Chen, X.; Hu, W.; Zhang, L.; Shi, Z.; Li, M. Integration of low-cost gnss and monocular cameras for simultaneous localization and mapping. Sensors 2018, 18, 2193. [Google Scholar] [CrossRef] [PubMed]
- Mikhail, E.M.; Bethel, J.S.; McGlone, J.C. Introduction to Modern Photogrammetry; John Wiley & Sons, Inc.: New York, NY, USA, 2001; Volume 19. [Google Scholar]
- Caccavale, F.; Natale, C.; Siciliano, B.; Villani, L. Six-dof impedance control based on angle/axis representations. IEEE Trans. Robot. Autom. 1999, 15, 289–300. [Google Scholar] [CrossRef]
- Cheng, P.L. A spherical rotation coordinate system for the description of three-dimensional joint rotations. Ann. Biomed. Eng. 2000, 28, 1381–1392. [Google Scholar] [CrossRef]
- Harwin, S.; Lucieer, A. Assessing the accuracy of georeferenced point clouds produced via multi-view stereopsis from unmanned aerial vehicle (UAV) imagery. Remote Sens. 2012, 4, 1573–1599. [Google Scholar] [CrossRef]
- National Land Survey of Finland, “Finnref GNSS RINEX Service”. Available online: https://www.maanmittauslaitos.fi/en/maps-and-spatial-data/positioning-services/rinex-palvelu (accessed on 28 September 2020).
- Takasu, T. RTKlib: An Open-source Program Package for GNSS Positioning. Tech. Rep. 2013. Available online: http://www.rtklib.com/ (accessed on 28 September 2020).
- Muja, M.; Lowe, D.G. Fast approximate nearest neighbors with automatic algorithm configuration. VISAPP 1 2009, 2, 331–340. [Google Scholar]
- Engel, J.; Schöps, T.; Cremers, D. LSD-SLAM: Large-scale direct monocular SLAM. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 834–849. [Google Scholar]






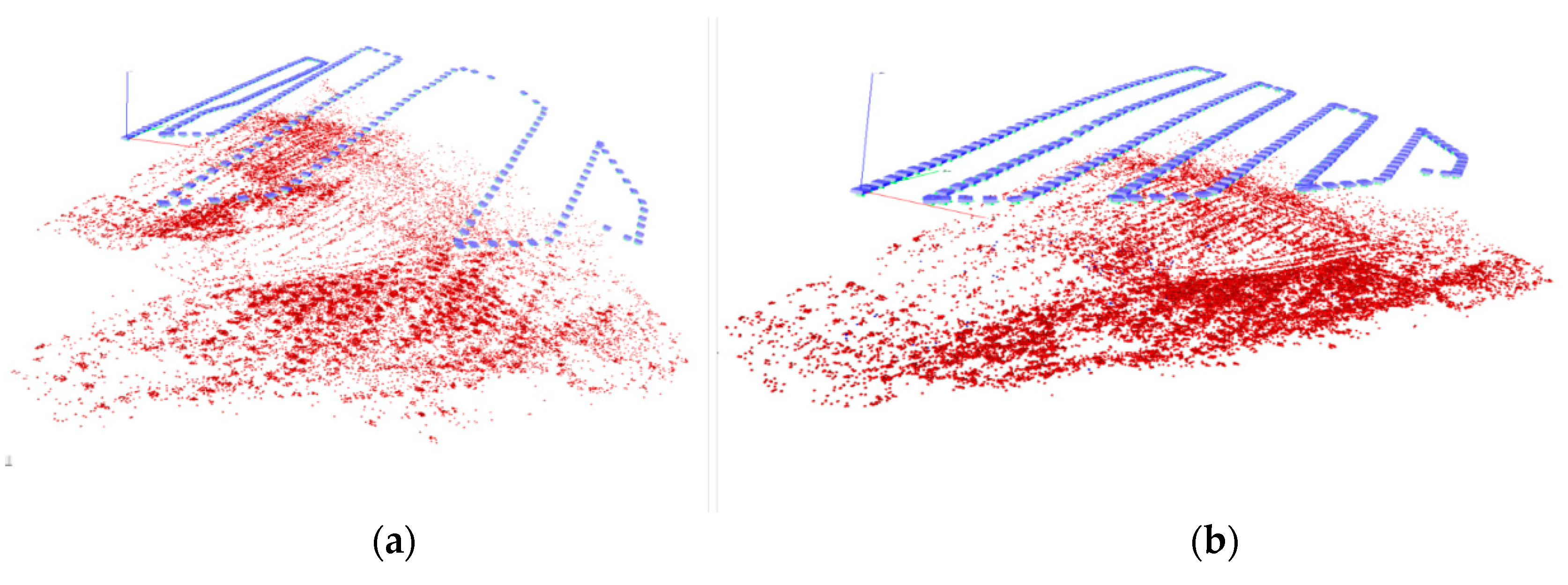
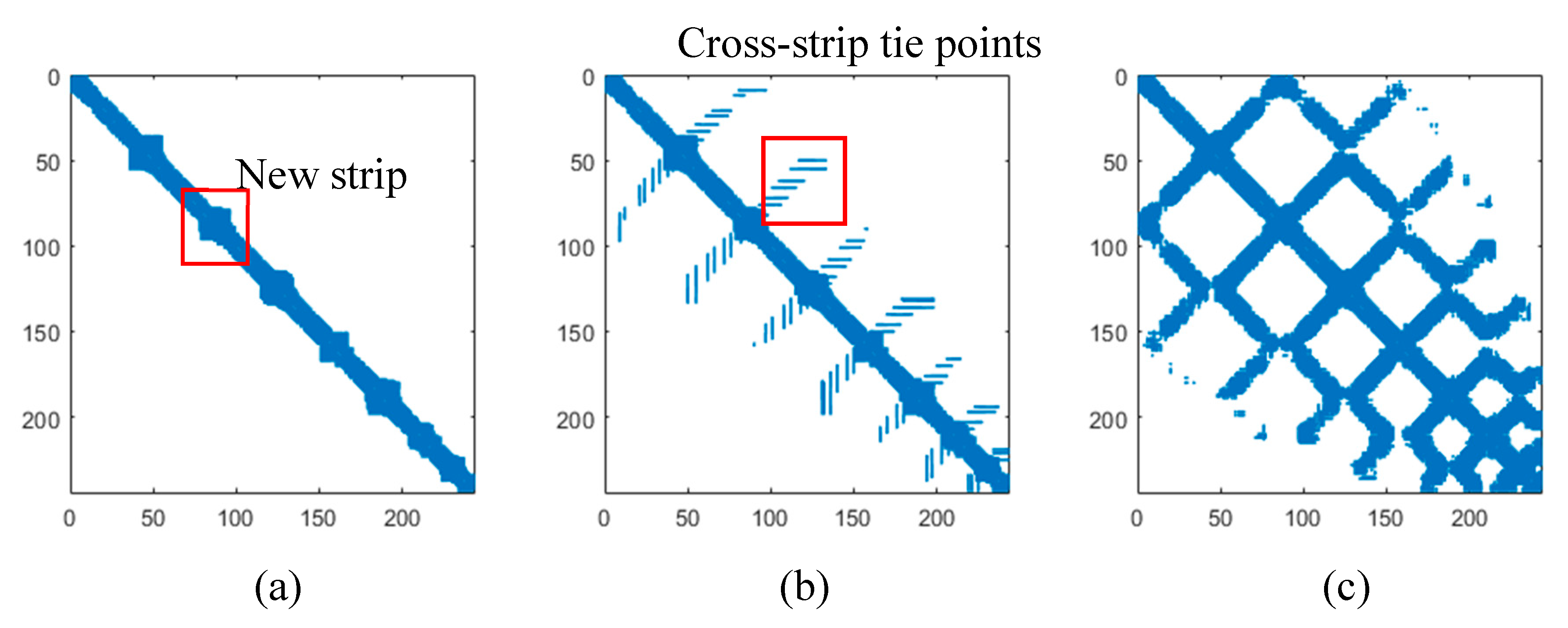

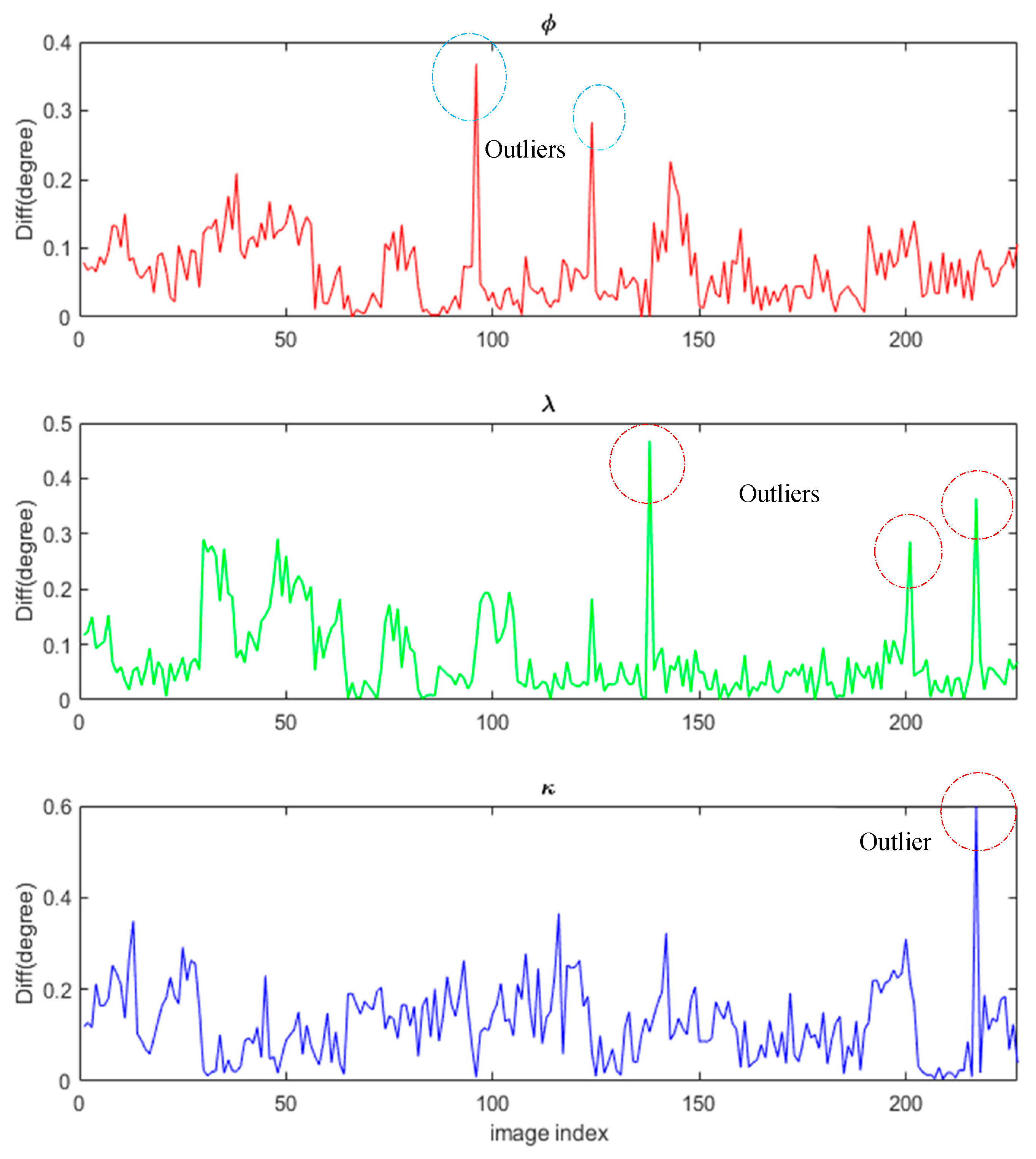
| Name | Dataset | Image Size (MPix) | Key-Point Time (s) | Matching Time (s) | Overall Time (s) | Memory (MB) | Number of Key Points | Number of Inliers | Inlier % |
|---|---|---|---|---|---|---|---|---|---|
| SIFT | DS3 | 35 | 16.1 | 39.0 | 55.1 | 9700 | 175k | 37k | 21.5% |
| DS1 | 24 | 11 | 49 | 60 | 9500 | 215k | 28k | 13.3% | |
| SURF | DS3 | 35 | 11 | 45 | 56 | 440 | 204k | 39k | 19.4% |
| DS1 | 24 | 12 | 53 | 65 | 440 | 221k | 34k | 15.6% | |
| DS3 | 35 | 0.9 | 1.2 | 2.1 | 380 | 10k | 4.1k | 41.1% | |
| ORB | DS1 | 24 | 1.2 | 200.7 | 201.9 | 390 | 200k | 55k | 27.8% |
| DS1 | 24 | 1.0 | 0.9 | 1.9 | 380 | 10k | 3.7k | 37.8% | |
| DS3 | 35 | 1.4 | 212 | 213.4 | 391 | 200k | 83k | 41.7% | |
| * Multilevel match with SIFT kernel | |||||||||
| DS1 | 24 | 0.031 | 0.144 | 6 | 232 | 4k | 3k | 92% | |
| Point Name | No. Rays | Residual | Unit | Residual Vector | Unit |
|---|---|---|---|---|---|
| 25 | 11 | 3.1 | cm | (−1.2, −2.0, −2.0) | cm |
| 27 | 10 | 4.4 | cm | (−2.0, 2.6, −3.0) | cm |
| 29 | 10 | 0.9 | cm | (0.3, 0.6, −0.6) | cm |
| 31 | 11 | 0.8 | cm | (−0.2, 0.2, −0.8) | cm |
| 32 | 16 | 1.8 | cm | (−1.0, 0.1, −1.5) | cm |
| 33 | 12 | 1.9 | cm | (−0.8, −0.5, 1.6) | cm |
| 34 | 13 | 4.0 | cm | (0.1, 0.4, −4.0) | cm |
| 36 | 10 | 1.9 | cm | (1.0, −1.1, −1.2) | cm |
| 37 | 12 | 1.6 | cm | (1.0, 0.4, −1.2) | cm |
| 38 | 11 | 0.6 | cm | (−0.2, 0.2, 0.5) | cm |
| 40 | 10 | 3.6 | cm | (2.2, −1.1, −2.6) | cm |
| 41 | 11 | 2.2 | cm | (1.5, 0.9, −1.3) | cm |
| Residual mean: 2.24 (cm), RMSE: 1.26 (cm) | |||||
| Point Name | No. Rays | Residual | Unit | Residual Vector | Unit |
|---|---|---|---|---|---|
| 9 | 9 | 0.1 | cm | (−0.1, −0.1, −0.0) | cm |
| 30 | 14 | 0.9 | cm | (−0.3, −0.1, −0.9) | cm |
| 35 | 11 | 2.4 | cm | (0.5, −0.9, −2.2) | cm |
| 39 | 10 | 1.8 | cm | (0.6, −0.4, −1.7) | Cm |
| Residual mean: 1.32 (cm), RMSE: 0.99 (cm) | |||||
| Point Name | No. Rays | Residual | Unit | Res. Vector | Unit |
|---|---|---|---|---|---|
| 25 | 10 | 2.6 | cm | (−0.8, −2.4,−0.6) | cm |
| 27 | 17 | 1.6 | cm | (−0.5, 1.3, −0.7) | cm |
| 29 | 10 | 0.6 | cm | (0.4, 0.4, −0.1) | cm |
| 31 | 11 | 0.6 | cm | (−0.3, 0.3, −0.4) | cm |
| 32 | 10 | 1.2 | cm | (−1.1, 0.1, −0.5) | cm |
| 33 | 11 | 1.7 | cm | (−0.9, −0.6, −1.2) | cm |
| 34 | 10 | 1.6 | cm | (−0.6, 0.3, −1.5) | cm |
| 36 | 10 | 1.4 | cm | (0.0, −0.4, 1.3) | cm |
| 37 | 10 | 1.0 | cm | (0.2, 0.2, 1.0) | cm |
| 38 | 10 | 1.1 | cm | (0.3, 0.6, −0.8) | cm |
| 40 | 10 | 0.5 | cm | (0.4, −0.3, 0.1) | cm |
| 41 | 10 | 2.9 | cm | (1.8, 1.0, −2.1) | cm |
| Residual mean: 1.4 (cm),RMSE: 0.76 (cm) | |||||
| Point Name | No. Rays | Residual | Unit | Residual Vector | Unit |
|---|---|---|---|---|---|
| 9 | 10 | 1.0 | cm | (0.2, −0.4, 0.9) | cm |
| 30 | 10 | 0.5 | cm | (−0.2, 0.1, 0.4) | cm |
| 35 | 10 | 1.6 | cm | (0.2, −0.5, −1.5) | cm |
| 39 | 10 | 0.5 | cm | (−0.3, −0.3, −0.3) | cm |
| Sample mean: 0.9 (cm), RMSE: 0.52 (cm) | |||||
| No | Param. Name | Unit | Front (DS2) | Back (DS3) | ||
|---|---|---|---|---|---|---|
| Value | Std. | Value | Std. | |||
| 1 | Principal Distance | px. | 8006.8 | 0.20 | 7995.16 | 0.39 |
| 2 | Principal Distance | mm. | 36.24 | 9e−4 | 36.18 | 9e−4 |
| 3 | Principal Point x dir. | px. | 4002.7 | 0.11 | 3986.79 | 0.13 |
| 4 | Principal Point y dir. | px. | 2623.4 | 0.14 | 2604.41 | 0.21 |
| 5 | K1 | N/A | −0.0395 | 7e−5 | −0.04583 | 7e−5 |
| 6 | K2 | N/A | 0.169570 | 4e−4 | 0.185436 | 4e−4 |
| 7 | K3 | N/A | 0.137138 | 9e−4 | 0.08950 | 9e−4 |
| 8 | P1 | N/A | 0.00104 | 4e−5 | −5e−4 | 6e−6 |
| 9 | P2 | N/A | −4e-4 | 3e−6 | −0.0017 | 3e−6 |
| 10 | Scale factor | N/A | −1e-4 | 4e−5 | 1e−4 | 5e−6 |
| 11 | Shear factor | N/A | 7e-6 | 2e−6 | −1e−4 | 2e−6 |
| 12 | Pixel size | 4.526 | N/A | 4.526 | N/A | |
| 13 | Lever-arm ( | ◦ | −105.12 | 0.01 | −75.28 | 0.03 |
| 14 | Lever-arm ( | ◦ | −1.76 | 2e−3 | −1.39 | 0.01 |
| 15 | Lever-arm ( | ◦ | −1.74 | 0.01 | 179.10 | 0.04 |
| 16 | Lever-arm ( | cm | −0.07 | 0.04 | 3.84 | 0.09 |
| 17 | Lever-arm ( | cm | −3.73 | 0.07 | −14.55 | 0.20 |
| 18 | Lever-arm ( | cm | −15.79 | 0.04 | −9.59 | 0.09 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khoramshahi, E.; Oliveira, R.A.; Koivumäki, N.; Honkavaara, E. An Image-Based Real-Time Georeferencing Scheme for a UAV Based on a New Angular Parametrization. Remote Sens. 2020, 12, 3185. https://doi.org/10.3390/rs12193185
Khoramshahi E, Oliveira RA, Koivumäki N, Honkavaara E. An Image-Based Real-Time Georeferencing Scheme for a UAV Based on a New Angular Parametrization. Remote Sensing. 2020; 12(19):3185. https://doi.org/10.3390/rs12193185
Chicago/Turabian StyleKhoramshahi, Ehsan, Raquel A. Oliveira, Niko Koivumäki, and Eija Honkavaara. 2020. "An Image-Based Real-Time Georeferencing Scheme for a UAV Based on a New Angular Parametrization" Remote Sensing 12, no. 19: 3185. https://doi.org/10.3390/rs12193185
APA StyleKhoramshahi, E., Oliveira, R. A., Koivumäki, N., & Honkavaara, E. (2020). An Image-Based Real-Time Georeferencing Scheme for a UAV Based on a New Angular Parametrization. Remote Sensing, 12(19), 3185. https://doi.org/10.3390/rs12193185






