Ground Moving Target Tracking and Refocusing Using Shadow in Video-SAR
Abstract
1. Introduction
- (1)
- The characteristics of the ground moving target’s shadow are analyzed in detail. Not only the size of the target, the influence of wavelength, angle of incidence, synthetic aperture time for the shadow in the SAR video are also discussed in this paper, which is significant for future SAR system and algorithm design.
- (2)
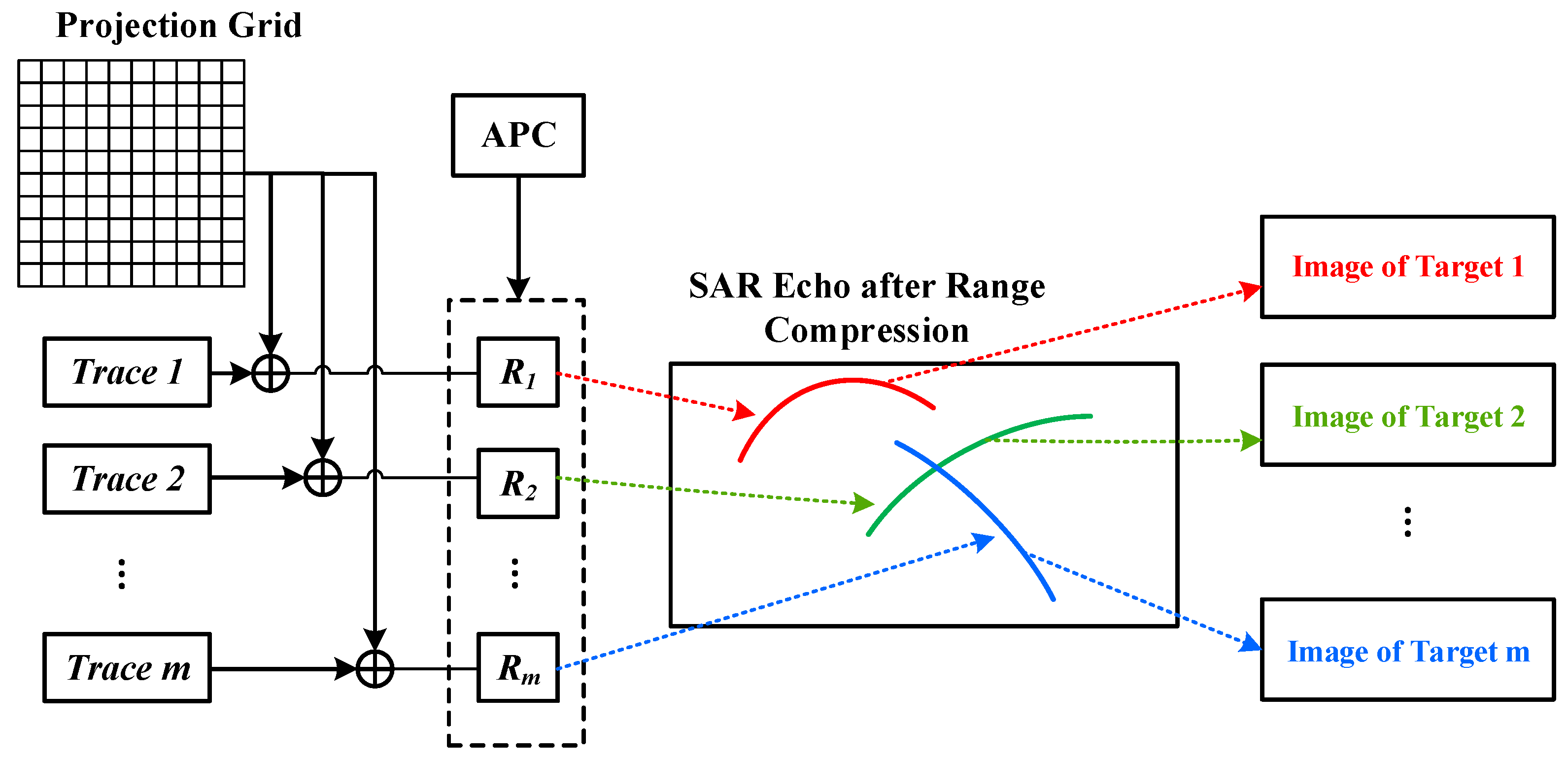
- To obtain SAR videos quickly and efficiently, a video-SAR imaging method v-BP is designed. With this method, repeated processing of multiplexed data segments can be avoided to improve the efficiency of multi-frame imaging and achieve real-time high frame rate monitoring. Furthermore, due to its fixed projection grid, the imaging results are registered automatically, which is convenient for estimating the position and velocity of moving targets.
- (3)
- The m-BP algorithm is proposed to refocus the ground moving target, and a deep-learning-based tracking network SiamFc is introduced to reconstruct the trajectory of the target. Our m-BP can refocus the ground moving target with rich geometrical features by using the trajectory obtained by SiamFc.
2. Signal Model and Imaging Analysis of the Ground Moving Target
2.1. Signal Model
2.2. Imaging Analysis
- (a)
- Range compression: range compression is implemented via pulse compression technique on the received SAR echoes at different times to achieve aggregation of scattering point energy along the range direction.
- (b)
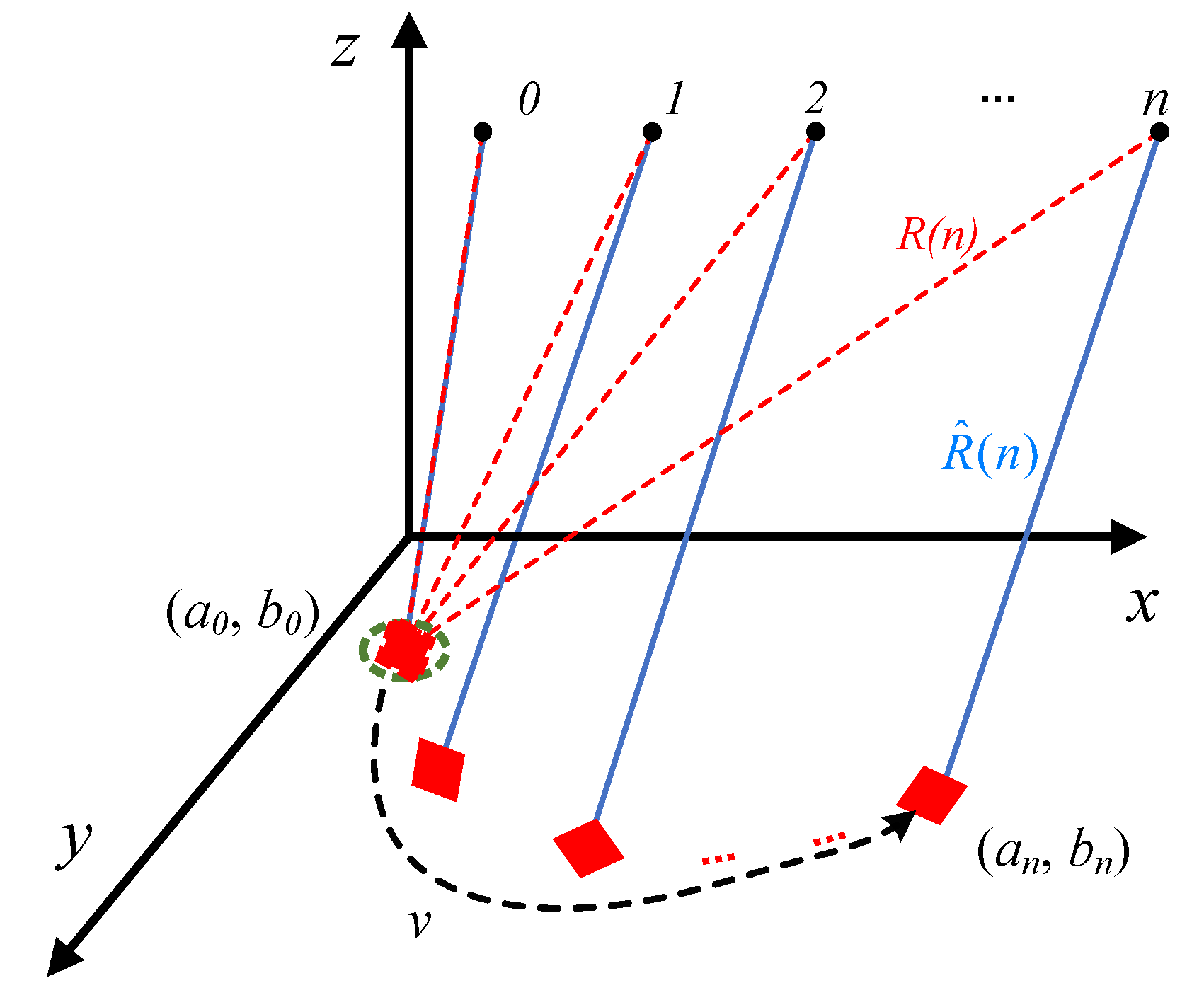
- Calculating echo delay: calculating echo delay from scattering point to SAR at different times:where isis the position of APC at time n, is the position of and w is the projected height. The projection coordinate system is usually a Cartesian coordinate system and w is 0.
- (c)
- Data interpolation/resampling in range: since the range compressed SAR data obtained in (a) is discrete and the echo delay calculated in (b) is continuous, to acquire echo at time , interpolation is essential to the discrete SAR data after range compression and resampling is necessary at time .
- (d)
- Coherent accumulation: compensate the Doppler phase generated by the scattering point at different times and add the compensated data at different times to obtain the scattering coefficient of . The signal with the compensated Doppler phase can be calculated by the following formula:where is the slant range of stationary target.
2.2.1. Defocusing in Azimuth
2.2.2. Offset in Azimuth
3. Shadow Characteristics of Moving Target
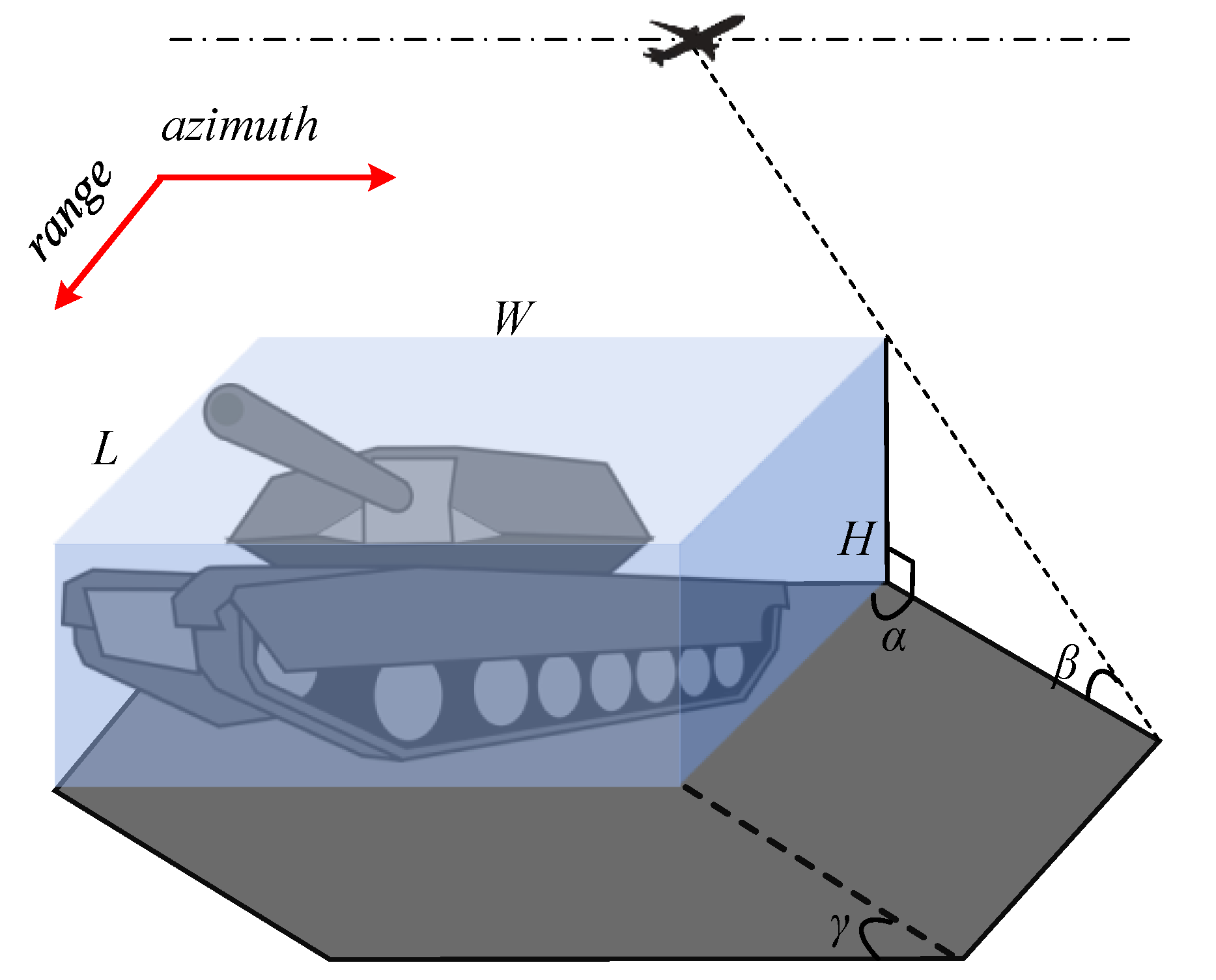
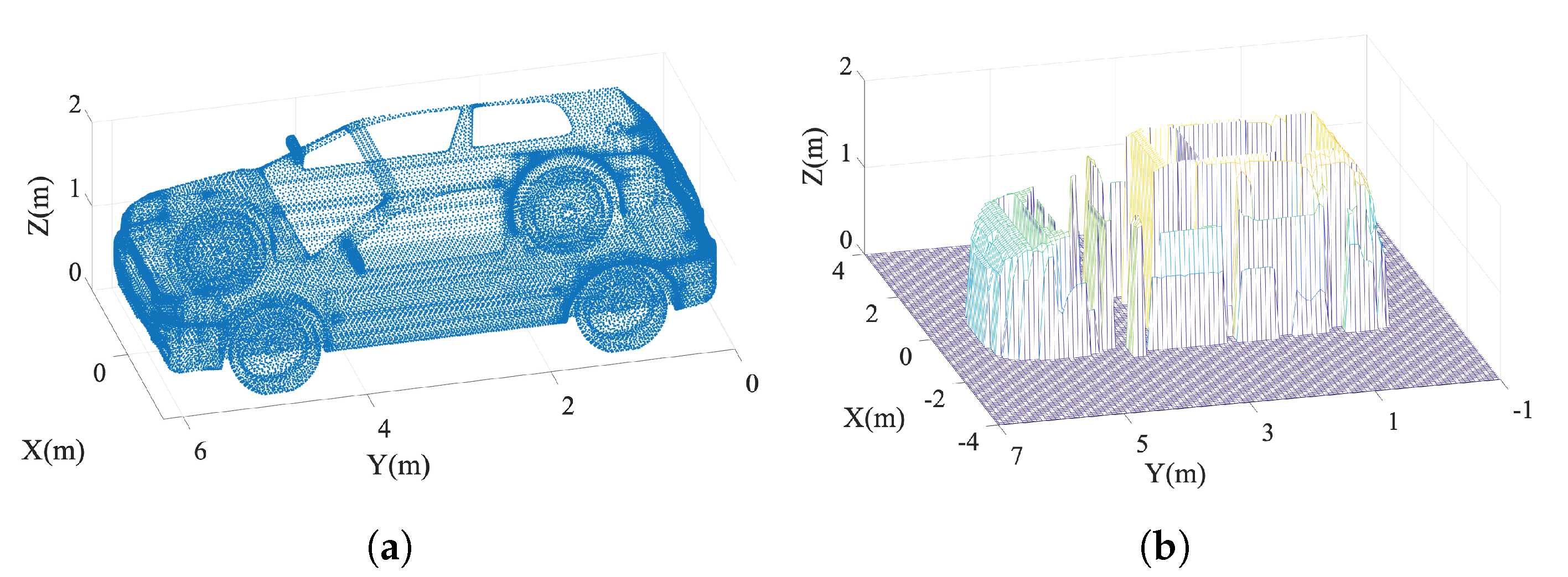
3.1. Size of Shadow
3.2. Effect of Shadow on Echo
3.3. The Degradation of Shadow
3.3.1. Blur Due to Small Aperture
3.3.2. Fading Due to Large Aperture
4. Methodology
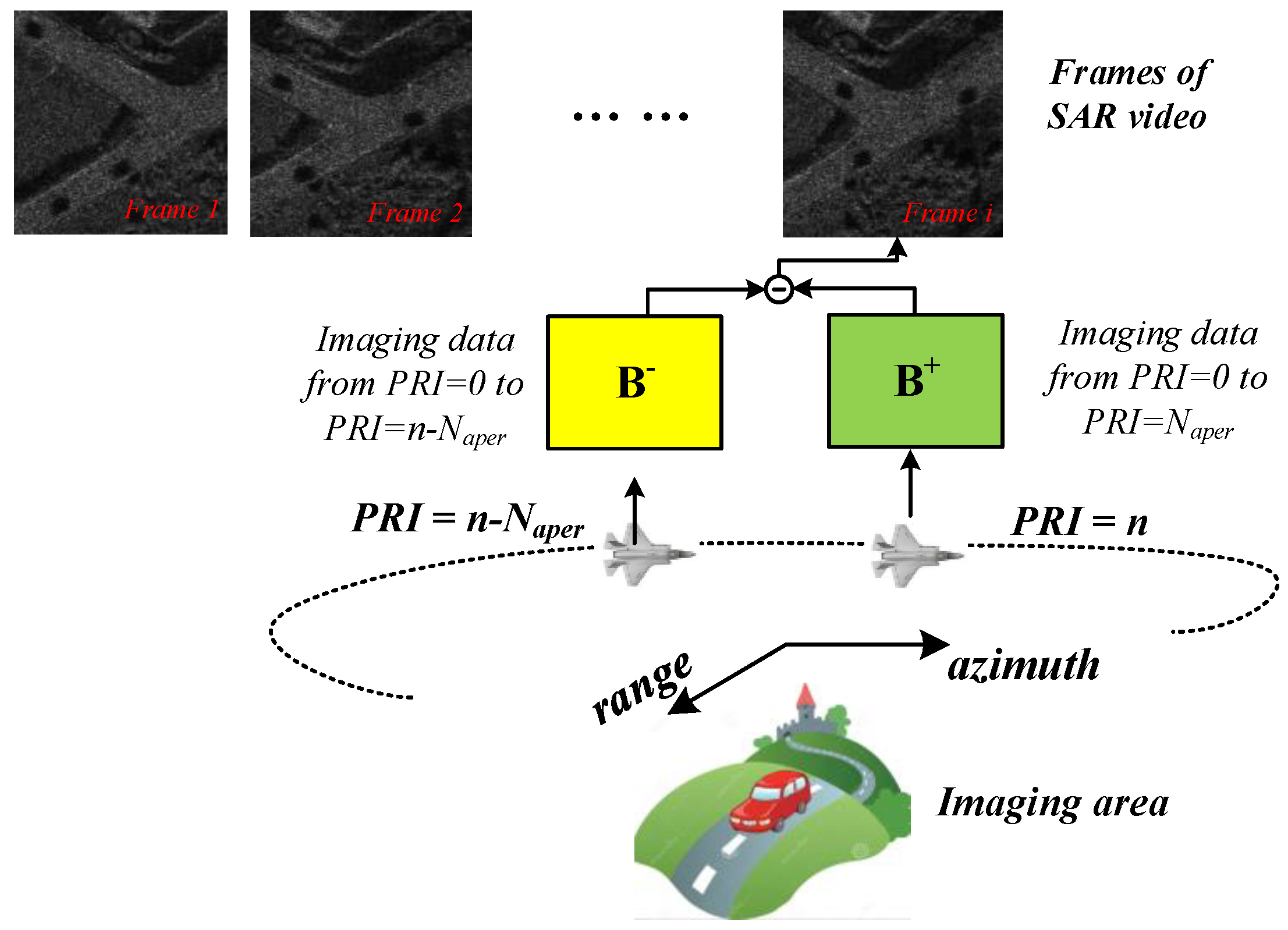
4.1. Video-Sar Back-Projection
| Algorithm 1 Video-SAR back-projection algorithm. |
| Ensure: ; ; ; for n in all PRIs do ; if then if then ; ; ; end if if then ; ; ; end if end if end if |
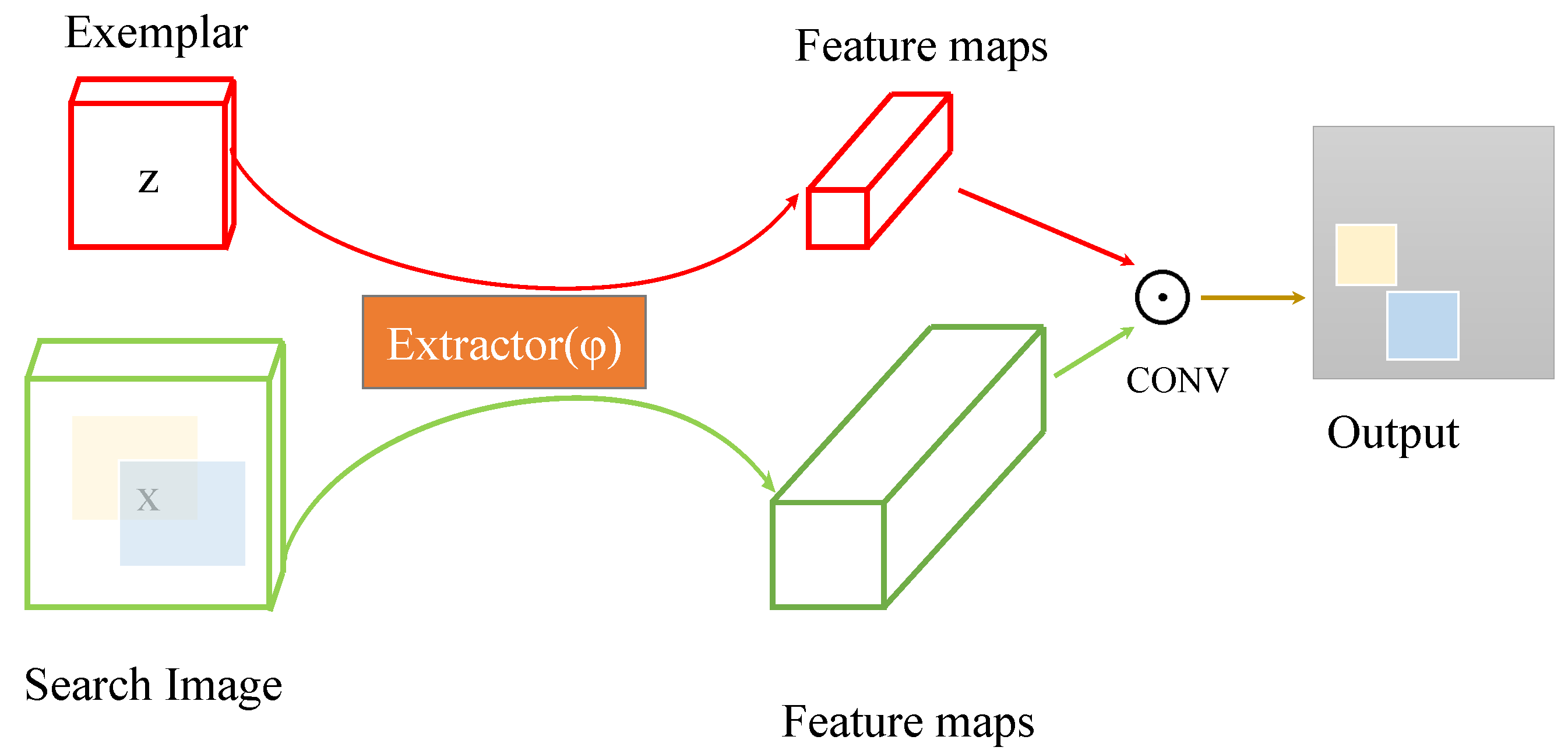
4.2. Tracking Via Shadow
4.3. Moving Target Back-Projection
5. Experiment and Analysis
5.1. Shadow Feature
5.1.1. Effect of System Parameters on Shadow
5.1.2. Effect of Target Parameters on Shadow
5.2. Shadow Tracking
5.3. Moving Target Refocusing
5.3.1. Refocusing Analysis of Moving Target in Precise Compensation
5.3.2. Refocusing of Moving Target Based on Tracking Results
5.3.3. Effect of Motion Parameters on Refocusing
6. Discussion
| Algorithm 2 Moving Target Back-projection (m-BP). |
|
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, B.; Hong, W.; Wu, Y. Sparse microwave imaging: Principles and applications. Sci. China Inf. Sci. 2012, 55, 1722–1754. [Google Scholar] [CrossRef]
- Chen, F.; Lasaponara, R.; Masini, N. An overview of satellite synthetic aperture radar remote sensing in archaeology: From site detection to monitoring. J. Cult. Herit. 2017, 23, 5–11. [Google Scholar] [CrossRef]
- Jing, W.; Xing, M.; Qiu, C.W.; Bao, Z.; Yeo, T.S. Unambiguous reconstruction and high-resolution imaging for multiple-channel SAR and airborne experiment results. IEEE Geosci. Remote Sens. Lett. 2008, 6, 102–106. [Google Scholar] [CrossRef]
- Ji, P.; Xing, S.; Dai, D.; Pang, B. Deceptive Targets Generation Simulation Against Multichannel SAR. Electronics 2020, 9, 597. [Google Scholar] [CrossRef]
- Kim, S.; Yu, J.; Jeon, S.Y.; Dewantari, A.; Ka, M.H. Signal processing for a multiple-input, multiple-output (MIMO) video synthetic aperture radar (SAR) with beat frequency division frequency-modulated continuous wave (FMCW). Remote Sens. 2017, 9, 491. [Google Scholar] [CrossRef]
- Li, L.; Zhang, X.; Pu, L.; Pu, L.; Tian, B.; Zhou, L.; Wei, S. 3D SAR Image Background Separation Based on Seeded Region Growing. IEEE Access 2019, 7, 179842–179863. [Google Scholar] [CrossRef]
- Garcia-Fernandez, M.; Alvarez-Lopez, Y.; Las Heras, F. Autonomous airborne 3d sar imaging system for subsurface sensing: Uwb-gpr on board a uav for landmine and ied detection. Remote Sens. 2019, 11, 2357. [Google Scholar] [CrossRef]
- Liu, X.W.; Zhang, Q.; Yin, Y.F.; Chen, Y.C.; Zhu, F. Three-dimensional ISAR image reconstruction technique based on radar network. Int. J. Remote Sens. 2020, 41, 5399–5428. [Google Scholar] [CrossRef]
- Tian, B.; Zhang, X.; Wei, S.; Ming, J.; Shi, J.; Li, L.; Tang, X. A Fast Sparse Recovery Algorithm via Resolution Approximation for LASAR 3D Imaging. IEEE Access 2019, 7, 178710–178725. [Google Scholar] [CrossRef]
- Pu, W.; Wang, X.; Wu, J.; Huang, Y.; Yang, J. Video SAR Imaging Based on Low-Rank Tensor Recovery. IEEE Trans. Neural Networks Learn. Syst. 2020. [Google Scholar] [CrossRef]
- Esposito, C.; Natale, A.; Palmese, G.; Berardino, P.; Lanari, R.; Perna, S. On the Capabilities of the Italian Airborne FMCW AXIS InSAR System. Remote Sens. 2020, 12, 539. [Google Scholar] [CrossRef]
- Filippo, B. COSMO-SkyMed staring spotlight SAR data for micro-motion and inclination angle estimation of ships by pixel tracking and convex optimization. Remote Sens. 2019, 11, 766. [Google Scholar] [CrossRef]
- Bao, J.; Zhang, X.; Tang, X.; Wei, S.; Shi, J. Moving Target Detection and Motion Parameter Estimation VIA Dual-Beam Interferometric SAR. In Proceedings of the IGARSS 2019-2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 1350–1353. [Google Scholar]
- Li, J.; Huang, Y.; Liao, G.; Xu, J. Moving Target Detection via Efficient ATI-GoDec Approach for Multichannel SAR System. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1320–1324. [Google Scholar] [CrossRef]
- Bollian, T.; Osmanoglu, B.; Rincon, R.; Lee, S.K.; Fatoyinbo, T. Adaptive antenna pattern notching of interference in synthetic aperture radar data using digital beamforming. Remote Sens. 2019, 11, 1346. [Google Scholar] [CrossRef]
- Zhou, L.; Yu, H.; Lan, Y. Deep Convolutional Neural Network-Based Robust Phase Gradient Estimation for Two-Dimensional Phase Unwrapping Using SAR Interferograms. IEEE Trans. Geosci. Remote Sens. 2020. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, S.; Li, T.; Chen, Q.; Zhang, X.; Li, S. Refined two-stage programming approach of phase unwrapping for multi-baseline SAR interferograms using the unscented Kalman filter. Remote Sens. 2019, 11, 199. [Google Scholar] [CrossRef]
- Perry, R.; Dipietro, R.; Fante, R. SAR imaging of moving targets. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 188–200. [Google Scholar] [CrossRef]
- Zhu, D.; Li, Y.; Zhu, Z. A keystone transform without interpolation for SAR ground moving-target imaging. J. Appl. Remote Sens. 2007, 4, 18–22. [Google Scholar] [CrossRef]
- Wells, L.; Sorensen, K.; Doerry, A.; Remund, B. Developments in SAR and IFSAR systems and technologies at Sandia National Laboratories. In Proceedings of the 2003 IEEE Aerospace Conference Proceedings (Cat. No.03TH8652), Big Sky, MT, USA, 8–15 March 2003; Volume 2, pp. 2_1085–2_1095. [Google Scholar]
- Raynal, A.M.; Bickel, D.L.; Doerry, A.W. Stationary and moving target shadow characteristics in synthetic aperture radar. Radar Sens. Technol. XVIII 2014, 9077, 90771B. [Google Scholar]
- Miller, J.; Bishop, E.; Doerry, A.; Raynal, A.M. Impact of ground mover motion and windowing on stationary and moving shadows in synthetic aperture radar imagery. In Proceedings of the SPIE 2015 Defense & Security Symposium, Algorithms for Synthetic Aperture Radar Imagery XXII, Baltimore, MD, USA, 23 April 2015; Volume 9475. [Google Scholar]
- Xu, H.; Yang, Z.; Tian, M.; Sun, Y.; Liao, G. An extended moving target detection approach for high-resolution multichannel SAR-GMTI systems based on enhanced shadow-aided decision. IEEE Trans. Geosci. Remote Sens. 2017, 56, 715–729. [Google Scholar] [CrossRef]
- Zhang, Y.; Mao, X.; Yan, H.; Zhu, D.; Hu, X. A novel approach to moving targets shadow detection in VideoSAR imagery sequence. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 606–609. [Google Scholar]
- Liu, Z.; An, D.; Huang, X. Moving Target Shadow Detection and Global Background Reconstruction for VideoSAR Based on Single-Frame Imagery. IEEE Access 2019, 7, 42418–42425. [Google Scholar] [CrossRef]
- Wang, C.; Shi, J.; Yang, X.; Zhou, Y.; Wei, S.; Li, L.; Zhang, X. Geospatial Object Detection via Deconvolutional Region Proposal Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3014–3027. [Google Scholar] [CrossRef]
- Wei, S.; Su, H.; Ming, J.; Wang, C.; Yan, M.; Kumar, D.; Shi, J.; Zhang, X. Precise and Robust Ship Detection for High-Resolution SAR Imagery Based on HR-SDNet. Remote Sens. 2020, 12, 167. [Google Scholar] [CrossRef]
- Su, H.; Wei, S.; Liu, S.; Liang, J.; Wang, C.; Shi, J.; Zhang, X. HQ-ISNet: High-Quality Instance Segmentation for Remote Sensing Imagery. Remote Sens. 2020, 12, 989. [Google Scholar] [CrossRef]
- Du, K.; Deng, Y.; Wang, R.; Zhao, T.; Li, N. SAR ATR based on displacement-and rotation-insensitive CNN. Remote Sens. Lett. 2016, 7, 895–904. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, T.; Tian, J.; Zhou, Z.; Wang, C.; Yang, X.; Shi, J. Complex Background SAR Target Recognition Based on Convolution Neural Network. In Proceedings of the 2019 6th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Xiamen, China, 26–29 November 2019; pp. 1–4. [Google Scholar]
- Zhang, Z.; Wang, H.; Xu, F.; Jin, Y.Q. Complex-valued convolutional neural network and its application in polarimetric SAR image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7177–7188. [Google Scholar] [CrossRef]
- Wang, C.; Shi, J.; Zhou, Y.; Yang, X.; Zhou, Z.; Wei, S.; Zhang, X. Semisupervised Learning-Based SAR ATR via Self-Consistent Augmentation. IEEE Trans. Geosci. Remote Sens. 2020, 1–12. [Google Scholar] [CrossRef]
- Yang, X.; Zhou, Y.; Wang, C.; Shi, J. SAR Images Enhancement Via Deep Multi-Scale Encoder-Decoder Neural Network. In Proceedings of the IGARSS 2019-2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 3368–3371. [Google Scholar]
- Zhou, Y.; Shi, J.; Yang, X.; Wang, C.; Kumar, D.; Wei, S.; Zhang, X. Deep multi-scale recurrent network for synthetic aperture radar images despeckling. Remote Sens. 2019, 11, 2462. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, S.; Li, H.; Xu, Z. Shadow Tracking of Moving Target Based on CNN for Video SAR System. In Proceedings of the IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 4399–4402. [Google Scholar]
- Ding, J.; Wen, L.; Zhong, C.; Loffeld, O. Video SAR Moving Target Indication Using Deep Neural Network. IEEE Trans. Geosci. Remote Sens. 2020. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2015; pp. 91–99. [Google Scholar]
- Jun, S.; Long, M.; Xiaoling, Z. Streaming BP for non-linear motion compensation SAR imaging based on GPU. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 2035–2050. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, X.; Shi, J.; Wei, S.; Tian, B. Ground Moving Target 2-D Velocity Estimation and Refocusing for Multichannel Maneuvering SAR with Fixed Acceleration. Sensors 2019, 19, 3695. [Google Scholar] [CrossRef] [PubMed]
- Jin, G.; Dong, Z.; He, F.; Yu, A. Background-Free Ground Moving Target Imaging for Multi-PRF Airborne SAR. IEEE Trans. Geosci. Remote Sens. 2018, 57, 1949–1962. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, X.; Shi, J.; Wei, S.; Pu, L. Ground slowly moving target detection and velocity estimation via high-speed platform dual-beam synthetic aperture radar. J. Appl. Remote Sens. 2019, 13, 026516. [Google Scholar] [CrossRef]
- Zhu, S.; Liao, G.; Qu, Y.; Zhou, Z.; Liu, X. Ground moving targets imaging algorithm for synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 2010, 49, 462–477. [Google Scholar] [CrossRef]
- Suwa, K.; Yamamoto, K.; Tsuchida, M.; Nakamura, S.; Wakayama, T.; Hara, T. Image-based target detection and radial velocity estimation methods for multichannel SAR-GMTI. IEEE Trans. Geosci. Remote Sens. 2016, 55, 1325–1338. [Google Scholar] [CrossRef]
- Moses, R.L.; Ash, J.N. An autoregressive formulation for SAR backprojection imaging. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 2860–2873. [Google Scholar] [CrossRef]
- Moss, R.L.; Ash, J.N. Recursive SAR imaging. In Algorithms for Synthetic Aperture Radar Imagery XV; Zelnio, E.G., Garber, F.D., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2008; Volume 6970, pp. 180–191. [Google Scholar] [CrossRef]
- Song, X.; Yu, W. Processing video-SAR data with the fast backprojection method. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2838–2848. [Google Scholar] [CrossRef]
- Zuo, F.; Li, J.; Hu, R.; Pi, Y. Unified Coordinate System Algorithm for Terahertz Video-SAR Image Formation. IEEE Trans. Terahertz Sci. Technol. 2018, 8, 725–735. [Google Scholar] [CrossRef]
- Bolme, D.S.; Beveridge, J.R.; Draper, B.A.; Lui, Y.M. Visual object tracking using adaptive correlation filters. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 2544–2550. [Google Scholar]
- Henriques, J.F.; Caseiro, R.; Martins, P.; Batista, J. High-speed tracking with kernelized correlation filters. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 37, 583–596. [Google Scholar] [CrossRef]
- Bertinetto, L.; Valmadre, J.; Henriques, J.F.; Vedaldi, A.; Torr, P.H. Fully-convolutional siamese networks for object tracking. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2016; pp. 850–865. [Google Scholar]
- Chu, Q.; Ouyang, W.; Li, H.; Wang, X.; Liu, B.; Yu, N. Online multi-object tracking using CNN-based single object tracker with spatial-temporal attention mechanism. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 4836–4845. [Google Scholar]
- Zhai, M.; Chen, L.; Mori, G.; Javan Roshtkhari, M. Deep learning of appearance models for online object tracking. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Dong-an, F.C.S.; Zhi-xiong, W. Simulation of RCS of Ship by Using Feko and Hypermesh. Equip. Environ. Eng. 2008, 5, 61–64. [Google Scholar]
- Farhadi, D.G.A.; Fox, D. Re 3: Real-Time Recurrent Regression Networks for Visual Tracking of Generic Objects. IEEE Robot. Autom. Lett. 2018, 3, 788–795. [Google Scholar]
- Čehovin, L.; Kristan, M.; Leonardis, A. Is my new tracker really better than yours? In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, Steamboat Springs, CO, USA, 24–26 March 2014; pp. 540–547. [Google Scholar]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 1, pp. 886–893. [Google Scholar]
- Chen, Z.; Hong, Z.; Tao, D. An experimental survey on correlation filter-based tracking. arXiv 2015, arXiv:1509.05520. [Google Scholar]
















| Imaging Resolution | Carrier Frequency | PRF | Platform Speed | Platform Height |
|---|---|---|---|---|
| 0.125 m | 35 GHz | 2000 Hz | 330 m/s | 10 km |
| squint angle | bandwidth | image size | FPS | PRI interval |
| 45 | 2GH | 1024 × 1024 | 1 | 640 |
| Index | Accuracy | Robustness | Distance |
|---|---|---|---|
| MOSSE | 0.506 | 0.81 | 17.26 |
| KCF | 0.721 | 1.00 | 6.25 |
| Re | 0.764 | 0.98 | 6.01 |
| SiamFc | 0.739 | 1.00 | 6.13 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Shi, J.; Zhou, Y.; Wang, C.; Hu, Y.; Zhang, X.; Wei, S. Ground Moving Target Tracking and Refocusing Using Shadow in Video-SAR. Remote Sens. 2020, 12, 3083. https://doi.org/10.3390/rs12183083
Yang X, Shi J, Zhou Y, Wang C, Hu Y, Zhang X, Wei S. Ground Moving Target Tracking and Refocusing Using Shadow in Video-SAR. Remote Sensing. 2020; 12(18):3083. https://doi.org/10.3390/rs12183083
Chicago/Turabian StyleYang, Xiaqing, Jun Shi, Yuanyuan Zhou, Chen Wang, Yao Hu, Xiaoling Zhang, and Shunjun Wei. 2020. "Ground Moving Target Tracking and Refocusing Using Shadow in Video-SAR" Remote Sensing 12, no. 18: 3083. https://doi.org/10.3390/rs12183083
APA StyleYang, X., Shi, J., Zhou, Y., Wang, C., Hu, Y., Zhang, X., & Wei, S. (2020). Ground Moving Target Tracking and Refocusing Using Shadow in Video-SAR. Remote Sensing, 12(18), 3083. https://doi.org/10.3390/rs12183083





