Improved IMU Preintegration with Gravity Change and Earth Rotation for Optimization-Based GNSS/VINS

Abstract

IMU preintegration technology has been widely used in the optimization-based sensor fusion framework, in order to avoid reintegrating the high-frequency IMU measurements at each iteration and maintain the ability of bias correction when bias estimation changes. Since IMU preintegration technology was first proposed, several improved versions have been designed by changing the attitude parameterization or the numerical integration method in the most current related research. However, all of these versions have failed to take the change of gravity and the earth rotation into consideration. In this paper, we redesign the IMU preintegration algorithm in which the earth rotation and gravity vector are calculated from the geodetic position. Compared with the covariance matrix form, in this paper, the uncertainty of the preintegrated IMU measurements is propagated in the form of a square root information matrix (SRIM) for better numerical stability and easy use in the optimization-based framework. We evaluate the improved IMU preintegration algorithm by using the dataset collected by our sensor platform equipped with two different-grade IMUs. The test results show that the improved IMU preintegration algorithm can cope well with the gravity change and earth rotation. The earth rotation must be taken into consideration for the high-grade IMU that can effectively sense the earth rotation. If the change of gravity is omitted, the root-mean-square error (RMSE) of the horizontal attitude is about 1.38 times greater than the geodetic displacement. Additionally, the positioning RMSE does not increase obviously within a limited range, which means tens of kilometers and several hundred meters for the low-grade and high-grade IMU used in the experiment, respectively.

1. Introduction

Automatic robots have become a hot topic over the last few years due to a growing market demand for products such as autonomous cars, rescue robots, and military robots. In order to succeed in their missions, these robots usually require accurate motion information (position, velocity, and attitude) for control and navigation. Many kinds of sensors can provide useful information for motion estimation, locally or globally, such as a camera, the IMU, and the global navigation satellite system (GNSS). Typically, a modern robot is equipped with several kinds of sensors with complementary sensing capacities, in order to make motion information estimation accurate and robust. Specifically, the inertial navigation system (INS) can provide position, velocity, and attitude information at a high frequency by integrating IMU measurements [1,2,3,4]. However, IMU measurements are typically corrupted by several kinds of errors, such as the scale factor error, misalignment, biases, and sensor-induced random output noise [5]. Such measurement errors make the long-term integration of IMU measurements unreliable. In contrast to the short-term accuracy of the INS, the GNSS can provide position information in the geodetic reference frame with a relatively consistent accuracy and no position drift. However, the provided position information is low-frequency and discontinuous. For those reasons, the INS/GNSS integrated navigation system has been well-studied over the past several decades for providing high-precision, high-frequency motion information without drift [6,7,8]. However, the performance of the integrated system greatly depends on the availability of GNSS signals, especially for the low-grade IMU [7,8]. Unfortunately, satellite signals are vulnerable to electromagnetic interference and easily shielded by high buildings, which makes GNSS measurements unreliable. Another well-known technique with the capacity for local motion information estimation is the visual-inertial navigation system (VINS), which fuses the measurements provided by the camera and the IMU [9,10,11,12,13,14,15,16,17,18,19,20,21]. The two sensors are complementary in many ways. The IMU makes the metric scale and the gravity vector observable and provides accurate inter-frame motion information. The visual information aids the IMU in bias estimation. Nevertheless, the global position and yaw estimation of the VINS finally drifts [14], unless other sensors/systems that provide global measurements, such as the GNSS, are integrated with the VINS [15,16]. According to the above analyses, there is an irresistible trend to fuse the complementary information from the redundant sensors for motion information estimation.

Information fusion of the INS/GNSS integrated navigation system can be implemented by Bayesian filters, such as the Kalman filter or extended Kalman filter [6]. In comparison, the information fusion algorithms of the VINS become more complex, due to the high nonlinearity of visual residual functions and the high number of visual measurements. Generally, the information fusion algorithms of the VINS can be divided into two categories, namely the optimization-based methods [9,10,11,12,13,15,16] and the Bayesian filter-based methods [14,17,18,19,20,21]. The optimization-based methods typically can achieve a higher accuracy than the filter-based methods by benefitting from the ability of re-linearization. The computational complexity of the filtered-based methods is cubic with the number of visible mappoints. For achieving a real-time performance, the number of mappoints in the state of the filter is strictly limited, which also decreases the accuracy of information fusion [22]. The multistate constraint Kalman filter (MSCKF) is a special augmented Kalman filter. It keeps a sliding window of past poses in its state vector [20,21]. The positions of mappoints are marginalized first by using the left null space trick. Then, a probabilistic constraint between the poses is constructed. Hence, its computational complexity is linear with the number of mappoints and cubic with the number of poses in the window. For the optimization-based methods, by exploring the first- and second-order sparsity structure of the normal equation, they also become highly efficient [23,24]. However, full optimization finally becomes infeasible as the number of measurements increases. For limiting the computational complexity, sliding window optimization methods have been designed and widely used for solving the VINS problem. These kinds of methods work in the spirit of optimization, but only keep a sliding window of poses [9,10,11,12,13]. The states outside the sliding window are either directly fixed [9,12] or marginalized out [10,11,13].

Typically, the sampling frequency of the IMU is high—approximately hundreds of Hertz. For the filter-based methods, the time update is required to operate at the IMU sampling frequency. For the optimization-based methods, it is impracticable to perform optimization at the IMU sampling frequency. One possible solution to this problem is to integrate the IMU measurements during the sampling interval of the other sensors working at a low sampling frequency. However, this will cause another problem in that the initial integration values are unknown or inaccurate. Once the initial integration values are updated at each iteration of optimization, the IMU measurements need to be re-integrated, which makes the computational complexity increase. In order to achieve fusion with other sensors, uncertainty of the integrated IMU measurements is also necessary. For propagating the uncertainty, the initial uncertainty traditionally needs to be calculated by back propagating the measurement uncertainties of sensors after each iteration. Then, the uncertainty of the integrated IMU measurements is re-propagated, which will also cause additional computation.

For coping with these two challenges, the IMU preintegration technique was first developed by Lupton et al. [25,26] for the optimization-based VINS. The technique can also be used in other optimization-based multi-sensor fusion frameworks, such as the LiDAR/IMU/GNSS integrated navigation system [27]. In [25,26], the attitude is parametrized by the Euler angles, which causes a singularity in specific cases [28]. In [29,30], the attitude is parametrized by the specific rotation group SO (3), in order to avoid the singularity and carefully cope with uncertainty propagation of the preintegrated IMU measurements. In [10], the attitude is parametrized by the attitude quaternion. The covariance propagation of the preintegrated IMU measurements is calculated by using the dynamic equations of the preintegration error states. In [31,32], closed-form solutions of IMU preintegration are derived by using linear system theory. However, all of the above IMU preintegration algorithms assume that the gravity vector is constant in the VINS reference frame. In practice, the gravity vector changes with the position relative to the VINS reference frame. The longer the relative position, the more obvious the change of gravity. The earth rotation is also not considered in the above IMU preintegration algorithms. In comparison, the gravity change and earth rotation are well-modeled in the strap-down inertial navigation algorithms [1,2,3,4], the INS/GNSS, and the INS/GNSS/Vision integrated navigation systems [6,7,8], in order to remove their influence from the IMU measurements. Motivated by these conventional INS relevant algorithms, we redesigned the IMU preintegration algorithm by taking the change of gravity and the earth rotation into consideration. Both terms are functions of the geodetic position. There are several kinds of geodetic reference models for the earth, such as the geodetic reference system 1980 (GRS-80), the world geodetic system 1984 (WGS-84), and the Chinese Geodetic Coordinate System 2000 (CGCS-2000). In the INS relevant algorithms, the WGS-84 model has been widely used. In this paper, the WGS-84 model is also adopted.

The preintegrated IMU measurements can be used to construct a preintegration factor, and the preintegration factor needs to be weighted by its square-root information matrix before being added to the optimization. In this paper, the uncertainty of the preintegrated IMU measurements is propagated in the form of a square root information matrix [33]. Compared with the covariance propagation form [25,26,29,30,31,32], the square-root information matrix is directly available for weighting the preintegrated IMU measurements and theoretically has a better numerical stability [33]. IMU measurements are typically corrupted by several kinds of errors. In this paper, we assume that the IMU has been well-calibrated offline. Then, the remaining IMU measurement errors include the sensor-induced random output noise and the slowly time-varying biases. In this paper, the sensor-induced random output noise is modeled as a white noise process. Additionally, the slowly time-varying bias is modeled as a one-order Markov process.

In order to evaluate the performance of the improved IMU preintegration algorithm, we implement a tightly-coupled monocular visual-inertial system [34], and the GNSS positioning results are fused in a loosely-coupled way. We perform experiments by using the dataset collected by our sensor platform. The sensor platform is equipped with two different-grade IMUs, in order to analyze the influence of the earth rotation and the change of gravity on different-grade IMUs.

Our contributions can be summarized as follows:

• We have redesigned the IMU preintegration algorithm by taking the earth rotation and the change of gravity into consideration;
• The uncertainty of the preintegrated IMU measurements has been propagated in the form of a square-root information matrix;
• We have evaluated the influence of the earth rotation and the change of gravity on the preintegrated IMU measurements by using two different-grade IMUs.

The remainder of this paper is organized as follows. In Section 2, the coordinate frames, notations, attitude parameterizations, and geodetic reference model of the earth are introduced. In Section 3, all of the details of the improved IMU preintegration algorithm are given, including the position, velocity, and attitude dynamic equations in the W frame; the IMU error model; the uncertainty propagation of preintegrated IMU measurements; and the IMU preintegration factors. In Section 4, the joint optimization framework of the VINS is briefly described. In Section 5, all of the details of experiment setup are introduced. In Section 6, all experimental results are given. In Section 7, we discuss the influence of the gravity change and the earth rotation on the IMU preintegration, according to the experimental results. In Section 8, we draw the conclusions.

2. Preliminaries

In this section, some fundamental professional knowledge used in designing the IMU preintegration algorithm is introduced, including the definitions of coordinate frames and notations, the attitude parameterizations, and the earth geodetic reference model. This fundamental professional knowledge has been well-developed in the INS and GNSS research communities for several decades.

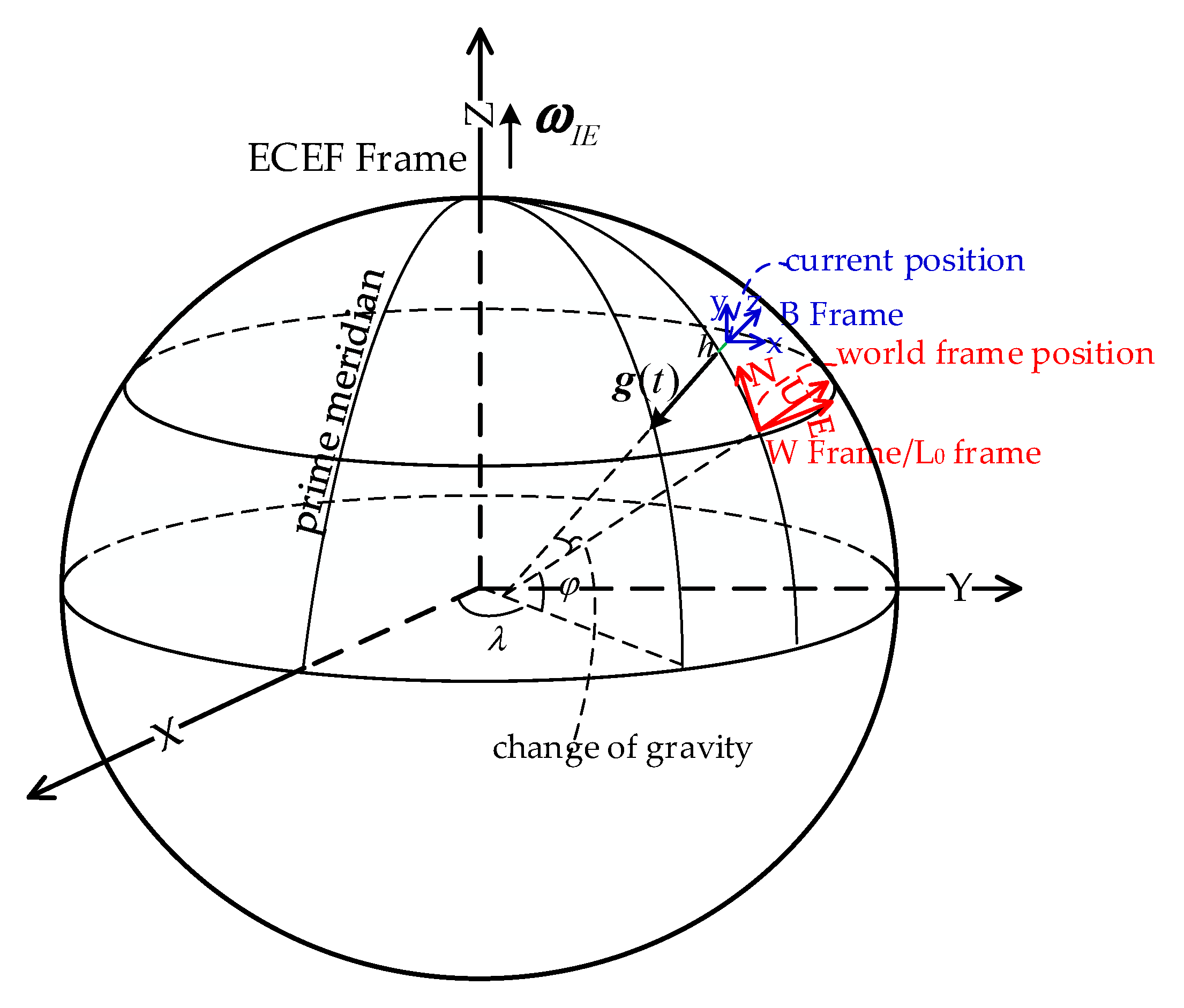
2.1. Coordinate Frames

A coordinate frame is defined by three unit vectors that are perpendicular to each other in a right-hand form. For making a mathematical operation valid, all related free vectors and points should be projected into the same reference coordinate frame.

The E frame is the earth-centered, earth-fixed coordinate frame, with its Z axis parallel to the earth polar axis, its X axis passing through the Greenwich meridian, and its Y axis lying in the equatorial plane to form a right-handed coordinate frame.

The I frame is the non-rotating and non-accelerating inertial coordinate frame used as the reference coordinate frame for the IMU measurement. Theoretically, its orientation can be arbitrary. In this paper, the E frame at the initial time is selected as a historically fixed inertial coordinate frame.

The L frame is the local level coordinate frame, with its X axis parallel to the east, Y axis parallel to the north, and Z axis vertical to the local earth surface.

The B frame is the IMU coordinate frame with axes parallel to the nominal orthogonal input axes.

The C frame is the camera coordinate frame with the origin at the optical center, the X axis horizontal and pointing to the right, and the Y axis vertical and pointing downwards.

The W frame is the reference coordinate frame for the VINS. In this paper, the L frame at the initial position or another fixed position is selected as the W frame.

2.2. Nomenclature

A0, A1, A2	arbitrary orthogonal right-handed coordinate frames;
$\mathit{f}$	specific force measured by the accelerometer, which is produced by a non-gravitational force;
$\mathit{g}$	local plumb-bob gravity vector that is a function of the geodetic position;
${\mathit{p}}_{A_1{A}_2}^{A_0}$	position vector of frame A2 relative to frame A1, with projection in frame A0;
${\mathit{v}}_{A_1{A}_2}^{A_0}$	velocity vector of frame A2 relative to frame A1, with projection in frame A0;
${\mathit{\omega }}_{A_1{A}_2}^{A_0}$	angular velocity vector of frame A2 relative to frame A1, with projection in frame A0;
${\mathit{C}}_{A_2}^{A_1}$	direction cosine matrix that transforms a vector from frame A2 to frame A1;
${\mathit{q}}_{A_2}^{A_1}$	attitude quaternion corresponding to ${\mathit{C}}_{A_2}^{A_1}$;
${\mathit{\theta }}_{A_2}^{A_1}$	rotation/angle-axis vector defined by the axis of rotation and the magnitude of rotation around the axis;
${\mathit{I}}_n$	n-dimension identity matrix;
${\mathbf{0}}_{m\times n}$	zero matrix with m rows and n columns.
Set an arbitrary vector as $\mathit{V}={[V_1,V_2,V_3]}^T$, then
$[\mathit{V}\times ]$	the skew-symmetric matrix of the vector, as follows: $[\mathit{V}\times ]=\left[\begin{array}{ccc}0& -V_3& V_2\\ V_3& 0& -V_1\\ -V_2& V_1& 0\end{array}\right]$;
${\lfloor \mathit{V}\rfloor }_q$	the quaternion form of the vector, as follows: ${\lfloor \mathit{V}\rfloor }_q=\left[\begin{array}{c}0\\ \mathit{V}\end{array}\right]$;
$\overline{\mathit{V}}$	the bar above the vector means it is a constant vector;
$\widehat{\mathit{V}}$	the hat above the vector means it is an estimation;
$\tilde{\mathit{V}}$	the tilde above the vector means it is a measurement;
$\dot{\mathit{V}}$	the point above the vector means it is the time derivative of the vector.

2.3. Attitude Parameterization

The direction cosine matrix, the rotation vector, and the attitude quaternion can be used to parameterize the attitude (rotation) between two coordinate frames with no singularity. Moreover, the three parameterization methods are mathematically equivalent.

The direction cosine matrix ${\mathit{C}}_{A_2}^{A_1}$ is a unit and orthogonal matrix, and the columns are equal to the projections of the unit vectors along the axes of frame A₂ into frame A₁. For an arbitrary vector $\mathit{V}\in {ℝ}^3$ with projections ${\mathit{V}}^{A_1}$, ${\mathit{V}}^{A_2}$ in the coordinate frame A₁, A₂, respectively, the following relationship holds [1]:

$${\mathit{V}}^{A_1}={\mathit{C}}_{A_2}^{A_1}{\mathit{V}}^{A_2},{\mathit{V}}^{A_2}={({\mathit{C}}_{A_2}^{A_1})}^T{\mathit{V}}^{A_1}.$$

(1)

According to Equation (1), it is easy to derive the chain rule of the direction cosine matrix:

$${\mathit{C}}_{A_2}^{A_0}={\mathit{C}}_{A_1}^{A_0}{\mathit{C}}_{A_2}^{A_1}.$$

(2)

The rotation vector ${\mathit{\theta }}_{A_2}^{A_1}=\varphi {\mathit{u}}_{A_2}^{A_1}$ is defined by a unit vector ${\mathit{u}}_{A_2}^{A_1}$ and the magnitude $\varphi$ around the unit vector. According to the Rodrigues formula [1,35], the counterpart direction cosine matrix ${\mathit{C}}_{A_2}^{A_1}$ is a function of the rotation vector, as follows:

$$\mathit{C}({\mathit{\theta }}_{A_2}^{A_1})=\mathrm{c}\mathrm{o}\mathrm{s}\varphi {\mathit{I}}_3+(1-\mathrm{c}\mathrm{o}\mathrm{s}\varphi ){\mathit{u}}_{A_2}^{A_1}{({\mathit{u}}_{A_2}^{A_1})}^T+\sin \varphi [{\mathit{u}}_{A_2}^{A_1}\times ].$$

(3)

The attitude quaternion is composed of four elements, as follows:

$${\mathit{q}}_{A_2}^{A_1}=q_w+q_x\mathit{i}+q_y\mathit{j}+q_z\mathit{k}=\left[\begin{array}{c}{q}_w\\ {\mathit{q}}_v\end{array}\right],$$

(4)

where $q_w,q_x,q_y,q_z\in ℝ$, ${\mathit{q}}_v={[q_x,q_y,q_z]}^T\in {ℝ}^3$, $\left|\right|{\mathit{q}}_{A_2}^{A_1}\left|\right|=q_w^2+q_x^2+q_y^2+q_z^2=\mathbf{1}$. We refer readers to reference [35] for more details about the quaternion. The attitude quaternion is also a function of the rotation vector, as follows:

$$\mathit{q}({\mathit{\theta }}_{A_2}^{A_1})=\left[\begin{array}{c}\cos (0.5\varphi )\\ \sin (0.5\varphi ){\mathit{u}}_{A_2}^{A_1}\end{array}\right].$$

(5)

The chain rule of the attitude quaternion is defined on the basis of quaternion multiplication, as follows:

$${\mathit{q}}_{A_2}^{A_0}={\mathit{q}}_{A_1}^{A_0}\otimes {\mathit{q}}_{A_2}^{A_1}={[{\mathit{q}}_{A_1}^{A_0}]}_L{\mathit{q}}_{A_2}^{A_1}={[{\mathit{q}}_{A_2}^{A_1}]}_R{\mathit{q}}_{A_1}^{A_0},$$

(6)

where $\otimes$ is the quaternion multiplication operator and ${\mathit{q}}_{A_1}^{A_0}={[{q^{\prime }}_w{{\mathit{q}}^{\prime }}_v^T]}^T$. The left and right quaternion multiplication matrices are as follows:

$${[{\mathit{q}}_{A_1}^{A_0}]}_L=\left[\begin{array}{cc}{q^{\prime }}_w& -{{\mathit{q}}^{\prime }}_v^T\\ {{\mathit{q}}^{\prime }}_v& {q^{\prime }}_w{\mathit{I}}_3+[{{\mathit{q}}^{\prime }}_v\times ]\end{array}\right],$$

(7)

$${[{\mathit{q}}_{A_2}^{A_1}]}_R=\left[\begin{array}{cc}{q}_w& -{\mathit{q}}_v^T\\ {\mathit{q}}_v& q_w{\mathit{I}}_3-[{\mathit{q}}_v\times ]\end{array}\right].$$

(8)

The conversion relationships between the direction cosine matrix and the attitude quaternion are as follows:

$$\mathit{q}({\mathit{C}}_{A_2}^{A_1})=\left[\begin{array}{c}{q}_w\\ {\mathit{q}}_v\end{array}\right],\{\begin{array}{l}{q}_w=\sqrt{tr({\mathit{C}}_{A_2}^{A_1})+1}/2\\ {\mathit{q}}_v={\left[\frac{C_{32}-C_{23}}{4q_w}\frac{C_{13}-C_{31}}{4q_w}\frac{C_{21}-C_{12}}{4q_w}\right]}^T\end{array},$$

(9)

$$\mathit{C}({\mathit{q}}_{A_2}^{A_1})=(2q_w^2-1){\mathit{I}}_3+2q_w[{\mathit{q}}_v\times ]+2{\mathit{q}}_v{\mathit{q}}_v^T,$$

(10)

where ${\mathit{C}}_{A_2}^{A_1}=\left\{C_{ij}\right\}$, $C_{ij}\in ℝ$, $i,j\in \{1,2,3\}$. $tr({\mathit{C}}_{A_2}^{A_1})$ is the trace of ${\mathit{C}}_{A_2}^{A_1}$, i.e., the sum of the diagonal elements of the direction cosine matrix.

2.4. Time Derivative of the Attitude Parameter

The time derivative of the direction cosine matrix ${\mathit{C}}_{A_2}^{A_1}$ is as follows:

$${\dot{\mathit{C}}}_{A_2}^{A_1}={\mathit{C}}_{A_2}^{A_1}[{\mathit{\omega }}_{A_1{A}_2}^{A_2}\times ].$$

(11)

The time derivative of the attitude quaternion ${\mathit{q}}_{A_2}^{A_1}$ is as follows:

$${\dot{\mathit{q}}}_{A_2}^{A_1}=\frac{1}{2}{\mathit{q}}_{A_2}^{A_1}\otimes {\lfloor {\mathit{\omega }}_{A_1{A}_2}^{A_2}\rfloor }_q.$$

(12)

2.5. The Earth Model

In this paper, the WGS-84 geodetic reference model is adopted for modeling the earth as shown in Figure 1. Set the geodetic position (latitude, longitude, and altitude) in the WGS-84 reference frame as $\phi$, $\lambda$, and $h$. Then, the direction cosine matrix between the L frame and E frame is as follows:

$$C_L^E(\phi ,\lambda )=\left[\begin{array}{ccc}-\sin \lambda & -\cos \lambda \sin \phi & \cos \lambda \cos \phi \\ \cos \lambda & -\sin \lambda \sin \phi & \sin \lambda \cos \phi \\ 0& \cos \phi & \sin \phi \end{array}\right].$$

(13)

The XYZ position in the E frame can be recovered from the geodetic position, as follows:

$${\mathit{p}}_{EL}^E(\phi ,\lambda ,h)=\left[\begin{array}{c}(R_N+h)\cos \phi \cos \lambda \\ (R_N+h)\cos \phi \sin \lambda \\ [R_N(1-e^2)+h]\sin \phi \end{array}\right],$$

(14)

where $e=0.08181919104282$ is the eccentricity of the earth and $R_N$ is the radius of curvature of the prime vertical plane. It is a function of the latitude, i.e., $R_N(\phi )=a/\sqrt{1-e^2{\sin }^2\phi }$. $a=6378137\mathrm{m}$ is the equatorial earth radius.

The geodetic position can also be recovered from the XYZ position in the E frame. The longitude can be recovered directly as follows:

$$\lambda =\arctan \left(\frac{{\mathit{p}}_{EL}^E(1)}{{\mathit{p}}_{EL}^E(0)}\right).$$

(15)

The latitude and altitude need to be recovered by the following iterative algorithm. The initial values are set as follows:

$$\begin{array}{c}h=0\\ R_N=a\\ r=\sqrt{{\mathit{p}}_{EL}^E{(0)}^2+{\mathit{p}}_{EL}^E{(1)}^2}\end{array}.$$

(16)

Then, the latitude and altitude are iteratively calculated until convergence, as follows:

$$\begin{array}{c}\sin \phi =\frac{{\mathit{p}}_{EL}^E(2)}{R_N(1-e^2)+h}\\ \phi =\arctan \left(\frac{{\mathit{p}}_{EL}^E(2)+e^2{R}_N(\phi )\sin \phi }{r}\right)\\ h=\frac{r}{\cos \phi }-R_N\end{array}.$$

(17)

For notation convenience, the computation process of Equations (15), (16), and (17) is donated as follows:

$$[\phi ,\lambda ,h]=LLA({\mathit{p}}_{EL}^E).$$

(18)

The normal gravity in the L frame is as follows:

$${\mathit{g}}_{\gamma }^L(\phi ,h)={\left[0,0,g_{\gamma }(\phi ,h)\right]}^T,$$

(19)

where $g_{\gamma }(\phi ,h)$ is calculated by the WGS-84 gravity model parameters, as follows:

$$\begin{array}{l}{g}_{\gamma }(\phi ,h)=g_{\gamma }(\phi )-(3.0877-0.0044{\sin }^2\phi )\times {10}^{-6}h+0.072\times {10}^{-12}{h}^2\\ g_{\gamma }(\phi )=9.7803253\times (1+0.0053022{\sin }^2\phi -0.0000058{\sin }^{2}2\phi )\end{array}$$

(20)

The gravity anomaly is omitted in our algorithm. Therefore, the normal gravity is approximately considered as the local gravity in this paper.

The earth rotation vector in the E frame is as follows:

$${\overline{\mathit{\omega }}}_{IE}^E={\left[0,0,{\mathsf{\Omega }}_{IE}\right]}^T,$$

(21)

where ${\mathsf{\Omega }}_{IE}=7.292115\times {10}^{-5}rad/s$.

The measurement of the accelerometer is a specific force. The influence of gravity needs to be removed from the preintegrated IMU measurements, in order to recover the metric motion. Therefore, we need to know the gravity vector projected in the W frame. The measurement of a gyroscope (rate sensor) is the angular velocity relative to the I frame. The influence of the earth rotation needs to be removed from the gyroscope measurement, in order to recover the real angular velocity relative to the earth.

Set the geodetic position of the W frame as ${\phi }_0$, ${\lambda }_0$, and $h_0$. The XYZ position ${\mathit{p}}_{EW}^E$ in the E frame can be calculated by Equation (14). Then, the direction cosine matrix ${\mathit{C}}_{L_0}^E={\mathit{C}}_W^E$ between the W frame and E frame can be calculated by Equation (13).

The earth rotation vector in the W frame is calculated as follows:

$${\overline{\mathit{\omega }}}_{IE}^W={({\mathit{C}}_{L_0}^E)}^T{\overline{\mathit{\omega }}}_{IE}^E.$$

(22)

Set the position of the IMU at time t in the W frame as ${\mathit{p}}_{W{B}_t}^W$. Then, its position in the E frame can be calculated as follows:

$${\mathit{p}}_{E{B}_t}^E={\mathit{p}}_{EW}^E+{\mathit{C}}_W^E{\mathit{p}}_{W{B}_t}^W.$$

(23)

Then, the geodetic position of IMU at time t can be calculated by Equation (18), i.e., $[{\phi }_t,{\lambda }_t,h_t]=LLA({\mathit{p}}_{E{B}_t}^E)$. The local normal gravity vector ${\mathit{g}}_{\gamma }^{L_t}({\phi }_t,h_t)$ in the L frame can be calculated by Equation (19). The direction cosine matrix ${\mathit{C}}_{L_t}^E({\phi }_t,{\lambda }_t)$ can be calculated by Equation (13). Therefore, the direction cosine matrix between the L frame and W frame is ${\mathit{C}}_{L_t}^W={({\mathit{C}}_W^E)}^T{\mathit{C}}_{L_t}^E$. Finally, the gravity vector in the W frame is calculated as follows:

$${\widehat{\mathit{g}}}^W={\mathit{C}}_{L_t}^W{\mathit{g}}_{\gamma }^{L_t}.$$

(24)

3. The Improved IMU Preintegration Technology

The position, velocity, and attitude are obtained by integrating the IMU measurements. For performing such integrations, the dynamic equations for the position, velocity, and attitude should be derived first. Generally, the position, velocity, and attitude of the VINS are parametrized in the W frame. Hence, the dynamic equations are also derived in the W frame.

First, the relationship of the positions parameterized in the W frame and I frame is as follows:

$${\mathit{p}}_{IB}^I={\mathit{C}}_E^I({\overline{\mathit{p}}}_{IW}^E+{\overline{\mathit{C}}}_W^E{\mathit{p}}_{WB}^W),$$

(25)

where ${\overline{\mathit{p}}}_{IW}^E={\overline{\mathit{p}}}_{EW}^E$ because the origins of the E frame and I frame are coincident, i.e., ${\overline{\mathit{p}}}_{IE}^E={\mathbf{0}}_{3\times 1}$, and the W frame is fixed with respect to the earth.

According to Equation (11), the time derivative of Equation (25) is as follows:

$${\mathit{v}}_{IB}^I={\mathit{C}}_E^I[{\overline{\mathit{\omega }}}_{IE}^E\times ]({\overline{\mathit{p}}}_{IW}^E+{\overline{\mathit{C}}}_W^E{\mathit{p}}_{WB}^W)+{\mathit{C}}_E^I{\overline{\mathit{C}}}_W^E{\mathit{v}}_{WB}^W,$$

(26)

where ${\mathit{v}}_{IB}^I={\dot{\mathit{p}}}_{IB}^I$, ${\mathit{v}}_{WB}^W={\dot{\mathit{p}}}_{WB}^W$. ${\overline{\mathit{\omega }}}_{IE}^E$ is the earth rotation in the E frame.

For obtaining the acceleration information, we need to further derive the time derivative of Equation (26) as follows:

$${\mathit{a}}_{IB}^I={\mathit{C}}_E^I[{\overline{\mathit{\omega }}}_{IE}^E\times ][{\overline{\mathit{\omega }}}_{IE}^E\times ]({\overline{\mathit{p}}}_{IW}^E+{\overline{\mathit{C}}}_W^E{\mathit{p}}_{WB}^W)+2{\mathit{C}}_E^I[{\overline{\mathit{\omega }}}_{IE}^E\times ]{\overline{\mathit{C}}}_W^E{\mathit{v}}_{WB}^W+{\mathit{C}}_E^I{\overline{\mathit{C}}}_W^E{\dot{\mathit{v}}}_{WB}^W,$$

(27)

where ${\mathit{a}}_{IB}^I={\dot{\mathit{v}}}_{IB}^I$.

Substituting the equation $[{\overline{\mathit{\omega }}}_{IE}^E\times ]={\overline{\mathit{C}}}_W^E[{\overline{\mathit{\omega }}}_{IE}^W\times ]{\overline{\mathit{C}}}_E^W$ into Equation (27), we have

$${\mathit{a}}_{IB}^I={\mathit{C}}_W^I[{\overline{\mathit{\omega }}}_{IE}^W\times ][{\overline{\mathit{\omega }}}_{IE}^W\times ]({\overline{\mathit{p}}}_{IW}^W+{\mathit{p}}_{WB}^W)+2{\mathit{C}}_W^I[{\overline{\mathit{\omega }}}_{IE}^W\times ]{\mathit{v}}_{WB}^W+{\mathit{C}}_W^I{\dot{\mathit{v}}}_{WB}^W.$$

(28)

Let us left-multiply both sides of Equation (28) by ${\mathit{C}}_I^B$. After re-organization, we have

$${\mathit{C}}_B^W{\mathit{a}}_{IB}^B=[{\overline{\mathit{\omega }}}_{IE}^W\times ][{\overline{\mathit{\omega }}}_{IE}^W\times ]({\overline{\mathit{p}}}_{IW}^W+{\mathit{p}}_{WB}^W)+2[{\overline{\mathit{\omega }}}_{IE}^W\times ]{\mathit{v}}_{WB}^W+{\dot{\mathit{v}}}_{WB}^W.$$

(29)

According to the theory of the force composition and decomposition, the acceleration ${\mathit{a}}_{IB}^B$ relative to the inertial space is the resultant force of the specific force ${\mathit{f}}^B$ and the gravitational force ${\mathit{G}}^B$, i.e., ${\mathit{a}}_{IB}^B={\mathit{f}}^B+{\mathit{G}}^B$. Substituting the equation into Equation (29), we have

$$\begin{array}{l}{\dot{\mathit{v}}}_{WB}^W={\mathit{C}}_B^W{\mathit{f}}^B+{\mathit{G}}^W-[{\overline{\mathit{\omega }}}_{IE}^W\times ][{\overline{\mathit{\omega }}}_{IE}^W\times ]({\overline{\mathit{p}}}_{IW}^W+{\mathit{p}}_{WB}^W)-2[{\overline{\mathit{\omega }}}_{IE}^W\times ]{\mathit{v}}_{WB}^W\\ \hspace{1em}\hspace{1em}={\mathit{C}}_B^W{\mathit{f}}^B+{\mathit{g}}^W-2[{\overline{\mathit{\omega }}}_{IE}^W\times ]{\mathit{v}}_{WB}^W\end{array},$$

(30)

where ${\mathit{g}}^W={\mathit{G}}^W-[{\overline{\mathit{\omega }}}_{IE}^W\times ][{\overline{\mathit{\omega }}}_{IE}^W\times ]({\overline{\mathit{p}}}_{IW}^W+{\mathit{p}}_{WB}^W)$ is the gravity in the W coordinate frame. $2[{\overline{\mathit{\omega }}}_{IE}^W\times ]{\mathit{v}}_{WB}^W$ is the well-known Coriolis acceleration.

Equation (30) is the velocity differential equation. The position differential equation can be easily expressed as follows:

$${\dot{\mathit{p}}}_{WB}^W={\mathit{v}}_{WB}^W.$$

(31)

The attitude is parameterized by the attitude quaternion. Furthermore, its time derivative can be derived according to Equation (12), as follows:

$$\begin{array}{l}{\dot{\mathit{q}}}_B^W=\frac{1}{2}{\mathit{q}}_B^W\otimes {\lfloor {\mathit{\omega }}_{WB}^B\rfloor }_q=\frac{1}{2}{\mathit{q}}_B^W\otimes {\lfloor {\mathit{\omega }}_{IB}^B-{\mathit{\omega }}_{IE}^B-{\overline{\mathit{\omega }}}_{EW}^B\rfloor }_q\\ \hspace{1em}\hspace{1em}\hspace{1em}=\frac{1}{2}{\mathit{q}}_B^W\otimes {\lfloor {\mathit{\omega }}_{IB}^B-\mathit{C}({\mathit{q}}_W^B){\overline{\mathit{\omega }}}_{IE}^W\rfloor }_q\end{array}.$$

(32)

Then, the position, velocity, and attitude can be reckoned by numerically integrating the three dynamic equations, as follows:

$$\begin{array}{l}{\mathit{p}}_{W{B}_{k+1}}^W={\mathit{p}}_{W{B}_k}^W+{\mathit{v}}_{W{B}_k}^W\mathsf{\Delta }{t}_{k.k+1}+{\displaystyle \int {\displaystyle {\int }_{t_k}^{t_{k+1}}{\mathit{C}}_{B_t}^W{\mathit{f}}^{B_t}\mathrm{d}t}}+{\displaystyle \int {\displaystyle {\int }_{t_k}^{t_{k+1}}{\mathit{g}}_t^W\mathrm{d}t}}-2[{\overline{\mathit{\omega }}}_{IE}^W\times ]{\displaystyle \int {\displaystyle {\int }_{t_k}^{t_{k+1}}{\mathit{v}}_{W{B}_t}^W\mathrm{d}t}}\\ \approx {\mathit{p}}_{W{B}_k}^W+{\mathit{v}}_{W{B}_k}^W\mathsf{\Delta }{t}_{k.k+1}+{\mathit{C}}_{B_k}^W{\mathit{\alpha }}_{k,k+1}+\frac{1}{2}{\mathit{g}}_k^W\mathsf{\Delta }{t}_{k.k+1}^2-2[{\overline{\mathit{\omega }}}_{IE}^W\times ]{\displaystyle {\sum }_{i=1}^{i=N}({\mathit{p}}_{W{B}_i}^W-{\mathit{p}}_{W{B}_k}^W)\mathsf{\Delta }{t}_i}\end{array},$$

(33)

where $\mathsf{\Delta }{t}_{k.k+1}=t_{k+1}-t_k$. $t_k$ is written as k in many subscripts and superscripts for convenience. $N$ is the sampling number during $[t_k,t_{k+1}]$ and $\mathsf{\Delta }{t}_i$ is the IMU sampling interval. The change of gravity is negligible during $[t_k,t_{k+1}]$. Therefore, ${\mathit{g}}_k^W$ is used to represent the gravity during the time interval. Moreover, ${\mathit{\alpha }}_{k,k+1}$ is the so-called IMU position preintegration, as follows:

$${\mathit{\alpha }}_{k,k+1}={\displaystyle \int {\displaystyle {\int }_{t_k}^{t_{k+1}}{\mathit{C}}_{B_t}^{B_k}{\mathit{f}}^{B_t}\mathrm{d}t}}.$$

(34)

The velocity is reckoned as follows:

$$\begin{array}{l}{\mathit{v}}_{W{B}_{k+1}}^W={\mathit{v}}_{W{B}_k}^W+{\displaystyle {\int }_{t_k}^{t_{k+1}}{\mathit{C}}_{B_t}^W{\mathit{f}}^{B_t}\mathrm{d}t}+{\displaystyle {\int }_{t_k}^{t_{k+1}}{\mathit{g}}_t^W\mathrm{d}t}-2[{\overline{\mathit{\omega }}}_{IE}^W\times ]{\displaystyle {\int }_{t_k}^{t_{k+1}}{\mathit{v}}_{W{B}_t}^W\mathrm{d}t}\\ ={\mathit{v}}_{W{B}_k}^W+{\mathit{C}}_{B_k}^W{\mathit{\beta }}_{k,k+1}+{\mathit{g}}_k^W\mathsf{\Delta }{t}_{k,k+1}-2[{\overline{\mathit{\omega }}}_{IE}^W\times ]({\mathit{p}}_{W{B}_{k+1}}^W-{\mathit{p}}_{W{B}_k}^W)\end{array},$$

(35)

where ${\mathit{\beta }}_{k,k+1}$ is the so-called IMU velocity preintegration, as follows:

$${\mathit{\beta }}_{k,k+1}={\displaystyle {\int }_{t_k}^{t_{k+1}}{\mathit{C}}_{B_t}^{B_k}{\mathit{f}}^{B_t}\mathrm{d}t}.$$

(36)

Finally, the attitude increment is the so-called IMU attitude preintegration. It can be reckoned by integrating Equation (32), as follows:

$${\mathit{\gamma }}_{B_{k+1}}^{B_k}={\displaystyle {\int }_{t_k}^{t_{k+1}}\frac{1}{2}{\mathit{q}}_{B_t}^{B_k}{\lfloor {\mathit{\omega }}_{I{B}_t}^{B_t}-\mathit{C}({\mathit{q}}_W^{B_t}){\overline{\mathit{\omega }}}_{IE}^W\rfloor }_q\mathrm{d}t}.$$

(37)

3.1. IMU Error Model and Preintegrated IMU Measurements

Typically, the IMU measurements are corrupted by several kinds of errors, such as the scale factor error, misalignment, sensor-induced random output noise, and slowly time-varying biases. In this paper, we assume that the IMU has been well-calibrated offline. Therefore, the scale factor error and misalignment are negligible. The sensor-induced random output noise is modeled as a white noise process. The slowly time-varying biases are molded as one-order Markov processes. Then, the IMU measurements are modeled as follows:

$$\begin{array}{l}{\tilde{\mathit{f}}}^{B_t}={\mathit{f}}^{B_t}+{\mathit{b}}_{Acc,t}+{\mathit{\eta }}_{Acc,t}\\ {\tilde{\mathit{\omega }}}_{I{B}_t}^{B_t}={\mathit{\omega }}_{I{B}_t}^{B_t}+{\mathit{b}}_{Gyro,t}+{\mathit{\eta }}_{Gyro,t}\end{array},$$

(38)

where ${\mathit{\eta }}_{Acc,t}$ and ${\mathit{\eta }}_{Gyro,t}$ are Gaussian white noise processes, and ${\mathit{\eta }}_{Acc,t}~\mathcal{N}(0,{\mathit{\sigma }}_{Acc}^2)$, ${\mathit{\eta }}_{Gyro,t}~\mathcal{N}(0,{\mathit{\sigma }}_{Gyro}^2)$. $\mathcal{N}(*,*)$ denotes a normal distribution. ${\mathit{b}}_{Acc,t}$ and ${\mathit{b}}_{Gyro,t}$ are IMU time-varying biases and are modeled as follows:

$$\begin{array}{l}{\dot{\mathit{b}}}_{Acc,t}=-\frac{1}{{\tau }_{A\mathit{C}\mathit{C}}}{\mathit{b}}_{Acc,t}+{\mathit{n}}_{Acc,t}\\ {\dot{\mathit{b}}}_{Gyro,t}=-\frac{1}{{\tau }_{Gyro}}{\mathit{b}}_{Gyro,t}+{\mathit{n}}_{Gyro,t}\end{array},$$

(39)

where ${\tau }_{Acc}$ and ${\tau }_{Gyro}$ are the correlation times of Markov processes. ${\mathit{n}}_{Acc,t}$ and ${\mathit{n}}_{Gyro,t}$ are driving Gaussian white noise processes, and ${\mathit{n}}_{Acc,t}~\mathcal{N}(\mathbf{0},{\mathit{\sigma }}_{b_{Acc}}^2)$, $n_{Gyro,t}~\mathcal{N}(\mathbf{0},{\mathit{\sigma }}_{b_{Gyro}}^2)$.

The IMU preintegration Equations (34), (36), and (37) can be solved by numerical integration. The initial body frame $B_k$ is selected as the reference frame for integration. Additionally, the initial values are known and independent of the position, velocity, and attitude in the W coordinate frame, i.e., ${\mathit{\alpha }}_{k,k}={\mathbf{0}}_{3\times 1}$, ${\mathit{\beta }}_{k,k}={\mathbf{0}}_{3\times 1}$, $\mathit{C}({\mathit{q}}_{B_k}^{B_k})={\mathit{I}}_3$. This is the core idea of the IMU preintegration algorithm.

Set the IMU preintegrations at time $t_i$ as ${\widehat{\mathit{\alpha }}}_{k,i}$, ${\widehat{\mathit{\beta }}}_{k,i}$, and ${\widehat{\mathit{\gamma }}}_{B_i}^{B_k}$, and the IMU bias estimations as ${\widehat{\mathit{b}}}_{Gyro,k}$ and ${\widehat{\mathit{b}}}_{Acc,k}$. When new IMU measurements ${\tilde{\mathit{f}}}^{B_j}$ and ${\tilde{\mathit{\omega }}}_{I{B}_j}^{B_j}$ are received, $t_i<t_j\in [t_k,t_{k+1}]$, and the IMU preintegrations are updated recursively, as follows:

$$\begin{array}{l}{\widehat{\mathit{\gamma }}}_{B_j}^{B_k}={\widehat{\mathit{q}}}_{B_j}^{B_k}={\widehat{\mathit{\gamma }}}_{B_i}^{B_k}\otimes \left[\begin{array}{c}1.0\\ 0.5({\tilde{\mathit{\omega }}}_{I{B}_j}^{B_j}-\mathit{C}({\widehat{\mathit{q}}}_W^{B_i}){\overline{\mathit{\omega }}}_{IE}^W-{\widehat{\mathit{b}}}_{Gyro,k})\mathsf{\Delta }{t}_{ij}\end{array}\right]\\ {\widehat{\mathit{\alpha }}}_{k,j}={\widehat{\mathit{\alpha }}}_{k,i}+{\widehat{\mathit{\beta }}}_{k,i}\mathsf{\Delta }{t}_{ij}+0.5\times \mathit{C}({\widehat{\mathit{\gamma }}}_{B_j}^{B_k})({\tilde{\mathit{f}}}^{B_j}-{\widehat{\mathit{b}}}_{Acc,k})\mathsf{\Delta }{t}_{ij}^2\\ {\widehat{\mathit{\beta }}}_{k,j}={\widehat{\mathit{\beta }}}_{k,i}+\mathit{C}({\widehat{\mathit{\gamma }}}_{B_j}^{B_k})({\tilde{\mathit{f}}}^{B_j}-{\widehat{\mathit{b}}}_{Acc,k})\mathsf{\Delta }{t}_{ij}\end{array},$$

(40)

where $\mathsf{\Delta }{t}_{ij}=t_j-t_i$.

3.2. Uncertainty Propagation and Jacobian Matrix of Bias Correction

The uncertainty propagation of IMU preintegration is similar to the time update of the Bayesian filter used in the INS/GNSS integrated navigation system. Due to the IMU preintegration errors being time-varying, we also need linear dynamic equations for tracking the errors, just like Psi- and Phi- angle error equations in the INS/GNSS integrated navigation system [36]. The Jacobian matrices for belated bias correction are contained in the transition matrix of the IMU preintegration errors. For iteratively updating the transition matrix, we also need the linear dynamic equations of the IMU preintegration errors. Hence, in this section, we will derive the linear dynamic equations first.

(1). Attitude preintegration error dynamic equation: The attitude preintegration error is defined in a right perturbation form. Set the attitude preintegration error at time t as $\delta {\mathit{\theta }}_{B_t}^{B_k}$. Then we have

$${\mathit{C}}_{B_t}^{B_k}={\widehat{\mathit{C}}}_{B_t}^{B_k}(\mathit{I}+[\delta {\mathit{\theta }}_{B_t}^{B_k}\times ]),$$

(41)

where ${\widehat{\mathit{C}}}_{B_t}^{B_k}=\mathit{C}({\widehat{\mathit{q}}}_{B_t}^{B_k})=\mathit{C}({\widehat{\mathit{\gamma }}}_{B_t}^{B_k})$.

The gyroscope bias error is defined as follows:

$${\mathit{b}}_{Gyro,k}={\widehat{\mathit{b}}}_{Gyro,k}+\delta {\mathit{b}}_{Gyro,k}.$$

(42)

Substituting the Equations (41) and (42) into Equation (2), we have

$$\begin{array}{l}{\widehat{\mathit{C}}}_{B_t}^{B_k}({\mathit{I}}_3+[\delta {\mathit{\theta }}_{B_t}^{B_k}\times ])={\widehat{\mathit{C}}}_{B_i}^{B_k}({\mathit{I}}_3+[\delta {\mathit{\theta }}_{B_i}^{B_k}\times ]){\mathit{C}}_{B_t}^{B_i}\\ {\mathit{C}}_{B_t}^{B_i}\approx {\mathit{I}}_3+\mathsf{\Delta }t[({\tilde{\mathit{\omega }}}_{I{B}_t}^{B_t}-{\widehat{\mathit{C}}}_W^{B_t}({\mathit{I}}_3+[\delta {\mathit{\theta }}_W^{B_t}\times ]){\overline{\mathit{\omega }}}_{IE}^E-{\widehat{\mathit{b}}}_{Gyro,k}-\delta {\mathit{b}}_{Gyro,k}-{\mathit{\eta }}_{Gyro,t})\times ]\end{array},$$

(43)

where $t_k<t_i<t$, and $\mathsf{\Delta }t=t-t_i$, $\mathsf{\Delta }t$ is sufficiently small.

The expanded form of Equation (43) is as follows:

$$\begin{array}{l}[\delta {\mathit{\theta }}_{B_t}^{B_k}\times ]={\widehat{\mathit{C}}}_{B_i}^{B_t}[\delta {\mathit{\theta }}_{B_i}^{B_k}\times ]{\widehat{\mathit{C}}}_{B_t}^{B_i}-{\widehat{\mathit{C}}}_{B_i}^{B_t}({\mathit{I}}_3+[\delta {\mathit{\theta }}_{B_i}^{B_k}\times ])[(\delta {\mathit{b}}_{Gyro,k}+{\eta }_{Gyro,t})\mathsf{\Delta }t\times ]\\ \approx [\delta {\mathit{\theta }}_{B_i}^{B_k}\times ]-[{\widehat{\omega }}_{W{B}_t}^{B_t}\times ][\delta {\mathit{\theta }}_{B_i}^{B_k}\times ]\mathsf{\Delta }t+[\delta {\mathit{\theta }}_{B_i}^{B_k}\times ][{\widehat{\omega }}_{W{B}_t}^{B_t}\times ]\mathsf{\Delta }t-[(\delta {\mathit{b}}_{Gyro,k}+{\eta }_{Gyro,t})\mathsf{\Delta }t\times ]\\ =[\delta {\mathit{\theta }}_{B_i}^{B_k}\times ]-[([{\widehat{\mathit{\omega }}}_{W{B}_t}^{B_t}\times ]\delta {\mathit{\theta }}_{B_i}^{B_k})\times ]\mathsf{\Delta }t-[(\delta {\mathit{b}}_{Gyro,k}+{\eta }_{Gyro,t})\times ]\mathsf{\Delta }t\end{array},$$

(44)

where ${\widehat{\omega }}_{W{B}_t}^{B_t}={\tilde{\omega }}_{I{B}_t}^{B_t}-{\widehat{\mathit{C}}}_W^{B_t}{\overline{\mathit{\omega }}}_{IE}^E-{\widehat{\mathit{b}}}_{Gyro,k}$, ${\widehat{\mathit{C}}}_W^{B_t}{\overline{\mathit{\omega }}}_{\mathit{I}E}^E\approx {\widehat{\mathit{C}}}_W^{B_t}({\mathit{I}}_3+[\delta {\mathit{\theta }}_W^{B_t}\times ]){\overline{\mathit{\omega }}}_{IE}^E$ because the magnitudes of ${\overline{\mathit{\omega }}}_{IE}^E$ and $\delta {\mathit{\theta }}_W^{B_t}$ are both quite small. Moreover, ${\widehat{\mathit{C}}}_{B_i}^{B_t}={\mathit{I}}_3-[{\widehat{\omega }}_{W{B}_t}^{B_t}\mathsf{\Delta }t\times ]$. All second-order small terms are omitted.

Then, the attitude preintegration error dynamic equation can be derived as follows:

$$\delta {\dot{\mathit{\theta }}}_{B_i}^{B_k}=\underset{\mathsf{\Delta }t\to 0}{\lim }\frac{\delta {\mathit{\theta }}_{B_t}^{B_k}-\delta {\mathit{\theta }}_{B_i}^{B_k}}{\mathsf{\Delta }t}=-[{\widehat{\omega }}_{W{B}_i}^{B_i}\times ]\delta {\mathit{\theta }}_{B_i}^{B_k}-\delta {\mathit{b}}_{Gyro,k}-{\eta }_{Gyro,i}.$$

(45)

(2). Velocity preintegration error dynamic equation: The velocity preintegration error is defined as follows:

$${\mathit{\beta }}_{k,t}={\widehat{\mathit{\beta }}}_{k,t}+\delta {\mathit{\beta }}_{k,t},$$

(46)

where $\delta {\mathit{\beta }}_{k,t}$ is the velocity preintegration error at time t.

The accelerometer bias error is defined as follows:

$${\mathit{b}}_{Acc,k}={\widehat{\mathit{b}}}_{Acc,k}+\delta {\mathit{b}}_{Acc,k}.$$

(47)

According to the Equations (40), (41), (46), and (47), we have

$${\widehat{\mathit{\beta }}}_{k,t}+\delta {\mathit{\beta }}_{k,t}={\widehat{\mathit{\beta }}}_{k,i}+\delta {\mathit{\beta }}_{k,i}+{\widehat{\mathit{C}}}_{B_t}^{B_k}({\mathit{I}}_3+[\delta {\mathit{\theta }}_{B_t}^{B_k}\times ])({\tilde{\mathit{f}}}^{B_t}-{\widehat{\mathit{b}}}_{Acc,k}-\delta {\mathit{b}}_{Acc,k}-{\mathit{\eta }}_{Acc,t}).$$

(48)

The expanded form of Equation (48) is as follows:

$$\delta {\mathit{\beta }}_{k,t}\approx \delta {\mathit{\beta }}_{k,i}+{\widehat{\mathit{C}}}_{B_t}^{B_k}[\delta {\mathit{\theta }}_{B_t}^{B_k}\times ]{\widehat{\mathit{f}}}^{B_t}\mathsf{\Delta }t-{\widehat{\mathit{C}}}_{B_t}^{B_k}(\delta {\mathit{b}}_{Acc,k}+{\mathit{\eta }}_{Acc,t})\mathsf{\Delta }t,$$

(49)

where ${\widehat{\mathit{f}}}^{B_t}={\tilde{\mathit{f}}}^{B_t}-{\widehat{b}}_{Acc,k}$.

Then, the velocity preintegration error dynamic equation can be derived as follows:

$$\delta {\dot{\mathit{\beta }}}_{k,i}=\underset{\mathsf{\Delta }t\to 0}{\lim }\frac{\delta {\mathit{\beta }}_{k,t}-\delta {\mathit{\beta }}_{k,i}}{\mathsf{\Delta }t}=-{\widehat{\mathit{C}}}_{B_i}^{B_k}[{\widehat{\mathit{f}}}^{B_i}\times ]\delta {\mathit{\theta }}_{B_i}^{B_k}-{\widehat{\mathit{C}}}_{B_i}^{B_k}\delta b_{Acc,k}-{\widehat{\mathit{C}}}_{B_i}^{B_k}{\mathit{\eta }}_{Acc,i}.$$

(50)

(3). Position preintegration error dynamic equation: The position preintegration error is defined as follows:

$${\mathit{\alpha }}_{k,t}={\widehat{\mathit{\alpha }}}_{k,t}+\delta {\mathit{\alpha }}_{k,t},$$

(51)

where $\delta {\mathit{\alpha }}_{k,t}$ is the position preintegration error at time t.

The position preintegration is the integration of velocity preintegration, so

$$\delta {\dot{\mathit{\alpha }}}_{k,i}=\delta {\mathit{\beta }}_{k,i}.$$

(52)

Rewriting the Equations (39), (45), (50), and (52) in a matrix form, we have

$$\begin{array}{l}\left[\begin{array}{c}\delta {\dot{\mathit{\alpha }}}_{k,i}\\ \delta {\dot{\mathit{\beta }}}_{k,i}\\ \delta {\dot{\mathit{\theta }}}_{B_i}^{B_k}\\ \delta {\dot{\mathit{b}}}_{Acc,i}\\ \delta {\dot{\mathit{b}}}_{Gyro,i}\end{array}\right]=\left[\begin{array}{ccccc}{\mathbf{0}}_{3\times 3}& {\mathit{I}}_3& {\mathbf{0}}_{3\times 3}& {\mathbf{0}}_{3\times 3}& {\mathbf{0}}_{3\times 3}\\ {\mathbf{0}}_{3\times 3}& {\mathbf{0}}_{3\times 3}& -{\widehat{\mathit{C}}}_{B_i}^{B_k}[{\widehat{\mathit{f}}}^{B_i}\times ]& -{\widehat{\mathit{C}}}_{B_i}^{B_k}& {\mathbf{0}}_{3\times 3}\\ {\mathbf{0}}_{3\times 3}& {\mathbf{0}}_{3\times 3}& -[{\widehat{\omega }}_{W{B}_i}^{B_i}\times ]& {\mathbf{0}}_{3\times 3}& -{\mathit{I}}_3\\ {\mathbf{0}}_{3\times 3}& {\mathbf{0}}_{3\times 3}& {\mathbf{0}}_{3\times 3}& -\frac{1}{{\tau }_{Acc}}{\mathit{I}}_3& {\mathbf{0}}_{3\times 3}\\ {\mathbf{0}}_{3\times 3}& {\mathbf{0}}_{3\times 3}& {\mathbf{0}}_{3\times 3}& {\mathbf{0}}_{3\times 3}& -\frac{1}{{\tau }_{Gyro}}{\mathit{I}}_3\end{array}\right] \left[\begin{array}{c}\delta {\mathit{\alpha }}_{k,i}\\ \delta {\mathit{\beta }}_{k,i}\\ \delta {\mathit{\theta }}_{B_i}^{B_k}\\ \delta b_{Acc,i}\\ \delta b_{Gyro,i}\end{array}\right]+\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\left[\begin{array}{cccc}{\mathbf{0}}_{3\times 3}& {\mathbf{0}}_{3\times 3}& {\mathbf{0}}_{3\times 3}& {\mathbf{0}}_{3\times 3}\\ -{\widehat{\mathit{C}}}_{B_i}^{B_k}& {\mathbf{0}}_{3\times 3}& {\mathbf{0}}_{3\times 3}& {\mathbf{0}}_{3\times 3}\\ {\mathbf{0}}_{3\times 3}& -{\mathit{I}}_3& {\mathbf{0}}_{3\times 3}& {\mathbf{0}}_{3\times 3}\\ {\mathbf{0}}_{3\times 3}& {\mathbf{0}}_{3\times 3}& {\mathit{I}}_3& {\mathbf{0}}_{3\times 3}\\ {\mathbf{0}}_{3\times 3}& {\mathbf{0}}_{3\times 3}& {\mathbf{0}}_{3\times 3}& {\mathit{I}}_3\end{array}\right] \left[\begin{array}{c}{\mathit{\eta }}_{A\mathit{C}\mathit{C},i}\\ {\mathit{\eta }}_{Gyro,i}\\ n_{A\mathit{C}\mathit{C},i}\\ n_{Gyro,i}\end{array}\right]\end{array}.$$

(53)

Rewriting Equation (53) in compact form,

$$\delta {\dot{\mathit{𝓏}}}_i={\mathit{F}}_i\delta {\mathit{𝓏}}_i+{\mathit{B}}_i{\mathit{u}}_i,$$

(54)

where $\delta {\mathit{𝓏}}_i={[\delta {\mathit{\alpha }}_{k,i}^T,\delta {\mathit{\beta }}_{k,i}^T,\delta {\mathit{\theta }}_{B_i}^{B_k}{}^T,\delta {\mathit{b}}_{Acc,i}^T,\delta {\mathit{b}}_{Gyro,i}^T]}^T$ and ${\mathit{u}}_i={[{\mathit{\eta }}_{Acc,i}^T,{\mathit{\eta }}_{Gyro,i}^T,{\mathit{n}}_{Acc,i}^T,{\mathit{n}}_{Gyro,i}^T]}^T$.

According to the linear system theorem [37], the system can be discretized as follows:

$$\delta {\mathit{𝓏}}_j\approx ({\mathit{I}}_{15}+{\mathit{F}}_i\mathsf{\Delta }{t}_{ij})\delta {\mathit{𝓏}}_i+\mathsf{\Delta }{t}_{ij}{\mathit{B}}_i{\mathit{u}}_{ij}^{eq\mathit{u}}={\mathit{\Phi }}_{ji}\delta {\mathit{𝓏}}_i+{\mathit{G}}_i{\mathit{u}}_{ij}^{equ},$$

(55)

where ${\mathit{u}}_{ij}^{equ}$ is the equivalent noise during $[t_i,t_j]$, as follows:

$${\mathit{u}}_{ij}^{equ}=\frac{1}{\mathsf{\Delta }{t}_{ij}}{\displaystyle {\int }_{t_i}^{t_j}{\mathit{u}}_{\tau }\mathrm{d}\tau }.$$

(56)

The mean of ${\mathit{u}}_{ij}^{equ}$ is zero. The covariance is calculated as follows:

$$\mathrm{c}\mathrm{o}\mathrm{v}({\mathit{u}}_{ij}^{equ})=\frac{1}{\mathsf{\Delta }{t}_{ij}^2}{\displaystyle {\int }_{t_i}^{t_j}\mathrm{c}\mathrm{o}\mathrm{v}({\mathit{u}}_{\tau })\mathrm{d}\tau }=\frac{\mathit{Q}}{\mathsf{\Delta }{t}_{ij}}={\mathit{Q}}_{ij}^{equ},$$

(57)

where $\mathit{Q}=\mathrm{diag}({\mathit{\sigma }}_{Acc}^2,{\mathit{\sigma }}_{Gyro}^2,{\mathit{\sigma }}_{b_{Acc}}^2,{\mathit{\sigma }}_{b_{Gyro}}^2)$. Additionally, the equivalent noise ${\mathit{u}}_{ij}^{equ}$ is a Gaussian white noise sequence.

Hence, the square root information matrix of the equivalent noise is as follows:

$${\mathit{\Lambda }}_{ij}^{eq\mathit{u}}=\mathrm{diag}\left(\frac{\sqrt{\mathsf{\Delta }{t}_{ij}}}{{\mathit{\sigma }}_{Acc}}{\mathit{I}}_3,\frac{\sqrt{\mathsf{\Delta }{t}_{ij}}}{{\mathit{\sigma }}_{Gyro}}{\mathit{I}}_3,\frac{\sqrt{\mathsf{\Delta }{t}_{ij}}}{{\mathit{\sigma }}_{b_{A\mathit{C}\mathit{C}}}}{\mathit{I}}_3,\frac{\sqrt{\mathsf{\Delta }{t}_{ij}}}{{\mathit{\sigma }}_{b_{Gyro}}}{\mathit{I}}_3\right).$$

(58)

The transition matrix from $t_k$ to $t_{k+1}$ is propagated as follows:

$${\mathit{\Phi }}_{k+1,k}={\displaystyle \mathbf{\prod }_{t_i<t_j}{\mathit{\Phi }}_{ji}},$$

(59)

where $t_i$ and $t_j$ are adjacent IMU sampling epochs, and $t_i,t_j\in [t_k,t_{k+1}]$.

Set the square root information matrix of the IMU preintegration errors at time $t_i$ as ${\mathit{\Lambda }}_i$. Then, the square root information matrix ${\mathit{\Lambda }}_j$ can be calculated by performing QR decomposition on the following data matrix [33], as follows:

$${\mathit{U}}_{ij}\left[\begin{array}{cc}{\mathit{\Lambda }}_{ij}^{eq\mathit{u}}& {\mathbf{0}}_{3\times 3}\\ {\mathit{\Lambda }}_i{\mathit{\Phi }}_{ji}^{-1}{G}_i& -{\mathit{\Lambda }}_i{\mathit{\Phi }}_{ji}^{-1}\end{array}\right]=\left[\begin{array}{cc}{\mathit{\Lambda }}_a& {\mathit{\Lambda }}_b\\ {\mathbf{0}}_{3\times 3}& {\mathit{\Lambda }}_j\end{array}\right],$$

(60)

where ${\mathit{U}}_{ij}$ is a unitary matrix. The right side of Equation (60) is an upper triangular matrix. The initial square-root information matrix at time $t_k$ should be large enough, because the initial values of IMU preintegration are deterministic. In our implementation, the initial square-root information matrix is set as ${\mathit{\Lambda }}_k={10}^8\times {\mathit{I}}_{15}$.

3.3. IMU Preintegration Factor

Given the preintegrated IMU measurements, all residual functions are listed as follows:

$$\begin{array}{l}{\mathit{r}}_{\alpha }={\left({\mathit{C}}_{B_k}^W\right)}^T\{{\mathit{r}}_{W{B}_{k+1}}^W-{\mathit{r}}_{W{B}_k}^W-{\mathit{v}}_{W{B}_k}^W\mathsf{\Delta }{t}_{k,k+1}-0.5\times {\widehat{\mathit{g}}}_k^W\mathsf{\Delta }{t}_{k,k+1}^2\\ \hspace{1em}\hspace{1em}\hspace{1em}+2[{\overline{\mathit{\omega }}}_{IE}^W\times ]{\displaystyle {\sum }_{i=0}^{i=N}({\widehat{\mathit{p}}}_{W{B}_i}^W-{\widehat{\mathit{p}}}_{W{B}_k}^W)\mathsf{\Delta }{t}_i}\}-{\widehat{\mathit{\alpha }}}_{k,k+1}\\ \hspace{1em}\hspace{1em}\hspace{1em}-{\mathit{J}}_{k,k+1}^{\partial \mathit{\alpha }/\partial {\mathit{b}}_{Acc}}({\mathit{b}}_{Acc,k}-{\widehat{b}}_{Acc,k})-{\mathit{J}}_{k,k+1}^{\partial \mathit{\alpha }/\partial {\mathit{b}}_{Gy\mathit{r}o}}({\mathit{b}}_{Gy\mathit{r}o,k}-{\widehat{b}}_{Gy\mathit{r}o,k})\\ {\mathit{r}}_{\mathit{\beta }}={\left({\mathit{C}}_{B_k}^W\right)}^T({\mathit{v}}_{W{B}_{k+1}}^W-{\mathit{v}}_{W{B}_k}^W-{\widehat{\mathit{g}}}_k^W\mathsf{\Delta }{t}_{k,k+1}+2[{\overline{\mathit{\omega }}}_{IE}^W\times ]({\widehat{\mathit{p}}}_{W{B}_{k+1}}^W-{\widehat{\mathit{p}}}_{W{B}_k}^W))\\ \hspace{1em}-{\widehat{\mathit{\beta }}}_{k,k+1}-{\mathit{J}}_{k,k+1}^{\partial \mathit{\beta }/\partial {\mathit{b}}_{A\mathit{C}\mathit{C}}}({\mathit{b}}_{Acc,k}-{\widehat{\mathit{b}}}_{Acc,k})-{\mathit{J}}_{k,k+1}^{\partial \mathit{\beta }/\partial {\mathit{b}}_{Gy\mathit{r}o}}({\mathit{b}}_{Gy\mathit{r}o,k}-{\widehat{\mathit{b}}}_{Gy\mathit{r}o,k})\\ {\mathit{r}}_{\gamma }=2{[{\left({\mathit{q}}_{B_{k+1}}^W\right)}^{-1}\otimes {\mathit{q}}_{B_k}^W\otimes {\widehat{\mathit{\gamma }}}_{B_{k+1}}^{B_k}\otimes \delta {\mathit{\gamma }}_{B_{k+1}}^{B_k}]}_{\mathit{v}}\\ {\mathit{r}}_{{\mathit{b}}_{A\mathit{C}\mathit{C}}}={\mathit{J}}_{k+1,k}^{Acc}{\mathit{b}}_{Acc,k}-{\mathit{b}}_{Acc,k+1}\\ {\mathit{r}}_{b_{Gy\mathit{r}o}}={\mathit{J}}_{k+1,k}^{Gy\mathit{r}o}{\mathit{b}}_{Gy\mathit{r}o,k}-{\mathit{b}}_{Gy\mathit{r}o,k+1}\end{array},$$

(61)

where ${\mathit{J}}_{k,k+1}^{\partial \mathit{\alpha }/\partial b_{A\mathit{C}\mathit{C}}}={\mathit{\Phi }}_{k+1,k}[1:3,10:12]$, ${\mathit{J}}_{k,k+1}^{\partial \mathit{\alpha }/\partial b_{Gyro}}={\mathit{\Phi }}_{k+1,k}[1:3,13:15]$,${\mathit{J}}_{k,k+1}^{\partial \mathit{\beta }/\partial b_{A\mathit{C}\mathit{C}}}={\mathit{\Phi }}_{k+1,k}[4:6,10:12]$, ${\mathit{J}}_{k,k+1}^{\partial \mathit{\beta }/\partial b_{Gyro}}={\mathit{\Phi }}_{k+1,k}[4:6,13:15]$, ${\mathit{J}}_{k,k+1}^{\partial \gamma /\partial b_{Gyro}}={\mathit{\Phi }}_{k+1,k}[7:9,13:15]$, ${\mathit{J}}_{k+1,k}^{Acc}=\mathit{\Phi }[10:12,10:12]$, and ${\mathit{J}}_{k+1,k}^{Gyro}=\mathit{\Phi }[13:15,13:15]$. The function ${\mathit{\Phi }}_{k+1,k}[a:b,c:d]$ means the sub-block of ${\mathit{\Phi }}_{k+1,k}$ from $a$ to $b$ rows and $C$ to $d$ columns. Additionally,

$$\delta {\mathit{\gamma }}_{B_{k+1}}^{B_k}=\left[\begin{array}{c}1\\ 0.5{\mathit{J}}_{k,k+1}^{\partial \gamma /\partial b_{Gyro}}({\mathit{b}}_k-{\widehat{\mathit{b}}}_k)\end{array}\right].$$

All of the above residual functions should be weighted by the square-root information matrix ${\mathit{\Lambda }}_{k+1}$ before adding them to optimization.

4. Nonlinear Joint Optimization

We use the hybrid sliding window nonlinear optimization for state estimation (more details can be found in our previous work [34]).

The full state vector is defined as follows:

$$\mathit{\chi }=[{\mathit{x}}_n,\cdots ,{\mathit{x}}_{n+N},{\mathit{t}}_{B\mathit{C}},{\mathit{\psi }}_m,\cdots ,{\mathit{\psi }}_{m+M}],$$

(62)

where

$$\begin{array}{c}{\mathit{x}}_k=[{\mathit{p}}_{W{B}_k}^W,{\mathit{v}}_{W{B}_k}^W,{\mathit{q}}_{B_k}^W,{\mathit{b}}_{Acc,k},{\mathit{b}}_{Gyro,k}],k\in [n,n+N],\\ {\mathit{t}}_{BC}=[{\mathit{p}}_{BC}^B,{\mathit{q}}_C^B]\end{array}$$

where ${\mathit{\psi }}_m$ is the inverse depth parameter of the m-th mappoint from its first observing keyframe, N is the number of keyframes in the sliding window, M is the number of visible mappoints, and ${\mathit{t}}_{BC}$ is the camera-IMU calibration parameter.

The joint optimization problem can be formulated as a nonlinear least-squares problem. The cost function is the sum of the prior and the Mahalanobis norm of all measurement residuals within the sliding window, as follows:

$$\begin{array}{l}{\mathit{\chi }}^{*}=\arg {\min }_{\mathit{\chi }}\left|\right|{\mathit{r}}_p-{\mathit{H}}_p\mathit{\chi }|{|}^2+{\displaystyle \sum _{k\in 𝔅}\left|\right|{\mathit{r}}_{k+1,k}^{IMU}(\mathit{\chi })|{|}_{{\mathit{\Lambda }}_{k+1}}}+\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\displaystyle \sum _{(l,j)\in 𝒞}\rho \left(\left|\right|{\mathit{r}}_l^{C_j}(\mathit{\chi })|{|}_{{\mathit{\Lambda }}_l^{{\mathit{C}}_j}}\right)+{\displaystyle \sum _{k\in 𝒢}\left|\right|{\mathit{r}}_k^G(\mathit{\chi })|{|}_{{\mathit{\Lambda }}_k^G}}}\end{array},$$

(63)

where ${\mathit{r}}_p$ and ${\mathit{H}}_p$ represent the prior information; $𝔅$, $𝒞$, and $𝒢$ are the measurement set of the IMU, camera, and GNSS, respectively; ${\mathit{r}}_{k+1,k}^{IMU}(\mathit{\chi })$ is the IMU preintegration residual function, as shown in Equation (61); ${\mathit{r}}_l^{C_j}(\mathit{\chi })$ is the re-projection residual function of the l-th mappoint in the j-th image (more details can be found in [34]); $\rho (*)$ is the Huber loss function for coping with potential outliers [38]; ${\mathit{\Lambda }}_l^{C_j}$ is the square root information matrix of the visual measurement; and ${\mathit{r}}_k^G(\mathit{\chi })$ is the GNSS residual at time $t_k$, as follows:

$${\mathit{r}}_k^G={\mathit{p}}_{W{B}_k}^W+\mathit{C}({\mathit{q}}_{B_k}^W){\overline{\mathit{p}}}_{Bgnss}^B-{\overline{\mathit{C}}}_E^W({\tilde{\mathit{p}}}_{Egnss}^E-{\overline{\mathit{p}}}_{EW}^E),$$

(64)

where ${\overline{\mathit{C}}}_E^W$ and ${\overline{\mathit{p}}}_{EW}^E$ are functions of the geodetic position of the selected world frame; ${\overline{\mathit{p}}}_{Bgnss}^B$ is the lever arm vector between the GNSS antenna and IMU, measured manually; and ${\tilde{\mathit{p}}}_{Egnss}^E$ is the XYZ position of the GNSS antenna in the E frame, and provided by the GNSS receiver.

5. Experiments

In order to evaluate the performance of the proposed IMU preintegration algorithm, we conducted experiments by using the dataset collected by our sensor platform. Our sensor platform consists of a left-right stereo camera and two different grades of IMU, as shown in Figure 2. The stereo camera consists of two Prosilica GT 1910 monocular cameras by AVT. Both of them are global shutter monochrome CCD cameras which deliver 1920 × 1080 images. The cameras are synchronously triggered by an Arduino Uno R3 microcontroller at 10 Hz. The microcontroller parses GPS time from the NMEA messages provided by Ublox NEO-M8N. The two cameras are equipped with LM8HC lenses by Kowa. The horizontal field of view of the lens is about 60 degrees. The two IMUs are MTi-G-710 and POS620, respectively. The MTi-G-710 is an industrial-grade MEMS-based IMU by Xsens. The POS620 is a quasi-navigation-grade IMU by the MPSTNAV company of China, and contains three-axis high-precision fiber optic gyroscopes (FOGs).

The technical parameters of the two different-grade IMUs are listed in

Table 1. The technical parameters of MTi-G-710 and POS620.

IMU	Gyroscope		Accelerometer
	Angular Random Walk $(\mathit{d}\mathit{e}\mathit{g}/\sqrt{\mathit{h}})$	Bias Instability $(\mathit{d}\mathit{e}\mathit{g}/\mathit{h})$	Velocity Random Walk $\left(\mathit{m}/\mathit{s}/\sqrt{\mathit{h}}\right)$	Bias Instability $\left(\mathit{m}\mathit{G}\mathit{a}\mathit{l}\right)$
MTi-G-710	0.6	100	0.048	2000
POS620	0.005	0.02	0.01	25

. During data collection, the two IMUs were sampled at 200 Hz.

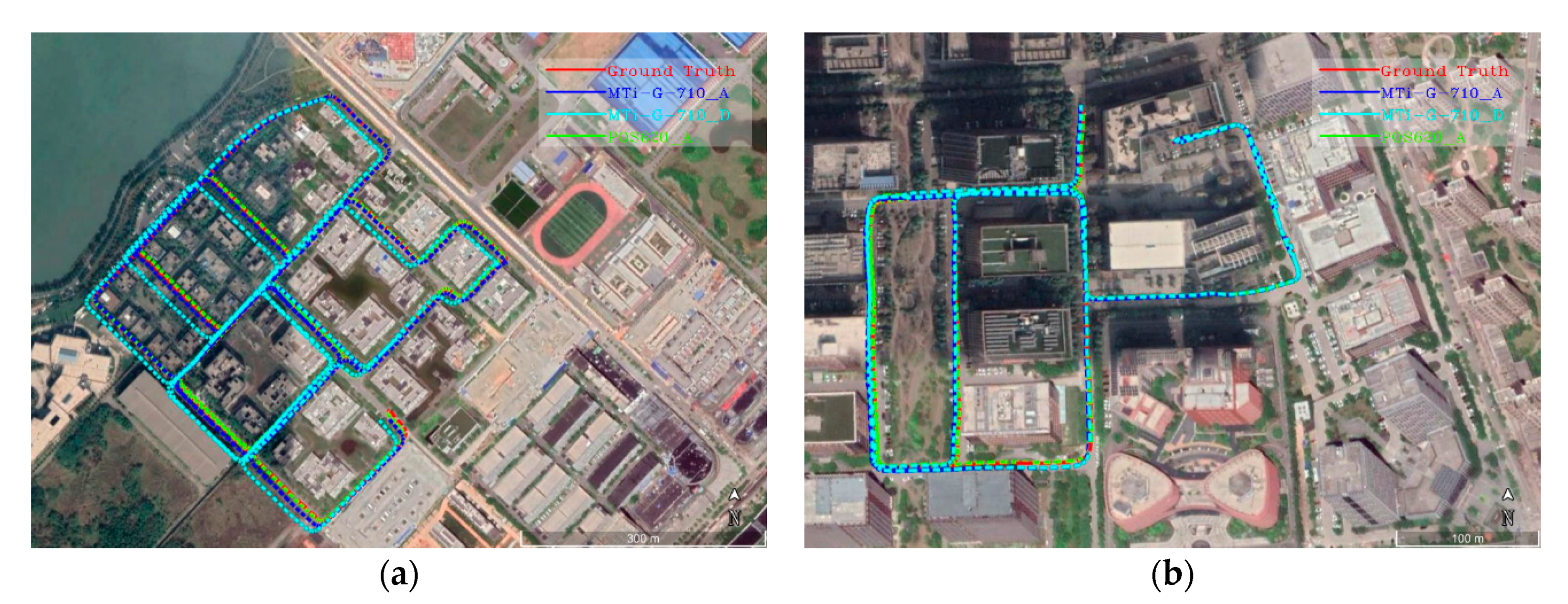
Our dataset contains two sequences collected at two different places in Wuhan city of China, namely the Wuhan Research and Innovation Center (WRIC) and the Guanggu financial harbor (GFH). There are many low-slung buildings and trees in the two places. These static objects provide a high-quality texture for visual measurements, as shown in Figure 3. Additionally, navigation satellite signals are not easily shielded or reflected in the two places. The GNSS raw data was recorded by the Trimble receiver. Furthermore, we used the GINS software developed by the MPSTNAV company of China to post-process the recorded GNSS raw data, in order to obtain high-precision real-time kinematic (RTK) positioning results.

Generally, the RTK positioning error was less than 0.10 m. The integrated navigation results of fusing the RTK positions and the POS620 measurements by Rauch-Tung-Striebel (RTS) smoothing served as the ground truth data. The dataset was used to evaluate the proposed IMU preintegration algorithm. It did not contain GNSS deny environment and visual challenges, such as overexposure, illumination changes, and poorly textured scenes. The motions performed by the vehicle during data collection were variable, including linear acceleration and deceleration, zero-speed motion, turning motion, and backward motion, i.e., almost all motions that can be performed by a ground vehicle. Additionally, changing slopes also exist in the two places. Therefore, the motions in the collected dataset were complicated enough to evaluate the proposed IMU preintegration algorithm.

Because it is quite difficult to obtain sufficient disparities from images recorded by a monocular camera when a vehicle runs along a straight road, we could not initialize the monocular visual-inertial system. For coping with this issue, stereo images were used to initialize the VINS. After initialization, only the images of the left side camera were used in optimization.

It is well-known that the earth is an approximate spheroid, and the direction of gravity approximately points to the center of the earth. Therefore, the direction and amplitude of gravity change with the position on the earth. For two positions that are far apart, the gravity vectors will be quite different. Therefore, it is imprecise for the traditional IMU preintegration algorithms to assume that the gravity vector is constant in the W frame, especially after the vehicle has traveled a long distance. An example is where the VINS system (maybe another system where the IMU preintegration technology is used) was initialized at city A and traveled to city B, where the W coordinate frame was located at city A. To simulate this situation, i.e., to amplify the influence of the change of gravity, we deliberately moved the W coordinate frame a certain distance from the starting position of the testing dataset. Specifically, if the geodetic position of the starting position was $\phi$, $\lambda$, and $h$, the geodetic displacement was $\delta \phi$, $\delta \lambda$, and $\delta h$, respectively. Then, the new position of the W coordinate frame was $\phi +\delta \phi$, $\lambda +\delta \lambda$, and $h+\delta h$, respectively. The new position of the W frame may not be located in a living area, and may be a mountain or a lake. However, this does not affect the evaluation of the proposed algorithm mathematically. In order to systematically evaluate the influence of the change of gravity, the geodetic displacement of the world frame was incrementally set as 0, 0.1, 0.25, 0.5, 1.0, and 2.0 degrees, where $\delta \phi =\delta \lambda$, $\delta h=0$. The corresponding Euclidean displacements were 0, 14.7, 36.7, 73.3, 146.4, and 292.1 kilometers. The new positions of the W frame were drawn in Google Earth, as shown in Figure 4.

In order to achieve good alignment with the geodetic frame, the RTK positions were added into optimization during the initial period, i.e., we directly used the RTK positioning results. Then, the RTK positions were removed after initialization, for better reflecting the impact of the IMU preintegration. At this time, the VINS system will have accurate prior information. For analyzing the influence of the earth rotation, the performance of the proposed IMU preintegration algorithm was also evaluated with or without a consideration of the earth rotation. Finally, the performance of the proposed IMU preintegration algorithm was evaluated under one of the four settings, as follows:

Setting A: Both the change of gravity and the earth rotation are considered, i.e., the proposed algorithm is used in a normal way;

Setting B: The change of gravity is considered, but the earth rotation is omitted;

Setting C: The change of gravity is omitted, but the earth rotation is considered;

Setting D: Both the change of gravity and the earth rotation are omitted, and the proposed IMU preintegration algorithm degenerates to a traditional IMU preintegration algorithm.

During the initial period, the proposed IMU preintegration algorithm was used under Setting A.

6. Results

The root-mean-square errors (RMSEs) of the estimated position, horizontal attitude, and yaw were calculated by comparing the estimated states with the ground truth data. All results are listed in

Table 2. The root-mean-square errors (RMSEs) of the position, horizontal attitude, and yaw of MTi-G-710 under different settings for the sequence at the test area of the Wuhan Research and Innovation Center (WRIC).

Shifting Distance (deg)	Setting A The Proposed Solution			Setting B With Gravity ChangeNo Earth Rotation			Setting C No Gravity ChangeWith Earth Rotation			Setting D The Traditional Solution
	P(m)	H(deg)	Y(deg)	P(m)	H(deg)	Y(deg)	P(m)	H(deg)	Y(deg)	P(m)	H(deg)	Y(deg)
0	5.46	0.077	0.52	5.53	0.064	0.37	4.23	0.073	0.25	5.00	0.065	0.47
0.1	4.90	0.068	0.42	5.26	0.070	0.56	4.65	0.161	0.41	3.84	0.172	0.61
0.25	5.54	0.066	0.51	5.34	0.074	0.44	5.51	0.350	0.49	4.75	0.355	0.66
0.5	4.44	0.079	0.35	5.67	0.082	0.41	8.73	0.680	0.37	8.75	0.681	0.57
1.0	5.11	0.076	0.49	4.28	0.085	0.50	9.55	1.338	0.64	9.13	1.339	0.67
2.0	5.03	0.070	0.36	5.69	0.073	0.33	20.9	2.640	0.42	15.9	2.654	0.49

,

Table 3. The RMSEs of the position, horizontal attitude, and yaw of MTi-G-710 under different settings for the sequence at the test area of the Guanggu financial harbor (GFH).

Shifting Distance (deg)	Setting A The Proposed Solution			Setting B With Gravity Change No Earth Rotation			Setting C No Gravity Change With Earth Rotation			Setting D The Traditional Solution
	P(m)	H(deg)	Y(deg)	P(m)	H(deg)	Y(deg)	P(m)	H(deg)	Y(deg)	P(m)	H(deg)	Y(deg)
0	3.05	0.064	0.48	2.72	0.066	0.48	2.58	0.064	0.55	3.07	0.065	0.73
0.1	2.67	0.070	0.42	2.45	0.059	0.68	2.64	0.154	0.51	2.83	0.162	0.69
0.25	2.96	0.076	0.63	2.42	0.065	0.54	2.59	0.339	0.59	3.02	0.347	0.54
0.5	2.40	0.065	0.52	3.18	0.064	0.36	3.76	0.673	0.57	3.83	0.674	0.36
1.0	3.03	0.068	0.50	2.59	0.074	0.55	5.21	1.334	0.50	4.92	1.330	0.49
2.0	2.74	0.065	0.68	3.17	0.065	0.48	9.04	2.643	0.75	9.16	2.644	0.50

and

Table 4. The RMSEs of the position, horizontal attitude, and yaw of POS620 under Setting A and Setting C for the dataset.

Shifting Distance (deg)	Setting A The Proposed Solution						Setting C No Gravity Change With Earth Rotation
	Sequence WRIC			Sequence GFH			Sequence WRIC			Sequence GFH
	P(m)	H(deg)	Y(deg)	P(m)	H(deg)	Y(deg)	P(m)	H(deg)	Y(deg)	P(m)	H(deg)	Y(deg)
0	1.50	0.017	0.45	0.55	0.011	0.09	1.27	0.017	0.38	0.55	0.011	0.10
0.1	1.78	0.017	0.52	0.81	0.012	0.19	2.36	0.133	0.34	1.83	0.134	0.23
0.25	1.52	0.017	0.49	0.70	0.012	0.11	8.28	0.323	1.90	---	---	---
0.5	1.86	0.017	0.60	0.62	0.012	0.09	---	---	---	---	---	---
1.0	1.28	0.018	0.41	0.78	0.012	0.18	---	---	---	---	---	---
2.0	1.40	0.019	0.44	0.63	0.012	0.09	---	---	---	---	---	---

Note: The notation --- means that the estimation diverged and crashed under this setting.

. Because all states were estimated from noisy sensor measurements by joint optimization, the final results were random due to the keyframe selection method and the change of the initial condition. However, the variation tendency of RMSEs was still obvious under different settings, especially for the RMSEs of the POS620 due to its high-precision measurements. The estimation results were diverged under Setting B and Setting D if the POS620 measurements were used in our implementation. Therefore, the RMSEs are not listed in Table 4. Additionally, the diverged estimation errors of POS620 are plotted in Figure 5.

The trajectories of the two IMUs for the sequences WRIC and GFH under different settings and two-degree geodetic displacements are plotted in Figure 6.

Due to the limited space of the paper, only some of the RMSEs obtained under different settings and different geodetic displacements are plotted in Figure 5, Figure 7, Figure 8 and Figure 9.

7. Discussion

In this section, we will discuss the influence of the gravity change and the earth rotation on the IMU preintegration, according to the results presented in the previous section.

According to the RMSEs of the horizontal attitude of the MTi-G-710 and POS620 under Setting A and Setting C presented in Table 2, Table 3 and Table 4, we can observe that ignoring the change of gravity makes the horizontal attitude errors increase as the geodetic displacement increases linearly. The RMSEs of the horizontal attitude error are about 1.38 times greater than the geodetic displacement. This tendency is also obvious in Figure 8b and Figure 9b, where the pitch and roll errors fluctuate sharply. If the vehicle moves in a small area, i.e., the geodetic displacement is almost 0 degrees, ignoring the change of gravity does not have much of an influence on the horizontal attitude errors, as shown in Table 2, Table 3 and Table 4, under Setting C. This phenomenon can also be directly observed in Figure 7.

According to the position RMSEs of MTi-G-710 under Setting A and Setting C presented in Table 2, we can observe that the RMSEs of the position are lower than 5.6 m under Setting A. The position RMSEs increase and become greater than 8.73 m under Setting C in Table 2, if the geodetic displacement is greater than 0.5 degrees. We can also observe a similar tendency under Setting A and Setting C in Table 3. The increase of the position RMSE becomes obvious when the geodetic displacement is greater than 1 degree, due to the short length of the sequence GFH.

According to the position RMSEs of POS620 under Setting A and Setting C presented in Table 4, we can observe that the position RMSEs are lower than 1.9 m in sequence WRIC and lower than 0.85 m in sequence GFH under Setting A. Additionally, the position RMSEs become greater than 2.36 m in sequence WRIC and 1.83 m in sequence GFH, if the geodetic displacement is greater than 0.1 degrees. The motion estimation results diverge under Setting C, if the geodetic displacement is greater than 0.25 degrees in the sequence WRIC and 0.1 degrees in the sequence GFH. Compared with the MTi-G-710, the POS620 is more sensitive to the change of gravity, due to its high-precision measurements, which means that it has a greater weight during information fusion. If the vehicle moves in a small area, i.e., the geodetic displacement is almost 0 degrees, ignoring the change of gravity has no obvious influence on the position errors for both low-grade and high-grade IMUs, as shown in Table 2, Table 3 and Table 4 under Setting C.

According to the RMSEs of the MTi-G-710 under Setting A and Setting B presented in Table 2 and Table 3, we can observe that ignoring the earth rotation has no obvious influence on the accuracy of the position and the horizontal attitude. From another perspective, the RMSEs of MTi-G-710 under Setting B and Setting D presented in Table 2 and Table 3 show that the positioning accuracy is obviously increased under large geodetic displacement by taking the change of gravity into consideration, but ignoring the earth rotation. Therefore, the earth rotation can be safely omitted for the industrial-grade MEMS-based IMU. In contrast, the motion estimation results diverge if the earth rotation is omitted from the measurements of the navigation-grade IMU (POS620), as shown in Figure 5. This is because the earth rotation is about $15\mathrm{deg}/h$, and the gyro bias instability and noise density of the angler random walk of the MTi-G-710 are $100\mathrm{deg}/h$ and $0.6\mathrm{deg}/\sqrt{h}$, respectively, making it impossible to sense the earth rotation. In contrast, the gyro bias instability and noise density of the angler random walk of the POS620 are about $0.02\mathrm{deg}/h$ and $0.005\mathrm{deg}/\sqrt{h}$, respectively. Therefore, the POS620 can sense the earth rotation effectively. At the same time, it should be noted that the higher noise density of MTi-G-710 makes the weight of its preintegrated IMU measurements lower, which makes the visual constrains more significant. However, the high grade of POS620 results in a greater weight of the preintegrated IMU measurements and reduces the effect of the visual constrains, making the system solution more sensitive to the modeling error of the earth rotation.

Since the yaw state is unobservable for the VINS and therefore cannot be estimated effectively [14], the drift of the yaw angle is completely random, making the yaw RMSEs stochastic under different settings and geodetic displacements, as shown in Table 2, Table 3 and Table 4.

8. Conclusions

In this paper, we have redesigned the IMU preintegration algorithm used in the optimization-based sensor fusion framework by taking the earth rotation and the change of gravity into consideration. Both of the two terms are functions of the geodetic position. In order to evaluate the proposed algorithm, we collected a dataset by using our sensor platform equipped with two different-grade IMUs. Then, the proposed algorithm was systematically evaluated by using the collected field dataset under different settings and test conditions. The test results led to the following conclusions: (1) The earth rotation can be safely omitted for industrial-grade MEMS-based IMUs that cannot sense the rotation effectively. However, for quasi-navigation-grade IMUs that can effectively sense the earth rotation, the earth rotation must be considered so as to maintain the positioning accuracy of the VINS; (2) if the change of gravity is omitted, the horizontal attitude error increases linearly as the geodetic displacement increases. Moreover, the RMSEs of the horizontal attitude error are about 1.38 times greater than the geodetic displacement. If the accuracy of the horizontal attitude matters, the change of gravity must be carefully considered; (3) if the change of gravity is omitted, the position error does not increase much within the limited working area. Furthermore, the threshold of the size of the limited working area is related to the IMU grade. According to the test results, for industrial-grade IMUs, the positioning error will not obviously increase within 0.25-degree geodetic displacement (36.7 km) if the gravity change is omitted. Additionally, for quasi-navigation-grade IMUs, the positioning error will also not increase if the limited size is about several hundred meters; (4) the performance of the proposed algorithm is consistent under different geodetic displacements and settings. Therefore, the proposed algorithm can cope well with the change of gravity and the earth rotation, forming a more robust GNSS/VINS solution.