Coral Reef Monitoring by Scuba Divers Using Underwater Photogrammetry and Geodetic Surveying
Abstract
1. Introduction
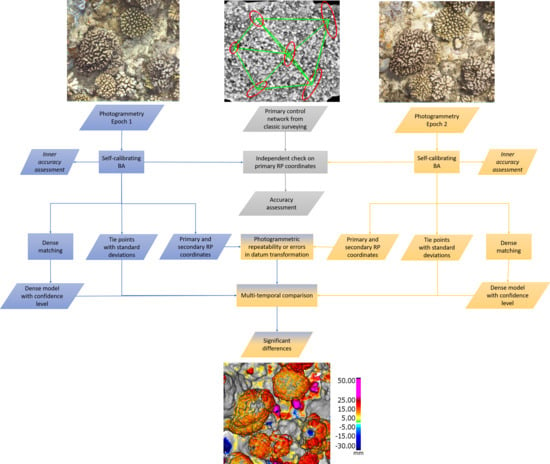
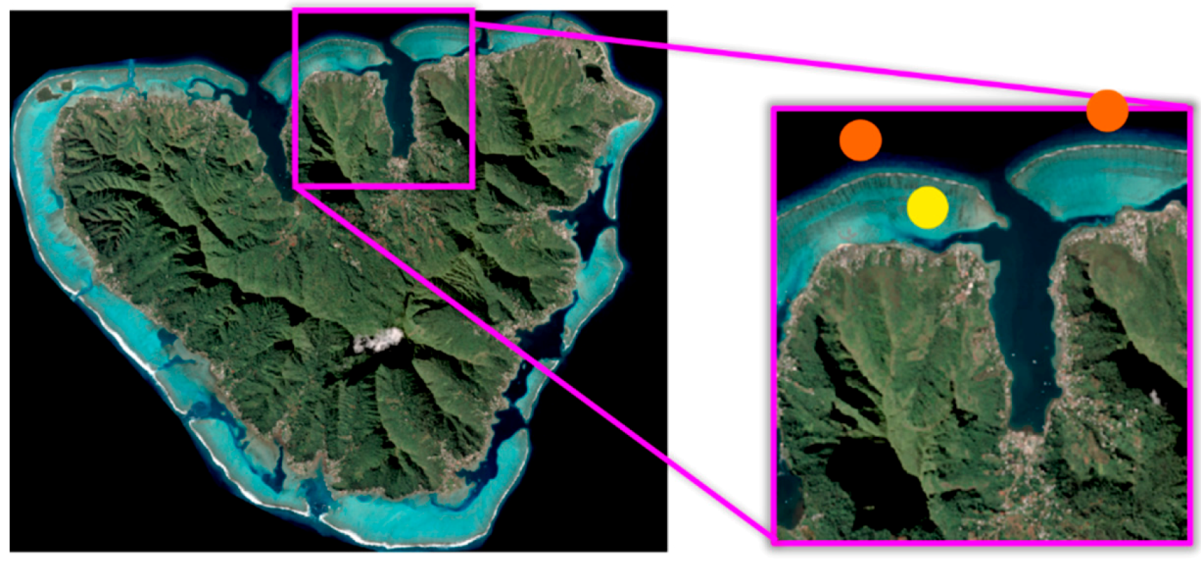
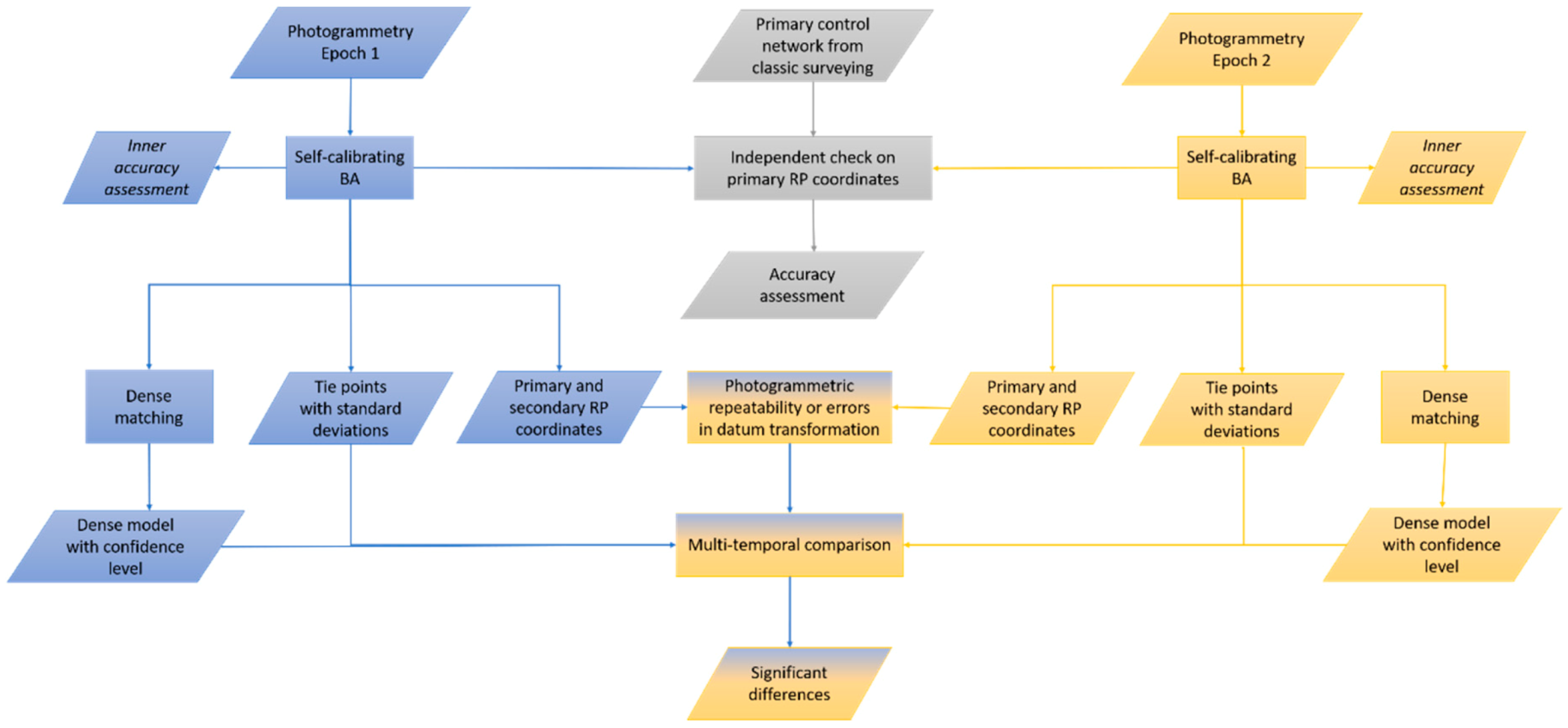
2. Four-Dimensional (4D) Monitoring and Change Detection of Moorea Coral Reefs
Primary and Secondary Control Networks for Coral Reef Monitoring
3. Comparison of Diver-Operated Underwater Photogrammetric Systems
- PL41: Panasonic Lumix GH4 (MIL)
- PL51-PL52: stereo system with two Panasonic Lumix GH5 (MIL)
- N750: Nikon D750 (DSLR)
- N300: Nikon D300 (DSLR)
- 5-GoPro: 5-head camera system with GoPro cameras named GoPro41 to GoPro45, where GoPro45 is the nadir looking camera.
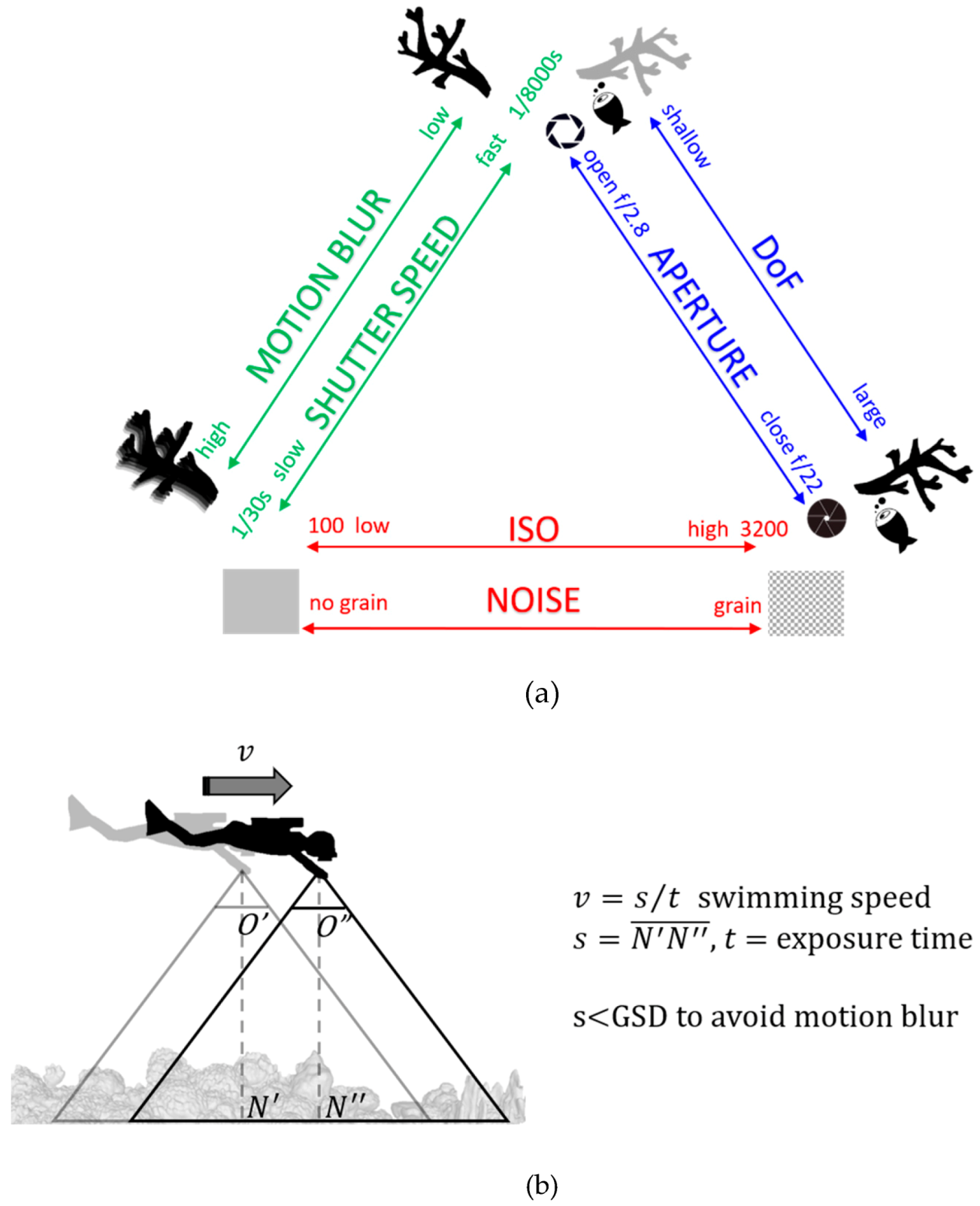
3.1. Camera Systems’ Set-Up
3.2. White Balance, Color Correction and Image Quality
3.3. Photogrammetric Processing
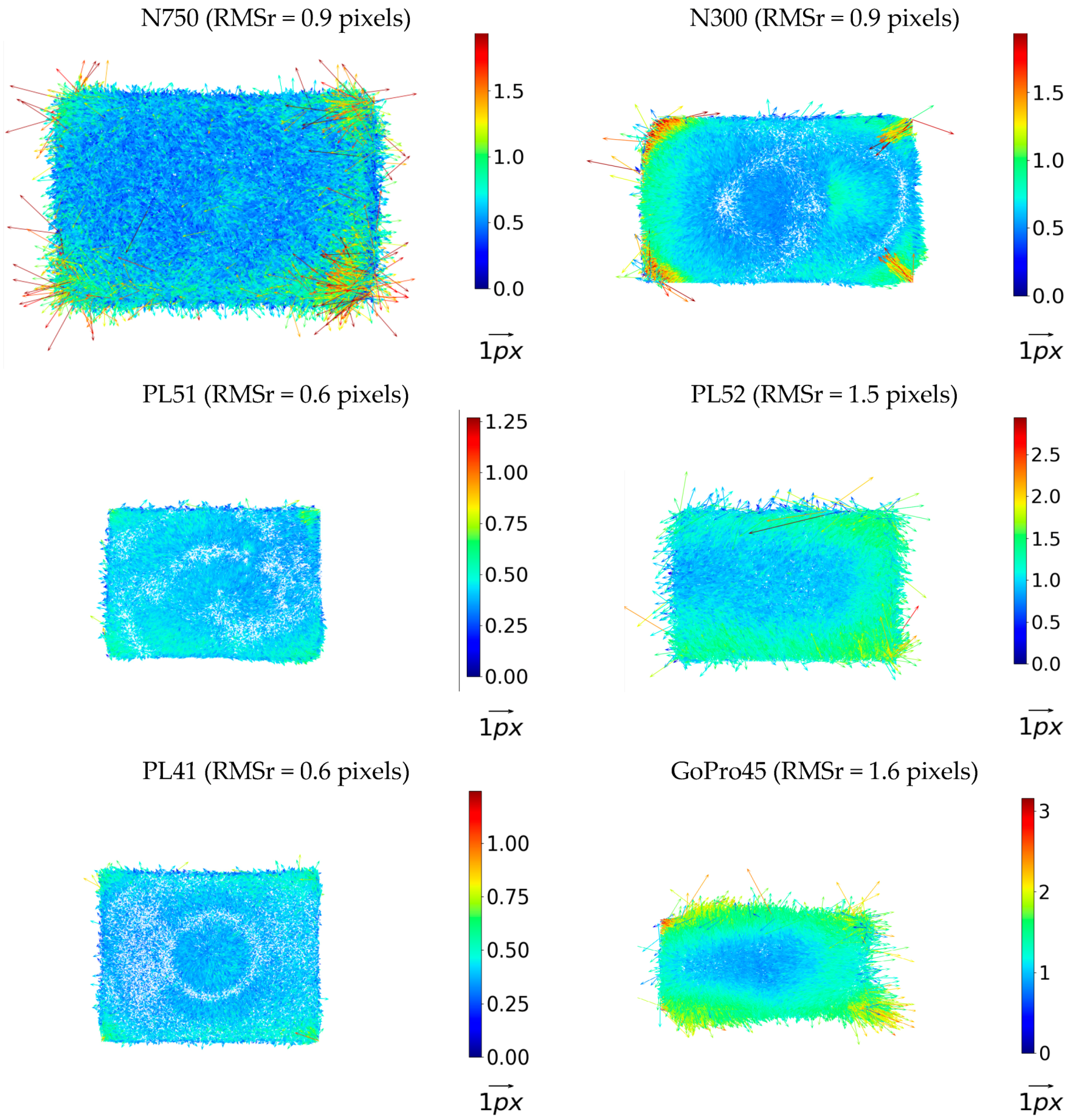
3.3.1. Residual Systematic Patterns
3.3.2. Object Space Analysis
4. Camera Network Analysis
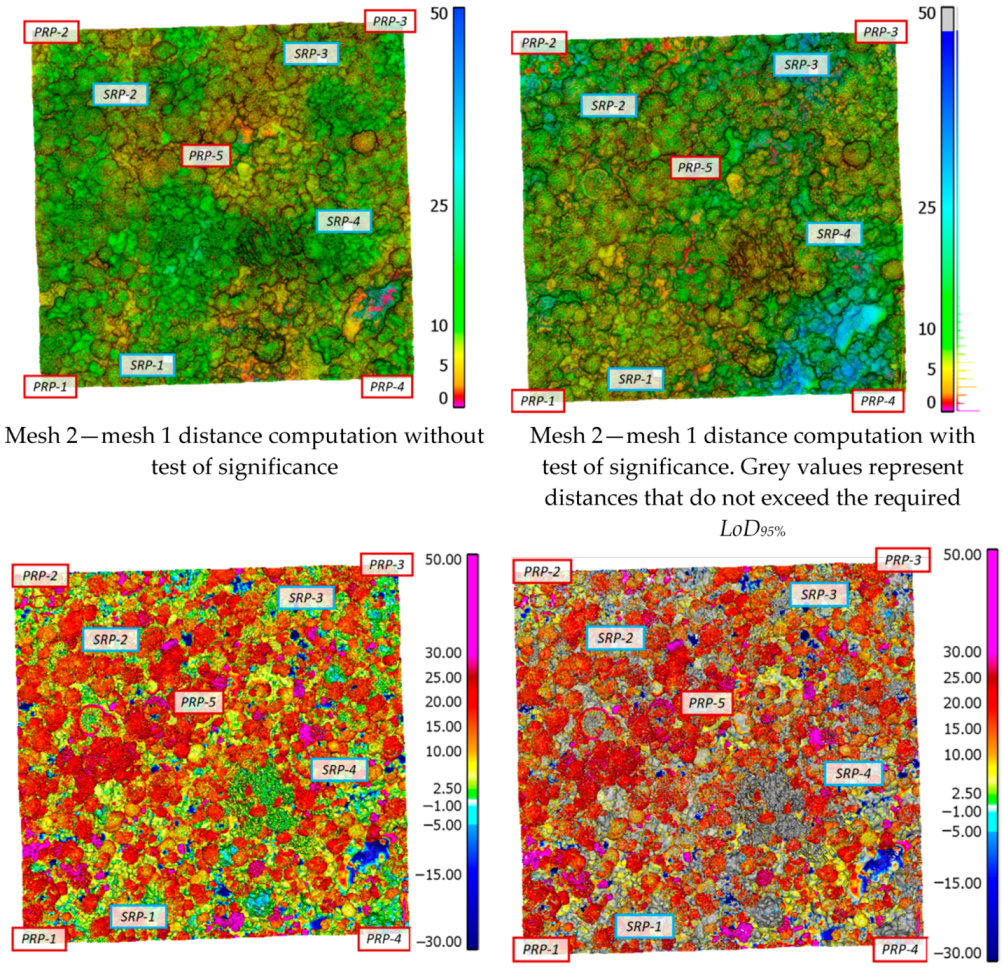
5. Level of Detection or Significance of Changes in Coral Reef Monitoring
- is computed for each vertex according to the t-statistics, which replaces the standard normal distribution when and , with a confidence level of 95% and a degree of freedom (DoF) computed as (Borradile, 2003; Langue et al., 2013):
- and are the tie points’ standard deviations from the covariance matrix and are transferred to the mesh vertices for epoch 1 and epoch 2,
- and are the number of stereo pairs for each vertex in the mesh for epoch 1 and epoch 2, respectively. The distances are disregarded if or < 2,
- is the registration error from epoch 2 to epoch 1.
6. Conclusions and Future Developments
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Drap, P.; Seinturier, J.; Hijazi, B.; Merad, D.; Boi, J.M.; Chemisky, B.; Seguin, E.; Long, L. The ROV 3D Project: Deep-sea underwater survey using photogrammetry: Applications for underwater archaeology. J. Comput. Cult. Herit. (JOCCH) 2015, 8, 1–24. [Google Scholar] [CrossRef]
- Menna, F.; Agrafiotis, P.; Georgopoulos, A. State of the art and applications in archaeological underwater 3D recording and mapping. J. Cult. Herit. 2018, 33, 231–248. [Google Scholar] [CrossRef]
- Figueira, W.; Ferrari, R.; Weatherby, E.; Porter, A.; Hawes, S.; Byrne, M. Accuracy and precision of habitat structural complexity metrics derived from underwater photogrammetry. Remote Sens. 2015, 7, 16883–16900. [Google Scholar] [CrossRef]
- Leon, J.X.; Roelfsema, C.M.; Saunders, M.I.; Phinn, S.R. Measuring coral reef terrain roughness using ‘Structure-from-Motion’ close-range photogrammetry. Geomorphology 2015, 242, 21–28. [Google Scholar] [CrossRef]
- Storlazzi, C.D.; Dartnell, P.; Hatcher, G.A.; Gibbs, A.E. End of the chain? Rugosity and fine-scale bathymetry from existing underwater digital imagery using structure-from-motion (SfM) technology. Coral Reefs 2016, 35, 889–894. [Google Scholar] [CrossRef]
- Menna, F.; Nocerino, E.; Nawaf, M.M.; Seinturier, J.; Torresani, A.; Drap, P.; Remondino, F.; Chemisky, B. Towards real-time underwater photogrammetry for subsea metrology applications. In Proceedings of the IEEE OCEANS 2019-Marseille, Marseille, France, 17–19 June 2019; pp. 1–10. [Google Scholar]
- Piazza, P.; Cummings, V.J.; Lohrer, D.M.; Marini, S.; Marriott, P.; Menna, F.; Nocerino, E.; Peirano, A.; Schiaparelli, S. Divers-operated underwater photogrammetry: Applications in the study of antarctic benthos. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 42, 885–892. [Google Scholar] [CrossRef]
- Capra, A.; Dubbini, M.; Bertacchini, E.; Castagnetti, C.; Mancini, F. 3D reconstruction of an underwater archaelogical site: Comparison between low cost cameras. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 40, 67–72. [Google Scholar] [CrossRef]
- Guo, T.; Capra, A.; Troyer, M.; Grün, A.; Brooks, A.J.; Hench, J.L.; Schmitt, R.J.; Holbrook, S.J.; Dubbini, M. Accuracy assessment of underwater photogrammetric three dimensional modelling for coral reefs. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 821–828. [Google Scholar] [CrossRef]
- Burns, J.H.R.; Delparte, D.; Gates, R.D.; Takabayashi, M. Integrating structure-from-motion photogrammetry with geospatial software as a novel technique for quantifying 3D ecological characteristics of coral reefs. PeerJ 2015, 3, e1077. [Google Scholar] [CrossRef]
- Mangeruga, M.; Bruno, F.; Cozza, M.; Agrafiotis, P.; Skarlatos, D. Guidelines for underwater image enhancement based on benchmarking of different methods. Remote Sens. 2018, 10, 1652. [Google Scholar] [CrossRef]
- Menna, F.; Nocerino, E.; Fassi, F.; Remondino, F. Geometric and optic characterization of a hemispherical dome port for underwater photogrammetry. Sensors 2016, 16, 48. [Google Scholar] [CrossRef] [PubMed]
- Maas, H.G. On the accuracy potential in underwater/multimedia photogrammetry. Sensors 2015, 15, 18140–18152. [Google Scholar] [CrossRef] [PubMed]
- Neyer, F.; Nocerino, E.; Grün, A. Monitoring coral growth–the dichotomy between underwater photogrammetry and geodetic control network. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, XLII-2, 759–766. [Google Scholar] [CrossRef]
- Capra, A.; Castagnetti, C.; Dubbini, M.; Gruen, A.; Guo, T.; Mancini, F.T.; Neyer, F.; Rossi, P.; Troyer, M. High Accuracy Underwater Photogrammetric Surveying. In Proceedings of the 3rd IMEKO International Conference on Metrology for Archeology and Cultural Heritage, Castello Carlo, Italy, 23–25 October 2017. [Google Scholar]
- Skarlatos, D.; Agrafiotis, P.; Menna, F.; Nocerino, E.; Remondino, F. Ground control networks for underwater photogrammetry in archaeological excavations. In Proceedings of the 3rd IMEKO International Conference on Metrology for Archaeology and Cultural Heritage, Lecce, Italy, 23–25 October 2017; pp. 23–25. [Google Scholar]
- Skarlatos, D.; Menna, F.; Nocerino, E.; Agrafiotis, P. Precision potential of underwater networks for archaeological excavation through trilateration and photogrammetry. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 42, 175–180. [Google Scholar] [CrossRef]
- Bryson, M.; Ferrari, R.; Figueira, W.; Pizarro, O.; Madin, J.; Williams, S.; Byrne, M. Characterization of measurement errors using structure-from-motion and photogrammetry to measure marine habitat structural complexity. Ecol. Evol. 2017, 7, 5669–5681. [Google Scholar] [CrossRef]
- Raoult, V.; Reid-Anderson, S.; Ferri, A.; Williamson, J.E. How reliable is Structure from Motion (SfM) over time and between observers? A case study using coral reef bommies. Remote Sens. 2017, 9, 740. [Google Scholar] [CrossRef]
- Moorea Island Digital Ecosystem Avatar Project. Available online: https://mooreaidea.ethz.ch/ (accessed on 27 July 2020).
- Nocerino, E.; Neyer, F.; Grün, A.; Troyer, M.; Menna, F.; Brooks, A.J.; Capra, A.; Castagnetti, C.; Rossi, P. Comparison of diver-operated underwater photogrammetric systems for coral reef monitoring. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 42, 143–150. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S.; Smith, M.W. 3-D uncertainty-based topographic change detection with structure-from-motion photogrammetry: Precision maps for ground control and directly georeferenced surveys. Earth Surf. Process. Landf. 2017, 42, 1769–1788. [Google Scholar] [CrossRef]
- Rodarmel, C.A.; Lee, M.P.; Brodie, K.L.; Spore, N.J.; Bruder, B. Rigorous Error Modeling for sUAS Acquired Image-Derived Point Clouds. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6240–6253. [Google Scholar] [CrossRef]
- Rossi, P.; Castagnetti, C.; Capra, A.; Brooks, A.J.; Mancini, F. Detecting change in coral reef 3D structure using underwater photogrammetry: Critical issues and performance metrics. Appl. Geomat. 2019, 12, 3–17. [Google Scholar] [CrossRef]
- Cressey, D. Tropical paradise inspires virtual ecology lab. Nature 2015, 517, 255–256. Available online: https://www.nature.com/news/tropical-paradise-inspires-virtual-ecology-lab-1.16710 (accessed on 27 July 2020). [CrossRef] [PubMed]
- Gruen, A.; Troyer, M.; Guo, T. Spatiotemporal physical modeling of tropical islands within the Digital Ecosystem Avatar (IDEA) Project. In Proceedings of the 19 Internationale Geodätische Woche Obergurgl 2017, Obergurgl, Austria, 12–18 February 2017; pp. 174–179. [Google Scholar]
- Guillaume, S.; Muller, C.; Cattin, P.-H. Trinet+, Logiciel de Compensation 3D Version 6.1, Mode d’Emploi, HEIG-VD; Yverdon, Switzerland, 2008. [Google Scholar]
- GAMA. Available online: http://www.gnu.org/software/gama/ (accessed on 27 July 2020).
- Menna, F.; Nocerino, E.; Remondino, F. Optical aberrations in underwater photogrammetry with flat and hemispherical dome ports. In Proceedings of the Videometrics, Range Imaging, and Applications XIV, Munich, Germany, 26–27 June 2017; International Society for Optics and Photonics: Bellingham, WA, USA; Volume 10332, p. 1033205. [Google Scholar]
- Nocerino, E.; Nawaf, M.M.; Saccone, M.; Ellefi, M.B.; Pasquet, J.; Royer, J.P.; Drap, P. Multi-camera system calibration of a low-cost remotely operated vehicle for underwater cave exploration. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 42, 329–337. [Google Scholar] [CrossRef]
- Akkaynak, D.; Treibitz, T. Sea-thru: A method for removing water from underwater images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 1682–1691. [Google Scholar]
- Neyer, F.; Nocerino, E.; Grün, A. Image Quality Improvements in Low-Cost Underwater Photogrammetry. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 42, 135–142. [Google Scholar] [CrossRef]
- Agisoft Metashape, Version 1.6 Professional Edition. Available online: http://www.agisoft.com/ (accessed on 27 July 2020).
- DBAT. Available online: https://github.com/niclasborlin/dbat/ (accessed on 27 July 2020).
- Börlin, N.; Grussenmeyer, P. Bundle adjustment with and without damping. Photogramm. Rec. 2013, 28, 396–415. [Google Scholar] [CrossRef]
- Menna, F.; Nocerino, E.; Remondino, F. Flat versus hemispherical dome ports in underwater photogrammetry. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 481–487. [Google Scholar]
- James, M.R.; Robson, S. Mitigating systematic error in topographic models derived from UAV and ground-based image networks. Earth Surf. Process. Landf. 2014, 39, 1413–1420. [Google Scholar] [CrossRef]
- Nocerino, E.; Menna, F.; Remondino, F. Accuracy of typical photogrammetric networks in cultural heritage 3D modeling projects. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, XL-5, 465–472. [Google Scholar] [CrossRef]
- Menna, F.; Nocerino, E.; Ural, S.; Gruen, A. Mitigating image residuals systematic patterns in underwater photogrammetry. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 43, 977–984. [Google Scholar] [CrossRef]
- Lague, D.; Brodu, N.; Leroux, J. Accurate 3D comparison of complex topography with terrestrial laser scanner: Application to the Rangitikei canyon (NZ). ISPRS J. Photogramm. Remote Sens. 2013, 82, 10–26. [Google Scholar]
- Furukawa, Y.; Hernández, C. Multi-view stereo: A tutorial. Found. Trends Comput. Graph. Vis. 2015, 9, 1–48. [Google Scholar] [CrossRef]
- Vu, H.H.; Labatut, P.; Pons, J.P.; Keriven, R. High accuracy and visibility-consistent dense multiview stereo. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 34, 889–901. [Google Scholar] [CrossRef] [PubMed]
- Kuhn, A.; Mayer, H.; Hirschmüller, H.; Scharstein, D. A TV prior for high-quality local multi-view stereo reconstruction. In Proceedings of the IEEE 2014 2nd International Conference on 3D Vision, Tokyo, Japan, 8–11 December 2014; Volume 1, pp. 65–72. [Google Scholar]
- Gruen, A.; Baltsavias, E.P. Adaptive least squares correlation with geometrical constraints. In Computer Vision for Robots; International Society for Optics and Photonics: Bellingham, WA, USA, 1986; Volume 595, pp. 72–82. [Google Scholar]
- Borradaile, G.J. Statistics of Earth Science Data: Their Distribution in Time, Space and Orientation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Zach, C.; Pock, T.; Bischof, H. A globally optimal algorithm for robust tv-l 1 range image integration. In Proceedings of the 2007 IEEE 11th International Conference on Computer Vision, Rio de Janeiro, Brazil, 14–21 October 2007; pp. 1–8. [Google Scholar]
- Cloud-to-Mesh Distance, CloudCompare. Available online: https://www.cloudcompare.org/doc/wiki/index.php?title=Cloud-to-Mesh_Distance (accessed on 27 July 2020).
- Menna, F.; Nocerino, E.; Drap, P.; Remondino, F.; Murtiyoso, A.; Grussenmeyer, P.; Börlin, N. Improving underwater accuracy by empirical weighting of image observations. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 42, 699–705. [Google Scholar] [CrossRef]
- d’Autume, M.G. Le traitement des erreurs systematique dans l’aerotriangulation. In Proceedings of the XIIth Congress of the ISP, Commission 3, Ottawa, ON, Canada, 24 July–4 August 1972. [Google Scholar]
- Pavoni, G.; Corsini, M.; Callieri, M.; Palma, M.; Scopigno, R. Semantic segmentation of benthic communities rom ortho-mosaic maps. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-2, 151–158. [Google Scholar] [CrossRef]









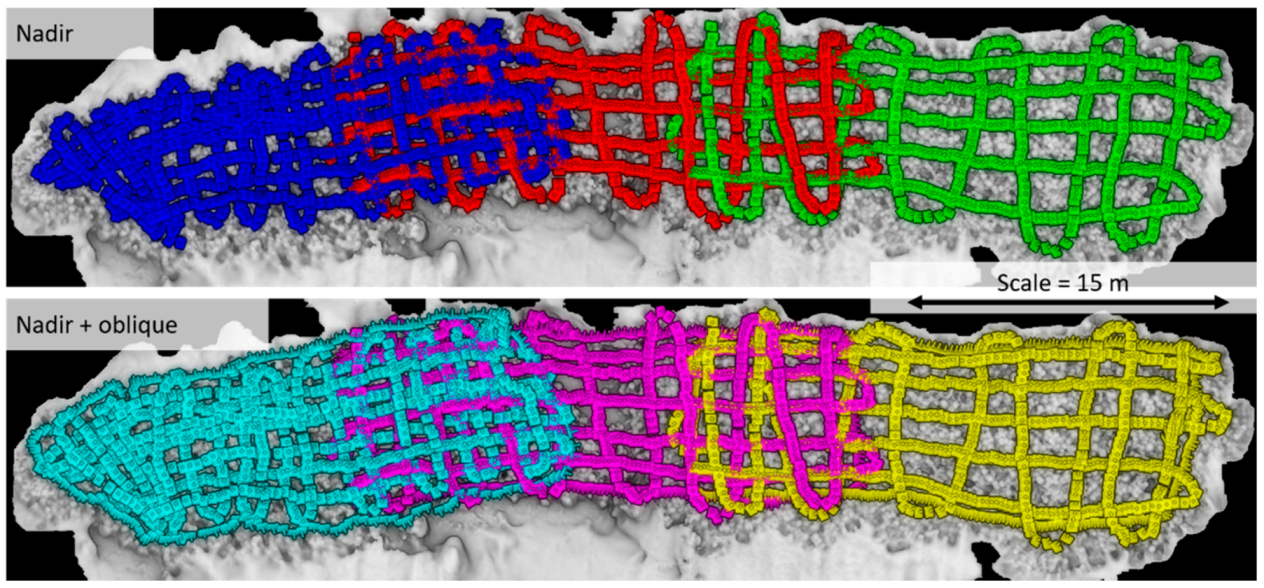



| 16 × 8 m Plot—Fringing Reef | 5 × 5 m Plots—Fore Reef 1 | 20 × 5 m Plot—Fore Reef | 50 × 10 m Plot—Fore Reef | |
|---|---|---|---|---|
| #PRP | 13 | 5 | 11 | 32 |
| DOF | 78 | 16 | 51 | 175 |
| σXY | 3.2 mm | 2.3 mm | 4.4 mm | 5.4 mm |
| σZ | 2.6 mm | 2.0 mm | 3.0 mm | 4.2 mm |
| Average Depth | 5 m | 10 m | 10 m | 12 m |
| Depth Range | 3 m | 2 m | 1 m | 4 m |
| System Acronym | N750 | N300 | PL51-PL52 | PL41 | 5-GoPro (GoPro41 to GoPro45) |
|---|---|---|---|---|---|
| Camera Type | DSLR | DSLR | MIL | MIL | Action cam |
| Camera Body | Nikon D750 | Nikon D300 | Panasonic Lumix GH5S | Panasonic Lumix GH4 | GoPro Hero 4 Black edition |
| Sensor Type (Dimensions (mm)) | Full frame (35.9 × 24) | APS-C (23.6 × 15.8) | Four thirds (17.3 × 13) | Four thirds (17.3 × 13) | 1/2.3 inch (6.17 × 4.55) |
| Pixel Size (um) | 6.0 | 5.6 | 4.6 | 3.8 | 1.5 |
| Image Size (pixel) | 6016 × 4016 | 4288 × 2848 | 3680 × 2760 | 4608 × 3456 | 3840 × 2160 |
| Lens (For zoom lenses, focused at focal length) | Nikkor 24 mm f/2.8 D | Nikkor 18–105 mm f/3.5–5.6 (at 18 mm) with +4 diopter 1 | Lumix G 14 mm f/2.5 | Olympus M. 12–50 mm f/3.25–6.3 (at 22 mm) | 3 mm |
| Underwater Pressure Housing (material) | NiMAR NI3D750ZM (polycarbonate) | Ikelite 6812.3 iTTL (polycarbonate) | Nauticam NA-GH5 (aluminum) | Nauticam NA-GH4 (aluminum) | GoPro housing (polycarbonate) |
| Port lens (material) | NiMAR NI320 dome-port (acrylic) | Ikelite 5503.55 dome-port (acrylic) | Nauticam N85 3.5” wide-angle dome-port (acrylic) | Nauticam N85 Macro Port (glass) with Wet Wide-Lens 1 (WWL-1) dome-port (glass) | Flat with red filters (glass) |
| N750 | N300 | PL41 | PL51 | PL52 | GoPro45 | |
|---|---|---|---|---|---|---|
| Working distance: 2 m | ||||||
| GSD (mm) | 0.5 | 0.6 | 0.6 | 0.8 | 0.7 | 1.2 |
| Number of images | 304 | 581 | 451 | 523 | 523 | 431 |
| Working distance: 5 m | ||||||
| GSD (mm) | 1.2 | - | 1.4 | 1.4 | 1.4 | 2.2 |
| Number of images | 101 | - | 139 | 166 | 166 | 430 |
| Mean intersection angle (degrees) | 27.9 | - | 30.4 | 24.9 | 25.5 | 27.8 |
| N750 | N300 | PL51 | PL52 | PL41 | 5-GoPro | ||
|---|---|---|---|---|---|---|
| Acquisition Mode | Single shot | Single shot | Time lapse @ 2 s shooting interval | Single shot | Video @ 30 frame per seconds (Field of view = wide) | |
| Original Images/Video Format | raw | raw | raw | raw | MP4 | |
| Exported Images/Extracted Frames Format | JPG @ highest quality | JPG @ highest quality | JPG @ highest quality | JPG @ highest quality | PNG (then converted to JPG @ highest quality) | |
| Shooting Mode | Aperture priority | Aperture priority | Aperture priority | Shutter priority | - | |
| Aperture Value | f/8 | f/5.6 | f/5.6 | - | f/2.8 | |
| Shutter Speed | - | - | - | 1/250 | 1/120 | |
| Minimum Shutter Speed | 1/250 | 1/125 | 1/250 | - | - | |
| Shutter Mode | mechanical | mechanical | Mechanical | electronic | Mechanical | Electronic | |
| Iso Mode | AUTO | AUTO | AUTO | AUTO | MAX 1 | |
| Iso lower | Upper auto Limit | 100 | 3200 | 200 | 1600 | 100 | 1600 | 200 | 1600 | 400 | 1600 | |
| Focus | First Shot | Auto focus | Auto focus | Auto focus | Auto focus continuous | - |
| Entire Acquisition | Manual | Manual | Manual | - | ||
| N750 | N300 | PL41 | PL51 | PL52 | GoPro45 | |
|---|---|---|---|---|---|---|
| Working distance: 2m | ||||||
| RMSr (pixel) | 0.9 | 0.8 | 0.6 | 0.6 | 1.5 | 1.6 |
| RMSEXY on PRPs (mm) | 3.8 | 3.9 | 3.8 | 2.9 | 3.5 | 4.0 |
| RMSEZ on PRPs (mm) | 2.6 | 5.0 | 2.3 | 2.1 | 3.6 | 2.6 |
| RMSEXYZ on PRPs (mm) | 3.5 | 4.3 | 3.4 | 3.2 | 3.5 | 3.6 |
| 3D_RMSEXYZ on PRPs (mm) | 6.0 | 7.4 | 5.8 | 5.5 | 6.1 | 6.3 |
| MAX ERROR [on PRP] (mm) | 9.4 [2] | 10.3 [2] | 9.3 [2] | 8.4 [2] | 7.7 [2] | 9.6 [2] |
| σX | σY | σZ (mm) | 0.9|0.9|1.3 | 0.6|0.6|1.1 | 1.5|1.5|1.8 | 0.8|0.8|1.1 | 1.6|1.6|3.7 | 2.2|2.1|3.8 |
| Working distance: 5m | ||||||
| RMSr (pixel) | 0.8 | - | 0.4 | 0.4 | 1.2 | 1.7 |
| RMSEXY on PRPs (mm) | 3.8 | - | 3.9 | 3.5 | 4.1 | 3.5 |
| RMSEZ on PRPs (mm) | 3.1 | - | 2.9 | 2.6 | 6.2 | 3.1 |
| RMSEXYZ on PRPs (mm) | 3.6 | - | 3.6 | 3.2 | 4.9 | 3.4 |
| 3D_RMSEXYZ on PRPs (mm) | 6.2 | - | 6.2 | 5.6 | 8.4 | 5.8 |
| MAX ERROR [on PRP] (mm) | 10.1 [2] | - | 9.1 [2] | 7.4 [2] | 11.5 [5] | 8.6 [1] |
| σX | σY | σZ (mm) | 0.8|0.8|1.8 | - | 0.5|0.5|1.2 | 0.6|0.5|1.2 | 1.7|1.7|3.7 | 3.2|3.4|5.8 |
| 5 vs. 2m | |||||
|---|---|---|---|---|---|
| N750 | N300 | PL41 | PL51 | PL52 | GoPro45 |
| 0.4|1.0|1.2 | - | 0.8|2.5|2.7 | 0.6|1.7|1.9 | 2.1|4.3|5.2 | 1.2|3.3|3.8 |
| N750 | N300 | PL41 | PL51 | PL52 | GoPro45 | |
|---|---|---|---|---|---|---|
| Working distance: 2 m | ||||||
| N750 | - | |||||
| N300 | 1.1|3.4|3.7 | - | ||||
| PL41 | 0.4|0.6|0.8 | 1.0|3.8|4.1 | - | |||
| PL51 | 1.0|1.4|2.0 | 0.8|2.9|3.1 | 0.8|1.8|2.2 | - | ||
| PL52 | 1.6|1.4|2.7 | 1.5|3.4|4.0 | 1.6|1.4|2.6 | 1.0|2.5|2.9 | - | |
| GoPro45 | 0.9|1.3|1.8 | 0.7|2.5|2.7 | 0.8|1.9|2.1 | 0.8|1.0|1.5 | 1.3|2.2|3.0 | - |
| Working distance: 5 m | ||||||
| N750 | - | - | ||||
| N300 | - | - | ||||
| PL41 | 0.6|3.6|3.8 | - | - | |||
| PL51 | 0.6|1.9|2.1 | - | 1.0|5.0|5.2 | - | ||
| PL52 | 1.1|4.2|4.5 | - | 1.4|7.5|7.8 | 1.2|3.3|3.7 | - | |
| GoPro45 | 1.1|3.1|3.5 | - | 1.1|4.2|4.5 | 1.1|3.8|4.1 | 1.0|6.0|6.2 | - |
| Nadir | Nadir + Oblique | |
|---|---|---|
| # images | 2600 | 3300 |
| Average GSD (mm) | 0.69 | 0.74 |
| RMS reprojection error (pixel) | 0.74 | 0.71 |
| RMSEXY | RMSEZ | 3D_RMSEXYZ (mm) | 16.5 | 107.3 | 109.8 | 13.4 | 12.8 | 22.9 |
| Epoch 1 (2018) | Epoch 2 (2019) | |
|---|---|---|
| Working distance (m) | 2.0 | 2.0 |
| GSD (mm) | 0.8 | 0.9 |
| Number of Images | 523 | 318 |
| RMS Reprojection Error (pixel) | 0.6 | 0.6 |
| RMSEXY | RMSEZ | RMSEXYZ on PRP (mm) from Geodetic Network | 2.9 | 2.3 | 3.2 | 2.3|1.8|3.8 |
| RMSEXY | RMSEZ | RMSEXYZ on PRP + SRPs (mm) from Epoch 1 | - | 1.3|0.9|1.6 |
| σX | σY | σZ | σXYZ (mm) | 0.8|0.8|1.1|1.6 | 0.8|0.7|1.5|1.9 |
| Mesh Resolution (mm) | 0.1 | 0.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nocerino, E.; Menna, F.; Gruen, A.; Troyer, M.; Capra, A.; Castagnetti, C.; Rossi, P.; Brooks, A.J.; Schmitt, R.J.; Holbrook, S.J. Coral Reef Monitoring by Scuba Divers Using Underwater Photogrammetry and Geodetic Surveying. Remote Sens. 2020, 12, 3036. https://doi.org/10.3390/rs12183036
Nocerino E, Menna F, Gruen A, Troyer M, Capra A, Castagnetti C, Rossi P, Brooks AJ, Schmitt RJ, Holbrook SJ. Coral Reef Monitoring by Scuba Divers Using Underwater Photogrammetry and Geodetic Surveying. Remote Sensing. 2020; 12(18):3036. https://doi.org/10.3390/rs12183036
Chicago/Turabian StyleNocerino, Erica, Fabio Menna, Armin Gruen, Matthias Troyer, Alessandro Capra, Cristina Castagnetti, Paolo Rossi, Andrew J. Brooks, Russell J. Schmitt, and Sally J. Holbrook. 2020. "Coral Reef Monitoring by Scuba Divers Using Underwater Photogrammetry and Geodetic Surveying" Remote Sensing 12, no. 18: 3036. https://doi.org/10.3390/rs12183036
APA StyleNocerino, E., Menna, F., Gruen, A., Troyer, M., Capra, A., Castagnetti, C., Rossi, P., Brooks, A. J., Schmitt, R. J., & Holbrook, S. J. (2020). Coral Reef Monitoring by Scuba Divers Using Underwater Photogrammetry and Geodetic Surveying. Remote Sensing, 12(18), 3036. https://doi.org/10.3390/rs12183036