Comparison of Different Missing-Imputation Methods for MAIAC (Multiangle Implementation of Atmospheric Correction) AOD in Estimating Daily PM2.5 Levels
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Satellite-Retrieved Product
2.1.2. Daily Monitoring Data
2.1.3. Meteorological Data and Land-Cover Data
2.2. Methodology
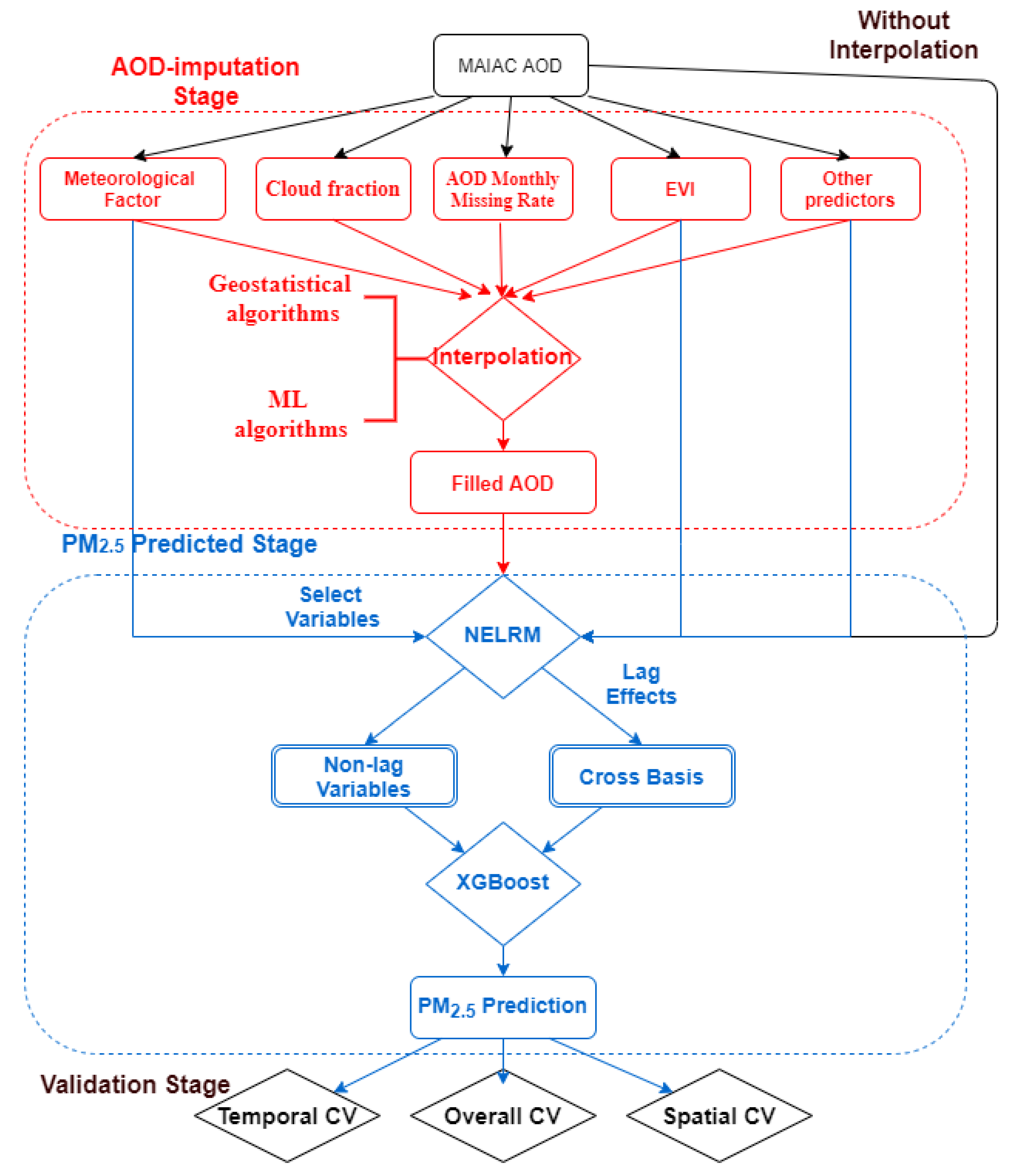
2.2.1. AOD-Imputation Stage for MAIAC AOD
2.2.2. PM2.5-Prediction Stage
2.2.3. Validation Stage
3. Results
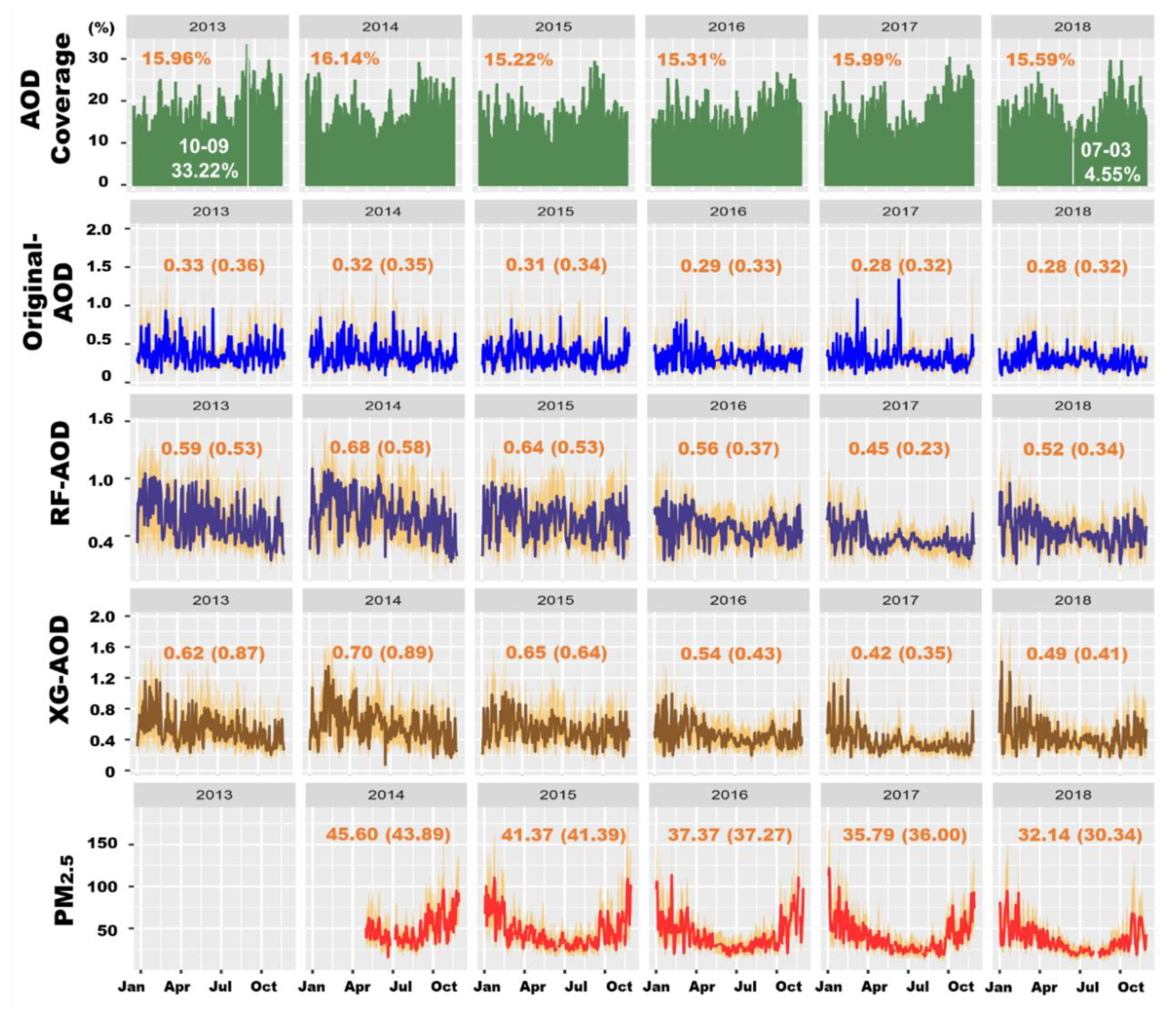
3.1. Descriptive Statistics of MAIAC AOD and PM2.5 Concentration
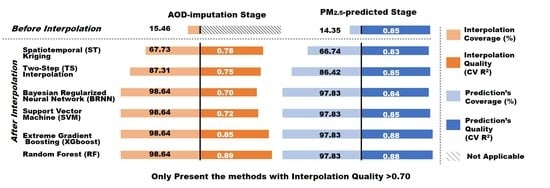
3.2. AOD-Imputation Stage
3.3. PM2.5 Predicted Stage
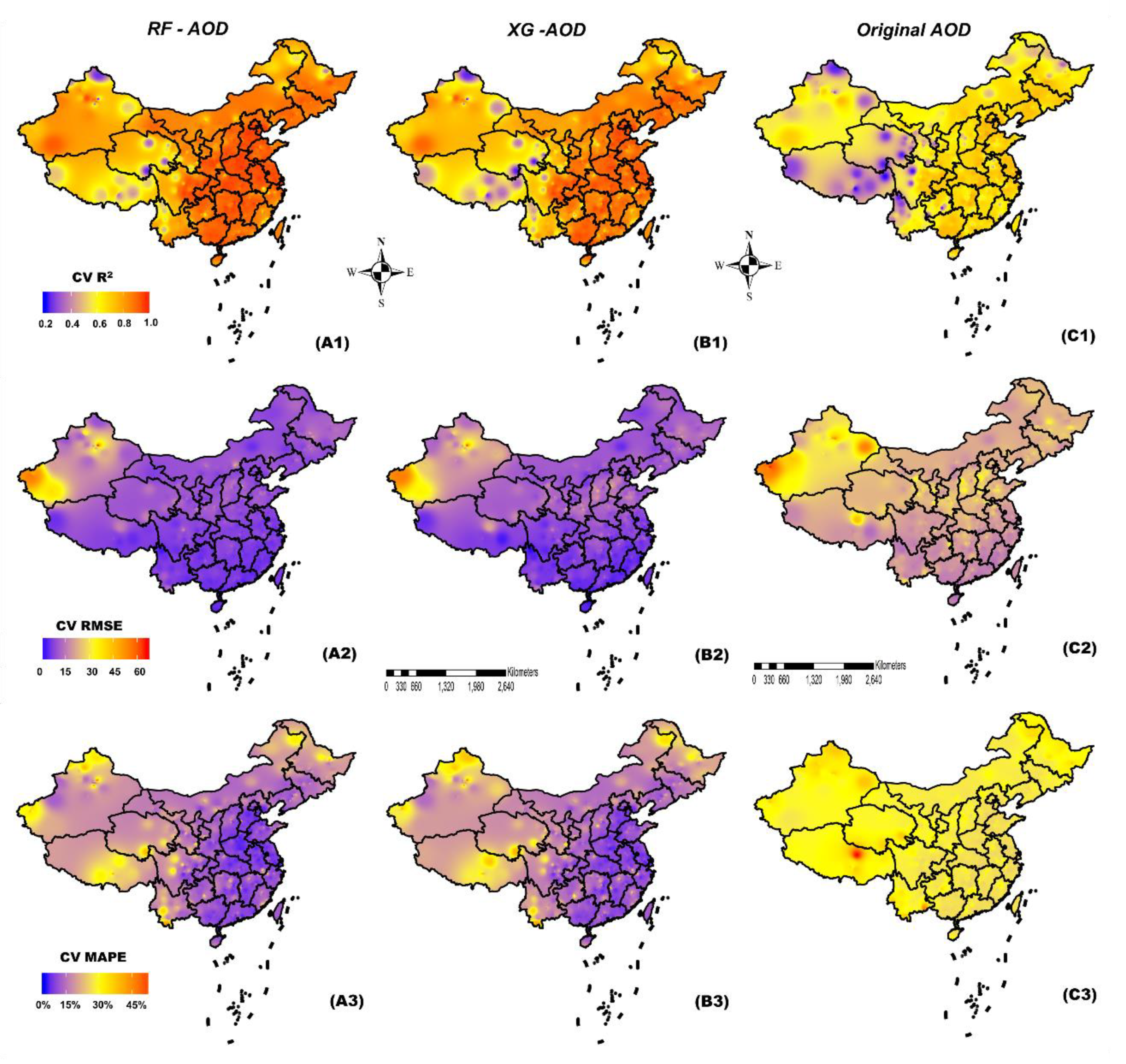
3.4. Spatial and Temporal Cross-Validation
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- International Energy Agency. Key World Energy Statistics 2018; OECD Publishing: Paris, France, 2018. [Google Scholar]
- Cohen, A.J.; Brauer, M.; Burnett, R.; Anderson, H.R.; Frostad, J.; Estep, K.; Balakrishnan, K.; Brunekreef, B.; Dandona, L.; Dandona, R.; et al. Estimates and 25-year trends of the global burden of disease attributable to ambient air pollution: An analysis of data from the Global Burden of Diseases Study 2015. Lancet 2017, 389, 1907–1918. [Google Scholar] [CrossRef]
- Lee, S.; Lee, W.; Kim, D.; Kim, E.; Myung, W.; Kim, S.-Y.; Kim, H. Short-term PM2.5 exposure and emergency hospital admissions for mental disease. Environ. Res. 2019, 171, 313–320. [Google Scholar] [CrossRef]
- Shah, A.S.V.; Lee, K.K.; McAllister, D.A.; Hunter, A.; Nair, H.; Whiteley, W.; Langrish, J.P.; Newby, D.E.; Mills, N.L. Short term exposure to air pollution and stroke: Systematic review and meta-analysis. BMJ 2015, 350, h1295. [Google Scholar] [CrossRef] [PubMed]
- Guaita, R.; Pichiule, M.; Maté, T.; Linares, C.; Díaz, J. Short-term impact of particulate matter (PM2.5) on respiratory mortality in Madrid. Int. J. Environ. Health Res. 2011, 21, 260–274. [Google Scholar] [CrossRef] [PubMed]
- Kloog, I.; Ridgway, B.; Koutrakis, P.; Coull, B.A.; Schwartz, J.D. Long-and short-term exposure to PM2.5 and mortality: Using novel exposure models. Epidemiology 2013, 24, 555. [Google Scholar] [CrossRef] [PubMed]
- Mar, T.F.; Jansen, K.; Shepherd, K.; Lumley, T.; Larson, T.V.; Koenig, J.Q. Exhaled nitric oxide in children with asthma and short-term PM2.5 exposure in Seattle. Environ. Health Perspect. 2005, 113, 1791–1794. [Google Scholar] [CrossRef]
- WHO. Air Quality Deteriorating in Many of the World’s Cities; WHO: Geneva, Switzerland, 2014. [Google Scholar]
- Chen, Z.-Y.; Zhang, T.-H.; Zhang, R.; Zhu, Z.-M.; Yang, J.; Chen, P.-Y.; Ou, C.-Q.; Guo, Y. Extreme gradient boosting model to estimate PM2.5 concentrations with missing-filled satellite data in China. Atmos. Environ. 2019, 202, 180–189. [Google Scholar] [CrossRef]
- Kahn, R.A.; Nelson, D.L.; Garay, M.J.; Levy, R.C.; Bull, M.A.; Diner, D.J.; Martonchik, J.V.; Paradise, S.R.; Hansen, E.G.; Remer, L.A. MISR aerosol product attributes and statistical comparisons with MODIS. IEEE Trans. Geosci. Remote Sens. 2009, 47, 4095–4114. [Google Scholar] [CrossRef]
- Paciorek, C.J.; Liu, Y. Limitations of remotely sensed aerosol as a spatial proxy for fine particulate matter. Environ. Health Perspect. 2009, 117, 904–909. [Google Scholar] [CrossRef]
- Zhang, T.; Gong, W.; Zhu, Z.; Sun, K.; Huang, Y.; Ji, Y. Semi-physical estimates of national-scale PM10 concentrations in China using a satellite-based geographically weighted regression model. Atmosphere 2016, 7, 88. [Google Scholar] [CrossRef]
- Liu, Y.; Paciorek, C.J.; Koutrakis, P. Estimating regional spatial and temporal variability of PM2.5 concentrations using satellite data, meteorology, and land use information. Environ. Health Perspect. 2009, 117, 886. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Zhang, T.; Zhang, R.; Zhu, Z.; Ou, C.; Guo, Y. Estimating PM2.5 concentrations based on non-linear exposure-lag-response associations with aerosol optical depth and meteorological measures. Atmos. Environ. 2018, 173, 30–37. [Google Scholar] [CrossRef]
- Kloog, I.; Koutrakis, P.; Coull, B.A.; Lee, H.J.; Schwartz, J. Assessing temporally and spatially resolved PM 2.5 exposures for epidemiological studies using satellite aerosol optical depth measurements. Atmos. Environ. 2011, 45, 6267–6275. [Google Scholar] [CrossRef]
- Lv, B.; Hu, Y.; Chang, H.H.; Russell, A.G.; Bai, Y. Improving the accuracy of daily PM2.5 distributions derived from the fusion of ground-level measurements with aerosol optical depth observations, a case study in North China. Environ. Sci. Technol. 2016, 50, 4752. [Google Scholar] [CrossRef]
- Xiao, Q.Y.; Wang, Y.; Howard, H.C.; Xia, M.; Geng, G. Full-coverage high-resolution daily PM2.5 estimation using MAIAC AOD in the Yangtze River Delta of China. Remote Sens. Environ. 2017, 199, 437–446. [Google Scholar] [CrossRef]
- Di, Q.; Kloog, I.; Koutrakis, P.; Lyapustin, A.; Wang, Y.; Schwartz, J. Assessing PM2.5 exposures with high spatiotemporal resolution across the continental United States. Environ. Sci. Technol. 2016, 50, 4712–4721. [Google Scholar] [CrossRef]
- Lyapustin, A.; Wang, Y.; Laszlo, I.; Kahn, R.; Korkin, S.; Remer, L.; Levy, R.; Reid, J. Multiangle implementation of atmospheric correction (MAIAC): 2. Aerosol algorithm. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Lyapustin, A.; Wang, Y.; Korkin, S.; Huang, D. MODIS Collection 6 MAIAC algorithm. Atmos. Meas. Tech. 2018, 11, 5741–5765. [Google Scholar] [CrossRef]
- Li, L.; Franklin, M.; Girguis, M.; Lurmann, F.; Wu, J.; Pavlovic, N.; Breton, C.; Gilliland, F.; Habre, R. Spatiotemporal imputation of MAIAC AOD using deep learning with downscaling. Remote Sens. Environ. 2020, 237, 111584. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, W.; Fan, M.; Wei, J.; Tan, Y.; Wang, Q. Evaluation of MAIAC aerosol retrievals over China. Atmos. Environ. 2019, 202, 8–16. [Google Scholar] [CrossRef]
- Hu, X.; Waller, L.A.; Lyapustin, A.; Wang, Y.; Al-Hamdan, M.Z.; Crosson, W.L.; Estes, M.G., Jr.; Estes, S.M.; Quattrochi, D.A.; Puttaswamy, S.J. Estimating ground-level PM2.5 concentrations in the Southeastern United States using MAIAC AOD retrievals and a two-stage model. Remote Sens. Environ. 2014, 140, 220–232. [Google Scholar] [CrossRef]
- CHINA MEE. Ambient Air Quality Standardss.GB 3095-2012; China Environmental: Beijing, China, 2016. [Google Scholar]
- San Martini, F.M.; Hasenkopf, C.A.; Roberts, D.C. Statistical analysis of PM2.5 observations from diplomatic facilities in China. Atmos. Environ. 2015, 110, 174–185. [Google Scholar] [CrossRef]
- Lv, B.; Hu, Y.; Chang, H.H.; Russell, A.G.; Cai, J.; Xu, B.; Bai, Y. Daily estimation of ground-level PM2.5 concentrations at 4 km resolution over Beijing-Tianjin-Hebei by fusing MODIS AOD and ground observations. Sci. Total Environ. 2017, 580, 235–244. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Liu, D.; Chen, J. A new geostatistical approach for filling gaps in Landsat ETM+ SLC-off images. Remote Sens. Environ. 2012, 124, 49–60. [Google Scholar] [CrossRef]
- Wikle, C.; Zammit-Mangion, A.; Cressie, N. Spatio-Temporal Statistics with R; CRC Press: Boca Raton, FL, USA, 2019; ISBN 9781351769723. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and regression by RandomForest. R News 2002, 2, 18–22. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. Knowl. Discov. Data Min. 2016, 785–794. [Google Scholar] [CrossRef]
- Wang, L. Support Vector Machines: Theory and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005; Volume 177, p. 3887. [Google Scholar]
- Ridgeway, G. Generalized Boosted Models: A guide to the gbm package. Update 2007, 1, 2007. [Google Scholar]
- Brenning, A. Statistical geocomputing combining R and SAGA: The example of landslide susceptibility analysis with generalized additive models. Hamburg. Beiträge zur Phys. Geogr. und Landschaftsökologie 2008, 19, 410. [Google Scholar]
- Pérez-Rodríguez, P.; Gianola, D.; Weigel, K.A.; Rosa, G.J.M.; Crossa, J. An R package for fitting Bayesian regularized neural networks with applications in animal breeding. J. Anim. Sci. 2013, 91, 3522–3531. [Google Scholar] [CrossRef]
- Kuhn, M. Building predictive models in R using the caret package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Just, A.C.; De Carli, M.M.; Shtein, A.; Dorman, M.; Lyapustin, A.; Kloog, I. Correcting measurement error in satellite aerosol optical depth with machine learning for modeling PM2.5 in the Northeastern USA. Remote Sens. 2018, 10, 803. [Google Scholar] [CrossRef] [PubMed]
- He, Q.; Huang, B. Satellite-based mapping of daily high-resolution ground PM2.5 in China via space-time regression modeling. Remote Sens. Environ. 2018, 206, 72–83. [Google Scholar] [CrossRef]
- Xue, T.; Zheng, Y.; Geng, G.; Zheng, B.; Jiang, X.; Zhang, Q.; He, K. Fusing observational, satellite remote sensing and air quality model simulated data to estimate spatiotemporal variations of PM2.5 exposure in China. Remote Sens. 2017, 9, 221. [Google Scholar] [CrossRef]
- Belle, J.; Liu, Y. Evaluation of Aqua MODIS Collection 6 AOD parameters for air quality research over the Continental United States. Remote Sens. 2016, 8, 815. [Google Scholar] [CrossRef]
- You, W.; Zang, Z.; Zhang, L.; Li, Y.; Pan, X.; Wang, W. National-scale estimates of ground-level PM2.5 concentration in China using geographically weighted regression based on 3 km resolution MODIS AOD. Remote Sens. 2016, 8, 184. [Google Scholar] [CrossRef]
- Zhang, T.; Gong, W.; Wang, W.; Ji, Y.; Zhu, Z.; Huang, Y. Ground Level PM2.5 Estimates over China Using Satellite-Based Geographically Weighted Regression (GWR) Models Are Improved by Including NO2 and Enhanced Vegetation Index (EVI). Int. J. Environ. Res. Public Health 2016, 13, 1215. [Google Scholar] [CrossRef]
- Kim, M.; Zhang, X.; Holt, J.B.; Liu, Y. Spatio-Temporal Variations in the Associations between Hourly PM2.5 and Aerosol Optical Depth (AOD) from MODIS Sensors on Terra and Aqua. Health 2013, 5, 8–13. [Google Scholar] [CrossRef]
- McGuinn, L.; Schneider, A.E.; Ward-Caviness, C.; Di, Q.; Schwartz, J.D.; Russell, A.; Hauser, E.; Kraus, W.; Neas, L.; Cascio, W. Comparison of Long-Term PM2.5 Concentrations from Ground-Based Monitoring, CMAQ Models and Satellite-Derived AOD to Characterize Adverse Cardiovascular Outcomes. In ISEE Conference Abstracts; Environmental Health Perspectives: Ottawa, Canada, 2018; Volume 2018. [Google Scholar]
- Liu, X.; Yan, L.; Yang, P.; Yin, Z.-Y.; North, G.R. Influence of Indian summer monsoon on aerosol loading in East Asia. J. Appl. Meteorol. Climatol. 2011, 50, 523–533. [Google Scholar] [CrossRef]
- Li, Z.; Lau, W.; Ramanathan, V.; Wu, G.; Ding, Y.; Manoj, M.G.; Liu, J.; Qian, Y.; Li, J.; Zhou, T. Aerosol and monsoon climate interactions over Asia. Rev. Geophys. 2016, 54, 866–929. [Google Scholar] [CrossRef]
- Zhang, R.; Di, B.; Luo, Y.; Deng, X.; Grieneisen, M.L.; Wang, Z.; Yao, G.; Zhan, Y. A nonparametric approach to filling gaps in satellite-retrieved aerosol optical depth for estimating ambient PM2.5 levels. Environ. Pollut. 2018, 243, 998–1007. [Google Scholar] [CrossRef]
- Yang, J.; Hu, M. Filling the missing data gaps of daily MODIS AOD using spatiotemporal interpolation. Sci. Total Environ. 2018, 633, 677. [Google Scholar] [CrossRef] [PubMed]
- Goldberg, D.L.; Gupta, P.; Wang, K.; Jena, C.; Zhang, Y.; Lu, Z.; Streets, D.G. Using gap-filled MAIAC AOD and WRF-Chem to estimate daily PM2.5 concentrations at 1 km resolution in the Eastern United States. Atmos. Environ. 2019, 199, 443–452. [Google Scholar] [CrossRef]
- Sorek-Hamer, M.; Strawa, A.W.; Chatfield, R.B.; Esswein, R.; Cohen, A.; Broday, D.M. Improved retrieval of PM2.5 from satellite data products using non-linear methods. Environ. Pollut. 2013, 182, 417–423. [Google Scholar] [CrossRef] [PubMed]
- Geng, G.; Zhang, Q.; Martin, R.V.; van Donkelaar, A.; Huo, H.; Che, H.; Lin, J.; He, K. Estimating long-term PM2.5 concentrations in China using satellite-based aerosol optical depth and a chemical transport model. Remote Sens. Environ. 2015, 166, 262–270. [Google Scholar] [CrossRef]
- Liu, Y.; He, K.; Li, S.; Wang, Z.; Christiani, D.C.; Koutrakis, P. A statistical model to evaluate the effectiveness of PM2.5 emissions control during the Beijing 2008 Olympic Games. Environ. Int. 2012, 44, 100–105. [Google Scholar] [CrossRef]
- He, Q.; Li, C.; Tang, X.; Li, H.; Geng, F.; Wu, Y. Validation of MODIS derived aerosol optical depth over the Yangtze River Delta in China. Remote Sens. Environ. 2010, 114, 1649–1661. [Google Scholar] [CrossRef]
- Zhang, T.; Zhu, Z.; Gong, W.; Zhu, Z.; Sun, K.; Wang, L.; Huang, Y.; Mao, F.; Shen, H.; Li, Z. Estimation of ultrahigh resolution PM2.5 concentrations in urban areas using 160 m Gaofen-1 AOD retrievals. Remote Sens. Environ. 2018, 216, 91–104. [Google Scholar] [CrossRef]
- Na, K.; Kumar, K.R.; Yan, Y.; Diao, Y.; Yu, X. Correlation Analysis between AOD and Cloud Parameters to Study Their Relationship over China Using MODIS Data (2003–2013): Impact on Cloud Formation and Climate Change. Aerosol Air Qual. Res. 2014, 15, 958–973. [Google Scholar]
- Bi, J.; Belle, J.H.; Wang, Y.; Lyapustin, A.I.; Wildani, A.; Liu, Y. Impacts of snow and cloud covers on satellite-derived PM2.5 levels. Remote Sens. Environ. 2019, 221, 665–674. [Google Scholar] [CrossRef]
- Feng, X.; Wang, S. Influence of different weather events on concentrations of particulate matter with different sizes in Lanzhou, China. J. Environ. Sci. 2012, 24, 665–674. [Google Scholar] [CrossRef]

| Methods | Main Features | Merits | Demerits |
|---|---|---|---|
| Geostatistical Algorithms | |||
| TS [9] | step I: mixed effect model Step II: IDW | using different satellite products | more steps |
| ST Kriging [28] | regionalize spatio-temporal variable to obtain semi-variance for kriging | maximize use spatio-temporal neighborhood information | extensive computation for large spatial and temporal scale |
| IDW [28] | inversed distance weighted-average within search radius | easier and quicker to calculated | less accurate for complex spatial distribution |
| Kriging [28] | using semi-variance to explore spatial distribution within search radius | commonly used | not considering temporal variation |
| NN [28] | nearest neighbors within search radius | easiest and quickest to calculate | less spatial variation |
| Machine Learning Algorithms | |||
| LASSO [35] | L1 regularization term was used to penalize nonessential or correlated features in model | prevent over fitting and ensure generalization | difficult to capture complex non-linear or interacting relationship |
| GAM [33] | use smooth functions to describe the relationship | fit non-linear relationship | easier to over fit |
| GBM [32] | an ensemble of weak prediction models, such as decision trees. | optimized by negative gradient of loss function. | over fitting and more computation time |
| BRNN [34] | Bayesian Inference was used to regularize the Maximum Likelihood in Neural Nets (similar regularization in Ridge Regression) | more robust than standard back-propagation nets | higher computation than L1 regularization |
| SVM [31] | Using kernel to map data into higher dimension, and then to fit the error within a certain threshold | produces higher accuracy with less computation power | weaker extrapolating ability in data with more noise |
| RF [29] | a meta estimator with numbers of classifying decision trees based on different sub-samples | control the overfitting by sub-samples | more computation time |
| XG [30] | a weighted ensemble of weak prediction models with regularized boosting and parallel processing | regularized boosting and parallel processing | less stable results in early stopping |
| Interpolation Method | Coverage (%) | Computation Time a | CV RMSE | CV R2 | CV MAPE (%) |
|---|---|---|---|---|---|
| Before Interpolation | 15.46 | \ | |||
| Geostatistical Algorithms | |||||
| TS | 87.31 | 55:38:56.56 | 0.17 | 0.75 | 20.56 |
| ST Kriging | 67.73 | 128:56:43.56 | 0.17 | 0.78 | 20.36 |
| IDW | 45.22 | 45:35:28.39 | 0.18 | 0.65 | 21.35 |
| Kriging | 42.37 | 88:46:37.24 | 0.17 | 0.66 | 20.89 |
| NN | 21.43 | 15:39:27.93 | 0.19 | 0.49 | 25.38 |
| ML Algorithms | |||||
| RF | 98.64 | 120:55:28.65 | 0.15 | 0.89 | 18.00 |
| XG | 98.64 | 18:00:38.20 | 0.15 | 0.85 | 19.06 |
| SVM | 98.64 | 19:04:47.64 | 0.17 | 0.72 | 19.41 |
| BRNN | 98.64 | 18:45:36.22 | 0.17 | 0.70 | 22.39 |
| GBM | 98.64 | 06:35:47.65 | 0.18 | 0.69 | 25.17 |
| GAM | 98.64 | 01:05:38.20 | 0.17 | 0.62 | 21.88 |
| LASSO | 98.64 | 01:18:30.23 | 0.19 | 0.49 | 28.03 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.-Y.; Jin, J.-Q.; Zhang, R.; Zhang, T.-H.; Chen, J.-J.; Yang, J.; Ou, C.-Q.; Guo, Y. Comparison of Different Missing-Imputation Methods for MAIAC (Multiangle Implementation of Atmospheric Correction) AOD in Estimating Daily PM2.5 Levels. Remote Sens. 2020, 12, 3008. https://doi.org/10.3390/rs12183008
Chen Z-Y, Jin J-Q, Zhang R, Zhang T-H, Chen J-J, Yang J, Ou C-Q, Guo Y. Comparison of Different Missing-Imputation Methods for MAIAC (Multiangle Implementation of Atmospheric Correction) AOD in Estimating Daily PM2.5 Levels. Remote Sensing. 2020; 12(18):3008. https://doi.org/10.3390/rs12183008
Chicago/Turabian StyleChen, Zhao-Yue, Jie-Qi Jin, Rong Zhang, Tian-Hao Zhang, Jin-Jian Chen, Jun Yang, Chun-Quan Ou, and Yuming Guo. 2020. "Comparison of Different Missing-Imputation Methods for MAIAC (Multiangle Implementation of Atmospheric Correction) AOD in Estimating Daily PM2.5 Levels" Remote Sensing 12, no. 18: 3008. https://doi.org/10.3390/rs12183008
APA StyleChen, Z.-Y., Jin, J.-Q., Zhang, R., Zhang, T.-H., Chen, J.-J., Yang, J., Ou, C.-Q., & Guo, Y. (2020). Comparison of Different Missing-Imputation Methods for MAIAC (Multiangle Implementation of Atmospheric Correction) AOD in Estimating Daily PM2.5 Levels. Remote Sensing, 12(18), 3008. https://doi.org/10.3390/rs12183008