A Cluster Approach to Cloud Cover Classification over South America and Adjacent Oceans Using a k-means/k-means++ Unsupervised Algorithm on GOES IR Imagery
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
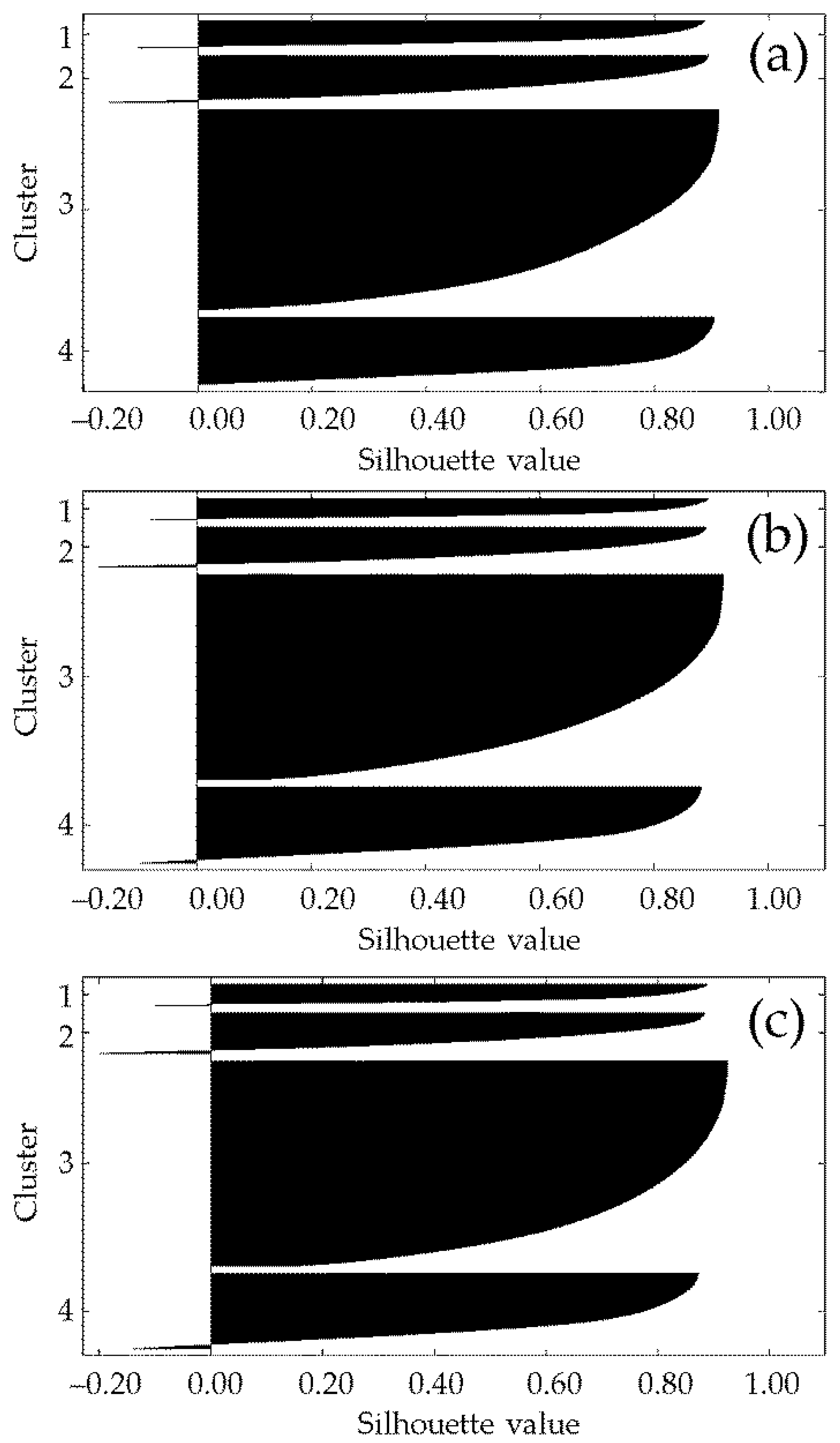
2.2. The k-means/k-means++ Clustering Algorithm
- A pixel from is randomly selected as the first centroid ;
- All individual Euclidean distances from each pixel to , denoted as , are computed;
- The second centroid is randomly selected with probability.
- 4.
- The process is repeated until all centroids are obtained. Similar to step 3), the k-th centroid is selected from with probability.
- 5.
- The distances for are computed;
- 6.
- Each grid point is assigned to the cluster with the closest centroid;
- 7.
- For , the average distance of all the pixels belonging to the cluster is calculated so as to reassign this value to the corresponding centroid.
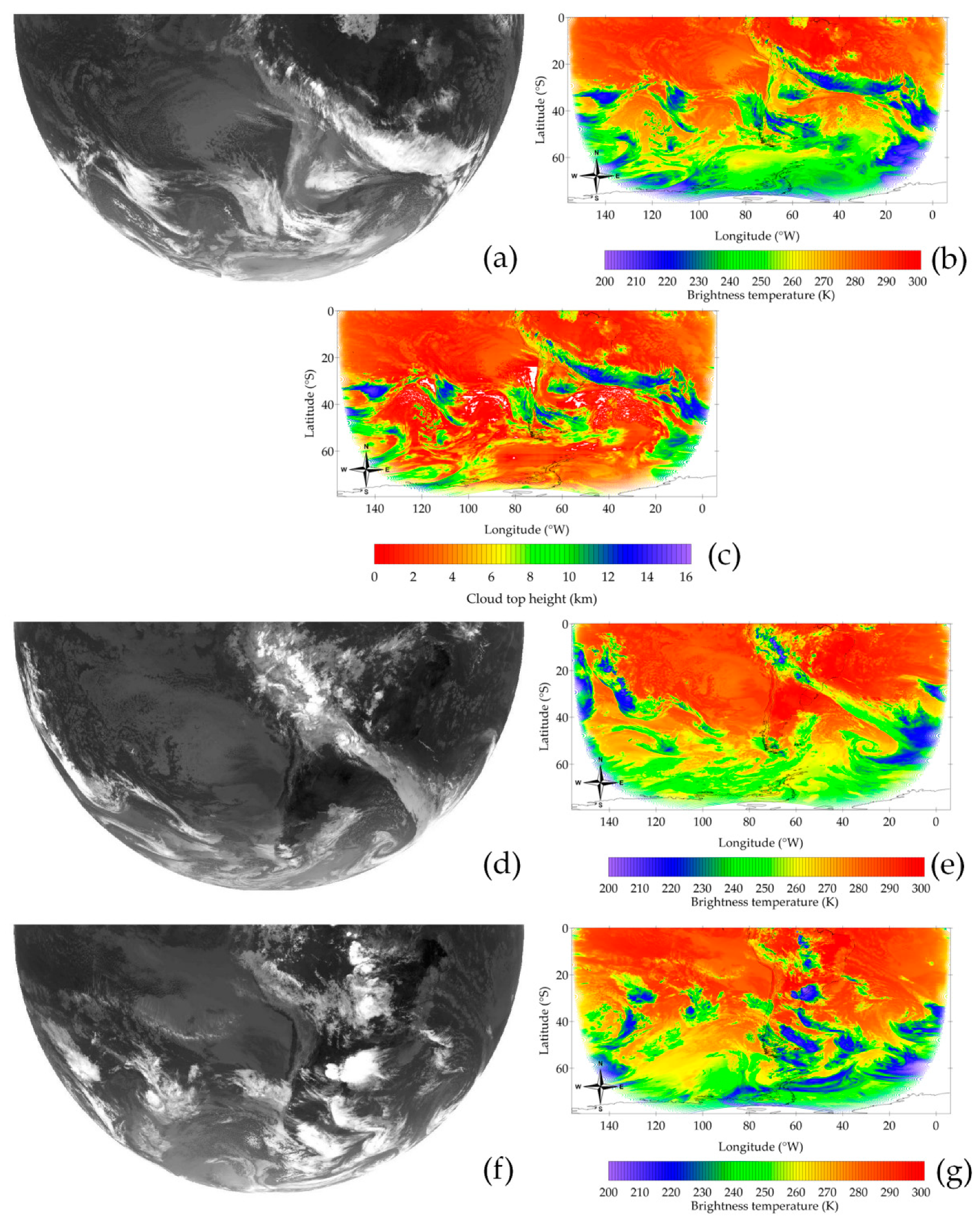
2.3. Evaluation of Cloud Top Heights
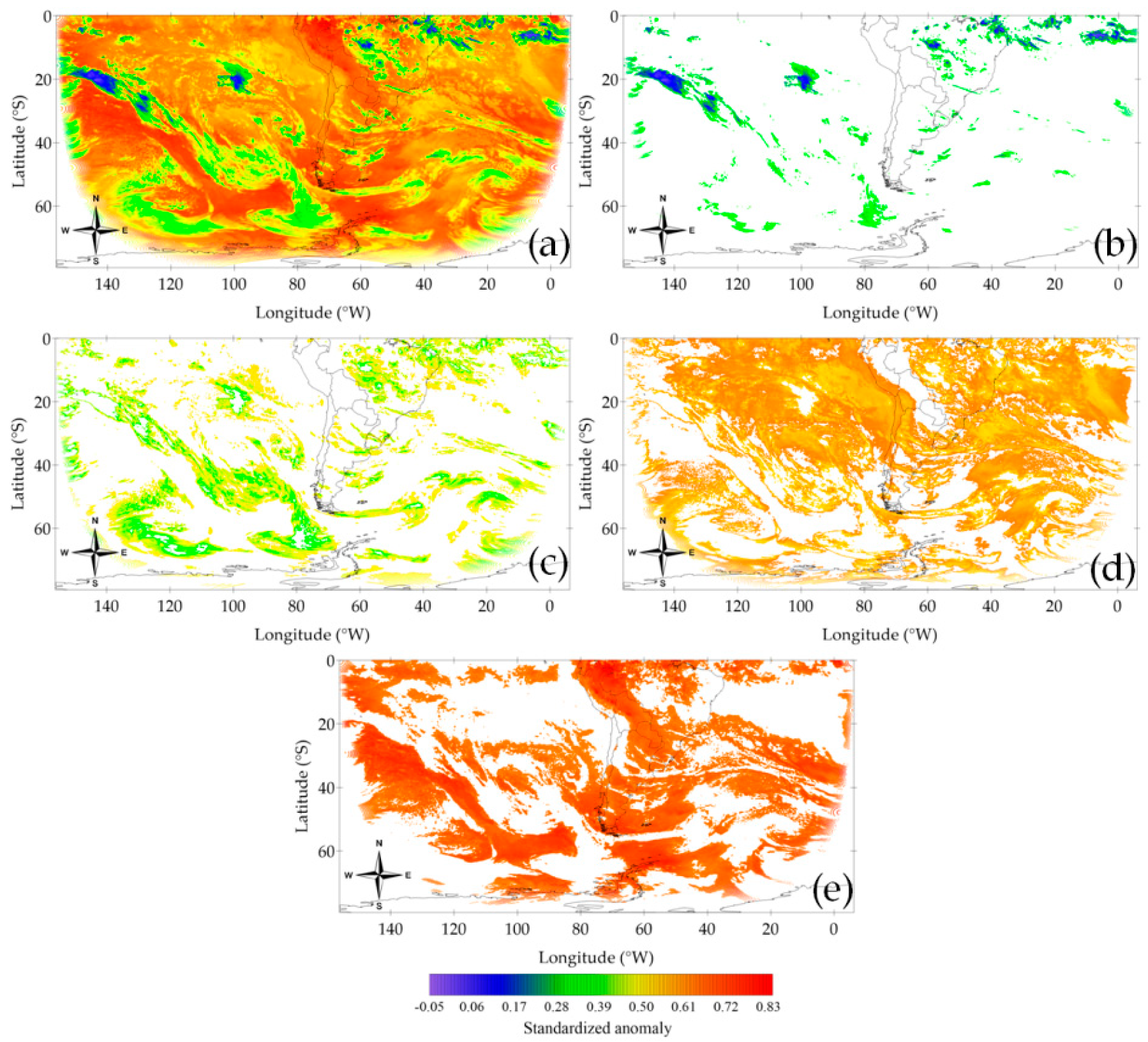
3. Results
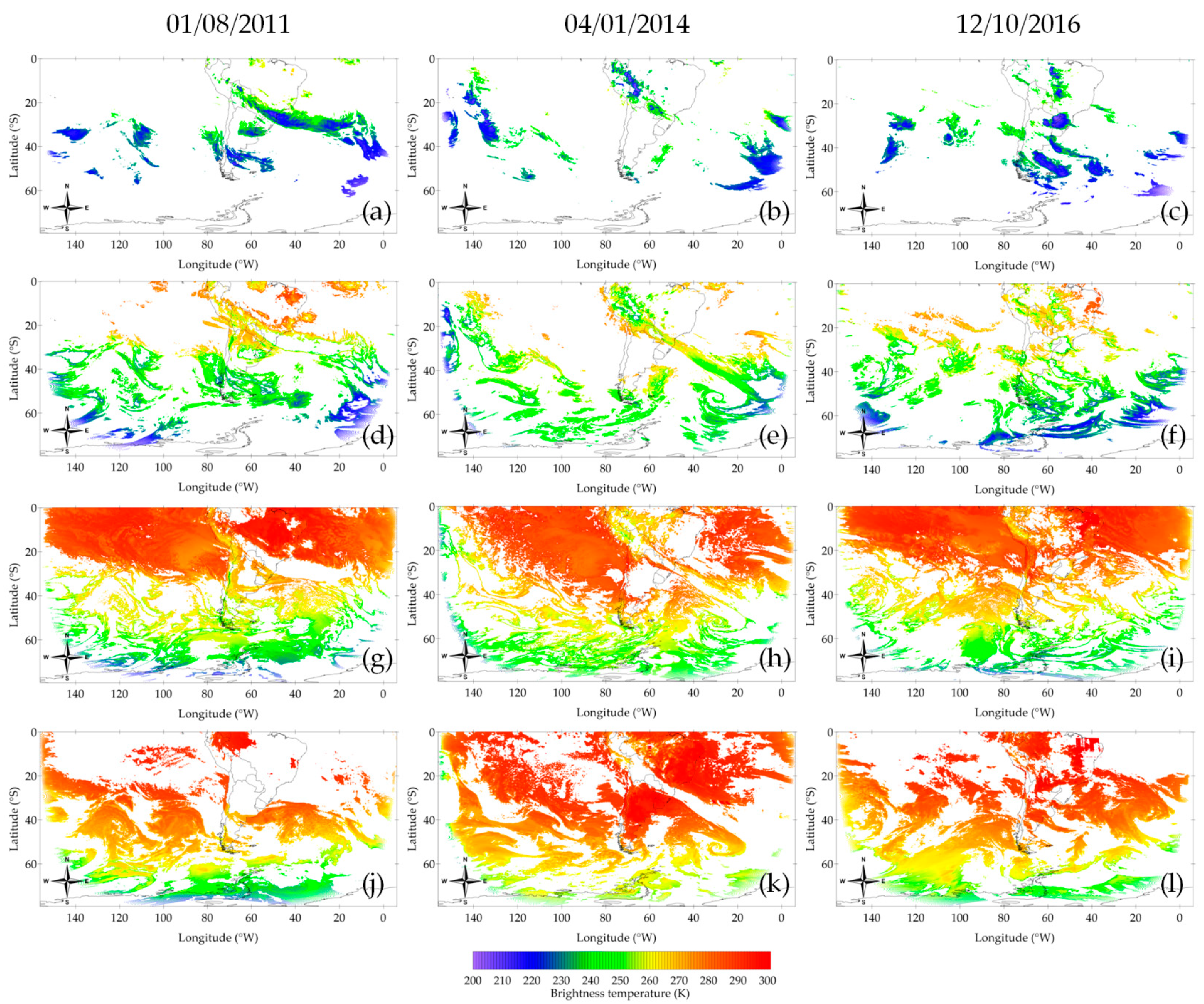
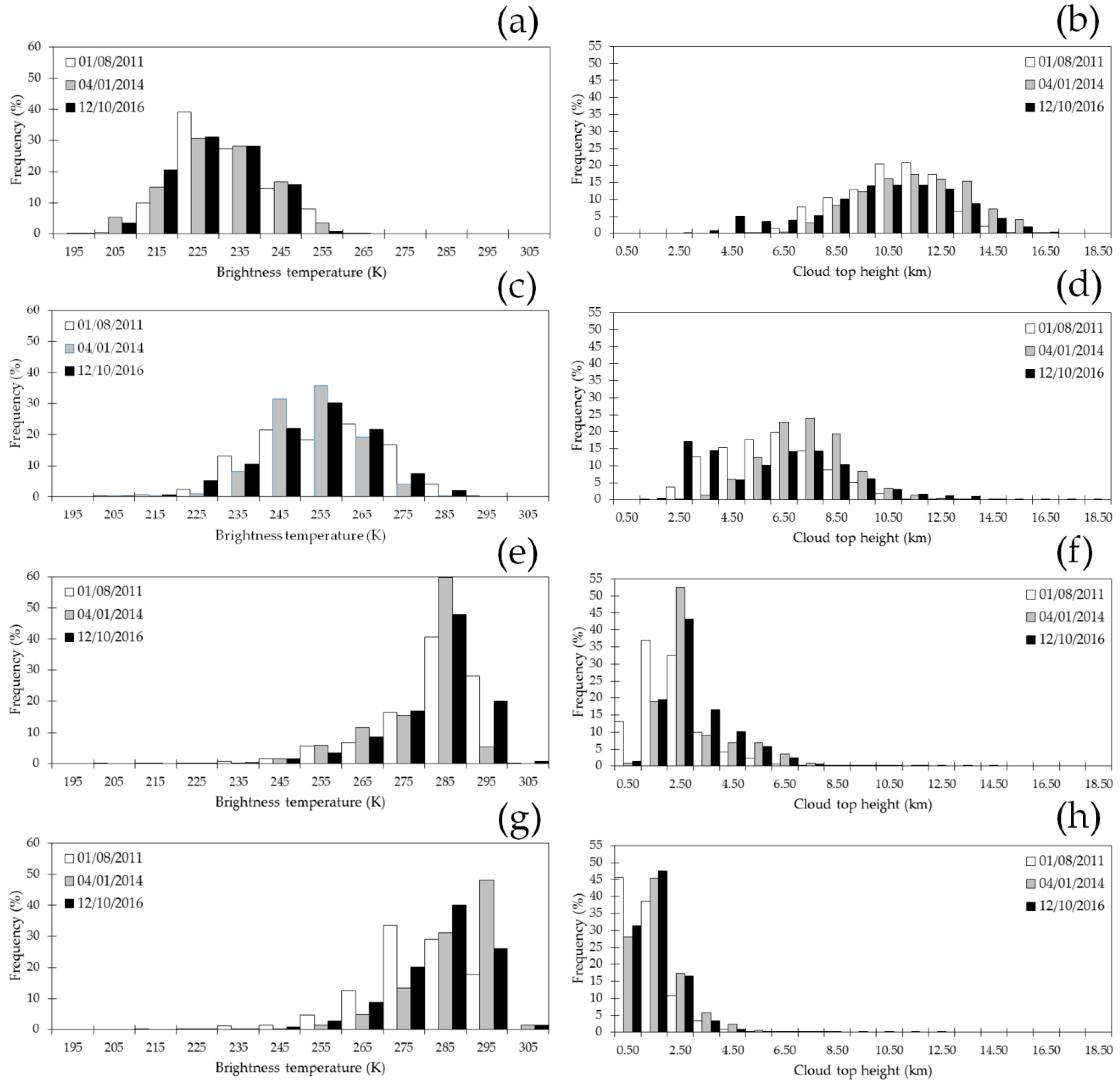
3.1. Sample Dates
3.1.1. Weather Analysis
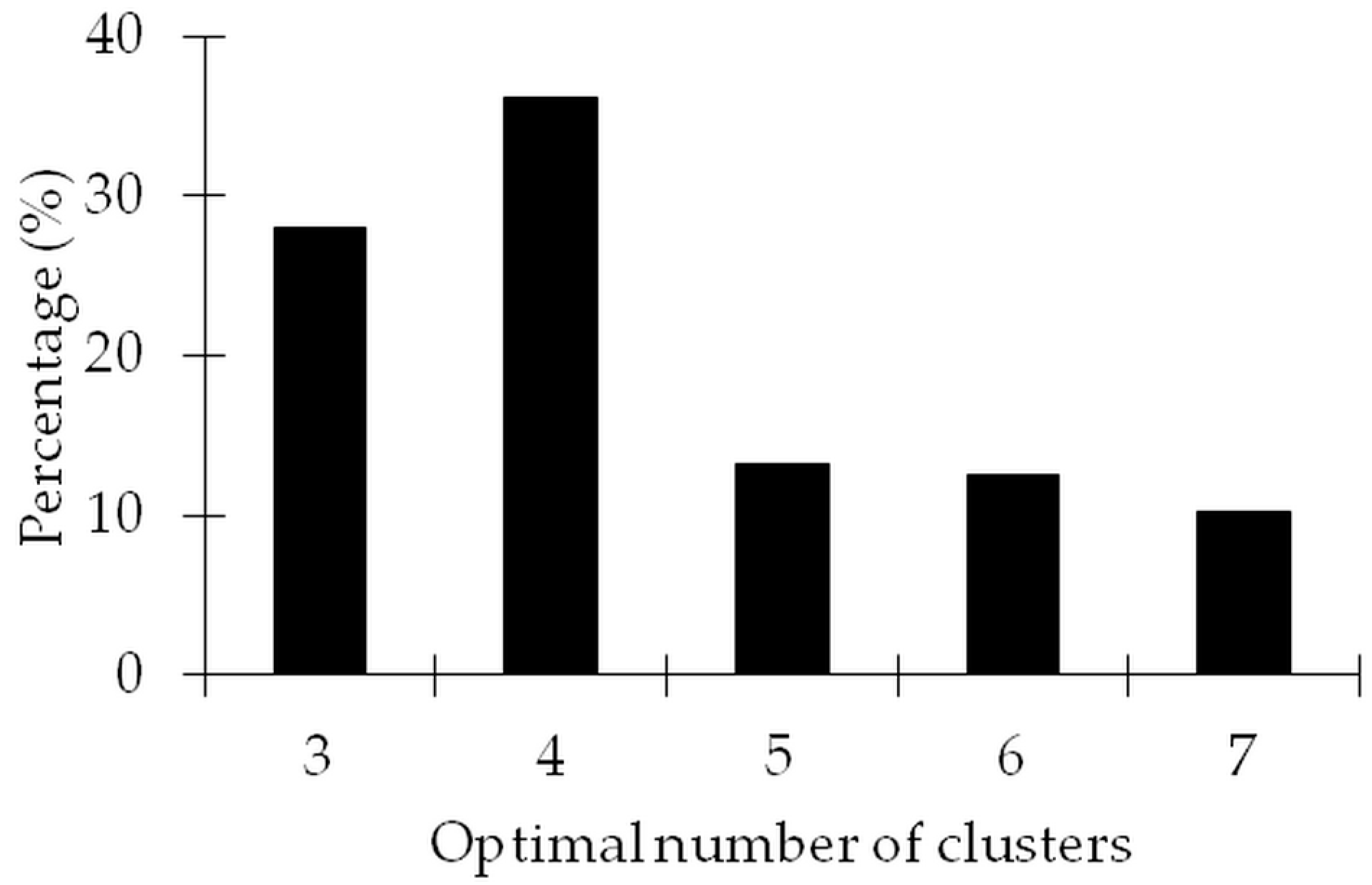
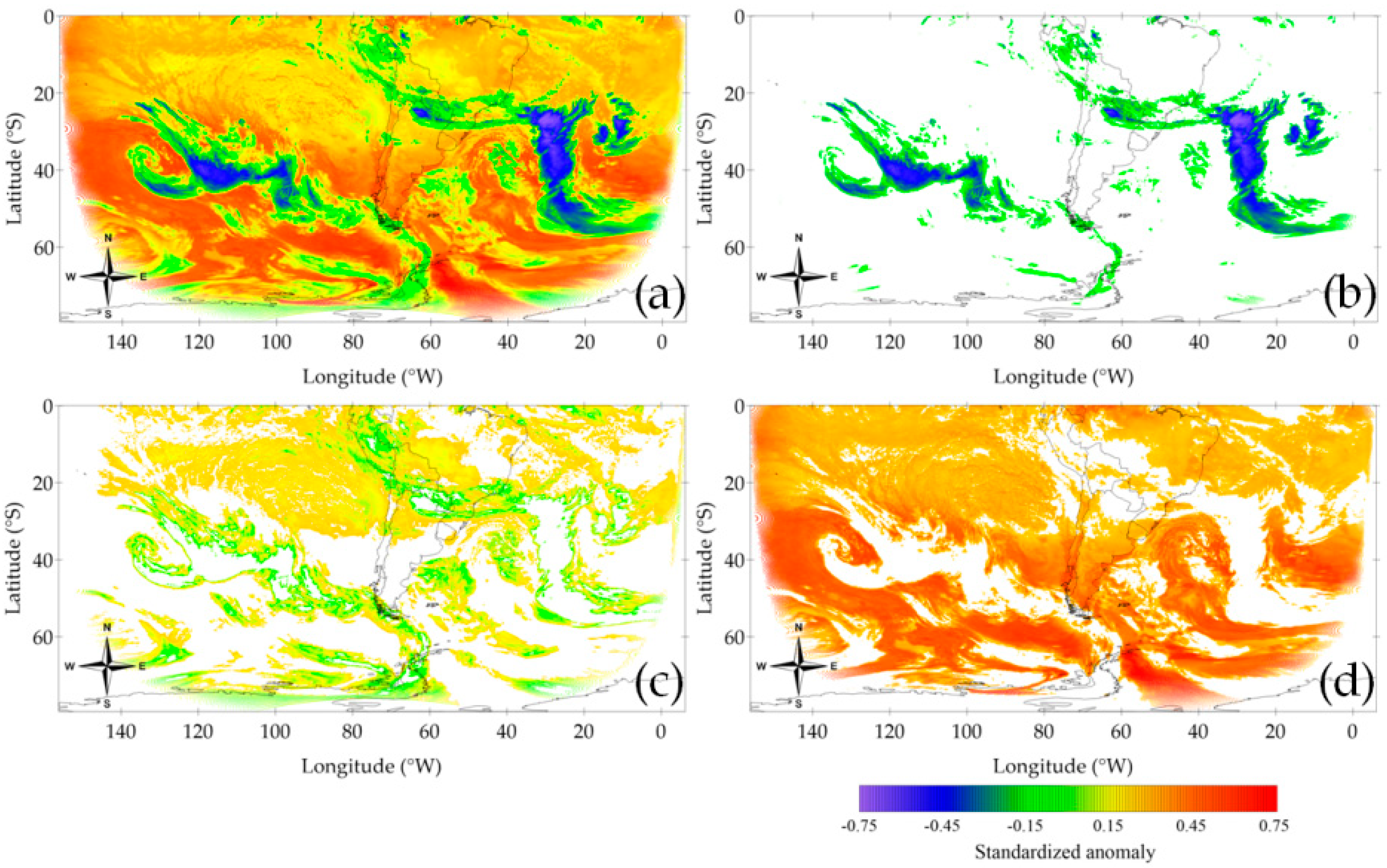
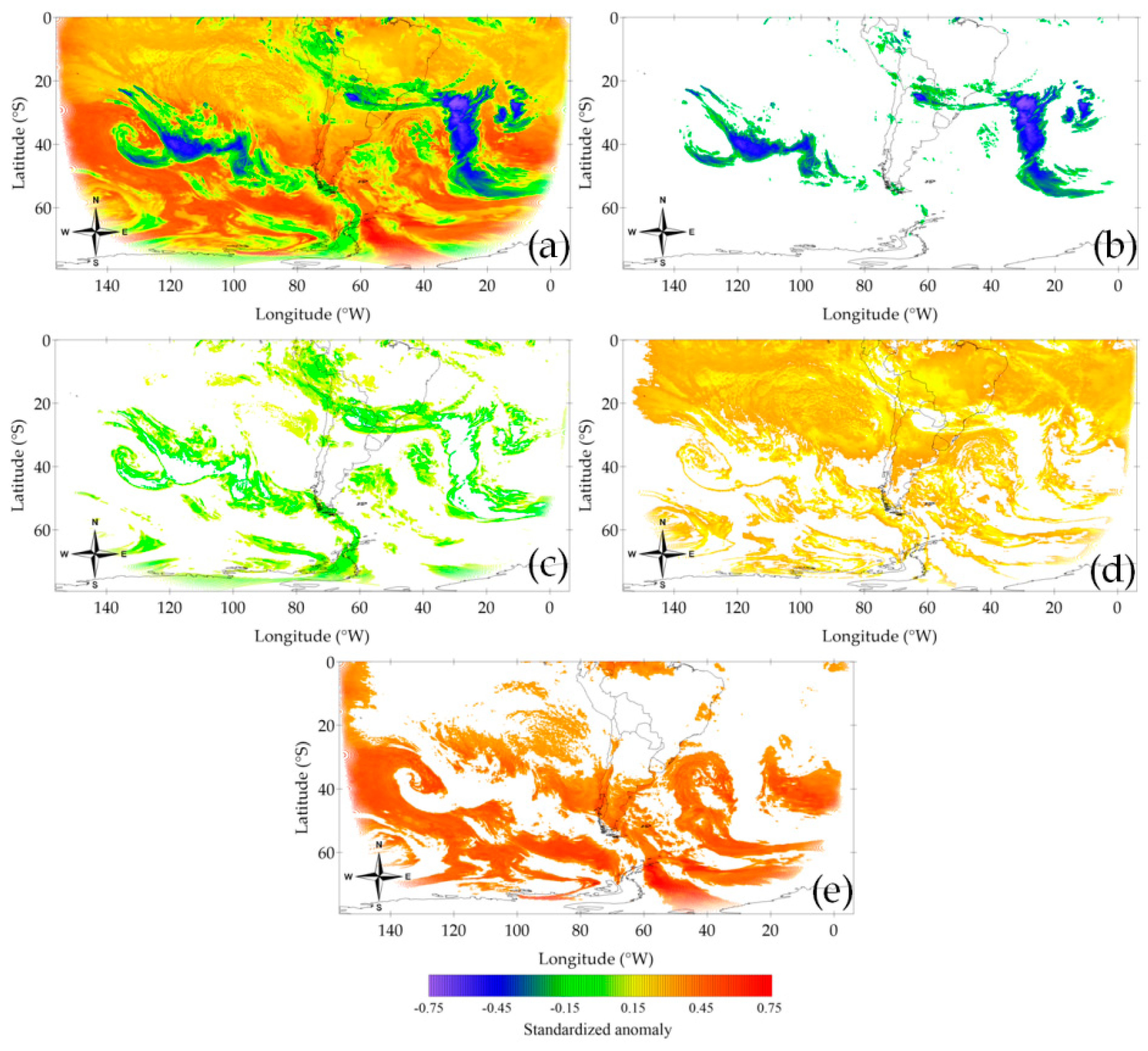
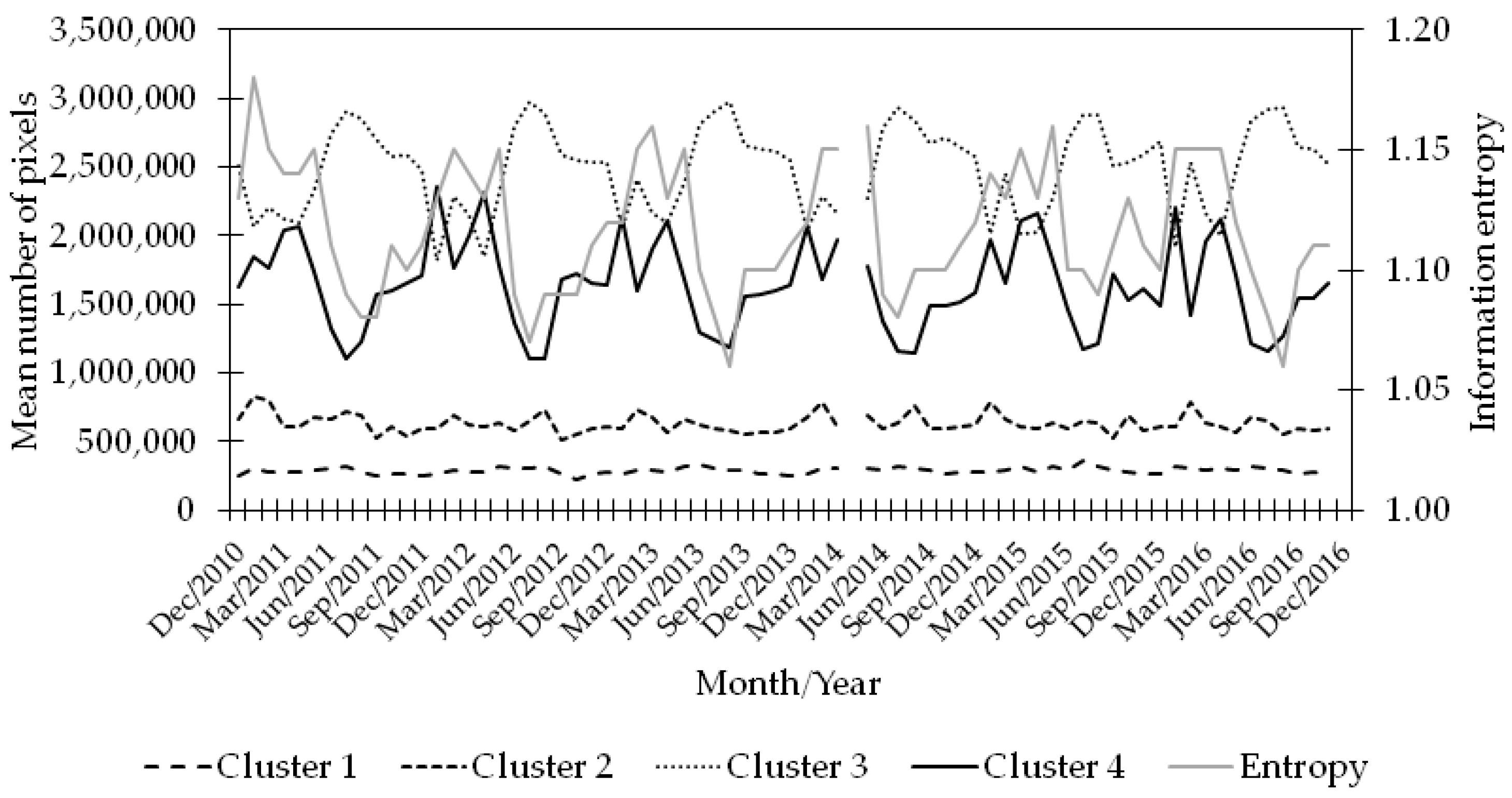
3.1.2. Cluster Analysis
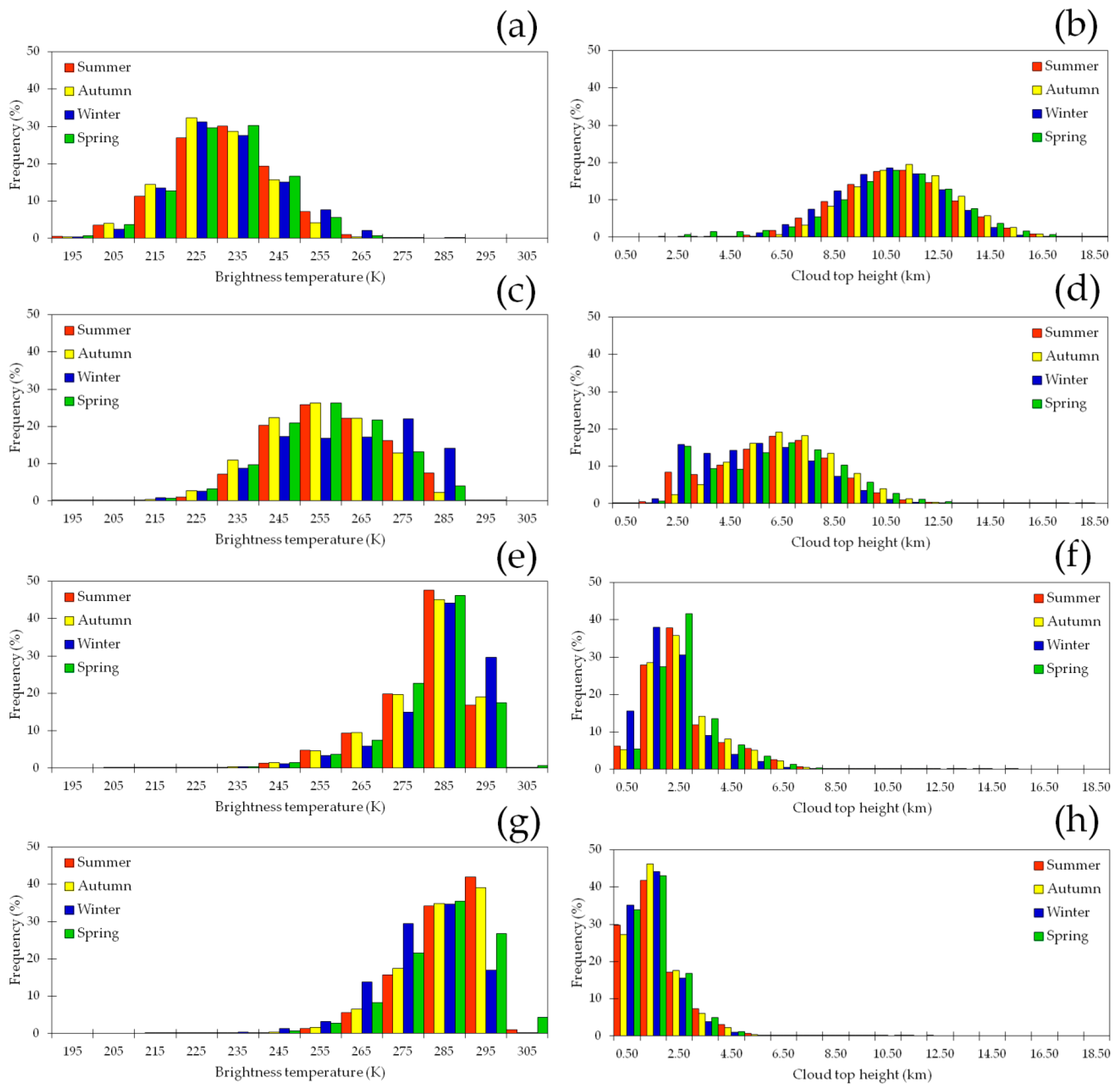
3.2. Seasonal Features
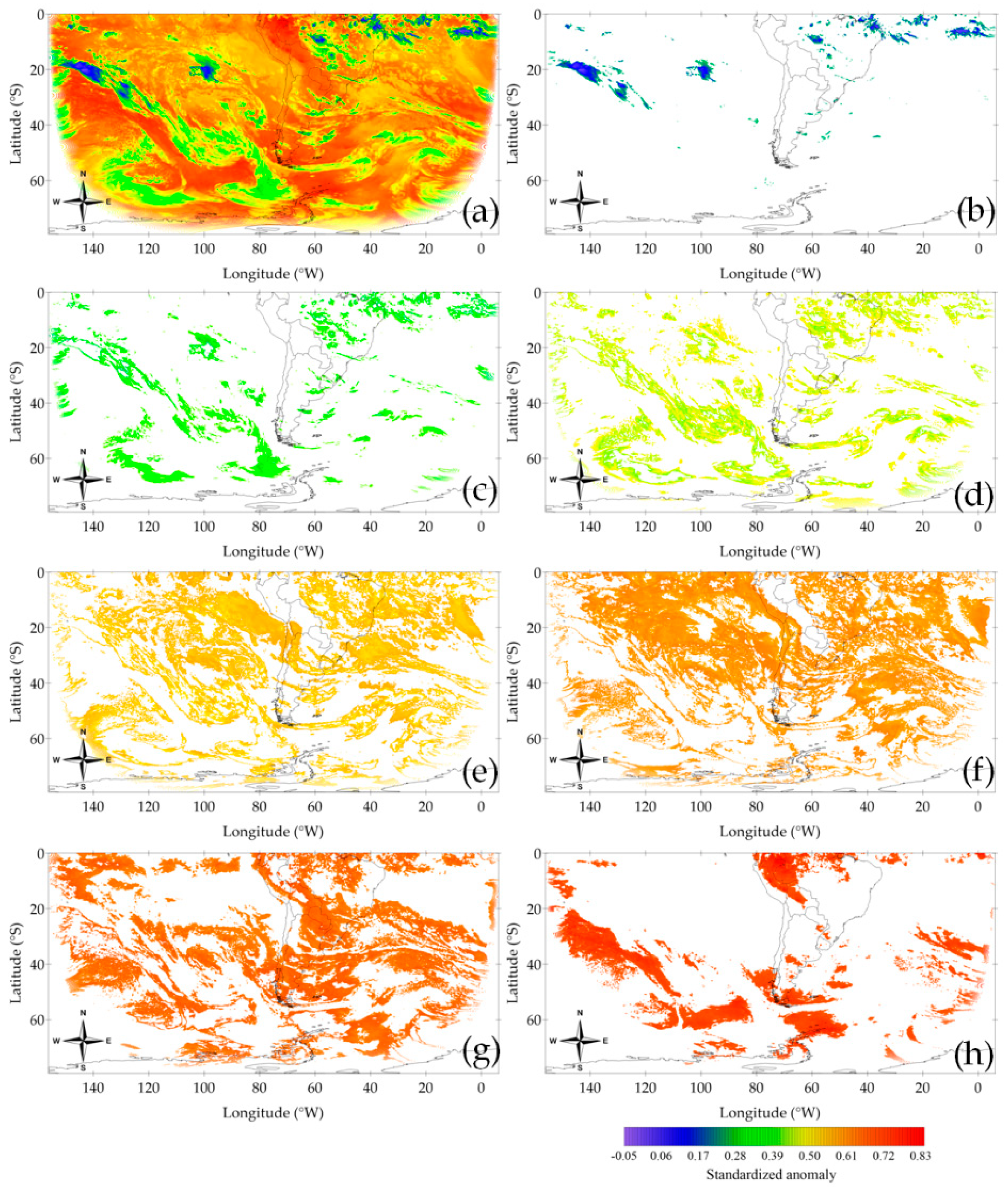
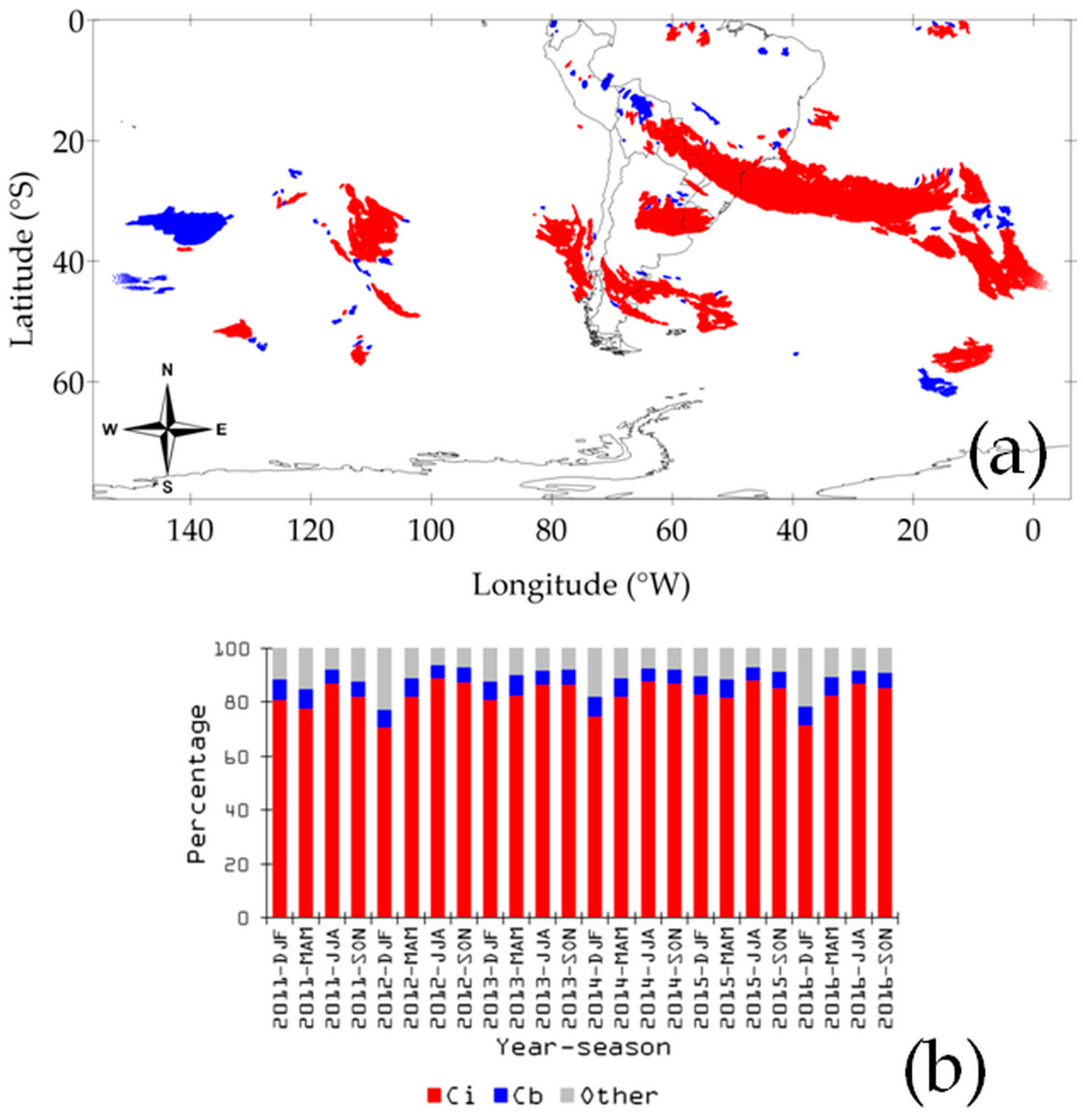
3.3. Identification of Cirrus and Cumulonimbus in Cluster 1
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Boucher, O.; Randall, D.; Artaxo, P.; Bretherton, C.; Feingold, G.; Fortster, P.; Kerminen, V.-M.; Kondo, Y.; Liao, H.; Lohmann, U.; et al. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the IPCC; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: New York, NY, USA, 2013; pp. 571–657. [Google Scholar]
- Ramanathan, V.; Cess, R.D.; Harrison, E.F.; Minnis, P.; Barkstrom, B.R.; Ahmad, E.; Hartmann, D. Cloud-radiative forcing and climate: Results from the Earth Radiation Budget Expermient. Science 1989, 243, 57–63. [Google Scholar] [CrossRef] [PubMed]
- Petty, G.W. The first law and its consequences. In A First Course in Atmospheric Thermodynamics; Sundog Publishing: Madison, WI, USA, 2008; pp. 123–160. [Google Scholar]
- Cess, R.D.; Briegleb, B.P.; Lian, M.S. Low-latitude cloudiness and climate feedback: Comparative Estimates from Satellite Data. J. Atmos. Sci. 1982, 39, 53–59. [Google Scholar] [CrossRef][Green Version]
- Liou, K.-N. Influence of cirrus clouds on weather and climate processes: A global perspective. Mon. Weather Rev. 1986, 114, 1167–1199. [Google Scholar] [CrossRef]
- Kiehl, J.T. Clouds and their effects on the climate system. Phys. Today 1994, 47, 36–42. [Google Scholar] [CrossRef]
- Stephens, G.L. Cloud feedbacks in the climate system: A critical review. J. Clim. 2005, 18, 237–273. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Fasullo, J.T. Global warming due to increasing absorbed solar radiation. Geophys. Res. Lett. 2009, 36, L07706. [Google Scholar] [CrossRef]
- Bony, S.; Stevens, B.; Frierson, D.M.W.; Jakob, C.; Kageyama, M.; Pincus, R.; Shepherd, T.G.; Sherwood, S.C.; Siebesma, A.P.; Sobel, A.H.; et al. Clouds, circulation and climate sensitivity. Nat. Geosci. 2015, 8, 261–268. [Google Scholar] [CrossRef]
- Schneider, T.; Teixeira, J.; Bretherton, C.S.; Brient, F.; Pressel, K.G.; Schär, C.; Siebesma, A.P. Climate goals and computing the future of clouds. Nat. Clim. Chang. 2017, 7, 3–5. [Google Scholar] [CrossRef]
- Dai, A.; Karl, T.R.; Sun, B.; Trenberth, K.E. Recent trends in cloudiness over the United States: A tale of monitoring inadequacies. Bull. Am. Meteorol. Soc. 2006, 87, 597–606. [Google Scholar] [CrossRef]
- Martucci, G.; Milroy, C.; O’Dowd, C.D. Detection of cloud-base height using Jenoptik CHM15K and Vaisala CL31 ceilometers. J. Atmos. Ocean Technol. 2010, 27, 305–318. [Google Scholar] [CrossRef]
- Yuchechen, A.E.; Lakkis, S.G.; Lavorato, M.B. On the stability of the troposphere/lower stratosphere and its relationships with cirrus clouds and three mandatory levels over Buenos Aires. Int. J. Remote Sens. 2016, 37, 1541–1552. [Google Scholar] [CrossRef]
- Saunders, R.W.; Krieble, K.T. An improved method for detecting clear sky and cloudy radiances from AVHRR data. Int. J. Remote Sens. 1988, 9, 123–150. [Google Scholar] [CrossRef]
- Rossow, W.B.; Schiffer, R.A. ISCCP Cloud data products. Bull. Am. Meteorol. Soc. 1991, 72, 2–20. [Google Scholar] [CrossRef]
- King, M.D.; Kaufman, Y.J.; Menzel, W.P.; Tanré, D. Remote sensing of cloud, aerosol, and water vapor properties from the Moderate Resolution Imaging Spectrometer (MODIS). IEEE Trans. Geosci. Remote Sens. 1992, 30, 2–27. [Google Scholar] [CrossRef]
- Wielicki, B.A.; Barkstrom, B.R.; Baum, B.A.; Charlock, T.P.; Green, R.N.; Kratz, D.P.; Lee, R.B., III; Minnis, P.; Smith, G.L.; Wong, T.; et al. Clouds and the Earth’s Radiant Energy System (CERES): Algorithm Overview. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1127–1141. [Google Scholar] [CrossRef]
- Zhuge, X.-Y.; Zou, X.; Wang, Y. A fast cloud detection algorithm applicable to monitoring and nowcasting of daytime cloud systems. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6111–6119. [Google Scholar] [CrossRef]
- Cheng, G.; Han, J. A survey on object detection in optical remote sensing images. ISPRS J. Photogramm. Remote Sens. 2016, 117, 11–28. [Google Scholar] [CrossRef]
- Anderson, R.K.; Oliver, V.J.; Ferguson, E.W.; Parmenter, F.C.; Amacher, L.R.; Cottrell, W.N.; Bittner, F.E. Application of meteorological satellite data in analysis and forecasting. In Reprint of ESSA Technical Report NESC 51 (including Supplement, November 1971, and Supplement #2, March 1973); United States Department of Commerce, National Oceanic and Atmospheric Administration, National Environmental Satellite Service: Washington, DC, USA, 1974. [Google Scholar]
- Lovejoy, S.; Austin, G.L. The delineation of rain areas from visible and IR satellite data for GATE and mid-latitudes. Atmos. Ocean 1979, 17, 77–92. [Google Scholar] [CrossRef]
- Scofield, R.A.; Purdom, J.F.W. The use of satellite data for mesoscale analyses and forecasting applications. In Mesoscale Meteorology and Forecasting; Ray, P.S., Ed.; American Meteorological Society: Boston, MA, USA, 1986; pp. 118–150. [Google Scholar]
- Stowe, L.L.; McClain, E.P.; Carey, R.; Pellegrino, P.; Gutman, G.G.; Davis, P.; Long, C.; Hart, S. Global distribution of cloud cover derived from NOAA/AVHRR operational satellite data. Adv. Space Res. 1991, 11, 51–54. [Google Scholar] [CrossRef]
- Reynolds, R.W.; Rayner, N.A.; Smith, T.M.; Stokes, D.C.; Wang, W. An improved in situ and satellite SST analysis for climate. J. Clim. 2002, 15, 1609–1625. [Google Scholar] [CrossRef]
- Christy, J.R.; Spencer, R.W.; Braswell, W.D.; Junod, R. Examination of space-based bulk atmospheric temperatures used in climate research. Int. J. Remote Sens. 2018, 39, 3580–3607. [Google Scholar] [CrossRef]
- Rosenfeld, D.; Lensky, I.M. Satellite-based insights into precipitation formation processes in continental and maritime convective clouds. Bul. Am. Meteorol. Soc. 1998, 79, 2457–2476. [Google Scholar] [CrossRef]
- Zhao, G.; Di Girolamo, L. Statistics on the macrophysical properties of trade wind cumuli over the tropical western Atlantic. J. Geophys. Res. 2007, 112, D10204. [Google Scholar] [CrossRef]
- Zhu, Y.; Rosenfled, D.; Yu, X.; Liu, G.; Dai, J.; Xu, X. Satellite retrieval of convective cloud base temperature based on the NPP/VIIRS Imager. Geophys. Res. Lett. 2014, 41, 1308–1313. [Google Scholar] [CrossRef]
- Seaman, C.J.; Noh, Y.-J.; Miller, S.D.; Heidinger, A.K.; Lindsey, D.T. Cloud-base height estimation from VIIRS. Part I: Operational algorithm validation against Cloudsat. J. Atmos. Ocean. Technol. 2017, 34, 567–583. [Google Scholar] [CrossRef]
- NOAA GOES-N,O,P—The Next Generation; NASA, Goddard Space Flight Centre: Greenbelt, MD, USA; U.S. Department of Commerce, National Oceanic and Atmospheric Administration, National Environmental Satellite, Data and Information Service: Suitland, MD, USA, 2005. Available online: https://www.nasa.gov/pdf/112855main_GOESNOPWeb1.pdf (accessed on 25 May 2020).
- NOAA Retires GOES-13 Satellite After 10 Years of Stellar Service. National Environmental Satellite, Data and Information Service, 8 January 2018. Available online: https://www.nesdis.noaa.gov/content/noaa-retires-goes-13-satellite-after-10-years-stellar-service (accessed on 25 May 2020).
- Hillger, D.W.; Schmit, T.J. The GOES-15 science test: Imager and sounder radiance and product validations. In NOAA Technical Report NESDIS 141; National Environmental Satellite, Data, and Information Service, National Oceanic and Atmospheric Administration, U.S. Department of Commerce: Washington, DC, USA, 2011. [Google Scholar]
- Minnis, P.; Harrison, E.F. Diurnal variability of regional cloud and clear-sky radiative parameters derived from GOES data. Part II: November 1978 cloud distributions. J. Clim. Appl. Meteorol. 1984, 23, 1012–1031. [Google Scholar] [CrossRef]
- Lee, T.F.; Turk, F.J.; Richardson, K. Stratus and fog products using GOES-8-9 3.9-μm data. Weather Forecast. 1997, 12, 664–677. [Google Scholar] [CrossRef]
- Weaver, J.F.; Knaff, J.A.; Bikos, D.; Wade, G.S.; Daniels, J.M. Satellite observations of a severe supercell thunderstorm on 24 July 2000 made during the GOES-11 science test. Weather Forecast. 2002, 17, 124–138. [Google Scholar] [CrossRef][Green Version]
- Xu, W.; Wooster, M.J.; Roberts, G.; Freebron, P. New GOES imager algorithms for cloud and active fire detection and fire radiative power assessment across North, South and Central America. Remote Sens. Environ. 2010, 114, 1876–1895. [Google Scholar] [CrossRef]
- NOAA’s Geostationary and Polar-Orbiting Weather Satellites. Available online: http://web.archive.org/web/20190601142029/https://noaasis.noaa.gov/NOAASIS/ml/genlsatl.html (accessed on 25 May 2020).
- GOES History. Available online: https://www.goes-r.gov/mission/history.html (accessed on 25 May 2020).
- Azimi-Sadjadi, M.R.; Zekavat, S.A. Cloud classification using support vector machines. In Proceedings of the IEEE 2000 International Geoscience and Remote Sensing Symposium, Taking the Pulse of the Planet: The Role of Remote Sensing in Managing the Environment, Honolulu, HI, USA, 24–28 July 2000. [Google Scholar] [CrossRef]
- Tian, B.; Shaikh, M.A.; Azimi-Sadjadi, M.R.; Vonder Haar, T.H.; Reinke, D.L. A study of cloud classification with neural networks using spectral and textural features. IEEE Trans. Neural Netw. 1999, 10, 138–151. [Google Scholar] [CrossRef]
- Bankert, R.L.; Mitrescu, C.; Miller, S.D.; Wade, R.H. Comparison of GOES cloud classification algorithms employing explicit and implicit physics. J. Appl. Meteorol. Climatol. 2009, 48, 1411–1421. [Google Scholar] [CrossRef]
- Bottino, M.J.; Ceballos, J.C. Daytime cloud classification over South American region using multispectral GOES-8 imagery. Int. J. Remote Sens. 2015, 36, 1–19. [Google Scholar] [CrossRef]
- Pankiewicz, G.S. Pattern recognition techniques for the identification of cloud and cloud systems. Meteorol. Appl. 1995, 2, 257–271. [Google Scholar] [CrossRef]
- Rossow, W.B.; Tselioudis, G.; Polak, A.; Jakob, C. Tropical climate described as a distribution of weather states indicated by distinct mesoscale cloud property mixtures. Geophys. Res. Lett. 2005, 32, 1–4. [Google Scholar] [CrossRef]
- Tselioudis, G.; Rossow, W.; Zhang, Y.; Konsta, D. Global weather statets and their properties from passive and active satellite cloud retrievals. J. Clim. 2013, 26, 7734–7746. [Google Scholar] [CrossRef]
- Oreopoulos, L.; Cho, N.; Lee, D.; Kato, S.; Huffman, G.J. An examination of the nature of global MODIS cloud regimes. J. Geophys. Res. 2014, 119, 8362–8383. [Google Scholar] [CrossRef]
- Oreopoulos, L.; Cho, N.; Lee, D.; Kato, S. Radiative effects of global MODIS cloud regimes. J. Geophys. Res. 2016, 121, 2299–2317. [Google Scholar] [CrossRef]
- Tan, J.; Jakob, C. A three-hourly data set of the state of tropical convection based on cloud regimes. Geophys. Res. Lett. 2013, 40, 1415–1419. [Google Scholar] [CrossRef]
- Weinreb, M.; Han, D. Conversion of GVAR Infrared Data to Scene Radiance or Temperature. NOAA Office of Satellite and Product Operations. Available online: https://www.ospo.noaa.gov/Operations/GOES/calibration/gvar-conversion.html (accessed on 25 May 2020).
- Garrett, K.J.; Yang, P.; Nasiri, S.L.; Yost, C.R.; Baum, B.A. Influence of cloud-top height and geometric thickness on a MODIS infrared-based ice cloud retrieval. J. Appl. Meteorol. Climatol. 2009, 48, 818–832. [Google Scholar] [CrossRef]
- Chang, F.-L.; Li, Z. A near-global climatology of single-layer and overlapped clouds and their optical properties retrieved from Terra/MODIS data using a new algorithm. J. Clim. 2005, 18, 4752–4771. [Google Scholar] [CrossRef]
- Szejwach, G. Determination of semi-transparent cirrus cloud temperature from infrared radiances: Application to METEOSAT. J. Appl. Meteorol. 1982, 21, 384–393. [Google Scholar] [CrossRef]
- Ackerman, S.A.; Strabala, K.I.; Menzel, W.P.; Frey, R.A.; Moeller, C.C.; Gumley, L.E. Discriminating clear sky from clouds with MODIS. J. Geophys. Res. 1998, 103, 32141–32157. [Google Scholar] [CrossRef]
- Berkhin, P.A. Survey of clustering data mining techniques. In Grouping Multidimensional Data; Kogan, J., Nicholas, C., Teboulle, M., Eds.; Springer: Berlin, Germany, 2006; pp. 25–71. [Google Scholar]
- Baraldi, A.; Blonda, P. Survey of fuzzy clustering algorithms for pattern recognition—Part I. IEEE Trans. Syst. Man Cybern. Part B Cybern. 1999, 29, 778–785. [Google Scholar] [CrossRef] [PubMed]
- Baraldi, A.; Blonda, P. A survey of fuzzy clustering algorithms for pattern recognition—Part II. IEEE Trans. Syst. Man Cybern. Part B Cybern. 1999, 29, 786–801. [Google Scholar] [CrossRef] [PubMed]
- Gentleman, R.; Carey, V.J. Unsupervised machine learning. In Bioconductor Case Studies; Springer: New York, NY, USA, 2008; pp. 137–157. [Google Scholar]
- Lloyd, S.P. Least square quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Arthur, D.; Vassilvitskii, S. K-means++: The Advantages of Careful Seeding. In Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 7–9 January 2007; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA; pp. 1027–1035.
- Xu, Y.; Qu, W.; Li, Z.; Min, G.; Li, K.; Liu, Z. Efficient k-Means++ Approximation with MapReduce. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 3135–3144. [Google Scholar] [CrossRef]
- Caliński, T.; Harabasz, J. A dendrite method for cluster analysis. Commun. Stat. 1974, 3, 1–27. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef]
- Shapiro, M.A.; Keyser, D. Fronts, jet streams and the tropopause. In Extratropical Cyclones: The Erik Palmén Memorial Volume; Newton, C.W., Holopainen, E.O., Eds.; American Meteorological Society: Boston, MA, USA, 1990; pp. 167–191. [Google Scholar]
- Satyamurty, P.; Nobre, C.A.; Silva Dias, P.L. Meteorology of the tropics: South America. In Meteorology of the Southern Hemisphere; Karoly, D.J., Vincent, D.G., Eds.; American Meteorological Society: Boston, MA, USA, 1998; Volume 27, pp. 119–139. [Google Scholar]
- Archer, C.L.; Caldeira, K. Historical trends in the jet streams. Geophys. Res. Lett. 2008, 35, L08803. [Google Scholar] [CrossRef]
- Hoskins, B.J.; Hodges, K.I. A new perspective on Southern hemisphere storm tracks. J. Clim. 2005, 18, 4105–4129. [Google Scholar] [CrossRef]
- Trenberth, K.E. Storm tracks in the Southern hemisphere. J. Atmos. Sci. 1991, 48, 2159–2178. [Google Scholar] [CrossRef]
- Silva, V.B.S.; Berbery, E.H. Intense rainfall events affecting the La Plata basin. J. Hydrometeorol. 2006, 7, 769–787. [Google Scholar] [CrossRef]
- Gan, M.A.; Kousky, V.E.; Ropelewski, C.F. The South America monsoon circulation and its relationship to rainfall over West-Central Brazil. J. Clim. 2004, 17, 47–66. [Google Scholar] [CrossRef]
- Laing, A.G.; Fritsch, J.M. The global population of mesoscale convective complexes. Q. J. R. Meteorolog. Soc. 1997, 123, 389–405. [Google Scholar] [CrossRef]
- Richter, I.; Mechoso, C.R. Orographic influences on the annual cycle of Namibian stratocumulus clouds. Geophys. Res. Lett. 2004, 31, L24108. [Google Scholar] [CrossRef]
- Zuidema, P.; Painemal, D.; de Szoeke, S.; Fairall, C. Stratocumuls cloud-top height estimates and their climatic implications. J. Clim. 2009, 22, 4652–4666. [Google Scholar] [CrossRef]
- Jakob, C.; Tselioudis, G. Objective identification of cloud regimes in the Tropical Western Pacific. Geophys. Res. Lett. 2003, 30, 2082. [Google Scholar] [CrossRef]
- Jakob, C.; Tselioudis, G.; Hume, T. The radiative, cloud, and thermodynamic properties of the major tropical western pacific cloud regimes. J. Clim. 2005, 18, 1203–1215. [Google Scholar] [CrossRef][Green Version]
- International Cloud Atlas, Definition of Clouds. World Meteorological Organization. Available online: https://cloudatlas.wmo.int/en/clouds-definitions.html (accessed on 4 July 2020).
- Wilks, D.S. Empirical distributions and exploratory analysis. In Statistical Methods in the Atmospheric Sciences; International Geophysical Series; Dmowska, R., Hartmann, D., Rossby, H.T., Eds.; Academic Press: Burlington, MA, USA, 2006; Volume 91, pp. 23–70. [Google Scholar]
- Saji, N.H.; Goswami, B.N.; Vinayachandran, P.N.; Yamagata, T. A dipole mode in the tropical Indian Ocean. Nature 1999, 401, 360–363. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C. Madden-Julian oscillation. Rev. Geophys. 2005, 43, RG2003. [Google Scholar] [CrossRef]
- Mantua, N.J.; Hare, S.R.; Zhang, Y.; Wallace, J.M.; Francis, R.C. A Pacific interdecadal climate oscillation with impacts on salmon production. Bul. Am. Meteorol. Soc. 1997, 78, 1069–1079. [Google Scholar] [CrossRef]
- Baldwin, M.P.; Gray, L.J.; Dunkerton, T.J.; Hamilton, K.; Haynes, P.H.; Randel, W.J.; Holton, J.R.; Alexander, M.J.; Hirota, I.; Horinouchi, T.; et al. The Quasi-biennial oscillation. Rev. Geophys. 2001, 39, 179–229. [Google Scholar] [CrossRef]
- Ropelewski, C.F.; Jones, P.D. An extension of the Tahiti-Darwin Southern oscillation index. Mon. Weather Rev. 1987, 115, 2161–2165. [Google Scholar] [CrossRef]
- Shi, N.; Tian, P.; Zhang, L. Simultaneous influence of the Southern Hemisphere annular mode on the atmospheric circulation of the Northern Hemisphere during the boreal winter. Int. J. Climatol. 2019, 39, 2685–2696. [Google Scholar] [CrossRef]
- Barrucand, M.G.; Zitto, M.E.; Piotrkowski, R.; Canziani, P.; O’Neill, A. Historical SAM index time series: Linear and nonlinear analysis. Int. J. Climatol. 2018, 38, e1091–e1106. [Google Scholar] [CrossRef]
- Teleconnection Pattern Calculation Procedures. NOAA/National Weather Service, National Centers for Environmental Prediction, Climate Prediction Center. 2005. Available online: https://www.cpc.ncep.noaa.gov/products/precip/CWlink/daily_ao_index/history/method.shtml (accessed on 26 May 2020).
- Antarctic Oscillation (AAO). National Oceanic and Atmospheric Administration/National Weather Service, National Centers for Environmental Prediction, Climate Prediction Center. 2005. Available online: https://www.cpc.ncep.noaa.gov/products/precip/CWlink/daily_ao_index/aao/aao.loading.shtml (accessed on 26 May 2020).
- Thompson, D.W.; Wallace, J.M. Annular modes in the extratropical circulation. Part I: Month-to-month variability. J. Clim. 2000, 13, 1000–1016. [Google Scholar] [CrossRef]
- Limpasuvan, V.; Hartmann, D.L. Wave-maintained annular modes of climate variability. J. Clim. 2000, 13, 4414–4429. [Google Scholar] [CrossRef]
- Velasco, I.; Fritsch, J.M. Mesoscale convective complexes in the Americas. J. Geophys. Res. 1987, 92, 9591–9613. [Google Scholar] [CrossRef]
- Newman, M.; Alexander, M.A.; Ault, T.R.; Cobb, K.M.; Deser, C.; Di Lorenzo, E.; Mantua, N.J.; Miller, A.J.; Minobe, S.; Nakamura, H.; et al. The Pacific decadal oscillation, revisited. J. Clim. 2016, 29, 4399–4427. [Google Scholar] [CrossRef]
- Tsonis, A.A.; Elsner, J.B.; Hunt, A.G.; Jagger, T.H. Unfolding the relation between global temperature and ENSO. Geophys. Res. Lett. 2005, 32, 1–4. [Google Scholar] [CrossRef]
- Yuchechen, A.E.; Lakkis, S.G.; Canziani, P.O. A seasonal climatology of UV reflectivity for southern South America. Int. J. Remote Sens. 2017, 38, 28–56. [Google Scholar] [CrossRef]
- Barrett, B.S.; Carrasco, J.F.; Testino, A.P. Madden-Julian Oscillation (MJO) modulation of atmospheric circulation and Chilean winter precipitation. J. Clim. 2012, 25, 1678–1688. [Google Scholar] [CrossRef]
- Batista-Tomás, A.R.; Díaz, O.; Batista-Leyva, A.J.; Altshuler, E. Classification and dynamics of tropical clouds by their fractal dimension. Q. J. R. Meteorolog. Soc. 2016, 142, 983–988. [Google Scholar] [CrossRef]
- Zhao, F.; Tang, C.; Dai, C.; Wu, X.; Wei, H. The global distribution of cirrus clouds reflectance based on MODIS level-3 data. Atmosphere 2020, 11, 219. [Google Scholar] [CrossRef]
- Lynch, D.K. Cirrus: History and definition. In Cirrus; Lynch, D.K., Sassen, D., Starr, D.O.C., Stephens, G., Eds.; Oxford University Press: New York, NY, USA, 2002; pp. 3–10. [Google Scholar]
- World Meteorological Organization (WMO). International Meteorological Vocabulary, 2nd ed.; Secretariat of the WMO: Geneva, Switzerland, 1992. [Google Scholar]
- Carlson, T.N. Upper-tropospheric fronts and jet streaks. In Mid-Latitude Weather Systems; American Meteorological Society: Boston, MA, USA, 1998; pp. 404–447. [Google Scholar]
- Juckes, M.; Smith, R.K. Convective destabilization by upper-level troughs. Q. J. R. Meteorolog. Soc. 2000, 126, 111–123. [Google Scholar] [CrossRef]
- Griffiths, M.; Thorpe, A.J.; Browning, K.A. Convective destabilization by a tropopause fold diagnosed using potential-vorticity inversion. Q. J. R. Meteorolog. Soc. 2000, 126, 125–144. [Google Scholar] [CrossRef]
- Goering, M.A.; Gallus, W.A., Jr.; Olsen, M.A.; Stanford, J.L. Role of stratospheric air in a severe weather event: Analysis of potential vorticity and total ozone. J. Geophys. Res. Atmos. 2001, 106, 11813–11823. [Google Scholar] [CrossRef]
- Inoue, T. On the temperature and effective emissivity determination of semi-transparent cirrus clouds by bi-spectral measurements in the 10μm window region. J. Meteorolog. Soc. Jpn. 1985, 63, 88–99. [Google Scholar] [CrossRef]
- Greenwald, T.J.; Christopher, S.A. Effect of cold clouds on satellite measurements near 183 GHz. J. Geophys. Res. 2002, 107, 4170. [Google Scholar] [CrossRef]
- Wylie, D.P.; Menzel, W.P. Two years of cloud cover statistics using VAS. J. Clim. 1989, 2, 380–392. [Google Scholar] [CrossRef]
- Wylie, D.P.; Menzel, W.P.; Woolf, H.M.; Strabala, K.I. Four years of global cirrus cloud statistics using HIRS. J. Clim. 1994, 7, 1972–1986. [Google Scholar] [CrossRef]
- Liu, Y.; Xia, J.; Shi, C.-X.; Hong, Y. An improved cloud classification algorithm for China’s FY-2C multi-channel images using artificial neural network. Sensors 2009, 9, 5558–5579. [Google Scholar] [CrossRef] [PubMed]
- Croft, P.J. Fog. In Encyclopedia of Atmospheric Sciences; Holton, J.R., Curry, J.A., Pyle, J.A., Eds.; Academic Press: London, UK, 2003; Volume 2, pp. 777–792. [Google Scholar]

| Cluster # | Date | |||
|---|---|---|---|---|
| 4 July 2011 | 24 April 2013 | |||
| 1 | 465,021 (9.22%) | 311,922 (6.18%) | 86,072 (1.71%) | 182,495 (3.62%) |
| 2 | 1,813,436 (35.94%) | 748,304 (14.83%) | 228,091 (4.52%) | 622,275 (12.33%) |
| 3 | 2,767,078 (54.84%) | 2,984,436 (59.15%) | 405,573 (8.04%) | 2,523,610 (50.02%) |
| 4 | 1,000,873 (19.84%) | 1,092,484 (21.65%) | 1,717,155 (34.03%) | |
| 5 | 1,549,494 (30.71%) | |||
| 6 | 1,175,199 (23.29%) | |||
| 7 | 508,622 (10.08%) | |||
| Total | 5,045,535 (100.00%) | 5,045,535 (100.00%) | 5,045,535 (100.00%) | 50,455,535 (100.00%) |
| Date | (K) | CTH (km) | ||||||
|---|---|---|---|---|---|---|---|---|
| Mean (SD) | Mean (SD) | |||||||
| #1 | #2 | #3 | #4 | #1 | #2 | #3 | #4 | |
| 01/08/2011 | 232 (11) | 256 (15) | 278 (13) | 278 (12) | 10.71 (1.79) | 6.04 (1.91) | 2.16 (1.15) | 1.22 (0.92) |
| 04/01/2014 | 230 (12) | 253 (10) | 280 (10) | 285 (9) | 11.56 (2.01) | 7.34 (1.63) | 2.94 (1.39) | 1.61 (1.00) |
| 12/10/2016 | 228 (11) | 253 (13) | 279 (11) | 284 (11) | 10.26 (2.75) | 6.06 (2.67) | 2.98 (1.28) | 1.44 (0.84) |
| Season | (K) | CTH (km) | ||||||
|---|---|---|---|---|---|---|---|---|
| Mean (SD) | Mean (SD) | |||||||
| #1 | #2 | #3 | #4 | #1 | #2 | #3 | #4 | |
| Summer | 233 (10) | 259 (7) | 280 (5) | 284 (4) | 11.07 (1.66) | 6.37 (1.28) | 2.68 (0.69) | 1.64 (0.57) |
| Autumn | 230 (9) | 255 (8) | 280 (6) | 284 (5) | 11.34 (1.52) | 6.82 (1.35) | 2.70 (0.72) | 1.61 (0.55) |
| Winter | 232 (10) | 261 (10) | 279 (5) | 279 (6) | 10.43 (1.51) | 5.39 (1.27) | 2.06 (0.57) | 1.40 (0.54) |
| Spring | 231 (10) | 256 (9) | 279 (5) | 284 (6) | 10.47 (2.06) | 5.98 (1.38) | 2.56 (0.67) | 1.45 (0.49) |
| Cluster/ Entropy | Season | AAO | PDO | QBO | SOI | MJO | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 20°E | 70°E | 80°E | 100°E | 120°E | 140°E | 160°E | 120°W | 40°W | 10°W | ||||||
| #1 | All | −0.27 | −0.53 | −0.37 | 0.42 | 0.46 | 0.53 | 0.46 | −0.30 | −0.50 | |||||
| DJF | −0.74 | −0.72 | 0.53 | 0.75 | 0.78 | −0.62 | |||||||||
| MAM | −0.63 | 0.51 | 0.57 | 0.61 | 0.51 | −0.56 | |||||||||
| JJA | |||||||||||||||
| SON | 0.50 | 0.50 | −0.52 | ||||||||||||
| #2 | All | 0.24 | −0.31 | −0.25 | 0.31 | 0.29 | −0.27 | ||||||||
| DJF | |||||||||||||||
| MAM | |||||||||||||||
| JJA | −0.51 | ||||||||||||||
| SON | 0.47 | ||||||||||||||
| #3 | All | ||||||||||||||
| DJF | |||||||||||||||
| MAM | |||||||||||||||
| JJA | |||||||||||||||
| SON | 0.49 | ||||||||||||||
| #4 | All | ||||||||||||||
| DJF | |||||||||||||||
| MAM | |||||||||||||||
| JJA | 0.48 | ||||||||||||||
| SON | |||||||||||||||
| Entropy | All | 0.25 | 0.25 | 0.24 | −0.24 | ||||||||||
| DJF | −0.60 | −0.71 | 0.54 | 0.76 | |||||||||||
| MAM | −0.74 | −0.49 | 0.53 | 0.64 | 0.72 | 0.64 | −0.66 | ||||||||
| JJA | |||||||||||||||
| SON | 0.59 | 0.51 | −0.52 | −0.49 | 0.52 | ||||||||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuchechen, A.E.; Lakkis, S.G.; Caferri, A.; Canziani, P.O.; Muszkats, J.P. A Cluster Approach to Cloud Cover Classification over South America and Adjacent Oceans Using a k-means/k-means++ Unsupervised Algorithm on GOES IR Imagery. Remote Sens. 2020, 12, 2991. https://doi.org/10.3390/rs12182991
Yuchechen AE, Lakkis SG, Caferri A, Canziani PO, Muszkats JP. A Cluster Approach to Cloud Cover Classification over South America and Adjacent Oceans Using a k-means/k-means++ Unsupervised Algorithm on GOES IR Imagery. Remote Sensing. 2020; 12(18):2991. https://doi.org/10.3390/rs12182991
Chicago/Turabian StyleYuchechen, Adrián E., S. Gabriela Lakkis, Agustín Caferri, Pablo O. Canziani, and Juan Pablo Muszkats. 2020. "A Cluster Approach to Cloud Cover Classification over South America and Adjacent Oceans Using a k-means/k-means++ Unsupervised Algorithm on GOES IR Imagery" Remote Sensing 12, no. 18: 2991. https://doi.org/10.3390/rs12182991
APA StyleYuchechen, A. E., Lakkis, S. G., Caferri, A., Canziani, P. O., & Muszkats, J. P. (2020). A Cluster Approach to Cloud Cover Classification over South America and Adjacent Oceans Using a k-means/k-means++ Unsupervised Algorithm on GOES IR Imagery. Remote Sensing, 12(18), 2991. https://doi.org/10.3390/rs12182991





