Inter-Calibration of AMSU-A Window Channels
Abstract
1. Introduction
2. Materials and Methods
2.1. Sno Overview
2.1.1. Temporal Features and Number of SNO Pairs
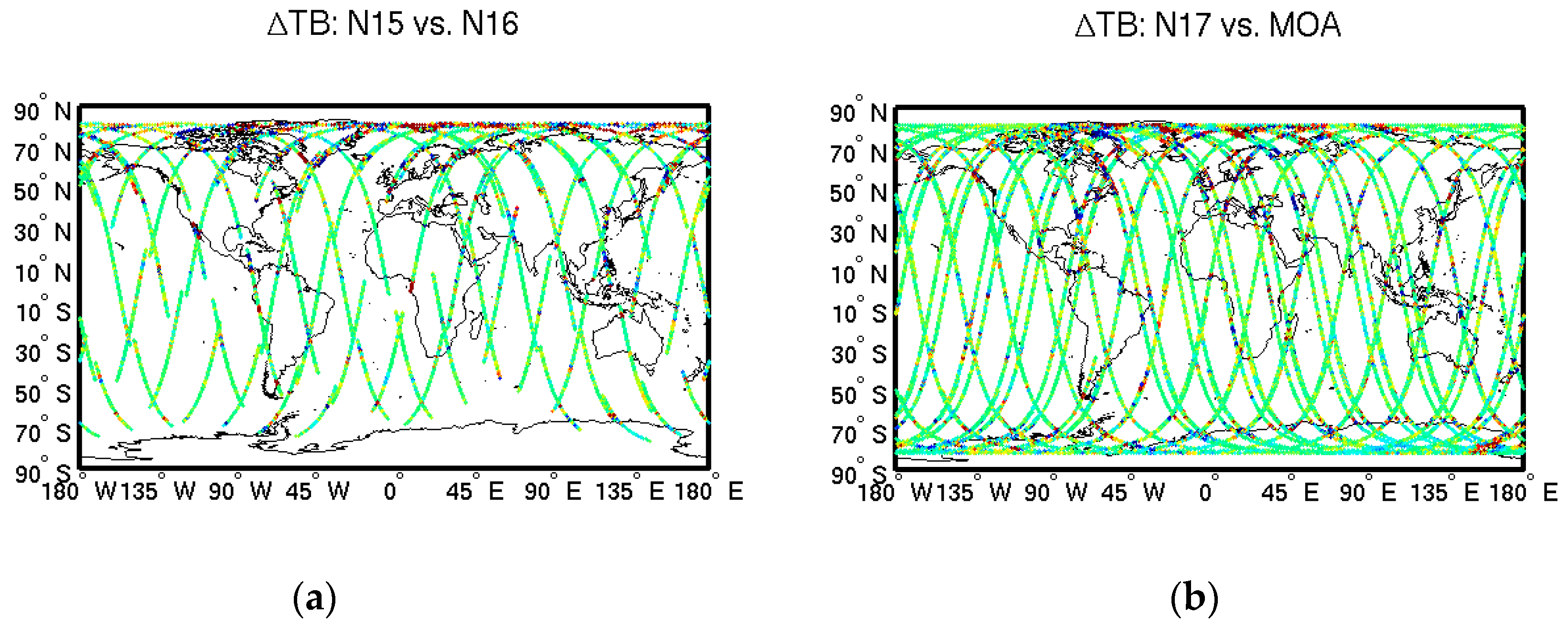
2.1.2. Spatial Features
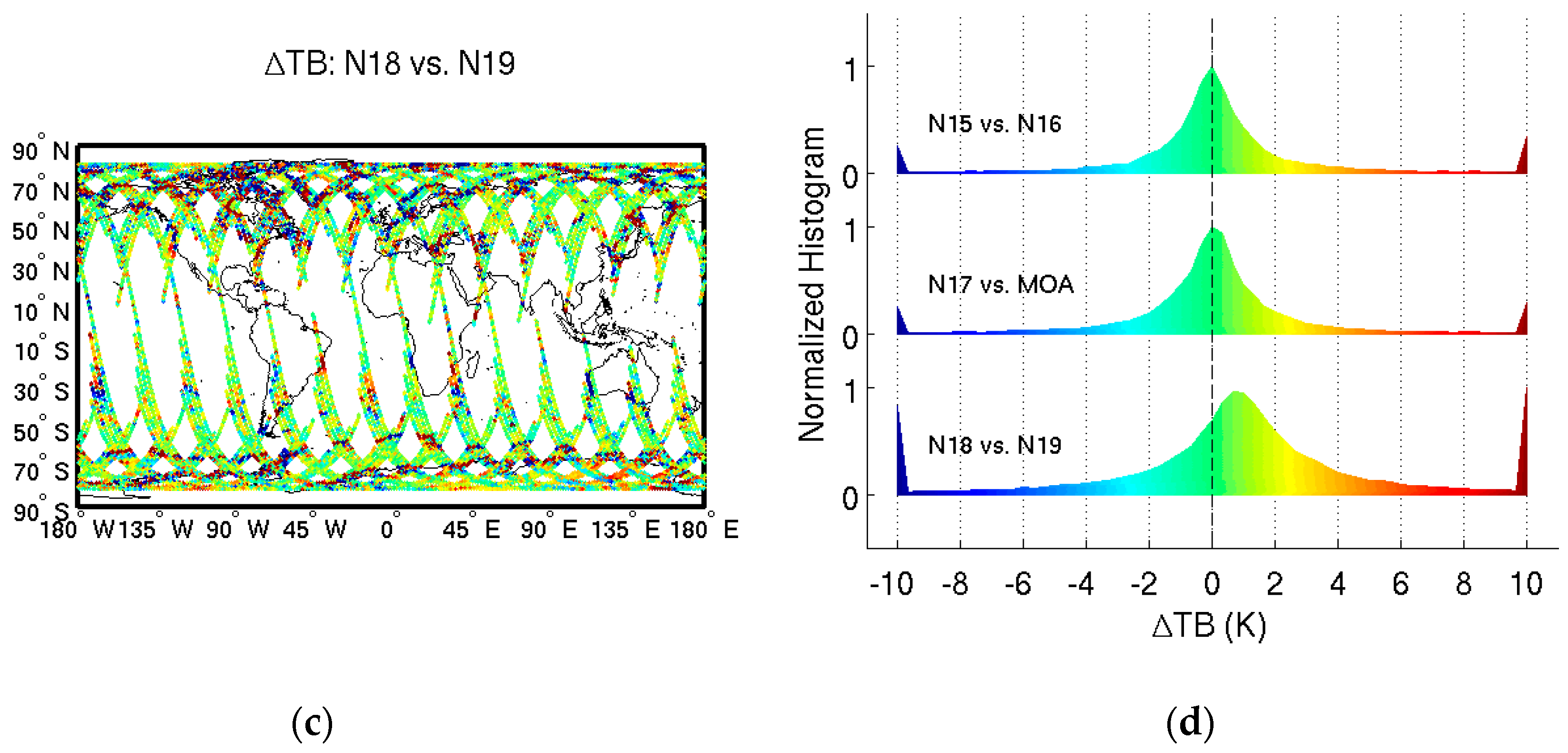
2.1.3. Brightness Temperature Time Series of SNO Pairs
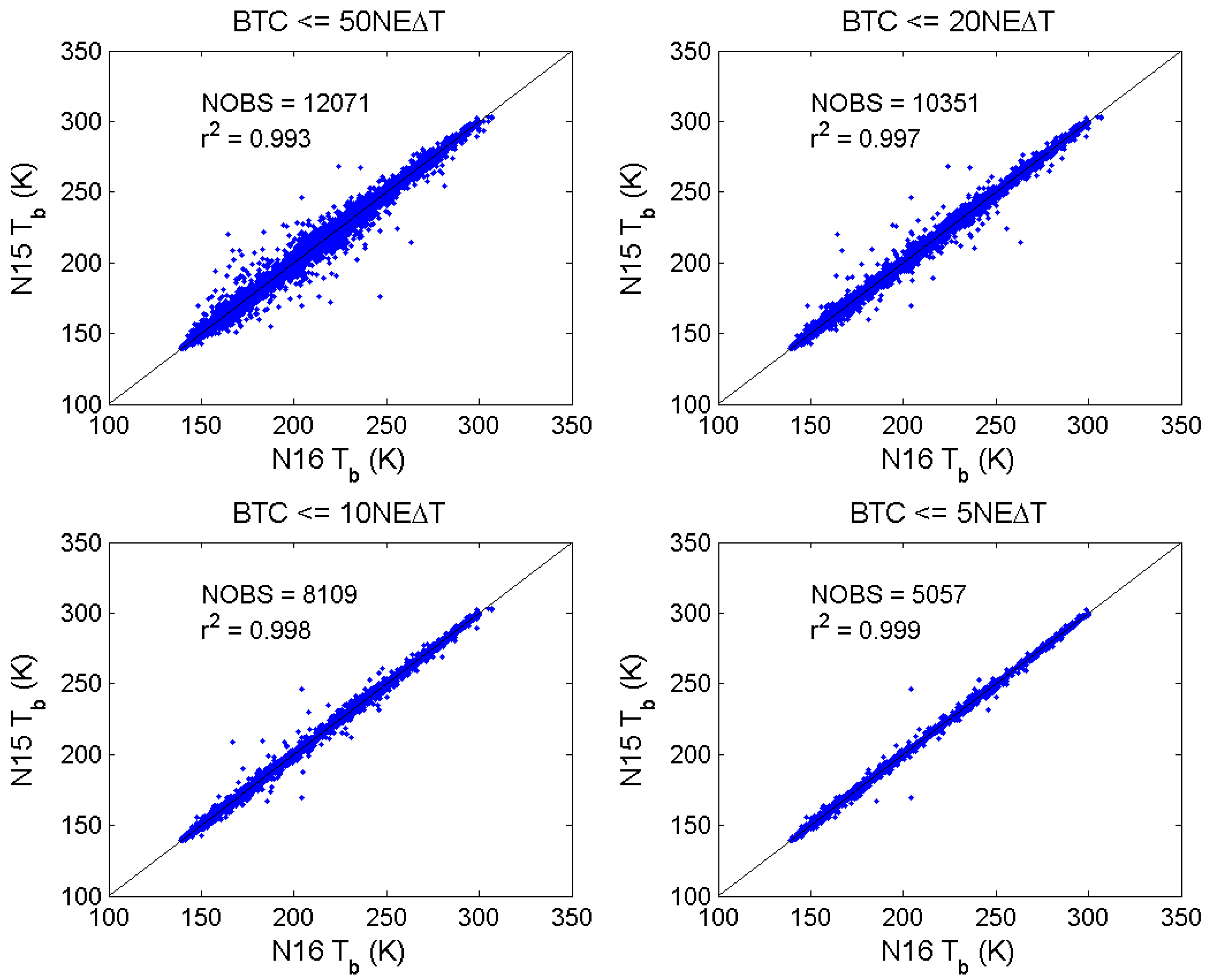
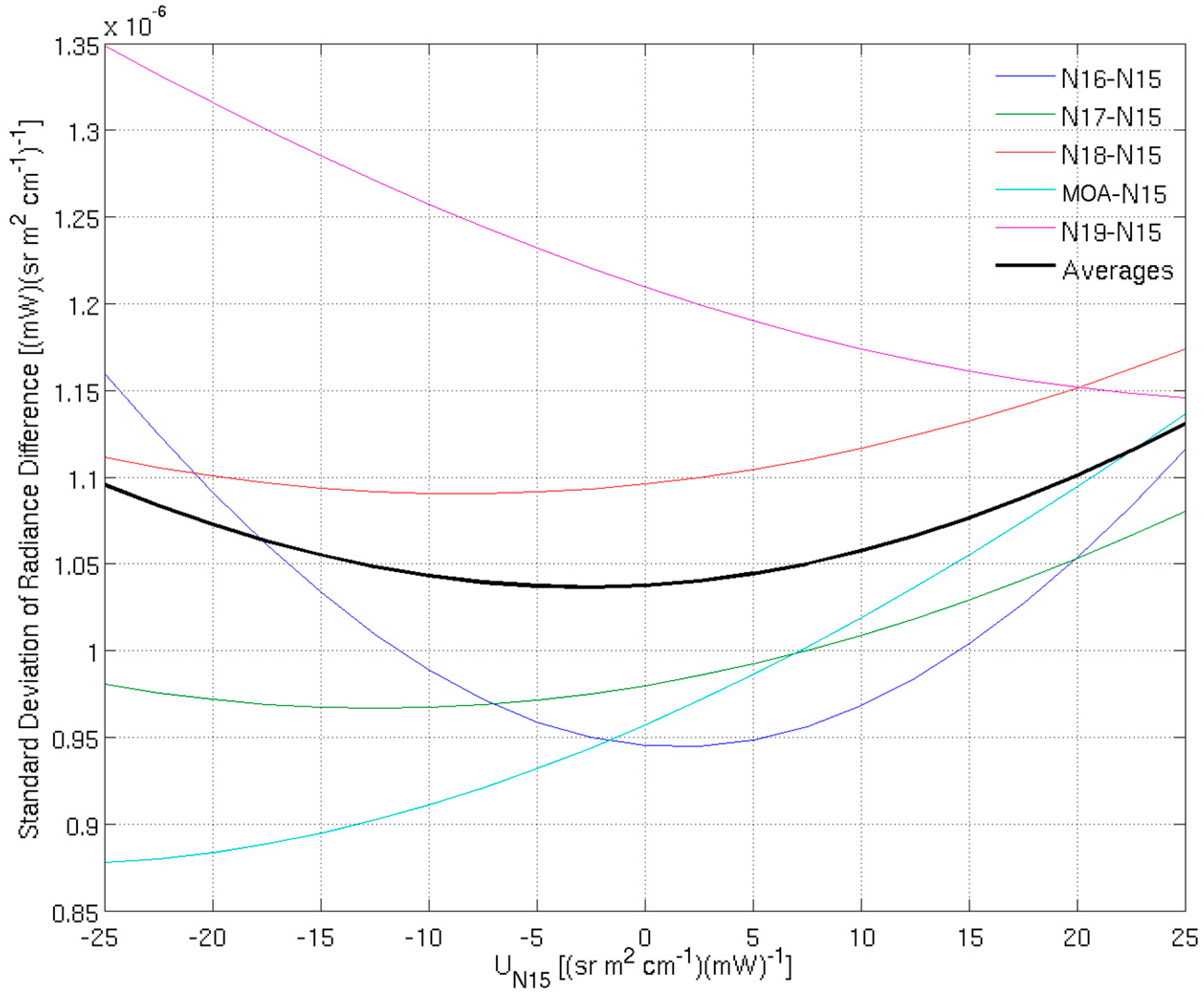
2.1.4. Sensitivity Test of Brightness Temperature Difference
2.2. Warm Target Contamination and Correction
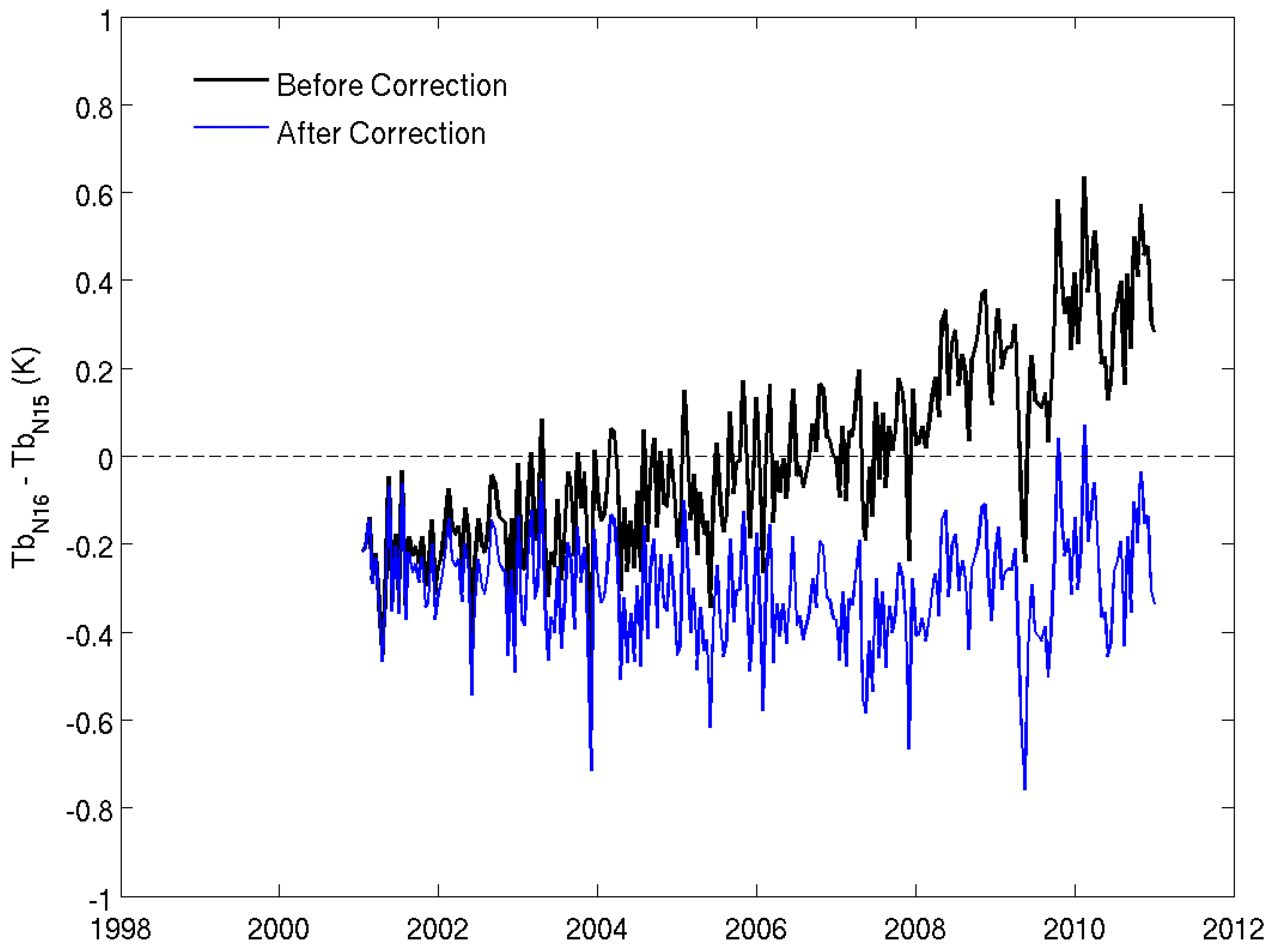
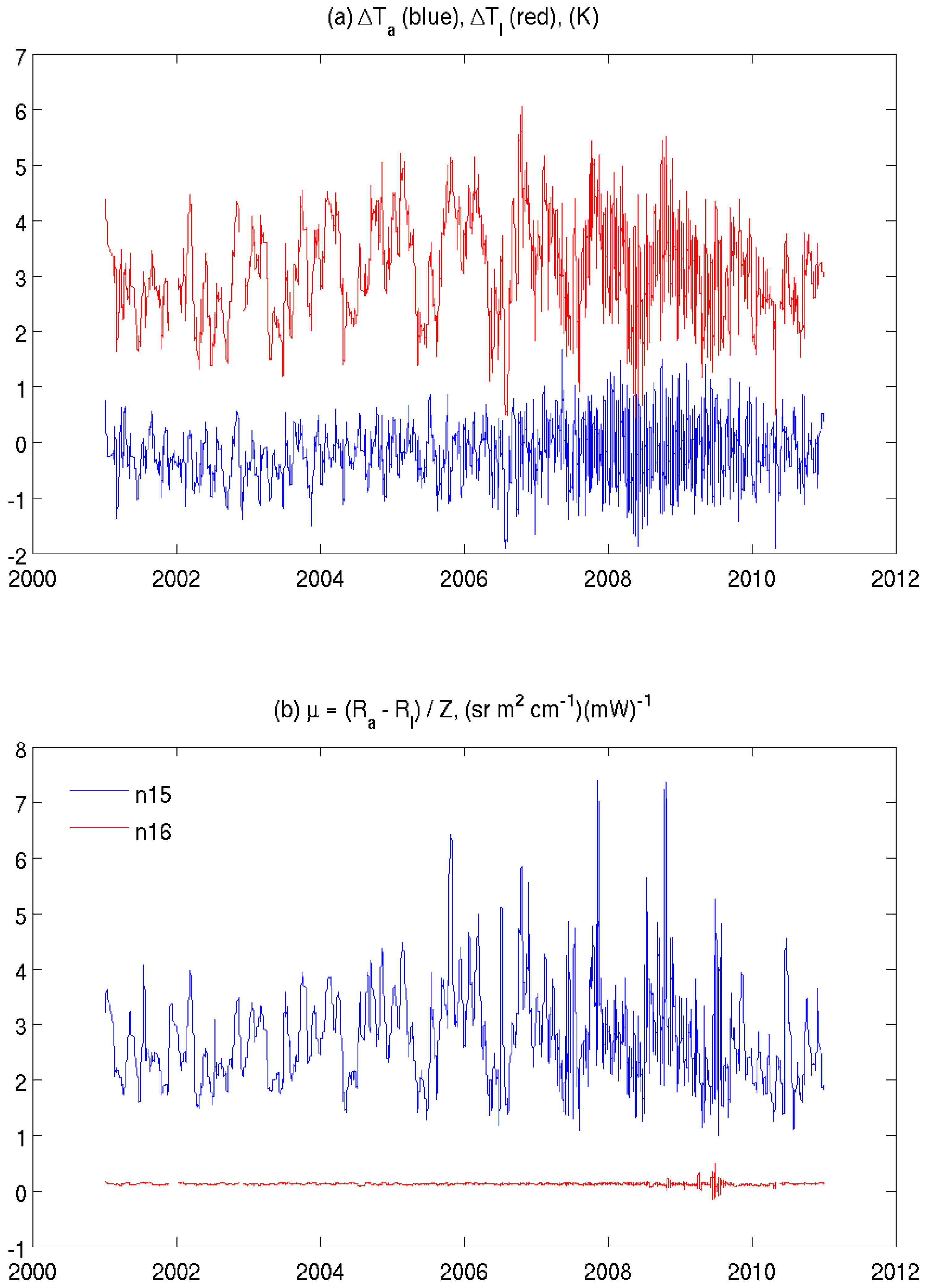
2.2.1. Identification of Warm Target Contamination
2.2.2. Correction Utilizing Integrated Microwave Inter-Calibration Approach
2.3. Other Satellite Specific Corrections
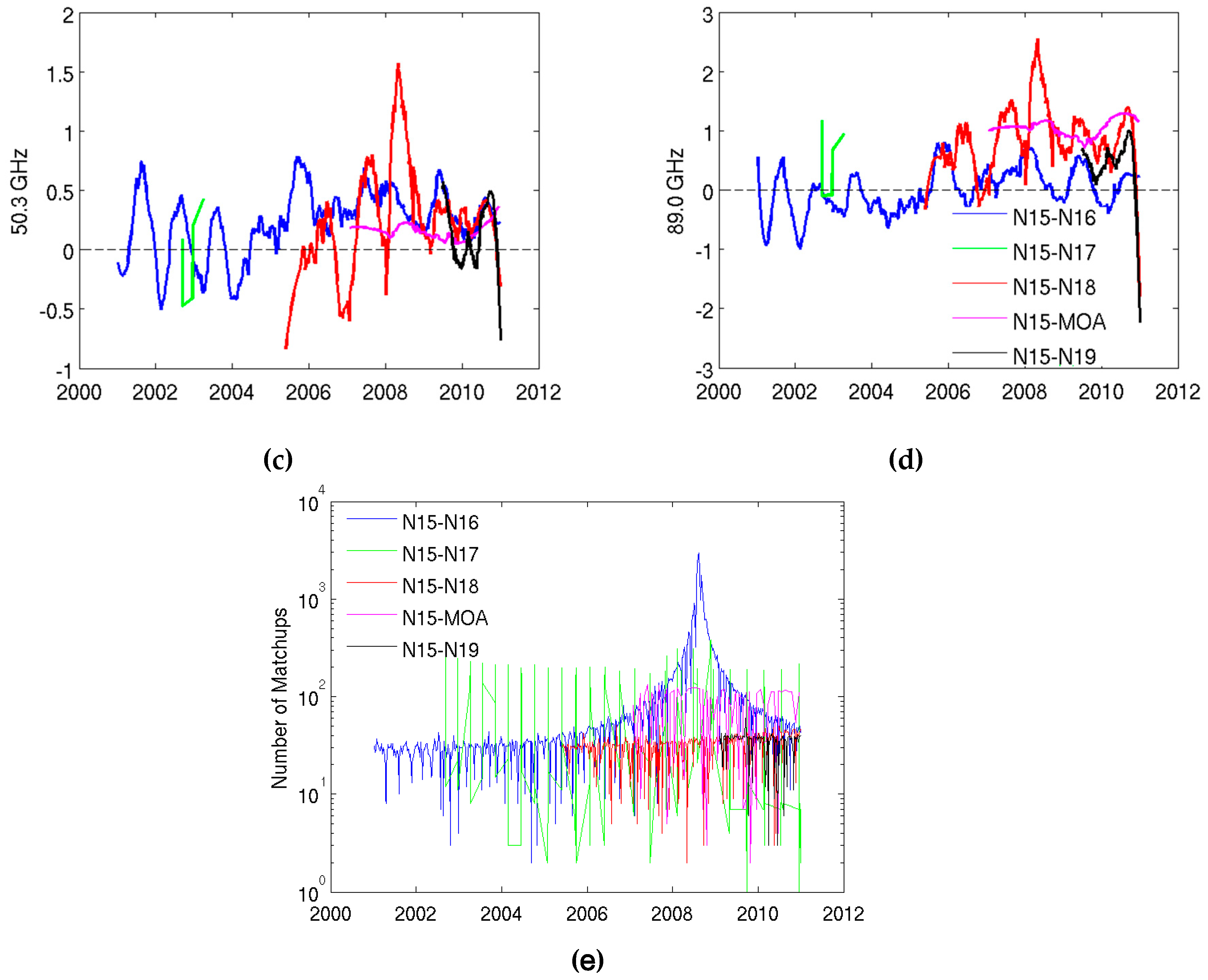
2.3.1. Slope Correction on 50.3 GHz, NOAA-16
2.3.2. Possible Frequency Shift in 89 GHz, NOAA-15
3. Results
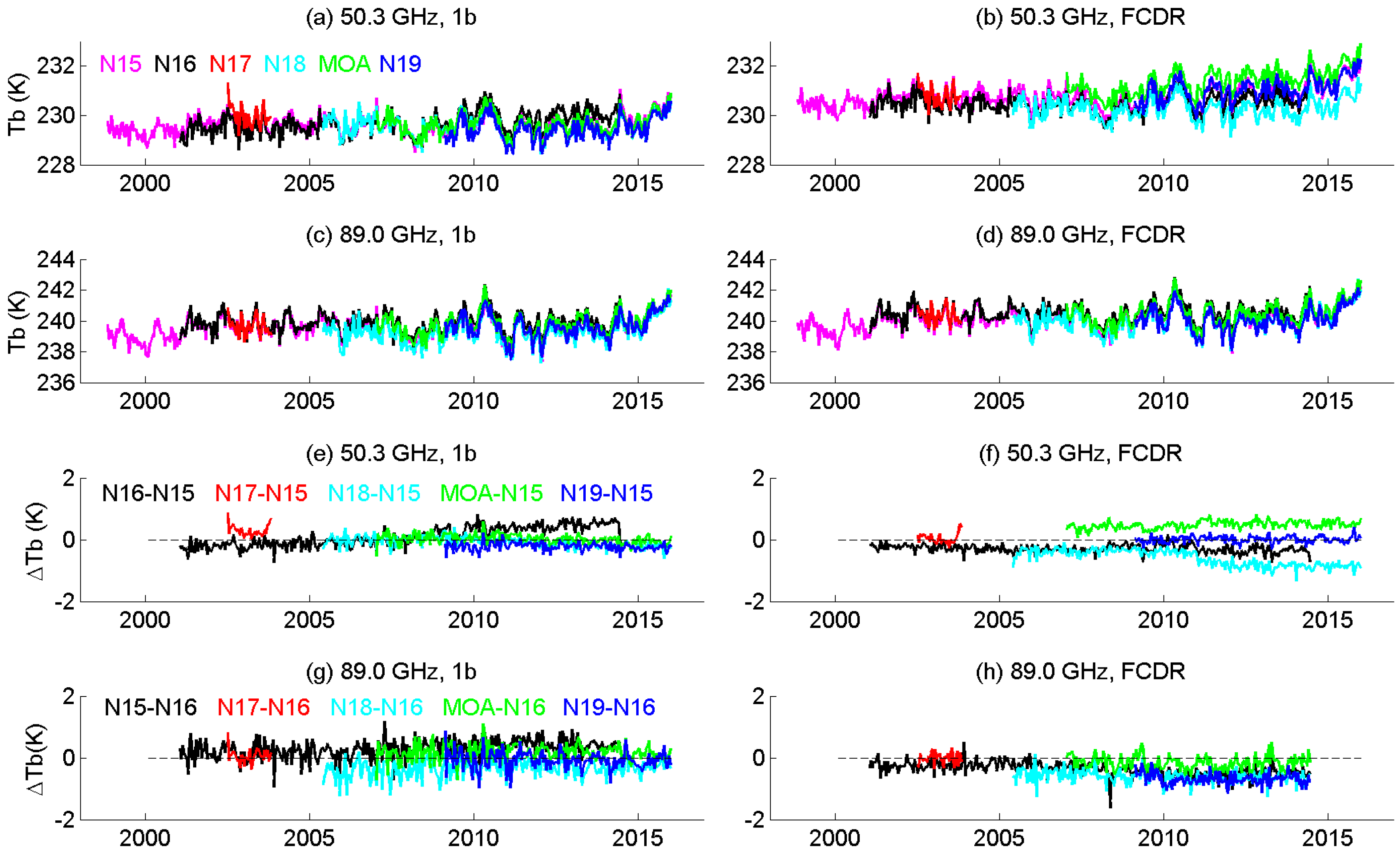
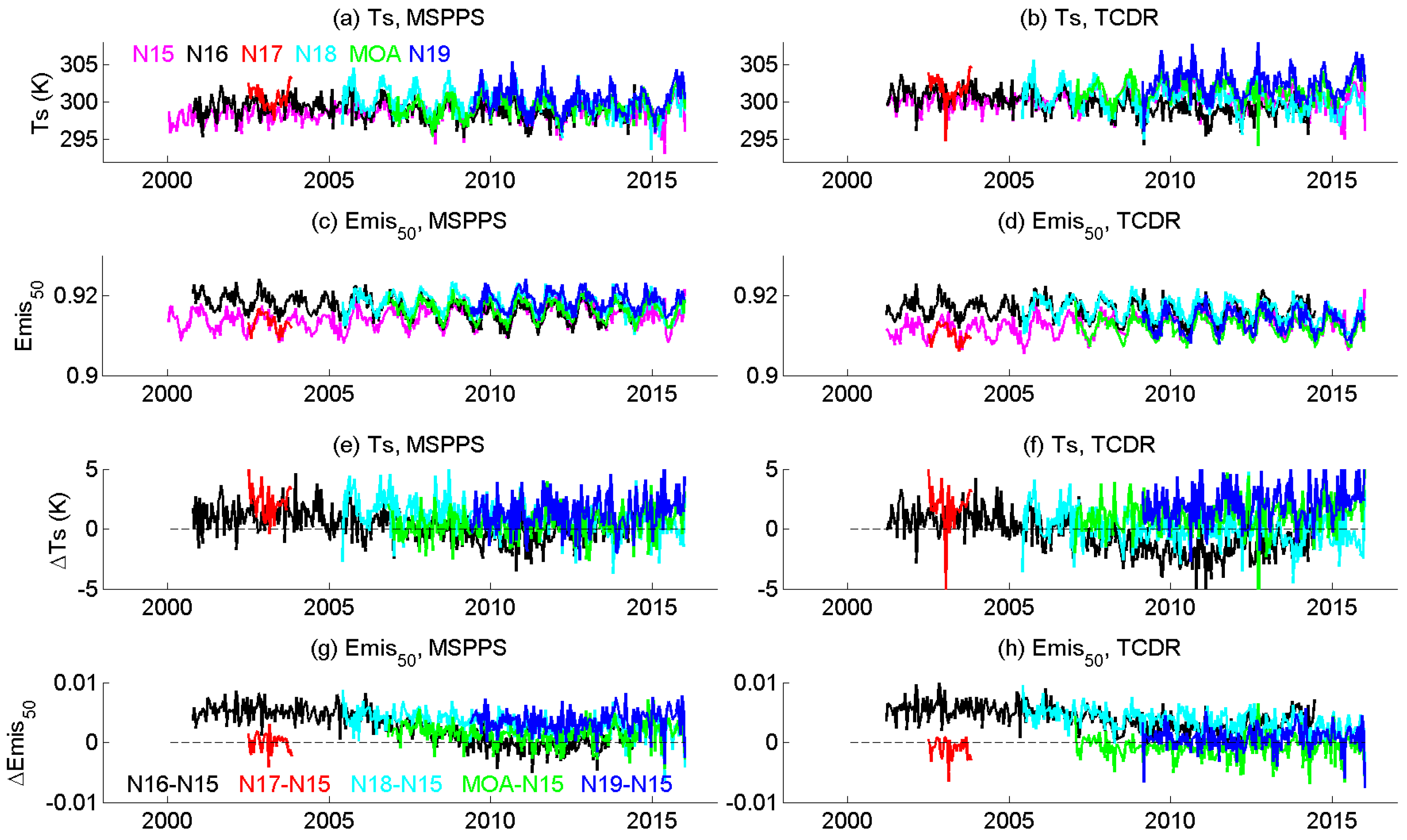
3.1. Fundamental CDR
3.2. Thematic CDR
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- National Research Council. Climate Data Records from Environmental Satellites; National Research Council of the National Academies: Washington, DC, USA, 2004; p. 150.
- Goldberg, M.; Ohring, G.; Butler, J.; Cao, C.; Datla, R.; Doelling, D.; Gärtner, V.; Hewison, T.; Iacovazzi, B.; Kim, D.; et al. The global space-based inter-calibration system. Bull. Am. Meteorol. Soc. 2011, 92, 467–475. [Google Scholar] [CrossRef]
- Hewison, T.J.; Wu, X.; Yu, F.; Tahara, Y.; Koenig, M. GSICS Inter-Calibration of Infrared Channels of Geostationary Imagers using Metop/IASI. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1160–1170. [Google Scholar] [CrossRef]
- Chander, G.; Hewison, T.J.; Fox, N.; Wu, X.; Xiong, X.; Blackwell, W.J. Overview of intercalibration of satellite instruments. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1056–1080. [Google Scholar] [CrossRef]
- Iacovazzi, R.A., Jr.; Cao, C.Y. Reducing uncertainties of SNO-estimated inter-satellite AMSU-A brightness temperature biases for surface-sensitive channels. J. Atmos. Ocean. Technol. 2008, 25, 1048–1054. [Google Scholar] [CrossRef]
- Yang, S.; Weng, F.; Yan, B.; Sun, N.; Goldberg, M. Special Sensor Microwave Imager (SSM/I) intersonsor calibration using s simultaneous conical overpass technique. J. Appl. Meteorol. Climatol. 2011, 50, 77–95. [Google Scholar] [CrossRef]
- Ruf, C.S. Detection of calibration drifts in spaceborne microwave radiometers using a vicarious cold reference. IEEE Trans. Geosci. Remote Sens. 2000, 38, 44–52. [Google Scholar] [CrossRef]
- Brown, S.T.; Ruf, C.S. Determination of an Amazon hot reference target for the on-orbit calibration of microwave radiometers. J. Atmos. Ocean. Technol. 2005, 22, 1340–1352. [Google Scholar] [CrossRef][Green Version]
- Wilheit, T.; Berg, W.; Jones, L.; Kroodsma, R.; McKague, D.; Ruf, C.; Sapiano, M. A consensus calibration based on TMI and WindSat. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 2641–2644. [Google Scholar]
- Sapiano, M.R.P.; Berg, W.K.; McKague, D.S.; Kummerow, C.D. Toward an intercalibrated fundamental climate data record of the SSM/I sensors. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1492–1503. [Google Scholar] [CrossRef]
- Cardinali, C. Data Assimilation: Observation Impact on the Short Range Forecast. ECMWF Lecture Notes. Available online: https://software.ecmwf.int/wiki/download/attachments/31064618/ObservationImpactForecast.pdf (accessed on 9 September 2020).
- Ferraro, R.R.; Weng, F.; Grody, N.; Zhao, L.; Meng, H.; Kongoli, C.; Pellegrino, P.; Qiu, S.; Dean, C. NOAA operational hydrological products derived from the AMSU. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1036–1049. [Google Scholar] [CrossRef]
- Boukabara, S.A.; Garrett, K.; Chen, W.; Iturbide-Sanchez, F.; Grassotti, C.; Kongoli, C.; Chen, R.; Liu, Q.; Yan, B.; Weng, F.; et al. MiRS: An all-weather 1DVAR satellite data assimilation and retrieval system. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3249–3272. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Pan, H.L.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Kistler, R.; Woollen, J.; Behringer, D.; et al. The NCEP climate forecast system reanalysis. Bull. Am. Meteorol. Soc. 2010, 91, 1015–1058. [Google Scholar] [CrossRef]
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.K.; et al. MERRA: NASA’s modern-era retrospective analysis for research and applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, D.P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Moradi, I.; Meng, H.; Ferraro, R.R.; Bilanow, S. Correcting geolocation errors for microwave instruments aboard NOAA satellites. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3625–3637. [Google Scholar] [CrossRef]
- Yang, W.; Meng, H.; Ferraro, R.R.; Moradi, I.; Devaraj, C. Cross scan asymmetry of AMSU-A window channels: Characterization, correction and verification. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1514–1530. [Google Scholar] [CrossRef]
- Zou, C.Z.; Wang, W. Inter-satellite calibration of AMSU-A observations for weather and climate applications. J. Geophys. Res. 2011, 116, D23113. [Google Scholar] [CrossRef]
- Zou, C.Z.; Goldberg, M.; Cheng, Z.; Grody, N.; Sullivan, J.; Cao, C.; Tarpley, D. Recalibration of microwave sounding unit for climate studies using simultaneous nadir overpasses. J. Geophys. Res. 2006, 111, D19114. [Google Scholar] [CrossRef]
- Christy, J.R.; Spencer, R.W.; Norris, W.B.; Braswell, W.D.; Parker, D.E. Error estimates of version 5.0 of MSU-AMSU bulk atmospheric temperature. J. Atmos. Ocean. Technol. 2003, 20, 613–629. [Google Scholar] [CrossRef]
- Mears, C.A.; Wentz, F.J. Construction of the Remote Sensing Systems V3.2 atmospheric temperature records from the MSU and AMSU microwave sounders. J. Atmos. Ocean. Technol. 2009, 26, 1040–1056. [Google Scholar] [CrossRef]
- Robertson, F.R.; Bosilovich, M.G.; Chen, J.; Miller, T.L. The effect of satellite observing system changes on MERRA water and energy fluxes. J. Clim. 2011, 24, 5197–5217. [Google Scholar] [CrossRef]
- Cao, C.; Weinreb, M.; Xu, H. Predicting simultaneous nadir overpasses among polar-orbiting meteorological satellites for the intersatellite calibration of radiometers. J. Atmos. Ocean. Technol. 2004, 21, 537–542. [Google Scholar] [CrossRef]
- Cao, C.; Xu, H.; Sullivan, J.; McMillin, L.; Ciren, P.; Hou, Y.T. Inter-satellite radiance biases for the High-Resolution infrared Radiation Sounders (HIRS) on board NOAA-15, -16, and -17 from simultaneous nadir observations. J. Atmos. Ocean. Technol. 2005, 22, 381–395. [Google Scholar] [CrossRef]
- Wang, L.; Goldberg, M.; Wu, X.; Cao, C.; Iacovazzi, R.; Yu, F.; Li, Y. Consistency assessment of Atmospheric Infrared Sounder and Infrared Atmospheric Sounding Interferometer radiances: Double differences versus simultaneous nadir overpasses. J. Geophys. Res. 2011, 116, D11. [Google Scholar] [CrossRef]
- POSE Operational Status–POSE Status–OSPO. Available online: www.ospo.noaa.gov/Operations/POES/status.html (accessed on 9 September 2020).
- John, V.O.; Holl, G.; Buehler, S.A.; Candy, B.; Saunders, R.W.; Parker, D.E. Understanding intersatellite biases of microwave humidity sounders using global simultaneous nadir overpasses. J. Geophys. Res. 2012, 117, D02305. [Google Scholar] [CrossRef]
- Mo, T. Prelaunch calibration of the Advanced Microwave Sounding Unit-A for NOAA-K. IEEE Trans. Microw. Theory Tech. 1996, 44, 1460–1469. [Google Scholar] [CrossRef]
- Mo, T.; Kigawa, S. A study of lunar contamination and on-orbit performance of the NOAA-18 Advanced Microwave Sounding Unit-A. J. Geophys. Res. 2007, 112, D20124. [Google Scholar] [CrossRef]
- Mo, T. AMSU-A antenna pattern corrections. IEEE Trans. Geosci. Remote Sens. 1999, 37, 103–112. [Google Scholar]
- Zou, C.Z.; Gao, M.; Goldberg, M. Error structure and atmospheric temperature trends in observations from the Microwave sounding Unit. J. Clim. 2009, 22, 1661–1681. [Google Scholar] [CrossRef]
- Zou, C.Z.; Wang, W. Stability of the MSU-derived atmospheric temperature trend. J. Atmos. Ocean. Technol. 2010, 27, 1960–1971. [Google Scholar] [CrossRef]
- Lu, Q.; Bell, W. Characterizing Channel Center Frequencies in AMSU-A and MSU Microwave Sounding Instruments. J. Atmos. Ocean. Technol. 2014, 31, 1713–1732. [Google Scholar] [CrossRef][Green Version]
- Han, Y.; Van Delst, P.; Liu, Q.; Weng, F.; Yan, B.; Treadon, R.; Derber, J. JCSDA Community Radiative Transfer Model (CRTM)—Version 1; NOAA Technical Report NESDIS 122; U.S. DOC NOAA: Washington, DC, USA, 2006.
- Meissner, T.; Wentz, F.J. The emissivity of the ocean surface between 6 and 90 GHz over a large range of wind speeds and earth incidence angles. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3004–3026. [Google Scholar] [CrossRef]
- Norouzi, H.; Rossow, W.; Temimi, M.; Prigent, C.; Azarderakhsh, M.; Boukabara, S.; Khanbilvardi, R. Using microwave brightness temperature diurnal cycle to improve emissivity retrievals over land. Remote Sens. Environ. 2012, 123, 470–482. [Google Scholar] [CrossRef]
- Tian, M.; Zou, X.; Weng, F. Use of Allan Deviation for characterizing satellite microwave sounder noise equivalent differential temperature (NEDT). IEEE Geosci. Remote Sens. Lett. 2015, 12, 2477–2480. [Google Scholar] [CrossRef]
- Ferraro, R.R.; Nelson, B.R.; Smith, T.; Prat, O.P. The AMSU-based hydrological bundle climate data record—Description and comparison with other data sets. Remote Sens. 2018, 10, 1640. [Google Scholar] [CrossRef]
- Yang, W.; John, V.O.; Zhao, X.; Lu, H.; Knapp, K.R. Satellite Climate Data Records: Development, Applications, and Societal Benefits. Remote Sens. 2016, 8, 331. [Google Scholar] [CrossRef]





| Launch Date | Decommission Date | Altitude (km) | Period (min) | Inclination (deg) | Precession Rate (min/mon) | |
|---|---|---|---|---|---|---|
| NOAA-15 | 05/13/1998 | 807 | 101.10 | 98.5 | 1.05 | |
| NOAA-16 | 09/21/2000 | 06/09/2014 | 849 | 102.00 | 99.0 | 3.00 |
| NOAA-17 | 06/24/2002 | 04/10/2013 | 810 | 101.20 | 98.7 | −4.62 |
| NOAA-18 | 05/20/2005 | 854 | 102.12 | 98.7 | 3.52 | |
| MetOP-A | 10/19/2006 | 817 | 101.36 | 98.7 | ||
| NOAA-19 | 02/06/2009 | 870 | 102.14 | 98.7 | 0.77 |
| Central Frequency (GHz) | ||||
|---|---|---|---|---|
| Channel 1 | Channel 2 | Channel 3 | Channel 15 | |
| NOAA-15 | 23.800013593 | 31.399992238 | 50.299988043 | 89.000016571 |
| NOAA-16 | 23.800013593 | 31.399992238 | 50.299988043 | 89.000016571 |
| NOAA-17 | 23.799204154 | 31.399662466 | 50.299178603 | 89.000076529 |
| NOAA-18 | 23.799204154 | 31.399662466 | 50.299178603 | 88.999986591 |
| MetOP-A | 23.799204154 | 31.399662466 | 50.299178603 | 89.000076529 |
| NOAA-19 | 23.799204154 | 31.399662466 | 50.299178603 | 89.000076529 |
| NOAA-16 | NOAA-17 | NOAA-18 | MetOP-A | NOAA-19 | |
|---|---|---|---|---|---|
| NOAA-15 | 1 (8.16) | 4.5 (104) | 1 (7.31) | 1 (31.7) | 1 (7.14) |
| NOAA-16 | 1 (8.44) | 3 (82.0) | 1 (11.2) | 2 (66.0) | |
| NOAA-17 | 1 (7.66) | 2 (40.0) | 1 (7.52) | ||
| NOAA-18 | 1 (9.81) | 8 (326.0) | |||
| MetOP-A | 1 (9.62) |
| Correlation Coefficients | 23.8 GHz | 31.4 GHz | 50.3 GHz | 89 GHz |
|---|---|---|---|---|
| (NOBS) | (53,531) | (53,531) | (53,534) | (53,506) |
| Distance | 0.19 | 0.18 | 0.15 | 0.18 |
| S1 * BTC | 0.53 | 0.53 | 0.47 | 0.43 |
| S2 * BTC | 0.55 | 0.55 | 0.5 | 0.44 |
| Time Difference | −0.01 | −0.01 | −0.01 | −0.01 |
| Ch # | NOAA-15 | NOAA-16 | NOAA 17 | NOAA-18 | MetOP A | NOAA-19 | |
|---|---|---|---|---|---|---|---|
| 1 | −3.00870 | −7.25050 | −7.22996 | −0.88067 | −0.98053 | 0.10012 | |
| 2 | −1.05123 | −3.35409 | −2.84701 | 1.51212 | −1.28394 | −2.30045 | |
| 3 | −2.37781 | −2.31567 | −2.20964 | −2.09040 | −2.62705 | −1.28555 | |
| 15 | 0 | −0.16528 | −0.25743 | 0.36618 | 0.21446 | 0.25637 | |
| 1 | 0 | −3.874 × | −5.459 × | 1.675 × | −4.635 × | −3.931 × | |
| 2 | 0 | −6.009 × | −6.199 × | −2.792 × | −5.270 × | −4.772 × | |
| 3 | 0 | −1.496 × | −1.750 × | 1.051 × | −5.953 × | −4.744 × | |
| 15 | 0 | 0 | −7.220 × | −2.927 × | −6.715 × | −2.017 × | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 3 | 0 | 1.448 × | 0 | 0 | 0 | 0 | |
| 15 | 0 | 0 | 0 | 0 | 0 | 0 |
| Before | After | |||||||
|---|---|---|---|---|---|---|---|---|
| Channel | 1 | 2 | 3 | 15 | 1 | 2 | 3 | 15 |
| N16-N15 | 0.374 | 0.263 | 0.267 | 0.315 | 0.217 | 0.193 | 0.126 | 0.227 |
| N17-N15 | 0.285 | 0.217 | 0.191 | 0.225 | 0.191 | 0.191 | 0.171 | 0.132 |
| N18-N15 | 0.386 | 0.259 | 0.168 | 0.337 | 0.239 | 0.197 | 0.13 | 0.242 |
| M02-N15 | 0.37 | 0.384 | 0.167 | 0.328 | 0.215 | 0.207 | 0.108 | 0.227 |
| N19-N15 | 0.424 | 0.276 | 0.174 | 0.374 | 0.263 | 0.187 | 0.115 | 0.208 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, W.; Meng, H.; Ferraro, R.R.; Chen, Y. Inter-Calibration of AMSU-A Window Channels. Remote Sens. 2020, 12, 2988. https://doi.org/10.3390/rs12182988
Yang W, Meng H, Ferraro RR, Chen Y. Inter-Calibration of AMSU-A Window Channels. Remote Sensing. 2020; 12(18):2988. https://doi.org/10.3390/rs12182988
Chicago/Turabian StyleYang, Wenze, Huan Meng, Ralph R. Ferraro, and Yong Chen. 2020. "Inter-Calibration of AMSU-A Window Channels" Remote Sensing 12, no. 18: 2988. https://doi.org/10.3390/rs12182988
APA StyleYang, W., Meng, H., Ferraro, R. R., & Chen, Y. (2020). Inter-Calibration of AMSU-A Window Channels. Remote Sensing, 12(18), 2988. https://doi.org/10.3390/rs12182988








