SLRL4D: Joint Restoration of Subspace Low-Rank Learning and Non-Local 4-D Transform Filtering for Hyperspectral Image
Abstract
1. Introduction
1.1. Restoration by Low-Rank Property
1.2. Restoration by Non-Local Similarity
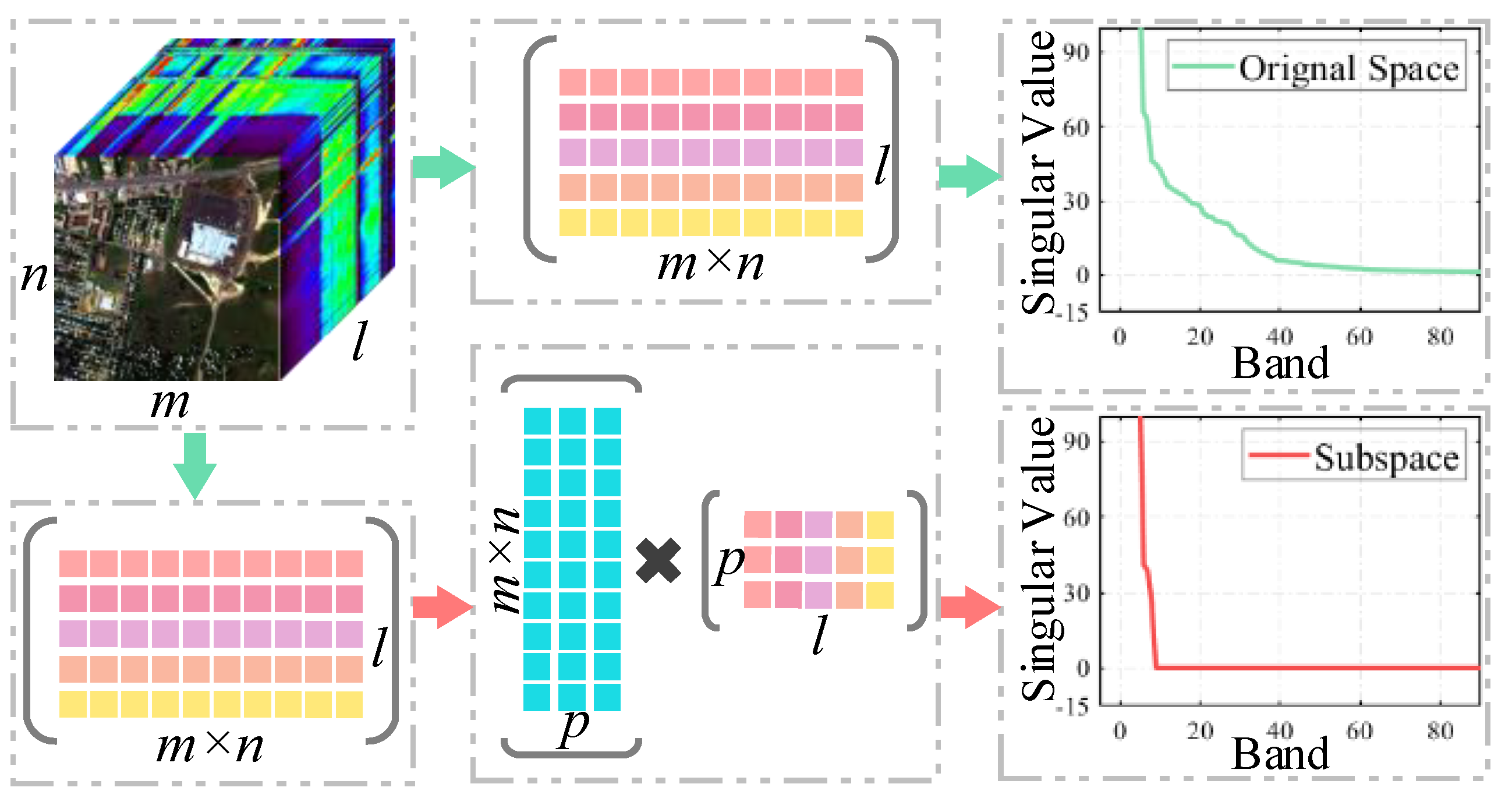
1.3. Restoration by Subspace Projection
- The subspace low-rank learning method is designed to restore the clean HSI from the contaminated HSI which is degraded by mixed noises. An orthogonal dictionary with far lower dimensions is learned during the process of alternating updates, thus leading to precise restoration of the clean principal signal of HSI.
- Based on the full exploration of low-rank property in subspace, BM4D filtering is employed to further explore the NSS property within the subspace of HSI rather than the original space. By preserving the details of the spatial domain more precisely, the complete parameter-free BM4D filtering leads to easier application in real world.
- Each term in the proposed restoration model is convex after careful design, thus, the convex optimization algorithm based on the alternating direction method of multipliers (ADMM) could be derived to solve and optimize this model. Meanwhile, due to the HSI being decomposed into two sub-matrices of lower dimensions, computational consumption of the proposed SLRL4D algorithm is much lower than other existing restoration methods.
- Extensive experiments of quantitative analysis and visual evaluation are conducted on several simulated and real datasets, and it is demonstrated that our proposed method not only achieves better restoration results, but also improves reliability and efficiency compared with the latest HSI restoration methods.
2. Problem Formulation
2.1. Degradation Model
2.2. Low-Rank Regularization
2.3. Non-Local Regularization
- For the low-rank regularization, when stripes or deadlines emerge at the same location in HSI, they also appear to have structured low-rank property, hence it is difficult to isolate sparse noise from low-rank signals. Meanwhile, its denoising ability is highly degraded when encountering heavy Gaussian noise.
- For the non-local regularization, the performance of restoration relies on the selection of search window and the neighborhood window, better performance is often achieved with much higher computational complexity. In practical applications, the excessively high time consumption of processing is fatal.
3. Methodology Design
3.1. Subspace Low-Rank Representation
- The use of clean HSI as the dictionary will inevitably cause the situation . Hence the dimension of the coefficients matrix will increase to immediately. The velocity of calculation and the rate of convergence will be decreased remarkably.
- In the face of heavy Gaussian noise, this model is not able to perform satisfied restoration results. The main reason is the plentiful sharp feature of the spatial domain in the original HSI are directly ignored.
3.2. Proposed SLRL4D Model
- The low-rank property of the spectral dimension lives in multiple subspaces and NSS of the spatial dimension is synchronously exploited in the process of restoration. Better restoration results would be achieved consequently.
- The dimension of subspace p is far lesser than the dimension of original space l which brings far lesser resource consumption and computational time in the practical experimentation. Higher restoration performance would be achieved consequently.
- Each term of this model is convex, thereby it is solvable with the employment of distributed ADMM algorithm. Easier restoration solution and optimization would be achieved consequently.
3.3. Model Optimization
- Update (Line 4): The subproblem of updating is given by:The soft-thresholding algorithm is employed to efficiently solve this subproblem:where is the soft-thresholding operator with threshold value . is the absolute value of each element in matrix .
- Update (Line 6):The subproblem of updating is given by:According to the reduced-rank Procrustes rotation algorithm [49], the solution of this subproblem is formulated aswhere , and are the left singular vector and right singular vector of . In this way, the solution to is given by the form.
Algorithm 1 ADMM-based algorithm for solving Equation (9). - Require:
- The contaminated HSI , dimension of subspace r, regularization parameters and , stop criterion , maximum iteration .
- Ensure:
- The latent denoised HSI .
- 1:
- Initialization: Estimate with the HySime algorithm [55], set = = = =0, set , , set .
- 2:
- while not converged do
- 3:
- Update with , , , fixed
- 4:
- 5:
- Update with , , , fixed
- 6:
- 7:
- Update with , , , fixed
- 8:
- 9:
- Update with , , , fixed
- 10:
- 11:
- Update with , , , fixed
- 12:
- 13:
- Update lagrange multipliers ,
- 14:
- 15:
- 16:
- 17:
- Update iteration
- 18:
- 19:
- end while
- 20:
- return.
- Update (Line 8):The subproblem of updating is given by:Under our design, BM4D filtering could efficiently solve this non-local regularized subproblem at lightning speed:
- Update (Line 10):The subproblem of updating is given by:Inviting the well-known singular value shrinkage method [56] to solve this nuclear norm subproblem, thus the solution could be formulated as:where is the singular value thresholding operator, which is defined as:and represents the singular value decomposition of , represents first r singular values of .
- Update (Line 12):The subproblem of updating is given by:Through the calculation of partial derivative, the solution of this convex subproblem is equivalent to the beneath linear equation:where , , , and is the identity matrix, is the transpose of the matrix .
4. Experimental Configurations
4.1. Datasets
- HYDICE Washington DC Mall (WDC): This dataset was acquired in the Washington DC mall by the HYDICE sensor, which contains intricate ground substances for example, rooftops, rubble roads, streets, lawn, vegetation, aquatoriums, and shadows. The spectral and spatial resolutions of corrected data are 191 high-quality clean bands ranging from 0.4–2.4 μm and 1208 × 307 pixels with 2.0 m/pixel. A sub-cube with the size of 256 × 256 × 191 is cropped for our simulated experiment.
- ROSIS Pavia University (PU): This dataset was acquired in the Pavia University by the ROSIS sensor, which contains intricate ground substances for example, asphalt roads, meadows, buildings, Bricks, vegetation and shadows. The spectral and spatial resolutions of corrected data are 103 high-quality clean bands ranging from 0.43–0.86 μm and 610 × 340 pixels with 1.3 m/pixel. A sub-cube with the size of 256 × 256 × 103 is cropped for our simulated experiment.
- HYDICE Urban: This dataset was acquired in the Copperas Cove by the HYDICE sensor, which also contains intricate ground substances. The spectral and spatial resolutions of this dataset are 210 bands and 307 × 307 pixels. Multiple bands are severely corrupted by the heavy mixed noises and watervapour absorption hence this data is employed to validate the performance of the proposed method in the real application.
- EO-1 Australia: This dataset was acquired in Australia by the EO-1 HYPERION sensor, the spectral and spatial resolutions of this dataset are 150 bands and 200 × 200 pixels. Multiple bands are severely corrupted by a series of deadlines, stripes and Gaussian noise, hence this data is also employed to validate the performance of SLRL4D in the real application.
4.2. Comparison Methods
- NLR-CPTD [41]: One of the latest HSI restoration methods which combine the low-rank CP tensor decomposition and non-local patches segmentation. It achieves state-of-the-art performance in removing Gaussian-stripes mixed noises removal.
- LRTDGS [57]: One of the latest HSI restoration methods that combine the low-rank Tucker tensor decomposition and group sparsity regularization. It achieves state-of-the-art performance in isolating structured sparse noise.
- LRTDTV [34]: A combination method of the tensor tucker decomposition and anisotropic TV, the piecewise smooth property of spatial-spectral domains and the global correlation of all bands are successfully explored.
- LLRSSTV [30]: Local overlapping patches of HSI are first cropped, then SSTV is embedded in the LRMR framework, therefore, the isolation of clean HSI patch and mixed noises is achieved.
- FSSLRL [49]: Superpixel segmentation is creatively introduced into the subspace low-rank learning architecture, and both spatial and spectral correlations are exploited simultaneously.
- TDL [58]: A dictionary learning denoising method based on the well-known Tucker tensor decomposition technique, outstanding Gaussian noise removal is achieved with the splitting rate of convergence.
- PCABM4D [47]: An enhanced principal component analysis method based on BM4D, BM4D filtering is employed to eliminate the remaining low-energy noisy component after PCA is executed in HSI.
- LRMR [21]: A patch-based restoration method under the framework of low-rank matrix recovery, the low-rank property of HSI is explored by dividing the original HSI into several local patches.
- BM4D [46]: An improved version of the well-known BM3D denoising algorithm, NSS of HSI is efficiently utilized in voxels instead of pixels.
4.3. Simulation Configurations
- Case 1: Zero-mean Gaussian noise with the same standard deviation was added to each band, and the variance of Gaussian noise was set to 0.25.
- Case 2: Zero-mean Gaussian noise with the different standard deviations was added to each band, and the variances were randomly selected from 0.15 to 0.25.
- Case 3: The variances and added bands of Gaussian noise were selected in the same manner as in Case 2. Meanwhile, impulse noise was added to 20 continuous bands with a percentage of 10%.
- Case 4: Deadlines were added to 20 continuous bands, and their widths and number were randomly selected, ranging from [1, 3] and [3, 10], respectively. The variances and added bands of Gaussian noise were selected in the same manner as in Case 2 still.
- Case 5: The stripes were added to 20 continuous bands, whose numbers were also randomly selected, ranging from [3, 10]. And the added manner of Gaussian noise were also selected same as in Case 2.
- Case 6: Mixed noises composed of multiple diverse types were added to different bands of datasets, that is, Gaussian noise, impulse noise, deadlines and stripes were added in the same manner as Case 2–5 simultaneously.
5. Results
5.1. Experimental Results on Simulated Datasets
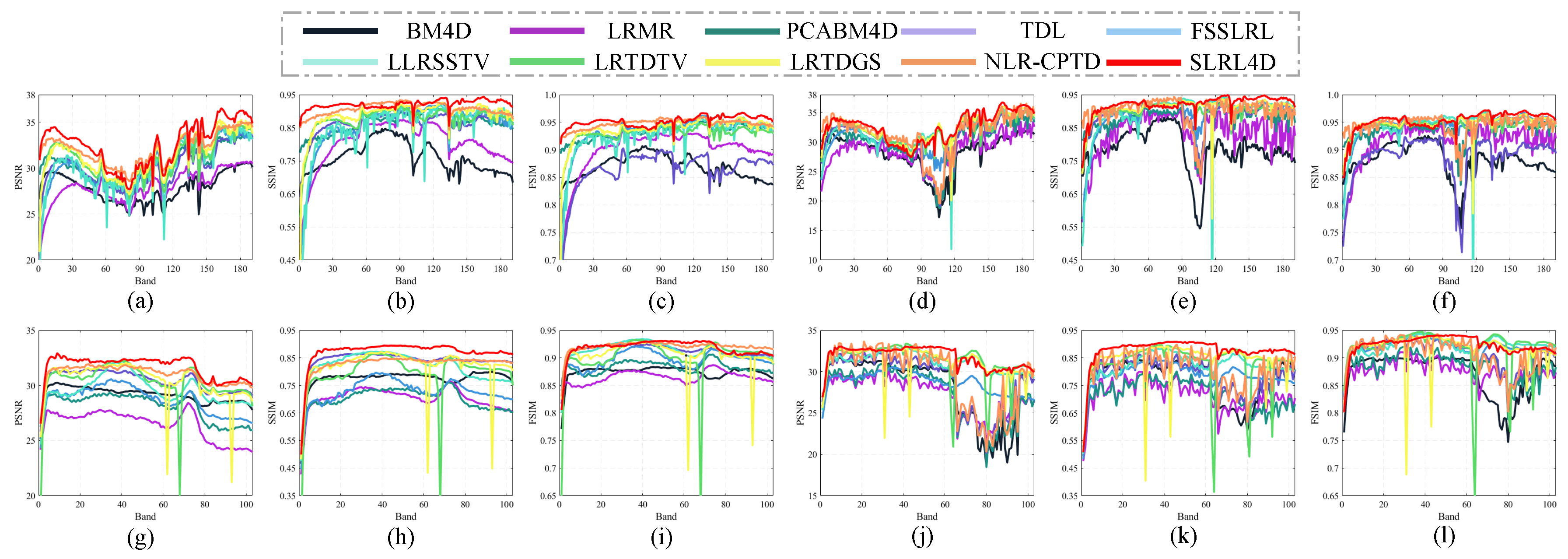
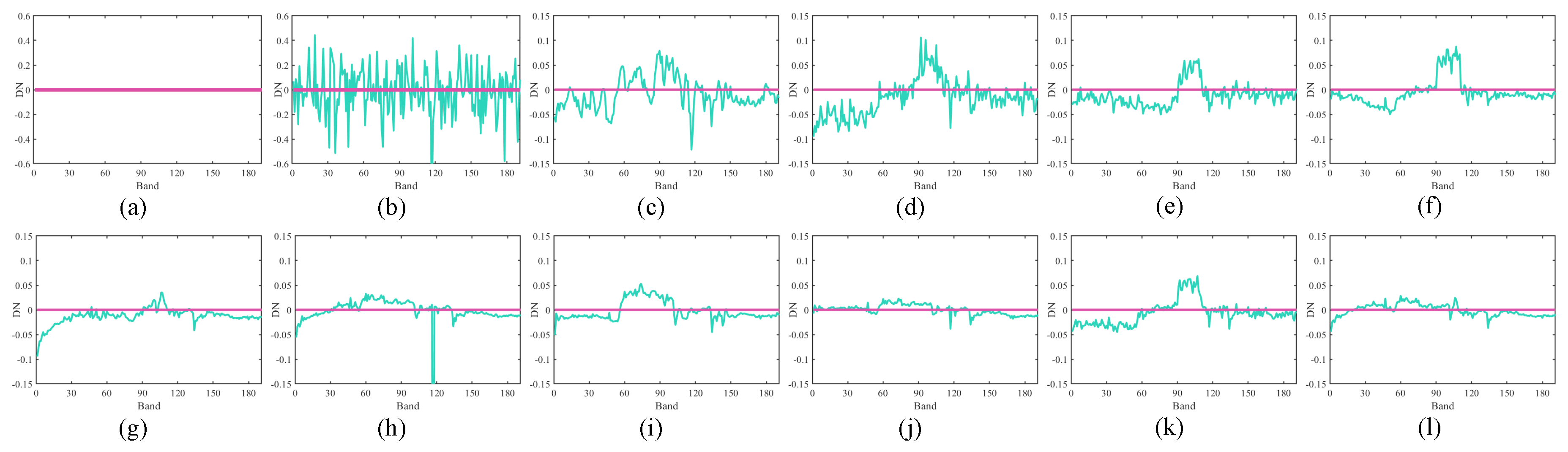
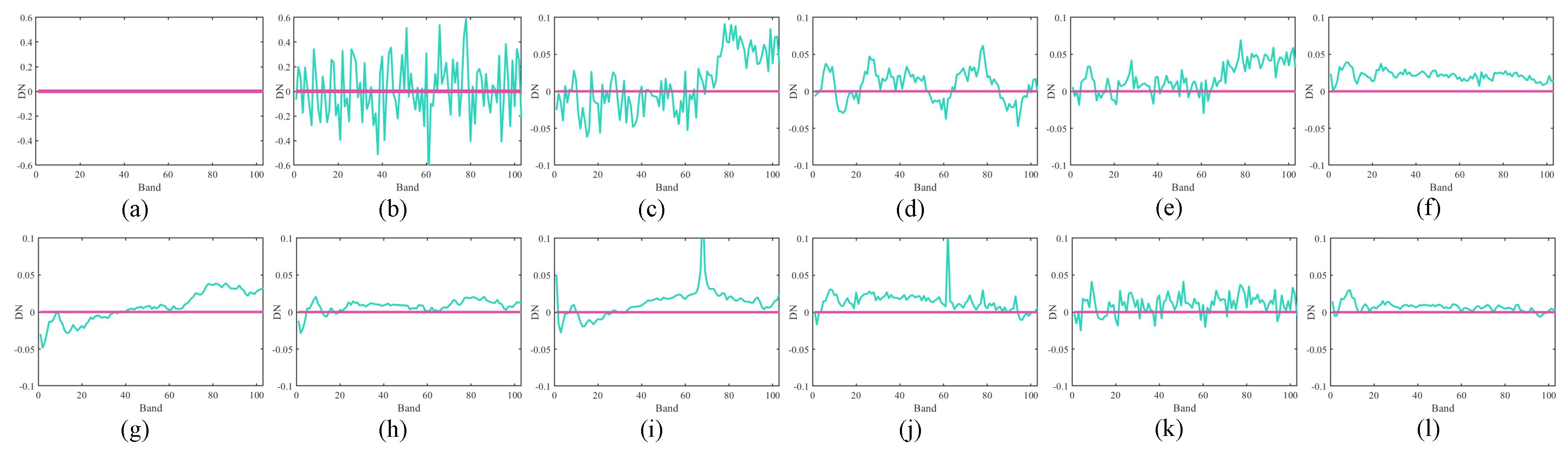
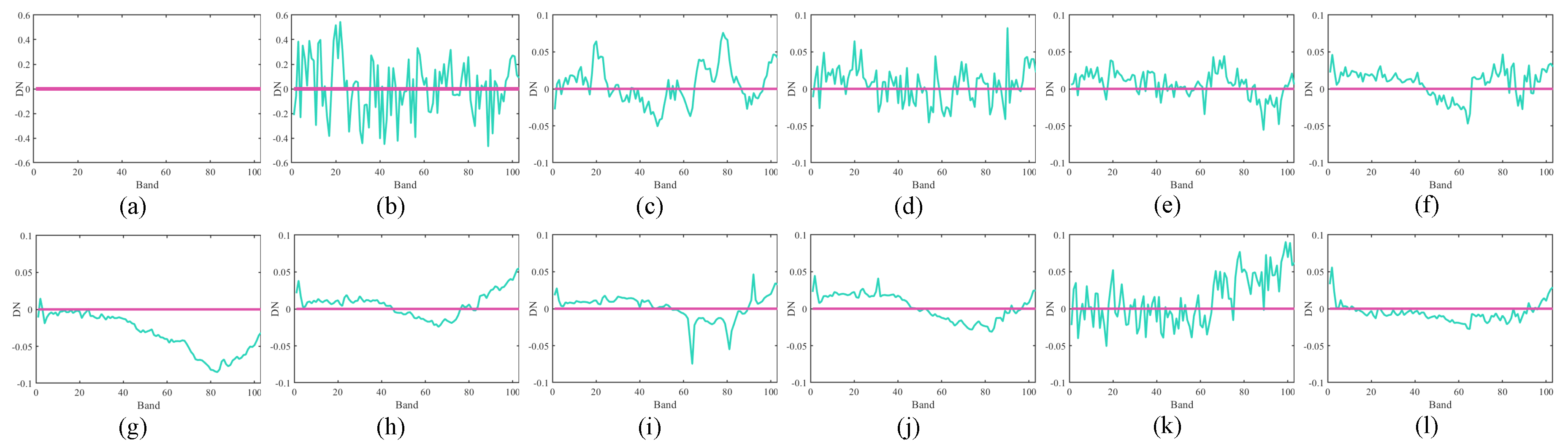
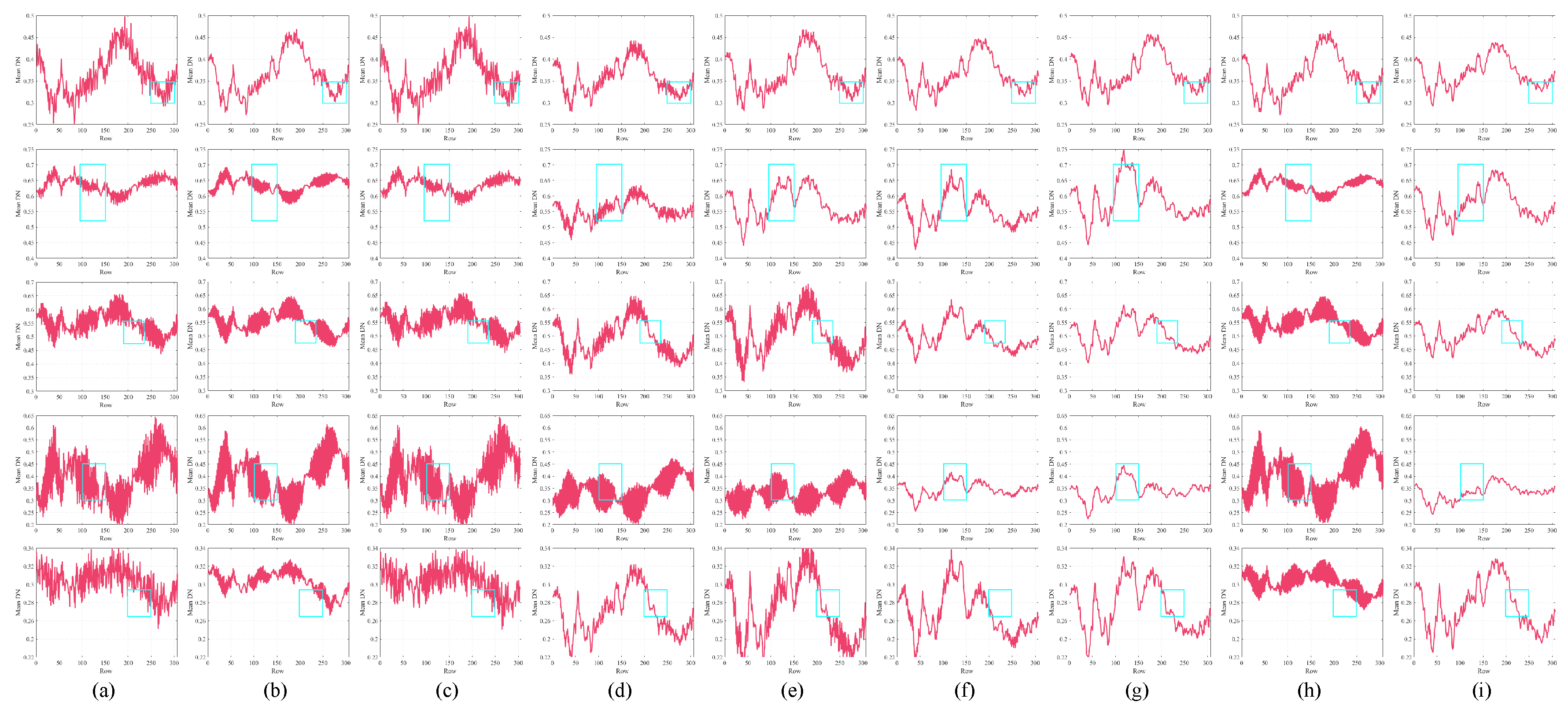
5.1.1. Visual Evaluation Results
5.1.2. Quantitative Evaluation Results
5.1.3. Qualitative Evaluation Results
5.1.4. Classification Evaluation Results
5.1.5. Comparison with Deep Learning Methods
5.2. Experimental Results on Real Datasets
5.2.1. Visual Evaluation Results
5.2.2. Quantitative Evaluation Results
6. Discussion
6.1. The Impact of Parameters , and
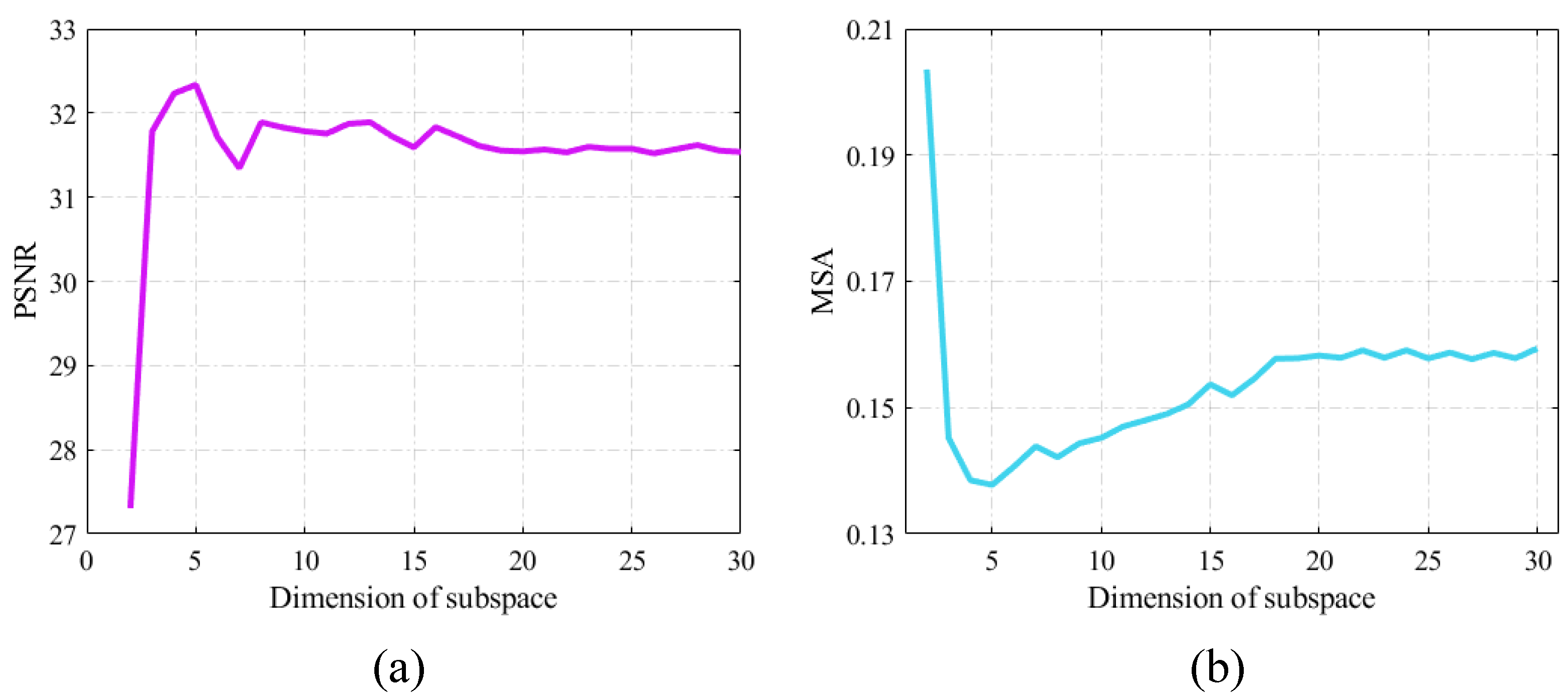
6.2. The Dimension of Subspace p
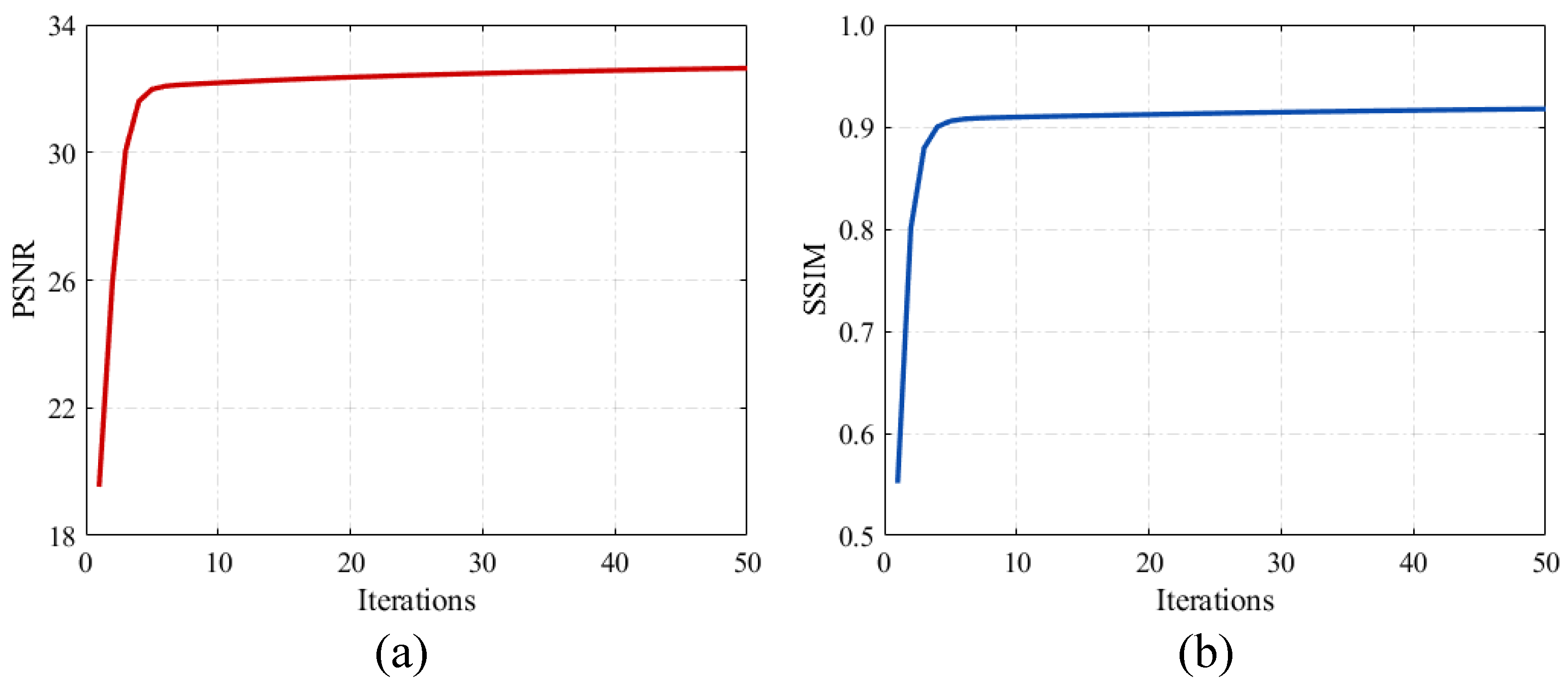
6.3. Convergence Analysis
7. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| HSI | Hyperspectral image |
| LRMR | Low-rank matrix recovery |
| NSS | Non-local self-similarity |
| CP | CANDECOMP/PARAFAC |
| BM4D | Block-matching and 4D filtering |
| SLR | Subspace low-rank |
| ADMM | Alternating direction method of multipliers |
| PSNR | Peak signal-to-noise ratio |
| SSIM | Structure similarity |
| FSIM | Feature similarity |
| ERGAS | Erreur relative globale adimensionnellede synthese |
| MSA | Mean spectral angle |
References
- Bioucas-Dias, J.M.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.; Chanussot, J. Hyperspectral remote sensing data analysis and future challenges. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–36. [Google Scholar] [CrossRef]
- Imani, M.; Ghassemian, H. An overview on spectral and spatial information fusion for hyperspectral image classification: Current trends and challenges. Inf. Fusion 2020, 59, 59–83. [Google Scholar] [CrossRef]
- Lu, X.; Dong, L.; Yuan, Y. Subspace clustering constrained sparse NMF for hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3007–3019. [Google Scholar] [CrossRef]
- Moeini Rad, A.; Abkar, A.A.; Mojaradi, B. Supervised distance-based feature selection for hyperspectral target detection. Remote Sens. 2019, 11, 2049. [Google Scholar] [CrossRef]
- Sun, L.; Ma, C.; Chen, Y.; Zheng, Y.; Shim, H.J.; Wu, Z.; Jeon, B. Low rank component Induced spatial-spectral kernel method for hyperspectral image classification. IEEE Trans. Circuits Syst. Video Technol. 2020, 1. [Google Scholar] [CrossRef]
- Chen, Y.; Li, J.; Zhou, Y. Hyperspectral image denoising by total variation-regularized bilinear factorization. Signal Process. 2020, 174, 107645. [Google Scholar] [CrossRef]
- Othman, H.; Qian, S.E. Noise reduction of hyperspectral imagery using hybrid spatial-spectral derivative-domain wavelet shrinkage. IEEE Trans. Geosci. Remote Sens. 2006, 44, 397–408. [Google Scholar] [CrossRef]
- Chen, G.; Qian, S.E. Denoising of hyperspectral imagery using principal component analysis and wavelet shrinkage. IEEE Trans. Geosci. Remote Sens. 2010, 49, 973–980. [Google Scholar] [CrossRef]
- Zhang, X.; Peng, F.; Long, M. Robust coverless image steganography based on DCT and LDA topic classification. IEEE Trans. Multimed. 2018, 20, 3223–3238. [Google Scholar] [CrossRef]
- Buades, A.; Coll, B.; Morel, J.M. A non-local algorithm for image denoising. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 2, pp. 60–65. [Google Scholar]
- Qian, Y.; Ye, M. Hyperspectral imagery restoration using nonlocal spectral-spatial structured sparse representation with noise estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 6, 499–515. [Google Scholar] [CrossRef]
- Song, Y.; Cao, W.; Shen, Y.; Yang, G. Compressed sensing image reconstruction using intra prediction. Neurocomputing 2015, 151, 1171–1179. [Google Scholar] [CrossRef]
- Song, Y.; Yang, G.; Xie, H.; Zhang, D.; Sun, X. Residual domain dictionary learning for compressed sensing video recovery. Multimed. Tools Appl. 2017, 76, 10083–10096. [Google Scholar] [CrossRef]
- Shen, Y.; Li, J.; Zhu, Z.; Cao, W.; Song, Y. Image reconstruction algorithm from compressed sensing measurements by dictionary learning. Neurocomputing 2015, 151, 1153–1162. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhang, Q.; Li, J.; Shen, H.; Zhang, L. Hyperspectral image denoising employing a spatial–spectral deep residual convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1205–1218. [Google Scholar] [CrossRef]
- Maffei, A.; Haut, J.M.; Paoletti, M.E.; Plaza, J.; Bruzzone, L.; Plaza, A. A single model CNN for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2516–2529. [Google Scholar] [CrossRef]
- Long, M.; Zeng, Y. Detecting iris liveness with batch normalized convolutional neural network. Comput. Mater. Contin. 2019, 58, 493–504. [Google Scholar] [CrossRef]
- Zhang, J.; Jin, X.; Sun, J.; Wang, J.; Sangaiah, A.K. Spatial and semantic convolutional features for robust visual object tracking. Multimed. Tools Appl. 2020, 79, 15095–15115. [Google Scholar] [CrossRef]
- Zeng, D.; Dai, Y.; Li, F.; Wang, J.; Sangaiah, A.K. Aspect based sentiment analysis by a linguistically regularized CNN with gated mechanism. J. Intell. Fuzzy Syst. 2019, 36, 3971–3980. [Google Scholar] [CrossRef]
- Candès, E.J.; Li, X.; Ma, Y.; Wright, J. Robust principal component analysis? J. ACM (JACM) 2011, 58, 1–37. [Google Scholar] [CrossRef]
- Zhang, H.; He, W.; Zhang, L.; Shen, H.; Yuan, Q. Hyperspectral image restoration using low-rank matrix recovery. IEEE Trans. Geosci. Remote Sens. 2013, 52, 4729–4743. [Google Scholar] [CrossRef]
- Wang, Q.; He, X.; Li, X. Locality and structure regularized low rank representation for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 57, 911–923. [Google Scholar] [CrossRef]
- Zhao, Y.Q.; Yang, J. Hyperspectral image denoising via sparse representation and low-rank constraint. IEEE Trans. Geosci. Remote Sens. 2014, 53, 296–308. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, T.Z.; Zhao, X.L.; Deng, L.J. Hyperspectral image restoration using framelet-regularized low-rank nonnegative matrix factorization. Appl. Math. Model. 2018, 63, 128–147. [Google Scholar] [CrossRef]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D: Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Aggarwal, H.K.; Majumdar, A. Hyperspectral image denoising using spatio-spectral total variation. IEEE Geosci. Remote Sens. Lett. 2016, 13, 442–446. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, Q.; Wu, Z.; Shen, Y. Total variation-regularized weighted nuclear norm minimization for hyperspectral image mixed denoising. J. Electron. Imaging 2016, 25, 013037. [Google Scholar] [CrossRef]
- Wang, Q.; Wu, Z.; Jin, J.; Wang, T.; Shen, Y. Low rank constraint and spatial spectral total variation for hyperspectral image mixed denoising. Signal Process. 2018, 142, 11–26. [Google Scholar] [CrossRef]
- He, W.; Zhang, H.; Zhang, L.; Shen, H. Total-variation-regularized low-rank matrix factorization for hyperspectral image restoration. IEEE Trans. Geosci. Remote Sens. 2015, 54, 178–188. [Google Scholar] [CrossRef]
- He, W.; Zhang, H.; Shen, H.; Zhang, L. Hyperspectral image denoising using local low-rank matrix recovery and global spatial–spectral total variation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 713–729. [Google Scholar] [CrossRef]
- Fang, Y.; Li, H.; Ma, Y.; Liang, K.; Hu, Y.; Zhang, S.; Wang, H. Dimensionality reduction of hyperspectral images based on robust spatial information using locally linear embedding. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1712–1716. [Google Scholar] [CrossRef]
- Xue, J.; Zhao, Y.; Liao, W.; Chan, J.C.W. Nonconvex tensor rank minimization and its applications to tensor recovery. Inf. Sci. 2019, 503, 109–128. [Google Scholar] [CrossRef]
- Fan, H.; Chen, Y.; Guo, Y.; Zhang, H.; Kuang, G. Hyperspectral image restoration using low-rank tensor recovery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4589–4604. [Google Scholar] [CrossRef]
- Wang, Y.; Peng, J.; Zhao, Q.; Leung, Y.; Zhao, X.L.; Meng, D. Hyperspectral image restoration via total variation regularized low-rank tensor decomposition. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1227–1243. [Google Scholar] [CrossRef]
- Yang, J.H.; Zhao, X.L.; Ma, T.H.; Chen, Y.; Huang, T.Z.; Ding, M. Remote sensing images destriping using unidirectional hybrid total variation and nonconvex low-rank regularization. J. Comput. Appl. Math. 2020, 363, 124–144. [Google Scholar] [CrossRef]
- Mairal, J.; Bach, F.; Ponce, J.; Sapiro, G.; Zisserman, A. Non-local sparse models for image restoration. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 2272–2279. [Google Scholar]
- Katkovnik, V.; Foi, A.; Egiazarian, K.; Astola, J. From local kernel to nonlocal multiple-model image denoising. Int. J. Comput. Vis. 2010, 86, 1. [Google Scholar] [CrossRef]
- Zhu, R.; Dong, M.; Xue, J.H. Spectral nonlocal restoration of hyperspectral images with low-rank property. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 8, 3062–3067. [Google Scholar]
- Bai, X.; Xu, F.; Zhou, L.; Xing, Y.; Bai, L.; Zhou, J. Nonlocal similarity based nonnegative tucker decomposition for hyperspectral image denoising. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 701–712. [Google Scholar] [CrossRef]
- Xue, J.; Zhao, Y.; Liao, W.; Kong, S.G. Joint spatial and spectral low-rank regularization for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 2017, 56, 1940–1958. [Google Scholar] [CrossRef]
- Xue, J.; Zhao, Y.; Liao, W.; Chan, J.C.W. Nonlocal low-rank regularized tensor decomposition for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5174–5189. [Google Scholar] [CrossRef]
- Xie, Q.; Zhao, Q.; Meng, D.; Xu, Z.; Gu, S.; Zuo, W.; Zhang, L. Multispectral images denoising by intrinsic tensor sparsity regularization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1692–1700. [Google Scholar]
- Huang, Z.; Li, S.; Fang, L.; Li, H.; Benediktsson, J.A. Hyperspectral image denoising with group sparse and low-rank tensor decomposition. IEEE Access 2017, 6, 1380–1390. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, L.; He, W.; Zhang, L. Hyperspectral image denoising with total variation regularization and nonlocal low-rank tensor decomposition. IEEE Trans. Geosci. Remote Sens. 2019, 58, 3071–3084. [Google Scholar] [CrossRef]
- Chen, Y.; He, W.; Yokoya, N.; Huang, T.Z.; Zhao, X.L. Nonlocal tensor-ring decomposition for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 2019, 58, 1348–1362. [Google Scholar] [CrossRef]
- Maggioni, M.; Katkovnik, V.; Egiazarian, K.; Foi, A. Nonlocal transform-domain filter for volumetric data denoising and reconstruction. IEEE Trans. Image Process. 2012, 22, 119–133. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Bui, T.D.; Quach, K.G.; Qian, S.E. Denoising hyperspectral imagery using principal component analysis and block-matching 4D filtering. Can. J. Remote Sens. 2014, 40, 60–66. [Google Scholar] [CrossRef]
- Sun, L.; Jeon, B. A novel subspace spatial-spectral low rank learning method for hyperspectral denoising. In Proceedings of the 2017 IEEE Visual Communications and Image Processing (VCIP), St. Petersburg, FL, USA, 10–13 December 2017; pp. 1–4. [Google Scholar]
- Sun, L.; Jeon, B.; Soomro, B.N.; Zheng, Y.; Wu, Z.; Xiao, L. Fast superpixel based subspace low rank learning method for hyperspectral denoising. IEEE Access 2018, 6, 12031–12043. [Google Scholar] [CrossRef]
- Zhuang, L.; Bioucas-Dias, J.M. Fast hyperspectral image denoising and inpainting based on low-rank and sparse representations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 730–742. [Google Scholar] [CrossRef]
- He, W.; Yao, Q.; Li, C.; Yokoya, N.; Zhao, Q. Non-local meets global: An integrated paradigm for hyperspectral denoising. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 6861–6870. [Google Scholar]
- Zhuang, L.; Ng, M.K. Hyperspectral mixed noise temoval by l_1-norm-based subspace representation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1143–1157. [Google Scholar] [CrossRef]
- Huang, H.; Shi, G.; He, H.; Duan, Y.; Luo, F. Dimensionality reduction of hyperspectral imagery based on spatial–spectral manifold learning. IEEE Trans. Cybern. 2019, 50, 2604–2616. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Nascimento, J.M. Hyperspectral subspace identification. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2435–2445. [Google Scholar] [CrossRef]
- Sun, L.; Wu, F.; Zhan, T.; Liu, W.; Wang, J.; Jeon, B. Weighted nonlocal low-rank tensor decomposition method for sparse unmixing of hyperspectral images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1174–1188. [Google Scholar] [CrossRef]
- Chen, Y.; He, W.; Yokoya, N.; Huang, T.Z. Hyperspectral image restoration using weighted group sparsity-regularized low-rank tensor decomposition. IEEE Trans. Cybern. 2020, 50, 3556–3570. [Google Scholar] [CrossRef] [PubMed]
- Peng, Y.; Meng, D.; Xu, Z.; Gao, C.; Yang, Y.; Zhang, B. Decomposable nonlocal tensor dictionary learning for multispectral image denoising. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2949–2956. [Google Scholar]
- Kuang, F.; Zhang, S.; Jin, Z.; Xu, W. A novel SVM by combining kernel principal component analysis and improved chaotic particle swarm optimization for intrusion detection. Soft Comput. 2015, 19, 1187–1199. [Google Scholar] [CrossRef]
- Chen, Y.; Xiong, J.; Xu, W.; Zuo, J. A novel online incremental and decremental learning algorithm based on variable support vector machine. Clust. Comput. 2019, 22, 7435–7445. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, W.; Zuo, J.; Yang, K. The fire recognition algorithm using dynamic feature fusion and IV-SVM classifier. Clust. Comput. 2019, 22, 7665–7675. [Google Scholar] [CrossRef]
- Zeng, D.; Dai, Y.; Li, F.; Sherratt, R.S.; Wang, J. Adversarial learning for distant supervised relation extraction. Comput. Mater. Contin. 2018, 55, 121–136. [Google Scholar]
- Meng, R.; Rice, S.G.; Wang, J.; Sun, X. A fusion steganographic algorithm based on faster R-CNN. Comput. Mater. Contin. 2018, 55, 1–16. [Google Scholar]
- Zhou, S.; Ke, M.; Luo, P. Multi-camera transfer GAN for person re-identification. J. Vis. Commun. Image Represent. 2019, 59, 393–400. [Google Scholar] [CrossRef]
- He, S.; Li, Z.; Tang, Y.; Liao, Z.; Li, F.; Lim, S.J. Parameters compressing in deep learning. Comput. Mater. Contin. 2020, 62, 321–336. [Google Scholar] [CrossRef]
- Gui, Y.; Zeng, G. Joint learning of visual and spatial features for edit propagation from a single image. Vis. Comput. 2020, 36, 469–482. [Google Scholar] [CrossRef]








| Dataset | Case | Index | Noisy | PCABM4D [47] | TDL [58] | FSSLRL [49] | LLRSSTV [30] | LRTDTV [34] | LRTDGS [57] | NLR-CPTD [41] | SLRL4D |
|---|---|---|---|---|---|---|---|---|---|---|---|
| WDC | Case 1 | PSNR | 12.042 | 30.341 | 30.012 | 30.339 | 30.225 | 30.981 | 31.330 | 32.090 | 32.633 |
| SSIM | 0.1330 | 0.8639 | 0.8647 | 0.8586 | 0.8529 | 0.8740 | 0.8871 | 0.9070 | 0.9208 | ||
| FSIM | 0.4919 | 0.9328 | 0.9230 | 0.9330 | 0.9239 | 0.9299 | 0.9370 | 0.9475 | 0.9520 | ||
| ERGAS | 60.8209 | 7.0790 | 7.3258 | 7.1147 | 7.3759 | 6.5940 | 6.3424 | 5.7895 | 5.4803 | ||
| MSA | 0.8570 | 0.1307 | 0.1222 | 0.1302 | 0.1432 | 0.1050 | 0.1058 | 0.0976 | 0.0802 | ||
| Case 2 | PSNR | 14.129 | 31.534 | 31.422 | 31.611 | 31.539 | 32.150 | 32.410 | 33.396 | 33.439 | |
| SSIM | 0.1922 | 0.8966 | 0.8985 | 0.8985 | 0.8997 | 0.9008 | 0.9090 | 0.9288 | 0.9350 | ||
| FSIM | 0.5539 | 0.9460 | 0.9416 | 0.9493 | 0.9419 | 0.9446 | 0.9485 | 0.9590 | 0.9607 | ||
| ERGAS | 48.5655 | 6.1748 | 6.2320 | 6.1407 | 8.4325 | 5.7740 | 5.6087 | 5.0149 | 4.9961 | ||
| MSA | 0.7572 | 0.1136 | 0.1059 | 0.1092 | 0.1607 | 0.0927 | 0.0925 | 0.0858 | 0.0742 | ||
| Case 3 | PSNR | 13.826 | 30.656 | 30.445 | 31.196 | 31.515 | 32.081 | 32.314 | 32.341 | 32.969 | |
| SSIM | 0.1831 | 0.8846 | 0.8818 | 0.8924 | 0.8989 | 0.8995 | 0.9087 | 0.9148 | 0.9224 | ||
| FSIM | 0.5472 | 0.9428 | 0.9356 | 0.9469 | 0.9414 | 0.9441 | 0.9486 | 0.9540 | 0.9552 | ||
| ERGAS | 50.5963 | 7.4086 | 7.5494 | 6.5403 | 9.6627 | 5.8170 | 5.6860 | 6.3406 | 5.4038 | ||
| MSA | 0.7640 | 0.1486 | 0.1484 | 0.1260 | 0.1617 | 0.0926 | 0.0934 | 0.1280 | 0.0876 | ||
| Case 4 | PSNR | 13.948 | 30.427 | 31.408 | 31.503 | 31.809 | 31.893 | 32.248 | 32.144 | 33.312 | |
| SSIM | 0.1890 | 0.8816 | 0.8994 | 0.8957 | 0.8940 | 0.9005 | 0.9078 | 0.9143 | 0.9338 | ||
| FSIM | 0.5486 | 0.9360 | 0.9425 | 0.9480 | 0.9431 | 0.9429 | 0.9478 | 0.9494 | 0.9599 | ||
| ERGAS | 49.7693 | 7.6996 | 6.5065 | 6.2197 | 6.9987 | 6.0993 | 5.8574 | 6.3738 | 5.0699 | ||
| MSA | 0.7651 | 0.1455 | 0.1143 | 0.1115 | 0.1381 | 0.0983 | 0.0955 | 0.1136 | 0.0751 | ||
| Case 5 | PSNR | 14.005 | 31.446 | 31.458 | 31.530 | 31.581 | 32.080 | 32.292 | 33.244 | 33.390 | |
| SSIM | 0.1892 | 0.8946 | 0.8970 | 0.8969 | 0.8928 | 0.8994 | 0.9102 | 0.9271 | 0.9284 | ||
| FSIM | 0.5501 | 0.9451 | 0.9409 | 0.9481 | 0.9407 | 0.9438 | 0.9488 | 0.9577 | 0.9576 | ||
| ERGAS | 49.5954 | 6.2429 | 6.2088 | 6.1925 | 8.1999 | 5.8178 | 5.7303 | 5.1017 | 5.0423 | ||
| MSA | 0.7637 | 0.1146 | 0.1042 | 0.1099 | 0.1472 | 0.0935 | 0.0955 | 0.0869 | 0.0736 | ||
| Case 6 | PSNR | 13.790 | 30.141 | 30.639 | 31.110 | 31.788 | 32.047 | 32.217 | 31.748 | 32.919 | |
| SSIM | 0.1802 | 0.8765 | 0.8878 | 0.8925 | 0.8944 | 0.8995 | 0.9086 | 0.9059 | 0.9215 | ||
| FSIM | 0.5458 | 0.9366 | 0.9388 | 0.9468 | 0.9438 | 0.9437 | 0.9481 | 0.9483 | 0.9553 | ||
| ERGAS | 50.5140 | 8.4916 | 7.8616 | 6.6505 | 7.0572 | 5.8479 | 5.8564 | 7.2990 | 5.4843 | ||
| MSA | 0.7654 | 0.1684 | 0.1575 | 0.1308 | 0.1380 | 0.0929 | 0.0963 | 0.1467 | 0.0903 | ||
| PU | Case 1 | PSNR | 12.042 | 28.113 | 30.440 | 28.702 | 29.612 | 30.325 | 30.455 | 31.041 | 31.671 |
| SSIM | 0.0892 | 0.7018 | 0.8408 | 0.7291 | 0.8194 | 0.7954 | 0.8217 | 0.8290 | 0.8717 | ||
| FSIM | 0.4234 | 0.8831 | 0.9134 | 0.8970 | 0.9126 | 0.9016 | 0.9054 | 0.9206 | 0.9180 | ||
| ERGAS | 61.3613 | 9.5350 | 7.3390 | 8.9760 | 8.2130 | 8.1152 | 7.6081 | 6.8476 | 6.3751 | ||
| MSA | 0.9318 | 0.1885 | 0.1186 | 0.1764 | 0.1452 | 0.1702 | 0.1478 | 0.1385 | 0.0984 | ||
| Case 2 | PSNR | 14.097 | 29.555 | 31.599 | 30.144 | 30.529 | 31.744 | 31.549 | 32.495 | 32.643 | |
| SSIM | 0.1345 | 0.7656 | 0.8617 | 0.8035 | 0.8551 | 0.8435 | 0.8552 | 0.8672 | 0.8924 | ||
| FSIM | 0.4847 | 0.9079 | 0.9316 | 0.9246 | 0.9277 | 0.9251 | 0.9221 | 0.9372 | 0.9321 | ||
| ERGAS | 49.3741 | 8.1296 | 6.4632 | 7.6367 | 7.5414 | 6.9415 | 6.7190 | 5.9089 | 5.7106 | ||
| MSA | 0.8319 | 0.1625 | 0.1159 | 0.1441 | 0.1336 | 0.1520 | 0.1349 | 0.1223 | 0.0916 | ||
| Case 3 | PSNR | 13.756 | 28.407 | 29.684 | 30.064 | 31.210 | 31.565 | 31.420 | 30.847 | 31.906 | |
| SSIM | 0.1253 | 0.7435 | 0.8123 | 0.7962 | 0.8282 | 0.8385 | 0.8518 | 0.8348 | 0.8799 | ||
| FSIM | 0.4794 | 0.9014 | 0.9146 | 0.9221 | 0.9257 | 0.9240 | 0.9203 | 0.9240 | 0.9253 | ||
| ERGAS | 51.0981 | 9.5420 | 8.5100 | 7.7057 | 6.8000 | 7.0056 | 6.8903 | 7.6459 | 6.2219 | ||
| MSA | 0.8253 | 0.1930 | 0.1704 | 0.1432 | 0.1352 | 0.1517 | 0.1317 | 0.1646 | 0.1005 | ||
| Case 4 | PSNR | 14.056 | 28.232 | 30.186 | 30.278 | 31.354 | 31.750 | 31.386 | 30.635 | 32.506 | |
| SSIM | 0.1356 | 0.7452 | 0.8200 | 0.8049 | 0.8309 | 0.8442 | 0.8499 | 0.8449 | 0.8903 | ||
| FSIM | 0.4841 | 0.8911 | 0.9183 | 0.9250 | 0.9255 | 0.9261 | 0.9195 | 0.9212 | 0.9316 | ||
| ERGAS | 49.4070 | 10.1610 | 8.1262 | 7.5204 | 6.7023 | 6.8369 | 6.8518 | 8.2926 | 5.8021 | ||
| MSA | 0.8261 | 0.2126 | 0.1613 | 0.1434 | 0.1359 | 0.1540 | 0.1357 | 0.1697 | 0.0945 | ||
| Case 5 | PSNR | 13.903 | 29.384 | 31.368 | 29.999 | 30.462 | 31.520 | 31.305 | 32.272 | 32.578 | |
| SSIM | 0.1295 | 0.7587 | 0.8538 | 0.7973 | 0.8523 | 0.8356 | 0.8470 | 0.8615 | 0.8912 | ||
| FSIM | 0.4791 | 0.9054 | 0.9294 | 0.9228 | 0.9272 | 0.9216 | 0.9185 | 0.9345 | 0.9320 | ||
| ERGAS | 50.4128 | 8.2778 | 6.6221 | 7.7509 | 7.5701 | 7.0474 | 6.8714 | 6.0468 | 5.7400 | ||
| MSA | 0.8419 | 0.1648 | 0.1171 | 0.1465 | 0.1335 | 0.1552 | 0.1348 | 0.1245 | 0.0936 | ||
| Case 6 | PSNR | 13.469 | 27.448 | 28.899 | 29.932 | 31.067 | 31.334 | 31.238 | 29.485 | 31.811 | |
| SSIM | 0.1199 | 0.7197 | 0.7823 | 0.7892 | 0.8219 | 0.8289 | 0.8448 | 0.8109 | 0.8773 | ||
| FSIM | 0.4705 | 0.8849 | 0.9087 | 0.9189 | 0.9226 | 0.9196 | 0.9171 | 0.9086 | 0.9238 | ||
| ERGAS | 52.5291 | 11.0025 | 9.5224 | 7.8226 | 6.9016 | 7.1722 | 7.0374 | 9.2811 | 6.2780 | ||
| MSA | 0.8339 | 0.2239 | 0.1910 | 0.1456 | 0.1371 | 0.1562 | 0.1369 | 0.1916 | 0.1025 |
| Case | Index | Noisy | PCABM4D [47] | TDL [58] | FSSLRL [49] | LLRSSTV [30] | LRTDTV [34] | LRTDGS [57] | NLR-CPTD [41] | SLRL4D |
|---|---|---|---|---|---|---|---|---|---|---|
| Case 1 | OA | 0.57732 | 0.70891 | 0.74824 | 0.60057 | 0.65361 | 0.71816 | 0.73532 | 0.76189 | 0.84743 |
| AA | 0.52242 | 0.67714 | 0.68235 | 0.50377 | 0.55286 | 0.63976 | 0.66712 | 0.72033 | 0.80327 | |
| Kappa | 0.45628 | 0.63205 | 0.68247 | 0.46198 | 0.55072 | 0.64255 | 0.66595 | 0.70220 | 0.80847 | |
| Case 6 | OA | 0.59775 | 0.72702 | 0.73404 | 0.63980 | 0.66957 | 0.73811 | 0.75806 | 0.77881 | 0.86227 |
| AA | 0.54232 | 0.69083 | 0.67431 | 0.54924 | 0.57729 | 0.65813 | 0.69144 | 0.72933 | 0.83022 | |
| Kappa | 0.48407 | 0.65680 | 0.66464 | 0.53553 | 0.57537 | 0.66784 | 0.69498 | 0.72158 | 0.82752 |
| Noise Level | Index | BM4D [46] | HSID-CNN [15] | HSI-SDeCNN [16] | SLRL4D |
|---|---|---|---|---|---|
| PSNR | 26.752 | 28.968 | 29.612 | 29.722 | |
| SSIM | 0.9208 | 0.9532 | 0.9608 | 0.9656 | |
| PSNR | 24.261 | 26.753 | 27.351 | 28.045 | |
| SSIM | 0.8670 | 0.9273 | 0.9371 | 0.9489 | |
| PSNR | 22.577 | 25.296 | 25.753 | 26.783 | |
| SSIM | 0.8119 | 0.9014 | 0.9121 | 0.9321 |
| Dataset | Noisy | PCABM4D [47] | TDL [58] | FSSLRL [49] | LLRSSTV [30] | LRTDTV [34] | LRTDGS [57] | NLR-CPTD [41] | SLRL4D |
|---|---|---|---|---|---|---|---|---|---|
| Urban | 0.06293 | 0.07881 | 0.06306 | 0.06217 | 0.06830 | 0.07408 | 0.07077 | 0.09202 | 0.09818 |
| Hyperion | 0.02432 | 0.03426 | 0.03198 | 0.03144 | 0.03198 | 0.03385 | 0.03716 | 0.03966 | 0.04459 |
| Dataset | PCABM4D [47] | TDL [58] | FSSLRL [49] | LLRSSTV [30] | LRTDTV [34] | LRTDGS [57] | NLR-CPTD [41] | SLRL4D |
|---|---|---|---|---|---|---|---|---|
| Urban | 738.59 | 56.08 | 258.17 | 337.96 | 323.52 | 202.90 | >1000 | 269.24 |
| Hyperion | 235.21 | 13.47 | 80.64 | 101.66 | 77.50 | 55.82 | >1000 | 57.72 |
| Case | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 6 | |
|---|---|---|---|---|---|---|---|
| Parameter | |||||||
| 1 | 1 | 0.2 | 0.4 | 0.4 | 0.2 | ||
| 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | ||
| p | 4 | 4 | 5 | 4 | 5 | 4 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, L.; He, C.; Zheng, Y.; Tang, S. SLRL4D: Joint Restoration of Subspace Low-Rank Learning and Non-Local 4-D Transform Filtering for Hyperspectral Image. Remote Sens. 2020, 12, 2979. https://doi.org/10.3390/rs12182979
Sun L, He C, Zheng Y, Tang S. SLRL4D: Joint Restoration of Subspace Low-Rank Learning and Non-Local 4-D Transform Filtering for Hyperspectral Image. Remote Sensing. 2020; 12(18):2979. https://doi.org/10.3390/rs12182979
Chicago/Turabian StyleSun, Le, Chengxun He, Yuhui Zheng, and Songze Tang. 2020. "SLRL4D: Joint Restoration of Subspace Low-Rank Learning and Non-Local 4-D Transform Filtering for Hyperspectral Image" Remote Sensing 12, no. 18: 2979. https://doi.org/10.3390/rs12182979
APA StyleSun, L., He, C., Zheng, Y., & Tang, S. (2020). SLRL4D: Joint Restoration of Subspace Low-Rank Learning and Non-Local 4-D Transform Filtering for Hyperspectral Image. Remote Sensing, 12(18), 2979. https://doi.org/10.3390/rs12182979








