1. Introduction
Drought is recognized as one of the most important phenomena that seriously affects various elements of the environment and the economy. In particular, drought has a negative impact on agricultural production, resulting in a decrease in crop yield and causing a shortage of food. The recently observed global warming is exacerbating the drought problem, and climate change effects have also been recorded in Central Europe, where the increase in temperature is related to the decrease in rainfall. More often, winters become mild with low precipitation, resulting in low retention that further enhances the decrease in water storage for proper crop development. Extremely poor conditions for crop development occur more frequently, and a long-term water deficit in soil causes a significant decrease in crop yield. The effective, fast, and reliable assessment of the extent, duration, and intensity of drought is essential for ensuring the sustainable development of crops for food security. Therefore, across the decades, systems of monitoring drought events have been developed. These systems were originally based on using data collected by the networks of meteorological stations measuring precipitation and air temperature. The most popular drought indices based on these data include the Palmer Drought Severity Index (PDSI) [
1], the Standardized Precipitation Index (SPI) [
2], the Standardized Precipitation Evapotranspiration Index (SPEI) [
3], and the Selyaninov hydrothermal indicator (i.e., the hydrothermal coefficient (HTC)) [
4]. However, information on the extent of drought based on these indices is not spatially precise, due to the insufficient spatial distribution of meteorological stations in many regions of the world. Therefore, new methods of assessing drought phenomena based on satellite remote sensing data have been developed. Technology based on satellite images, collected continuously over land areas, has proved to be effective in drought estimation and mitigation [
5,
6,
7]. Wu et al. [
6] evaluated the Moderate-resolution Imaging Spectroradiometer (MODIS) indices to detect agricultural drought in relation to the anomaly of precipitation and moisture deficiency characterized by meteorological data in agricultural areas. The complexity of drought recovery analysis based on remotely sensed data has been studied in many research works. Among others, this problem has been addressed in publications, which emphasize the impact of drought on ecosystem water-use efficiency (WUE) and its components—gross primary productivity (GPP) and evapotranspiration (ET) [
8,
9].
Numerous approaches to developing remote sensing-based methods for drought monitoring have been applied, including methods based on vegetation indices, canopy temperature, thermal inertia, and microwaves. As vegetation growth is mainly related to soil moisture and temperature conditions, methods based on vegetation and temperature indices proved to be the most promising for drought assessment [
10]. The first works based on the Vegetation Condition Index (VCI) and the Temperature Condition Index (TCI) derived from NOAA AVHRR data revealed that these indices are capable of delivering information on the extent of drought over large areas [
11,
12,
13,
14]. Subsequently, more complex indices, which combine information derived from optical and thermal parts of the spectrum, have been developed. The Vegetation Health Index (VHI) takes into account both the reflectance and temperature of the vegetation canopy, characterizing better drought conditions [
15]. The Temperature Vegetation Dryness Index (TVDI) incorporates the relationship between the vegetation index and the land surface temperature (LST) to enhance drought detection [
16]. The Vegetation Supply Water Index (VSWI), which is the ratio of the Normalized Difference Vegetation Index (NDVI) and LST, when modified to the Normalized Vegetation Supply Water Index (NVSWI), proved to be effective for the analysis of time series, thus improving drought monitoring [
17,
18]. The EVI index of the Moderate-resolution Imaging Spectroradiometer (MODIS) was used in Germany in 2018 to identify potential regional differences in order to examine drought effects in various land cover types [
19]. The Fraction of Absorbed Photosynthetically Active Radiation (FAPAR) can reflect the greenness and health conditions of vegetation and has been used to monitor and assess the impact of drought [
20]. In particular, FAPAR has been chosen and operationally used in the formula of the Combined Drought Indicator (CDI) for monitoring drought in the European Drought Observatory (EDO) within the Copernicus Emergency Management Service [
21]. A study that compared the spatial occurrence of droughts, detected by the combination of satellite drought indices over the desert and arid area in Mongolia, proved that the areas of drought occurrence were better identified with FAPAR than using the Palmer Drought Severity Index (PDSI) and that it is rather difficult to point out the most valuable drought index [
22].
While analyzing the performance of various drought indices based on remotely sensed data, it was found that their capability for drought detection varies with spatial and temporal patterns, implying that the application of a specific approach is necessary for different regions of the world [
23,
24,
25]. Some authors have examined the models for drought detection applied to regions that are site-specific, adjusted to local environments [
26,
27,
28]. VHI is based on the NDVI and the brightness temperature, derived from the NOAA AVHRR satellite. NDVI and LST, supposed to have an inverse correlation with vegetation vigor, detect stress with low NDVI and high temperature values. However, Karnieli et al. [
29] found that northern ecosystems are characterized by positive correlations, which implies that a higher temperature has a favorable impact on vegetation activity. Thus, the conclusion is that VHI should be used with prudence, especially in high-latitude regions [
30,
31]. Furthermore, it is important to examine the reaction of vegetation to water deficit. For instance, the reaction of vegetation to precipitation anomalies has been studied for Inner Mongolia [
32], and it was found that vegetation has a 1–2 month lag response to precipitation anomalies and is significantly correlated with 2–6 months of cumulative precipitation anomalies.
Different drought indices provide different judgments of drought severity because of difficulties in determining the best method of evaluation. Most often, the indices based on meteorological data are applied for verification of satellite-derived indices to consider the climatic/environmental variability of the region [
33]. The authors indicated that different indices reflect the drought differently. The SPEI has a good correlation with yield loss at a 6 month scale and in the middle growth season, while the VegDRI (Vegetation Drought Response Index) and PADI (Process-based Accumulated Drought Index) demonstrated the highest correlation in the late growth season, which indicates that they are complementary and should be used together. There are advantages and limitations of drought indices often used jointly that are complementary for different growth seasons to indicate the yield loss. The Enhanced Combined Drought Index (ECDI) based on the weighted approach of using four independently derived satellite data: rainfall, soil moisture, land surface temperature, and vegetation vigor, has been introduced by Enenkel et al. [
34]. The index was developed in direct collaboration with “Doctors without Borders.” As stated by the authors, a dedicated approach has to be chosen for different needs of the users. It was pointed out that the drought impact is often neglected. Prediction of vegetation conditions and drought effects is also very important as they relate to the economic losses and food risk. Adede et al. [
35] predicted drought conditions up to three months ahead from the developed prediction model using artificial neural networks.
In this study, it was decided to develop a model for drought assessment and monitoring for Poland, which is based on the hydrothermal coefficient HTC characterizing climatic variability of the entire country and satellite-derived Temperature Condition Index (TCI). The HTC index has been used for estimates of drought for agriculture in the Central-Eastern part of Europe. The advantage of this indicator over others is that only readily available information is needed to determine the index, i.e., the amount of rainfall and average daily temperature. Strings of any length can be considered; however, those most frequently analyzed are 15 day and 30 day observation strings [
4].
The method is based on three main assumptions:
HTC is adequate for stratifying the water deficit regions;
TCI with lag steps characterizes the thermal conditions of the area;
fusion of meteorological and satellite data is cardinal in the drought detection model.
In this study, the development of the method for Poland is presented, and its performance is carefully assessed using an indirect method based on the reduction in cereal crop yield caused by severe drought events.
2. Materials and Methods
2.1. Study Area
The study area covers Poland, which is located in Central Europe in the temperate climate zone, with some stratification from a maritime climate in the west to a more continental climate in the east of the country. Poland’s topography is stratified from north to south, with plains in the central part and mountains in the southern part of the country. Both features, climate and topography, have an important impact on the development of drought conditions, predestinating lowlands in the western and central parts of Poland as the most vulnerable areas for the occurrence of drought. These regions are frequently and heavily affected by drought episodes, and according to official figures of the Central Statistical Office, the most serious droughts in Poland during the last 20 years appeared in 2003, 2006, 2010, 2015, and 2018, resulting in a reduction in cereal yield from 15% to 35%, depending on the region. The worst drought events appeared in 2018, characterized by a long duration (over a month) in the most critical phases of crop development. Poland is divided into sixteen Nomenclature of Territorial Units for Statistics level 2 (NUTS 2) units (see
Figure 1).
As drought conditions have a significant impact on agricultural areas, this type of land cover was primarily taken into analysis. The map representing agricultural land was produced on the basis of the CORINE Land Cover (CLC) database, generated for 2018 (see
Figure 2—orange layer). The land cover classes belonging to CLC class Level 1—agricultural areas: arable land (CLC 2.1.1), complex cultivation patterns (CLC 2.4.2), and pastures (CLC 2.3.1)—were used to produce a layer of agricultural land for Poland.
2.2. Meteorological Data
The main meteorological parameters—precipitation and air temperature—were collected from synoptic, climatological, and rainfall stations located throughout Poland (see
Figure 2) for the period 2001–2019 (data from 233 stations in the case of air temperature and from 1313 stations in the case of precipitation). The data were obtained from the Institute of Meteorology and Water Management’s National Research Institute (IMGW-PIB) and further processed at the Institute of Geodesy and Cartography. The aim of processing was to obtain the spatial distribution of the meteorological data measured at the stations.
Meteorological data collected at the stations were interpolated to obtain an image database at a 1 km spatial resolution. Air temperature data were interpolated using the method of ordinary kriging, reducing first the temperature values to sea level, adjusting the spherical model of the semivariogram for each day, and then estimating the final values at the real height above sea level. Interpolation of precipitation was done by applying the method of the average value weighted with distance (i.e., inverse distance weighting (IDW)), and 50 km was assumed as the maximum distance of the stations’ impact.
2.3. Hydrothermal Coefficient
For characterizing atmospheric moisture conditions, which are the basis for the drought phenomenon, the hydrothermal coefficient was selected, which combines both the parameters of air temperature and precipitation within a given period into the form of a synthetic index. The hydrothermal coefficient (HTC), developed by Selyaninov [
36], is defined through the following equation:
where
n—length of the preceding period in days;
—precipitation amount on the ith day (mm);
—daily average of the air temperature on the ith day (°C).
The HTC describes atmospheric drought if the accumulation of air temperature in the preceding period outperforms the accumulated precipitation during the period under consideration. Regarding the HTC values, very dry and dry conditions were assumed for HTC ≤ 0.7 and 0.7 < HTC ≤ 1.0, respectively [
4]; similar thresholds were found for studies in Central Europe, applying the HTC for analyzing moisture conditions
[37,38]. HTC is included in the Handbook of Drought Indicator and Indices [
39] as one of the indices useful for defining atmospheric drought. The accumulation period of precipitation and air temperature is usually assumed for drought assessment as multiples of ten days; such a principle was applied in the present work.
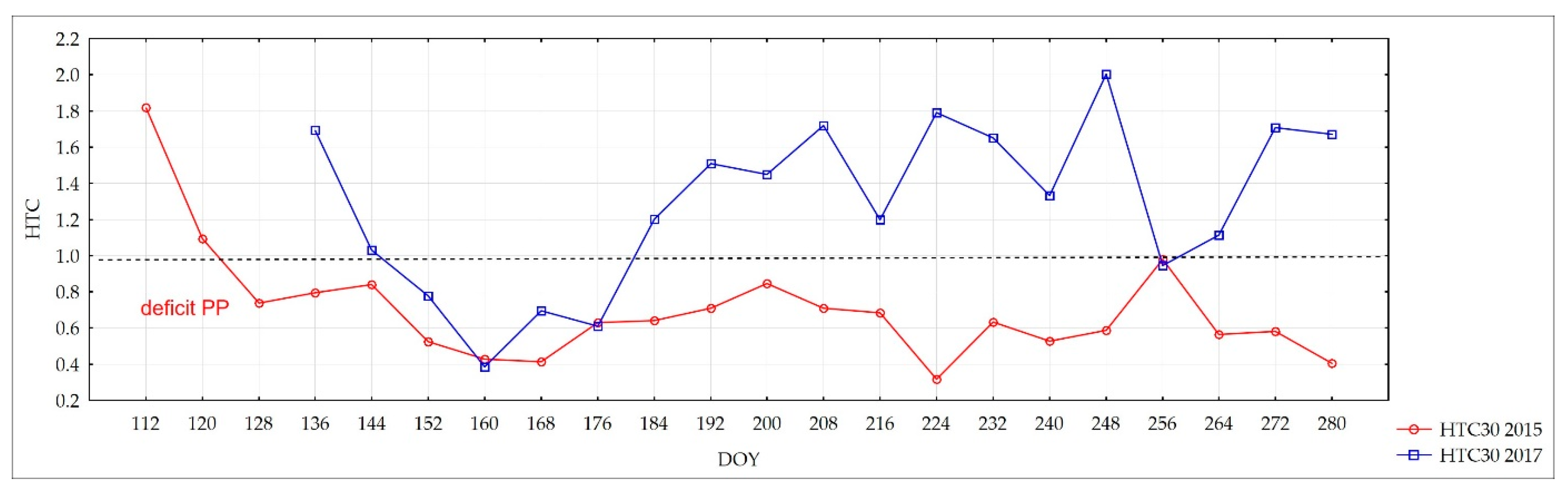
As HTC is based on the current course of precipitation and air temperature, it reveals well the dynamics of changes in moisture conditions for crop areas. A time series for a given area can be created, which provides information on the water deficit in particular parts of the growing season. The differences in the course of the HTC between the years 2015 and 2017 are presented in
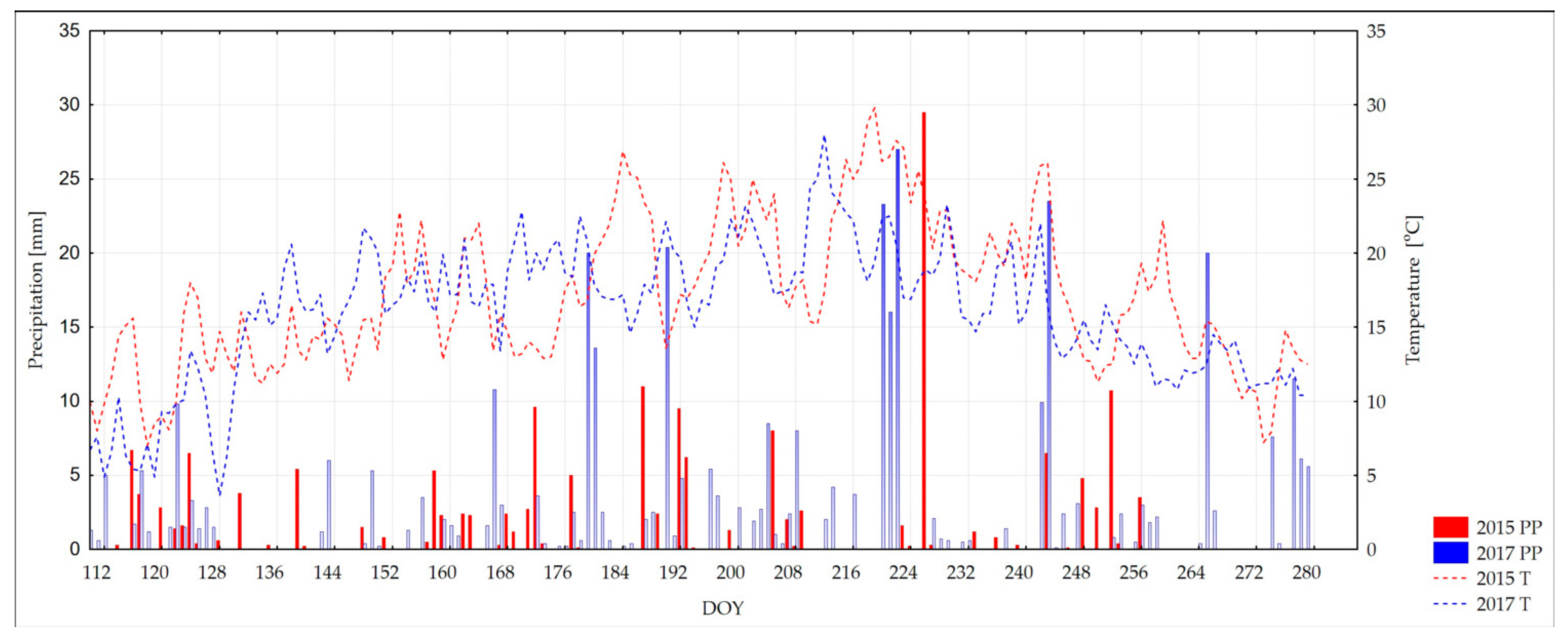
Figure 3. These are more explicit than the differences in precipitation and air temperature for the same years (
Figure 4), which proves that application of the HTC better explains the dynamics of changes of atmospheric moisture.
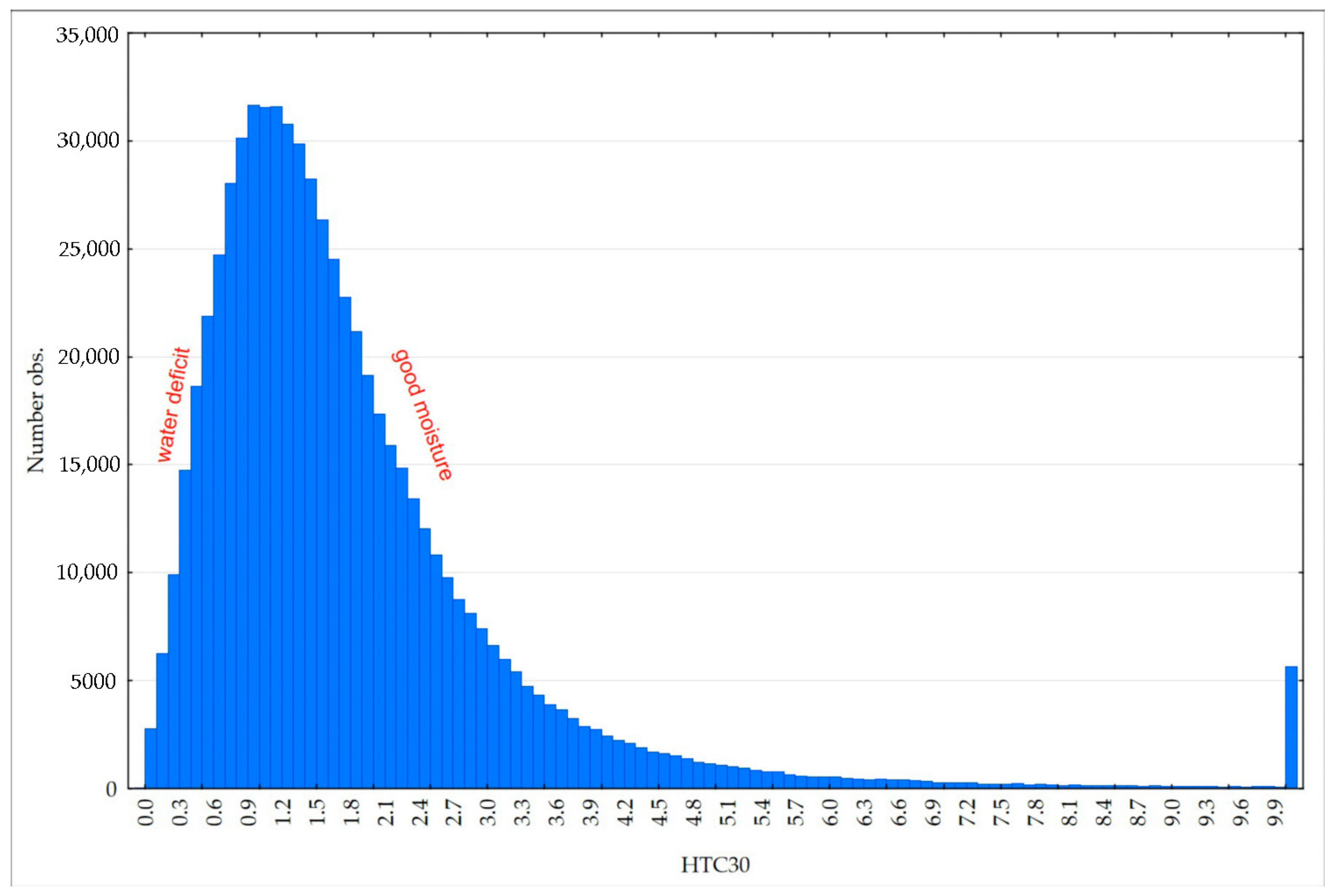
The distribution of all empirical HTC values for an accumulation length equal to 30 days and spanning the years 2001–2019, calculated for the original data from the meteorological stations in all growing periods, is close to log-normal (
Figure 5).
The median was used as the average value estimator of this set of observations: It is approximately equal to 1.0. The distribution of HTC shows that the values around 1.0 are those that occurred most frequently and represent the average state of atmospheric moisture on the territory of Poland. Thus, HTC < 1 is assumed to indicate water deficit, while HTC > 1 indicates good moisture conditions.
However, the spatial distribution of the HTC reveals various patterns; the local medians of the HTC comprise values significantly lower or higher than 1.0. In the case when the local median is lower than 1.0, rainfall deficit occurs more often within the corresponding area, and when it is higher than 1.0, good moisture conditions prevail within the area. Herein, such an approach was considered to characterize the climatic features of the area.
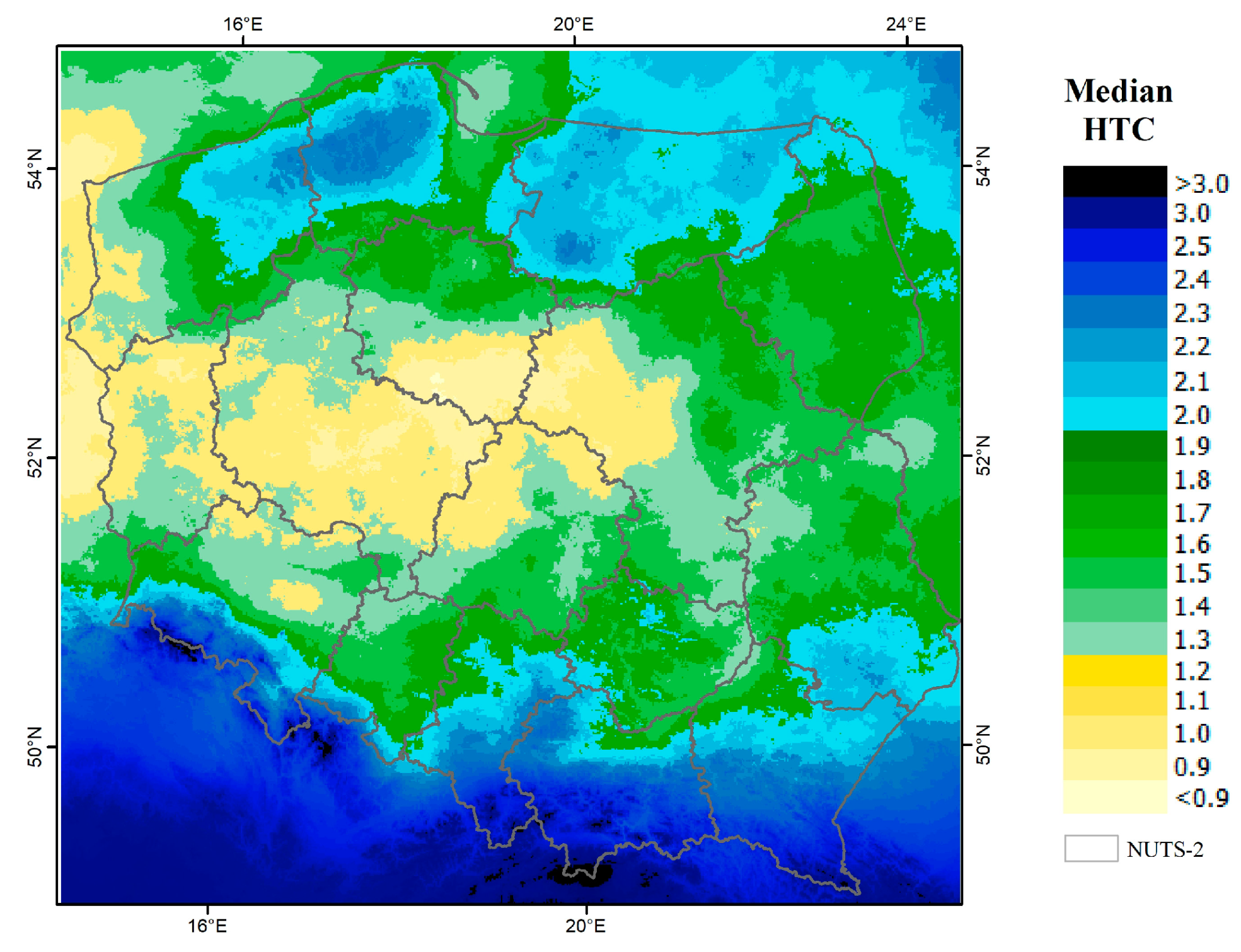
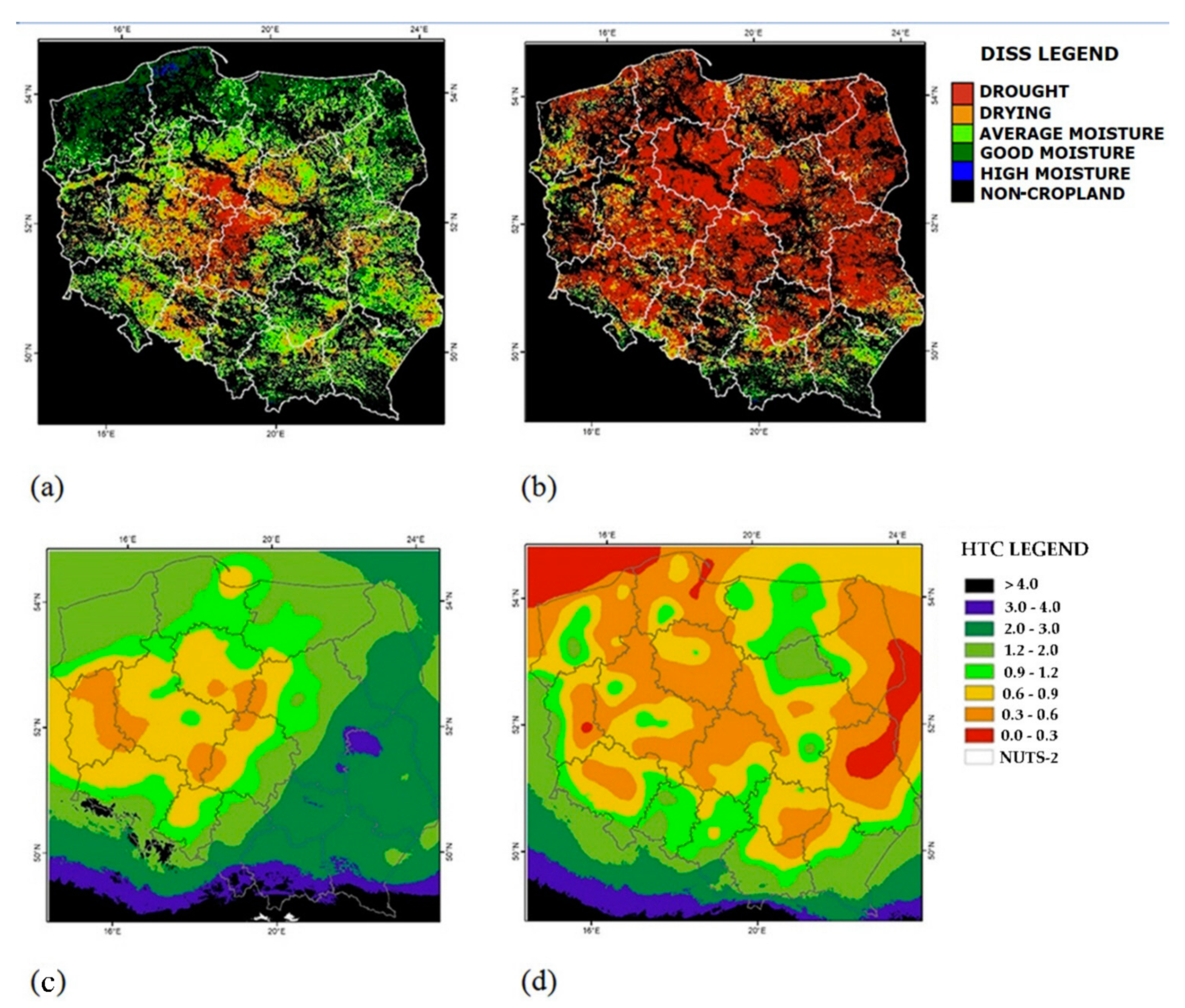
The median of HTC calculated for the selected area informs about the average atmospheric conditions (in relation to precipitation and air temperature). To obtain the median HTC values for the entirety of Poland, a database of 1 km raster images of HTC was created using the daily interpolated temperature and precipitation from the meteorological stations in the period 2001–2019. These images refer to the growing season (from the end of April to September) and were formed with a 10 day step. The spatial distribution of HTC median values in Poland (
Figure 6) is related to climatic conditions, which are influenced by Poland’s topography (
Figure 7). The lowland areas in western and central Poland are characterized by the prevailing water deficit (HTC median < 1.0), while the upland and mountain areas located in southern Poland, due to higher and more frequent rainfall, reveal good moisture conditions (HTC median > 1.0). Moreover, a high HTC median appears in northern Poland (Masurian and Pomeranian regions), where hilly landscapes filled with numerous lakes modify the climatic conditions, thus increasing the amount of rainfall. The same conditions are observed along the Baltic sea coastline—high HTC values are caused by the impact of a maritime-type climate in the northern part of the country. Relationships are noticed when comparing the maps (
Figure 6 and
Figure 7).
Figure 6 presents the cross-section of atmospheric conditions represented by HTC across the territory of Poland. Meanwhile,
Figure 7 presents a digital terrain model (DTM) for Poland. The spatial patterns of HTC and DTM are similar.
2.4. Satellite Data
The temperature product delivered by the MODIS satellite was applied in this study, namely Terra MODIS Land Surface Temperature/Emissivity 8 Day L3 Global 1 km (i.e., the MOD11A2 product); it was used for generating TCIs.
The MOD11A2 product offers land surface temperature (LST)/emissivity at a 1000 m resolution in an eight-day gridded Level 3. Band no. 1, named LST_Day_1km, was extracted for further work, which contains the mean daily temperature calculated as the average value from 2–8 non-cloudy days.
On the basis of the MOD11A2 product LST_Day_1km, the Temperature Condition Index (TCI) was calculated according to Equation (2):
where
LSTmax—maximum LST from the multiannual period;
LSTmin—minimum LST from the multiannual period;
LSTi—LST for the particular eight-day period.
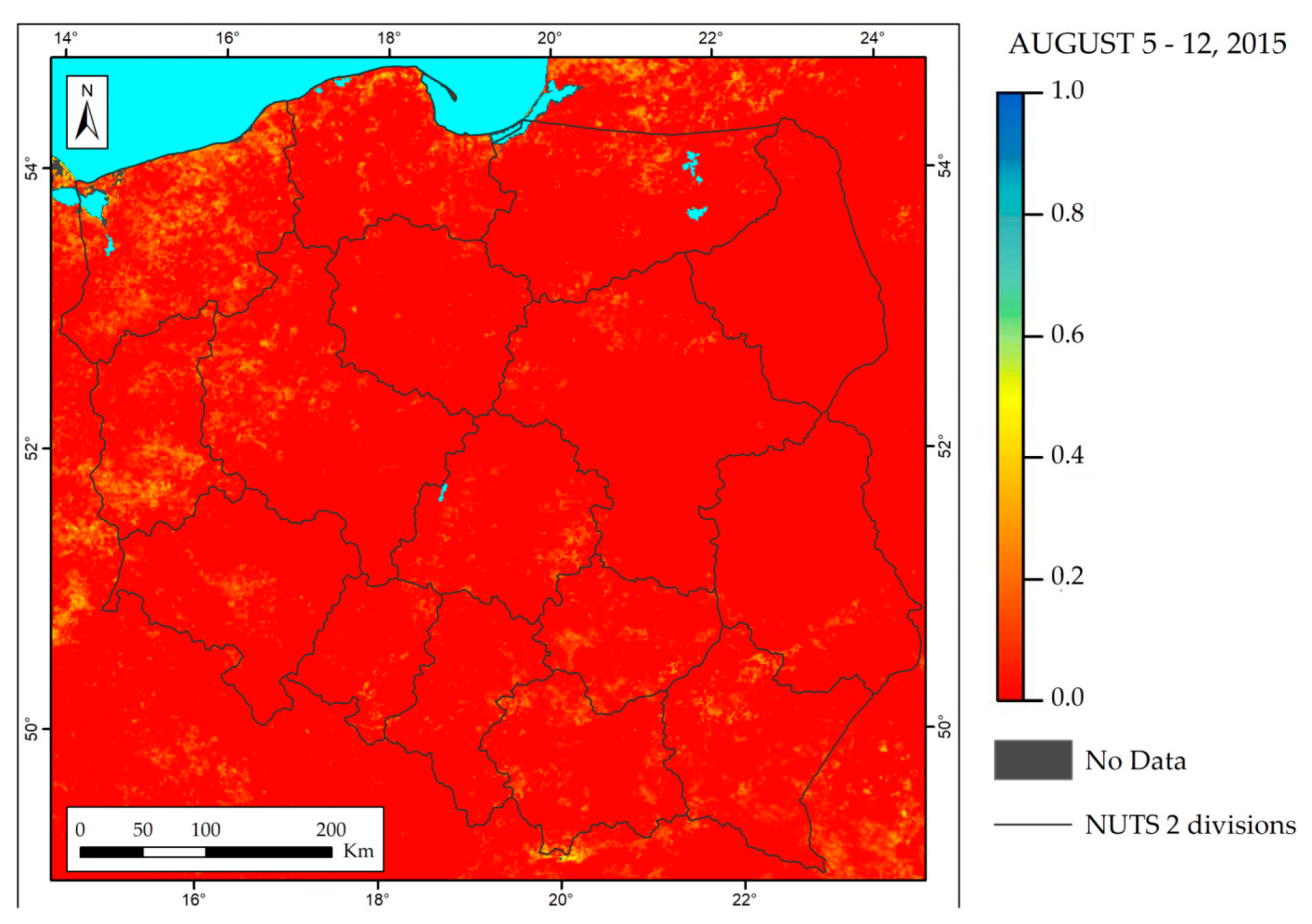
TCI is the normalized index of LST, which relates the current LST value to the range of multiannual values, placing it in the interval 0–1. The maximum LST value in a pixel corresponds to TCI = 0, while the minimum corresponds to TCI = 1.
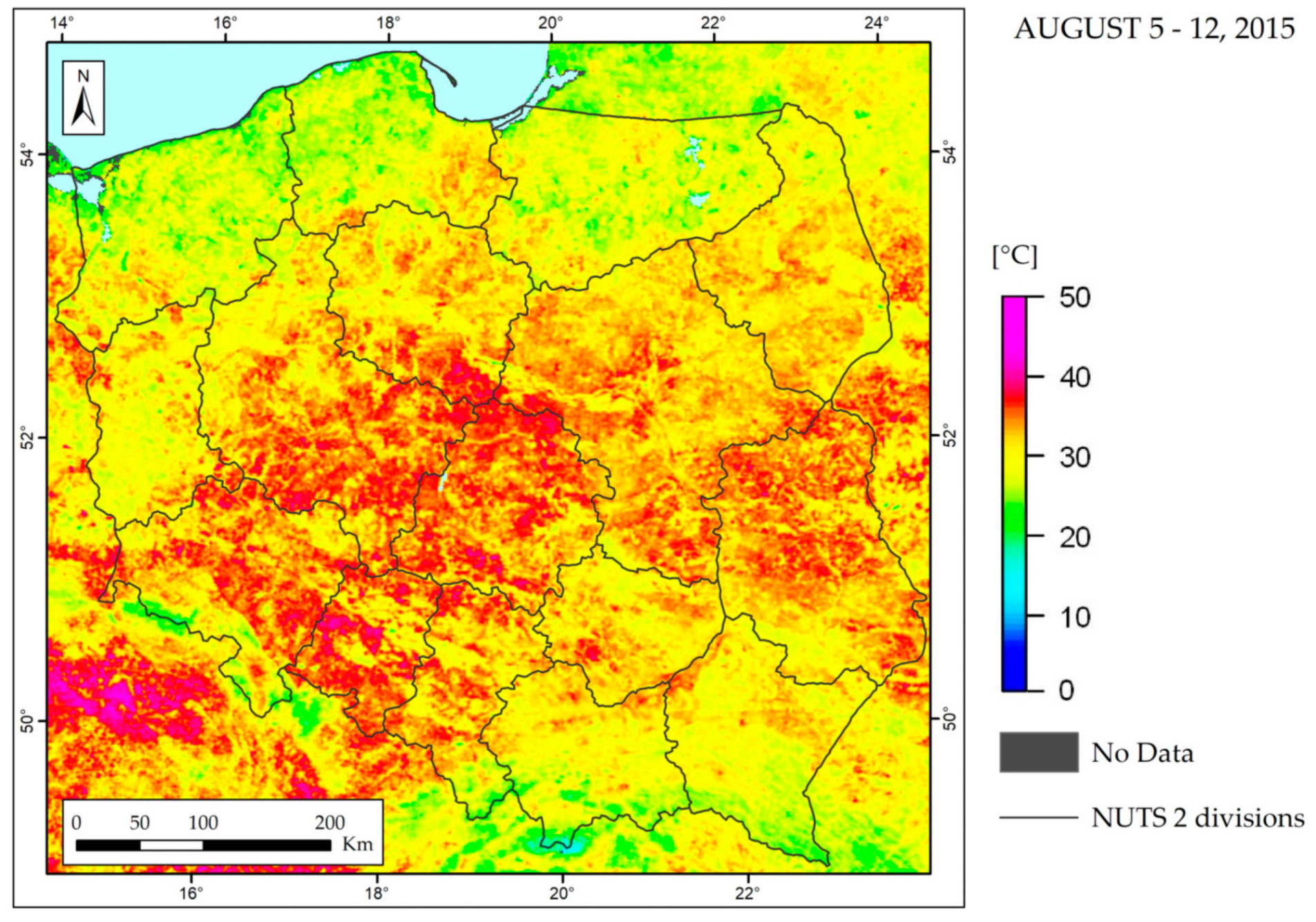
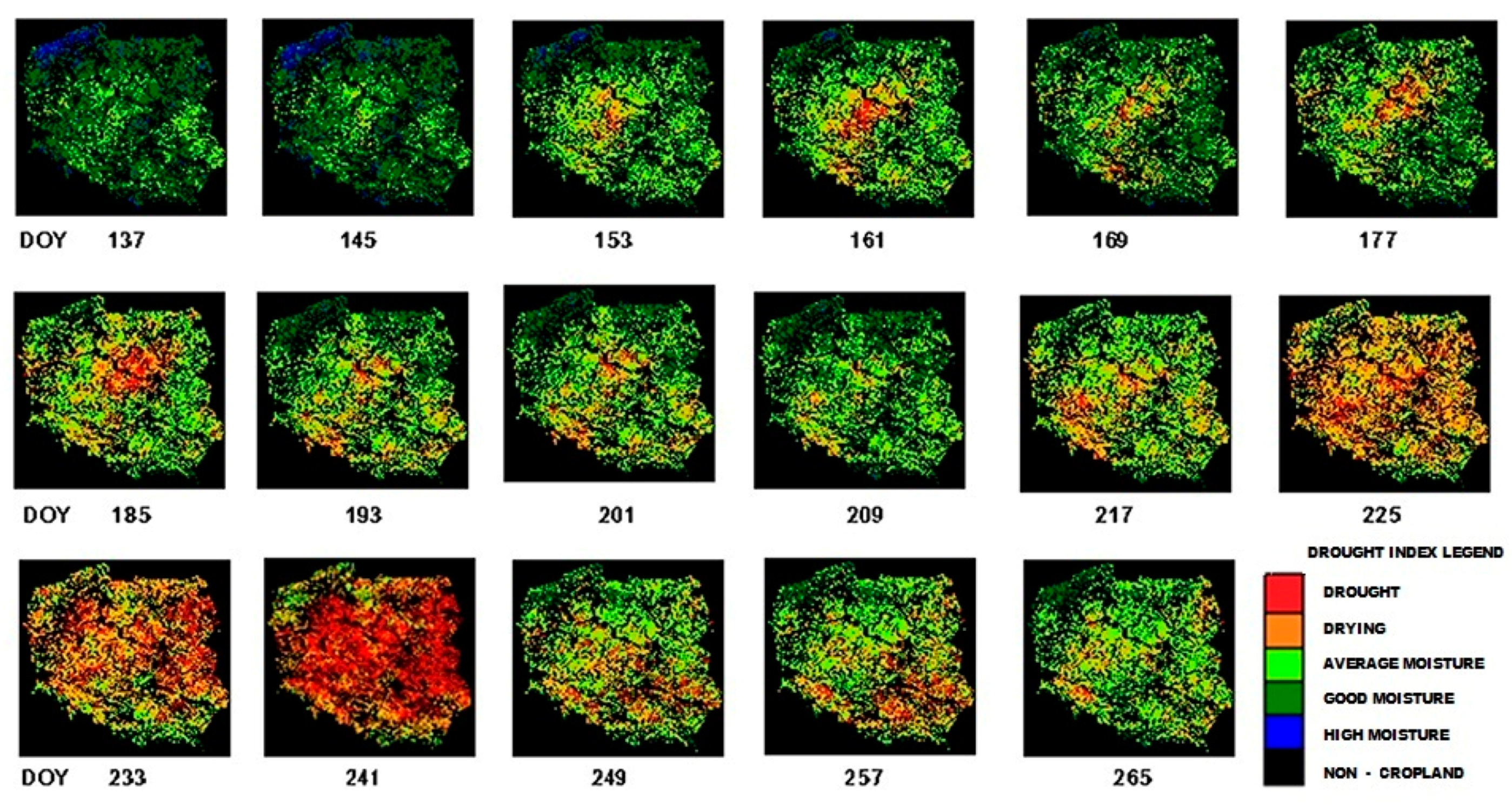
Figure 8 presents the conditions when the TCI is homogeneously equal to zero across Poland. In parallel, the maximum LST for day of year (DOY) 241 presented in
Figure 9 is spatially diversified within Poland.
The spatial diversification of the maximum LST is justified to a large extent by the climatic feature expressed by the HTC median (
Figure 6) coupled with topography (
Figure 7); in upland and mountainous areas, LST does not exceed 30–40 °C, while in the lowlands, it can even achieve 50 °C and incidentally higher.
The TCI describes the effect of vegetation stress in response to temperature [
11]. The vegetation condition is estimated in relation to the maximum/minimum temperatures. A low TCI, significantly lower than 0.5, implies that the vegetation is in a bad condition. However, spatial comparisons of TCI can be ambiguous, as the same values can present different levels of vegetation stress. In our approach, HTC is the factor that enables us to incorporate the variable climatic conditions into a final method of drought assessment. TCI was considered as the main input for constructing the drought index.
2.5. Approach for Drought Assessment Using Satellite and Meteorological Data
The aim of the present analysis was to describe the relationship between HTC representing the atmospheric moisture conditions and TCI satellite-derived index characterizing the vegetation response to these conditions for agricultural area in different climatic zones in Poland.
In this approach, the TCI was used in a time series form, which consists of consecutive observations in each vegetation period. The cross-sectional data structure was adopted to join observations from spatially diversified regions. The samples of meteorological and satellite data, which came directly from evenly distributed meteorological stations (
Figure 2) and the agricultural area around the stations, were pooled into a special structure, called
panel data. Such an approach allowed us to formulate a drought model based on meteorological and satellite data in a spatiotemporal scheme.
2.5.1. Panel Data and Fixed Effect Model
The cross-sectional data are a set of observations derived from various entities in one fixed point of time. The analysis takes into consideration the differences between the groups of observations from these entities. The time series describe a feature in a temporal aspect; observations are collected at equally spaced time intervals as ‘time points,’ and the ‘lag operator’ is defined, which indicates the preceding observation by a number of ‘time steps.’ In ‘panel data,’ one cross-sectional entity is considered over time, so the structure is pooled over space as well as over time. It enables us to apply more complex two-dimensional models, taking into account the dynamics of changes in combination with the diversity of the objects. We found it to be appropriate to develop the model using a combination of temporal satellite and spatially diversified meteorological data, described as the Fixed Effects Model [
40]. This approach affords the possibility to estimate the linear regression parameters (i.e., slope and intercept) for joint data from
n parallel sources under some assumptions. The first assumption is that the diversified relations within the groups of observations are represented by intercept parameters, which are independent of time, i.e., fixed in time. The second assumption is that the expected values of the variables are also fixed in time.
The system of equations for the fixed effects model is defined as
where
i—entity (one source of data) 1…n;
n—number of entities;
t—time point;
—intercept fixed in time for entity i;
—dependent variable;
—independent variable for entity i and time point t-k, k = 0,…,m;
m—number of lags;
—slope parameter for independent variable Xi,t-k, k = 0,…,m;
—error for entity i and time point t.
The intercept is specific for entity i and is unknown. It does not allow all entity observations to be combined into one system of equations to estimate the parameters .
The intragroup transformation of equations system (3) was done. It consists of the subtraction of the expected value in the group (entity) from each variable on the left and right sides of the equations:
where
, —the fixed-in-time expected values of variables X and Y;
= 0, because the mean of the residuum is zero by assumption of the least mean squares method (LMSQ) method.
The transformation eliminates the element that differentiates the groups of observations because it was constant on the level of one group. Expression (4) is the homogeneous system of linear equations, which can be estimated by the classical least mean squares method (LMSQ). It describes the model based on the anomalies of dependent and independent variables defined in Equation (3). The anomalies of variables erase the spatial diversification and allow for their comparison on a uniform scale.
2.5.2. Design of the Drought Index Based on the TCI under Different Climatic Areas
The data from one meteorological station were taken as the entity in Equation (3). HTC30 coefficients were calculated for 30 days back for the time points with an eight-day step coupled with the days of the year in the MODIS image database. The exemplary cases in the system of equations (3) for stations
i 1..233, years 2001..2019, and eight-day time steps
d 112..280 for the left and right side variables are presented in
Table 1.
A logarithmic operation was carried out on HTC30 to ensure a normal distribution. The expected value of it is log(MedHTC30). The number of lagged TCI variables in the model expression is determined during the estimation process. The value equal to 0.5 as the expected value of the TCI for each eight-day step of MODIS data was taken. It was confirmed by the Student’s t-test that there is no significant difference between the value 0.5 and the multiyear averages of the TCI for most entity areas and time points.
Thus, the formulation of the model, combining spatiotemporal satellite and meteorological data according to Equation (4) for 30 days of HTC accumulation, becomes
where
—HTC30 coefficient of station i at time point t (eight-day step in the growing season);
—median of all HTC30 observations at station i;
—TCI for the area close to station i at time point t;
0.5—the expected mean of the TCI variable for every station at every time point;
—the error for station i at time point t;
, —the parameters to estimate.
The dependent variable in Equation (5) has the form
YHTC30i,t = log(
HTC30i,t) – log(
MedHTC30i). The mean subtraction results in the dependent variable becoming free from the atmospheric characteristics represented by the median MedHTC30 of each station. The learning sample was limited to such cases where the number of agricultural pixels within 10 km of the meteorological station exceeded 200. Such a choice provides more averaging of area in the agricultural cover class, which is advantageous for modeling. TCI data come from the aggregation of 1 km
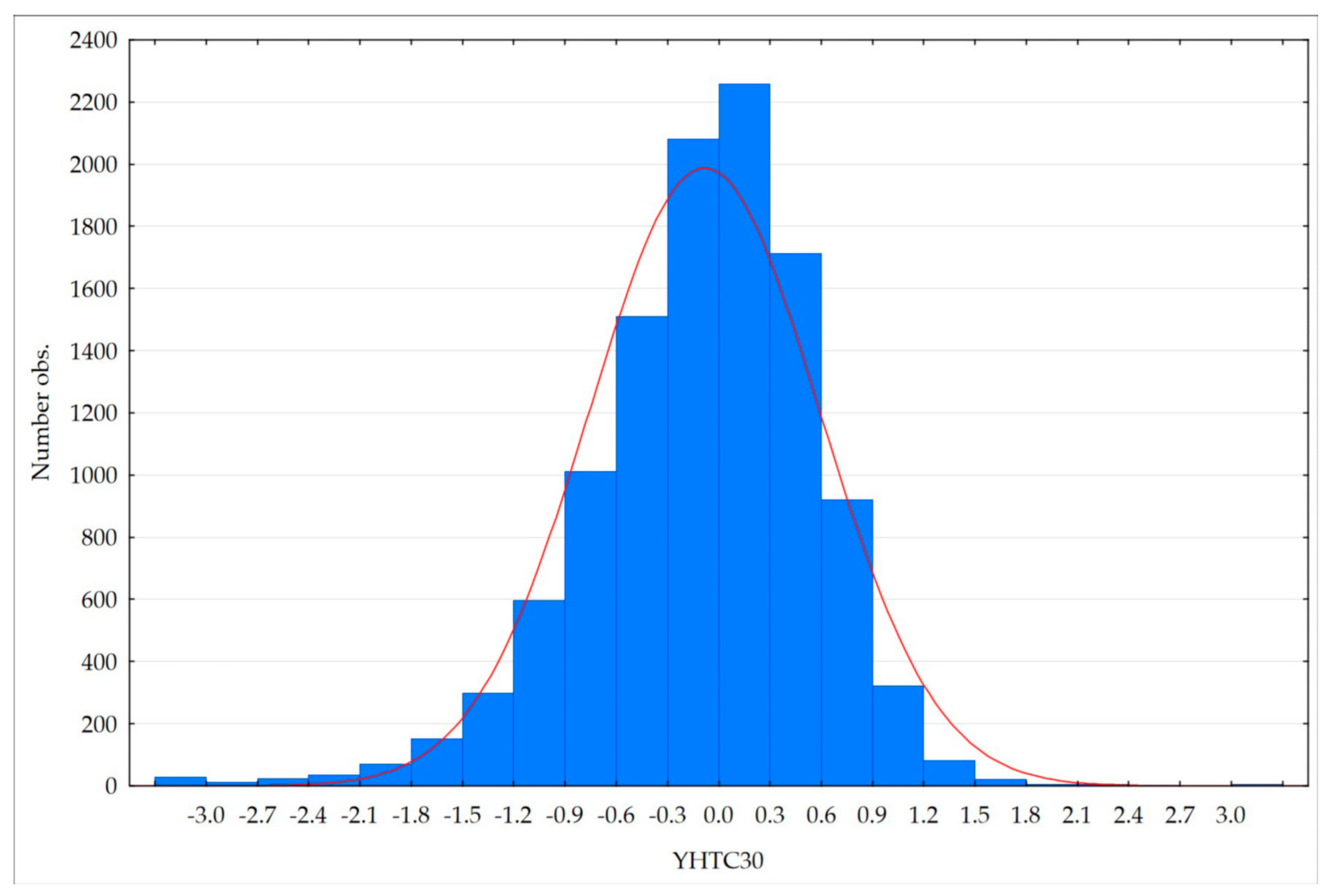
2 pixel values for the sample area. A histogram of the dependent variable, called YHTC30, presented in
Figure 10, shows the normal distribution necessary for using the LMSQ regression method.
The equation, being the result of regression after recalculating the estimated parameters (slope and intercept), can be presented in the form
where
t is the eight-day time point of the growing season; and
are the estimated parameters.
The length of the period for HTC accumulation was set to 30, 40, and 50 previous days. This allowed us to fit it to 3, 4, or 5 time steps back of aggregating TCI, respectively, according to Equation (4). The Pearson’s R coefficient as a goodness-of-fit measure and the standard errors for the models using the TCI in the 3, 4, and 5 time steps are presented in
Table 2. The standard errors decrease as the TCI lag increases; thus, more intensive agricultural drought is predicted with more precision in relation to atmospheric conditions.
The goodness-of-fit on individual meteorological stations is largely balanced for all variants of the model. The correlation coefficients change in the range presented in the last column of
Table 2, from R = 0.48 to 0.74, depending on station. The results included in
Table 2 highlight the feasibility of using the model that fuses meteorological and satellite data to detect drought in different climatic regions.
The exponential transformation of Equation (6) and the moving of MedHTC30 to the right side by multiplication affords an equation with HTC30 on the left side. The variability of the right side of the equation is based on TCI, while MedHTC30 is a fixed element characterizing the climatic aspect of a specific area. For the whole territory of Poland, the MedHTC30 image with a resolution of 1 km was prepared using interpolated meteorological data (
Figure 6). Equation (6) was adopted as the Drought Information Satellite System (DISS) index:
where
t is the eight-day time point in the growing season; and a is negative while b, c, and d are positive.
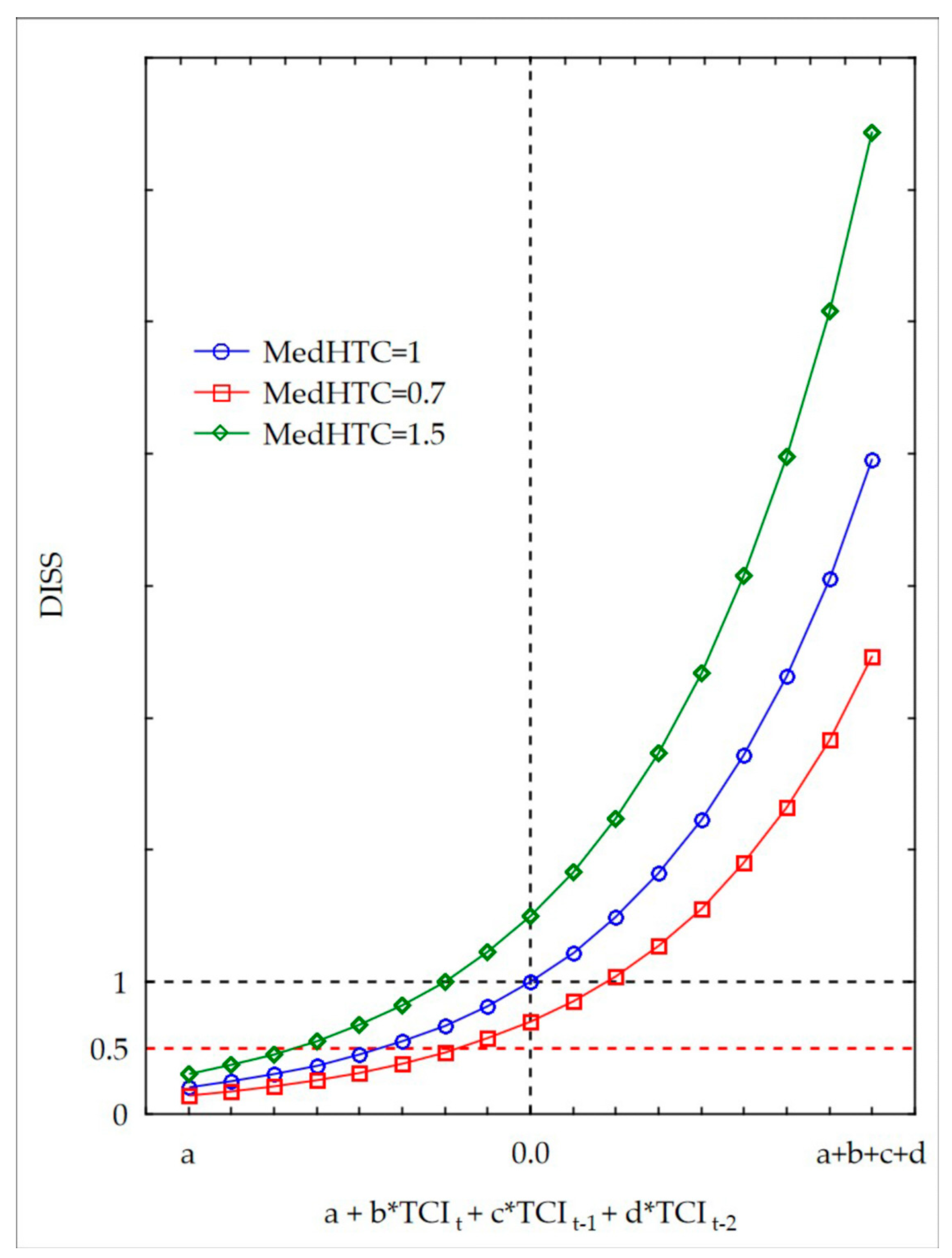
Figure 11 illustrates the simulation of the differences between the values of DISS for climatic areas represented by various MedHTC. For the same values of the satellite indices in (7), the drought index DISS is higher for areas characterized by a more humid climate and lower for drier areas than for the average hydrothermal conditions. This allows us to compare the results from various regions using the uniform scale. It also allows us to maintain the characteristics of the area, regarding the frequency of the occurrence of drought, compatible with HTC distribution.
The number of time steps in the moving average phase of (7) is flexible, depending on the period of accumulation of the precipitation and temperature in HTC equation (1). The more the preceding satellite indices are aggregated, the longer the horizon of agricultural moisture conditions that we are interested in. The number of lags of TCI used in the DISS formula determines the degree of intensity of the drought conditions. This information could be dedicated to a specific type of vegetation cover, describing their temporal response lag to drought [
41]. For mitigating drought effects on arable area, shorter periods are preferable, as 3–4 eight-day time steps of TCI. The 5 steps of the TCI model would be useful for detecting drought of the more drought-resistant plants.
The statistical analysis revealed that the period of accumulation for the meteorological coefficient is longer than the time horizon of the satellite response. The 30 day HTC is significantly related to three steps of the eight-day TCI (24 days), as well as the 40 day HTC, to 4*8 days and 50 to 5*8 days, respectively. This is in accordance with the nature of the vegetation’s condition, which is controlled by soil moisture, as well as with the delayed reaction to water deficit. Testing of the dependences between in situ and satellite indices in the moisture context was presented in [
42].
The equation of the DISS index based on the 3 time-step moving average of TCI for agriculture area is as follows:
The distribution of HTC values across the territory of Poland presented in
Figure 6 shows that the dominating values are around 1.0. Thus, HTC < 1, with some approximation, should be treated as indicating atmospheric conditions, which predestine drought conditions.
The selection of thresholds for the classification of drought levels was based on the statistical analysis presented in
Table 3, related to the probability of compliance of the DISS index in its particular ranges with the water deficit characterized by HTC. Statistical agreement with a water deficit above 80% was accepted as satisfactory for determining serious drought conditions; a value of 0.5 was chosen as the threshold of serious drought, because it is half of the 0–1 interval; and a value of 1 is related to average conditions in the area when the median HTC is equal to 1.0 (
Figure 11).
When the DISS values increase, the probability of water deficit decreases, until the level of DISS > 1.5; then, there is a high certainty that the area is not affected by drought. The probability grows with an increase in the time horizon when aggregating the satellite indices (three, four, and five time steps). Testing took place on a sample of approximately 50,000 observations using all available data. The percentage characteristics of the moisture conditions described by DISS within the agricultural area of Poland are presented in
Table 3.
Classification of the DISS index was done using the thresholds specified in
Table 3. Five levels of dry/moisture conditions were distinguished for the agricultural areas:
Drought—when DISS < 0.5
Drying—when DISS ≥ 0.5 and DISS < 0.8
Average conditions—when DISS ≥ 0.8 and DISS < 1.5
Good conditions—when DISS ≥ 1.5 and DISS < 3.0
Wet/cold conditions—when DISS ≥ 3.0
2.6. Areas of Drought versus Yield Reduction
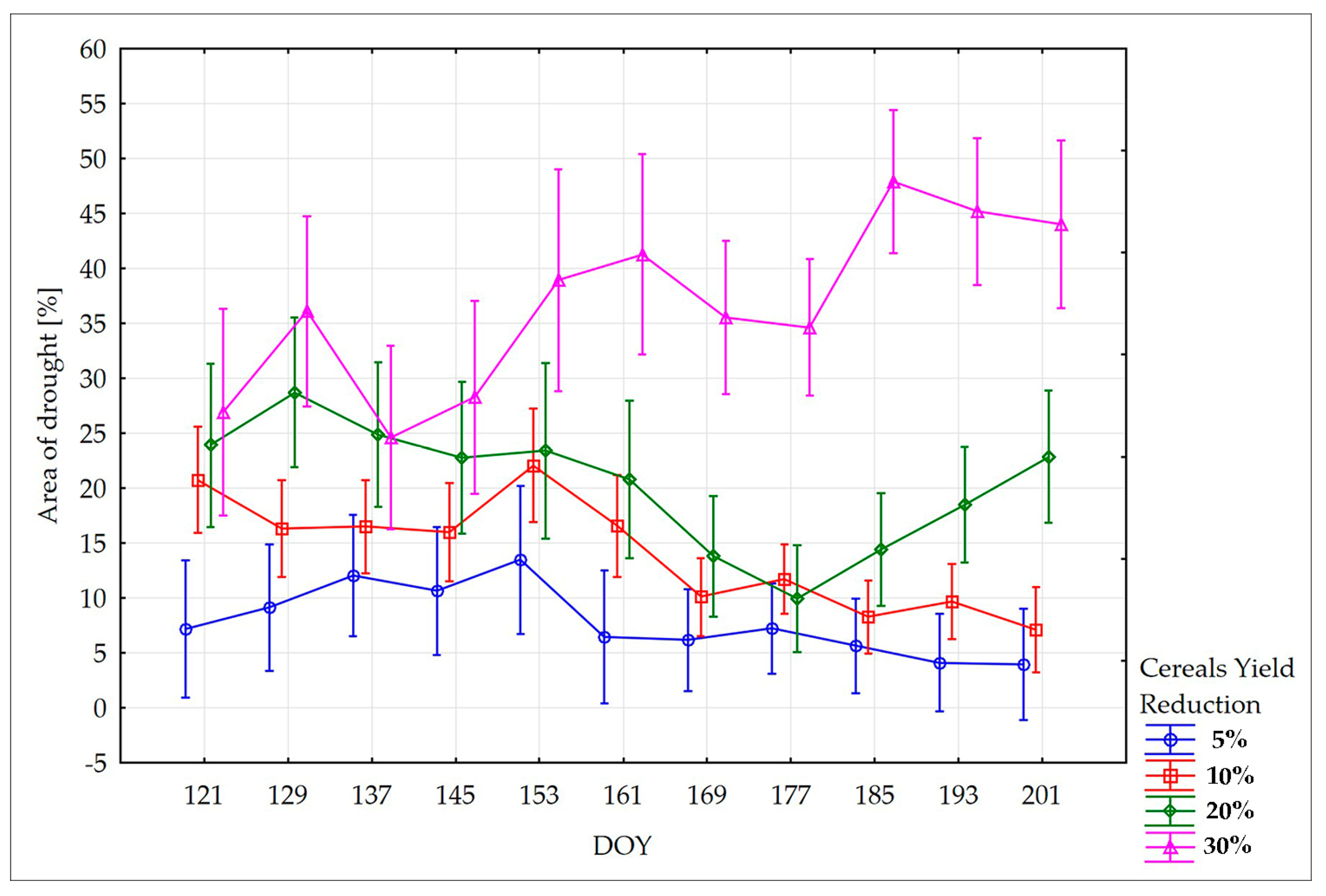
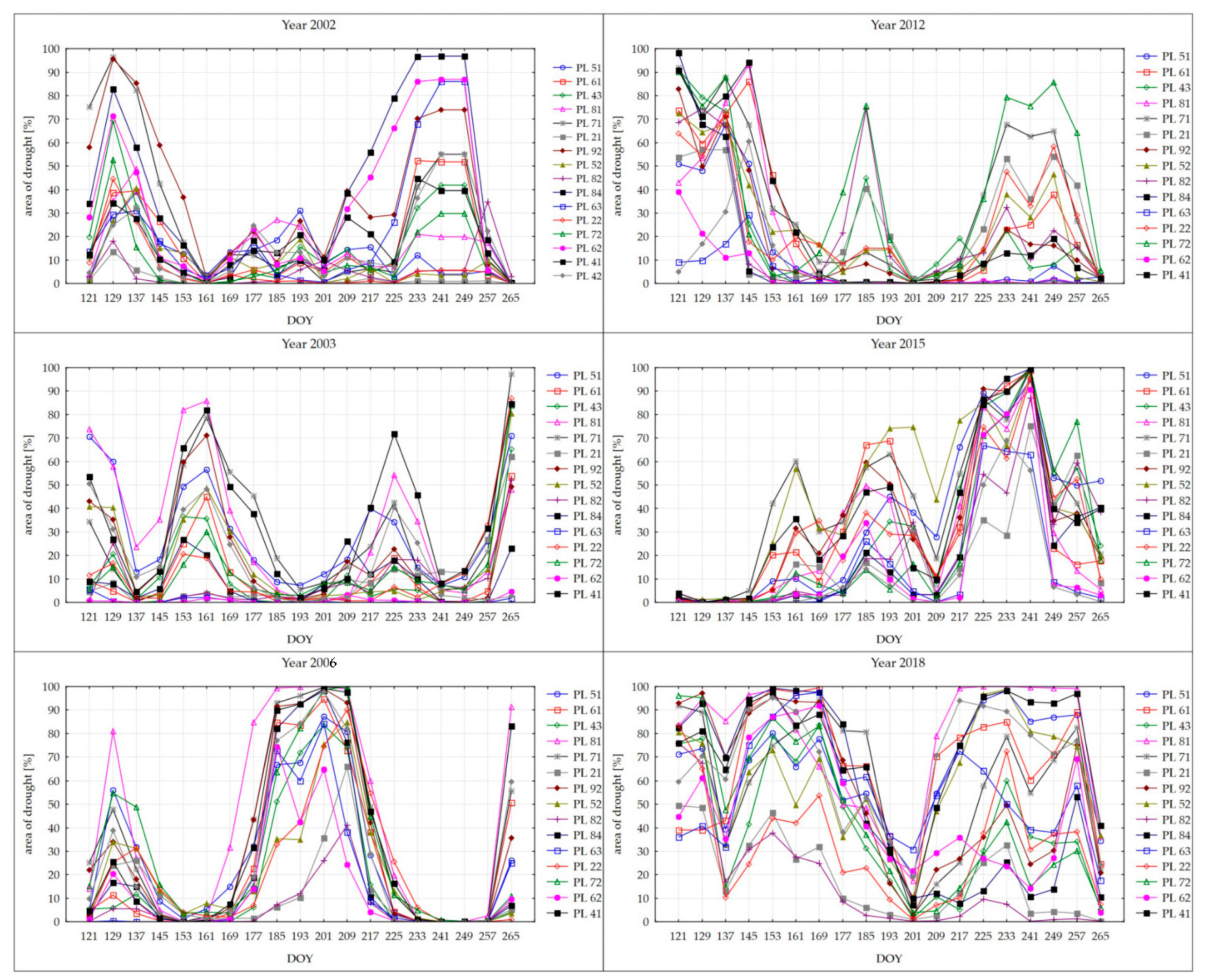
The relationship between the extent of drought area and the reduction in crop yield was investigated using the analysis of variance statistical method (ANOVA). In the development period of cereals (DOY 121–201), a comparison of the extent of drought area was made in groups of observations that varied in the level of yield reduction. The observations were divided into four groups of cases (year/voivodeship) where the yields were 5%, 10%, 20%, and 30% lower than the voivodeship multiyear maximum. ‘Multi-way ANOVA with repeated measurements’ describes the course of moisture conditions represented by the mean percentage of area affected by drought for the four groups of yield reduction level. High yield reductions (i.e., above 30%) are clearly related to a large scale of drought for most of the season. Besides, the differences between the means of the drought area percentage for the group of 30% yield reduction and the other groups were statistically significant in the subsequent periods, starting from day of year (DOY) 145. This was tested by ‘contrasts analysis’, in which the F-test was calculated for the means in the “30” group in contrast to the other groups for each DOY time point. The analysis was conducted on a sample of 288 cases and revealed that the percentage of drought area in the voivodeships detected by the DISS index corresponds to the level of yield reduction, especially for high yield reduction. It concerns the most important parts of the season of cereal growth (June–July).
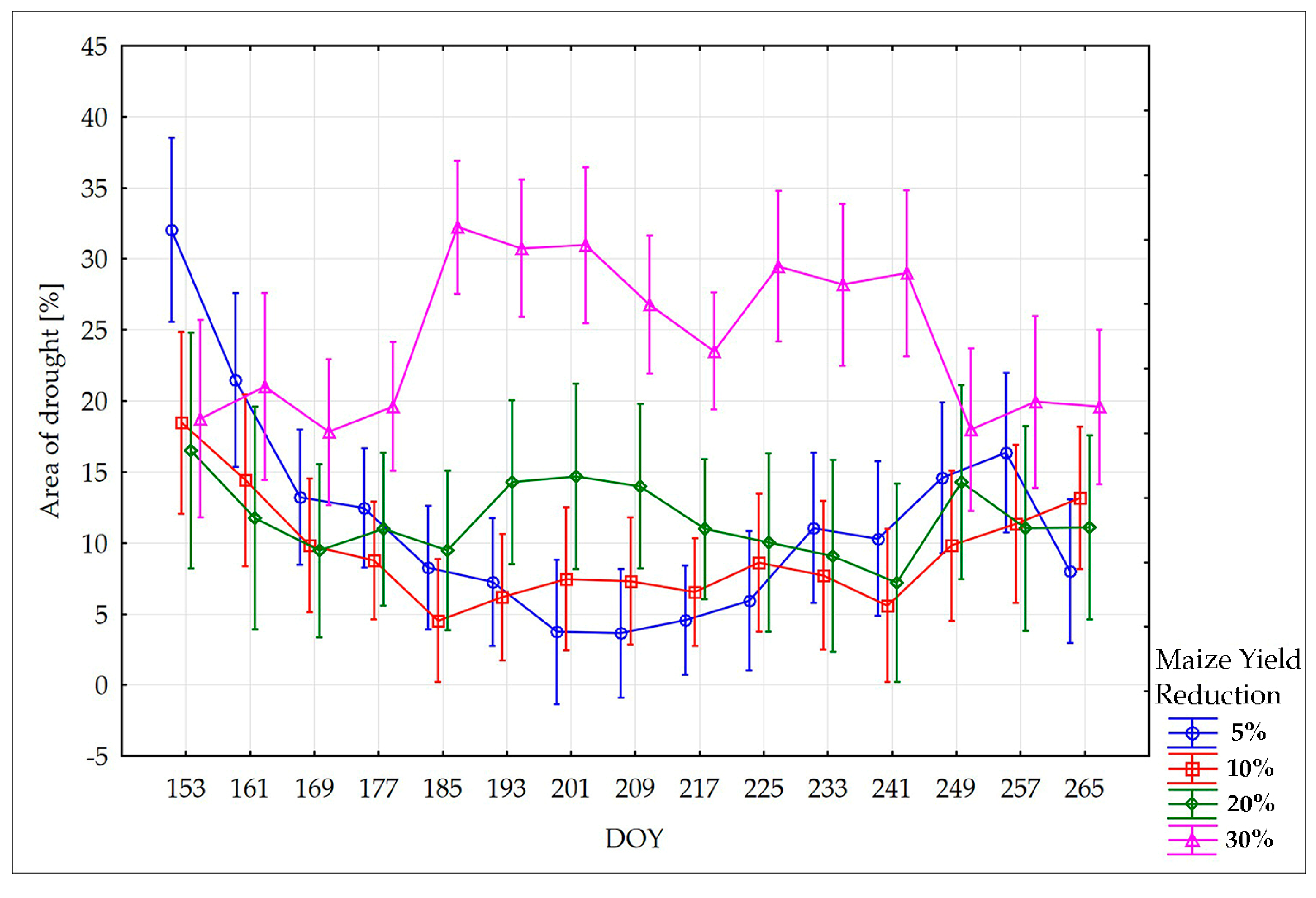
The same analysis was made for maize. The period with the greatest impact on the yield reduction of maize is a DOY from 177 to 241 (end of June to end of August). The results of the ANOVA for cereal and maize are presented in
Figure 12 and
Figure 13. The bars denote the 0.95 confidence interval for the mean value of the drought area. Statistical analysis was conducted for all 16 NUTS 2 regions within the 2001–2018 timeframe. Yield data covering this period were collected from the Central Statistical Office (CSO). The existing increasing linear trends concerning voivodeships data were taken into consideration.
4. Discussion
4.1. Verification of Drought Maps
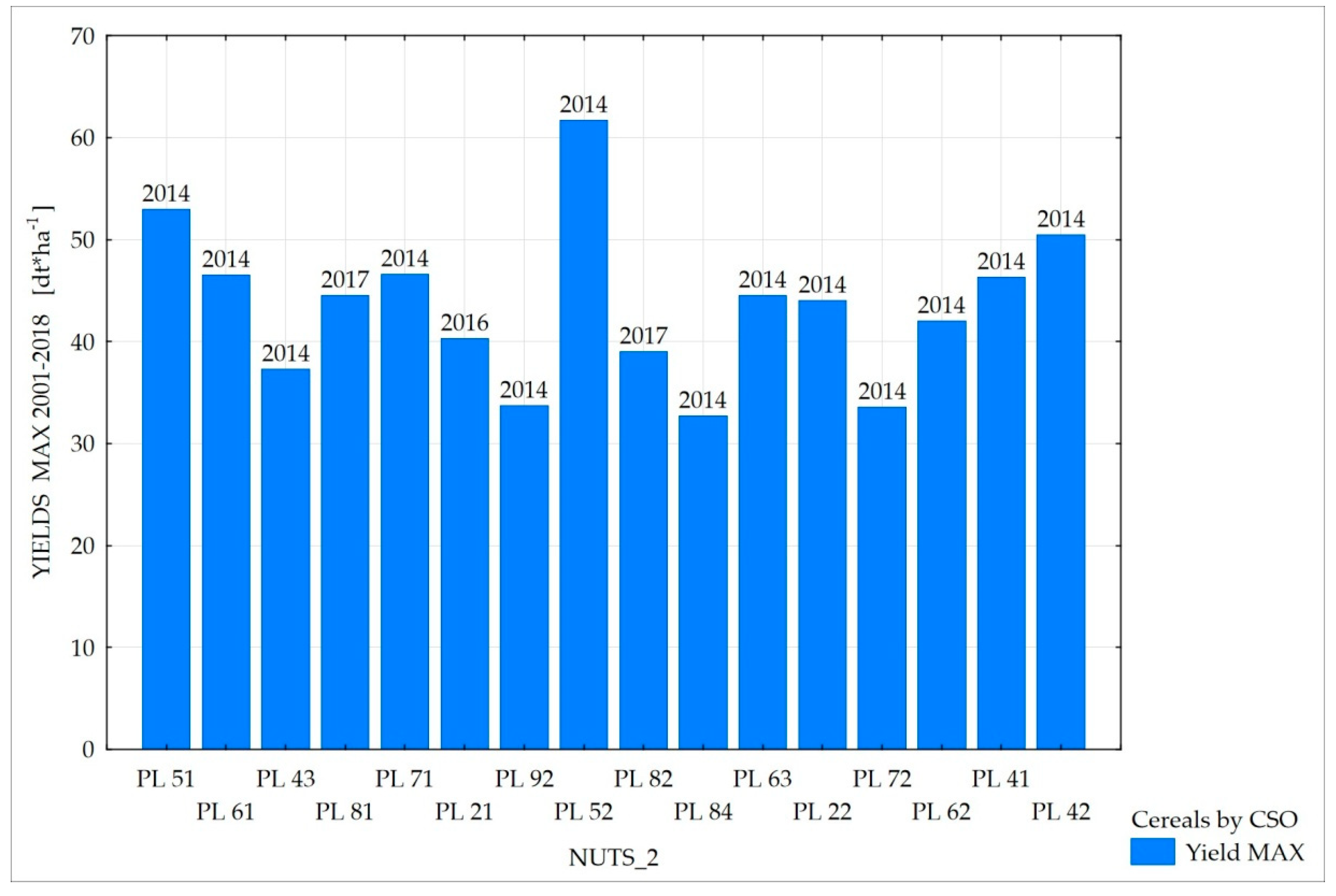
The method used for verification of the drought maps was based on the assumption that severe drought should have an impact on yield reduction of the main crops. Therefore, yield data covering the 2001–2018 period were collected from the Central Statistical Office (CSO) for all NUTS 2 regions (i.e., voivodeships) in Poland. Next, years with maximum yields were determined for each voivodeship in order to calculate at the next stage yield reductions.
Figure 19 demonstrates various levels of maximum yield depending on the region, highlighting three years when maximum yields appeared, namely 2014 (primarily), 2017, and 2016.
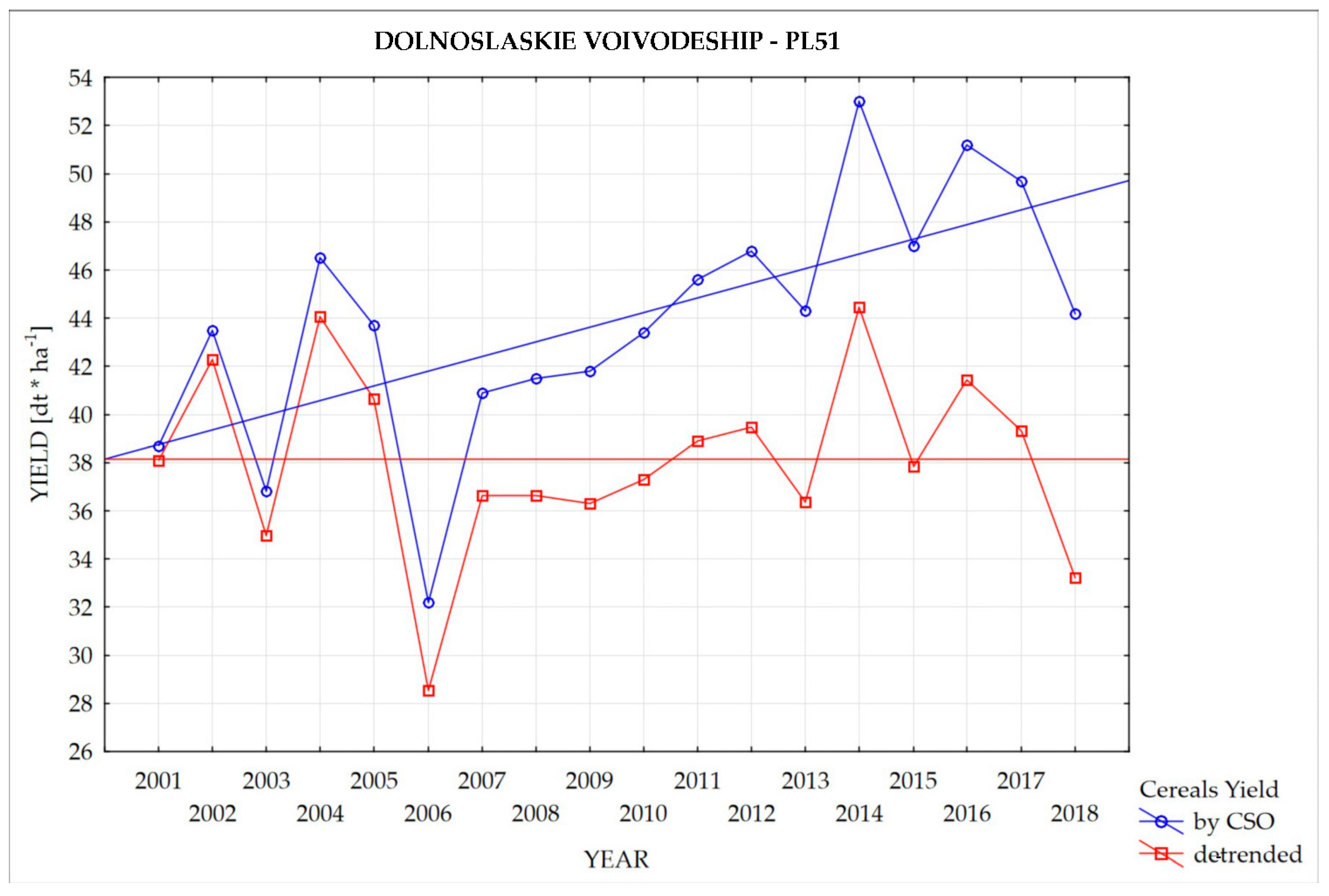
When analyzing time series of yield over the period 2001–2018, it was found that a significant increasing trend appears for each region (i.e., voivodeship); therefore, the de-trending procedure was applied. The increasing trend resulted from the gradually improved agricultural practices and from better crop varieties applied by the farmers. An example of yield values before and after application of the de-trending procedure is presented in
Figure 20.
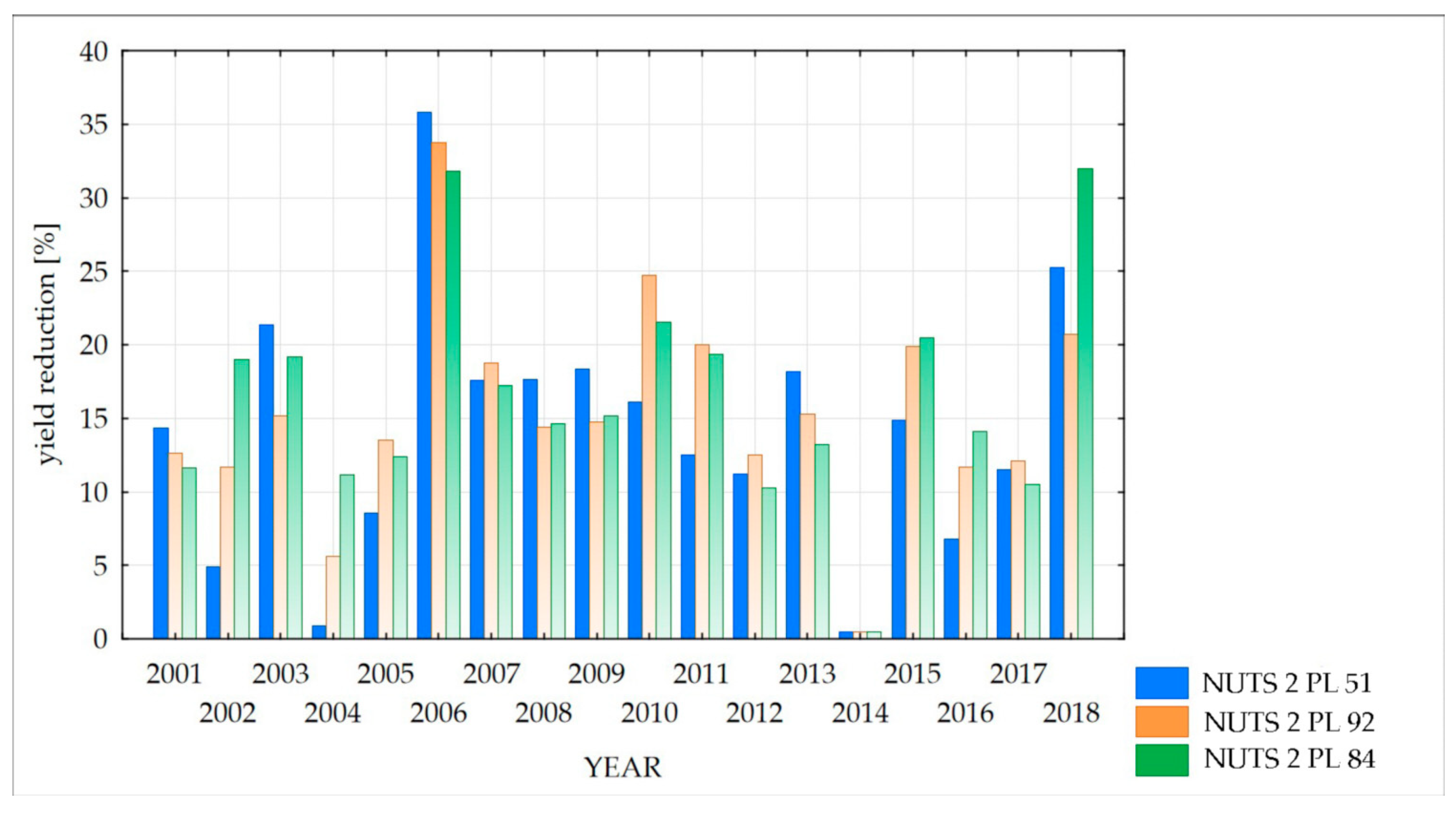
At the next stage, the percentage reduction of yield in relation to the maximum yield was calculated for each year and for each NUTS 2 region. The information on the yield reduction for cereal in graphical form is presented for the selected NUTS 2 regions in
Figure 21.
Finally, statistical analysis (ANOVA) described in the Method section has been applied to find the relationship between the level of yield reduction and percentage of drought occurrence; it revealed the correlation of these two parameters, especially for a group with high yield reductions.
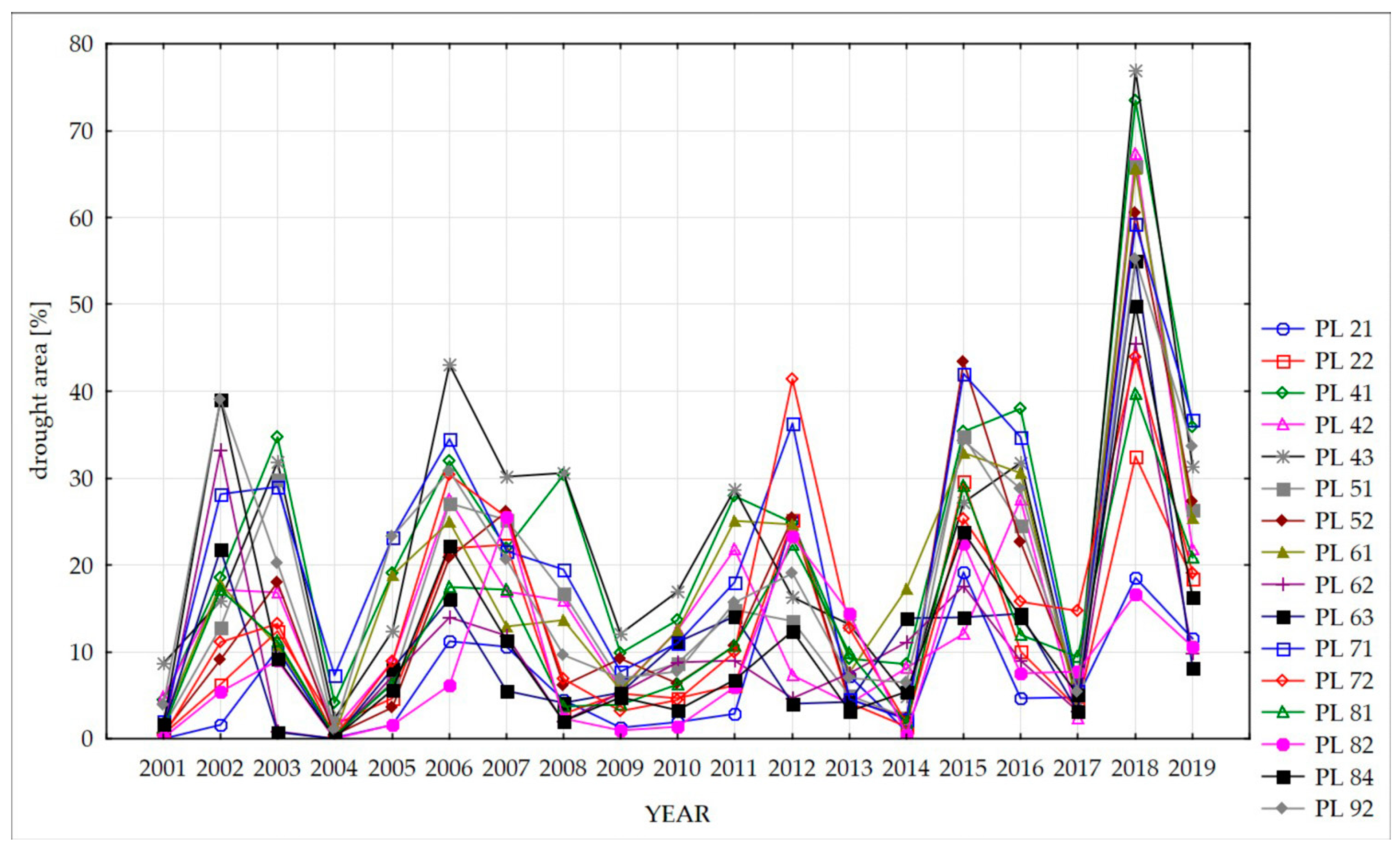
The maps of the drought index based on satellite data can be used for detailed spatial analysis of the variability of the drought conditions within the vegetation period, as presented in Figures 24–28. However, they can also be effectively applied for distinguishing areas (regions) with the highest intensity of drought from a multiyear perspective. Such an analysis was carried out by applying information on the percentage of drought occurrence within particular NUTS 2 regions (i.e., voivodeships) in the 2001–2019 timeframe. This information was derived from the maps of the DISS drought index, calculating the average percentage of drought area in the whole vegetation period. The results of the analysis are presented in
Figure 22.
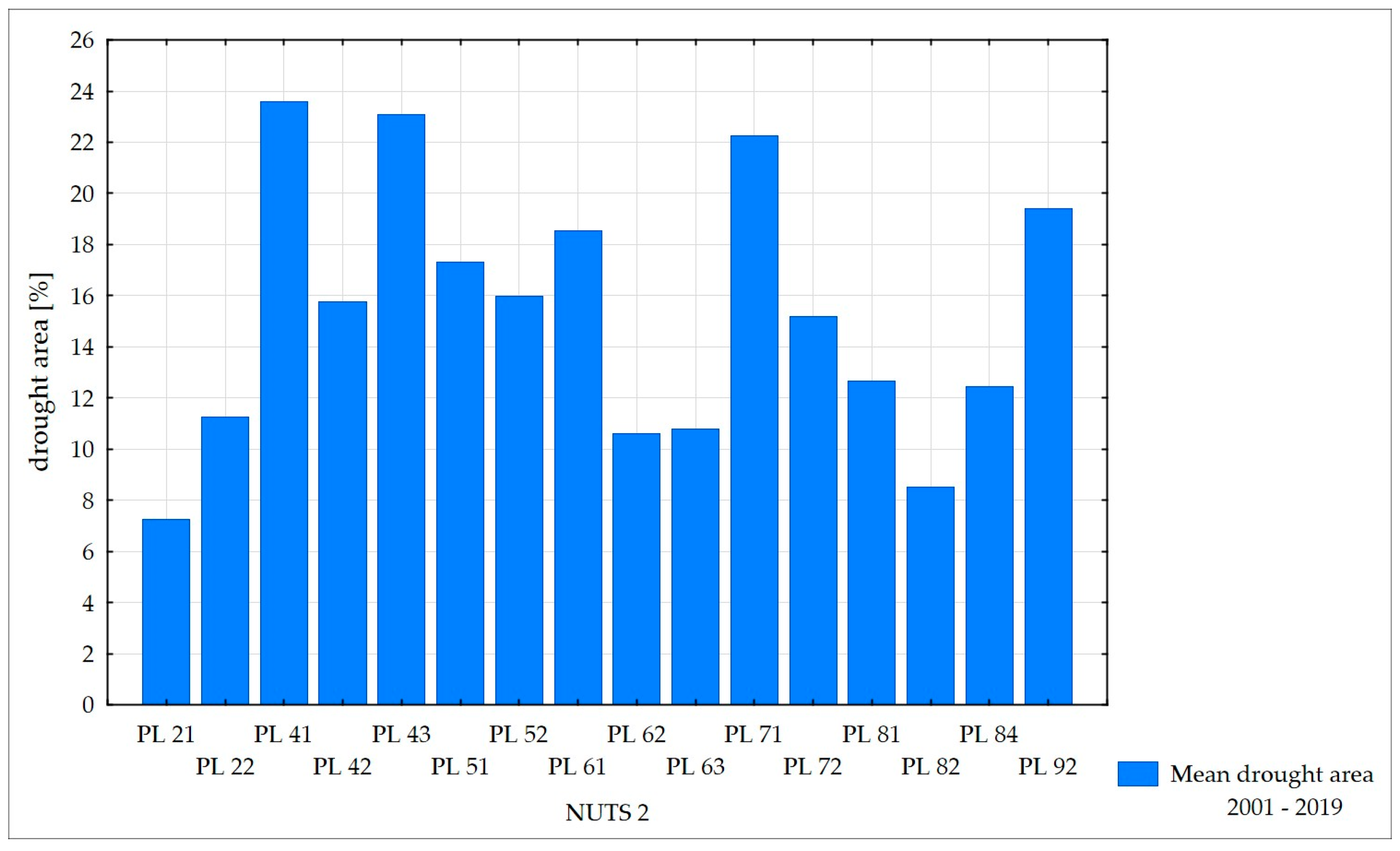
The study confirmed that in the years 2002, 2003, 2006, 2007, 2011, 2012, 2015, 2016, 2018, and 2019, the extent of the drought for the majority of NUTS 2 regions was the highest, for most voivodeships reaching over 20% of the agricultural area. In particular, it revealed extremely high drought in 2018, which reached over 40% of the agricultural area for almost all voivodeships. Simultaneously, a comparative analysis of the occurrence of drought within particular regions, performed for the whole 2001–2019 period, pointed out those voivodeships that are especially prone to drought conditions. The results of this analysis in graphical form are presented in
Figure 23.
The regions most heavily affected by drought were PL71 (Lodzkie), PL41 (Wielkopolskie), PL43 (Lubuskie), PL92 (Mazowieckie), PL61 (Kujawsko-Pomorskie), and PL51 (Dolnoslaskie), all located in central and western Poland. In these regions, drought hazards are also most frequently described by meteorological parameters, which correlate well with the satellite-based drought index.
4.2. Spatial Analysis of the Occurrence of Drought in Poland
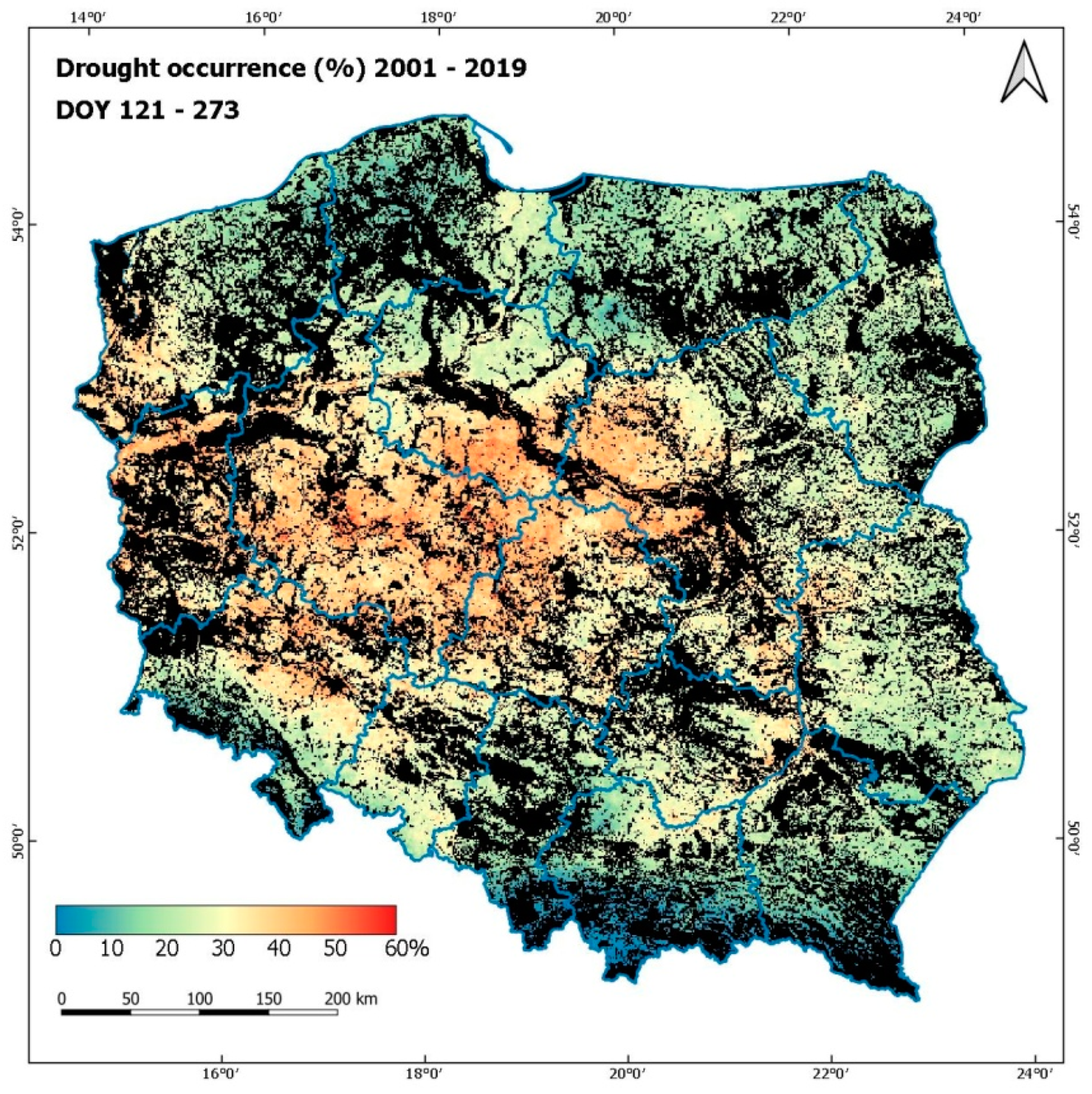
The information obtained in aggregated form for all regions was confirmed by spatial analysis of the raster DISS drought maps, which were used for calculating the percentage of the occurrence of drought within the whole vegetation season. The results of this analysis were prepared in the form of two maps, presenting the occurrence of drought in percentages across the 2001–2019 period (
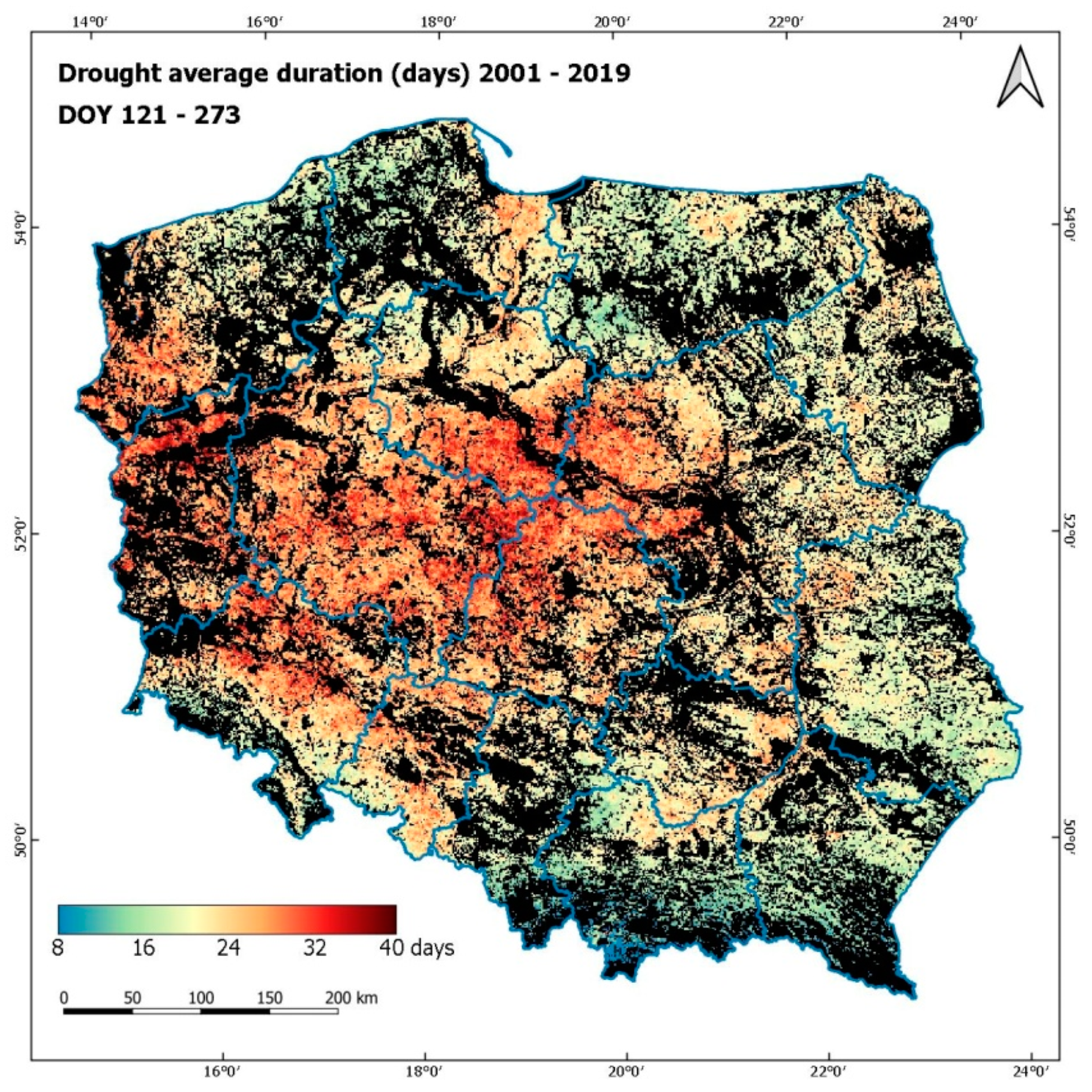
Figure 24) and showing the average duration of drought (in days) for the same period (
Figure 25). Both maps demonstrate the spatial distribution of the intensity of drought, which is consistent with the conclusions derived from the analysis of the regions (
Figure 23); the same areas located in the central and western parts of Poland proved to be seriously affected by drought, reaching similar percentage levels in terms of the occurrence of drought.
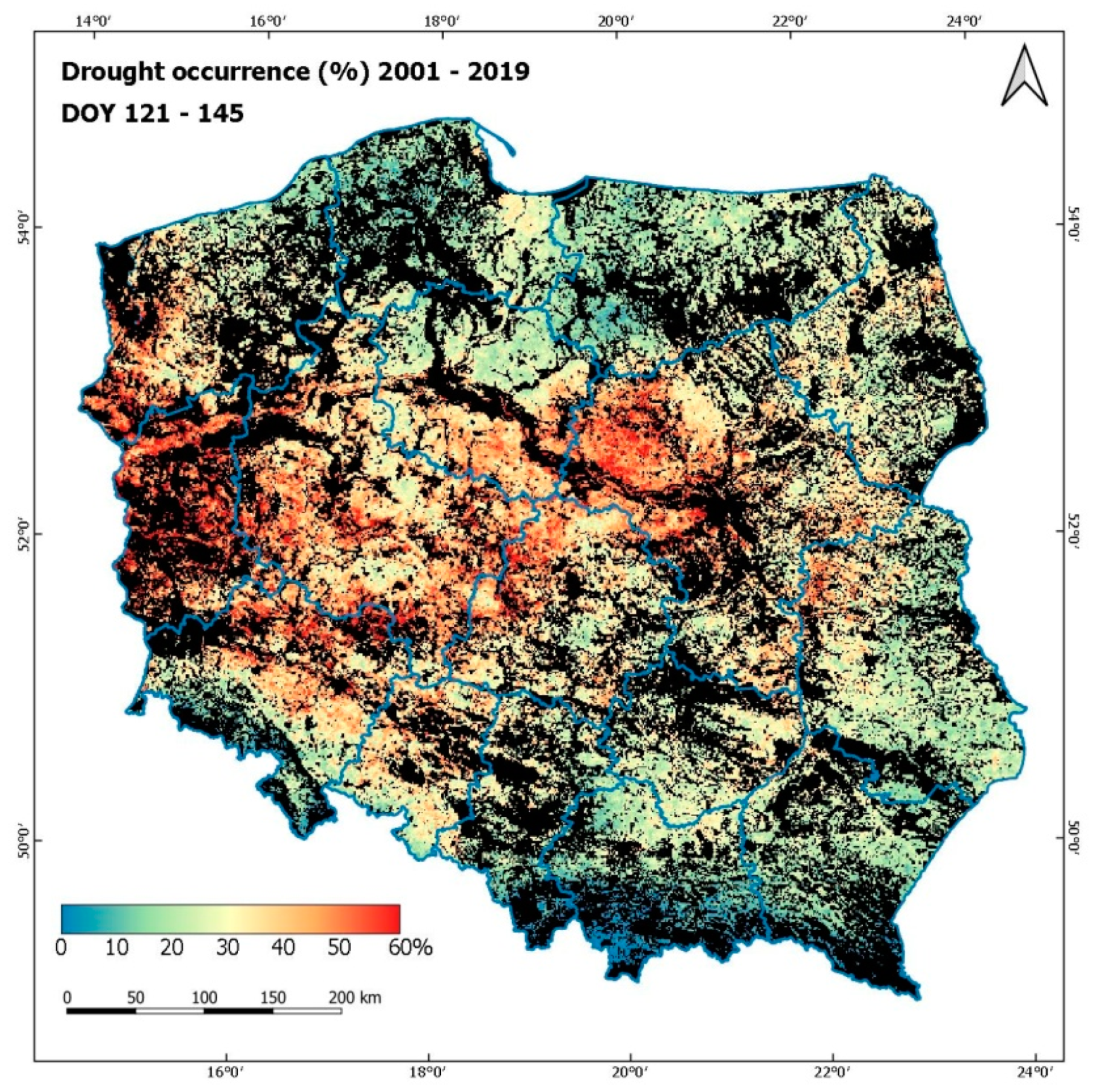
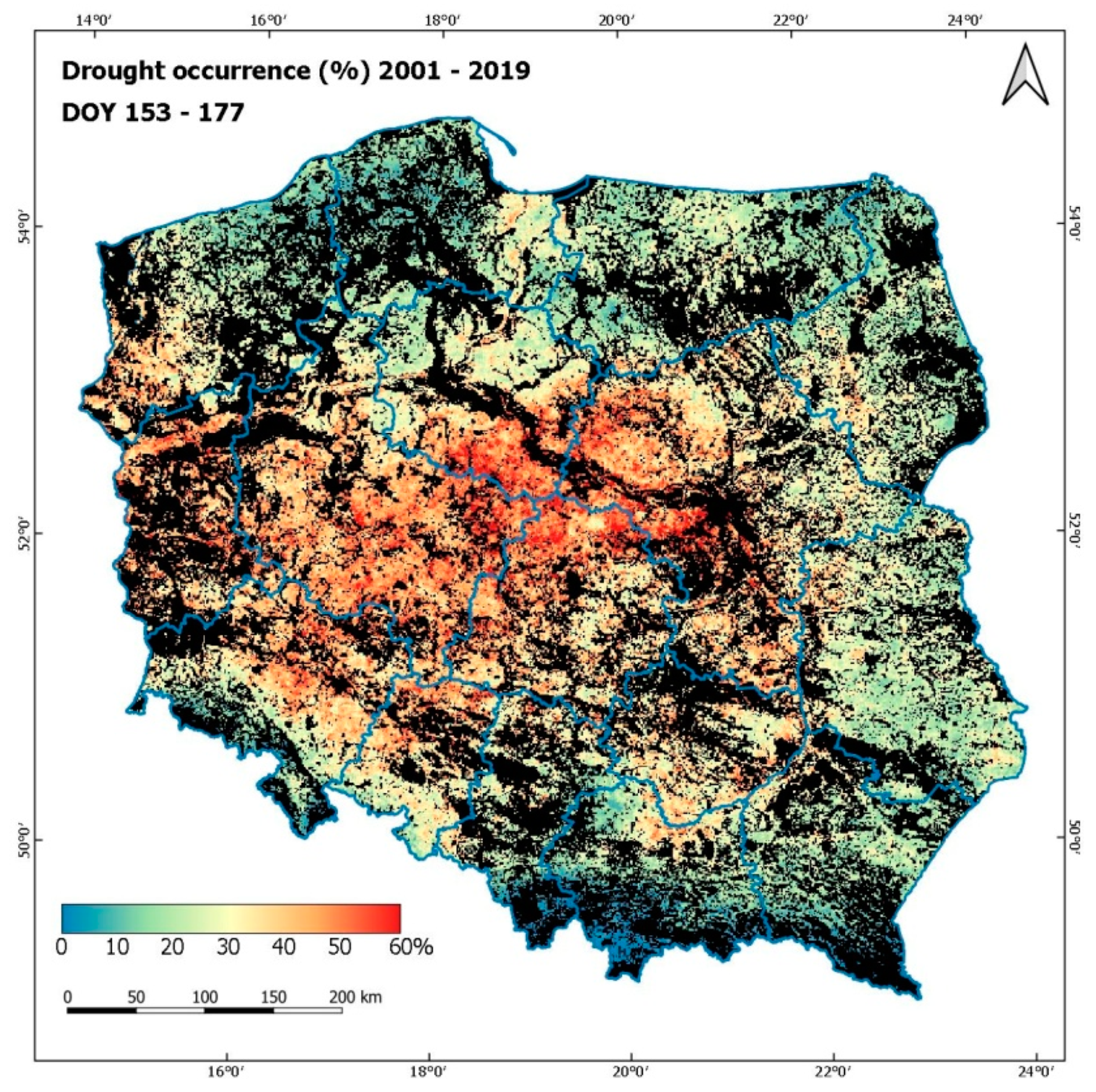
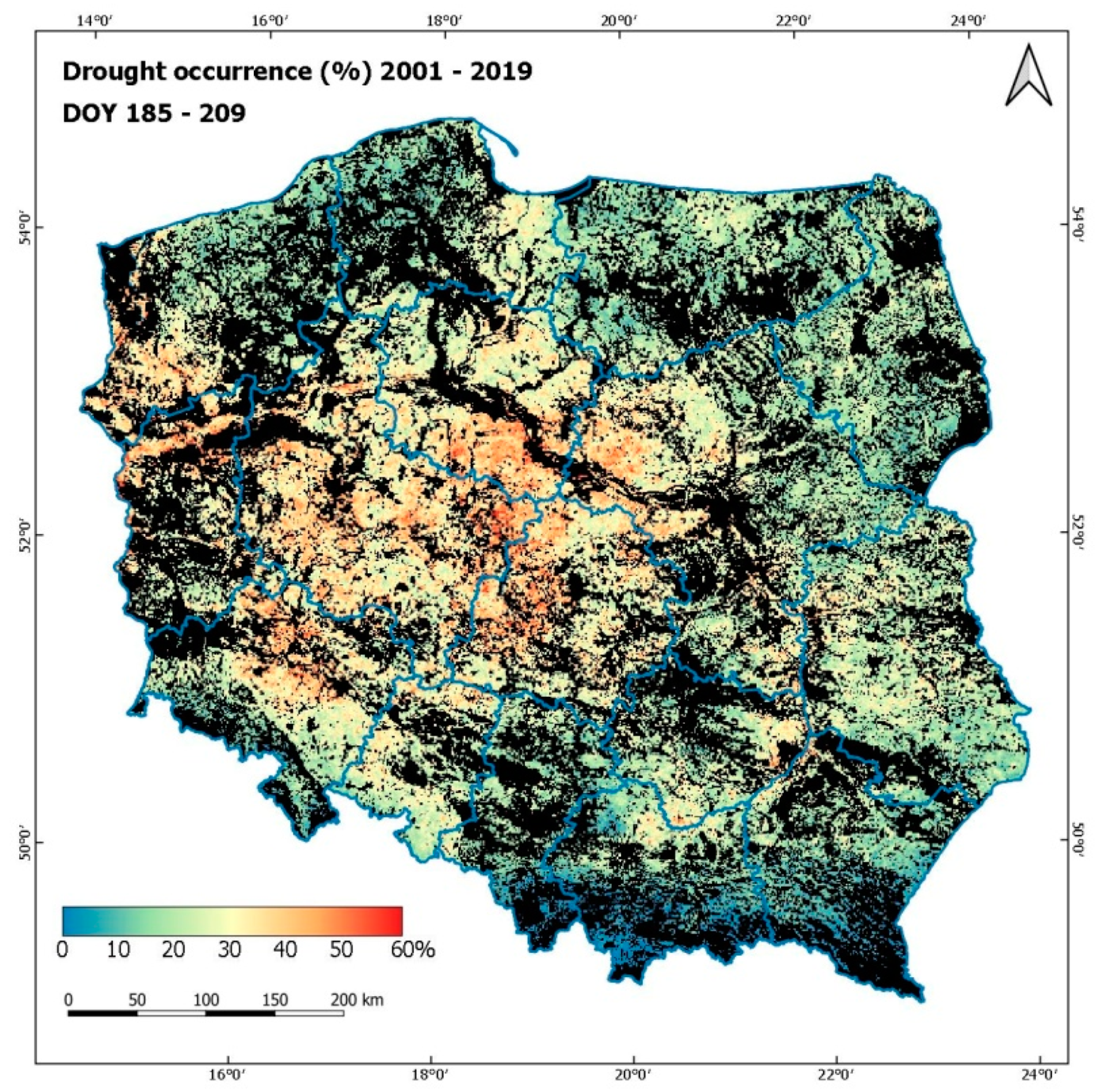
Maps of the percentage of drought occurrence can also be an effective tool for monitoring the changeability of drought conditions when prepared for important parts of the vegetation season. Such an analysis was carried in the course of this research; the maps of the percentage of drought occurrence were generated for three periods: May 1–May 24, June 3–June 26, and July 3–July 27 (presented in
Figure 26,
Figure 27 and
Figure 28, respectively).
The presented maps demonstrate that in the period covering May and June (
Figure 26 and
Figure 27, respectively), the area of the occurrence of drought in Poland is the highest. This period is critical for the development of cereals; such information is significant for agricultural producers, especially in regions of central and western Poland, where the occurrence of drought is the highest and the average duration is the longest.
4.3. General Discussion
The results from applying the present approach for estimating the occurrence of drought, based on utilizing the satellite-derived TCI and meteorological data, indicate that this approach is an effective tool for reliable assessment of drought hazards. Verification of the performance of the developed DISS drought index, conducted through a comparison of the extent of drought expressed by the area of drought in the analyzed region and the reduction in yield of the main crops revealed that there is a good statistical relationship between these two types of data. The figures of yield reduction obtained from the Central Statistical office suggest that the DISS index can be considered a good drought indicator. The relationship is particularly evident in the case of high yield reductions, as presented in
Figure 12 and
Figure 13.
The presented study also revealed that the intensity of drought estimated using the DISS drought index depends on the number of lags of TCI used in the DISS formula. Applying a time lag to the TCI results in a better correlation with the HTC meteorological index, and so the satellite response to atmospheric drought is better described. This is explained by observations that the reaction of vegetation to water shortage differs depending on the type of land cover, i.e., agricultural crops, grasslands, and forests. Applying DISS in versions of three, four, or four lags of TCI allows us to obtain information about drought suitable for particular vegetation environments. Our experience is that the application of three or four lags of TCI in the DISS formula is suitable to detect a water deficit within agricultural land and grasslands, which lasts, according to the HTC, 30–40 days. Application of five lags of TCI in the DISS formula is suitable to detect drought effects within forest areas, which are more resistant to drought, as a water deficit according to the HTC can last, in this case, 50 days. The period of satellite information is always shorter than the meteorological information because of the delayed response of vegetation to a lack of water.
The important asset of the presented approach is that it considers in the formula of DISS the variability of climatic conditions in the region through incorporation of the median of HTC. Such a solution allows us to adjust the values of the DISS index to local meteorological conditions characterized by levels of air temperature and precipitation.
5. Conclusions
The approach of assessing agricultural drought by the DISS index, developed at the Institute of Geodesy and Cartography, which is the fusion of meteorological and satellite data, combines, in one formula, both types of information, hence considering the variability in the environmental conditions expressed by HTC. HTC has been assumed as an atmospheric drought indicator; however, this study brought a better understanding of the relationship between water deficit characterized by the HTC index and the reaction of vegetation to the water deficit expressed by TCI calculated from MODIS data.
The DISS model is significant for its ability to derive drought information for local governments across different time scales. This information is important for decision-making at the local, regional, and national levels across multiple sectors such as agriculture, water resources, insurance, energy, and public health. The choice of the time scale for drought assessment (from 30 to 50 days, as presented) depends on the needs of the private and public sectors. Such information is important from an economic point of view; hence, satellite-based drought maps should start to be included as part of crop condition assessment systems at the farm level.
This study revealed that the percentage of drought area in the NUTS 2 regions detected by the DISS index corresponds to the level of yield reduction, especially for high yield reduction in the most important parts of the season of cereal growth (May–June). The central and western parts of Poland are usually heavily affected by the occurrence of drought and the longest drought duration, which is critical for the development of cereals. High yield reductions (i.e., over 30%) are clearly related, to a large extent, to drought for most of the growing season. Information on the areas where yield reduction occurs can serve as an indication for farmers on which crop they should grow, but also what kind of drought mitigation measures should be performed.
The DISS drought index should also have great importance in implementing adaptation and mitigation activities for agricultural areas related to the occurrence of drought. The model was validated only for Poland, applying data about the yield reduction. The spatial distribution of DISS was 1 km2, which is very important for the agriculture sector. In the future, the model will be tested for the global scale with the use of gridded meteorological data from models. Strong discussions are taking place in regional governments regarding the building of irrigation systems and the provision of capacity for local retention. Local retention is very important, as Poland is exposed to climate changes when drought frequently occurs.