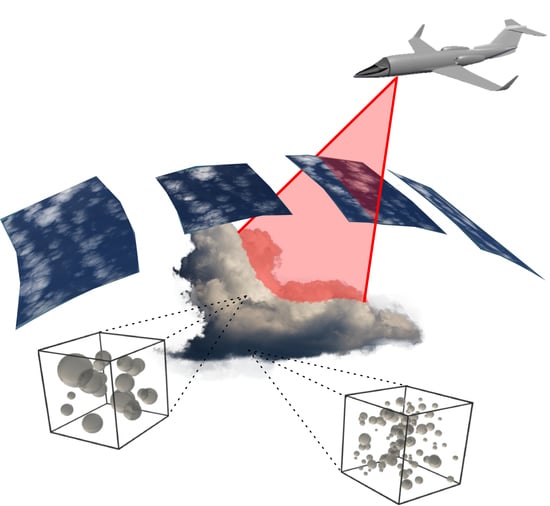
Multi-View Polarimetric Scattering Cloud Tomography and Retrieval of Droplet Size
Abstract
1. Motivation, Context & Outline
1.1. Why Polarized Light?
1.2. Why Passive Tomography?
1.3. Context
1.4. Outline
2. Theoretical Background
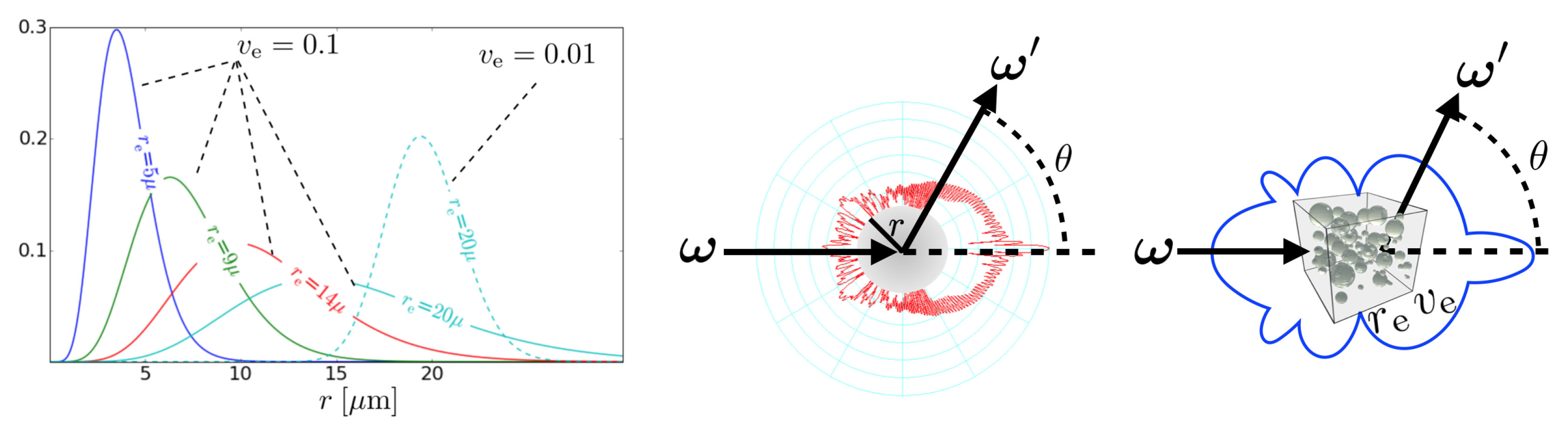
2.1. Scatterer Microphysical Properties
2.2. Single Scattering of Polarized Light
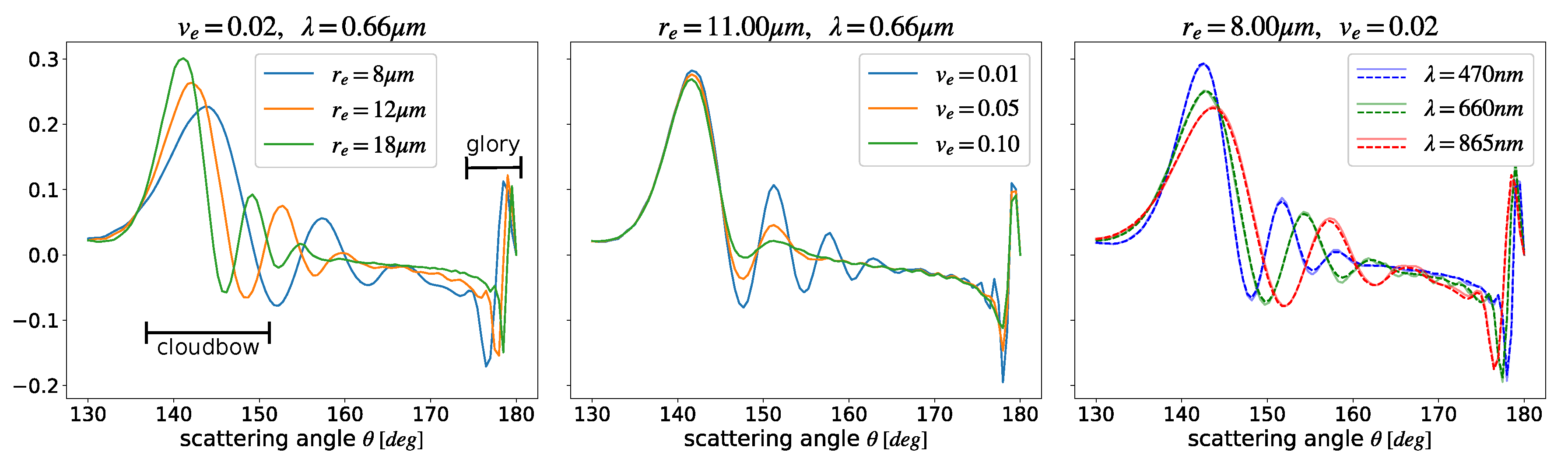
Mie Scattering
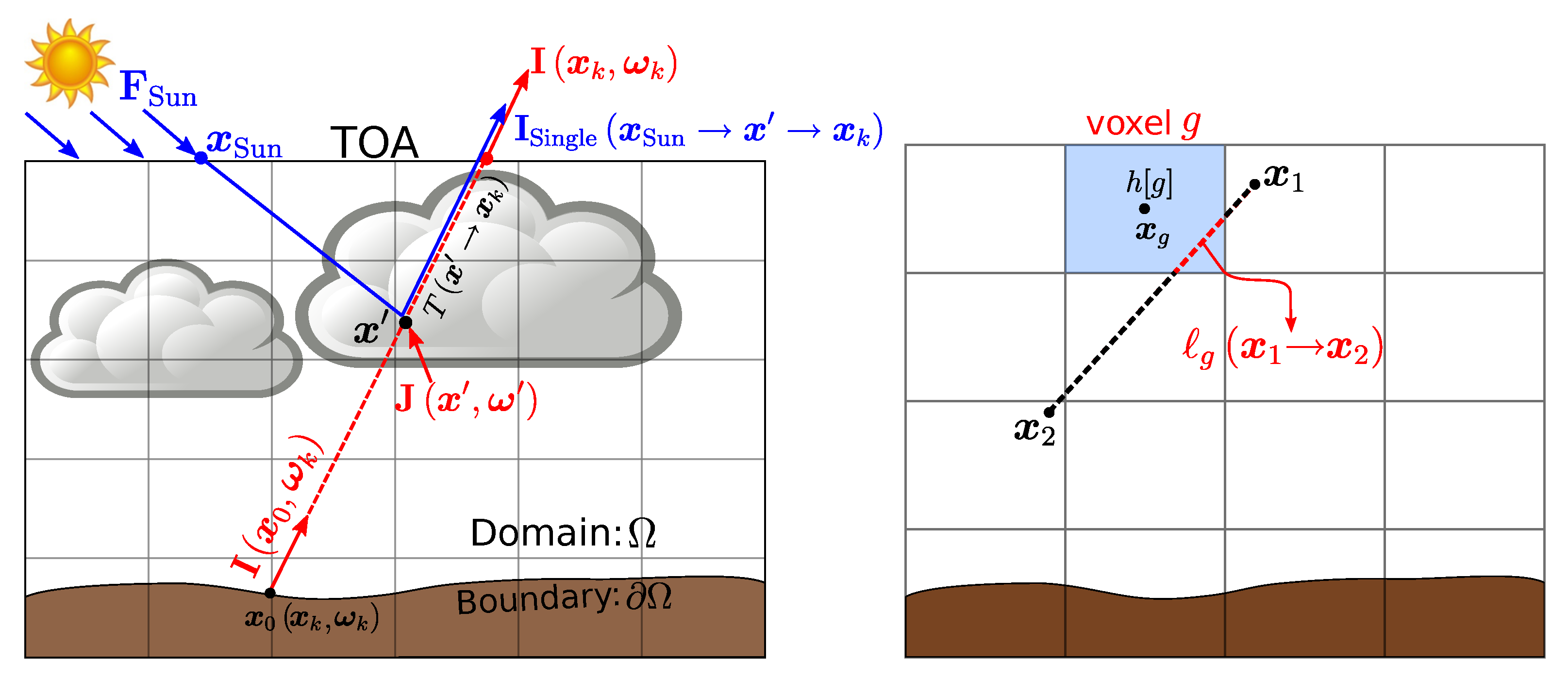
2.3. Multiple Scattering of Polarized Light
2.4. Single-Scattering Separation
2.5. Ray Tracing
3. Cloud Tomography
3.1. Polarimetric Information
3.2. Inverse Problem Formulation
3.3. Iterative Solution Approach
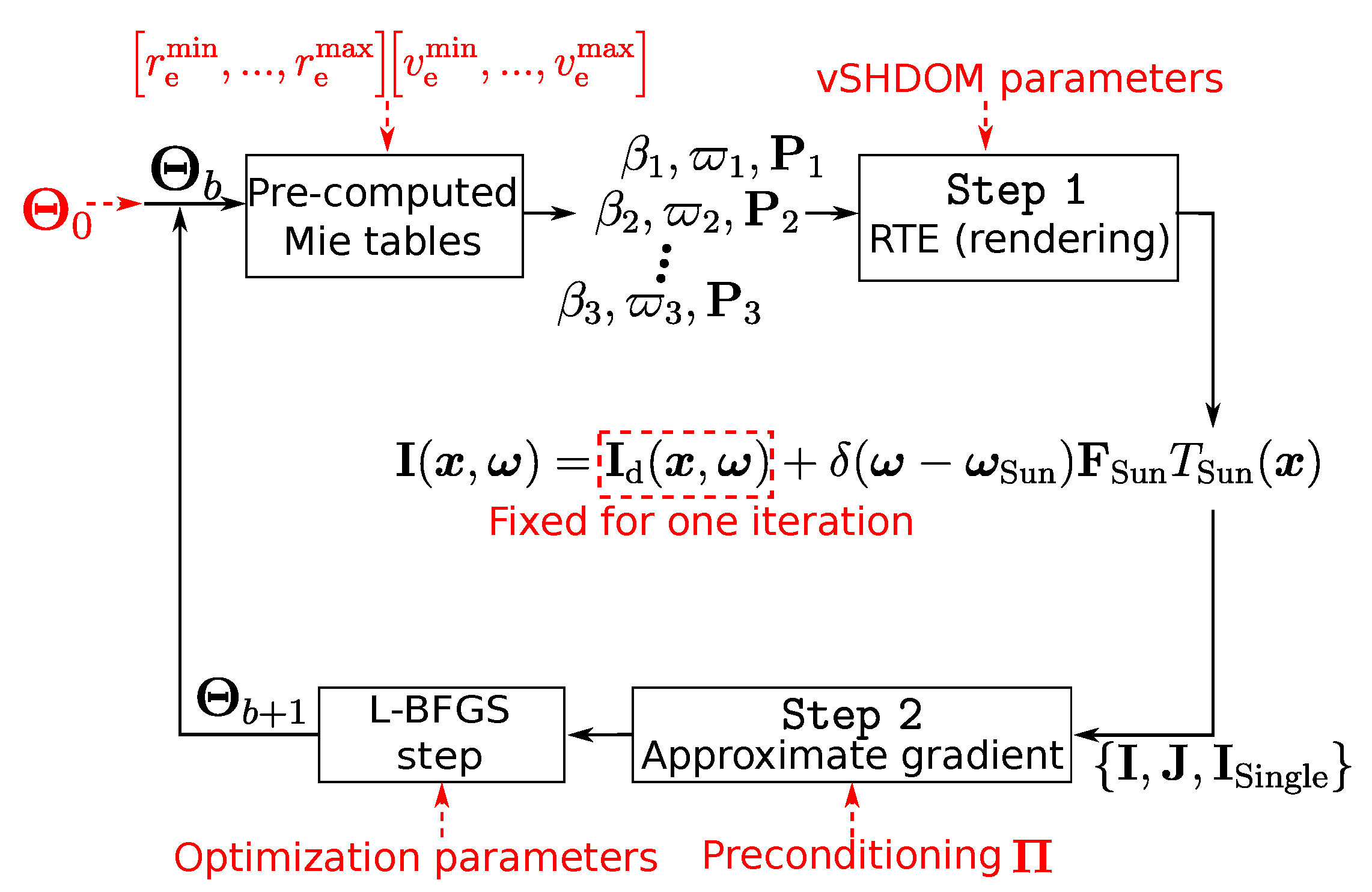
Step 1: RTE Forward Model
Step 2: Approximate Jacobian Computation
4. Computational Efficiency
5. Simulations
6. Discussion
7. Summary & Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Extended Theoretical Background
Appendix A.1. Scatterer Microphysical Properties
Appendix A.2. Polarized Light
Appendix A.3. Single Scattering of Polarized Light
Appendix A.3.1. Rayleigh Scattering
Appendix A.3.2. Mie Scattering
Appendix B. Jacobian Derivation
Appendix C. Measurement Noise

| 4.472 | 3.081 | 2.284 | 1.0 | 0.27 | 0.03 | 0.009 |
Appendix D. Numerical Considerations
Appendix D.1. Hyper-Parameters
Appendix D.2. Preconditioning
Appendix D.3. Initialization
- Each image is segmented into potentially cloudy and non-cloudy pixels (we use a simple radiance threshold).
- From each camera viewpoint, each potentially cloudy pixel back-projects a ray into the 3D domain. Voxels that this ray crosses are voted as potentially cloudy.
- Voxels which accumulate “cloudy” votes in at least 8 out of the 9 AirMSPI viewpoints are marked as cloudy.
Appendix D.4. Convergence
References
- Trenberth, K.E.; Fasullo, J.T.; Kiehl, J. Earth’s global energy budget. Bull. Am. Meteorol. Soc. 2009, 90, 311–324. [Google Scholar] [CrossRef]
- Boucher, O.; Randall, D.; Artaxo, P.; Bretherton, C.; Feingold, G.; Forster, P.; Kerminen, V.M.; Kondo, Y.; Liao, H.; Lohmann, U.; et al. Clouds and aerosols. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013; pp. 571–657. [Google Scholar]
- Rosenfeld, D.; Lensky, I.M. Satellite-based insights into precipitation formation processes in continental and maritime convective clouds. Bull. Am. Meteorol. Soc. 1998, 79, 2457–2476. [Google Scholar] [CrossRef]
- Platnick, S.; King, M.; Ackerman, S.; Menzel, W.; Baum, B.; Riedi, J.; Frey, R. The MODIS cloud products: Algorithms and examples from Terra. IEEE Trans. Geosci. Remote Sens. 2003, 41, 459–473. [Google Scholar] [CrossRef]
- Marshak, A.; Platnick, S.; Várnai, T.; Wen, G.; Cahalan, R.F. Impact of three-dimensional radiative effects on satellite retrievals of cloud droplet sizes. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Cho, H.M.; Zhang, Z.; Meyer, K.; Lebsock, M.; Platnick, S.; Ackerman, A.S.; Di Girolamo, L.; C.-Labonnote, L.; Cornet, C.; Riedi, J.; et al. Frequency and causes of failed MODIS cloud property retrievals for liquid phase clouds over global oceans. J. Geophys. Res. Atmos. 2015, 120, 4132–4154. [Google Scholar] [CrossRef]
- National Academies of Sciences, Engineering, and Medicine. Thriving on Our Changing Planet: A Decadal Strategy for Earth Observation from Space; The National Academies Press: Washington, DC, USA, 2018. [Google Scholar]
- Schilling, K.; Schechner, Y.Y.; Koren, I. CloudCT—computed tomography of clouds by a small satellite formation. In Proceedings of the IAA Symposium on Small Satellites for Earth Observation, Berlin, Germany, 6–10 May 2019. [Google Scholar]
- Nakajima, T.; King, M.D. Determination of the optical thickness and effective particle radius of clouds from reflected solar radiation measurements. Part I: Theory. J. Atmos. Sci. 1990, 47, 1878–1893. [Google Scholar] [CrossRef]
- Deschamps, P.Y.; Bréon, F.M.; Leroy, M.; Podaire, A.; Bricaud, A.; Buriez, J.C.; Seze, G. The POLDER mission: Instrument characteristics and scientific objectives. IEEE Trans. Geosci. Remote. Sens. 1994, 32, 598–615. [Google Scholar] [CrossRef]
- Bréon, F.M.; Goloub, P. Cloud droplet effective radius from spaceborne polarization measurements. Geophys. Res. Lett. 1998, 25, 1879–1882. [Google Scholar] [CrossRef]
- Kalashnikova, O.V.; Garay, M.J.; Davis, A.B.; Diner, D.J.; Martonchik, J.V. Sensitivity of multi-angle photo-polarimetry to vertical layering and mixing of absorbing aerosols: Quantifying measurement uncertainties. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 2149–2163. [Google Scholar] [CrossRef]
- Lukashin, C.; Wielicki, B.A.; Young, D.F.; Thome, K.; Jin, Z.; Sun, W. Uncertainty estimates for imager reference inter-calibration with CLARREO reflected solar spectrometer. IEEE Trans. Geosci. Remote. Sens. 2013, 51, 1425–1436. [Google Scholar] [CrossRef]
- Diner, D.; Xu, F.; Garay, M.; Martonchik, J.; Rheingans, B.; Geier, S.; Davis, A.; Hancock, B.; Jovanovic, V.; Bull, M.; et al. The Airborne Multiangle SpectroPolarimetric Imager (AirMSPI): A new tool for aerosol and cloud remote sensing. Atmos. Meas. Tech. 2013, 6, 2007–2025. [Google Scholar] [CrossRef]
- Diner, D.J.; Boland, S.W.; Brauer, M.; Bruegge, C.; Burke, K.A.; Chipman, R.; Di Girolamo, L.; Garay, M.J.; Hasheminassab, S.; Hyer, E.; et al. Advances in multiangle satellite remote sensing of speciated airborne particulate matter and association with adverse health effects: From MISR to MAIA. J. Appl. Remote. Sens. 2018, 12, 042603. [Google Scholar] [CrossRef]
- Martins, J.V.; Nielsen, T.; Fish, C.; Sparr, L.; Fernandez-Borda, R.; Schoeberl, M.; Remer, L. HARP CubeSat–An innovative hyperangular imaging polarimeter for earth science applications. In Proceedings of the Small Sat Pre-Conference Workshop, Logan, UT, USA, 3 August 2014; Volume 20. [Google Scholar]
- Emde, C.; Barlakas, V.; Cornet, C.; Evans, F.; Korkin, S.; Ota, Y.; Labonnote, L.C.; Lyapustin, A.; Macke, A.; Mayer, B.; et al. IPRT polarized radiative transfer model intercomparison project—Phase A. J. Quant. Spectrosc. Radiat. Transf. 2015, 164, 8–36. [Google Scholar] [CrossRef]
- Emde, C.; Barlakas, V.; Cornet, C.; Evans, F.; Wang, Z.; Labonotte, L.C.; Macke, A.; Mayer, B.; Wendisch, M. IPRT polarized radiative transfer model intercomparison project—Three-dimensional test cases (Phase B). J. Quant. Spectrosc. Radiat. Transf. 2018, 209, 19–44. [Google Scholar] [CrossRef]
- Kak, A.; Slaney, M. Principles of Computerized Tomographic Imaging IEEE Press; IEEE Press: Piscataway, NJ, USA, 1988. [Google Scholar]
- Gordon, R.; Bender, R.; Herman, G.T. Algebraic reconstruction techniques (ART) for three-dimensional electron microscopy and X-ray photography. J. Theor. Biol. 1970, 29, 471–481. [Google Scholar] [CrossRef]
- Marshak, A.; Davis, A.; Cahalan, R.; Wiscombe, W. Nonlocal independent pixel approximation: Direct and inverse problems. IEEE Trans. Geosci. Remote. Sens. 1998, 36, 192–204. [Google Scholar] [CrossRef]
- Faure, T.; Isaka, H.; Guillemet, B. Neural network retrieval of cloud parameters of inhomogeneous and fractional clouds: Feasibility study. Remote Sens. Environ. 2001, 77, 123–138. [Google Scholar] [CrossRef]
- Faure, T.; Isaka, H.; Guillemet, B. Neural network retrieval of cloud parameters from high-resolution multispectral radiometric data: A feasibility study. Remote Sens. Environ. 2002, 80, 285–296. [Google Scholar] [CrossRef]
- Cornet, C.; Isaka, H.; Guillemet, B.; Szczap, F. Neural network retrieval of cloud parameters of inhomogeneous clouds from multispectral and multiscale radiance data: Feasibility study. J. Geophys. Res. Atmos. 2004, 109, D12203. [Google Scholar] [CrossRef]
- Zinner, T.; Mayer, B.; Schröder, M. Determination of three-dimensional cloud structures from high-resolution radiance data. J. Geophys. Res. Atmos. 2006, 111, D08204. [Google Scholar] [CrossRef]
- Iwabuchi, H.; Hayasaka, T. A multi-spectral non-local method for retrieval of boundary layer cloud properties from optical remote sensing data. Remote Sens. Environ. 2003, 88, 294–308. [Google Scholar] [CrossRef]
- Diner, D.J.; Beckert, J.C.; Reilly, T.H.; Bruegge, C.J.; Conel, J.E.; Kahn, R.A.; Martonchik, J.V.; Ackerman, T.P.; Davies, R.; Gerstl, S.A.W.; et al. Multi-angle Imaging SpectroRadiometer (MISR) instrument description and experiment overview. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1072–1087. [Google Scholar] [CrossRef]
- Marchand, R.; Ackerman, T. Evaluation of radiometric measurements from the NASA Multiangle Imaging SpectroRadiometer (MISR): Two-and three-dimensional radiative transfer modeling of an inhomogeneous stratocumulus cloud deck. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Seiz, G.; Davies, R. Reconstruction of cloud geometry from multi-view satellite images. Remote. Sens. Environ. 2006, 100, 143–149. [Google Scholar] [CrossRef]
- Cornet, C.; Davies, R. Use of MISR measurements to study the radiative transfer of an isolated convective cloud: Implications for cloud optical thickness retrieval. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Evans, K.F.; Marshak, A.; Várnai, T. The Potential for Improved Boundary Layer Cloud Optical Depth Retrievals from the Multiple Directions of MISR. J. Atmos. Sci. 2008, 65, 3179–3196. [Google Scholar] [CrossRef]
- Romps, D.M.; Öktem, R. Observing Clouds in 4D with Multiview Stereophotogrammetry. Bull. Am. Meteorol. Soc. 2018, 99, 2575–2586. [Google Scholar] [CrossRef]
- Castro, E.; Ishida, T.; Takahashi, Y.; Kubota, H.; Perez, G.J.; Marciano, J.S. Determination of cloud-top Height through three-dimensional cloud Reconstruction using DIWATA-1 Data. Sci. Rep. 2020, 10, 1–13. [Google Scholar] [CrossRef]
- Alexandrov, M.D.; Cairns, B.; Emde, C.; Ackerman, A.S.; Ottaviani, M.; Wasilewski, A.P. Derivation of cumulus cloud dimensions and shape from the airborne measurements by the Research Scanning Polarimeter. Remote Sens. Environ. 2016, 177, 144–152. [Google Scholar] [CrossRef]
- Lee, B.; Di Girolamo, L.; Zhao, G.; Zhan, Y. Three-Dimensional Cloud Volume Reconstruction from the Multi-angle Imaging SpectroRadiometer. Remote Sens. 2018, 10, 1858. [Google Scholar] [CrossRef]
- Yu, H.; Ma, J.; Ahmad, S.; Sun, E.; Li, C.; Li, Z.; Hong, J. Three-Dimensional Cloud Structure Reconstruction from the Directional Polarimetric Camera. Remote Sens. 2019, 11, 2894. [Google Scholar] [CrossRef]
- Veikherman, D.; Aides, A.; Schechner, Y.Y.; Levis, A. Clouds in The Cloud. In Proceedings of the Asian Conference on Computer Vision (ACCV), Singapore, 1–5 November 2014; pp. 659–674. [Google Scholar]
- Zinner, T.; Marshak, A.; Lang, S.; Martins, J.V.; Mayer, B. Remote sensing of cloud sides of deep convection: Towards a three-dimensional retrieval of cloud particle size profiles. Atmos. Chem. Phys. 2008, 8, 4741–4757. [Google Scholar] [CrossRef]
- Alexandrov, M.D.; Miller, D.J.; Rajapakshe, C.; Fridlind, A.; van Diedenhoven, B.; Cairns, B.; Ackerman, A.S.; Zhang, Z. Vertical profiles of droplet size distributions derived from cloud-side observations by the research scanning polarimeter: Tests on simulated data. Atmos. Res. 2020, 239, 104924. [Google Scholar] [CrossRef] [PubMed]
- Okamura, R.; Iwabuchi, H.; Schmidt, K.S. Feasibility study of multi-pixel retrieval of optical thickness and droplet effective radius of inhomogeneous clouds using deep learning. Atmos. Meas. Tech. 2017, 10, 4747–4759. [Google Scholar] [CrossRef]
- Masuda, R.; Iwabuchi, H.; Schmidt, K.S.; Damiani, A.; Kudo, R. Retrieval of Cloud Optical Thickness from Sky-View Camera Images using a Deep Convolutional Neural Network based on Three-Dimensional Radiative Transfer. Remote Sens. 2019, 11, 1962. [Google Scholar] [CrossRef]
- Liou, K.N.; Ou, S.C.; Takano, Y.; Roskovensky, J.; Mace, G.G.; Sassen, K.; Poellot, M. Remote sensing of three-dimensional inhomogeneous cirrus clouds using satellite and mm-wave cloud radar data. Geophys. Res. Lett. 2002, 29, 1360. [Google Scholar] [CrossRef]
- Barker, H.; Jerg, M.; Wehr, T.; Kato, S.; Donovan, D.; Hogan, R. A 3D cloud-construction algorithm for the EarthCARE satellite mission. Q. J. R. Meteorol. Soc. 2011, 137, 1042–1058. [Google Scholar] [CrossRef]
- Fielding, M.D.; Chiu, J.C.; Hogan, R.J.; Feingold, G. A novel ensemble method for retrieving properties of warm cloud in 3-D using ground-based scanning radar and zenith radiances. J. Geophys. Res. Atmos. 2014, 119, 10–912. [Google Scholar] [CrossRef]
- Hasmonay, R.A.; Yost, M.G.; Wu, C.F. Computed tomography of air pollutants using radial scanning path-integrated optical remote sensing. Atmos. Environ. 1999, 33, 267–274. [Google Scholar] [CrossRef]
- Todd, L.A.; Ramanathan, M.; Mottus, K.; Katz, R.; Dodson, A.; Mihlan, G. Measuring chemical emissions using an open-path Fourier transform infrared (OP-FTIR) spectroscopy and computer-assisted tomography. Atmos. Environ. 2001, 35, 1937–1947. [Google Scholar] [CrossRef]
- Kazahaya, R.; Mori, T.; Kazahaya, K.; Hirabayashi, J. Computed tomography reconstruction of SO2 concentration distribution in the volcanic plume of Miyakejima, Japan, by airborne traverse technique using three UV spectrometers. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Wright, T.E.; Burton, M.; Pyle, D.M.; Caltabiano, T. Scanning tomography of SO2 distribution in a volcanic gas plume. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Warner, J.; Drake, J.; Snider, J. Liquid water distribution obtained from coplanar scanning radiometers. J. Atmos. Ocean. Technol. 1986, 3, 542–546. [Google Scholar] [CrossRef]
- Huang, D.; Liu, Y.; Wiscombe, W. Determination of cloud liquid water distribution using 3D cloud tomography. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Huang, D.; Liu, Y.; Wiscombe, W. Cloud tomography: Role of constraints and a new algorithm. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Garay, M.J.; Davis, A.B.; Diner, D.J. Tomographic reconstruction of an aerosol plume using passive multiangle observations from the MISR satellite instrument. Geophys. Res. Lett. 2016, 43, 12–590. [Google Scholar] [CrossRef]
- Aides, A.; Schechner, Y.Y.; Holodovsky, V.; Garay, M.J.; Davis, A.B. Multi-sky-view 3D aerosol distribution recovery. Opt. Express 2013, 21, 25820–25833. [Google Scholar] [CrossRef]
- Geva, A.; Schechner, Y.Y.; Chernyak, Y.; Gupta, R. X-ray computed tomography through scatter. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 34–50. [Google Scholar]
- Arridge, S.R. Optical tomography in medical imaging. Inverse Probl. 1999, 15, R41. [Google Scholar] [CrossRef]
- Boas, D.A.; Brooks, D.H.; Miller, E.L.; DiMarzio, C.A.; Kilmer, M.; Gaudette, R.J.; Zhang, Q. Imaging the body with diffuse optical tomography. IEEE Signal Process. Mag. 2001, 18, 57–75. [Google Scholar] [CrossRef]
- Arridge, S.R.; Schotland, J.C. Optical tomography: Forward and inverse problems. Inverse Probl. 2009, 25, 123010. [Google Scholar] [CrossRef]
- Che, C.; Luan, F.; Zhao, S.; Bala, K.; Gkioulekas, I. Inverse transport networks. arXiv 2018, arXiv:1809.10820. [Google Scholar]
- Evans, K.F. The spherical harmonics discrete ordinate method for three-dimensional atmospheric radiative transfer. J. Atmos. Sci. 1998, 55, 429–446. [Google Scholar] [CrossRef]
- Doicu, A.; Efremenko, D.; Trautmann, T. A multi-dimensional vector spherical harmonics discrete ordinate method for atmospheric radiative transfer. J. Quant. Spectrosc. Radiat. Transf. 2013, 118, 121–131. [Google Scholar] [CrossRef]
- Levis, A.; Schechner, Y.Y.; Aides, A.; Davis, A.B. Airborne three-dimensional cloud tomography. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 3379–3387. [Google Scholar]
- Holodovsky, V.; Schechner, Y.Y.; Levin, A.; Levis, A.; Aides, A. In-situ multi-view multi-scattering stochastic tomography. In Proceedings of the IEEE International Conference on Computational Photography (ICCP), Evanston, IL, USA, 13–14 May 2016; pp. 1–12. [Google Scholar]
- Levis, A.; Schechner, Y.Y.; Davis, A.B. Multiple-scattering microphysics tomography. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 6740–6749. [Google Scholar]
- Aides, A.; Levis, A.; Holodovsky, V.; Schechner, Y.Y.; Althausen, D.; Vainiger, A. Distributed Sky Imaging Radiometry and Tomography. In Proceedings of the IEEE International Conference on Computational Photography (ICCP), Saint Louis, MO, USA, 24–26 April 2020; pp. 1–12. [Google Scholar]
- Loeub, T.; Levis, A.; Holodovsky, V.; Schechner, Y.Y.; Chernyak, Y.; Gupta, R. Monotonicity Prior for Cloud Tomography. In Proceedings of the European Conference on Computer Vision (ECCV), Glasgow, Scotlang, 24–29 August 2020. [Google Scholar]
- Hansen, J.E. Multiple scattering of polarized light in planetary atmospheres, Part II. Sunlight reflected by terrestrial water clouds. J. Atmos. Sci. 1971, 28, 1400–1426. [Google Scholar] [CrossRef]
- Marshak, A.; Davis, A. 3D Radiative Transfer in Cloudy Atmospheres; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Chylek, P. Extinction and liquid water content of fogs and clouds. J. Atmos. Sci. 1978, 35, 296–300. [Google Scholar]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Chandrasekhar, S. Radiative Transfer; Oxford University Press: Oxford, UK, 1950. [Google Scholar]
- Mayer, B. Radiative transfer in the cloudy atmosphere. Eur. Phys. J. Conf. 2009, 1, 75–99. [Google Scholar] [CrossRef]
- Nakajima, T.; Tanaka, M. Algorithms for radiative intensity calculations in moderately thick atmospheres using a truncation approximation. J. Quant. Spectrosc. Radiat. Transf. 1988, 40, 51–69. [Google Scholar] [CrossRef]
- Zhu, C.; Byrd, R.H.; Lu, P.; Nocedal, J. Algorithm 778: L-BFGS-B: Fortran subroutines for large-scale bound-constrained optimization. ACM Trans. Math. Softw. 1997, 23, 550–560. [Google Scholar] [CrossRef]
- Doicu, A.; Efremenko, D.S. Linearizations of the Spherical Harmonic Discrete Ordinate Method (SHDOM). Atmosphere 2019, 10, 292. [Google Scholar] [CrossRef]
- Martin, W.; Cairns, B.; Bal, G. Adjoint methods for adjusting three-dimensional atmosphere and surface properties to fit multi-angle/multi-pixel polarimetric measurements. J. Quant. Spectrosc. Radiat. Transf. 2014, 144, 68–85. [Google Scholar] [CrossRef][Green Version]
- Martin, W.G.; Hasekamp, O.P. A demonstration of adjoint methods for multi-dimensional remote sensing of the atmosphere and surface. J. Quant. Spectrosc. Radiat. Transf. 2018, 204, 215–231. [Google Scholar] [CrossRef]
- Forster, L.; Davis, A.B.; Diner, D.J.; Mayer, B. Toward Cloud Tomography from Space using MISR and MODIS: Locating the “Veiled Core” in Opaque Convective Clouds. arXiv 2019, arXiv:1910.00077. [Google Scholar]
- Zhao, M.; Austin, P.H. Life cycle of numerically simulated shallow cumulus clouds. Part II: Mixing dynamics. J. Atmos. Sci. 2005, 62, 1291–1310. [Google Scholar] [CrossRef]
- Anderson, G.P.; Clough, S.A.; Kneizys, F.; Chetwynd, J.H.; Shettle, E.P. AFGL Atmospheric Constituent Profiles (0.120 km); Technical Report; Air Force Geophysics Lab: Hanscom AFB, MA, USA, 1986. [Google Scholar]
- Matheou, G.; Chung, D. Large-eddy simulation of stratified turbulence. Part 2: Application of the stretched-vortex model to the atmospheric boundary layer. J. Atmos. Sci. 2014, 71, 4439–4460. [Google Scholar] [CrossRef]
- Yau, M.K.; Rogers, R.R. A Short Course in Cloud Physics; Elsevier: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Seethala, C. Evaluating the State-Of-The-Art of and Errors in 1D Satellite Cloud Liquid Water Path Retrievals with Large Eddy Simulations and Realistic Radiative Transfer Models. Ph.D. Thesis, University of Hamburg, Hamburg, Germany, 2012. [Google Scholar]
- Ewald, F.; Zinner, T.; Kölling, T.; Mayer, B. Remote sensing of cloud droplet radius profiles using solar reflectance from cloud sides – Part 1: Retrieval development and characterization. Atmos. Meas. Tech. 2019, 12, 1183–1206. [Google Scholar] [CrossRef]
- Alexandrov, M.D.; Cairns, B.; Emde, C.; Ackerman, A.S.; van Diedenhoven, B. Accuracy assessments of cloud droplet size retrievals from polarized reflectance measurements by the research scanning polarimeter. Remote Sens. Environ. 2012, 125, 92–111. [Google Scholar] [CrossRef]
- Blyth, A.M.; Latham, J. A Climatological Parameterization for Cumulus Clouds. J. Atmos. Sci. 1991, 48, 2367–2371. [Google Scholar] [CrossRef]
- French, J.R.; Vali, G.; Kelly, R.D. Observations of microphysics pertaining to the development of drizzle in warm, shallow cumulus clouds. Q. J. R. Meteorol. Soc. 2000, 126, 415–443. [Google Scholar] [CrossRef]
- Gerber, H.E.; Frick, G.M.; Jensen, J.B.; Hudson, J.G. Entrainment, mixing, and microphysics in trade-wind cumulus. J. Meteorol. Soc. Jpn. Ser. II 2008, 86, 87–106. [Google Scholar] [CrossRef]
- Khain, P.; Heiblum, R.; Blahak, U.; Levi, Y.; Muskatel, H.; Vadislavsky, E.; Altaratz, O.; Koren, I.; Dagan, G.; Shpund, J.; et al. Parameterization of Vertical Profiles of Governing Microphysical Parameters of Shallow Cumulus Cloud Ensembles Using LES with Bin Microphysics. J. Atmos. Sci. 2019, 76, 533–560. [Google Scholar] [CrossRef]
- Pinsky, M.; Khain, A. Theoretical Analysis of the Entrainment–Mixing Process at Cloud Boundaries. Part I: Droplet Size Distributions and Humidity within the Interface Zone. J. Atmos. Sci. 2018, 75, 2049–2064. [Google Scholar] [CrossRef]
- Bera, S.; Prabha, T.V.; Grabowski, W.W. Observations of monsoon convective cloud microphysics over India and role of entrainment-mixing. J. Geophys. Res. Atmos. 2016, 121, 9767–9788. [Google Scholar] [CrossRef]
- Costa, A.A.; de Oliveira, C.J.; de Oliveira, J.C.P.; da Costa Sampaio, A.J. Microphysical observations of warm cumulus clouds in Ceara, Brazil. Atmos. Res. 2000, 54, 167–199. [Google Scholar] [CrossRef]
- Lu, M.L.; Feingold, G.; Jonsson, H.H.; Chuang, P.Y.; Gates, H.; Flagan, R.C.; Seinfeld, J.H. Aerosol-cloud relationships in continental shallow cumulus. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Martins, J.A.; Dias, M.A.F.S. The impact of smoke from forest fires on the spectral dispersion of cloud droplet size distributions in the Amazonian region. Environ. Res. Lett. 2009, 4, 015002. [Google Scholar] [CrossRef]
- Hudson, J.G.; Noble, S.; Jha, V. Cloud droplet spectral width relationship to CCN spectra and vertical velocity. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Pandithurai, G.; Dipu, S.; Prabha, T.V.; Maheskumar, R.S.; Kulkarni, J.R.; Goswami, B.N. Aerosol effect on droplet spectral dispersion in warm continental cumuli. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Igel, A.L.; van den Heever, S.C. The Importance of the Shape of Cloud Droplet Size Distributions in Shallow Cumulus Clouds. Part I: Bin Microphysics Simulations. J. Atmos. Sci. 2017, 74, 249–258. [Google Scholar] [CrossRef]
- Lu, M.L.; Seinfeld, J.H. Effect of aerosol number concentration on cloud droplet dispersion: A large-eddy simulation study and implications for aerosol indirect forcing. J. Geophys. Res. Atmos. 2006, 111, D02207. [Google Scholar] [CrossRef]
- Wang, X.; Xue, H.; Fang, W.; Zheng, G. A study of shallow cumulus cloud droplet dispersion by large eddy simulations. Acta Meteorol. Sin. 2011, 25, 166–175. [Google Scholar] [CrossRef]
- Milbrandt, J.A.; Yau, M.K. A Multimoment Bulk Microphysics Parameterization. Part I: Analysis of the Role of the Spectral Shape Parameter. J. Atmos. Sci. 2005, 62, 3051–3064. [Google Scholar] [CrossRef]
- Cairns, B.; Russell, E.E.; Travis, L.D. Research Scanning Polarimeter: Calibration and ground-based measurements. In Polarization: Measurement, Analysis, and Remote Sensing II; International Society for Optics and Photonics: Bellingham, WA, USA, 1999; Volume 3754, pp. 186–196. [Google Scholar]
- Levis, A.; Loveridge, J.; Aides, A. Pyshdom. 2020. Available online: https://github.com/aviadlevis/pyshdom (accessed on 1 January 2020).
- Sanghavi, S.; Davis, A.B.; Eldering, A. vSmartMOM: A vector matrix operator method-based radiative transfer model linearized with respect to aerosol properties. J. Quant. Spectrosc. Radiat. Transf. 2014, 133, 412–433. [Google Scholar] [CrossRef]
- Xu, F.; Davis, A.B. Derivatives of light scattering properties of a nonspherical particle computed with the T-matrix method. Opt. Lett. 2011, 36, 4464–4466. [Google Scholar] [CrossRef]
- Florescu, L.; Markel, V.A.; Schotland, J.C. Inversion formulas for the broken-ray Radon transform. Inverse Probl. 2011, 27, 025002. [Google Scholar] [CrossRef]
- Van Harten, G.; Diner, D.J.; Daugherty, B.J.; Rheingans, B.E.; Bull, M.A.; Seidel, F.C.; Chipman, R.A.; Cairns, B.; Wasilewski, A.P.; Knobelspiesse, K.D. Calibration and validation of Airborne Multiangle SpectroPolarimetric Imager (AirMSPI) polarization measurements. Appl. Opt. 2018, 57, 4499–4513. [Google Scholar] [CrossRef]
- Pincus, R.; Evans, K.F. Computational cost and accuracy in calculating three-dimensional radiative transfer: Results for new implementations of Monte Carlo and SHDOM. J. Atmos. Sci. 2009, 66, 3131–3146. [Google Scholar] [CrossRef]
- Scipy. L-BFGS-B. 2020. Available online: https://docs.scipy.org/doc/scipy/reference/optimize.minimize-lbfgsb.html (accessed on 1 January 2020).





© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Levis, A.; Schechner, Y.Y.; Davis, A.B.; Loveridge, J. Multi-View Polarimetric Scattering Cloud Tomography and Retrieval of Droplet Size. Remote Sens. 2020, 12, 2831. https://doi.org/10.3390/rs12172831
Levis A, Schechner YY, Davis AB, Loveridge J. Multi-View Polarimetric Scattering Cloud Tomography and Retrieval of Droplet Size. Remote Sensing. 2020; 12(17):2831. https://doi.org/10.3390/rs12172831
Chicago/Turabian StyleLevis, Aviad, Yoav Y. Schechner, Anthony B. Davis, and Jesse Loveridge. 2020. "Multi-View Polarimetric Scattering Cloud Tomography and Retrieval of Droplet Size" Remote Sensing 12, no. 17: 2831. https://doi.org/10.3390/rs12172831
APA StyleLevis, A., Schechner, Y. Y., Davis, A. B., & Loveridge, J. (2020). Multi-View Polarimetric Scattering Cloud Tomography and Retrieval of Droplet Size. Remote Sensing, 12(17), 2831. https://doi.org/10.3390/rs12172831