The Greening and Wetting of the Sahel Have Leveled off since about 1999 in Relation to SST
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.2. The Sahel Extension, Growing/Rainy Seasons, and the SST Indices
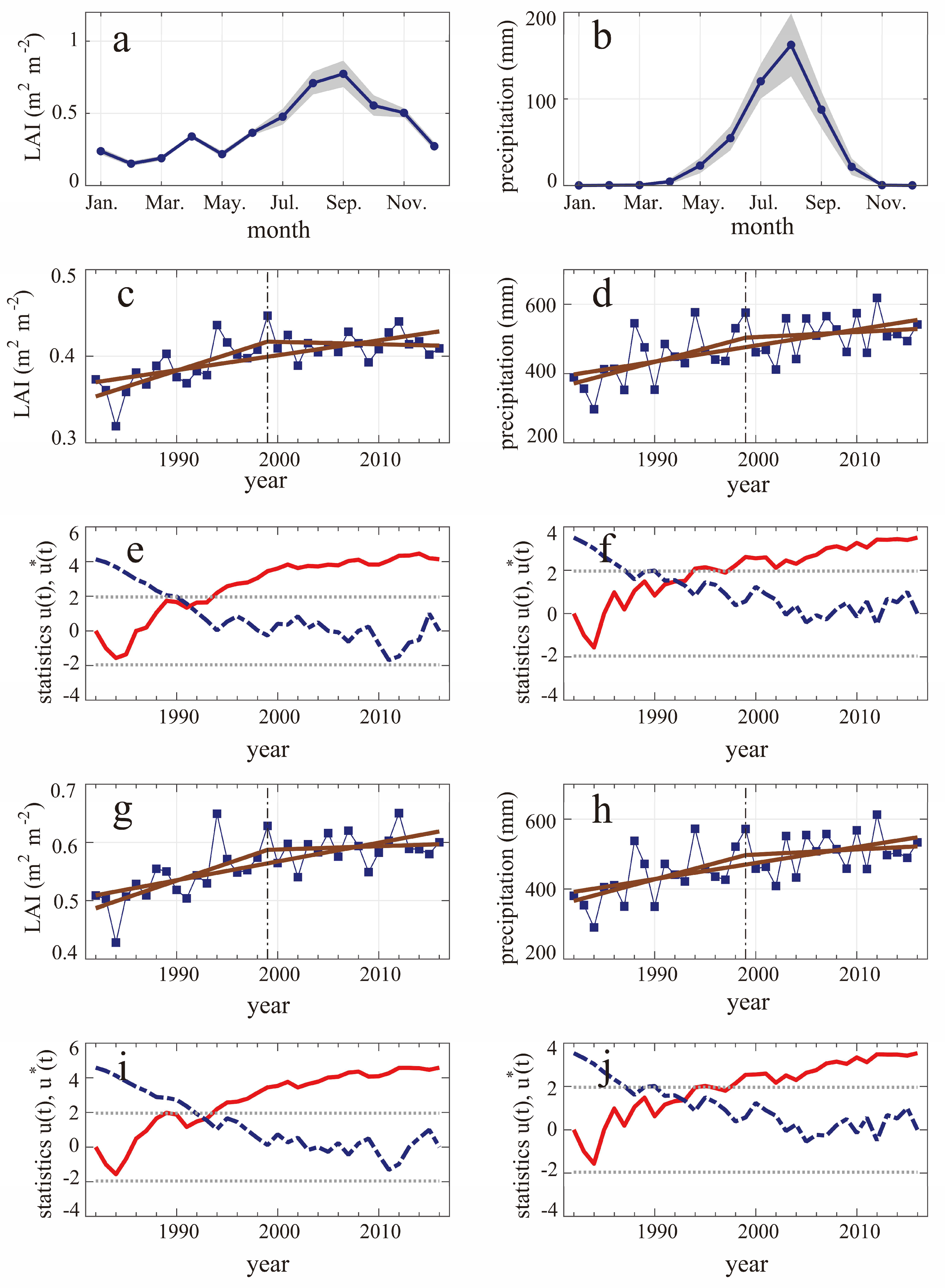
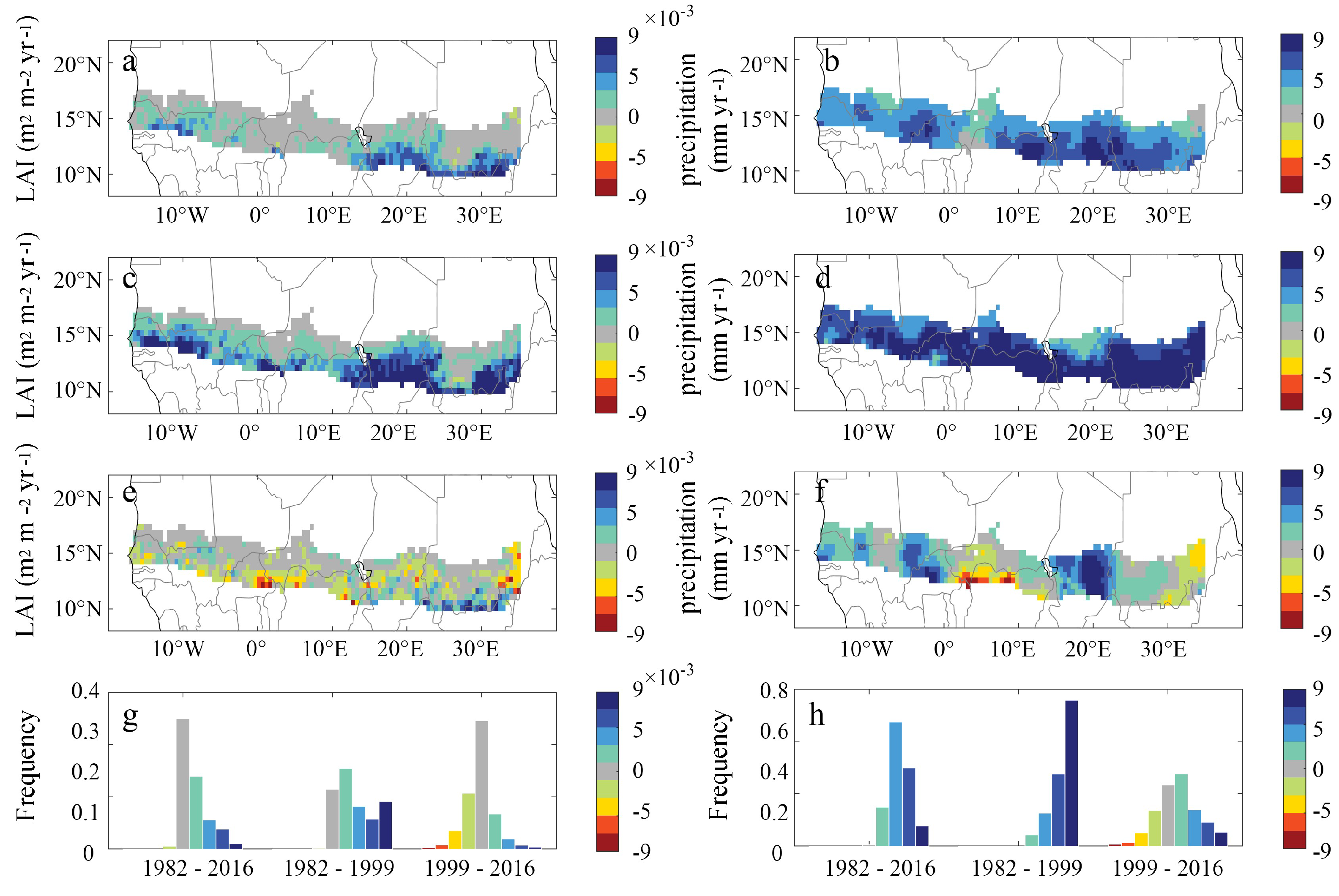
2.3. Trend Analysis
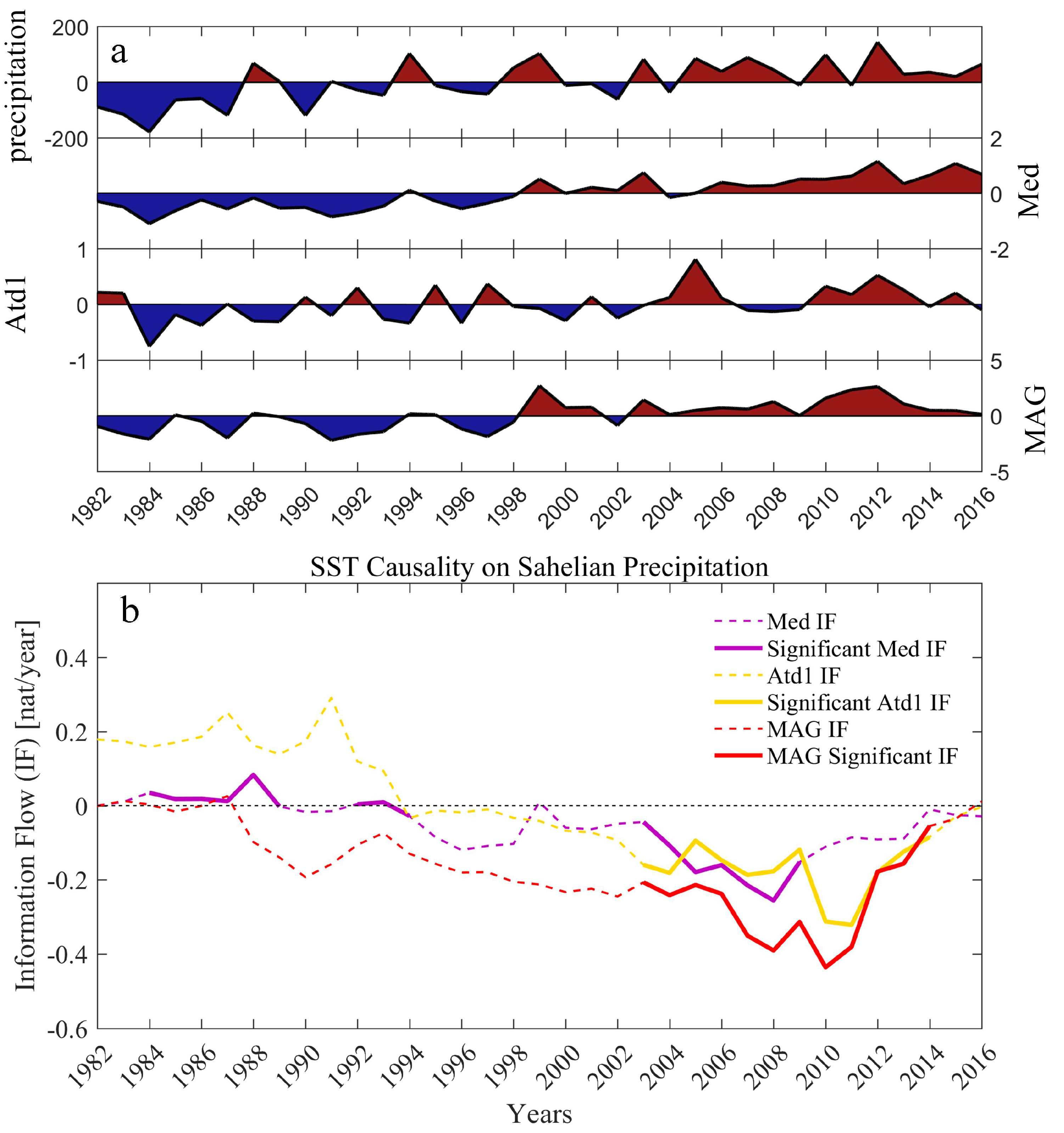
2.4. Teleconnection Analysis between SST and Precipitation
3. Results
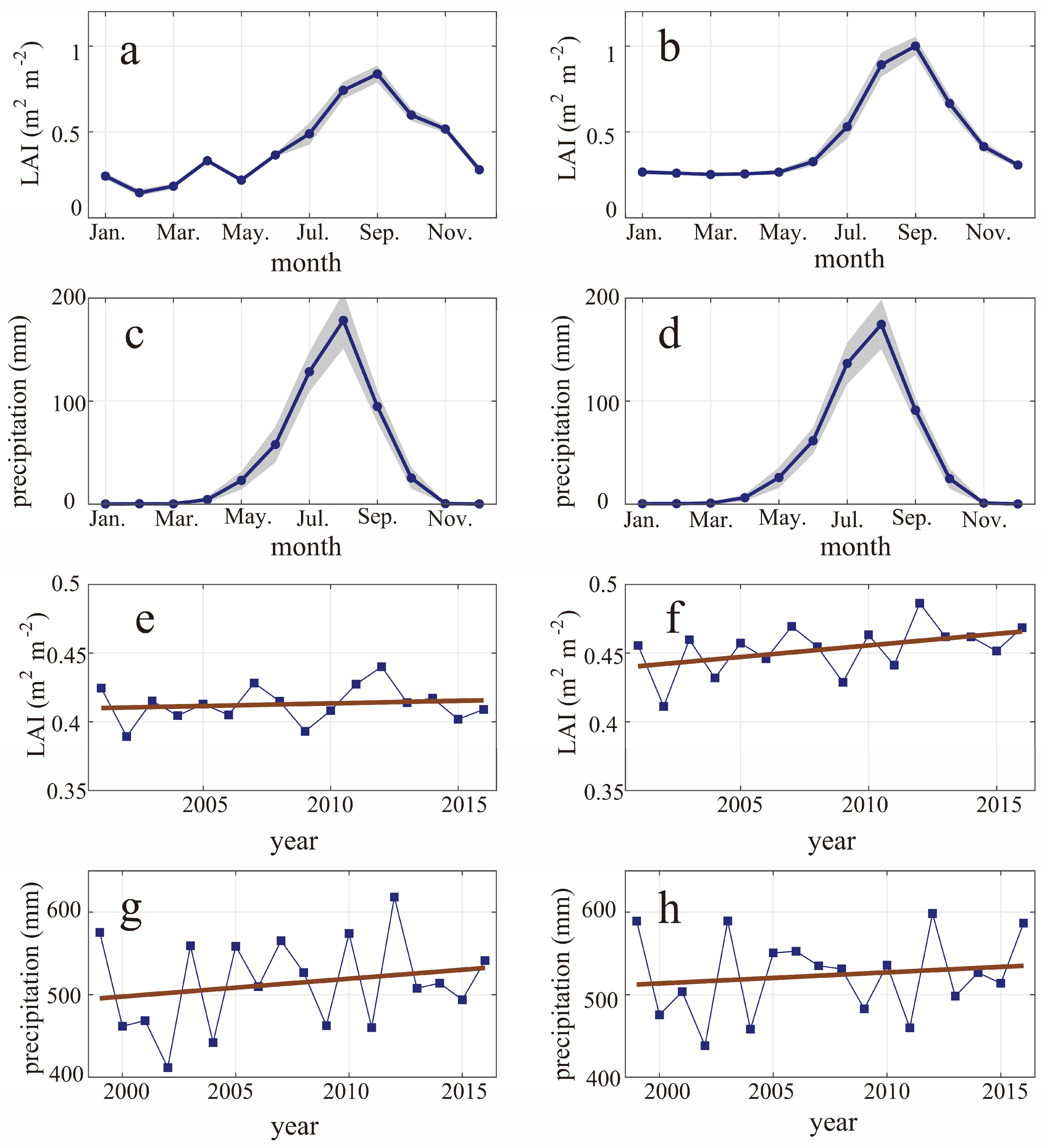
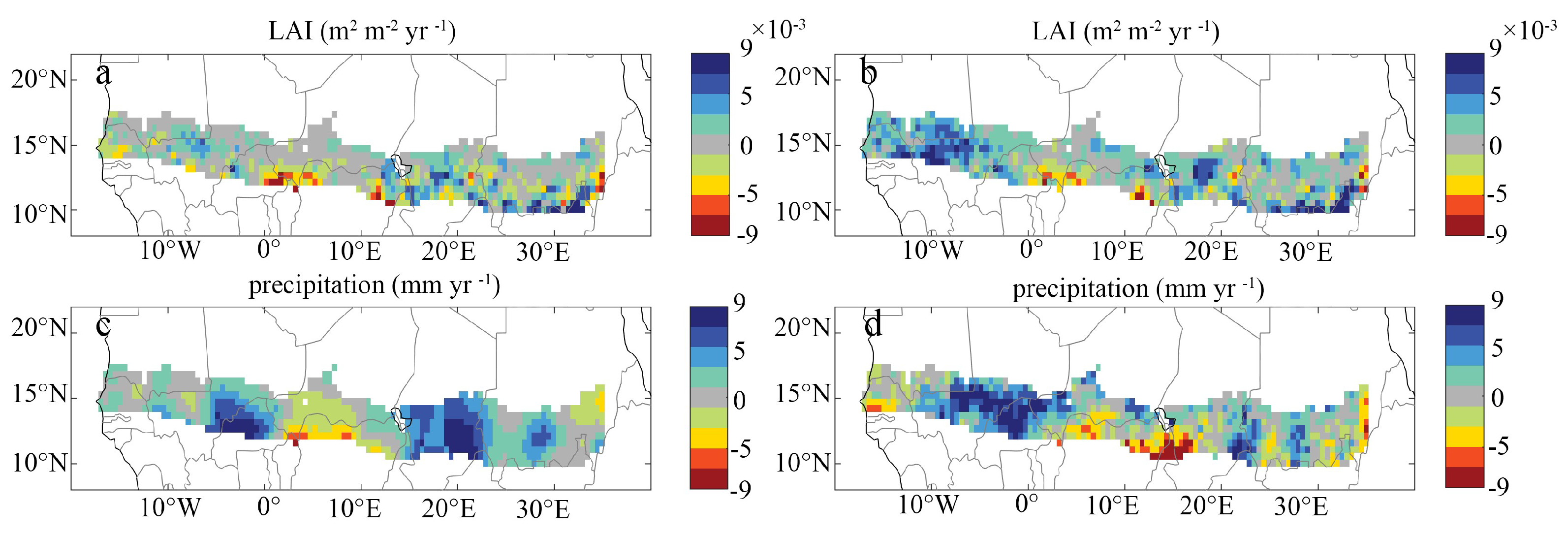
3.1. Coherent Trends of the LAI and Precipitation
3.2. The Relationship between SST Indices and Precipitation
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Koppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Koppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Dai, A.; Lamb, P.J.; Trenberth, K.E.; Hulme, M.; Jones, P.D.; Xie, P. The recent Sahel drought is real. Int. J. Climatol. 2004, 24, 1323–1331. [Google Scholar] [CrossRef]
- Held, I.M.; Delworth, T.L.; Lu, J.; Findell, K.L.; Knutson, T.R. Simulation of Sahel drought in the 20th and 21st centuries. Proc. Natl. Acad. Sci. USA 2005, 102, 17891–17896. [Google Scholar] [CrossRef]
- Ali, A.; Lebel, T. The Sahelian standardized rainfall index revisited. Int. J. Climatol. 2009, 29, 1705–1714. [Google Scholar] [CrossRef]
- Biasutti, M. Rainfall trends in the African Sahel: Characteristics, processes, and causes. Wiley Interdiscip. Rev. Clim. Chang. 2019, 10, e591. [Google Scholar] [CrossRef]
- Giannini, A.; Salack, S.; Lodoun, T.; Ali, A.; Gaye, A.T.; Ndiaye, O. A unifying view of climate change in the Sahel linking intra-seasonal, interannual and longer time scales. Environ. Res. Lett. 2013, 8, 024010. [Google Scholar] [CrossRef]
- Hagos, S.M.; Cook, K.H. Ocean warming and late-twentieth-century Sahel drought and recovery. J. Clim. 2008, 21, 3797–3814. [Google Scholar] [CrossRef]
- Nicholson, S.E.; Some, B.; Kone, B. An analysis of recent rainfall conditions in west Africa, including the rainy seasons of the 1997 El Niño and the 1998 La Niña years. J. Clim. 2000, 13, 2628–2640. [Google Scholar] [CrossRef]
- Pinzon, J.E.; Tucker, C.J. A non-stationary 1981–2012 AVHRR NDVI3g time series. Remote Sens. 2014, 6, 6929–6960. [Google Scholar] [CrossRef]
- Tucker, C.J.; Pinzon, J.E.; Brown, M.E.; Slayback, D.A.; Pak, E.W.; Mahoney, R.; Vermote, E.F.; El Saleous, N. An extended AVHRR 8-km NDVI dataset compatible with MODIS and SPOT vegetation NDVI data. Int. J. Remote Sens. 2005, 26, 4485–4498. [Google Scholar] [CrossRef]
- Anyamba, A.; Tucker, C.J. Analysis of Sahelian vegetation dynamics using NOAA-AVHRR NDVI data from 1981-2003. J. Arid Environ. 2005, 63, 596–614. [Google Scholar] [CrossRef]
- Eklundh, L.; Olsson, L. Vegetation index trends for the African Sahel 1982–1999. Geophys. Res. Lett. 2003, 30, 1430–1433. [Google Scholar] [CrossRef]
- Olsson, L.; Eklundh, L.; Ardo, J. A recent greening of the Sahel-trends, patterns and potential causes. J. Arid Environ. 2005, 63, 556–566. [Google Scholar] [CrossRef]
- Piao, S.; Wang, X.; Park, T.; Chen, C.; Lian, X.; He, Y.; Bjerke, J.W.; Chen, A.; Ciais, P.; Tømmervik, H.; et al. Characteristics, drivers and feedbacks of global greening. Nat. Rev. Earth Environ. 2020, 1, 14–27. [Google Scholar] [CrossRef]
- West, C.T.; Moody, A.J.; Nébié, E.K.; Sanon, O. Ground-truthing Sahelian greening: Ethnographic and spatial evidence from Burkina Faso. Hum. Ecol. 2017, 45, 89–101. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Park, T.; Wang, X.; Piao, S.; Xu, B.; Chaturvedi, R.K.; Fuchs, R.; Brovkin, V.; Ciais, P.; Fensholt, R.; et al. China and India lead in greening of the world through land-use management. Nat. Sustain. 2019, 2, 122–129. [Google Scholar] [CrossRef]
- Zhu, Z.; Piao, S.; Myneni, R.B.; Huang, M.; Zeng, Z.; Canadell, J.G.; Ciais, P.; Sitch, S.; Friedlingstein, P.; Arneth, A.; et al. Greening of the Earth and its drivers. Nat. Clim. Chang. 2016, 6, 791–795. [Google Scholar] [CrossRef]
- Georganos, S.; Abdi, A.M.; Tenenbaum, D.E.; Kalogirou, S. Examining the NDVI-rainfall relationship in the semi-arid Sahel using geographically weighted regression. J. Arid Environ. 2017, 146, 64–74. [Google Scholar] [CrossRef]
- Herrmann, S.M.; Anyamba, A.; Tucker, C.J. Recent trends in vegetation dynamics in the African Sahel and their relationship to climate. Glob. Environ. Chang. 2005, 15, 394–404. [Google Scholar] [CrossRef]
- Hickler, T.; Eklundh, L.; Seaquist, J.W.; Smith, B.; Ardö, J.; Olsson, L.; Sykes, M.T.; Sjöström, M. Precipitation controls Sahel greening trend. Geophys. Res. Lett. 2005, 32, L21415. [Google Scholar] [CrossRef]
- Abdi, A.M.; Boke-Olén, N.; Tenenbaum, D.E.; Tagesson, T.; Cappelaere, B.; Ardö, J. Evaluating water controls on vegetation growth in the semi-arid Sahel using field and earth observation data. Remote Sens. 2017, 9, 294. [Google Scholar] [CrossRef]
- Meroni, M.; Rembold, F.; Fasbender, D.; Vrieling, A. Evaluation of the standardized precipitation index as an early predictor of seasonal vegetation production anomalies in the Sahel. Remote Sens. Lett. 2017, 8, 301–310. [Google Scholar] [CrossRef]
- Nemani, R.R.; Keeling, C.D.; Hashimoto, H.; Jolly, W.M.; Piper, S.C.; Tucker, C.J.; Myneni, R.B.; Running, S.W. Climate-driven increases in global terrestrial net primary production from 1982 to 1999. Science 2003, 300, 1560–1563. [Google Scholar] [CrossRef]
- Charney, J.G. Dynamics of deserts and drought in the Sahel. Q. J. R. Meteorol. Soc. 1975, 101, 193–202. [Google Scholar] [CrossRef]
- Folland, C.K.; Palmer, T.N.; Parker, D.E. Sahel rainfall and worldwide sea temperatures, 1901–1985. Nature 1986, 320, 602. [Google Scholar] [CrossRef]
- Giannini, A.; Saravanan, R.; Chang, P. Oceanic forcing of sahel rainfall on interannual to interdecadal time scales. Science 2003, 302, 1027–1030. [Google Scholar] [CrossRef] [PubMed]
- Palmer, T.N. Influence of the Atlantic, Pacific and Indian Oceans on Sahel rainfall. Nature 1986, 322, 251. [Google Scholar] [CrossRef]
- Lamb, P.J. Case Studies of tropical Atlantic surface circulation patterns during recent sub-saharan weather anomalies: 1967 and 1968. Mon. Weather Rev. 1978, 106, 482–491. [Google Scholar] [CrossRef]
- Biasutti, M.; Held, I.M.; Sobel, A.H.; Giannini, A. SST forcings and Sahel rainfall variability in simulations of the twentieth and twenty-first centuries. J. Clim. 2008, 21, 3471–3486. [Google Scholar] [CrossRef]
- Losada, T.; Rodriguez-Fonseca, B.; Mohino, E.; Bader, J.; Janicot, S.; Mechoso, C.R. Tropical SST and Sahel rainfall: A non-stationary relationship. Geophys. Res. Lett. 2012, 39, L12705. [Google Scholar] [CrossRef]
- Pomposi, C.; Giannini, A.; Kushnir, Y.; Lee, D.E. Understanding Pacific Ocean influence on interannual precipitation variability in the Sahel. Geophys. Res. Lett. 2016, 43, 9234–9242. [Google Scholar] [CrossRef]
- Dyer, E.L.E.; Jones, D.B.A.; Li, R.; Sawaoka, H.; Mudryk, L. Sahel precipitation and regional teleconnections with the Indian Ocean. J. Geophys. Res. Atmos. 2017, 122, 5654–5676. [Google Scholar] [CrossRef]
- Park, J.Y.; Bader, J.; Matei, D. Anthropogenic Mediterranean warming essential driver for present and future Sahel rainfall. Nat. Clim. Chang. 2016, 6, 941–945. [Google Scholar] [CrossRef]
- Diatta, S.; Fink, A.H. Statistical relationship between remote climate indices and West African monsoon variability. Int. J. Climatol. 2014, 34, 3348–3367. [Google Scholar] [CrossRef]
- Rodríguez-Fonseca, B.; Mohino, E.; Mechoso, C.R.; Caminade, C.; Biasutti, M.; Gaetani, M.; Garcia-Serrano, J.; Vizy, E.K.; Cook, K.; Xue, Y.; et al. Variability and predictability of West African droughts: A review on the role of sea surface temperature anomalies. J. Clim. 2015, 28, 4034–4060. [Google Scholar] [CrossRef]
- Dong, B.; Sutton, R. Dominant role of greenhouse-gas forcing in the recovery of Sahel rainfall. Nat. Clim. Chang. 2015, 5, 757–760. [Google Scholar] [CrossRef]
- Biasutti, M. Hydrology: What Brings Rain to the Sahel? Nat. Clim. Chang. 2016, 6, 897–898. [Google Scholar] [CrossRef]
- Liang, X.S. Information flow and causality as rigorous notions ab initio. Phys. Rev. E 2016, 94, 52201. [Google Scholar] [CrossRef]
- Hagan, D.F.T.; Wang, G.; Liang, X.S.; Dolman, H.A.J. A time-varying causality formalism based on the Liang–Kleeman information flow for analyzing directed interactions in nonstationary climate systems. J. Clim. 2019, 32, 7521–7537. [Google Scholar] [CrossRef]
- Stips, A.; Macias, D.; Coughlan, C.; Garcia-Gorriz, E.; Liang, X.S. On the causal structure between CO2 and global temperature. Sci. Rep. 2016, 6, 21691. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Bi, J.; Pan, Y.; Ganguly, S.; Anav, A.; Xu, L.; Samanta, A.; Piao, S.; Nemani, R.; Myneni, R. Global data sets of vegetation leaf area index (LAI)3g and fraction of photosynthetically active radiation (FPAR)3g derived from Global Inventory Modeling and Mapping Studies (GIMMS) normalized difference vegetation index (NDVI3g) for the period 1981 to 2011. Remote Sens. 2013, 5, 927–948. [Google Scholar] [CrossRef]
- Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated high-resolution grids of monthly climatic observations—The CRU TS3.10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef]
- Huang, B.; Thorne, P.W.; Banzon, V.F.; Boyer, T.; Chepurin, G.; Lawrimore, J.H.; Menne, M.J.; Smith, T.M.; Vose, R.S.; Zhang, H.M. Extended reconstructed sea surface temperature, version 5 (ERSSTv5): Upgrades, validations, and intercomparisons. J. Clim. 2017, 30, 8179–8205. [Google Scholar] [CrossRef]
- Biasutti, M. Forced Sahel rainfall trends in the CMIP5 archive. J. Geophys. Res. Atmos. 2013, 118, 1613–1623. [Google Scholar] [CrossRef]
- USGS 30 ARC-second Global Elevation Data, GTOPO30. 1997. Available online: https://www.usgs.gov/centers/eros/science (accessed on 2 October 2018).
- Kendall, M.G. Rank Correlation Methods; Charles Griffin: London, UK, 1975; p. 202. [Google Scholar]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Sneyers, R. Sur L’analyse Statistique des Series D’observations; OMM: Geneve, Switzerland, 1975. [Google Scholar]
- Zhang, Y.; Guan, D.; Jin, C.; Wang, A.; Wu, J.; Yuan, F. Analysis of impacts of climate variability and human activity on streamflow for a river basin in northeast China. J. Hydrol. 2011, 410, 239–247. [Google Scholar] [CrossRef]
- Demaree, G.R.; Nicolis, C. Onset of Sahelian drought viewed as a fluctuation-induced transition. Q. J. R. Meteorol. Soc. 1990, 116, 221–238. [Google Scholar] [CrossRef]
- Moraes, J.M.; Pellegrino, G.Q.; Ballester, M.V.; Martinelli, L.A.; Victoria, R.L.; Krusche, A.V. Trends in hydrological parameters of a southern Brazilian watershed and its relation to human induced changes. Water Resour. Manag. 1998, 12, 295–311. [Google Scholar] [CrossRef]
- Toms, J.D.; Lesperance, M.L. Piecewise regression: A tool for identifying ecological thresholds. Ecology 2003, 84, 2034–2041. [Google Scholar] [CrossRef]
- Wang, X.; Piao, S.; Ciais, P.; Li, J.; Friedlingstein, P.; Koven, C.; Chen, A. Spring temperature change and its implication in the change of vegetation growth in North America from 1982 to 2006. Proc. Natl. Acad. Sci. USA 2011, 108, 1240–1245. [Google Scholar] [CrossRef] [PubMed]
- Myneni, R.; Knyazikhin, Y.; Park, T. MOD15A2H MODIS/Terra Leaf Area Index/FPAR 8-Day L4 Global 500 m SIN Grid V006; NASA EOSDIS Land Processes DAAC: Sioux Falls, SD, USA, 2015. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Bernardino, P.N.; Keersmaecker, W.D.; Fensholt, R.; Verbesselt, J.; Somers, B.; Horion, S. Global-scale characterization of turning points in arid and semi-arid ecosystem functioning. Glob. Ecol. Biogeogr. 2020, 29, 1230–1245. [Google Scholar] [CrossRef]
- Ackerley, D.; Booth, B.B.B.; Knight, S.H.E.; Highwood, E.J.; Frame, D.J.; Allen, M.R.; Rowell, D.P. Sensitivity of Twentieth-Century Sahel Rainfall to Sulfate Aerosol and CO2 Forcing. J. Clim. 2011, 24, 4999–5014. [Google Scholar] [CrossRef]

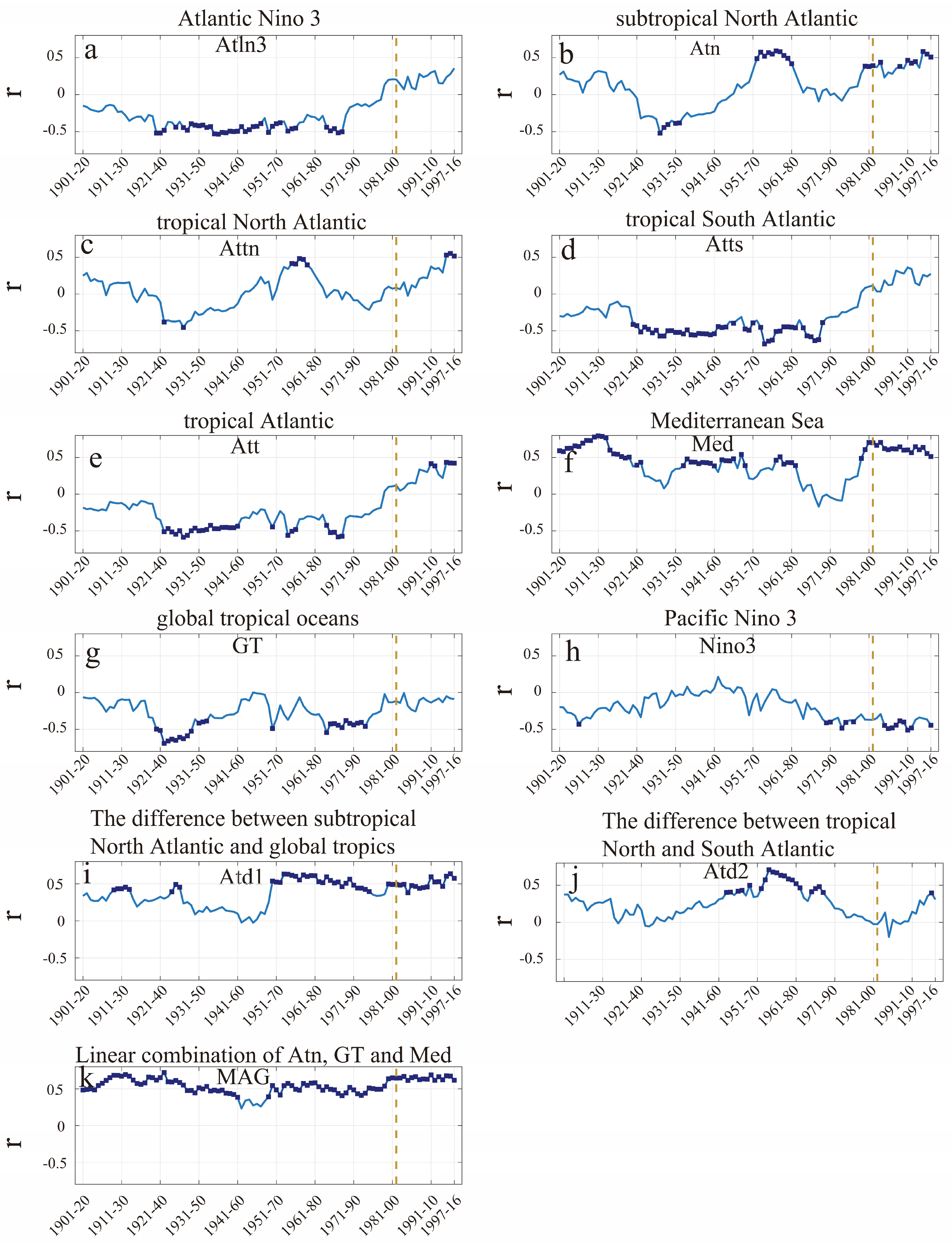
| NO. | SST Index | Spatial Extension | Comments | r (1901–2016) | r (1982–2016) |
|---|---|---|---|---|---|
| 1 | Atln3 | 3°S–3°N, 15°W–0°W | Atlantic Nino 3 | −0.29 ** | 0.20 |
| 2 | Atn | 10°N–40°N, 75°W–15°W | subtropical North Atlantic | 0.07 | 0.59 ** |
| 3 | Attn | 10°N–25°N, 75°W–15°W | tropical North Atlantic | −0.07 | 0.46 ** |
| 4 | Atts | 20°S–10°N, 75°W–15°E | tropical South Atlantic | −0.26 ** | 0.27 * |
| 5 | Att | 20°S–20°N, 75°W–15°E | tropical Atlantic | −0.20 ** | 0.38 |
| 6 | Med | 30°N–50°N, 0°–50°E | Mediterranean Sea | 0.32 ** | 0.70 ** |
| 7 | GT | 20°S–20°N, 180°W–180°E | global tropical oceans | −0.27 ** | 0.20 |
| 8 | Nino3 | 90°W–150°W, 5°S–5°N | Pacific Nino 3 | −0.28 ** | −0.29 |
| 9 | Atd1 | Atn minus GT | The difference between subtropical North Atlantic and global tropics | 0.51 ** | 0.60 ** |
| 10 | Atd2 | Attn minus Atts | The difference between tropical North and South Atlantic | 0.32 ** | 0.28 |
| 11 | MAG a | Med × α + Atn × β– GT × λ | Linear combination of Atn, GT and Med | 0.65 ** | 0.72 ** |
| LAI | Annual | R2 | J–N | R2 | Annual | PLR R2 | J–N | PLR R2 | |
| 1982–2016 | 1.72 × 10−3 ** | 0.45 | 3.23 × 10−3 ** | 0.50 | TP | 1999 | 0.60 | 1999 | 0.58 |
| 1982–1999 | 4.25 × 10−3 ** | 6.58 × 10−3 ** | β1 | 3.72 × 10−3 ** | 5.89 × 10−3 ** | ||||
| 1999–2016 | −0.27 × 10−3 | 0.53 | β2 | -4.00 × 10−3 ** | -5.32 × 10−3 ** | ||||
| Precipitation | Annual | R2 | M–O | R2 | Annual | PLR R2 | M–O | PLR R2 | |
| 1982–2016 | 4.63 ** | 0.39 | 4.60 ** | 0.39 | TP | 1999 | 0.44 | 1999 | 0.44 |
| 1982–1999 | 9.72 ** | 9.57 ** | β1 | 7.77 ** | 7.73 ** | ||||
| 1999–2016 | 2.17 | 1.99 | β2 | −6.28* | -6.27 * | ||||
| SST | Atd1 | MAG | Atd1 | MAG | |||||
| 1982–2016 | 1.18 × 10−2 * | 5.32 × 10−2 * | TP | 1999 | 1999 | ||||
| 1982–1999 | 1.38 × 10−2 | 5.05 × 10−2 | β1 | 1.68 × 10−2 * | 6.67 × 10-2 * | ||||
| 1999–2016 | −0.20 × 10−2 | −0.87 × 10−2 | β2 | −0.99 × 10−2 * | −2.70 × 10−2 * | ||||
| 2001–2016 | Annual | J–N | 1999–2016 | Annual | M–O |
|---|---|---|---|---|---|
| GIMMS LAI3g | 0.38 × 10−3 ** | 1.08 × 10−3 ** | CRU Precipitation | 2.17 ** | 1.99 ** |
| MODIS LAI | 1.69× 10−3 ** | 1.88 × 10−3 ** | TRMM Precipitation | 1.33 ** | 1.26 ** |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.; Zhou, S.; Liang, C.; Hagan, D.F.T.; Zeng, N.; Wang, J.; Shi, T.; Chen, X.; Dolman, A.J. The Greening and Wetting of the Sahel Have Leveled off since about 1999 in Relation to SST. Remote Sens. 2020, 12, 2723. https://doi.org/10.3390/rs12172723
Chen T, Zhou S, Liang C, Hagan DFT, Zeng N, Wang J, Shi T, Chen X, Dolman AJ. The Greening and Wetting of the Sahel Have Leveled off since about 1999 in Relation to SST. Remote Sensing. 2020; 12(17):2723. https://doi.org/10.3390/rs12172723
Chicago/Turabian StyleChen, Tiexi, Shengjie Zhou, Chuanzhuang Liang, Daniel Fiifi Tawia Hagan, Ning Zeng, Jun Wang, Tingting Shi, Xin Chen, and A.J. Dolman. 2020. "The Greening and Wetting of the Sahel Have Leveled off since about 1999 in Relation to SST" Remote Sensing 12, no. 17: 2723. https://doi.org/10.3390/rs12172723
APA StyleChen, T., Zhou, S., Liang, C., Hagan, D. F. T., Zeng, N., Wang, J., Shi, T., Chen, X., & Dolman, A. J. (2020). The Greening and Wetting of the Sahel Have Leveled off since about 1999 in Relation to SST. Remote Sensing, 12(17), 2723. https://doi.org/10.3390/rs12172723










