Using Apparent Electrical Conductivity as Indicator for Investigating Potential Spatial Variation of Soil Salinity across Seven Oases along Tarim River in Southern Xinjiang, China
Abstract
1. Introduction
- (1)
- establish quantitative RF–based EMI prediction model (horizontal and vertical modes, ECa, mS·m−1) using RF algorithm and other auxiliary remote sensing environmental products, then,
- (2)
- predict ECa spatial distribution at the predefined bulk soil depths (0–37.5 cm, 0–75 cm and 0–150 cm) and analyze the spatial distribution characteristics of soil salinity by the predicted ECa maps,
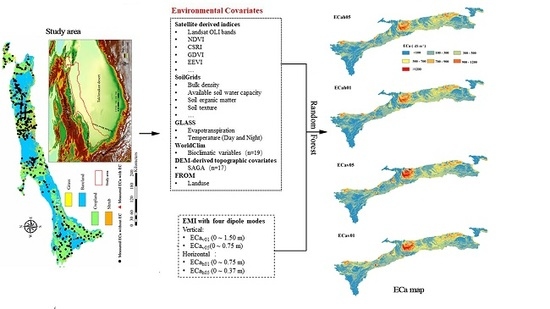
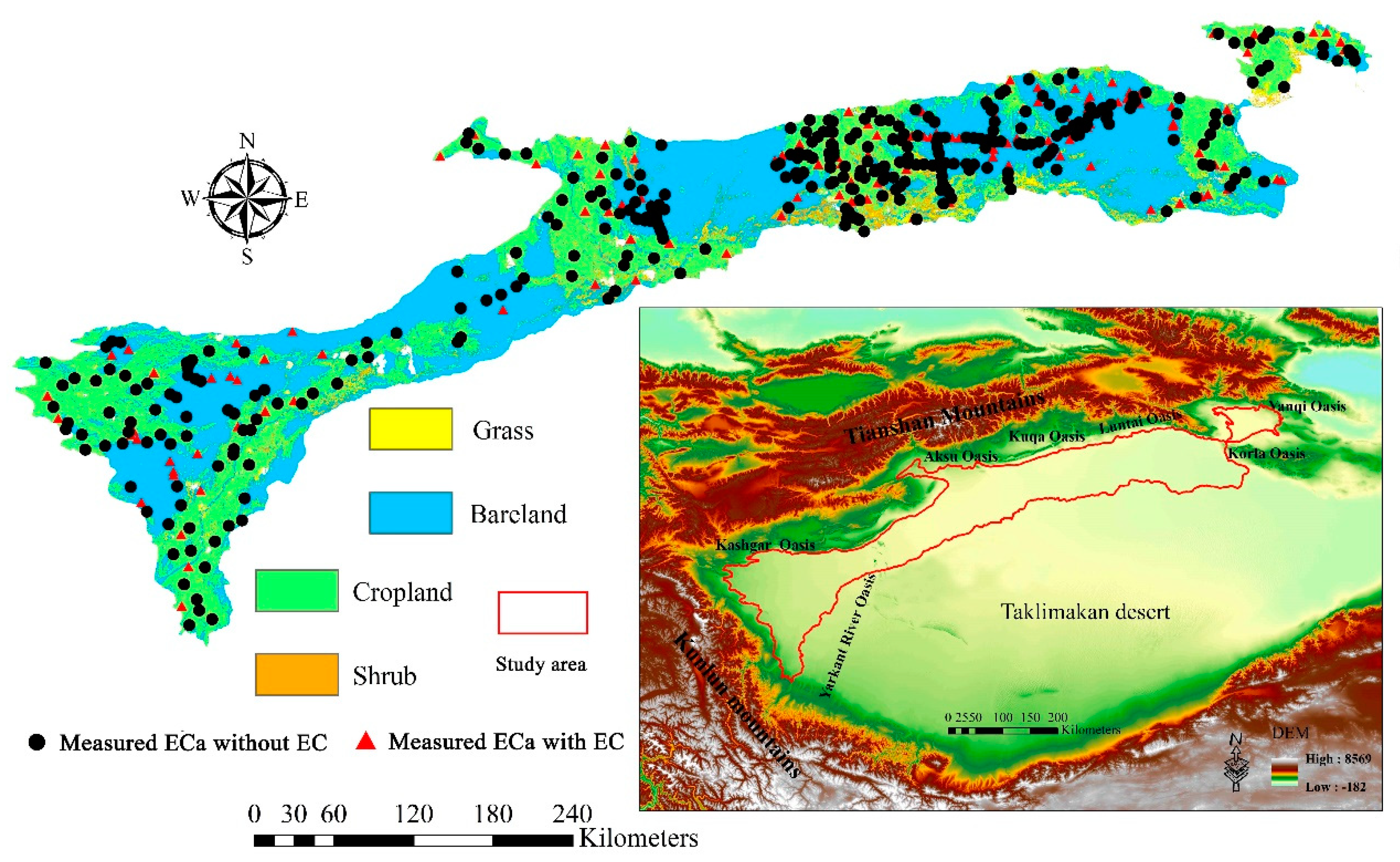
2. Study Area
3. Data and Methods
3.1. Environment Variables
3.2. Field Sampling
3.3. Machine Learning Algorithms
3.3.1. Random Forest
3.3.2. Variable Selection
3.4. Model Validation
4. Results
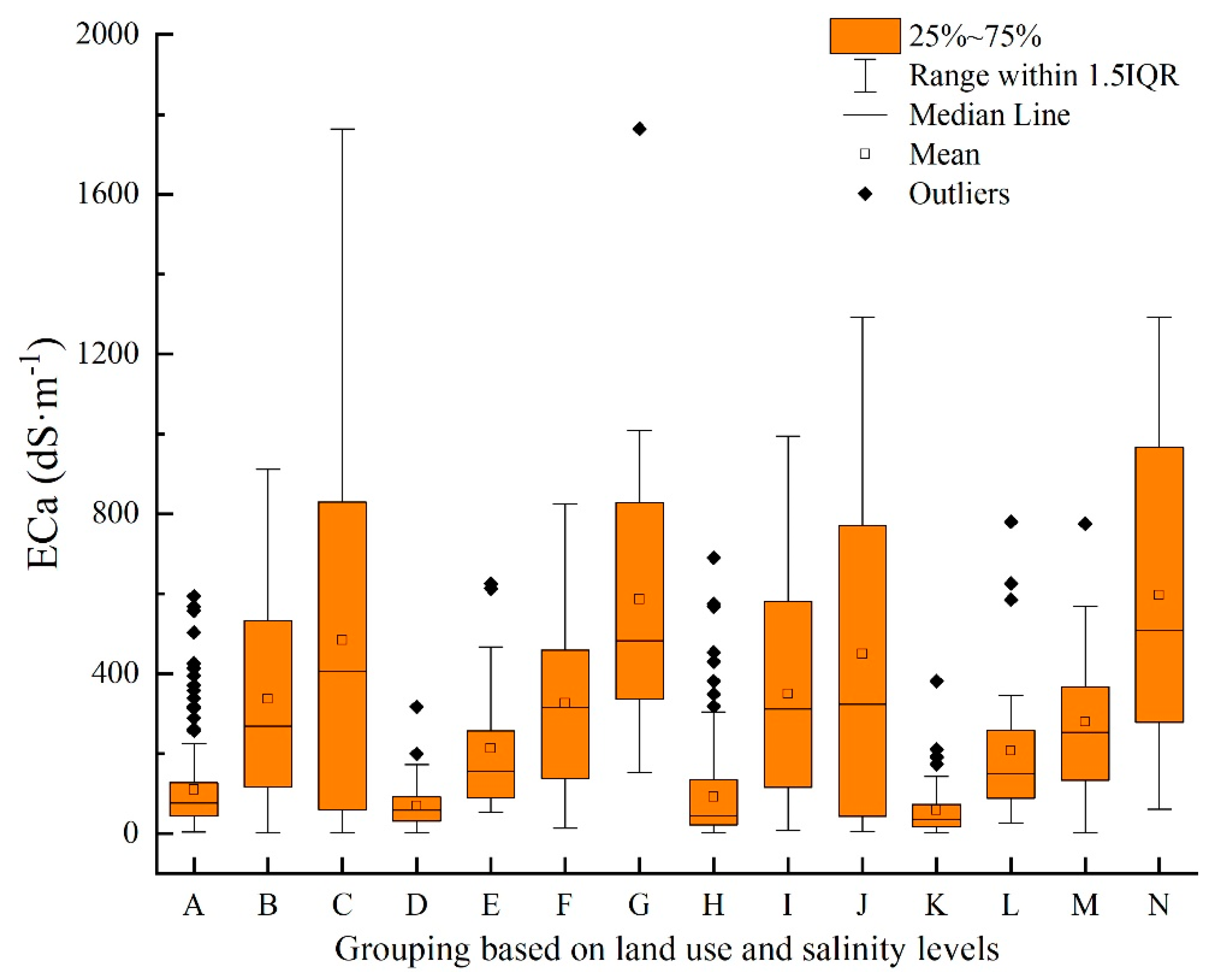
4.1. Statistical Description of ECa and EC Data
4.2. Correlation between ECa and EC at Different Depths
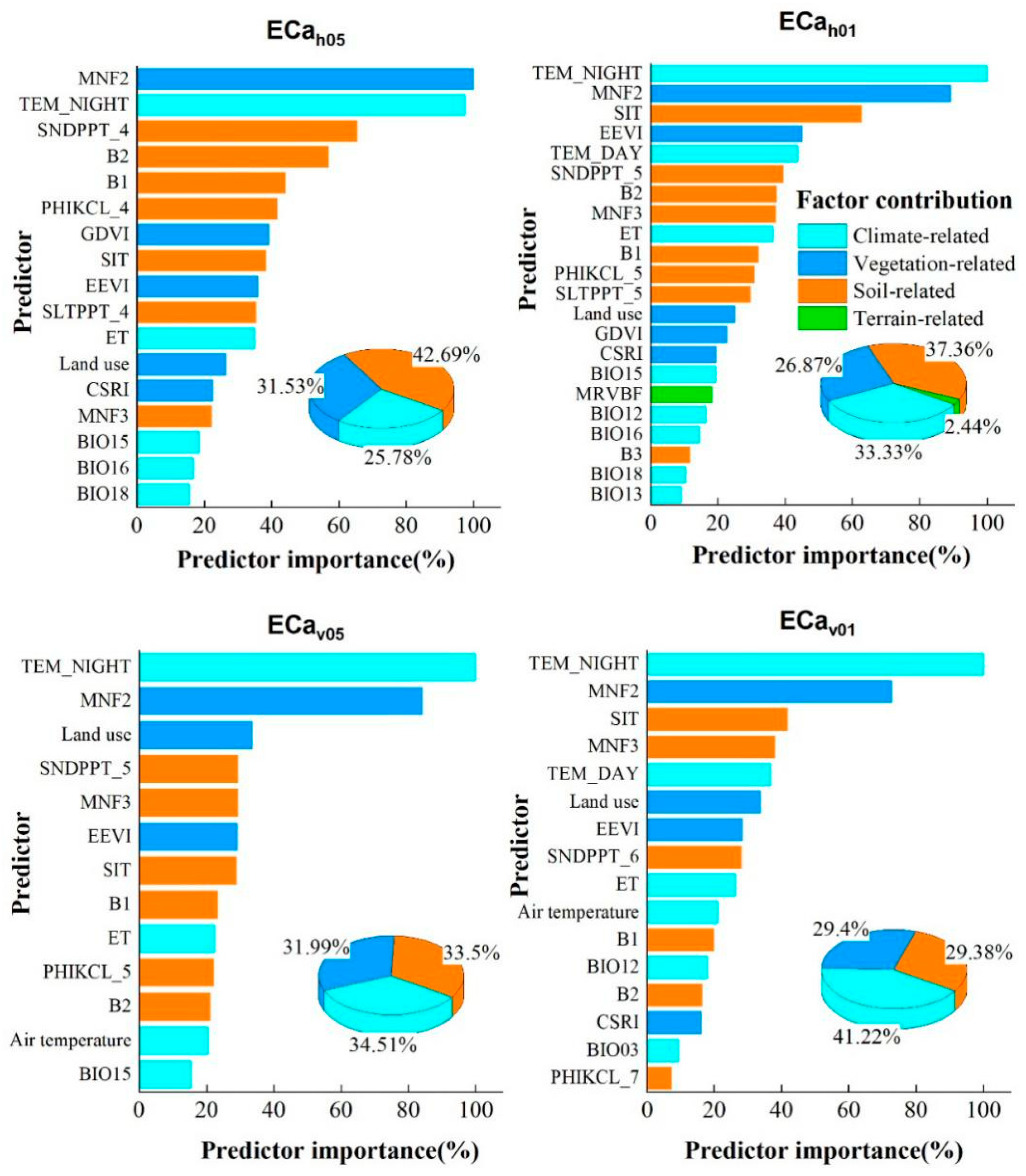
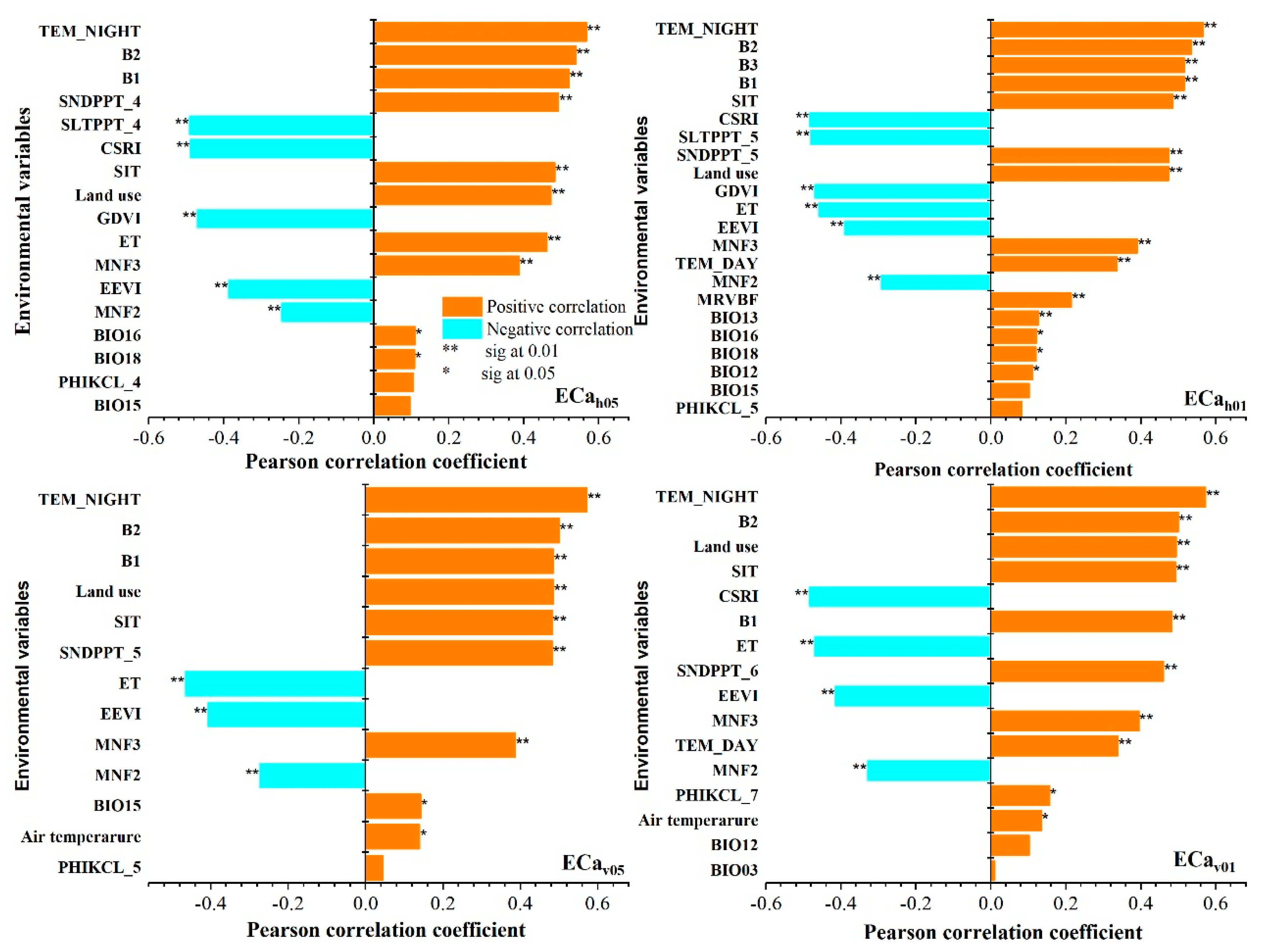
4.3. Important Variables
4.4. Correlation between Environmental Covariates and Measured ECa
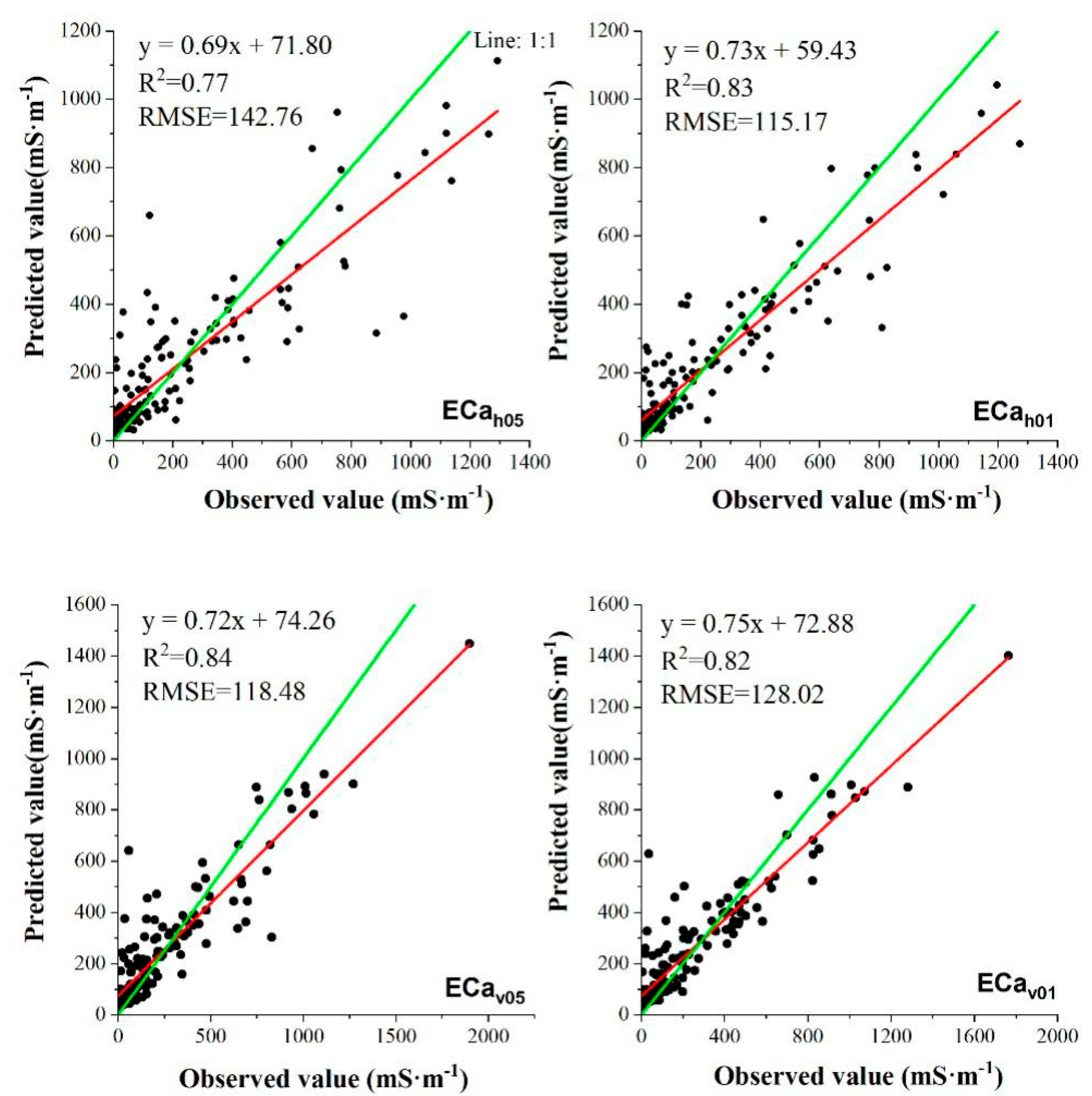
4.5. Calibration and Validation of the ECa Model
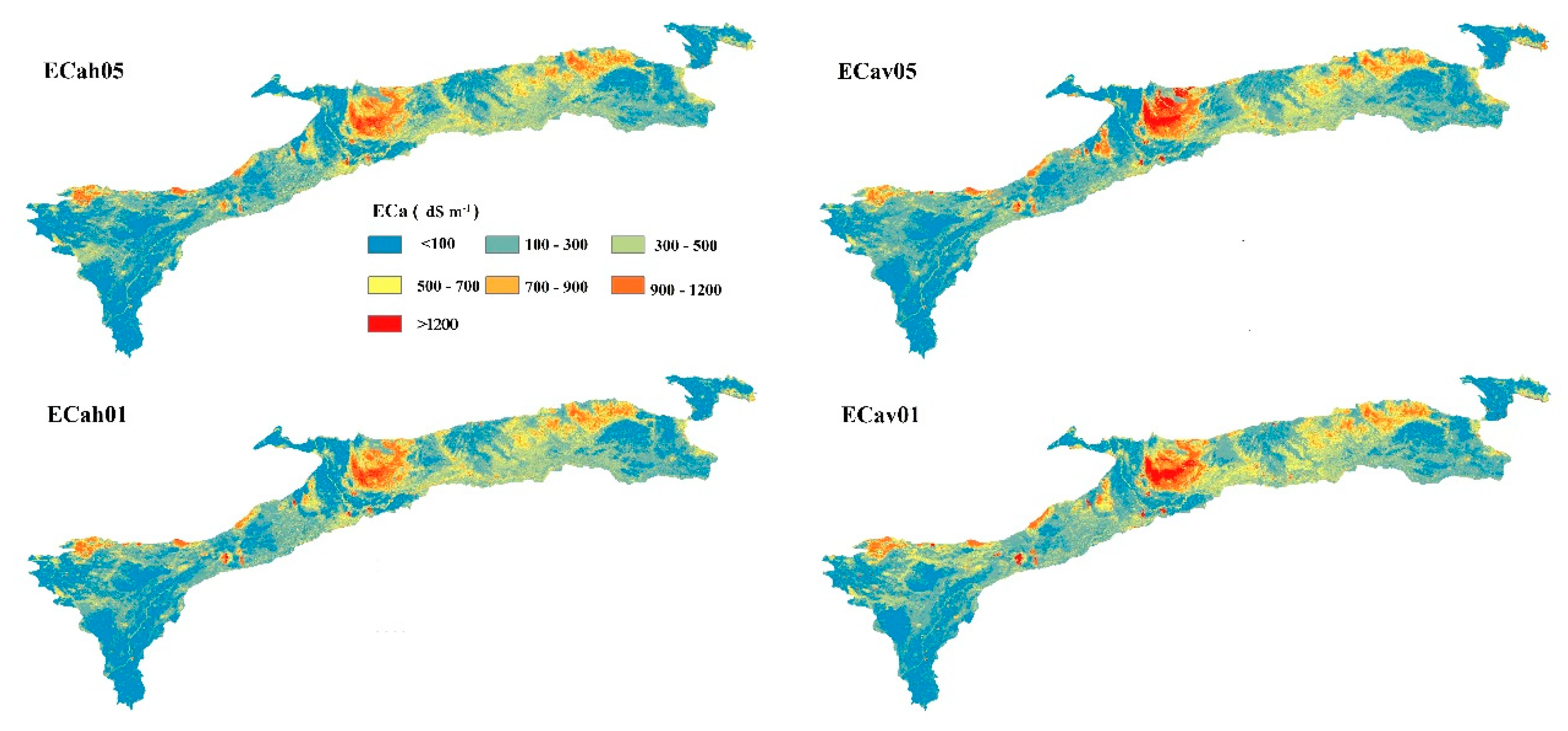
4.6. Spatial Distribution Characteristics of ECa
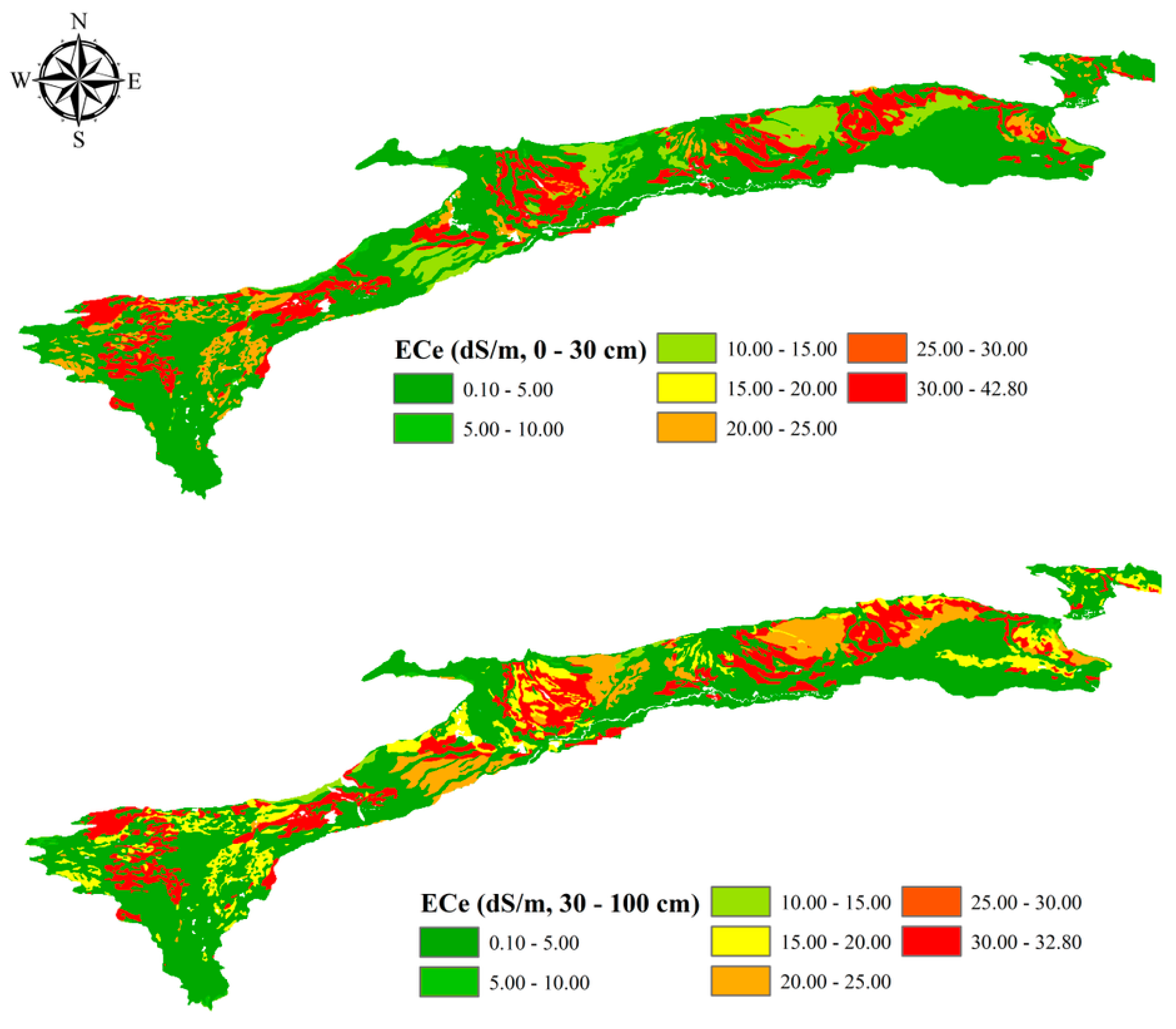
5. Discussion and Perspectives
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- FAO; ITPS. Status of the World’s Soil Resources (SWSR)—Main Report; Food and Agriculture Organization of the United Nations and Intergovernmental Technical Panel on Soils: Rome, Italy, 2015. [Google Scholar]
- Wei, Y.; Shi, Z.; Biswas, A.; Yang, S.; Ding, J.; Wang, F. Updated information on soil salinity in a typical oasis agroecosystem and desert-oasis ecotone: Case study conducted along the Tarim River, China. Sci. Total Environ. 2019, 135387, in press. [Google Scholar] [CrossRef]
- Fathizad, H.; Ardakani, M.A.H.; Sodaiezadeh, H.; Kerry, R.; Taghizadeh-Mehrjardi, R. Investigation of the spatial and temporal variation of soil salinity using random forests in the central desert of Iran. Geoderma 2020, 365, 114233. [Google Scholar] [CrossRef]
- Huang, J.; Prochazka, M.J.; Triantafilis, J. Irrigation salinity hazard assessment and risk mapping in the lower Macintyre Valley, Australia. Sci. Total Environ. 2016, 551–552, 460–473. [Google Scholar] [CrossRef]
- Scudiero, E.; Skaggs, T.H.; Corwin, D.L. Corwin; Regional-scale soil salinity assessment using Landsat ETM + canopy reflectance. Remote Sens. Environ. 2015, 169, 335–343. [Google Scholar] [CrossRef]
- Ivushkin, K.; Bartholomeus, H.; Bregt, A.K.; Pulatov, A.; Kempen, B.; De Sousa, L. Global mapping of soil salinity change. Remote Sens. Environ. 2019, 231, 111260. [Google Scholar] [CrossRef]
- Wang, Z. Saline Soil of China; Science Press: Beijing, China, 1993. [Google Scholar]
- Tian, C.; Mai, W.; Zhao, Z. Study on key technologies of ecological management of saline alkali land in arid area of Xinjiang. Acta Ecol. Sin. 2016, 3636, 7064–7068. [Google Scholar]
- Butcher, K.; Wick, A.F.; DeSutter, T.; Chatterjee, A.; Harmon, J. Soil Salinity: A Threat to Global Food Security. Agron. J. 2016, 108108, 2189–2200. [Google Scholar] [CrossRef]
- Popp, J.; Lakner, Z.; Harangi-Rákos, M.; Fári, M. The effect of bioenergy expansion: Food, energy, and environment. Renew. Sustain. Energy Rev. 2014, 32, 559–578. [Google Scholar] [CrossRef]
- Richards, J.A.; Nicholls, R.J. Impacts of climate change in coastal systems in Europe. PESETA-Coastal Systems study. JRC Work. Pap. 2009, 2009, 45–57. [Google Scholar]
- Liu, G.; Li, J.; Zhang, X.; Wang, X.; Lv, Z.; Yang, J.; Shao, H.; Yu, S. GIS-mapping spatial distribution of soil salinity for Eco-restoring the Yellow River Delta in combination with Electromagnetic Induction. Ecol. Eng. 2016, 94, 306–314. [Google Scholar] [CrossRef]
- Wang, Q.; Du, Y.; Sun, Y.; Wu, Z. Preliminary report on rice improvement experiment of Sea Rice in Yopurga county, Kashgar district, Xinjiang. Agr. Tech. 2019, 3939, 83–84. [Google Scholar]
- Wang, X.; Jiang, Z.; Li, Y.; Kong, F.; Xi, M. Inorganic carbon sequestration and its mechanism of coastal saline-alkali wetlands in Jiaozhou Bay, China. Geoderma 2019, 351, 221–234. [Google Scholar] [CrossRef]
- Mavi, M.S.; Marschner, B. Impact of Salinity on Respiration and Organic Matter Dynamics in Soils is More Closely Related to Osmotic Potential than to Electrical Conductivity. Pedosphere 2017, 27, 949–956. [Google Scholar] [CrossRef]
- Setia, R.; Smith, P.; Marschner, B.; Gottschalk, P.; Baldock, J.A.; Verma, V.; Setia, D.; Smith, J. Simulation of salinity effects on past, present, and future soil organic carbon stocks. Environ. Sci. Technol. 2012, 4646, 1624–1631. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.D.; Pan, Z.L.; Lei, Z.D.; Zhang, F.W. Study on Water Resources and Ecology of Tarim River in China; Xinjiang People’s Publishing House: Urumqi, China, 2000. [Google Scholar]
- He, K.; Wu, S.; Yang, Y.; Wang, D.; Zhang, S.; Yin, N. Dynamic changes of land use and oasis in Xinjiang in the past 40 years. Arid Land Geogr. 2018, 4141, 193–200. [Google Scholar]
- Wei, K.; Wang, L. Reexamination of the Aridity Conditions in Arid Northwestern China for the Last Decade. J. Clim. 2013, 26, 9594–9602. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Y.; Fang, G.; Li, Y. Multivariate assessment and attribution of droughts in Central Asia. Sci. Rep. 2017, 77, 1316. [Google Scholar] [CrossRef]
- Yao, J.; Zhao, Y.; Chen, Y.; Yu, X.; Zhang, R. Multi-scale assessments of droughts: A case study in Xinjiang, China. Sci. Total Environ. 2018, 630, 444–452. [Google Scholar] [CrossRef]
- Deng, H.; Chen, Y. The glacier and snow variations and their impact on water resources in mountain regions:A case study in Tianshan Mountains of Central Asia. Acta Geog. Sin. 2018, 7373, 1309–1323. [Google Scholar]
- Hengl, T.; De Jesus, J.M.; Macmillan, R.A.; Batjes, N.; Heuvelink, G.B.M.; Ribeiro, E.; Samuel-Rosa, A.; Kempen, B.; Leenaars, J.G.B.; Walsh, M.G.; et al. SoilGrids1km Global Soil Information Based on Automated Mapping. PLoS ONE 2014, 9, e105992. [Google Scholar] [CrossRef]
- Hengl, T.; De Jesus, J.M.; Heuvelink, G.B.M.; Gonzalez, M.R.; Kilibarda, M.; Blagotić, A.; Shangguan, W.; Wright, M.N.; Geng, X.; Bauer-Marschallinger, B.; et al. SoilGrids250m: Global gridded soil information based on machine learning. PLoS ONE 2017, 12, e0169748. [Google Scholar] [CrossRef] [PubMed]
- Qiao, M.; Zhou, S.B.; Lei, L.U.; Yan, J.J.; He-Ping, L.I. Temporal and spatial changes of soil salinization and improved countermeasures of Tarim Basin Irrigation District in recent 25 a. Arid Land Geogr. 2011, 39, 171–181. [Google Scholar]
- Doolittle, J.A.; Brevik, E.C. The use of electromagnetic induction techniques in soils studies. Geoderma 2014, 223, 33–45. [Google Scholar] [CrossRef]
- Scudiero, E.; Skaggs, T.H.; Corwin, D.L. Comparative regional-scale soil salinity assessment with near-ground apparent electrical conductivity and remote sensing canopy reflectance. Ecol. Indic. 2016, 70, 276–284. [Google Scholar] [CrossRef]
- Huang, J.; Koganti, T.; Santos, F.M.; Triantafilis, J. Mapping soil salinity and a fresh-water intrusion in three-dimensions using a quasi-3d joint-inversion of DUALEM-421S and EM34 data. Sci. Total Environ. 2017, 577, 395–404. [Google Scholar] [CrossRef]
- Casterad, M.A.; Herrero, J.; Betrán, J.A.; Ritchie, G.L. Sensor-Based Assessment of Soil Salinity during the First Years of Transition from Flood to Sprinkler Irrigation. Sensors 2018, 18, 616. [Google Scholar] [CrossRef]
- Yao, R.; Yang, J. Quantitative evaluation of soil salinity and its spatial distribution using electromagnetic induction method. Agric. Water Manag. 2010, 97, 1961–1970. [Google Scholar] [CrossRef]
- Hu, J.; Peng, J.; Zhou, Y.; Xu, D.; Zhao, R.; Jiang, Q.; Fu, T.; Wang, F.; Shi, Z. Quantitative Estimation of Soil Salinity Using UAV-Borne Hyperspectral and Satellite Multispectral Images. Remote Sens. 2019, 11, 736. [Google Scholar] [CrossRef]
- Metternicht, G.; Zinck, J. Remote sensing of soil salinity: Potentials and constraints. Remote Sens. Environ. 2003, 85, 1–20. [Google Scholar] [CrossRef]
- Allbed, A.; Kumar, L. Soil Salinity Mapping and Monitoring in Arid and Semi-Arid Regions Using Remote Sensing Technology: A Review. Adv. Remote Sens. 2013, 2, 373–385. [Google Scholar] [CrossRef]
- Fathololoumi, S.; Vaezi, A.R.; Alavipanah, S.K.; Ghorbani, A.; Biswas, A. Comparison of spectral and spatial-based approaches for mapping the local variation of soil moisture in a semi-arid mountainous area. Sci. Total Environ. 2020, 724, 138319. [Google Scholar] [CrossRef] [PubMed]
- Fathololoumi, S.; Vaezi, A.R.; Alavipanah, S.K.; Ghorbani, A.; Saurette, D.; Biswas, A. Improved digital soil mapping with multitemporal remotely sensed satellite data fusion: A case study in Iran. Sci. Total Environ. 2020, 721, 137703. [Google Scholar] [CrossRef] [PubMed]
- Heung, B.; Ho, H.C.; Zhang, J.; Knudby, A.; Bulmer, C.E.; Schmidt, M.G. An overview and comparison of machine-learning techniques for classification purposes in digital soil mapping. Geoderma 2016, 265, 62–77. [Google Scholar] [CrossRef]
- Barthold, F.; Wiesmeier, M.; Breuer, L.; Frede, H.-G.; Wu, J.; Blank, F. Land use and climate control the spatial distribution of soil types in the grasslands of Inner Mongolia. J. Arid. Environ. 2013, 88, 194–205. [Google Scholar] [CrossRef]
- Wang, F.; Shi, Z.; Biswas, A.; Yang, S.; Ding, J. Multi-algorithm comparison for predicting soil salinity. Geoderma 2020, 365, 114211. [Google Scholar] [CrossRef]
- Keskin, H.; Grunwald, S.; Harris, W.G. Digital mapping of soil carbon fractions with machine learning. Geoderma 2019, 339, 40–58. [Google Scholar] [CrossRef]
- Wang, B.; Waters, C.; Orgill, S.; Cowie, A.; Clark, A.; Liu, D.L.; Simpson, M.; McGowen, I.; Sides, T. Estimating soil organic carbon stocks using different modelling techniques in the semi-arid rangelands of eastern Australia. Ecol. Indic. 2018, 88, 425–438. [Google Scholar] [CrossRef]
- Chagas, C.D.S.; Júnior, W.D.C.; Bhering, S.B.; Filho, B.C. Spatial prediction of soil surface texture in a semiarid region using random forest and multiple linear regressions. Catena 2016, 139, 232–240. [Google Scholar] [CrossRef]
- Heung, B.; Bulmer, C.E.; Schmidt, M.G. Predictive soil parent material mapping at a regional-scale: A Random Forest approach. Geoderma 2014, 214, 141–154. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Mendes, M.P.; Garcia-Soldado, M.J.; Olmo, M.C.; Ribeiro, L. Predictive modeling of groundwater nitrate pollution using Random Forest and multisource variables related to intrinsic and specific vulnerability: A case study in an agricultural setting (Southern Spain). Sci. Total Environ. 2014, 476, 189–206. [Google Scholar] [CrossRef]
- Tajik, S.; Ayoubi, S.; Shirani, H.; Zeraatpisheh, M. Digital mapping of soil invertebrates using environmental attributes in a deciduous forest ecosystem. Geoderma 2019, 353, 252–263. [Google Scholar] [CrossRef]
- Jiapaer, G.; Chen, X.; Bao, A. A comparison of methods for estimating fractional vegetation cover in arid regions. Agr. Forest. Meteorol. 2011, 151, 1698–1710. [Google Scholar] [CrossRef]
- Zhou, H.; Shen, M.; Chen, J.; Xia, J.; Hong, S. Trends of natural runoffs in the Tarim River Basin during the last 60 years. Arid Land Geogr. 2018, 41, 4–12. [Google Scholar]
- IUSS-Working-Group-WRB. World Reference Base for Soil Resources 2014, updAte 2015 International Soil Classification System for Naming Soils and Creating Legends for Soil Maps. In World Soil Resources Reports No. 106; FAO: Rome, Italy, 2015. [Google Scholar]
- McBratney, A.B.; Santos, M.M.; Minasny, B. On digital soil mapping. Geoderma 2003, 117, 3–52. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Li, X.; Chen, J.; Wang, K.; Jia, K.; Cheng, J.; Jiang, B.; Fisher, J.; Mu, Q.; et al. A satellite-based hybrid algorithm to determine the Priestley–Taylor parameter for global terrestrial latent heat flux estimation across multiple biomes. Remote Sens. Environ. 2015, 165, 216–233. [Google Scholar] [CrossRef]
- Hijmans, R.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. 2005, 25, 1965–1978. [Google Scholar] [CrossRef]
- Chen, H.; Zhao, G.; Chen, J.; Wang, R.; Gao, M. Remote sensing inversion of saline soil salinity based on modified vegetation index in estuary area of Yellow River. Trans. Chin. Soc. Agric. Eng. 2015, 31, 107–114. [Google Scholar]
- Wu, W.; Mhaimeed, A.S.; Al-Shafie, W.M.; Ziadat, F.; Dhehibi, B.; Nangia, V.; De Pauw, E. Mapping soil salinity changes using remote sensing in Central Iraq. Geoderma Reg. 2014, 2, 21–31. [Google Scholar] [CrossRef]
- Allbed, A.; Kumar, L.; Aldakheel, Y.Y. Assessing soil salinity using soil salinity and vegetation indices derived from IKONOS high-spatial resolution imageries: Applications in a date palm dominated region. Geoderma 2014, 230, 1–8. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Minasny, B.; Sarmadian, F.; Malone, B. Digital mapping of soil salinity in Ardakan region, central Iran. Geoderma 2014, 213, 15–28. [Google Scholar] [CrossRef]
- Gong, P.; Liu, H.; Zhang, M.; Li, C.; Wang, J.; Huang, H.; Clinton, N.; Ji, L.; Li, W.; Bai, Y.; et al. Stable classification with limited sample: Transferring a 30-m resolution sample set collected in 2015 to mapping 10-m resolution global land cover in 2017. Sci. Bull. 2019, 64, 370–373. [Google Scholar] [CrossRef]
- Yang, L.; Li, X.; Shi, J.; Shen, F.; Qi, F.; Gao, B.; Chen, Z.; Zhu, A.-X.; Zhou, C. Evaluation of conditioned Latin hypercube sampling for soil mapping based on a machine learning method. Geoderma 2020, 369, 114337. [Google Scholar] [CrossRef]
- McNeill, J. Electrical Conductivity of Soils and Rock; Geonics Ltd.: Mississauga, ON, Canada, 1980. [Google Scholar]
- McNeill, J. Geonics EM38 Ground Conductivity meTer: EM38 Operating Manual; Geonics Limited: Mississauga, ON, Canada, 1990. [Google Scholar]
- Van Meerveld, H.J.I.; McDonnell, J.J. Assessment of multi-frequency electromagnetic induction for determining soil moisture patterns at the hillslope scale. J. Hydrol. 2009, 368, 56–67. [Google Scholar] [CrossRef]
- Rukun, L. Analytical Methods of Soil and Agricultural Chemistry; China Agricultural Science and Technology Press: Beijing, China, 1999. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News. 2002, 2, 18–22. [Google Scholar]
- Breiman, L. Random Forests. Machine. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Svetnik, V.; Liaw, A.; Tong, C.; Culberson, J.C.; Sheridan, R.P.; Feuston, B.P. Random Forest: A Classification and Regression Tool for Compound Classification and QSAR Modeling. J. Chem. Inf. Comput. Sci. 2003, 43, 1947–1958. [Google Scholar] [CrossRef]
- Strobl, C.S.; Boulesteix, A.-L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional variable importance for random forests. BMC Bioinform. 2008, 9, 307. [Google Scholar] [CrossRef]
- Grimm, R.; Behrens, T.; Märker, M.; Elsenbeer, H. Soil organic carbon concentrations and stocks on Barro Colorado Island—Digital soil mapping using Random Forests analysis. Geoderma 2008, 146, 102–113. [Google Scholar] [CrossRef]
- Genuer, R.; Poggi, J.-M.; Tuleau-Malot, C. Variable selection using random forests. Pattern. Recogn. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Nabiollahi, K.; Minasny, B.; Triantafilis, J. Comparing data mining classifiers to predict spatial distribution of USDA-family soil groups in Baneh region, Iran. Geoderma 2015, 253–254, 67–77. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2013. [Google Scholar]
- Efron, B.; Tibshirani, R. An Introduction to the Bootstrap; Chapman & Hall: London, UK, 1993. [Google Scholar]
- Adhikari, K.; Hartemink, A.E.; Minasny, B.; Kheir, R.B.; Greve, M.B.; Greve, M.H. Greve; Digital Mapping of Soil Organic Carbon Contents and Stocks in Denmark. PLoS ONE 2014, 9, 13. [Google Scholar] [CrossRef] [PubMed]
- Mamat, Z.; Halik, Ü.; Muhtar, P.; Abliz, A.; Nurmamat, I. Temporal variation of significant soil hydrological parameters in the Yutian oasis in Northwest China from 2001 to 2010. Environ. Earth Sci. 2016, 75, 16. [Google Scholar] [CrossRef]
- Bennett, D.; George, R. Using the EM38 to measure the effect of soil salinity on Eucalyptus globulus in south-western Australia. Agr. Water. Manag. 1995, 27, 69–85. [Google Scholar] [CrossRef]
- Mcfarlane, D.J.; Ryder, A.T. Salinity and Waterlogging on the Esperance Downs Research Station; Department of Agriculture and Food: Perth, Australia, 1990; p. 108.
- Misra, R.; Padhi, J. Assessing field-scale soil water distribution with electromagnetic induction method. J. Hydrol. 2014, 516, 200–209. [Google Scholar] [CrossRef]
- Wang, F.; Yang, S.; Yang, W.; Yang, X.; Jianli, D. Comparison of machine learning algorithms for soil salinity predictions in three dryland oases located in Xinjiang Uyghur Autonomous Region (XJUAR) of China. Eur.J. Remote Sens. 2019, 52, 256–276. [Google Scholar] [CrossRef]
- Jiang, Q.; Peng, J.; Biswas, A.; Hu, J.; Zhao, R.; He, K.; Shi, Z. Characterising dryland salinity in three dimensions. Sci. Total Environ. 2019, 682, 190–199. [Google Scholar] [CrossRef]
- Richards, L.A. Diagnosis and Improvement of Saline and Alkali Soils; USDA Agriculture Handbook; US Department of Agriculture: Washington, DC, USA, 1954; Volume 60, p. 290.
- Li, B.; Xiong, H.; Zhang, J. Dynamic of soil salt in soil profiles different in cultivation age and its affecting factors. Acta Geog. Sin. 2010, 47, 429–438. [Google Scholar]
- Lv, Z.Z.; Liu, G.M.; Yang, J. Soil salinity characteristics of Manas River valley in Xinjiang. Acta Geog. Sin. 2013, 50, 289–295. [Google Scholar]
- Wu, J.; Feng, C.; Liu, X.; Luo, D.; Qi, W.; Peng, J. Inversion of Soil Electrical Conductivity Based on Electromagnetic induction Data in the Arid Region of Southern Xinjiang. Chin. J. Soil. Sci. 2019, 50, 1278–1284. [Google Scholar]
- Altdorff, D.; Galagedara, L.; Nadeem, M.; Cheema, M.; Unc, A. Effect of agronomic treatments on the accuracy of soil moisture mapping by electromagnetic induction. Catena 2018, 164, 96–106. [Google Scholar] [CrossRef]
- Babaeian, E.; Sadeghi, M.; Franz, T.E.; Jones, S.B.; Tuller, M. Mapping soil moisture with the OPtical TRApezoid Model (OPTRAM) based on long-term MODIS observations. Remote Sens. Environ. 2018, 211, 425–440. [Google Scholar] [CrossRef]
- Toby, C. An Overview of the “Triangle Method” for Estimating Surface Evapotranspiration and Soil Moisture from Satellite Imagery. Sensors 2007, 7, 1612–1629. [Google Scholar]
- Liang, Z.; Chen, S.; Yang, Y.; Zhou, Y.; Shi, Z. High-resolution three-dimensional mapping of soil organic carbon in China: Effects of SoilGrids products on national modeling. Sci. Total Environ. 2019, 685, 480–489. [Google Scholar] [CrossRef] [PubMed]
- Bui, E.N. Soil salinity: A neglected factor in plant ecology and biogeography. J. Arid. Environ. 2013, 92, 14–25. [Google Scholar] [CrossRef]
- Akramkhanov, A.; Martius, C.; Park, S.; Hendrickx, J. Environmental factors of spatial distribution of soil salinity on flat irrigated terrain. Geoderma 2011, 163, 55–62. [Google Scholar] [CrossRef]
- Zhang, S. Spatial and Temporal Distribution of Soil Water and Its Stochastic Simulation in an Oasis Desert Ecotone; Northwest A & F univsersity: Shanxi, China, 2017. [Google Scholar]
- Li, X. Spatial-Temporal Variability of Soil Moisture and Influencing Factors in Northwest Arid Area of China; Institute of Soil and Water Conservation of Chinese Academy of Sciences: Beijing, China, 2019. [Google Scholar]
- Zhao, Z.Y.; Wang, R.H.; Yin, C.H.; Wang, L. Influence of spatial heterogeneity of soil salinity on plant community structure and composition of plain at south piedmont of Tianshan Mountains. Arid Land Geogr. 2007, 30, 839–845. [Google Scholar]
- Peng, J.; Biswas, A.; Jiang, Q.; Zhao, R.; Hu, J.; Hu, B.; Shi, Z. Estimating soil salinity from remote sensing and terrain data in southern Xinjiang Province, China. Geoderma 2019, 337, 1309–1319. [Google Scholar] [CrossRef]
- Xinjiang-agriculture-department-soil-census-office. Soil in Xinjiang; Science Press: Beijing, China, 1996. [Google Scholar]
- Huang, J.; McBratney, A.B.; Minasny, B.; Triantafilis, J. Monitoring and modelling soil water dynamics using electromagnetic conductivity imaging and the ensemble Kalman filter. Geoderma 2017, 285, 76–93. [Google Scholar] [CrossRef]
- Yang, X.-D.; Ali, A.; Xu, Y.-L.; Jiang, L.-M.; Lv, G.H. Soil moisture and salinity as main drivers of soil respiration across natural xeromorphic vegetation and agricultural lands in an arid desert region. Catena 2019, 177, 126–133. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Y.; Li, W.; Deng, H.; Fang, G. Potential impacts of climate change on vegetation dynamics in Central Asia. J. Geophys. Res. Atmos. 2015, 120, 12345–12356. [Google Scholar] [CrossRef]
- Price, J. Using spatial context in satellite data to infer regional scale evapotranspiration. IEEE Trans. Geosci. Remote Sens. 1990, 28, 940–948. [Google Scholar] [CrossRef]
- Gillies, R.R.; Carlson, T.N. Thermal Remote Sensing of Surface Soil Water Content With Partial Vegetation Cover for Incorporation Into Climate Models. J. Appl. Meteorol. 1995, 34, 745–756. [Google Scholar] [CrossRef]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar] [CrossRef]
- Petropoulos, G.P.; Carlson, T.; Wooster, M.J.; Islam, S. A review of Ts/VI remote sensing based methods for the retrieval of land surface energy fluxes and soil surface moisture. Prog. Phys. Geog. 2009, 33, 224–250. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, R.; Wan, Z.; Bi, Y.; Zhou, C.; Tang, B.-H.; Yan, G.; Zhang, X. A Review of Current Methodologies for Regional Evapotranspiration Estimation from Remotely Sensed Data. Sensors 2009, 9, 3801–3853. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Z.-Y.; Li, X.-Y.; Wu, H.-W.; Xiao, X.; Chen, H.-Y.; Wei, J.-Q. Using electromagnetic induction method to reveal dynamics of soil water and salt during continual rainfall events. Biosyst. Eng. 2016, 152, 3–13. [Google Scholar] [CrossRef]
- Brevik, E.C.; Fenton, T.E.; Lazari, A. Soil electrical conductivity as a function of soil water content and implications for soil mapping. Precis Agric. 2006, 7, 393–404. [Google Scholar] [CrossRef]
- Robinet, J.; Von Hebel, C.; Govers, G.; Van Der Kruk, J.; Minella, J.P.; Schlesner, A.; Ameijeiras-Mariño, Y.; Vanderborght, J. Spatial variability of soil water content and soil electrical conductivity across scales derived from Electromagnetic Induction and Time Domain Reflectometry. Geoderma 2018, 314, 160–174. [Google Scholar] [CrossRef]
- Peng, D.; Zhou, T. Why was the arid and semiarid northwest China getting wetter in the recent decades? J. Geophys. Res. Atmos. 2017, 122, 9060–9075. [Google Scholar] [CrossRef]
- Mao, X.; Li, M.; Shen, Y.; He, C. Analysis of the phreatic evaporation in Yarkant river basin, Xinjiang. Arid Land Geogr. 1998, 21, 44–49. [Google Scholar]
- Yao, J.; Chen, Y.; Zhao, Y.; Mao, W.; Xu, X.; Liu, Y.; Yang, Q. Response of vegetation NDVI to climatic extremes in the arid region of Central Asia: A case study in Xinjiang, China. Theor. Appl. Clim. Theor. 2017, 131, 1503–1515. [Google Scholar] [CrossRef]
- Liang, Z.; Chen, S.; Yang, Y.; Zhao, R.; Shi, Z.; Rossel, R.A.V. National digital soil map of organic matter in topsoil and its associated uncertainty in 1980’s China. Geoderma 2019, 335, 47–56. [Google Scholar] [CrossRef]
- Wisz, M.; Hijmans, R.; Elith, J.; Peterson, A.T.; Graham, C.; Guisan, A.; NCEAS Predicting Species Distributions Working Group. Effects of sample size on the performance of species distribution models. Divers. Distrib. 2008, 14, 763–773. [Google Scholar] [CrossRef]

| Auxiliary Data | Land Surface Parameters | Definition | Reference/Source | Soil Forming Factors |
|---|---|---|---|---|
| SoilGrids (250 m) | CRFVOL | Coarse fragments volumetric in % | [24] | S |
| OCSTHA | Soil organic carbon stock in tons/ha | S | ||
| OCDENS | Soil organic carbon density in kg/cubic-m | S | ||
| CECSOL | Cation exchange capacity of soil in cmolc/kg | S,P | ||
| PHIKCL | Soil pH × 10 in H2O | S,P | ||
| SNDPPT | Sand content (50–2000 micrometer) mass fraction in % | S,P | ||
| SLTPPT | Silt content (2–50 micrometer) mass fraction in % | S,P | ||
| Remote sensing data (30 m) | Landsat OLI | Band 1–7 | P,S,NS,A | |
| Minimum noise Fraction of OLI bands | MNF1,MNF2,MNF3 | P,S,NS,A | ||
| CSRI | Canopy response salinity index | [5] | O | |
| EEVI | Extended enhanced vegetation index | [51] | O | |
| GDVI | Generalized difference vegetation index | [52] | O | |
| CAI | carbonate index | [52] | P,S | |
| SIT | Salinity index | [53] | P,S | |
| CI | Clay index | [54] | P,S | |
| BI | Brightness index | [54] | P,S | |
| Land use (30 m) | Land use | Global 30-m surface land use\cover products (finer resolution observation and monitoring (FROM) | [69] | P,S,O,C |
| Climate (1 km) | AT | Air temperature | National Earth System Science Data Center | C |
| ET | evapotranspiration | |||
| TEM_NIGHT | Night surface temperature | |||
| TEM_DAY | Day surface temperature | |||
| Bioclimatic variables | Bio1, Bio2, Bio3… Bio19 | WorldClim | ||
| Terrain attributes (90 m) | VD | Valley depth | SAGA GIS | R |
| VDCN | Vertical distance to channel network | |||
| TWI | Topographic wetness index | |||
| SL | Slope length | |||
| SVF | Sky view factor | |||
| TPI | Topographic position index | |||
| MRVBF/MRRTF | Multiresolution index of valley bottom Flatness | |||
| SH | Slope height | |||
| NH | Normalized height | |||
| STH | Standardized height | |||
| MSP | Mid-slope position | |||
| TEX | Terrain surface texture | |||
| FA | Flow accumulation | |||
| CSC | Cross-section curvature | |||
| LC | Longitudinal curvature | |||
| RSP | Relative slope position |
| ECa/EC | Min | Max | Mean | SD | CV |
|---|---|---|---|---|---|
| ECah05 | 0.98 | 1292.41 | 329.45 | 315.10 | 1.18 |
| ECah01 | 1.53 | 1279.92 | 325.86 | 310.89 | 1.17 |
| ECav05 | 0.67 | 1898.60 | 350.14 | 336.87 | 1.15 |
| ECav01 | 1.39 | 1763.94 | 354.43 | 338.12 | 1.11 |
| EC0–10 cm | 0.08 | 88.35 | 7.27 | 12.75 | 1.75 |
| EC10–20 cm | 0.07 | 29.15 | 4.19 | 6.20 | 1.48 |
| EC20–40 cm | 0.05 | 21.23 | 3.33 | 5.14 | 1.54 |
| EC40–60 m | 0.06 | 18.88 | 2.96 | 4.47 | 1.51 |
| EC60–80 cm | 0.05 | 15.20 | 2.30 | 3.48 | 1.51 |
| EC80–100 cm | 0.07 | 13.75 | 2.08 | 2.94 | 1.41 |
| Depth | EC0–10 cm | EC10–20 cm | EC20–40 cm | EC40–60 m | EC60–80 cm | EC80–100 cm |
|---|---|---|---|---|---|---|
| EC0–10 cm | 1.00 ** | |||||
| EC10–20 cm | 0.83 ** | 1.00 ** | ||||
| EC20–40 cm | 0.71 ** | 0.94 ** | 1.00 ** | |||
| EC40–60 m | 0.67 ** | 0.90 ** | 0.95 ** | 1.00 ** | ||
| EC60–80 cm | 0.71 ** | 0.88 ** | 0.91 ** | 0.93 ** | 1.00 ** | |
| EC80–100 cm | 0.58 ** | 0.81 ** | 0.85 ** | 0.90 ** | 0.89 ** | 1.00 ** |
| Land Use | ECa/EC | EC0–10 cm | EC10–20 cm | EC20–40 cm | EC40–60 m | EC60–80 cm | EC80–100 cm |
|---|---|---|---|---|---|---|---|
| Farmland | ECah05 | 0.72 ** | 0.64 ** | 0.56 ** | 0.55 ** | 0.57 ** | 0.45 ** |
| ECah01 | 0.75 ** | 0.70 ** | 0.57 ** | 0.56 ** | 0.61 ** | 0.50 ** | |
| ECav05 | 0.63 ** | 0.61 ** | 0.57 ** | 0.55 ** | 0.58 ** | 0.52 ** | |
| ECav01 | 0.74 ** | 0.73 ** | 0.65 ** | 0.64 ** | 0.66 ** | 0.57 ** | |
| Shrub/grass | ECah05 | 0.29 | 0.40 ** | 0.57 ** | 0.54 ** | 0.56 ** | 0.34 * |
| ECah01 | 0.35 * | 0.40 ** | 0.58 ** | 0.53 ** | 0.64 ** | 0.47 ** | |
| ECav05 | 0.37 * | 0.43 ** | 0.64 ** | 0.63 ** | 0.56 ** | 0.40 ** | |
| ECav01 | 0.37 * | 0.44 ** | 0.65 ** | 0.64 ** | 0.62 ** | 0.53 ** | |
| Bare land | ECah05 | 0.33 * | 0.63 ** | 0.66 ** | 0.66 ** | 0.63 ** | 0.61 ** |
| ECah01 | 0.36 * | 0.70 ** | 0.74 ** | 0.75 ** | 0.71 ** | 0.68 ** | |
| ECav05 | 0.36 * | 0.64 ** | 0.71 ** | 0.69 ** | 0.66 ** | 0.62 ** | |
| ECav01 | 0.41 * | 0.71 ** | 0.77 ** | 0.76 ** | 0.72 ** | 0.68 ** |
| Land Use | Ecah05 | Ecah01 | Ecav05 | Ecav01 | ||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | |
| Farmland | 0.43 | 115.57 | 0.48 | 126.27 | 0.49 | 116.52 | 0.44 | 115.62 |
| Shrub/grass | 0.57 | 171.49 | 0.77 | 138.07 | 0.66 | 124.77 | 0.74 | 111.23 |
| Bare land | 0.84 | 151.27 | 0.88 | 129.27 | 0.89 | 143.24 | 0.91 | 120.70 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, J.; Yang, S.; Shi, Q.; Wei, Y.; Wang, F. Using Apparent Electrical Conductivity as Indicator for Investigating Potential Spatial Variation of Soil Salinity across Seven Oases along Tarim River in Southern Xinjiang, China. Remote Sens. 2020, 12, 2601. https://doi.org/10.3390/rs12162601
Ding J, Yang S, Shi Q, Wei Y, Wang F. Using Apparent Electrical Conductivity as Indicator for Investigating Potential Spatial Variation of Soil Salinity across Seven Oases along Tarim River in Southern Xinjiang, China. Remote Sensing. 2020; 12(16):2601. https://doi.org/10.3390/rs12162601
Chicago/Turabian StyleDing, Jianli, Shengtian Yang, Qian Shi, Yang Wei, and Fei Wang. 2020. "Using Apparent Electrical Conductivity as Indicator for Investigating Potential Spatial Variation of Soil Salinity across Seven Oases along Tarim River in Southern Xinjiang, China" Remote Sensing 12, no. 16: 2601. https://doi.org/10.3390/rs12162601
APA StyleDing, J., Yang, S., Shi, Q., Wei, Y., & Wang, F. (2020). Using Apparent Electrical Conductivity as Indicator for Investigating Potential Spatial Variation of Soil Salinity across Seven Oases along Tarim River in Southern Xinjiang, China. Remote Sensing, 12(16), 2601. https://doi.org/10.3390/rs12162601