A New Weighting Method by Considering the Physical Characteristics of Atmospheric Turbulence and Decorrelation Noise in SBAS-InSAR
Abstract
1. Introduction
2. Methodology
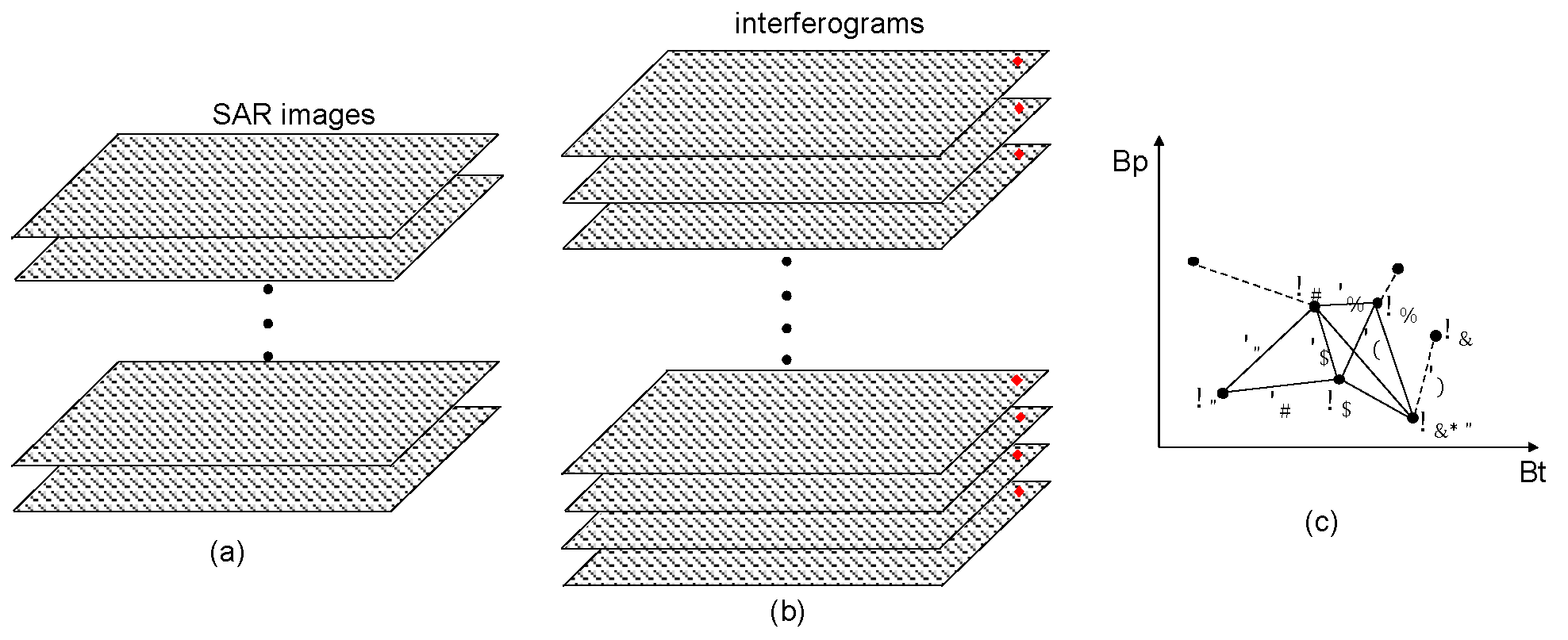
2.1. Review of SBAS-InSAR Technique
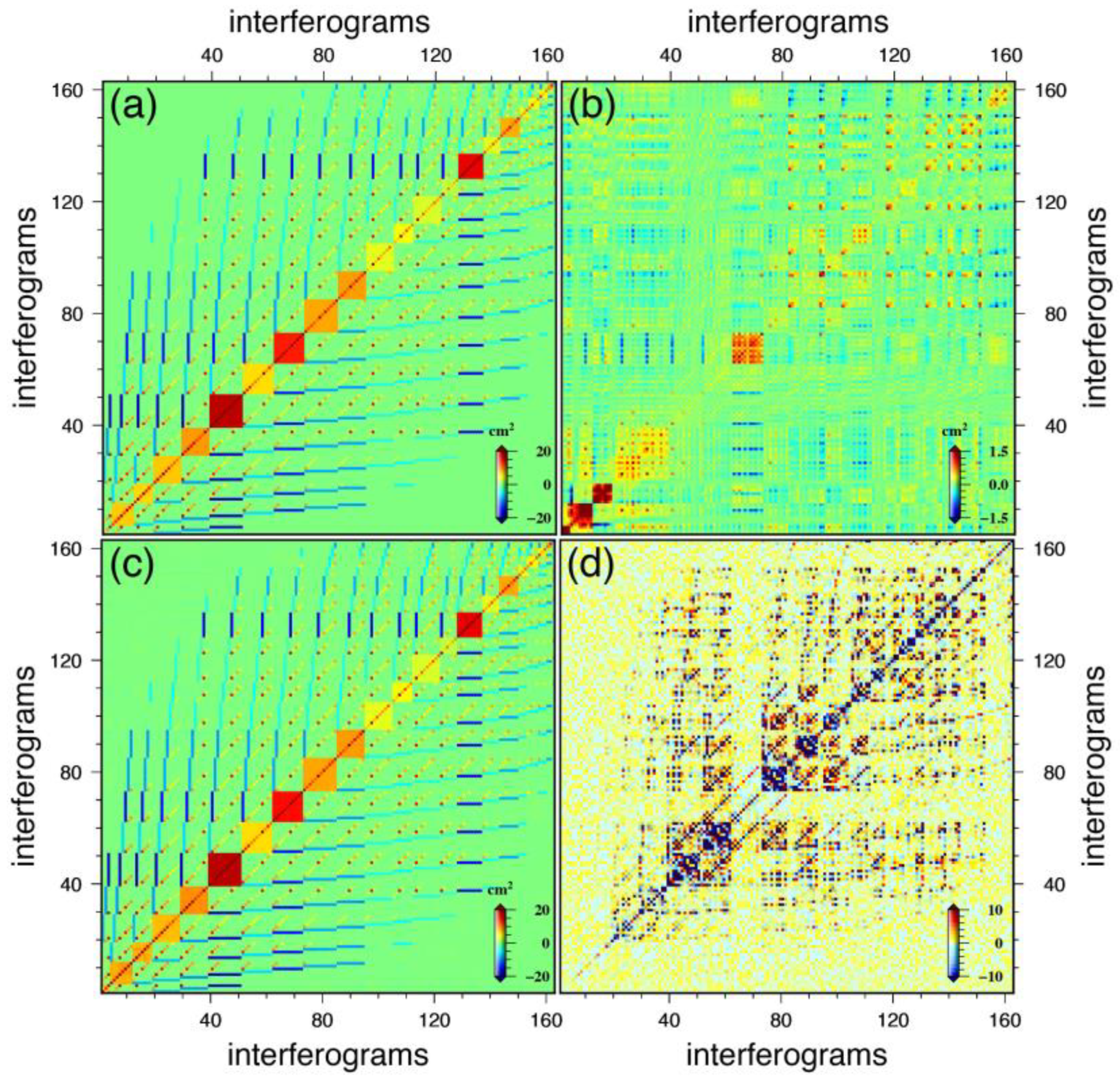
2.2. The Variance-Covariance Matrix of Atmospheric Phase in SBAS-InSAR
2.3. The Variance-Covariance Matrix of Decorrelation Noise in SBAS-InSAR
2.4. The Weight of Each Pixel in SBAS-InSAR
3. Results
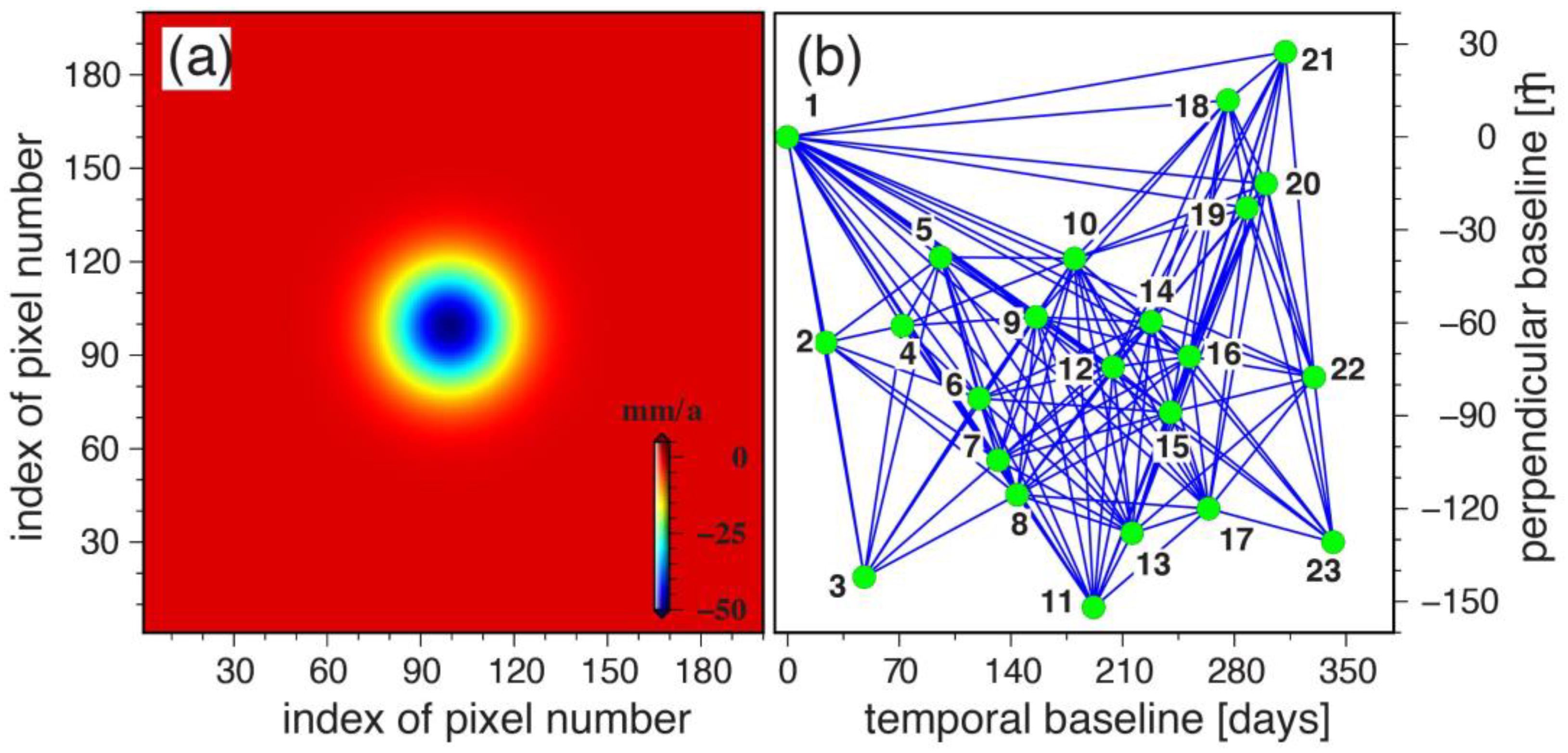
3.1. Synthetic Test and Results
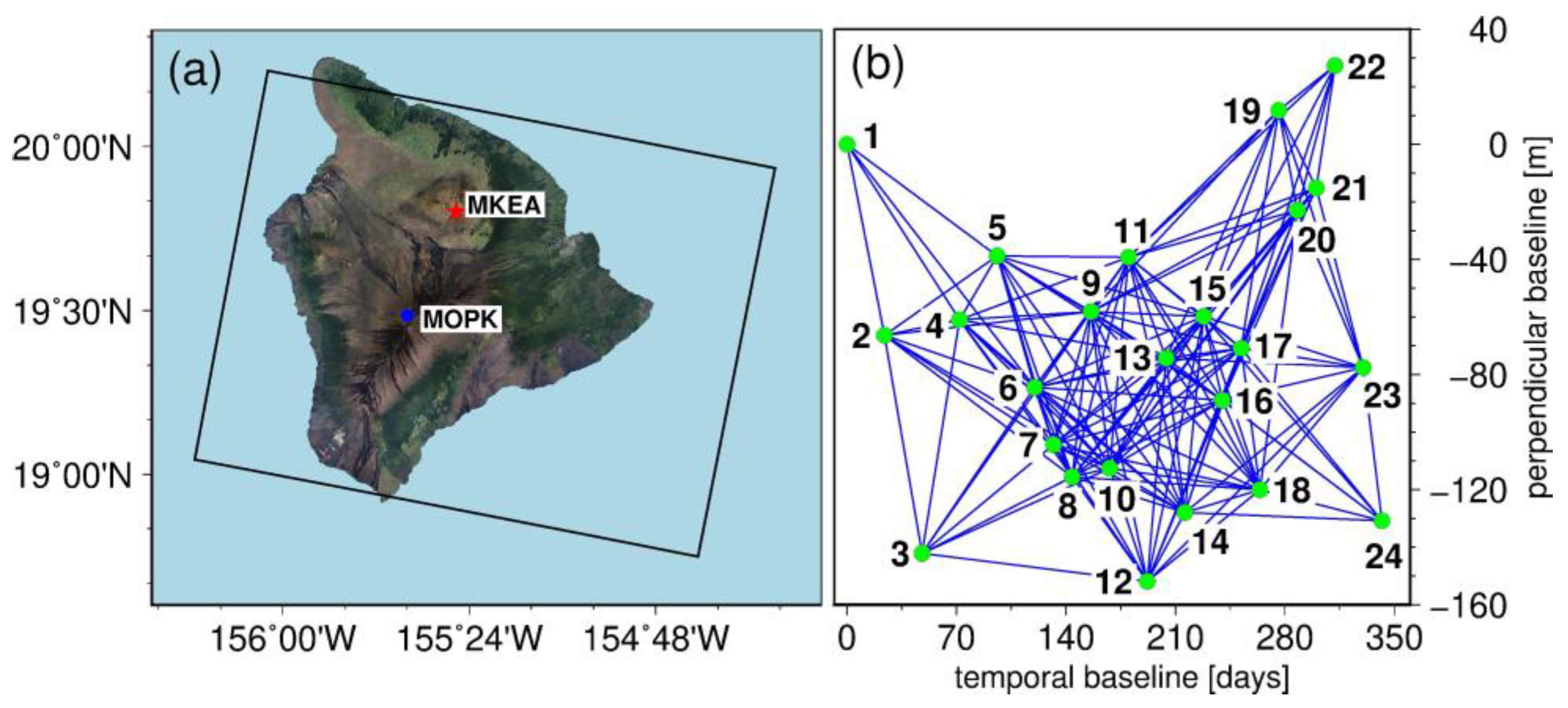
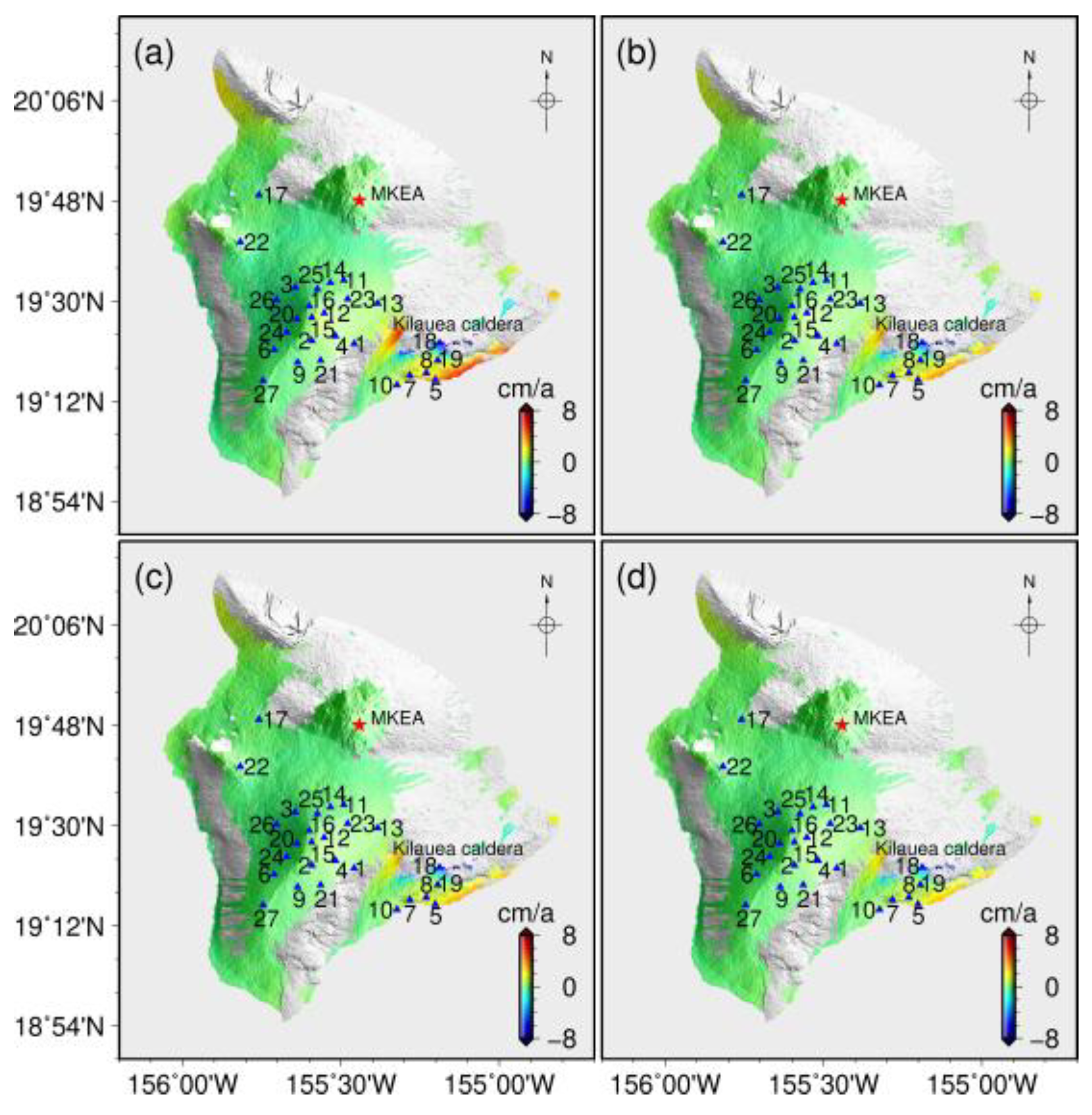
3.2. Real Test Case Example: Big Island of Hawaii
4. Discussions
4.1. The Necessity of Considering Decorrelation Noise
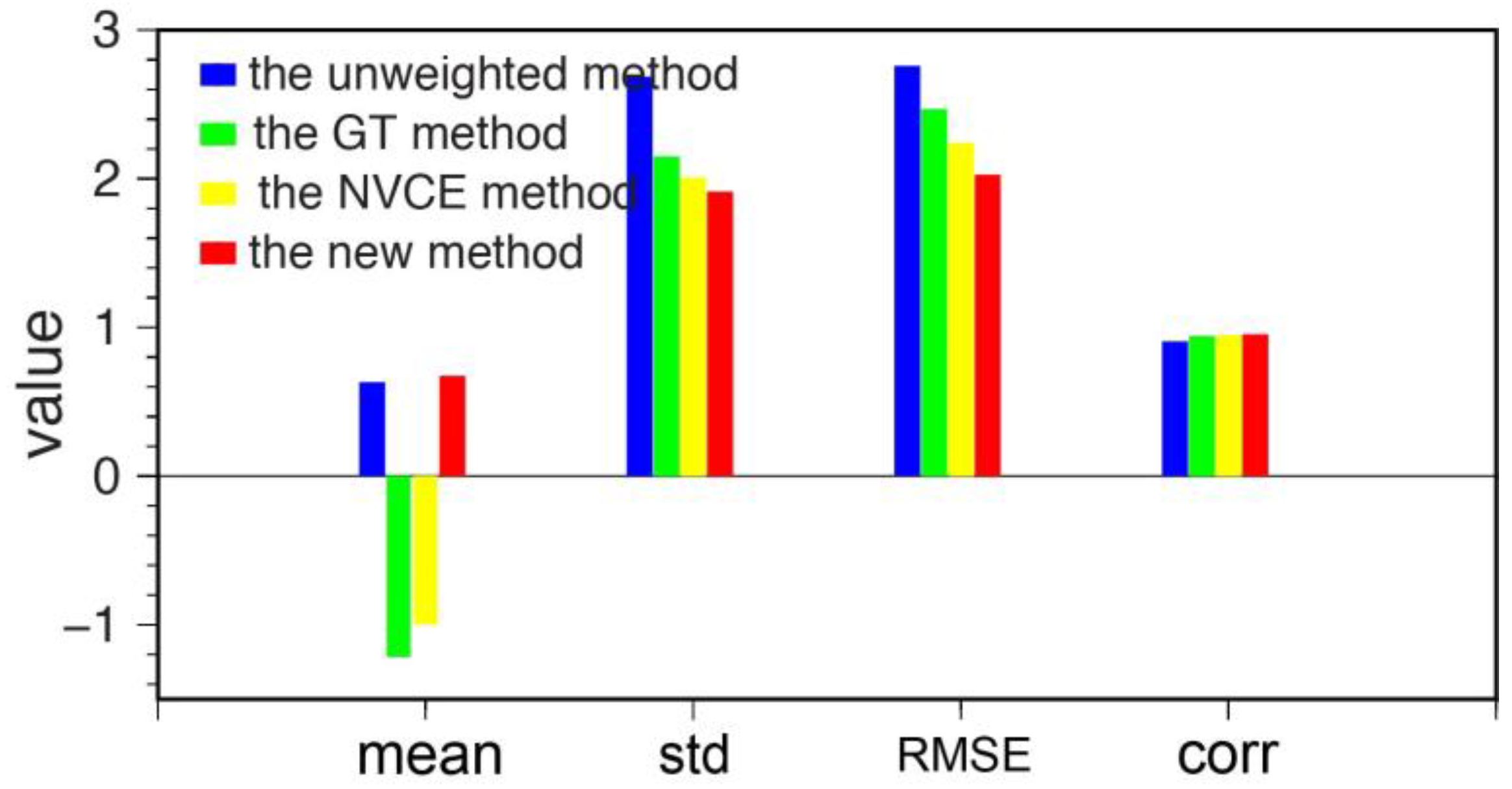
4.2. Average Performance
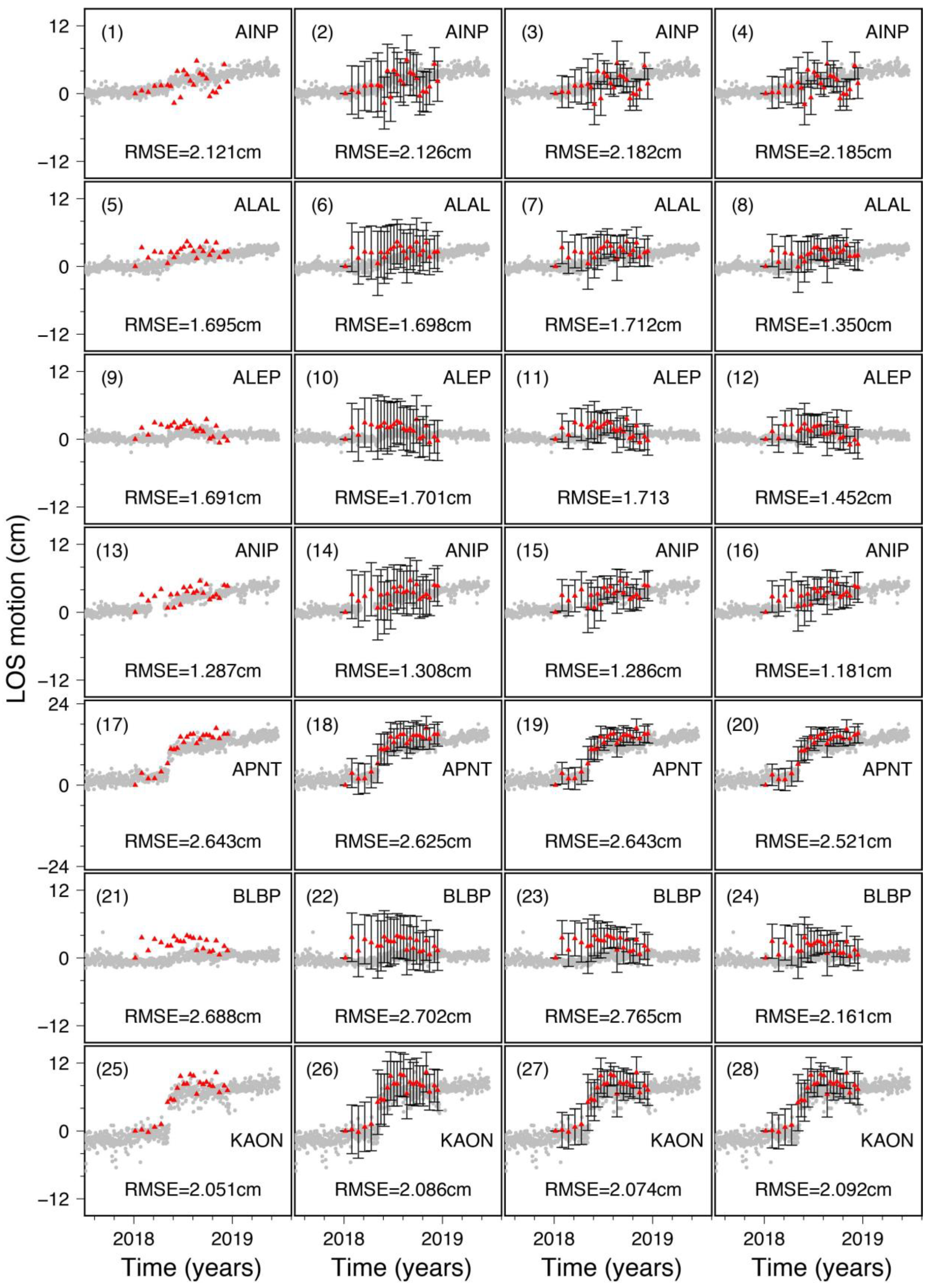
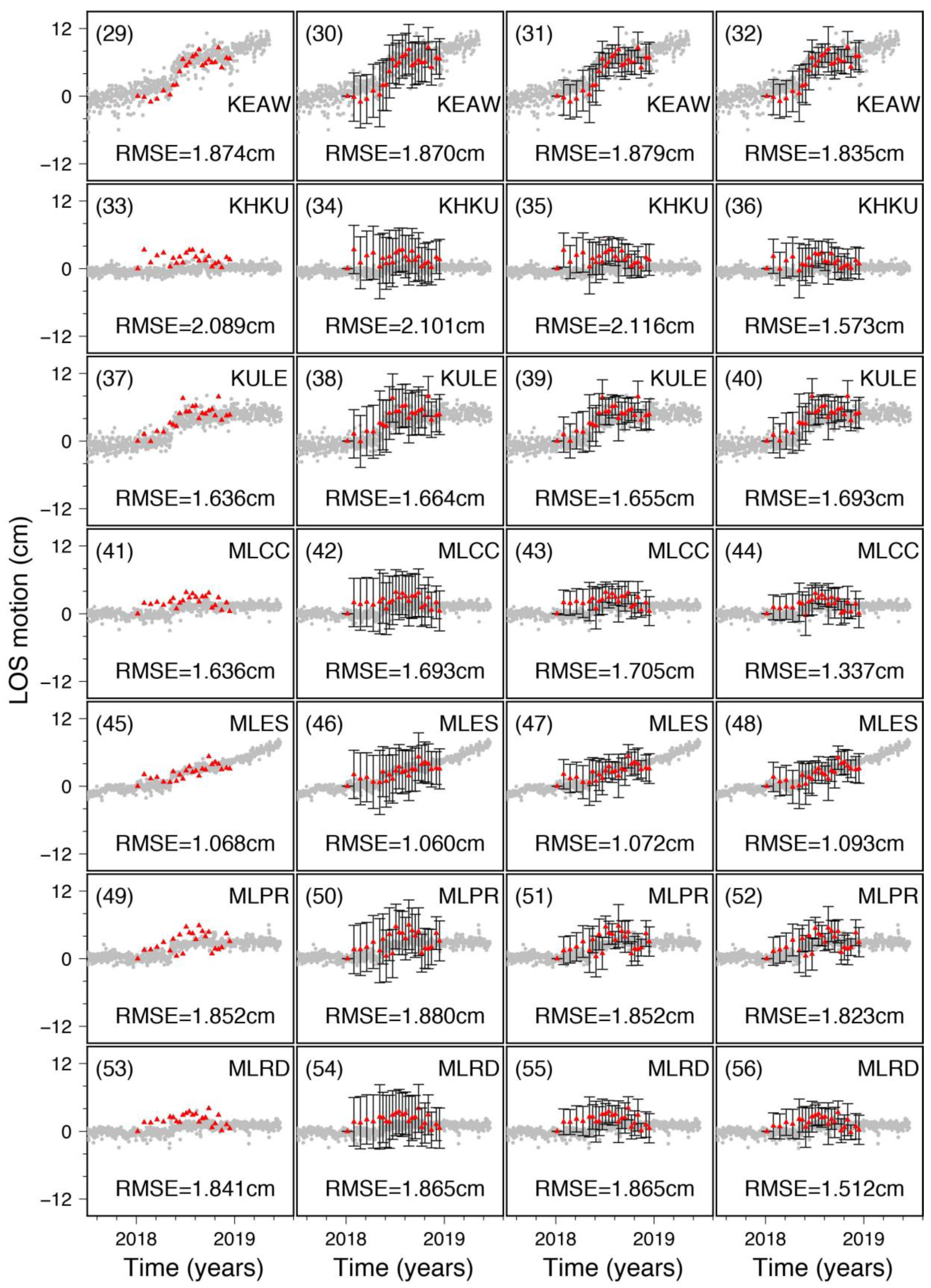
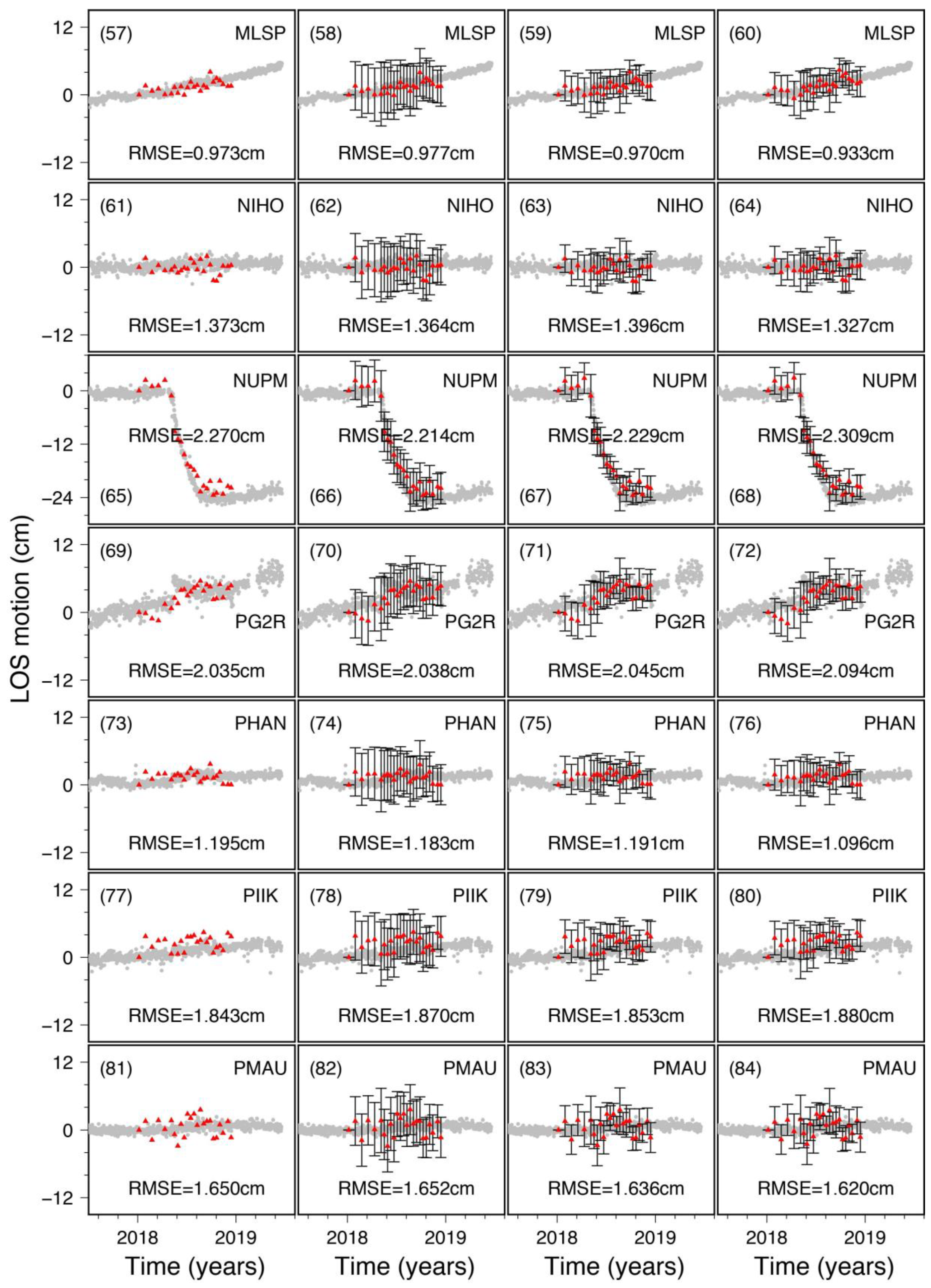
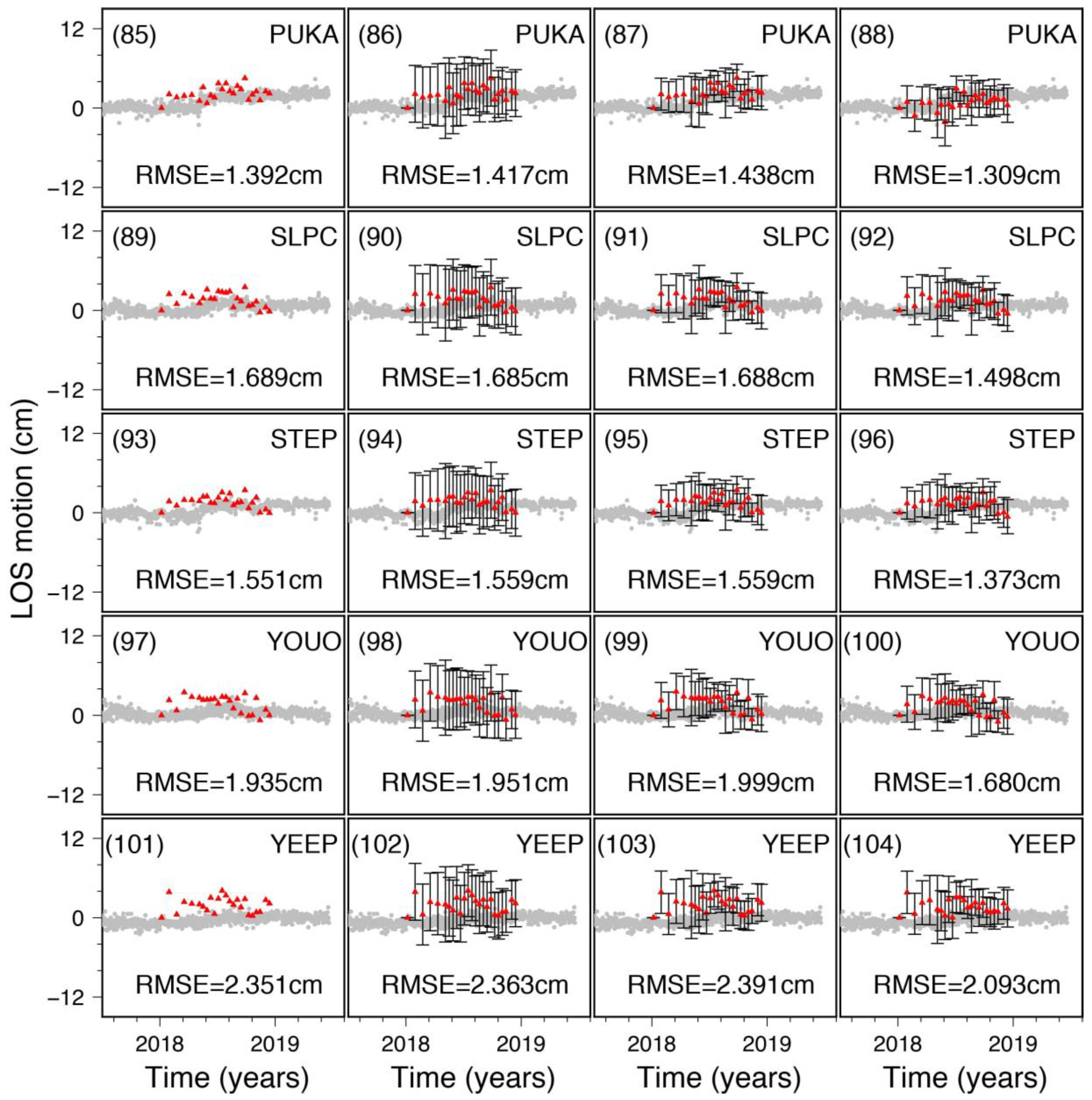
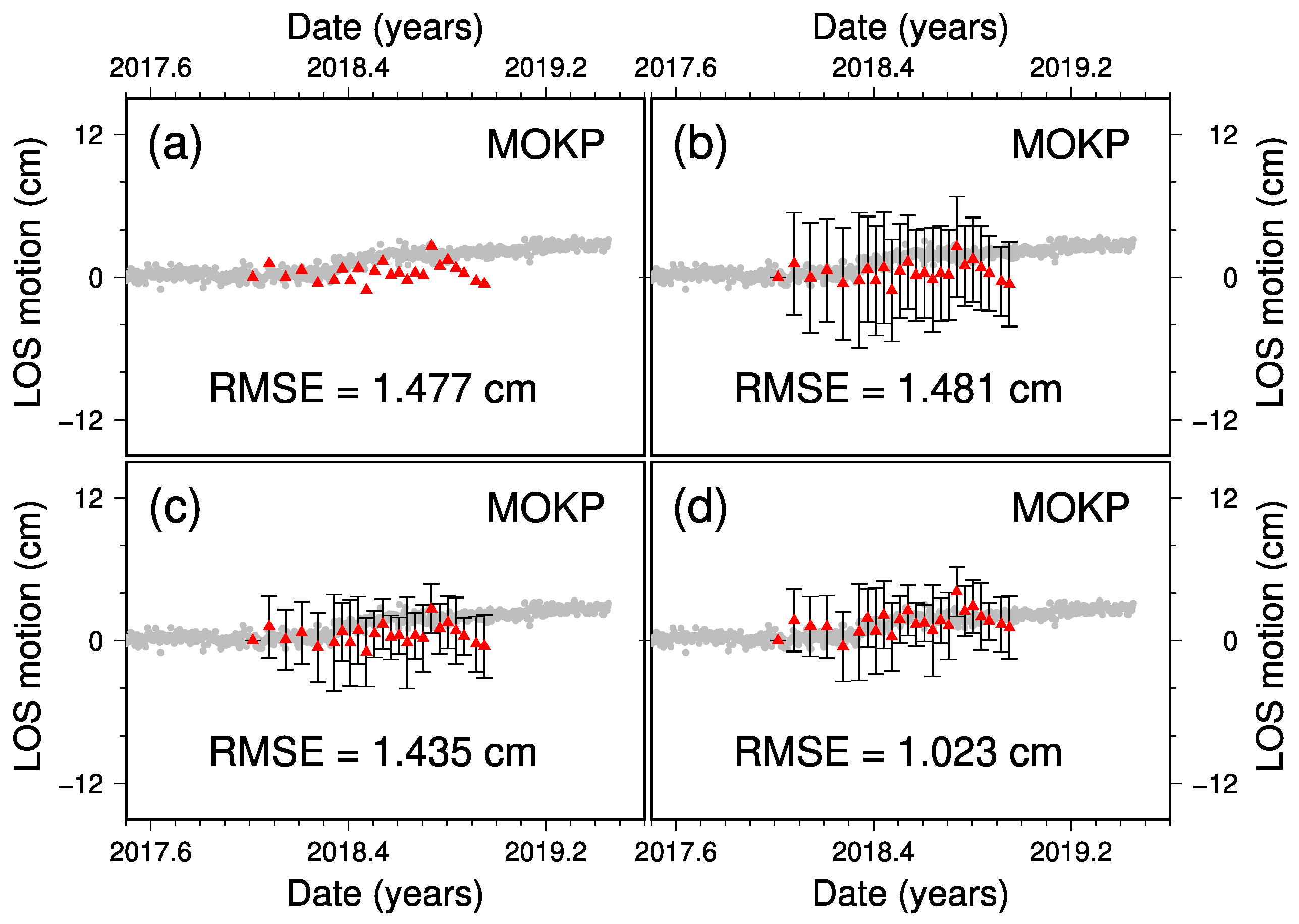
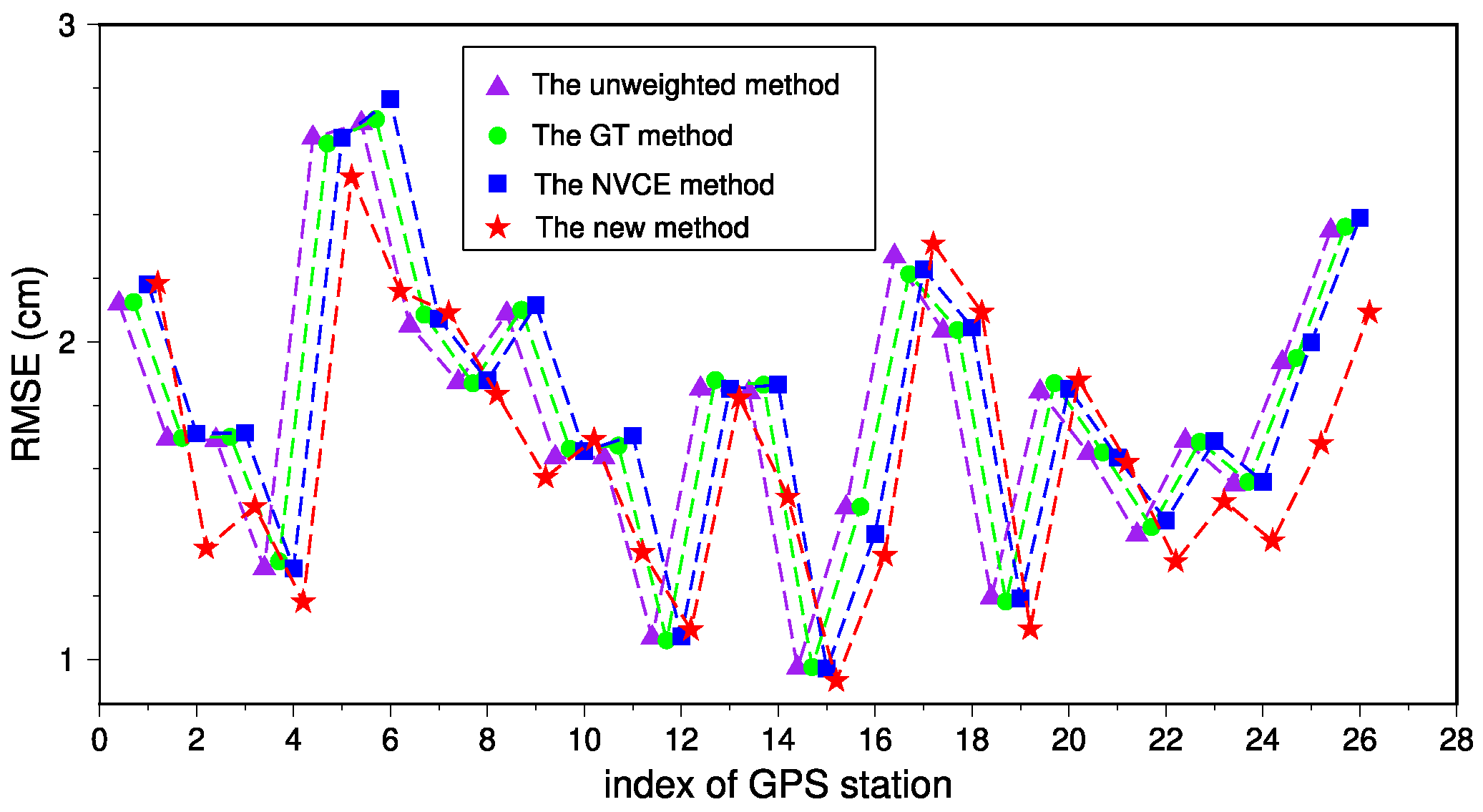
4.3. Validation of the Performances with GNSS Datasets
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Duan, M.; Xu, B.; Li, Z.W.; Cao, Y.M.; Hu, J.; Xu, W.B.; Wei, J.C.; Feng, G.C. Non-differential water vapor estimation from SBAS-InSAR. J. Atmos. Sol. Terr. Phys. 2020, 204, 105284. [Google Scholar] [CrossRef]
- Mateus, P.; Miranda, P.M.A.; Nico, G.; Catalão, J.; Pinto, P.; Tomé, R. Assimilating InSAR maps of water vapor to improve heavy rainfall forecasts: A case study with two successive storms. J. Geophys. Res. Atmos. 2018, 123, 3341–3355. [Google Scholar] [CrossRef]
- Miranda, P.M.; Mateus, P.; Nico, G.; Catalão, J.; Tomé, R.; Nogueira, M. InSAR meteorology: High-resolution geodetic data can increase atmospheric predictability. Geophys. Res. Lett. 2019, 46, 2949–2955. [Google Scholar] [CrossRef]
- Tang, W.; Liao, M.; Zhang, L.; Li, W.; Yu, W. High-spatial-resolution mapping precipitable water vapor using SAR interferograms, GPS observations and ERA-Interim reanalysis. Atmos. Meas. Tech. 2016, 9, 4487–4501. [Google Scholar] [CrossRef]
- Youhei, K.; Masanobu, S.; Masato, F. InSAR observation and numerical modeling of the water vapor signal during a heavy rain: A case study of the 2008 Seino event, central Japan. Geophys. Res. Lett. 2013, 40, 4740–4744. [Google Scholar]
- Du, Y.N.; Zhang, L.; Feng, G.C.; Lu, Z.; Sun, Q. On the accuracy of topographic residuals retrieved by MTInSAR. IEEE Trans. Geosci. Remote Sens. 2016, 55, 1053–1065. [Google Scholar] [CrossRef]
- Hu, J.; Li, Z.W.; Ding, X.L.; Zhu, J.J.; Zhang, L.; Sun, Q. Resolving three-dimensional surface displacements from InSAR measurements: A review. Earth Sci. Rev. 2014, 133, 1–17. [Google Scholar] [CrossRef]
- Yang, Z.F.; Li, Z.W.; Zhu, J.J.; Preusse, A.; Hu, J.; Feng, G.C.; Yi, H.W.; Papst, M. Time-series 3D Mining-Induced Large Displacement Modeling and Roubst Estimation from a Single-Geometry SAR Amplitude Dataset. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3600–3610. [Google Scholar] [CrossRef]
- Liu, J.H.; Hu, J.; Li, Z.W.; Zhu, J.J.; Sun, Q.; Gan, J. A method for measuring 3-D surface deformations with InSAR based on strain model and variance component estimation. IEEE Trans. Geosci. Remote Sens. 2018, 56, 239–250. [Google Scholar] [CrossRef]
- Liu, J.H.; Hu, J.; Xu, W.B.; Li, Z.W.; Zhu, J.J.; Ding, X.L.; Zhang, L. Complete three-dimensional coseismic deformation field of the 2016 central tottori earthquake by integrating left- and right-looking InSAR observations with the improved SM-VCE method. J. Geophys. Res. Solid Earth 2019, 124, 12099–12115. [Google Scholar] [CrossRef]
- Wu, S.B.; Zhang, L.; Ding, X.L.; Perissin, D. Pixel-wise MTInSAR estimator for integration of coherent point selection and unwrapped phase vector recovery. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2659–2668. [Google Scholar] [CrossRef]
- Wu, S.B.; Yang, Z.F.; Ding, X.L.; Zhang, B.C.; Zhang, L.; Lu, Z. Two decades settlement of Hong Kong international airpory measured with multi-temporal InSAR. Remote Sens. Environ. 2020, 248, 111976. [Google Scholar] [CrossRef]
- Zebker, H.A.; Rosen, P.A.; Hensley, S. Atmospheric effects in interferometric synthetic aperture radar surface deformation and topographic maps. J. Geophys. Res. Solid Earth 1997, 102, 7547–7563. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Springer Science & Business Media: Berlin, Germany, 2001. [Google Scholar]
- Li, Z.W.; Cao, Y.M.; Wie, J.C.; Duan, M.; Wu, L.X.; Hou, J.X.; Zhu, J.J. Time-Series InSAR Ground Deformation Monitoring: Atmospheric Delay Modeling and Estimating. Earth Sci. Rev. 2019, 192, 258–284. [Google Scholar] [CrossRef]
- Qu, C.Y.; Shan, X.J.; Zhang, G.H.; Song, X.G.; Guo, L.M. Influence of interferometric baseline on measurements of seismic deformation: A case study on the 1997 mani, tibet m 7.7 earthquake. Seismol. Geol. 2012, 34, 672–680. [Google Scholar]
- Xu, B.; Li, Z.W.; Zhu, Y.; Shi, J.C.; Feng, G.C. SAR interferometric baseline refinement based on flat-earth phase without a ground control point. Remote Sens. 2020, 12, 233. [Google Scholar] [CrossRef]
- Xu, B.; Li, Z.W.; Zhu, Y.; Shi, J.C.; Feng, G.C. Kinematic coregistration of Sentinel-1 TOPSAR images based on sequential least squares adjustment. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 3083–3093. [Google Scholar] [CrossRef]
- Xu, W.B.; Li, Z.W.; Ding, X.L.; Zhu, J.J. Interpolating Atmospheric Water Vapor Delay by Incorporating Terrain Elevation Information. J. Geod. 2012, 85, 555–564. [Google Scholar] [CrossRef]
- Li, Z.W.; Xu, W.B.; Feng, G.C.; Hu, J.; Wang, C.C.; Ding, X.L.; Zhu, J.J. Correcting atmospheric effects on InSAR with MERIS water vapor data and elevation-dependent interpolation model. Geophys. J. Int. 2012, 189, 898–910. [Google Scholar] [CrossRef]
- Liang, H.Y.; Zhang, L.; Ding, X.L.; Lu, Z.; Li, X. Toward Mitigating Stratified Tropospheric Delays in Multitemporal InSAR: A Quadtree Aided Joint Model. IEEE Trans. Geosci. Remote Sens. 2018, 57, 291–303. [Google Scholar] [CrossRef]
- Shirzaei, M.; Walter, T.R. Estimating the effect of satellite orbital error using wavelet-based robust regression applied to insar deformation data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4600–4605. [Google Scholar] [CrossRef]
- Xu, B.; Li, Z.W.; Wang, Q.J.; Jiang, M.; Zhu, J.J.; Ding, X.L. A Refine Strategy for Removing Composite Errors of SAR Interferogram. IEEE Trans. Geosci. Remote Sens. Lett. 2011, 11, 143–147. [Google Scholar] [CrossRef]
- Li, Z.H.; Fielding, E.J.; Cross, P.; Preusker, R. Advanced inSAR atmospheric correction: MERIS/MODIS combination and stacked water vapor models. Int. J. Remote Sens. 2009, 30, 3343–3363. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.H.; Penna, N.T. Interferometric synthetic aperture radar atmospheric correction using a GPS-based iterative tropospheric decomposition model. Remote Sens. Environ. 2018, 204, 109–121. [Google Scholar] [CrossRef]
- Doin, M.P.; Lasserre, C.; Peltzer, G.; Cavalié, O.; Doubre, C. Corrections of stratified tropospheric delays in SAR interferometry: Validation with global atmospheric models. J. Appl. Geophys. 2009, 69, 35–50. [Google Scholar] [CrossRef]
- Jolivet, R.; Grandin, R.; Lasserre, C.; Doin, M.P.; Peltzer, G. Systematic InSAR tropospheric phase delay corrections from global meteorological reanalysis data. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Azeriansyah, R.; Harintaka. Integration PS-InSAR and MODIS PWV data to monitor land subsidence in Semarang city 2015–2018. In Proceedings of the 1st International Conference on Geodesy, Geomatics, and Land Administration, Semarang, Indonesia, 24–25 July 2019; pp. 66–76. [Google Scholar]
- Xu, C.J.; Wang, H.; Jiang, G.Y. Study on crustal deformation of Wenchuan Ms8.0 earthquake using wide-swath ScanSAR and MODIS. Geod. Geodyn. 2011, 2, 1–6. [Google Scholar]
- Mateus, P.; Nico, G.; Catalão, J. Interpolating MERIS and GPS measurements of precipitable water vapor (PWV) to estimate atmospheric phase delay maps. Remote Sens. Clouds Atmos. XV 2010, 7827, 782713. [Google Scholar]
- Puyssegur, B.; Michek, R.; Avouac, P. Tropospheric Phase Delay in Interferometric Synthetic Aperture Radar Estimated from Meteorological Model and Multispectral imagery. J. Geophys. Res. Solid Earth 2007, 112, B05419. [Google Scholar] [CrossRef]
- Gong, W.; Meyer, F.; Webley, P.W.; Morton, D.; Liu, S. Performance analysis of atmospheric correction in InSAR data based on the Weather Research and Forecasting Model (WRF). In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 2900–2903. [Google Scholar]
- Mateus, P.; Nico, G.; Catalão, J. Uncertainty assessment of the estimated atmospheric delay obtained by a numerical weather model (NMW). IEEE Trans. Geosci. Remote Sens. 2015, 53, 6710–6717. [Google Scholar] [CrossRef]
- Thomas, H.; Youhei, K.; Shingo, S.; Ryuichi, I.; Masato, F.; Tetsuro, K.; Yasuhiro, K. On the importance of accurately ray-traced troposphere corrections for Interferometric SAR data. J. Geod. 2010, 84, 537–546. [Google Scholar]
- Kinoshita, Y.; Furuya, M.; Hobiger, T.; Ichikawa, R. Are numerical weather model outputs helpful to reduce tropospheric delay signals in InSAR data? J. Geod. 2012, 87, 267–277. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Bovenga, F.; Giacovazzo, V.M.; Refice, A.; Veneziani, N. Multichromatic analysis of InSAR data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4790–4799. [Google Scholar] [CrossRef]
- Biondi, F.; Clemente, C.; Orlando, D. An atmospheric phase screen estimation strategy based on multichromatic analysis for differential interferometric synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7269–7280. [Google Scholar] [CrossRef]
- González, P.J.; Fernández, J. Error Estimation in Multitemporal InSAR Deformation Time Series, with Application to Lanzarote, Canary Islands. J. Geophys. Res. Solid Earth 2011, 116, B10404. [Google Scholar] [CrossRef]
- Cao, Y.M.; Li, Z.W.; Wei, J.C.; Duan, M.; Feng, G.C. Stochastic Modeling for Time Series InSAR: With Emphasis on Atmospheric Effects. J. Geod. 2018, 92, 185–204. [Google Scholar] [CrossRef]
- Reinisch, E.C.; Cardiff, M.; Feigl, K.L. Graph Theory for Analyzing Pair-Wise Data: Application to Geophysical Model Parameters Estimated from Interferometric Synthetic Aperture Radar Data at Okmok Volcano, Alaska. J. Geod. 2018, 91, 9–24. [Google Scholar] [CrossRef]
- Cressie, N. Statistics for Spatial Data; John and Wiley and Sons: Hoboken, NJ, USA, 1993. [Google Scholar]
- Strozzi, T.; Wegmuller, U.; Werner, C.; Wiesmann, A. Measurement of slow uniform surface displacement with mm/year accuracy. In Proceedings of the IGARSS, Honolulu, HI, USA, 24–28 July 2000; Volume 5, pp. 24–28. [Google Scholar]
- Zebker, H.A.; Villasenor, J. Decorrelation in interferometric radar echos. IEEE Trans. Geosci. Remote Sens. 1992, 30, 950–959. [Google Scholar] [CrossRef]
- Esfahany, S.S. Exploitation of Distributed Scatterers in Synthetic Aperture Radar Interferometry. Ph.D. Thesis, Delft University of Technology, Delft, The Netherland, 2017. [Google Scholar]
- Chen, K.J.; Smith, J.D.; Avouac, J.P.; Liu, Z.; Song, Y.T.; Gualandi, A. Triggering of The Mw 7.2 Hawaii Earthquake of 4 May 2018 by A Dike Intrusion. Geophys. Res. Lett. 2019, 46, 2503–2510. [Google Scholar] [CrossRef]
- Casu, F.; Lanari, R.; Sansosti, E.; Poland, M.; Miklius, A.; Solaro, G.; Tzzani, P. SBAS-InSAR analysis of surface deformation at Mauna Loa and Kilauea volcanoes in Hawaii. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009; Volume 4, pp. 41–44. [Google Scholar]
- Gui, Q.; Guo, J. Study on methods for solving ill-condition equations. J. Geod. Geodyn. 2004, 24, 15–18. [Google Scholar]
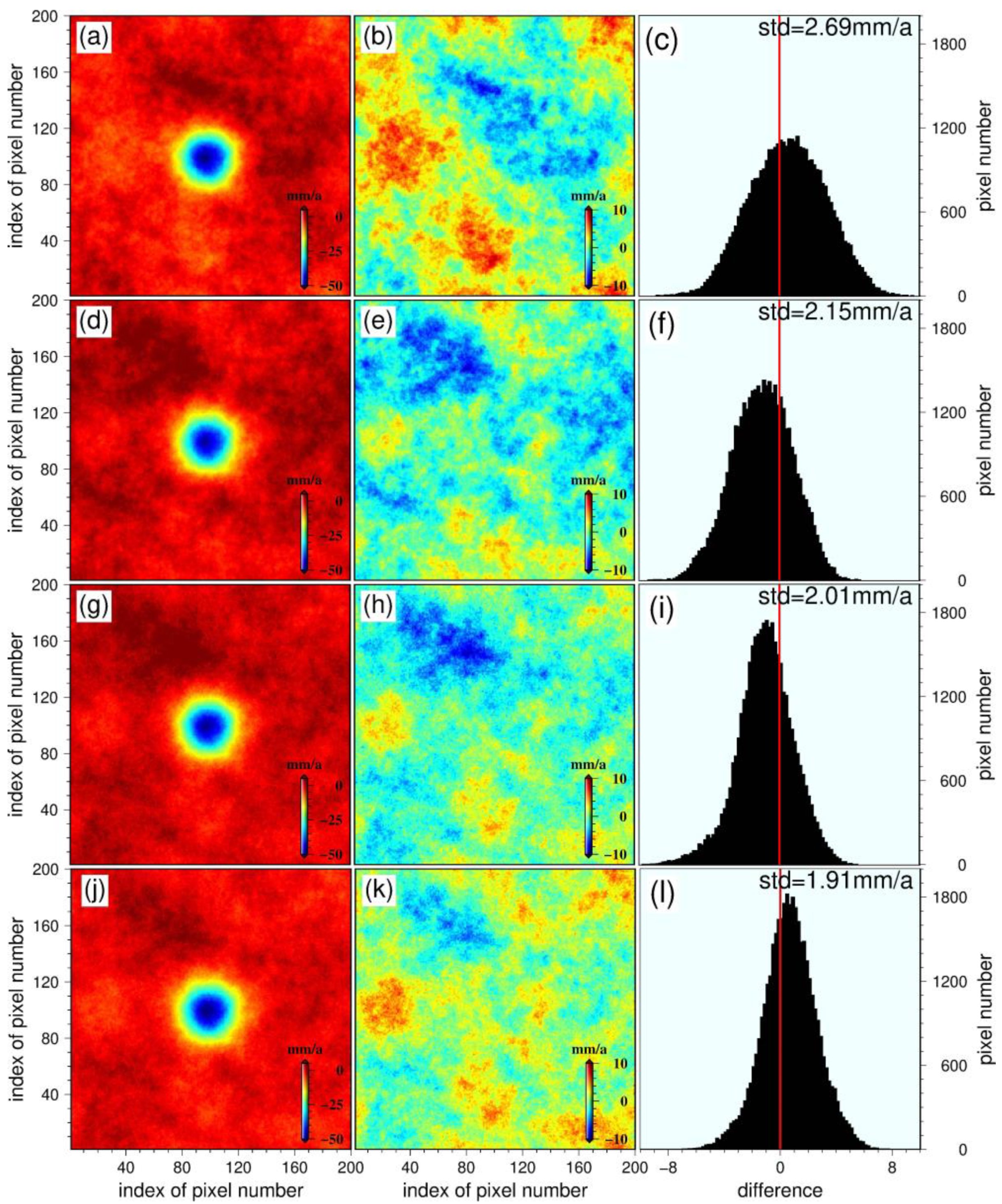
| Method | std(mm/a) | Kurtosis | Skewness |
|---|---|---|---|
| The NVCE method | 2.01 | 3.53 | −0.28 |
| The new method | 1.91 | 3.23 | −0.06 |
| Number | Orbit Model | Orbit Number | Imaging Time | Time Baseline (Day) | Perpendicular Baseline (m) |
|---|---|---|---|---|---|
| 1 | Descending | 09038 | 2018-01-05 | 0 | 0 |
| 2 | Descending | 09388 | 2018-01-29 | 24 | −66.35 |
| 3 | Descending | 09738 | 2018-02-22 | 48 | −142.10 |
| 4 | Descending | 10088 | 2018-03-18 | 72 | −60.95 |
| 5 | Descending | 10438 | 2018-04-11 | 96 | −38.77 |
| 6 | Descending | 10788 | 2018-05-05 | 120 | −84.43 |
| 7 | Descending | 10963 | 2018-05-17 | 132 | −104.36 |
| 8 | Descending | 11138 | 2018-05-29 | 144 | −115.50 |
| 9 | Descending | 11313 | 2018-06-10 | 156 | −58.11 |
| 10 | Descending | 11488 | 2018-06-22 | 168 | −112.54 |
| 11 | Descending | 11663 | 2018-07-04 | 180 | −39.20 |
| 12 | Descending | 11838 | 2018-07-16 | 192 | −151.86 |
| 13 | Descending | 12013 | 2018-07-28 | 204 | −74.30 |
| 14 | Descending | 12188 | 2018-08-09 | 216 | −127.93 |
| 15 | Descending | 12363 | 2018-08-21 | 228 | −59.77 |
| 16 | Descending | 12538 | 2018-09-02 | 240 | −88.92 |
| 17 | Descending | 12713 | 2018-09-14 | 252 | −70.85 |
| 18 | Descending | 12888 | 2018-09-26 | 264 | −120.01 |
| 19 | Descending | 13063 | 2018-10-08 | 276 | 11.81 |
| 20 | Descending | 13238 | 2018-10-20 | 288 | −22.91 |
| 21 | Descending | 13413 | 2018-11-01 | 300 | −15.14 |
| 22 | Descending | 13588 | 2018-11-13 | 312 | 27.40 |
| 23 | Descending | 24834 | 2018-12-01 | 330 | −77.53 |
| 24 | Descending | 25009 | 2018-12-13 | 342 | −130.78 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, M.; Xu, B.; Li, Z.; Wu, W.; Cao, Y.; Liu, J.; Wang, G.; Hou, J. A New Weighting Method by Considering the Physical Characteristics of Atmospheric Turbulence and Decorrelation Noise in SBAS-InSAR. Remote Sens. 2020, 12, 2557. https://doi.org/10.3390/rs12162557
Duan M, Xu B, Li Z, Wu W, Cao Y, Liu J, Wang G, Hou J. A New Weighting Method by Considering the Physical Characteristics of Atmospheric Turbulence and Decorrelation Noise in SBAS-InSAR. Remote Sensing. 2020; 12(16):2557. https://doi.org/10.3390/rs12162557
Chicago/Turabian StyleDuan, Meng, Bing Xu, Zhiwei Li, Wenhao Wu, Yunmeng Cao, Jihong Liu, Guanya Wang, and Jingxin Hou. 2020. "A New Weighting Method by Considering the Physical Characteristics of Atmospheric Turbulence and Decorrelation Noise in SBAS-InSAR" Remote Sensing 12, no. 16: 2557. https://doi.org/10.3390/rs12162557
APA StyleDuan, M., Xu, B., Li, Z., Wu, W., Cao, Y., Liu, J., Wang, G., & Hou, J. (2020). A New Weighting Method by Considering the Physical Characteristics of Atmospheric Turbulence and Decorrelation Noise in SBAS-InSAR. Remote Sensing, 12(16), 2557. https://doi.org/10.3390/rs12162557






