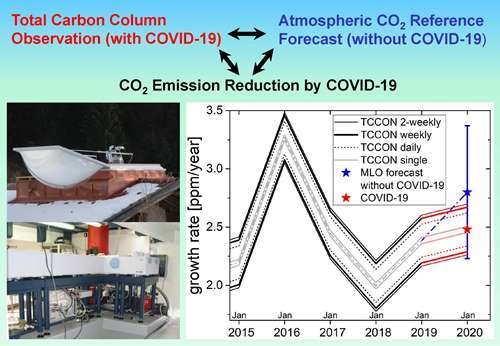
Can We Measure a COVID-19-Related Slowdown in Atmospheric CO2 Growth? Sensitivity of Total Carbon Column Observations
Abstract
1. Introduction
2. Data and Methods
2.1. Total Carbon Column Observations
2.1.1. XCO2 Data Set
2.1.2. TCCON Sites
2.1.3. TCCON Time Series and Averaging
2.2. Mathematics to Derive Trends, Annual Growth Rates, and Related Confidence Intervals
2.2.1. Model Fit
2.2.2. Confidence Intervals for Model Fit Parameters
2.2.3. Combined Trends from Multiple Sites
2.2.4. Annual Growth Rates
2.2.5. Confidence Intervals for Annual Growth Rates
2.2.6. Combined Annual Growth Rates from Multiple Sites
2.3. Forecast of 2020 Annual Growth Rate for Mauna Loa
3. Results
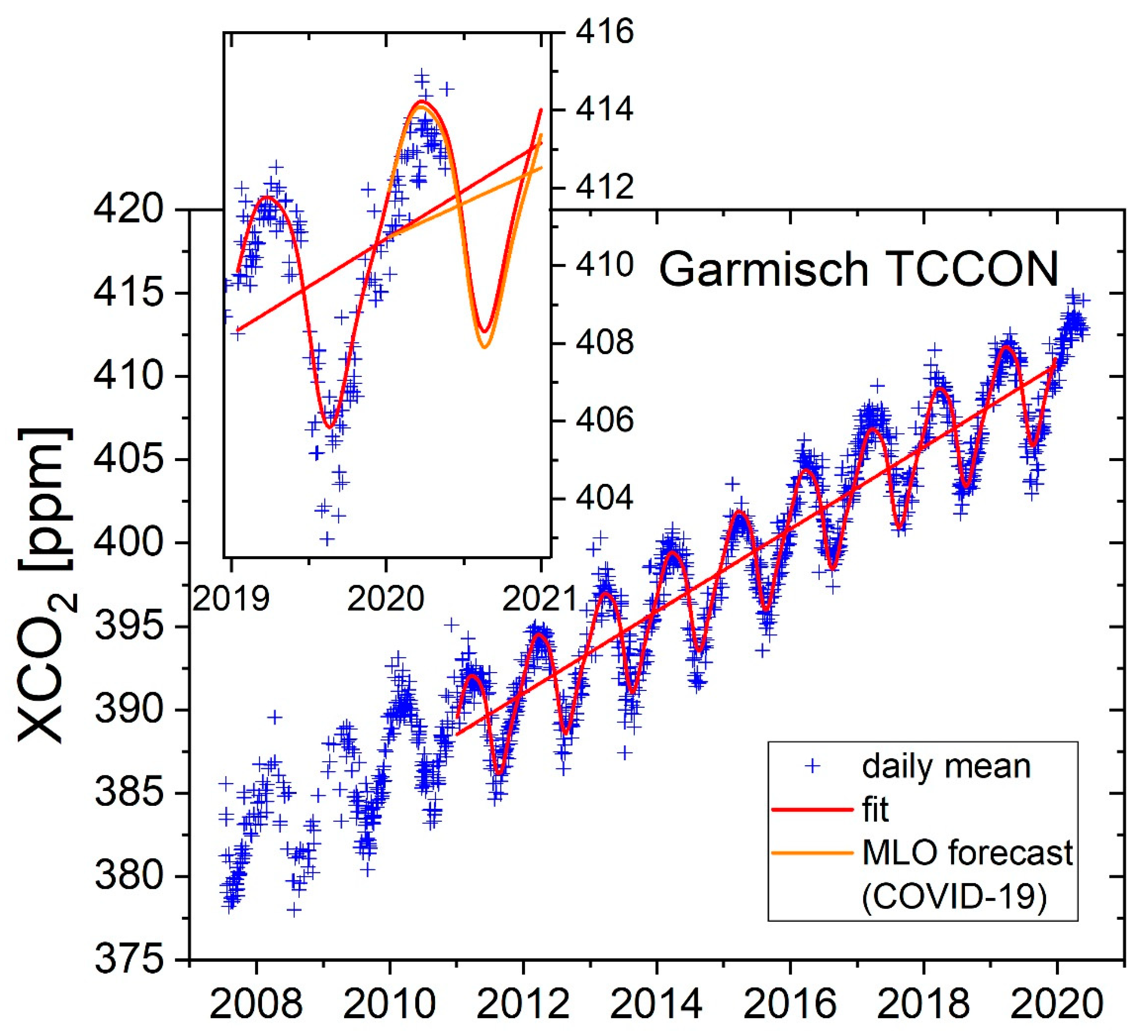
3.1. TCCON Trend
3.2. TCCON Annual Growth Rates
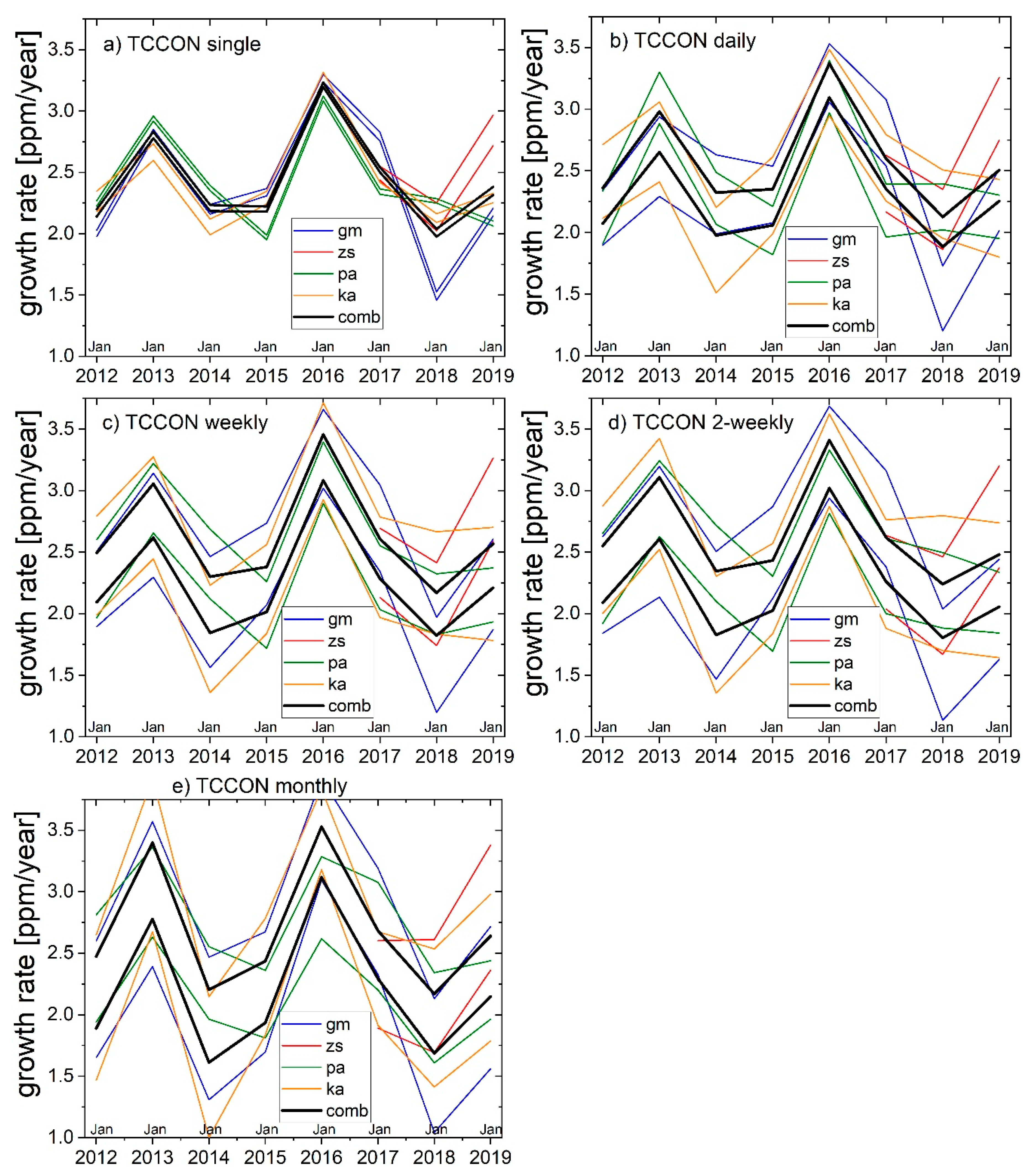
3.2.1. Interannual Variability of TCCON Annual Growth Rates
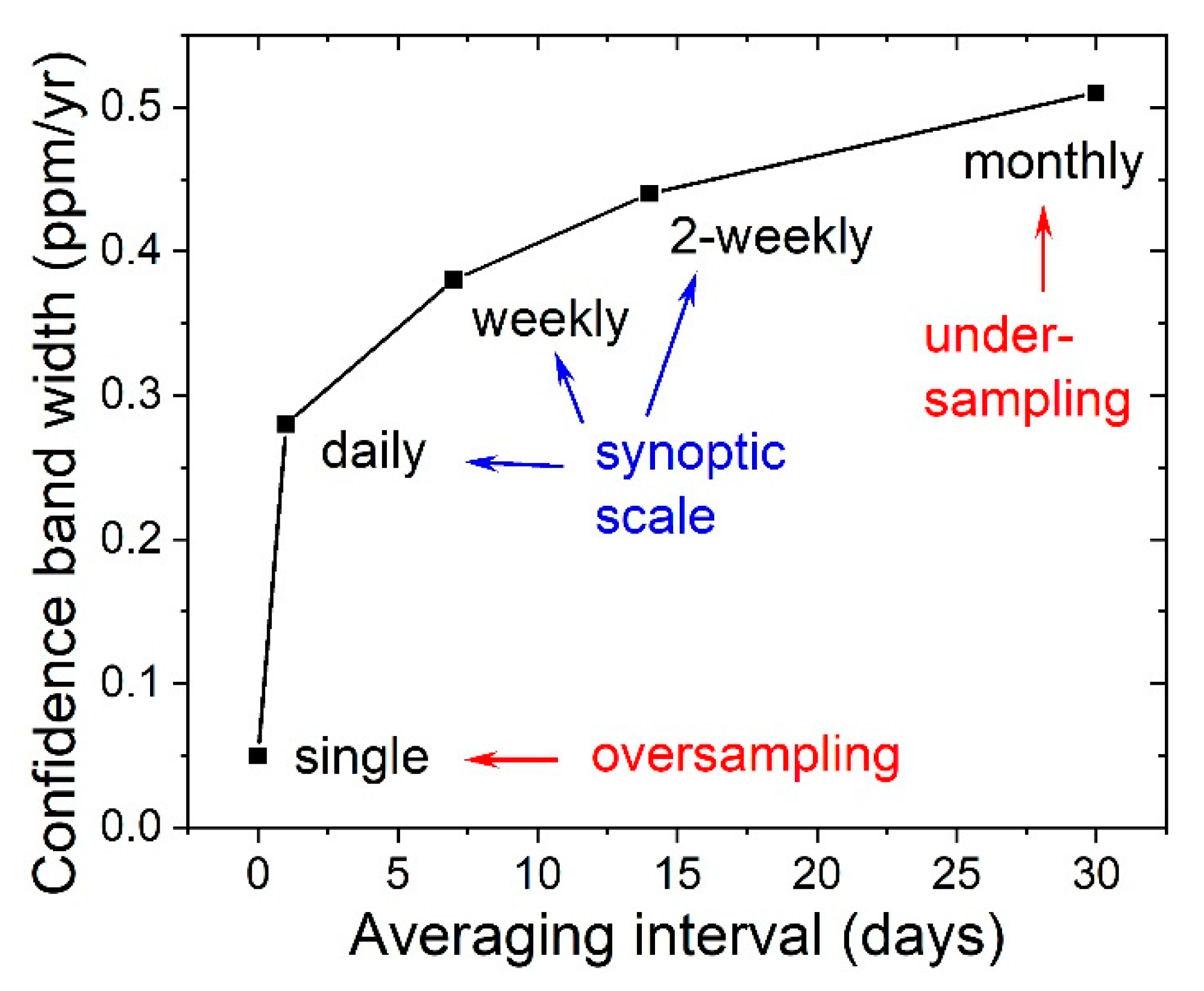
3.2.2. Confidence Bands for the TCCON Annual Growth Rates
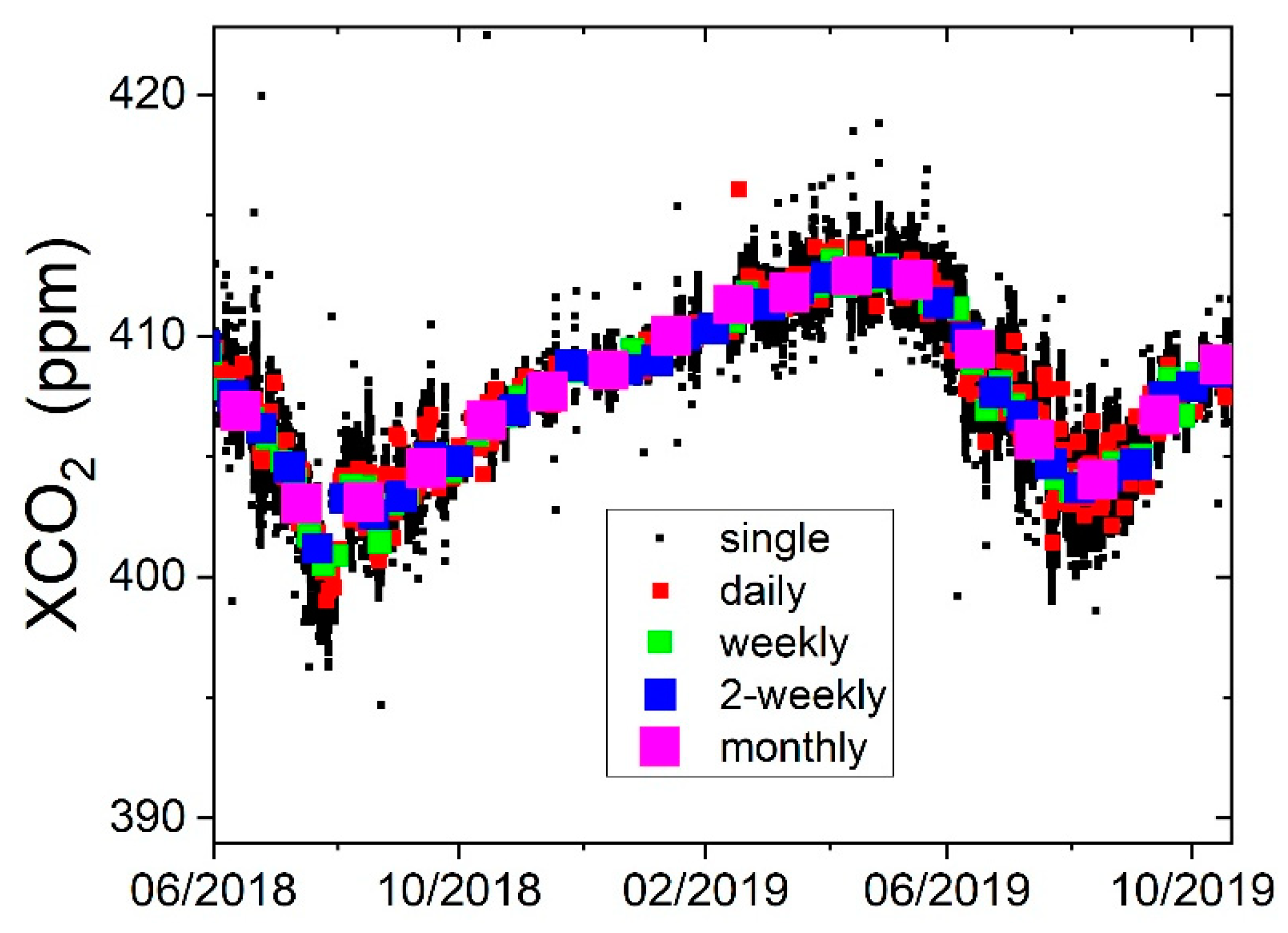
Oversampling with Single-Spectra Resolution
Sampling with Synoptic-Scale Temporal Resolution
Undersampling with Monthly-Scale Temporal Resolution
- The confidence bands in Figure 2a provide a measure for a contribution of ≈0.05 ppm/yr resulting from the propagation of single-measurement precision into TCCON-derived annual growth rates, but are no realistic measure for the total annual growth uncertainty (due to the oversampling/underrepresentation of the synoptic evolution).
- The black Figure 2b–d confidence bands from daily, weekly, and 2-weekly TCCON data (i.e., 0.38 [0.28, 0.44] ppm/yr) can be considered as the realistic total uncertainty estimate/range for the hemispherically representative annual growth rates attainable from the TCCON data; it is favorable to base the analysis of annual growth rates on the time series aggregated into synoptic-scale temporal resolution.
- For preferred synoptic-scale sampling, the annual growth rates from sites with differing sampling densities (see Table 1) become consistent (Figure 2). As a result, it makes sense to combine the annual growth rates of various sites to thereby reduce the confidence width as shown in Table 3 (i.e., not only use the site with the densest sampling).
- Aggregating TCCON time series into monthly means leads to an undersampling of the intra-annual XCO2 evolution and thereby to unreliable annual growth rates and too large confidence bands.
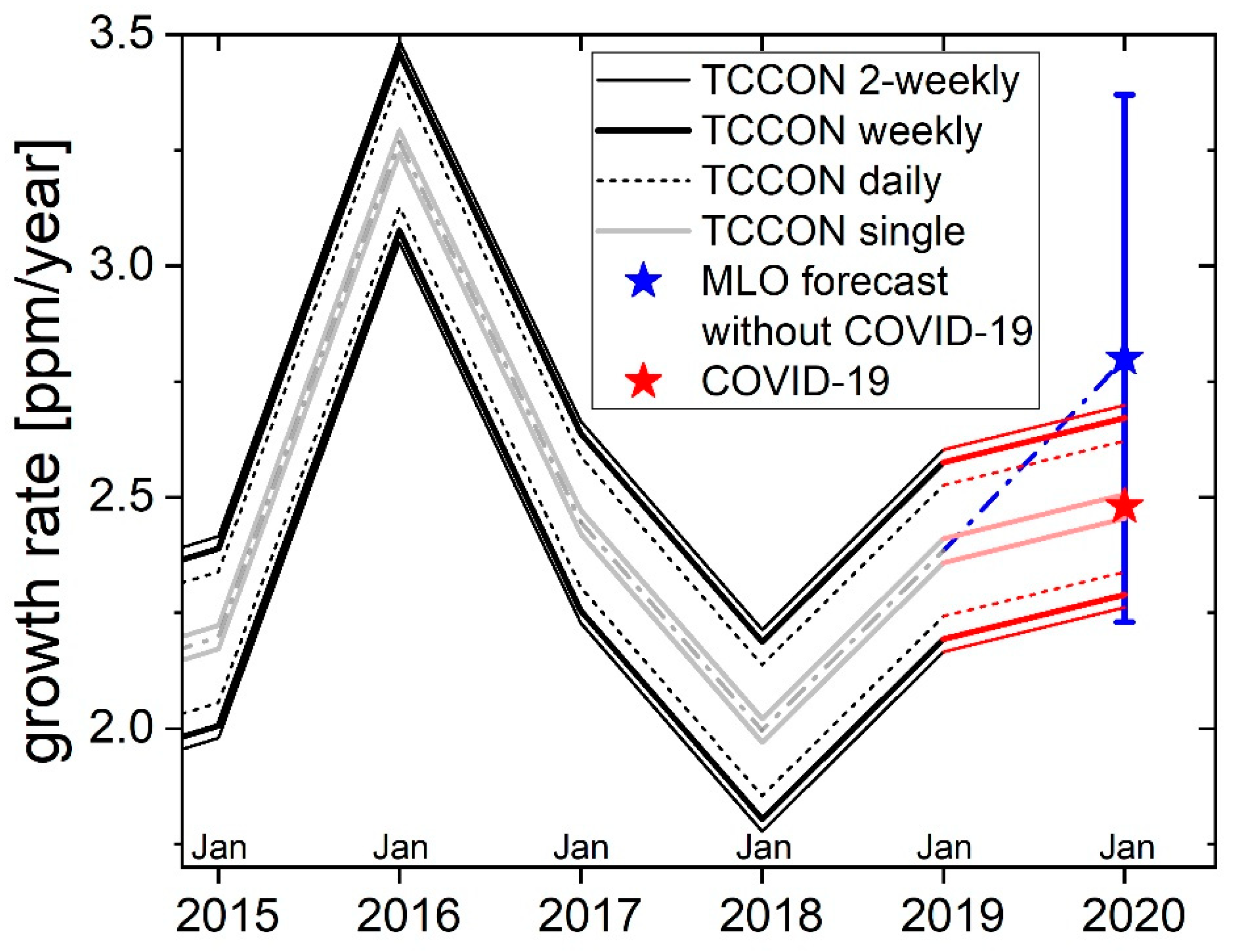
3.3. Synopsis of TCCON Annual Growth Rates with Mauna Loa 2020 Forecast
4. Discussion
4.1. Discussion of Trend Results
4.2. Discussion of TCCON Annual Growth Rates
4.3. Can TCCON Measure a COVID-19-Related Reduction of the Annual Growth Rate? Discussion of Five Cases
4.3.1. Case (i)
4.3.2. Case (ii)
4.3.3. Case (iii)
4.3.4. Case (iv)
4.3.5. Case (v)
5. Summary and Conclusions
- (i)
- There is a 0.6 [0.4, 0.7]-yr contribution to the detection delay due to the impact of synoptic variability on XCO2 observations. This was inferred solely from the TCCON data analysis. The forecast-based verification of this result, however, was not feasible. This is because the forecast uncertainty for the forecasted reference case (without the COVID-19 impact) exceeds the forecasted (and to-be-measured) 2020 growth rate reduction. The currently attainable forecast confidence is only ≈10% narrower than the max–min range observed by TCCON during the last 10 years.
- (ii)
- There is a ≈1-month (0.08-yr) contribution to the detection delay, originating from the (0.8 ppm) single-measurement precision of the TCCON measurements on the ≈1 min scale.
- (iii)
- Taking the reported forecast uncertainty of ±0.57 ppm/yr for the forecasted reference case (without the COVID-19 impact) fully into account, a one-time growth rate reduction of −0.32 ppm yr−2 in 2020 cannot be detected. The same holds true if the growth rate reduction would stay constant on the same level during the subsequent years.
- (iv)
- We assumed a growth rate reduction of −0.32 ppm yr−2 starting in 2020, as in the cases before based on a −8 % emissions reduction in 2020. However, we then additionally assumed a year-on-year increase in the growth rate reduction by −0.32 ppm yr−2. This describes a desirable progressive emission reduction over the years, which may or may not be COVID-19 related after 2020. This case is comparable to the rates of decrease needed over the next decades to limit climate change to a 1.5 °C warming. For this case, we derived an overall detection delay of 2.4 [2.2, 2.5] yr. This is limited by the forecast uncertainty with an additional contribution from synoptic variability.
- (v)
- Finally, assuming the same type of progressive growth rate reduction, we investigated the case that no forecast for the reference case (without the COVID-19 impact) would be available. The idea to derive a detection delay was that due to the progressive growth rate reduction assumed, that the growth rate will leave at a certain point the max–min range of the previous observations. The resulting overall detection delay is 5.2 [4.8, 5.3] yr.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Intergovernmental Panel on Climate Change (IPCC). Global Warming of 1.5 °C. An IPCC Special Report on the Impacts of Global Warming of 1.5 °C above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty; Masson-Delmotte, V., Zhai, P., Pörtner, H.-O., Roberts, D., Skea, J., Shukla, P.R., Pirani, A., Moufouma-Okia, W., Péan, C., Pidcock, R., et al., Eds.; World Meteorological Organization: Geneva, Switzerland, 2018; in press. [Google Scholar]
- Betts, R.A.; Jones, C.D.; Knight, J.R.; Keeling, R.F.; Kennedy, J.J. El Niño and a record CO2 rise. Nat. Clim. Chang. 2016, 6, 806–810. [Google Scholar] [CrossRef]
- Peters, G.P.; Le Quéré, C.; Andrew, R.M.; Canadell, J.G.; Friedlingstein, P.; Ilyina, Z.; Jackson, R.B.; Joos, F.; Korsbakken, J.I.; McKinley, G.A.; et al. Towards real-time verification of CO2 emissions. Nat. Clim. Chang. 2017, 7, 848–852. [Google Scholar] [CrossRef]
- Friedlingstein, P.; Jones, M.W.; O’Sullivan, M.; Andrew, R.M.; Hauck, J.; Peters, G.P.; Peters, W.; Pongratz, J.; Sitch, S.; Le Quéré, C.; et al. Global Carbon Budget 2019. Earth Syst. Sci. Data 2019, 11, 1783–1838. [Google Scholar] [CrossRef]
- Le Quéré, C.; Jackson, R.B.; Jones, M.W.; Smith, A.J.P.; Abernethy, S.; Andrew, R.M.; De-Gol, A.J.; Willis, D.R.; Shan, Y.; Canadell, J.G.; et al. Temporary reduction in daily global CO2 emissions during the COVID-19 forced confinement. Nat. Clim. Chang. 2020. [Google Scholar] [CrossRef]
- The International Energy Agency (IEA). Global Energy Review 2020; IEA: Paris, France, 2020; Available online: https://www.iea.org/reports/global-energy-review-2020 (accessed on 4 June 2020).
- Liu, Z.; Ciais, P.; Deng, Z.; Lei, R.; Davis, S.J.; Feng, S.; Zheng, B.; Cui, D.; Dou, X.; He, P.; et al. COVID-19 causes record decline in global CO2 emissions. arXiv 2020, arXiv:2004.13614v3. [Google Scholar]
- Wunch, D.; Toon, G.C.; Blavier, J.-F.L.; Washenfelder, R.A.; Notholt, J.; Connor, B.J.; Griffith, D.W.T.; Sherlock, V.; Wennberg, P.O. The Total Carbon Column Observing Network. Phil. Trans. R. Soc. A 2011, 369, 2087–2112. [Google Scholar] [CrossRef] [PubMed]
- Wunch, D.; Wennberg, P.O.; Toon, G.C.; Connor, B.J.; Fisher, B.; Osterman, G.B.; Frankenberg, C.; Mandrake, L.; O’Dell, C.; Ahonen, P.; et al. A method for evaluating bias in global measurements of CO2 total columns from space. Atmos. Chem. Phys. 2011, 11, 12317–12337. [Google Scholar] [CrossRef]
- Liang, A.; Gong, W.; Han, G.; Xiang, C. Comparison of Satellite-Observed XCO2 from GOSAT, OCO-2, and Ground-Based TCCON. Remote Sens. 2017, 9, 1033. [Google Scholar] [CrossRef]
- Wunch, D.; Wennberg, P.O.; Osterman, G.; Fisher, B.; Naylor, B.; Roehl, C.M.; O’Dell, C.; Mandrake, L.; Viatte, C.; Kiel, M.; et al. Comparisons of the Orbiting Carbon Observatory-2 (OCO-2) XCO2 measurements with TCCON. Atmos. Meas. Tech. 2017, 10, 2209–2238. [Google Scholar] [CrossRef]
- Wu, L.; Hasekamp, O.; Hu, H.; Landgraf, J.; Butz, A.; aan de Brugh, J.; Aben, I.; Pollard, D.F.; Griffith, D.W.T.; Feist, D.G.; et al. Carbon dioxide retrieval from OCO-2 satellite observations using the RemoTeC algorithm and validation with TCCON measurements. Atmos. Meas. Tech. 2018, 11, 3111–3130. [Google Scholar] [CrossRef]
- O’Dell, C.W.; Eldering, A.; Wennberg, P.O.; Crisp, D.; Gunson, M.R.; Fisher, B.; Frankenberg, C.; Kiel, M.; Lindqvist, H.; Mandrake, L.; et al. Improved retrievals of carbon dioxide from Orbiting Carbon Observatory-2 with the version 8 ACOS algorithm. Atmos. Meas. Tech. 2018, 11, 6539–6576. [Google Scholar] [CrossRef]
- Reuter, M.; Buchwitz, M.; Schneising, O.; Noël, S.; Bovensmann, H.; Burrows, J.P.; Boesch, H.; Di Noia, A.; Anand, J.; Parker, R.J.; et al. Ensemble-based satellite-derived carbon dioxide and methane column-averaged dry-air mole fraction data sets (2003–2018) for carbon and climate applications. Atmos. Meas. Tech. 2020, 13, 789–819. [Google Scholar] [CrossRef]
- Chevallier, F.; Deutscher, N.; Conway, T.J.J.; Ciais, P.; Ciattaglia, L.; Dohe, S.; Fröhlich, M.; Gomez-Pelaez, A.J.; Hase, F.; Haszpra, L.; et al. Global CO2 surface fluxes inferred from surface air-sample measurements and from TCCON retrievals of the CO2 total column. Geophys. Res. Lett. 2011, 38, L24810. [Google Scholar] [CrossRef]
- Reuter, M.; Buchwitz, M.; Hilker, M.; Heymann, J.; Schneising, O.; Pillai, D.; Bovensmann, H.; Burrows, J.P.; Bösch, H.; Parker, R.; et al. Satellite-inferred European carbon sink larger than expected. Atmos. Chem. Phys. 2014, 14, 13739–13753. [Google Scholar] [CrossRef]
- Feng, L.; Palmer, P.I.; Parker, R.J.; Deutscher, N.M.; Feist, D.G.; Kivi, R.; Morino, I.; Sussmann, R. Estimates of European uptake of CO2 inferred from GOSAT XCO2 retrievals: Sensitivity to measurement bias inside and outside Europe. Atmos. Chem. Phys. 2016, 16, 1289–1302. [Google Scholar] [CrossRef]
- Lindqvist, H.; O’Dell, C.W.; Basu, S.; Boesch, H.; Chevallier, F.; Deutscher, N.; Feng, L.; Fisher, B.; Hase, F.; Inoue, M.; et al. Does GOSAT capture the true seasonal cycle of carbon dioxide? Atmos. Chem. Phys. 2015, 15, 13023–13040. [Google Scholar] [CrossRef]
- Yuan, Y.; Sussmann, R.; Rettinger, M.; Ries, L.; Petermeier, H.; Menzel, A. Comparison of Continuous In-Situ CO2 Measurements with Co-Located Column-Averaged XCO2 TCCON/Satellite Observations and CarbonTracker Model Over the Zugspitze Region. Remote Sens. 2019, 11, 2981. [Google Scholar] [CrossRef]
- Keppel-Aleks, G.; Wennberg, P.O.; Washenfelder, R.A.; Wunch, D.; Schneider, T.; Toon, G.C.; Andres, R.J.; Blavier, J.-F.; Connor, B.; Davis, K.J.; et al. The imprint of surface fluxes and transport on variations in total column carbon dioxide. Biogeosciences 2012, 9, 875–891. [Google Scholar] [CrossRef]
- Olsen, S.C.; Randerson, J.T. Differences between surface and column atmospheric CO2 and implications for carbon cycle research. J. Geophys. Res. 2004, 109, D02301. [Google Scholar] [CrossRef]
- Betts, R.A.; Jones, C.D.; Jin, Y.; Keeling, R.F.; Kennedy, J.J.; Knight, J.R.; Scaife, A. Analysis: What Impact Will the Coronavirus Pandemic Have on Atmospheric CO2? CarbonBrief. 2020. Available online: https://www.carbonbrief.org/analysis-what-impact-will-the-coronavirus-pandemic-have-on-atmospheric-co2 (accessed on 4 June 2020).
- Messerschmidt, J.; Geibel, M.C.; Blumenstock, T.; Chen, H.; Deutscher, N.M.; Engel, A.; Feist, D.G.; Gerbig, C.; Gisi, M.; Hase, F.; et al. Calibration of TCCON column-averaged CO2: The first aircraft campaign over European TCCON sites. Atmos. Chem. Phys. 2011, 11, 10765–10777. [Google Scholar] [CrossRef]
- Sussmann, R.; Schäfer, K. Infrared spectroscopy of tropospheric trace gases: Combined analysis of horizontal and vertical column abundances. Appl. Opt. 1997, 36, 735–741. [Google Scholar] [CrossRef] [PubMed]
- Sussmann, R.; Rettinger, M. TCCON Data from Garmisch (DE), Release GGG2014.R2 [Data Set]; TCCON Data Archive, Hosted by CaltechDATA: Pasadena, CA, USA, 2018; R2. [Google Scholar]
- Sussmann, R.; Rettinger, M. TCCON Data from Zugspitze (DE), Release GGG2014.R1 [Data Set]; TCCON Data Archive, Hosted by CaltechDATA: Pasadena, CA, USA, 2018; R1. [Google Scholar]
- Hase, F.; Blumenstock, T.; Dohe, S.; Groß, J.; Kiel, M. TCCON Data from Karlsruhe (DE), Release GGG2014R1. [Data Set]; TCCON Data Archive, Hosted by CaltechDATA: Pasadena, CA, USA, 2015; R1. [Google Scholar] [CrossRef]
- Wennberg, P.O.; Roehl, C.M.; Wunch, D.; Toon, G.C.; Blavier, J.-F.; Washenfelder, R.; Keppel-Aleks, G.; Allen, N.T.; Ayers, J. TCCON data from Park Falls (US), Release GGG2014R1. [Data Set]; TCCON data archive, hosted by CaltechDATA: Pasadena, CA, USA, 2017; R1. [Google Scholar] [CrossRef]
- Masarie, K.A.; Tans, P.P. Extension and integration of atmospheric carbon dioxide data into a globally consistent measurement record. J. Geophys. Res. Atmos. 1995, 100, 11593–11610. [Google Scholar] [CrossRef]
- Gatz, D.F.; Smith, L. The standard error of a weighted mean concentration—I. Bootstrapping vs. other methods. Atmos. Environ. 1995, 29, 1185–1193. [Google Scholar] [CrossRef]
- Gatz, D.F.; Smith, L. The standard error of a weighted mean concentration—II. Estimating confidence intervals. Atmos. Environ. 1995, 29, 1195–1200. [Google Scholar] [CrossRef]
- Gardiner, T.; Forbes, A.; de Mazière, M.; Vigouroux, C.; Mahieu, E.; Demoulin, P.; Velazco, V.; Notholt, J.; Blumenstock, T.; Hase, F.; et al. Trend analysis of greenhouse gases over Europe measured by a network of ground-based remote FTIR instruments. Atmos. Chem. Phys. 2008, 8, 6719–6727. [Google Scholar] [CrossRef]
- Kohlhepp, R.; Ruhnke, R.; Chipperfield, M.P.; De Maziere, M.; Notholt, J.; Barthlott, S.; Batchelor, R.L.; Blatherwick, R.D.; Blumenstock, T.; Coffey, M.T.; et al. Observed and simulated time evolution of HCl, ClONO2, and HF total column abundances. Atmos. Chem. Phys. 2012, 12, 3527–3556. [Google Scholar] [CrossRef]
- Sussmann, R.; Borsdorff, T.; Rettinger, M.; Camy-Peyret, C.; Demoulin, P.; Duchatelet, P.; Mahieu, E.; Servais, C. Harmonized retrieval of column-integrated atmospheric water vapor from the FTIR network-first examples for long-term records and station trends. Atmos. Chem. Phys. 2009, 9, 8987–8999. [Google Scholar] [CrossRef]
- Sussmann, R.; Forster, F.; Rettinger, M.; Bousquet, P. Renewed methane increase for five years (2007–2011) observed by solar FTIR spectrometry. Atmos. Chem. Phys. 2012, 12, 4885–4891. [Google Scholar] [CrossRef]
- Met Office. Mauna Loa Carbon Dioxide Forecast for 2020. Available online: https://www.metoffice.gov.uk/research/climate/seasonal-to-decadal/long-range/forecasts/co2-forecast (accessed on 4 June 2020).
- Kennedy, J.J.; Rayner, N.A.; Smith, R.O.; Parker, D.E.; Saunby, M. Reassessing biases and other uncertainties in sea surface temperature observations measured in situ since 1850: 2. Biases and homogenization. J. Geophys. Res. Atmos. 2011, D14104. [Google Scholar] [CrossRef]
- MacLachlan, C.; Arribas, A.; Peterson, K.A.; Maidens, A.; Fereday, D.; Scaife, A.A.; Gordon, M.; Vellinga, M.; Williams, A.; Comer, R.E.; et al. Global Seasonal forecast system version 5 (GloSea5): A high-resolution seasonal forecast system. Q. J. R. Meteorol. Soc. 2015, 141, 1072–1084. [Google Scholar] [CrossRef]
- Prentice, I.C.; Farquhar, G.D.; Fasham, M.J.R.; Goulden, M.L.; Heimann, M.; Jaramillo, V.J.; Kheshgi, H.S.; Le Quéré, C.; Scholes, R.J.; Wallace, D.W.R. The Carbon Cycle and Atmospheric Carbon Dioxide. In Climate Change 2001: The Scientific Basis, Contribution of Working Group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change; Houghton, J.T., Ding, Y., Griggs, D.J., Noguer, M., van der Linden, P.J., Dai, X., Maskell, K., Johnson, C.A., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2001; pp. 183–237. [Google Scholar]
| Site | Lat. | Lon. | Alt. (km) | Measurement Days per Year (Average) | Spectra per Day (Average) | Single Spectra Integration Time (s) | Data Set |
|---|---|---|---|---|---|---|---|
| Garmisch (gm 1) | 47°N | 11°E | 0.74 | 127 | 79 | 95 | [25] |
| Zugspitze (zs) | 47°N | 11°E | 2.96 | 110 | 37 | 18/97 2 | [26] |
| Karlsruhe (ka) | 49°N | 8°E | 0.12 | 120 | 46 | 35 | [27] |
| Park Falls (pa) | 46°N | 90°W | 0.44 | 238 | 118 | 95 | [28] |
| Site | Fitted Period | Trend Slope [ppm/yr] | Confidence Interval [ppm/yr, 95%] |
|---|---|---|---|
| Garmisch | (Jan 2011–Dec 2019) | 2.46 | [2.44, 2.49] |
| Karlsruhe | (Jan 2011–Dec 2019) | 2.46 | [2.43, 2.49] |
| Park Falls | (Jan 2011–Dec 2019) | 2.44 | [2.42, 2.46] |
| Zugspitze | (Jan 2016–Dec 2019) | 2.42 | [2.33, 2.50] |
| Combined (gm, ka, pa) | (Jan 2011–Dec 2019) | 2.45 | [2.44, 2.47] |
| Site | Monthly (ppm/yr) | 2-Weekly (ppm/yr) | Weekly (ppm/yr) | Daily (ppm/yr) | Single (ppm/yr) |
|---|---|---|---|---|---|
| Garmisch | 1.02 | 0.86 | 0.73 | 0.53 | 0.07 |
| Karlsruhe | 1.03 | 0.91 | 0.82 | 0.60 | 0.10 |
| Park Falls | 0.69 | 0.60 | 0.53 | 0.40 | 0.04 |
| Zugspitze | 0.88 | 0.74 | 0.64 | 0.49 | 0.20 |
| Combined (gm, ka, pa, zs) | 0.51 | 0.44 | 0.38 | 0.28 | 0.05 |
| Case (i)−(v) Assumptions | Delay Type | Delay Time (yr) | Data Basis | Dominant Mechanism |
|---|---|---|---|---|
| (i) one-time growth rate reduction 2020 = −0.32 ppm yr−2; forecast error = 0; TCCON confidence (weekly sampling) = 0.38 ppm/yr | delay contribution | 0.6 [0.4, 0.7] | weekly TCCON data | weekly-scale synoptic variability of XCO2 |
| (ii) one-time growth rate reduction 2020 = −0.32 ppm yr−2; forecast error = 0; TCCON confidence (single-spectra sampling) = 0.05 ppm/yr | delay contribution | 0.08 | single-spectra TCCON data | TCCON single-measurement precision |
| (iii) growth rate reduction starting 2020 and constant afterwards = −0.32 ppm yr−2; forecast error = ±0.57 ppm/yr | overall delay | ∞ | forecast error | forecast error |
| (iv) growth rate reduction starting 2020 and linear annual increase afterwards = −0.32 ppm yr−2; forecast error = ±0.57 ppm/yr; TCCON confidence (weekly sampling) = 0.38 ppm/yr | overall delay | 2.4 [2.2, 2.5] | forecast error and weekly TCCON data | forecast error |
| (v) growth rate reduction starting 2020 and linear annual increase afterwards = −0.32 ppm yr−2; no forecast error available; TCCON max–min range (weekly sampling) = 1.27 ppm/yr; TCCON confidence (weekly sampling) = 0.38 ppm/yr | overall delay | 5.2 [4.8, 5.3] | forecast error and weekly TCCON data | observed max–min range of growth rates |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sussmann, R.; Rettinger, M. Can We Measure a COVID-19-Related Slowdown in Atmospheric CO2 Growth? Sensitivity of Total Carbon Column Observations. Remote Sens. 2020, 12, 2387. https://doi.org/10.3390/rs12152387
Sussmann R, Rettinger M. Can We Measure a COVID-19-Related Slowdown in Atmospheric CO2 Growth? Sensitivity of Total Carbon Column Observations. Remote Sensing. 2020; 12(15):2387. https://doi.org/10.3390/rs12152387
Chicago/Turabian StyleSussmann, Ralf, and Markus Rettinger. 2020. "Can We Measure a COVID-19-Related Slowdown in Atmospheric CO2 Growth? Sensitivity of Total Carbon Column Observations" Remote Sensing 12, no. 15: 2387. https://doi.org/10.3390/rs12152387
APA StyleSussmann, R., & Rettinger, M. (2020). Can We Measure a COVID-19-Related Slowdown in Atmospheric CO2 Growth? Sensitivity of Total Carbon Column Observations. Remote Sensing, 12(15), 2387. https://doi.org/10.3390/rs12152387