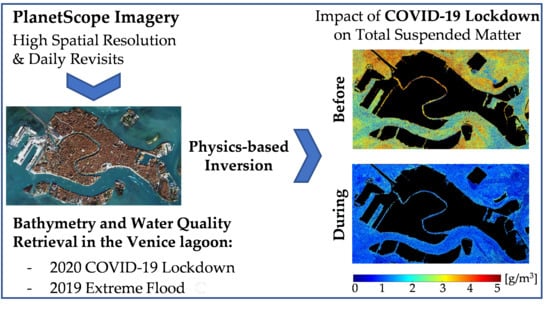
Physics-based Bathymetry and Water Quality Retrieval Using PlanetScope Imagery: Impacts of 2020 COVID-19 Lockdown and 2019 Extreme Flood in the Venice Lagoon
Abstract
1. Introduction
2. Study Area and Dataset
3. Method
3.1. Adaptation of WASI for Processing PlanetScope Imagery
3.2. Parametrization of WASI
3.2.1. Shallow-Water Inversion
3.2.2. Deep-Water Inversion
4. Results and Discussion
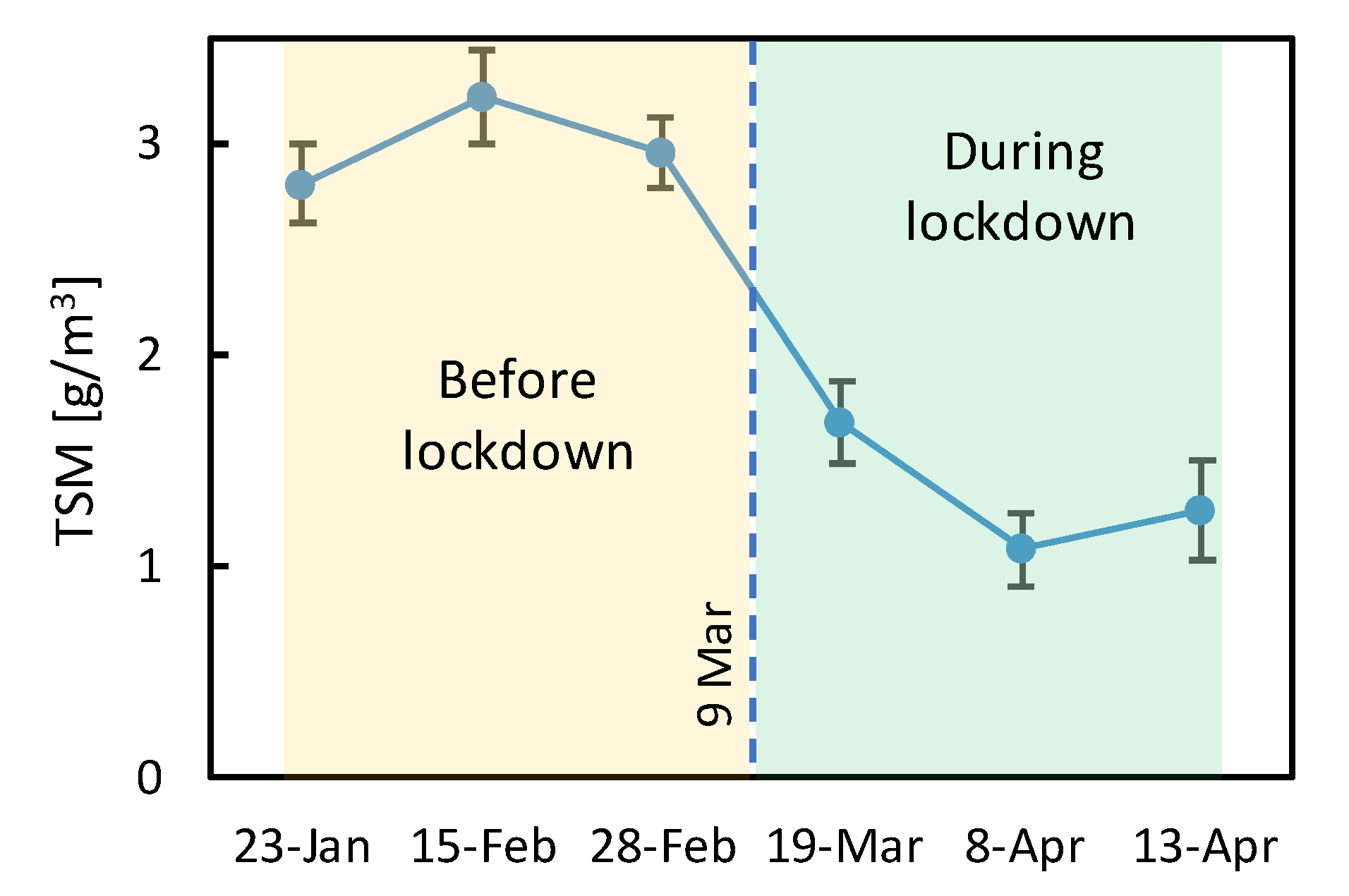
4.1. Retrievals of TSM
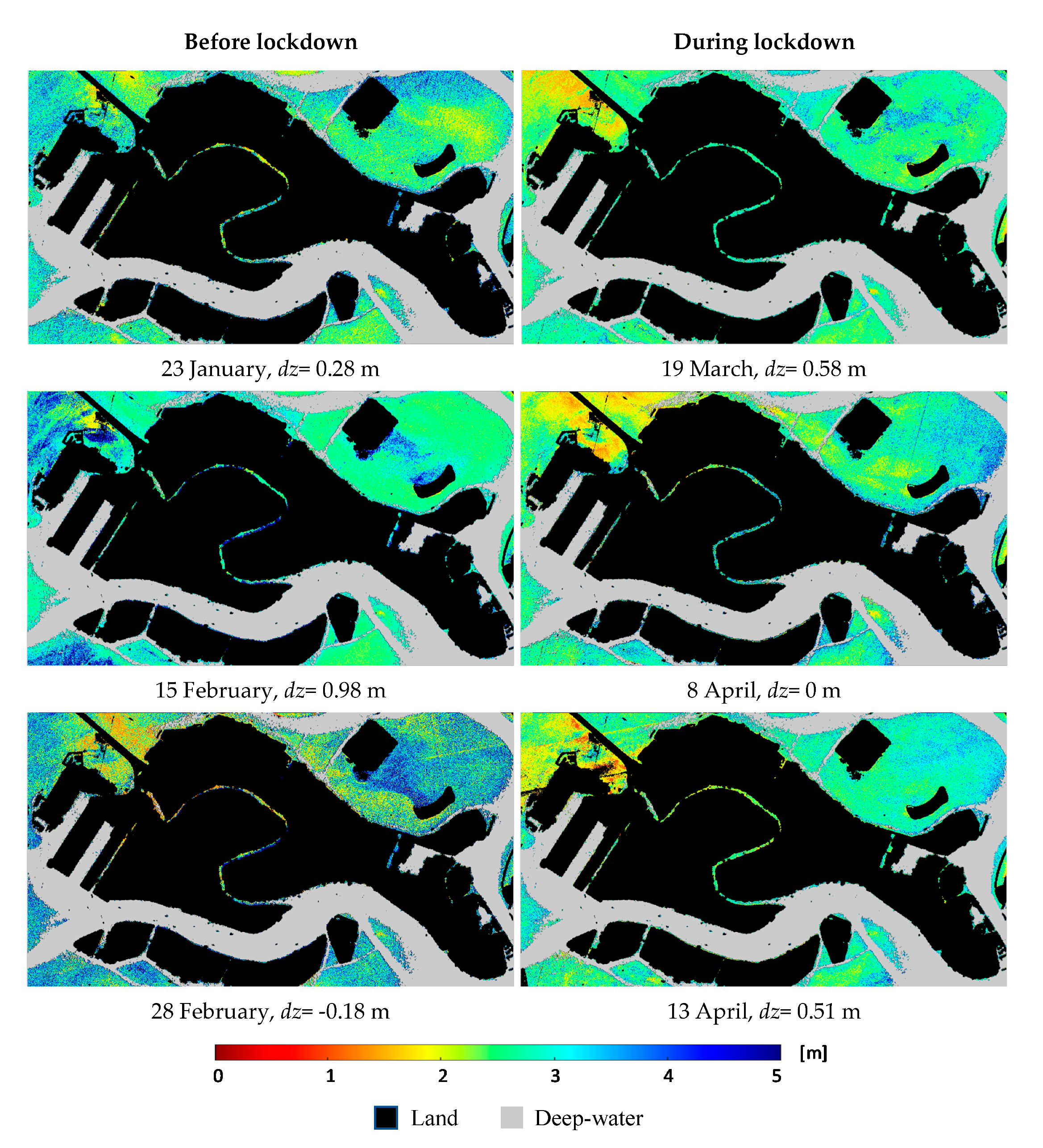
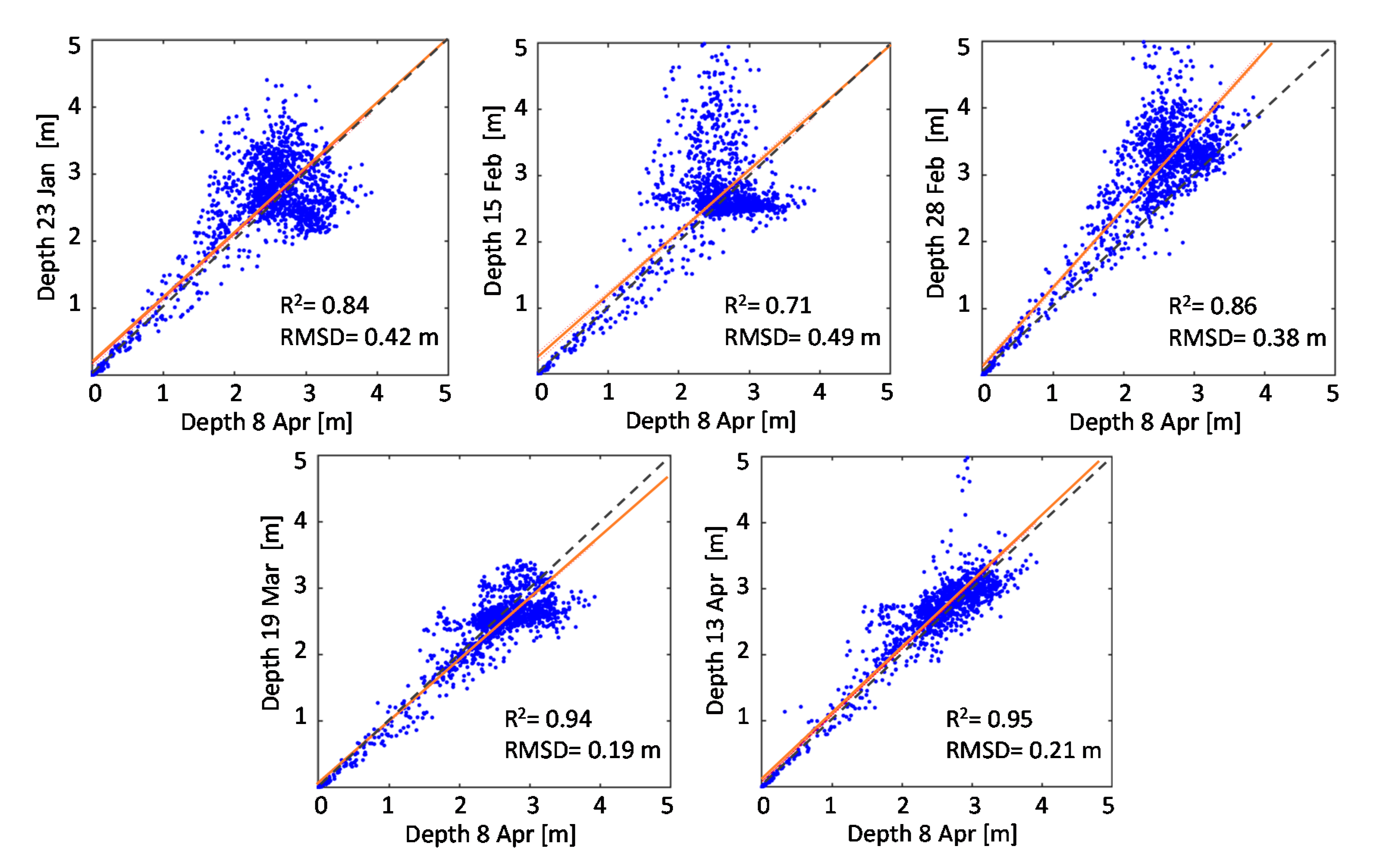
4.2. Retrievals of Bathymetry
5. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Poursanidis, D.; Traganos, D.; Chrysoulakis, N.; Reinartz, P. Cubesats allow high spatiotemporal estimates of satellite-derived bathymetry. Remote Sens. 2019, 11, 1299. [Google Scholar] [CrossRef]
- Planet, Planet Imagery Product Specifications. Available online: https://assets.planet.com/docs/Planet_Combined_Imagery_Product_Specs_letter_screen.pdf (accessed on 10 July 2020).
- Akiyanova, F.; Oleshko, A.; Karakulov, Y.; Shaimerdenova, A. Application of the methods of remote sensing of the Earth to study the bathymetry of the coastal part of the Astana reservoir (Kazakhstan). In Proceedings of the 19th International Multidisciplinary Scientific GeoConference SGEM 2019, Sofia, Bulgaria, 28 June–7 July 2019; pp. 457–464. [Google Scholar]
- Ahola, R.; Chénier, R.; Horner, B.; Faucher, M.-A.; Sagram, M. Satellite derived bathymetry for Arctic charting: A review of sensors and techniques for operational implementation within the Canadian Hydrographic Service. In Remote Sensing of the Ocean, Sea Ice, Coastal Waters, and Large Water Regions 2018; Bostater, C.R., Mertikas, S.P., Neyt, X., Eds.; SPIE: Bellingham, WA, USA, 2018; Volume 10784, p. 6. [Google Scholar]
- Gabr, B.; Ahmed, M.; Marmoush, Y. PlanetScope and Landsat 8 Imageries for Bathymetry Mapping. J. Mar. Sci. Eng. 2020, 8, 143. [Google Scholar] [CrossRef]
- Wicaksono, P.; Lazuardi, W. Assessment of PlanetScope images for benthic habitat and seagrass species mapping in a complex optically shallow water environment. Int. J. Remote Sens. 2018, 39, 5739–5765. [Google Scholar] [CrossRef]
- Houborg, R.; McCabe, M. High-Resolution NDVI from planet’s constellation of earth observing nano-satellites: A new data source for precision agriculture. Remote Sens. 2016, 8, 768. [Google Scholar] [CrossRef]
- Cooley, S.; Smith, L.; Stepan, L.; Mascaro, J. Tracking Dynamic Northern Surface Water Changes with High-Frequency Planet CubeSat Imagery. Remote Sens. 2017, 9, 1306. [Google Scholar] [CrossRef]
- Niroumand-Jadidi, M.; Vitti, A.; Lyzenga, D.R. Multiple Optimal Depth Predictors Analysis (MODPA) for river bathymetry: Findings from spectroradiometry, simulations, and satellite imagery. Remote Sens. Environ. 2018, 218, 132–147. [Google Scholar] [CrossRef]
- Toming, K.; Kutser, T.; Laas, A.; Sepp, M.; Paavel, B.; Nõges, T. First experiences in mapping lake water quality parameters with Sentinel-2 MSI imagery. Remote Sens. 2016, 8, 640. [Google Scholar] [CrossRef]
- Ansper, A.; Alikas, K. Retrieval of chlorophyll a from Sentinel-2 MSI Data for the European Union Water Framework Directive Reporting Purposes. Remote Sens. 2018, 11, 64. [Google Scholar] [CrossRef]
- Niroumand-Jadidi, M.; Vitti, A. Improving the accuracies of bathymetric models based on multiple regression for calibration (case study: Sarca River, Italy). In Proceedings of the SPIE - The International Society for Optical Engineering, Edinburgh, UK, 19 October 2016; SPIE: Bellingham, WA, USA, 2016; Volume 9999. [Google Scholar]
- Niroumand-Jadidi, M.; Vitti, A. Reconstruction of river boundaries at sub-pixel resolution: Estimation and spatial allocation of water fractions. ISPRS Int. J. Geo-Inf. 2017, 6, 383. [Google Scholar] [CrossRef]
- Niroumand-Jadidi, M.; Bovolo, F.; Vitti, A.; Bruzzone, L. A novel approach for bathymetry of shallow rivers based on spectral magnitude and shape predictors using stepwise regression. In Image and Signal Processing for Remote Sensing XXIV; Bruzzone, L., Bovolo, F., Benediktsson, J.A., Eds.; SPIE: Bellingham, WA, USA, 2018; Volume 10789, p. 23. [Google Scholar]
- Niroumand-Jadidi, M.; Vitti, A. Optimal band ratio analysis of WorldView-3 imagery for bathymetry of shallow rivers (case study: Sarca River, Italy). In International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences - ISPRS Archives; ISPRS: Pragure, Czech Republic, 2016; Volume 41. [Google Scholar]
- Gao, J. Bathymetric mapping by means of remote sensing: Methods, accuracy and limitations. Prog. Phys. Geogr. Earth Environ. 2009, 33, 103–116. [Google Scholar] [CrossRef]
- Niroumand-Jadidi, M.; Bovolo, F.; Bruzzone, L. Novel spectra-derived features for empirical retrieval of water quality parameters: Demonstrations for OLI, MSI, and OLCI Sensors. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10285–10300. [Google Scholar] [CrossRef]
- Ritchie, J.C.; Zimba, P.V.; Everitt, J.H. Remote sensing techniques to assess water quality. Photogramm. Eng. Remote Sens. 2003, 69, 695–704. [Google Scholar] [CrossRef]
- Lyzenga, D.R.; Malinas, N.P.; Tanis, F.J. Multispectral bathymetry using a simple physically based algorithm. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2251–2259. [Google Scholar] [CrossRef]
- Vanhellemont, Q. Daily metre-scale mapping of water turbidity using CubeSat imagery. Opt. Express 2019, 27, A1372. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; Doxaran, D.; Vanhellemont, Q. Retrieval and validation of water turbidity at metre-scale using pléiades satellite data: A case study in the gironde estuary. Remote Sens. 2020, 12, 946. [Google Scholar] [CrossRef]
- Soomets, T.; Uudeberg, K.; Jakovels, D.; Brauns, A.; Zagars, M.; Kutser, T. Validation and comparison of water quality products in baltic lakes using sentinel-2 msi and sentinel-3 OLCI data. Sensors 2020, 20, 742. [Google Scholar] [CrossRef]
- Nechad, B.; Ruddick, K.G.; Park, Y. Calibration and validation of a generic multisensor algorithm for mapping of total suspended matter in turbid waters. Remote Sens. Environ. 2010, 114, 854–866. [Google Scholar] [CrossRef]
- Mobley, C.D. Light and Water: Radiative Transfer in Natural Waters; Academic Press: Cambridge, MA, USA, 1994; ISBN 9780125027502. [Google Scholar]
- Gege, P. The water color simulator WASI: An integrating software tool for analysis and simulation of optical in situ spectra. Comput. Geosci. 2004, 30, 523–532. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41, 5755. [Google Scholar] [CrossRef]
- Niroumand-Jadidi, M.; Pahlevan, N.; Vitti, A. Mapping substrate types and compositions in shallow streams. Remote Sens. 2019, 11, 262. [Google Scholar] [CrossRef]
- Kutser, T.; Hedley, J.; Giardino, C.; Roelfsema, C.; Brando, V.E. Remote sensing of shallow waters - A 50 year retrospective and future directions. Remote Sens. Environ. 2020, 240, 111619. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral remote sensing for shallow waters. 2. Deriving bottom depths and water properties by optimization. Appl. Opt. 1999, 38, 3831–3843. [Google Scholar] [CrossRef] [PubMed]
- Kutser, T.; Pierson, D.C.; Kallio, K.Y.; Reinart, A.; Sobek, S. Mapping lake CDOM by satellite remote sensing. Remote Sens. Environ. 2005, 94, 535–540. [Google Scholar] [CrossRef]
- Mishra, S.; Mishra, D.R. Normalized difference chlorophyll index: A novel model for remote estimation of chlorophyll-a concentration in turbid productive waters. Remote Sens. Environ. 2012, 117, 394–406. [Google Scholar] [CrossRef]
- Kutser, T.; Paavel, B.; Verpoorter, C.; Ligi, M.; Soomets, T.; Toming, K.; Casal, G. Remote sensing of black lakes and using 810 nm reflectance peak for retrieving water quality parameters of optically complex waters. Remote Sens. 2016, 8, 497. [Google Scholar] [CrossRef]
- Dörnhöfer, K.; Klinger, P.; Heege, T.; Oppelt, N. Multi-sensor satellite and in situ monitoring of phytoplankton development in a eutrophic-mesotrophic lake. Sci. Total Environ. 2018, 612, 1200–1214. [Google Scholar] [CrossRef]
- Dekker, A.G.; Phinn, S.R.; Anstee, J.; Bissett, P.; Brando, V.E.; Casey, B.; Fearns, P.; Hedley, J.; Klonowski, W.; Lee, Z.P.; et al. Intercomparison of shallow water bathymetry, hydro-optics, and benthos mapping techniques in Australian and Caribbean coastal environments. Limnol. Oceanogr. Methods 2011, 9, 396–425. [Google Scholar] [CrossRef]
- Gege, P. WASI-2D: A software tool for regionally optimized analysis of imaging spectrometer data from deep and shallow waters. Comput. Geosci. 2014, 62, 208–215. [Google Scholar] [CrossRef]
- Jacobo, J. Venice Canals are Clear Enough to See Fish as Coronavirus Halts Tourism in the City. Available online: https://abcnews.go.com/International/venice-canals-clear-fish-coronavirushalts-%0Atourism-city/story?id=69662690 (accessed on 29 June 2020).
- Guy, J.; Di Donato, V. Venice’s Canal Water Looks Clearer as Coronavirus Keeps Visitors Away. 2020. Available online: https://edition.cnn.com/travel/article/venice-canals-clear-water-scli-intl/index.html (accessed on 20 July 2020).
- Carniello, L.; Silvestri, S.; Marani, M.; D’Alpaos, A.; Volpe, V.; Defina, A. Sediment dynamics in shallow tidal basins: In situ observations, satellite retrievals, and numerical modeling in the Venice Lagoon. J. Geophys. Res. Earth Surf. 2014, 119, 802–815. [Google Scholar] [CrossRef]
- Ruol, P.; Favaretto, C.; Volpato, M.; Martinelli, L. Flooding of Piazza San Marco (Venice): Physical model tests to evaluate the overtopping discharge. Water 2020, 12, 427. [Google Scholar] [CrossRef]
- Giardino, C.; Candiani, G.; Bresciani, M.; Lee, Z.; Gagliano, S.; Pepe, M. BOMBER: A tool for estimating water quality and bottom properties from remote sensing images. Comput. Geosci. 2012, 45, 313–318. [Google Scholar] [CrossRef]
- Brockmann, C.; Doerffer, R.; Peters, M.; Stelzer, K.; Embacher, S.; Ruescas, A. Evolution of the C2RCC neural network for Sentinel 2 and 3 for the retrieval of ocean colour products in normal and extreme optically complex waters. In Proceedings of the ESA Living Planet, Prague, Czech Republic, 9–13 May 2016. [Google Scholar]
- Gege, P. WASI (Water Colour Simulator). 2020. Available online: www.ioccg.org/data/software.html (accessed on 22 July 2020).
- Gege, P.; Albert, A. A Tool for inverse modeling of spectral measurements in deep and shallow waters. In Remote Sensing of Aquatic Coastal Ecosystem Processes; Richardson, L.L., LeDrew, E.F., Eds.; Springer: Dordrecht, The Netherlands, 2006; pp. 81–109. ISBN 978-1-4020-3968-3. [Google Scholar]
- Gege, P. Chapter 2 − Radiative Transfer Theory for Inland Waters. In Bio-Optical Modeling and Remote Sensing of Inland Waters; Mishra, D.R., Ogashawara, I., Gitelson, A.A., Eds.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 25–67. ISBN 978-0-12-804644-9. [Google Scholar]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral remote sensing for shallow waters. I. A semianalytical model. Appl. Opt. 1998, 37, 6329–6338. [Google Scholar] [CrossRef] [PubMed]
- Albert, A.; Mobley, C. An analytical model for subsurface irradiance and remote sensing reflectance in deep and shallow case-2 waters. Opt. Express 2003, 11, 2873. [Google Scholar] [CrossRef] [PubMed]
- Albert, A. Inversion Technique for Optical Remote Sensing in Shallow Water. Ph.D. Thesis, University of Hamburg, Hamburg, Germany, 2004. [Google Scholar]
- Pope, R.M.; Fry, E.S. Absorption spectrum (380–700 nm) of pure water II Integrating cavity measurements. Appl. Opt. 1997, 36, 8710. [Google Scholar] [CrossRef] [PubMed]
- Kou, L.; Labrie, D.; Chylek, P. Refractive indices of water and ice in the 065- to 25-μm spectral range. Appl. Opt. 1993, 32, 3531. [Google Scholar] [CrossRef] [PubMed]
- Morel, A. Optical properties of pure water and pure sea water. Opt. Asp. Oceanogr. 1974, 14, 1–24. [Google Scholar]
- Bricaud, A.; Morel, A.; Prieur, L. Absorption by dissolved organic matter of the sea (yellow substance) in the UV and visible domains1. Limnol. Oceanogr. 1981, 26, 43–53. [Google Scholar] [CrossRef]
- Carder, K.L.; Steward, R.G.; Harvey, G.R.; Ortner, P.B. Marine humic and fulvic acids: Their effects on remote sensing of ocean chlorophyll. Limnol. Oceanogr. 1989, 34, 68–81. [Google Scholar] [CrossRef]
- D’Sa, E.J.; Miller, R.L.; Del Castillo, C. Bio-optical properties and ocean color algorithms for coastal waters influenced by the Mississippi River during a cold front. Appl. Opt. 2006, 45, 7410–7428. [Google Scholar] [CrossRef]
- Santini, F.; Alberotanza, L.; Cavalli, R.M.; Pignatti, S. A two-step optimization procedure for assessing water constituent concentrations by hyperspectral remote sensing techniques: An application to the highly turbid Venice lagoon waters. Remote Sens. Environ. 2010, 114, 887–898. [Google Scholar] [CrossRef]
- Babin, M.; Stramski, D.; Ferrari, G.M.; Claustre, H.; Bricaud, A.; Obolensky, G.; Hoepffner, N. Variations in the light absorption coefficients of phytoplankton, nonalgal particles, and dissolved organic matter in coastal waters around Europe. J. Geophys. Res. C Oceans. 2003, 108. [Google Scholar] [CrossRef]
- Heege, T. Flugzeuggestützte Fernerkundung von Wasserinhaltsstoffen im Bodensee. Ph.D. Thesis, DLR-Forschungsbericht, Oberpfaffenhofen, Germany, 2000. [Google Scholar]
- Gege, P. Analytic model for the direct and diffuse components of downwelling spectral irradiance in water. Appl. Opt. 2012, 51, 1407–1419. [Google Scholar] [CrossRef] [PubMed]
- Gregg, W.W.; Carder, K.L. A simple spectral solar irradiance model for cloudless maritime atmospheres. Limnol. Oceanogr. 1990, 35, 1657–1675. [Google Scholar] [CrossRef]
- Jerlov, N.G. Marine Optics; Elsevier Scientific Publ. Company: Amaterdam, The Netherlands, 1976. [Google Scholar]
- Gege, P.; Groetsch, P. A spectral model for correcting sun glint and sky glint. In Proceedings of the Ocean Optics XXIII 2016, Victoria, BC, Canada, 23–28 October 2016. [Google Scholar]
- Dörnhöfer, K.; Göritz, A.; Gege, P.; Pflug, B.; Oppelt, N. Water Constituents and Water Depth Retrieval from Sentinel-2A—A First Evaluation in an Oligotrophic Lake. Remote Sens. 2016, 8, 941. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Caceci, M.S.; Cacheris, W.P. Fitting curves to data. Byte May 1984 1984, 340–362. [Google Scholar]
- Volpe, V.; Silvestri, S.; Marani, M. Remote sensing retrieval of suspended sediment concentration in shallow waters. Remote Sens. Environ. 2011, 115, 44–54. [Google Scholar] [CrossRef]
- Braga, F.; Scarpa, G.M.; Brando, V.E.; Manfè, G.; Zaggia, L. COVID-19 lockdown measures reveal human impact on water transparency in the Venice Lagoon. Sci. Total Environ. 2020, 736. [Google Scholar] [CrossRef]
- Gelinas, M.; Bokuniewicz, H.; Rapaglia, J.; Lwiza, K.M.M. Sediment resuspension by ship wakes in the venice lagoon. J. Coast. Res. 2013, 286, 8–17. [Google Scholar] [CrossRef]
- Madricardo, F.; Foglini, F.; Trincardi, F. Processed high-resolution ASCII: ESRI gridded bathymetry data (EM2040 and EM3002) from the Lagoon of Venice collected in 2013. Interdisciplinary Earth Data Alliance (IEDA). 2017. Available online: http://get.iedadata.org/doi/323605 (accessed on 2 June 2020). [CrossRef]
- Madricardo, F.; Foglini, F.; Kruss, A.; Ferrarin, C.; Pizzeghello, N.M.; Murri, C.; Rossi, M.; Bajo, M.; Bellafiore, D.; Campiani, E.; et al. High resolution multibeam and hydrodynamic datasets of tidal channels and inlets of the Venice Lagoon. Sci. Data 2017, 4, 1–14. [Google Scholar] [CrossRef]
- Philpot, W.D. Bathymetric mapping with passive multispectral imagery. Appl. Opt. 1989, 28, 1569. [Google Scholar] [CrossRef] [PubMed]
- Lovato, T.; Androsov, A.; Romanenkov, D.; Rubino, A. The tidal and wind induced hydrodynamics of the composite system Adriatic Sea/Lagoon of Venice. Cont. Shelf Res. 2010, 30, 692–706. [Google Scholar] [CrossRef]
- Zaggia, L.; Lorenzetti, G.; Manfé, G.; Scarpa, G.M.; Molinaroli, E.; Parnell, K.E.; Rapaglia, J.P.; Gionta, M.; Soomere, T. Fast shoreline erosion induced by ship wakes in a coastal lagoon: Field evidence and remote sensing analysis. PLoS ONE 2017, 12, e0187210. [Google Scholar] [CrossRef] [PubMed]
- Madricardo, F.; Foglini, F.; Campiani, E.; Grande, V.; Catenacci, E.; Petrizzo, A.; Kruss, A.; Toso, C.; Trincardi, F. Assessing the human footprint on the sea-floor of coastal systems: The case of the Venice Lagoon, Italy. Sci. Rep. 2019, 9. [Google Scholar] [CrossRef]



| Fit Parameter | Initial Value | Min | Max | Units | Description |
|---|---|---|---|---|---|
| 0.1 | 0 | 50 | m−1 | Absorption coefficient of CDOM at 440 nm | |
| 0.8 | 0.1 | 100 | g m−3 | Concentration of NAP | |
| 2 | 0 | 1000 | m | Bottom depth (water depth) | |
| 2 | 0 | 10 | Relative brightness of sand | ||
| 0.67 | −1 | 10 | sr−1 | Fraction of sky radiance due to direct solar radiation |
| Fit Parameter | Initial Value | Min | Max | Units | Description |
|---|---|---|---|---|---|
| 0.1 | 0 | 50 | m−1 | Absorption coefficient of CDOM at 440 nm | |
| 6 | 0.1 | 100 | g m−3 | Concentration of NAP | |
| 0.67 | −1 | 10 | sr−1 | Fraction of sky radiance due to direct solar radiation | |
| 0.318 | 0 | 10 | sr−1 | Fraction of sky radiance due to Rayleigh scattering | |
| 0.318 | 0 | 10 | sr−1 | Fraction of sky radiance due to aerosol scattering |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niroumand-Jadidi, M.; Bovolo, F.; Bruzzone, L.; Gege, P. Physics-based Bathymetry and Water Quality Retrieval Using PlanetScope Imagery: Impacts of 2020 COVID-19 Lockdown and 2019 Extreme Flood in the Venice Lagoon. Remote Sens. 2020, 12, 2381. https://doi.org/10.3390/rs12152381
Niroumand-Jadidi M, Bovolo F, Bruzzone L, Gege P. Physics-based Bathymetry and Water Quality Retrieval Using PlanetScope Imagery: Impacts of 2020 COVID-19 Lockdown and 2019 Extreme Flood in the Venice Lagoon. Remote Sensing. 2020; 12(15):2381. https://doi.org/10.3390/rs12152381
Chicago/Turabian StyleNiroumand-Jadidi, Milad, Francesca Bovolo, Lorenzo Bruzzone, and Peter Gege. 2020. "Physics-based Bathymetry and Water Quality Retrieval Using PlanetScope Imagery: Impacts of 2020 COVID-19 Lockdown and 2019 Extreme Flood in the Venice Lagoon" Remote Sensing 12, no. 15: 2381. https://doi.org/10.3390/rs12152381
APA StyleNiroumand-Jadidi, M., Bovolo, F., Bruzzone, L., & Gege, P. (2020). Physics-based Bathymetry and Water Quality Retrieval Using PlanetScope Imagery: Impacts of 2020 COVID-19 Lockdown and 2019 Extreme Flood in the Venice Lagoon. Remote Sensing, 12(15), 2381. https://doi.org/10.3390/rs12152381