Potential of UAS-Based Remote Sensing for Estimating Tree Water Status and Yield in Sweet Cherry Trees
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site
2.2. Experimental Design
2.3. Airborne Imagery
2.4. Field Measurements
2.5. Machine Learning Methodologies for Estimating Tree Crop Yield
2.6. Statistical Analysis
3. Results
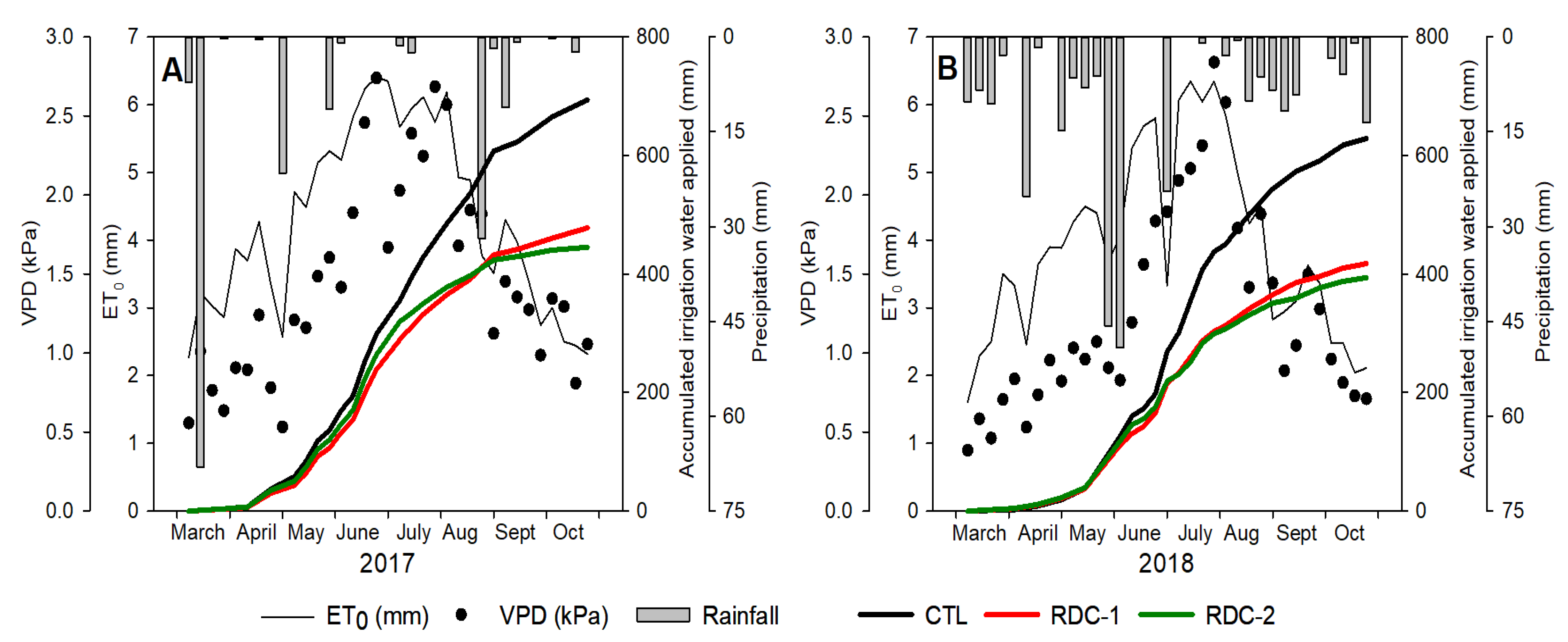
3.1. Environmental Conditions and Irrigation Water Applied
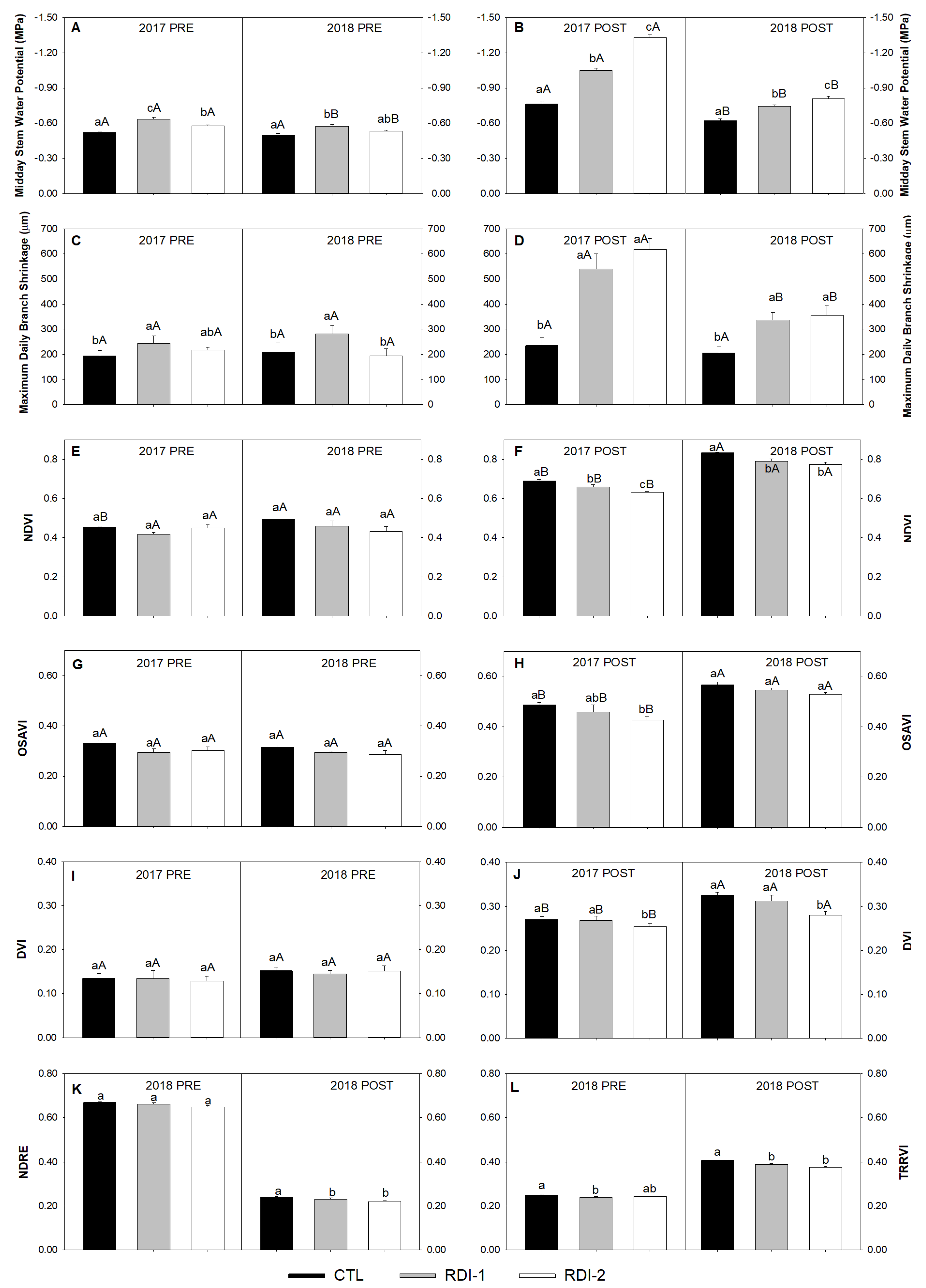
3.2. Conventional and Continuous Plant Water Status Indicators and Remote Vegetation Indices
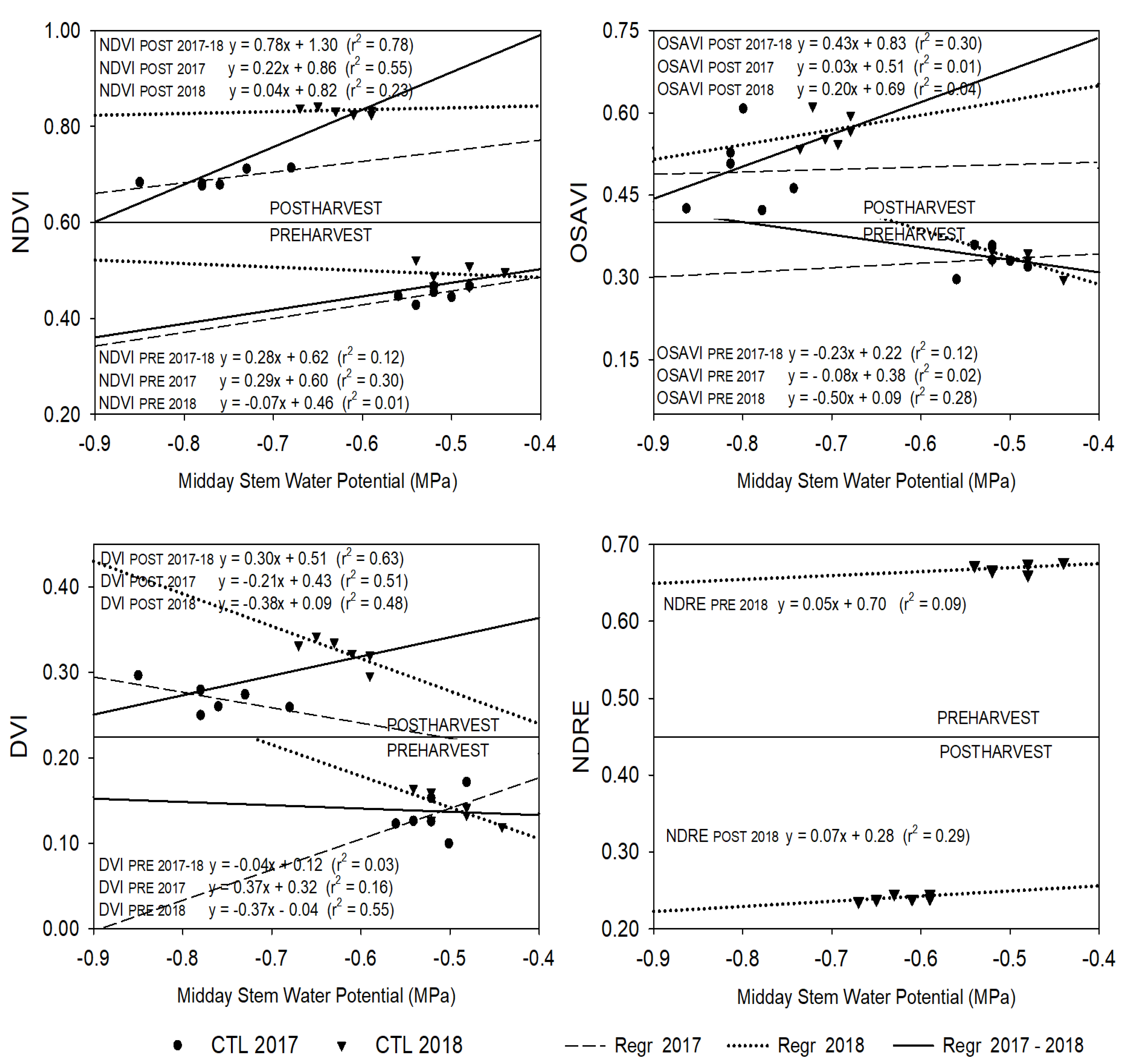
3.3. Relationship between Plant Water Status Indicators and Vegetation Indices
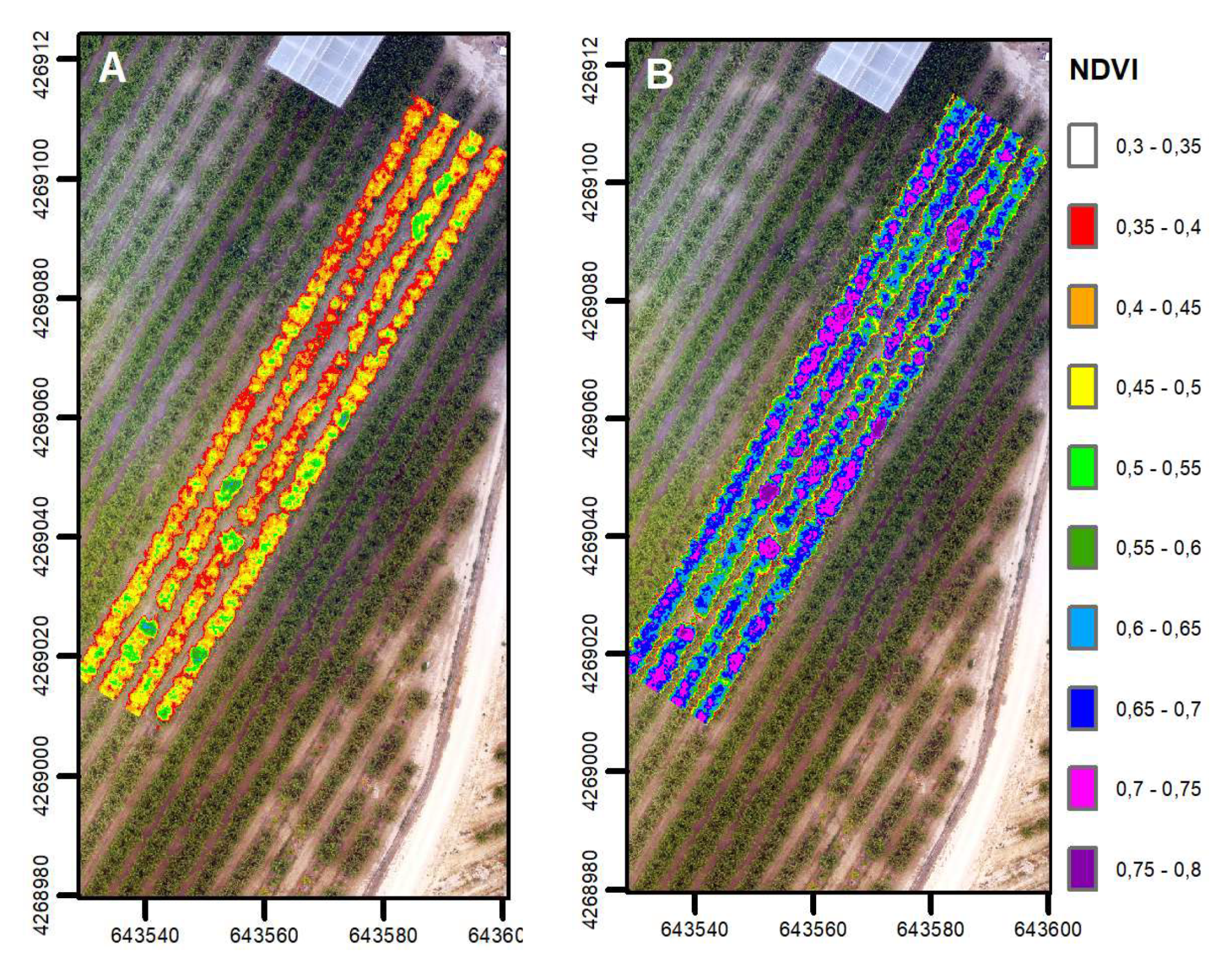
3.4. Assessment of Tree Vigor Using Remote Indices
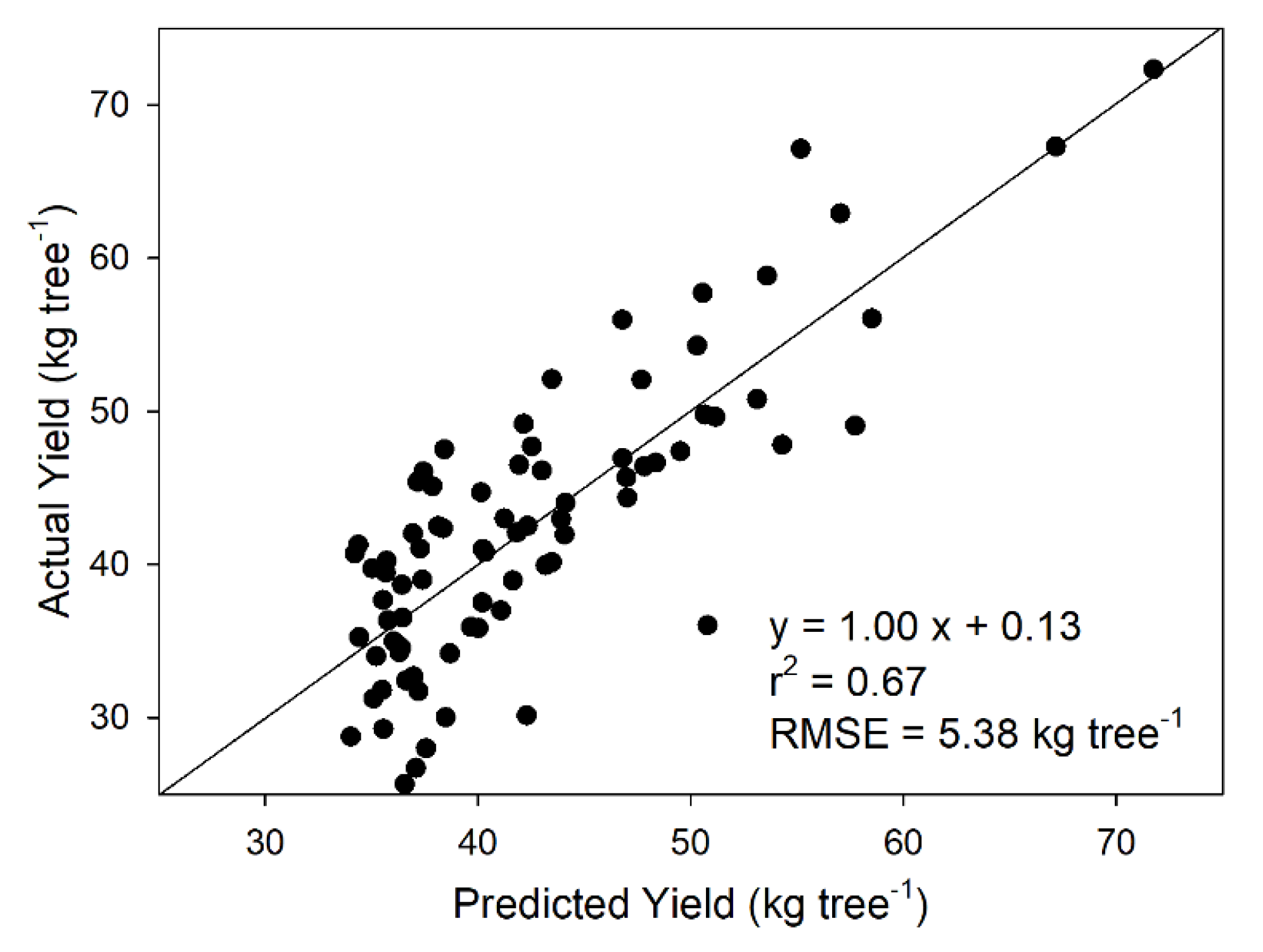
3.5. Tree Yield Estimation
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cammarano, D.; Fitzgerald, G.J.; Casa, R.; Basso, B. Assessing the Robustness of Vegetation Indices to Estimate Wheat N in Mediterranean Environments. Remote Sens. 2014, 6, 2827–2844. [Google Scholar] [CrossRef]
- Cancela, J.J.; Fandiño, M.; Rey, B.J.; Dafonte, J.; González, X.P. Discrimination of irrigation water management effects in pergola trellis system vineyards using a vegetation and soil index. Agric. Water Manag. 2017, 183, 70–77. [Google Scholar] [CrossRef]
- Gago, J.; Douthe, C.; Coopman, R.E.; Gallego, P.P.; Ribas-Carbo, M.; Flexas, J.; Escalona, J.; Medrano, H. UAVs challenge to assess water stress for sustainable agriculture. Agric. Water Manag. 2015, 153, 9–19. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, H.; Niu, Y.; Han, W. Mapping Maize Water Stress Based on UAV Multispectral. Remote Sens. 2019, 11, 605. [Google Scholar] [CrossRef]
- Zhao, T.; Stark, B.; Chen, Y.Q.; Ray, A.; Doll, D. More Reliable Crop Water Stress Quantification Using Small Unmanned Aerial Systems (sUAS). IFAC Pap. 2016, 49, 409–414. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the great plains with ERTS. In Third ERTS-1 Symposium; NASA: Washington, DC, USA, 1973; Volume 1, pp. 309–317. [Google Scholar]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Barnes, E.M.; Clarke, T.R.; Richards, S.E.; Colaizzi, P.D.; Haberland, J.; Kostrzewski, M.; Waller, P.; Choi, C.; Riley, E.; Thompson, T.; et al. Coincident Detection of Crop Water Stress, Nitrogen Status and Canopy Density Using Ground Based Multispectral Data. In Proceedings of the Fifth International Conference on Precision Agriculture, 16–19 July 2000, Bloomington, MN, USA; Robert, P.C., Rust, R.H., Larson, W.E., Eds.; ASA, CSSA and SSA: Madison, WI, USA, 2000; pp. 1–15. [Google Scholar]
- Conesa, M.R.; Conejero, W.; Vera, J.; Ramírez-Cuesta, J.M.; Ruiz-Sánchez, M.C. Terrestrial and Remote Indexes to Assess Moderate Deficit Irrigation in Early-Maturing Nectarine Trees. Agronomy 2019, 9, 630. [Google Scholar] [CrossRef]
- Gonzalez-Dugo, V.; Zarco-Tejada, P.J.; Nicolas, E.; Nortes, P.A.; Alarcón, J.J.; Intrigliolo, D.S.; Fereres, E. Using high resolution UAV thermal imagery to assess the variability in the water status of five fruit tree species within a commercial orchard. Precis. Agric. 2013, 14, 660–678. [Google Scholar] [CrossRef]
- Santesteban, L.G.; Di Gennaro, S.F.; Herrero-Langreo, A.; Miranda, C.; Royo, J.B.; Matese, A. High-resolution UAV-based thermal imaging to estimate the instantaneous and seasonal variability of plant water status within a vineyard. Agric. Water Manag. 2017, 183, 49–59. [Google Scholar] [CrossRef]
- Stagakis, S.; González-Dugo, V.; Cid., P.; Guillén-Climent, M.L.; Zarco-Tejada, P.J. Monitoring water stress and fruit quality in an orange orchard under regulated deficit irrigation using narrow-band structural and physiological remote sensing indices. ISPRS J. Photogramm. 2012, 71, 47–61. [Google Scholar] [CrossRef]
- Blando, F.; Oomah, B.D. Sweet and sour cherries: Origin, distribution, nutritional composition and health benefits. Trends Food Sci. Tech. 2019, 86, 517–529. [Google Scholar] [CrossRef]
- Blanco, V.; Torres-Sánchez, R.; Blaya-Ros, P.J.; Pérez-Pastor, A.; Domingo, R. Vegetative and reproductive response of ‘Prime Giant’ sweet cherry trees to regulated deficit irrigation. Sci. Hortic. 2019, 249, 478–489. [Google Scholar] [CrossRef]
- Marsal, J.; Lopez, G.; del Campo, J.; Mata, M.; Arbones, A.; Girona, J. Postharvest regulated deficit irrigation in ’Summit’ sweet cherry fruit yield and quality in the following season. Irrig. Sci. 2010, 28, 181–189. [Google Scholar] [CrossRef]
- Carrasco-Benavides, M.; Espinoza Meza, S.; Olguín-Cáceres, J.; Muñoz-Concha, D.; von Bennewitz, E.; Ávila-Sánchez, C.; Ortega-Farías, S. Effects of regulated post-harvest irrigation strategies on yield, fruit quality and water productivity in a drip-irrigated cherry orchard. N. Z. J. Crop. Hort. 2020, 48, 97–116. [Google Scholar] [CrossRef]
- Abdelfatah, A.; Aranda, X.; Savé, R.; de Herralde, F.; Biel, C. Evaluation of the response of maximum daily shrinkage in young cherry trees submitted to water stress cycles in a greenhouse. Agric. Water Manag. 2013, 118, 150–158. [Google Scholar] [CrossRef]
- Blanco, V.; Domingo, R.; Pérez-Pastor, A.; Blaya-Ros, P.J.; Torres-Sánchez, R. Soil and plant water indicators for deficit irrigation management of field-grown sweet cherry trees. Agric. Water Manag. 2018, 208, 83–94. [Google Scholar] [CrossRef]
- Livellara, N.; Saavedra, F.; Salgado, E. Plant based indicators for irrigation scheduling in young cherry trees. Agric. Water Manag. 2011, 98, 684–690. [Google Scholar] [CrossRef]
- Ortuño, M.F.; Alarcón, J.J.; Nicolás, E.; Torrecillas, A. Interpreting trunk diameter changes in young lemon trees under deficit irrigation. Plant Sci. 2004, 167, 275–280. [Google Scholar] [CrossRef]
- Puerto, P.; Domingo, R.; Torres, R.; Pérez-Pastor, A.; García-Riquelme, M. Remote management of deficit irrigation in almond trees based on maximum daily trunk shrinkage. Water relations and yield. Agric. Water Manag. 2013, 126, 33–45. [Google Scholar] [CrossRef]
- Aggelopoulou, K.D.; Wulfsohn, D.; Fountas, S.; Gemtos, T.A.; Nanos, G.D.; Blackmore, S. Spatial variation in yield and quality in a small apple orchard. Precis. Agric. 2009, 11, 538–556. [Google Scholar] [CrossRef]
- Mu, Y.; Fujii, Y.; Takata, D.; Zheng, K.N.; Honda, K.; Ninomiya, S.; Guo, W. Characterization of peach tree crown by using high-resolution images from an unmanned aerial vehicle. Hortic. Res. 2018, 74, 5. [Google Scholar] [CrossRef] [PubMed]
- Rahman, M.M.; Robson, A.; Bristow, M. Exploring the Potential of High Resolution WorldView-3 Imagery for Estimating Yield of Mango. Remote Sens. 2018, 10, 1866. [Google Scholar] [CrossRef]
- Whiting, M.D.; Perry, R.L. Chapter 18: Fruit Harvest Methods and Technologies. In Cherries: Botany, Production and Uses, 1st ed.; Quero-García, J., Iezzoni, A., Pulawska, J., Lang, G., Eds.; CABI: Oxfordshire, UK, 2017; pp. 442–459. [Google Scholar]
- Lee, B.-H.; Kendel, P.; Brorsen, B.W. Pre-harvest forecasting of county wheat yield and wheat quality using weather information. Agric. For. Meteorol. 2013, 15, 26–35. [Google Scholar] [CrossRef]
- Goldstein, A.; Fink, L.; Meitin, A.; Bohadana, S.; Lutenberg, O.; Ravid, G. Applying machine learning on sensor data for irrigation recommendations: Revealing the agronomist’s tacit knowledge. Precis. Agric. 2018, 19, 3. [Google Scholar] [CrossRef]
- Navarro-Hellín, H.; Martínez-del-Rincon, J.; Domingo-Miguel, R.; Soto-Valles, F.; Torres-Sánchez, R. A decision support system for managing irrigation in agriculture. Comput. Electron. Agric. 2016, 124, 121–131. [Google Scholar] [CrossRef]
- Romero, M.; Luo, Y.; Su, B.; Fuentes, S. Vineyard water status estimation using multispectral imagery from an UAV platform and machine learning algorithms for irrigation scheduling management. Comput. Electron. Agric. 2018, 147, 109–117. [Google Scholar] [CrossRef]
- Torres, R.; Navarro-Hellin, H.; Frutos, A.G.; Ruiz-Abellon, M.C.; Domingo, R. A Decision Support System for Irrigation Management: Analysis and Implementation of Different Learning Techniques. Water 2020, 12, 548. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. FAO Irrigation and drainage paper 56. In Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements; Food and Agriculture Organization: Rome, Italy, 1998. [Google Scholar]
- Marsal, J. FAO irrigation and drainage paper 66. Sweet Cherry. In Crop Yield Response to Water; Food and Agriculture Organization: Rome, Italy, 2012; pp. 449–457. [Google Scholar]
- Fereres, E.; Martinich, D.A.; Aldrich, T.M.; Castel, J.R.; Holzapfel, E.; Schulbach, H. Drip irrigation saves money in young almond orchards. Calif. Agric. 1982, 36, 12–13. [Google Scholar]
- McCutchan, H.; Shackel, K.A. SWP as a sensitive indicator of water stress in prune trees (Prunus domestica L. cv. French). J. Am. Soc. Hortic. Sci. 1992, 117, 607–611. [Google Scholar] [CrossRef]
- Gholipoor, M.; Nadali, F. Fruit yield prediction of pepper using artificial neural network. Sci. Hortic. 2019, 250, 249–253. [Google Scholar] [CrossRef]
- Fernandes, J.L.; Ebecken, N.F.F.; Esquerdo, J.C.D.M. Sugarcane yield prediction in Brazil using NDVI time series and neural networks ensemble. 2017. Int. J. Remote Sens. 2011, 38, 4631–4644. [Google Scholar] [CrossRef]
- Veenadhari, S.; Mishra, B.; Singh, C.D. Soybean Productivity Modelling using Decision Tree Algorithms. Int. J. Comp. Appl. 2011, 27, 11–15. [Google Scholar] [CrossRef]
- Bhatnagar, R.; Gohain, G.B. Crop Yield Estimation Using Decision Trees and Random Forest Machine Learning Algorithms on Data from Terra (EOS AM-1) & Aqua (EOS PM-1) Satellite Data. In Machine Learning and Data Mining in Aerospace Technology. Studies in Computational Intelligence, 1st ed.; Hassanien, A., Darwish, A., El-Askary, H., Eds.; Springer Int. Publishing: Cham, Switzerland, 2020; pp. 107–124. [Google Scholar]
- San-Segundo, R.; Navarro-Hellín, H.; Torres-Sánchez, R.; Hodgins, J.; de la Torre, F. Increasing robustness in the detection of freezing of gait in Parkinson’s disease. Electronics 2019, 8, 119. [Google Scholar] [CrossRef]
- Goldhamer, D.A.; Fereres, E. Irrigation scheduling protocols using continuously recorded trunk diameter measurements. Irrig. Sci. 2001, 20, 115–125. [Google Scholar] [CrossRef]
- Blanco, V.; Blaya-Ros, P.J.; Torres-Sánchez, R.; Domingo, R. Influence of Regulated Deficit Irrigation and Environmental Conditions on Reproductive Response of Sweet Cherry Trees. Plants. 2020, 9, 94. [Google Scholar] [CrossRef]
- Lauri, P.E.; Claverie, J. Sweet Cherry Tree Architecture, Physiology and Management: Towards an Integrated View. Acta Hort. 2008, 667, 361–366. [Google Scholar] [CrossRef]
- Baluja, J.; Diago, M.P.; Balda, P.; Zorer, R.; Meggio, F.; Morales, F.; Tardaguilla, J. Assessment of vineyard water status variability by thermal and multispectral imagery using an unmanned aerial vehicle (UAV). Irrig. Sci. 2012, 30, 511–522. [Google Scholar] [CrossRef]
- Ballester, C.; Zarco-Tejada, P.J.; Nicolás, E.; Alarcón, J.J.; Fereres, E.; Intrigliolo, D.S.; Gonzalez-Dugo, V. Evaluating the performance of xanthophyll, chlorophyll and structural-sensitive spectral indices to detect water stress in five fruit tree species. Prec. Agric. 2018, 19, 178–193. [Google Scholar] [CrossRef]
- Robson, A.; Rahman, M.M.; Muir, J. Using WorldView Satellite Imagery to Map Yield in Avocado (Persea americana): A Case Study in Bundaberg, Australia. Remote Sens. 2017, 9, 1223. [Google Scholar] [CrossRef]
- Vossen, P.M.; Silva, D. Chapter 16. Temperate Tree Fruit and Nut Crops. In California Master Gardener Handbook, 2nd ed.; Pittenger, D.R., Ed.; University of California, Pub.: Davis, CA, USA, 2015; Volume 3382, pp. 83–108. [Google Scholar]
- Bellvert, J.; Adeline, K.; Baram, S.; Pierce, L.; Sanden, B.L.; Smart, D.R. Monitoring Crop Evapotranspiration and Crop Coefficients over an Almond and Pistachio Orchard Throughout Remote Sensing. Remote Sens. 2018, 10, 2001. [Google Scholar] [CrossRef]
- Virlet, N.; Lebourgeois, V.; Martinez, S.; Costes, E.; Labbé, S.; Regnard, J.L. Stress indicators based on airborne thermal imagery for field phenotyping a heterogeneous tree population for response to water constraints. J. Exp. Bot. 2014, 65, 5429–5442. [Google Scholar] [CrossRef] [PubMed]
- Beeri, O.; Mey-tal, S.; Raz, Y.; Rud, R.; Pelta, R. Detecting variability in plant water potential with multi-spectral satellite imagery. In Proceedings of the 14th International Conference on Precision Agriculture, Montreal, QC, Canada, 24–27 June 2018; International Society of Precision Agriculture, Pub.: Monticello, IL, USA, 2018. [Google Scholar]
- Van Beek, J.; Tits, L.; Somers, B.; Coppin, P. Stem Water Potential Monitoring in Pear Orchards through WorldView-2 Multispectral Imagery. Remote Sens. 2013, 5, 6647–6666. [Google Scholar] [CrossRef]
- Matese, A.; Di Gennaro, S.F. Practical Applications of a Multisensor UAV Platform Based on Multispectral, Thermal and RGB High Resolution Images in Precision Viticulture. Agriculture 2018, 8, 116. [Google Scholar] [CrossRef]
- Papageorgiou, E.I.; Aggelopoulou, K.D.; Gemtos, T.A.; Nanos, G.D. Yield prediction in apples using Fuzzy Cognitive Map learning approach. Comput. Electron. Agric. 2013, 91, 19–29. [Google Scholar] [CrossRef]
- Cheng, H.; Damerow, L.; Sun, Y.; Blanke, M. Early Yield Prediction Using Image Analysis of Apple Fruit and Tree Canopy Features with Neural Networks. J. Imaging. 2017, 3, 6. [Google Scholar] [CrossRef]
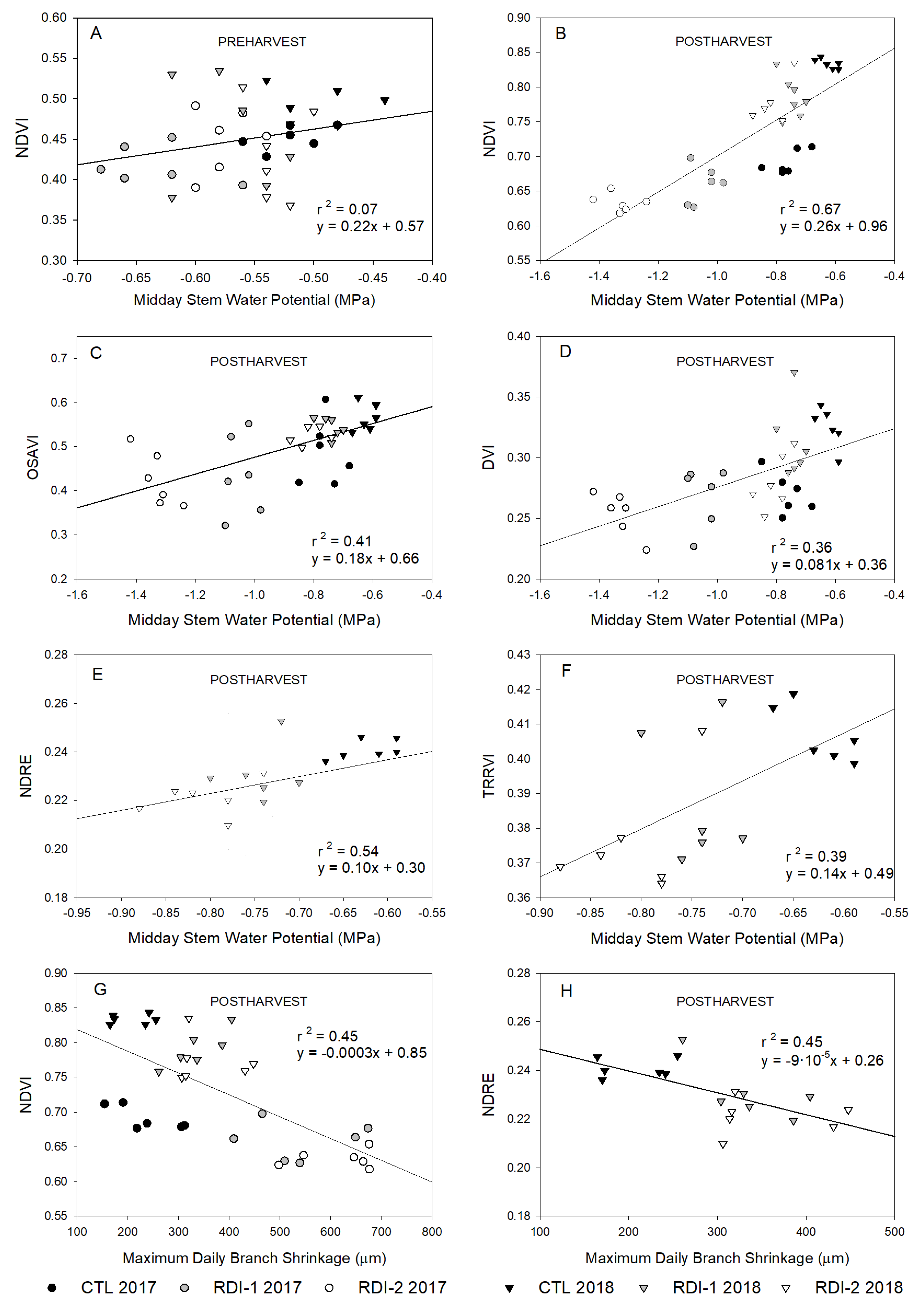
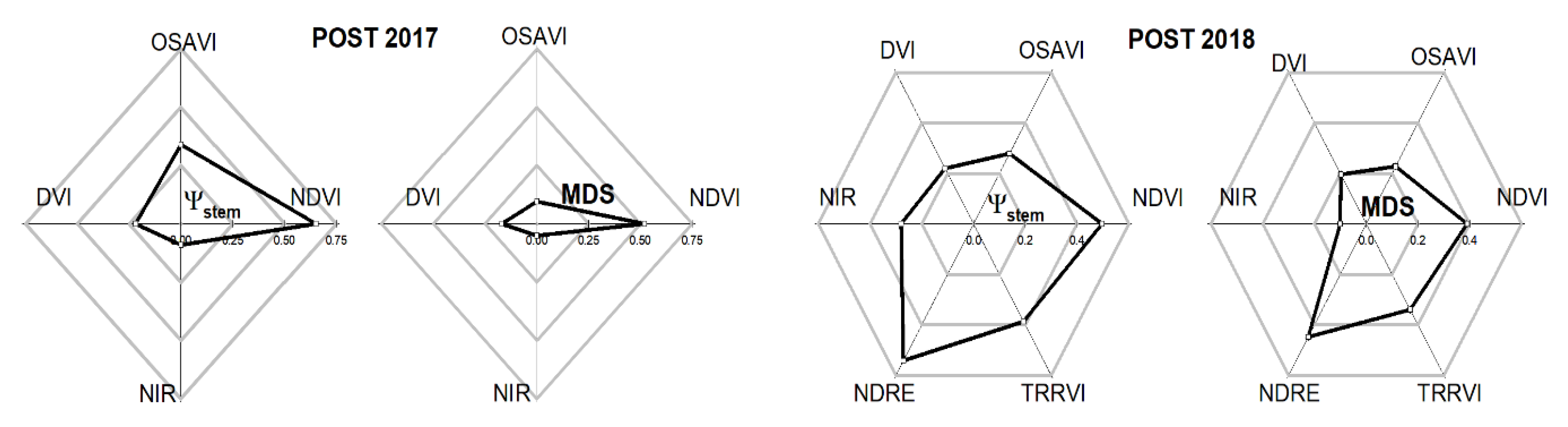
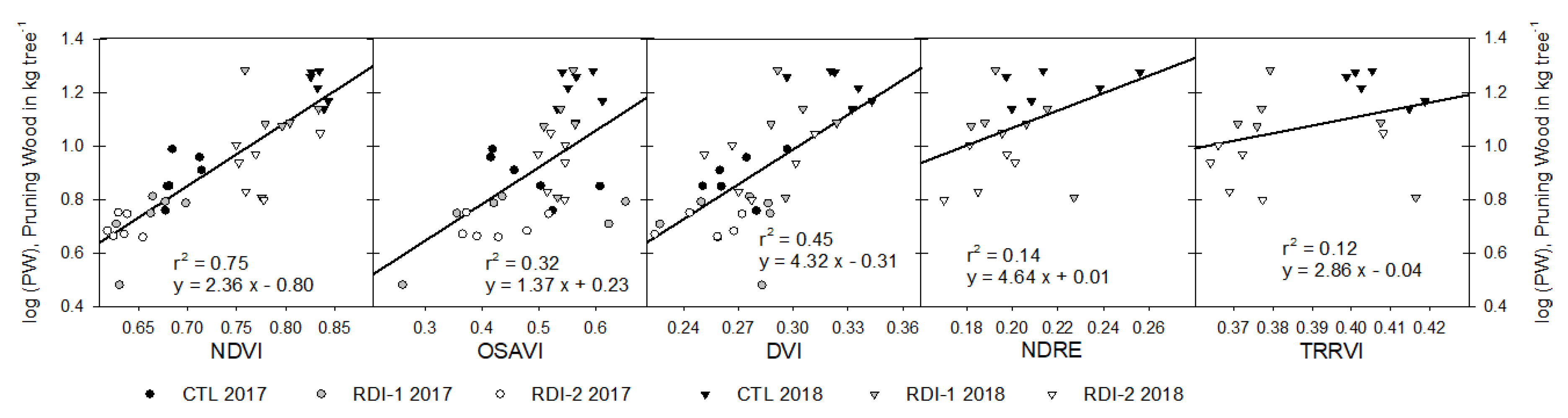
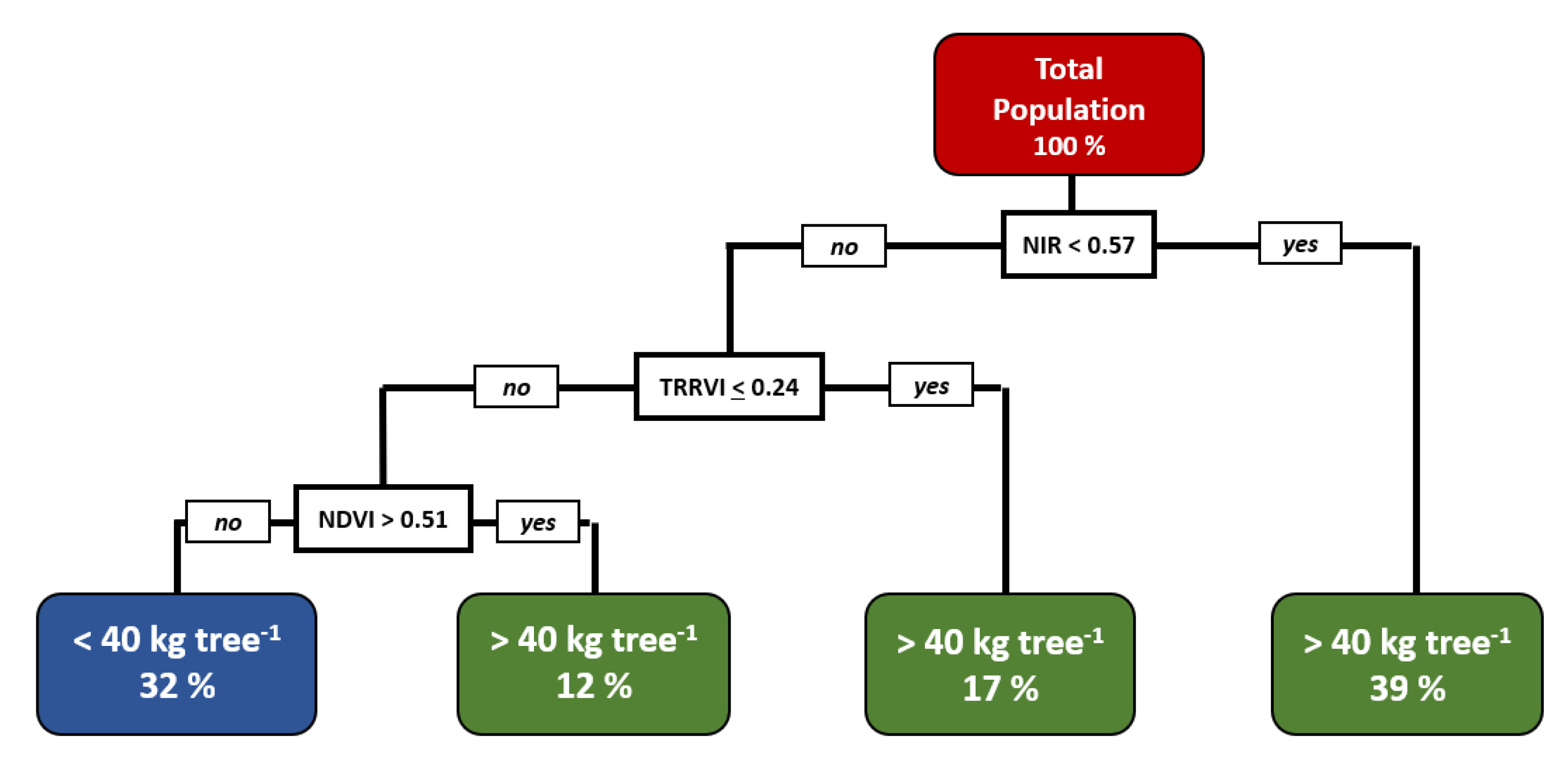
| Ψs | MDS | NDVI | OSAVI | DVI | NDRE | TRRVI | |||||||||
| RDI 1 | RDI 2 | RDI 1 | RDI 2 | RDI 1 | RDI 2 | RDI 1 | RDI 2 | RDI 1 | RDI 2 | RDI 1 | RDI 2 | RDI 1 | RDI 2 | ||
| PRE | SI | 1.15 | 1.07 | 1.36 | 0.93 | 0.93 | 0.88 | 0.88 | 0.88 | 0.97 | 0.93 | 0.99 | 0.98 | 0.95 | 0.96 |
| CV | 0.07 | 0.04 | 0.12 | 0.15 | 0.15 | 0.14 | 0.07 | 0.12 | 0.24 | 0.20 | 0.02 | 0.03 | 0.04 | 0.03 | |
| S | 16.0 | 27.7 | 11.6 | 6.2 | 6.21 | 6.5 | 15.2 | 9.3 | 4.9 | 4.7 | 48.0 | 36.4 | 24.9 | 32.7 | |
| POST | SI | 1.19 | 1.29 | 1.63 | 1.72 | 0.95 | 0.93 | 0.95 | 0.90 | 0.98 | 0.90 | 0.96 | 0.92 | 0.95 | 0.92 |
| CV | 0.05 | 0.06 | 0.16 | 0.18 | 0.03 | 0.04 | 0.19 | 0.12 | 0.09 | 0.08 | 0.05 | 0.03 | 0.05 | 0.04 | |
| S | 25.7 | 20.9 | 10.4 | 9.4 | 28.5 | 22.5 | 13.2 | 8.3 | 10.4 | 12.1 | 19.3 | 28.0 | 19.4 | 21.3 | |
| NDVI | OSAVI | DVI | NDRE | TRRVI | NIR | Yield (kg tree−1) | |
|---|---|---|---|---|---|---|---|
| Mean | 0.466 | 0.590 | 0.140 | 0.663 | 0.245 | 0.589 | 42.112 |
| SE | 0.007 | 0.007 | 0.002 | 0.002 | 0.001 | 0.006 | 1.119 |
| Yield kg tree−1 | Min | Max | Mean | SD | CV (%) | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|
| Actual | 25.67 | 72.32 | 42.46 | 9.40 | 22.15 | 0.83 | 1.01 |
| Predicted | 34.02 | 71.74 | 42.47 | 7.69 | 18.16 | 1.49 | 2.48 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blanco, V.; Blaya-Ros, P.J.; Castillo, C.; Soto-Vallés, F.; Torres-Sánchez, R.; Domingo, R. Potential of UAS-Based Remote Sensing for Estimating Tree Water Status and Yield in Sweet Cherry Trees. Remote Sens. 2020, 12, 2359. https://doi.org/10.3390/rs12152359
Blanco V, Blaya-Ros PJ, Castillo C, Soto-Vallés F, Torres-Sánchez R, Domingo R. Potential of UAS-Based Remote Sensing for Estimating Tree Water Status and Yield in Sweet Cherry Trees. Remote Sensing. 2020; 12(15):2359. https://doi.org/10.3390/rs12152359
Chicago/Turabian StyleBlanco, Víctor, Pedro José Blaya-Ros, Cristina Castillo, Fulgencio Soto-Vallés, Roque Torres-Sánchez, and Rafael Domingo. 2020. "Potential of UAS-Based Remote Sensing for Estimating Tree Water Status and Yield in Sweet Cherry Trees" Remote Sensing 12, no. 15: 2359. https://doi.org/10.3390/rs12152359
APA StyleBlanco, V., Blaya-Ros, P. J., Castillo, C., Soto-Vallés, F., Torres-Sánchez, R., & Domingo, R. (2020). Potential of UAS-Based Remote Sensing for Estimating Tree Water Status and Yield in Sweet Cherry Trees. Remote Sensing, 12(15), 2359. https://doi.org/10.3390/rs12152359





