Abstract
Coastal wetlands are productive ecosystems driven by highly dynamic hydrological processes such as tides and river discharge, which operate at daily to seasonal timescales, respectively. The scientific community has been calling for landscape-scale measurements of hydrological variables that could help understand the flow of water and transport of sediment across coastal wetlands. While in situ water level gauge data have enabled significant advances, they are limited in coverage and largely unavailable in many parts of the world. In preparation for the NISAR mission, we investigate the use of spaceborne Interferometric Synthetic Aperture Radar (InSAR) observations of phase and coherence at L-band for landscape-scale monitoring of water level change and vegetation cover in coastal wetlands across seasons. We use L-band SAR images acquired by ALOS/PALSAR from 2007 to 2011 to study the impact of seasonal changes in vegetation cover on InSAR sensitivity to water level change in the wetlands of the Atchafalaya basin located in coastal Louisiana, USA. Seasonal variations are observed in the interferometric coherence () time-series over wetlands, with higher coherence during the winter and lower coherence during the summer. We show with InSAR time-series that coherence is inversely correlated with Normalized Difference Vegetation Index (NDVI). Our analysis of polarimetric scattering mechanisms demonstrates that double-bounce is the dominant mechanism in swamps while its weakness in marshes hinders estimation of water level changes. In swamps, water level change maps derived from InSAR are highly correlated (r2 = 0.83) with in situ data from the Coastwide Reference Monitoring System (CRMS). From October to December, we observed that the water level may be below wetland elevation and thus not inundating wetlands significantly. Our analysis shows that water level can only be retrieved when both images used for InSAR are acquired when wetlands are inundated. The L-band derived-maps of water level change show large scale gradients originating from the Gulf Intracoastal Waterway rather than the main delta trunk channel, confirming its significant role as a source of hydrologic connectivity across these coastal wetlands. These results indicate that NISAR, with its InSAR observations every 12 days, will provide the measurements necessary to reveal large scale hydrodynamic processes that occur in swamps across seasons.
1. Introduction
River deltas along the world’s coasts connect the land and sea with highly productive wetland ecosystems accumulating soils through biomass production and capture of mineral sediments. These wetlands play a significant role in reducing the impact of flooding and erosion [1], protecting coastal infrastructure, acting as nurseries for fish, crustaceans and mammals, and providing livelihood of millions of people around the globe. However, river deltas are threatened by the impacts of climate change and human activity [2,3]. In particular, changes in hydrology and sediment supply exacerbate the devastating impact of subsidence and sea level rise on deltas [4,5]. In Louisiana, the Mississippi Delta has lost nearly 5000 km2 of wetlands between 1930 and 2010, at rates of loss of 43 km2/year since 1985 estimated with remote sensing [6,7]. As of 2014, they covered approximately 38,000 km2 [8]. In 2003, U.S. Geological Survey (USGS) implemented the Coastwide Reference Monitoring System (CRMS) as a mechanism to monitor and evaluate the effectiveness of Coastal Wetlands Planning, Protection and Restoration Act (CWPPRA) projects along the Louisiana coastline [9]. Among other measurements, CRMS stations monitor hourly water level across the landscape supporting analysis of temporal as well as spatial variations in water level [10]. However, spatially continuous observations of water level changes are needed to complement in situ measurements and understand the connectivity between the channel networks and wetlands.
Spaceborne remote sensing with Interferometric Synthetic Aperture Radar (InSAR) is a promising technique to monitor changes in water levels [1]. InSAR measures the image similarity (coherence) and range difference (phase) of a pair of SAR images, and higher coherence is needed to obtain accurate estimates of phase [11]. There are two main factors affecting InSAR observations over wetlands: vegetation structure and water level. The presence of vegetation increases the intensity of the backscattered microwave, in part because the specular scattering from the water surface is reflected back towards the radar by the vegetation [12]. This same backscatter signal, as measured consecutively by an orbiting radar, can be used to estimate water level changes through phase change using InSAR [13,14]. InSAR measurements of water level in wetlands have progressed significantly over the last two decades [15], in particular at L- and C-bands. Previous studies have found that L-band with HH polarization generally provides the best results, in particular over shorter temporal baselines [15]. This was demonstrated in several case studies using JERS-1 [14] and ALOS/PALSAR [16]. In Louisiana, Oliver–Cabrera and Wdowinski [17] mapped the tidal inundation extent along the entire Louisiana coastal wetlands using InSAR from ALOS/PALSAR and Radarsat-1. Their study demonstrated that tidal inundation is restricted to narrow areas along the coast, and InSAR observations in coastal wetlands are highly dependent on the tide-induced water level.
The InSAR coherence at C-band is known to decrease as herbaceous plants grow to maturity [18] and is generally higher in swamps (defined here as woody wetlands) than in marshes (herbaceous wetlands) [19,20]. In both biomes, coherence reaches its highest values during the leaf-off season [11]. Although it is known that water level change within wetlands can be estimated using InSAR, a more complete analysis of the impact of vegetation structure and phenology, and seasonal variations in water level, on the L-band InSAR signal is needed to develop algorithms for the upcoming NISAR mission.
In this paper, we seek to assess the potential of the NISAR mission [21] and develop operational methods to measure large scale changes in water level in coastal wetlands globally and across seasons. NISAR is an L-band radar instrument planned for launch in 2022 that will generate interferograms every 12 days. While NISAR offers the possibility of monitoring wetlands hydrology at the global scale, its capabilities will most likely depend on vegetation type and phenology. This study evaluates the water level change retrieval in coastal wetlands given L-band InSAR response to wetland vegetation type and seasonal changes.
We processed 17 InSAR pairs of ALOS/PALSAR (hereon PALSAR) data from 2007 to 2011 using InSAR Scientific Computing Environment (ISCE) [22]. ISCE will be used to process data from the upcoming NISAR mission. We first summarize the study site and the CRMS data set (Section 2). We then introduce the processing of the PALSAR L-band dataset in Section 3. In Section 4, we validate and discuss the results using CRMS’s in situ water level measurements before concluding in Section 5.
2. Wax Lake Wetlands and In Situ Data
Previous studies of water level change have focused primarily on inland swamp forest in Louisiana [11,19,23]. Our study area covers coastal wetlands within the Atchfalaya basin of coastal Louisiana, divided by a channel called the Wax Lake Outlet. The study area is influenced by tides. Figure 1 shows the land cover of swamps and marshes from the National Land Cover Database (NLCD) [24]. The study area is bounded on the north side by the engineered Gulf Intracoastal Waterway (GIWW). The GIWW is leveed on its northern boundary, but the southern boundary may be a source of floodwaters to the wetlands in the study area. The Wax Lake Delta (WLD) is located at the downstream end of the river.
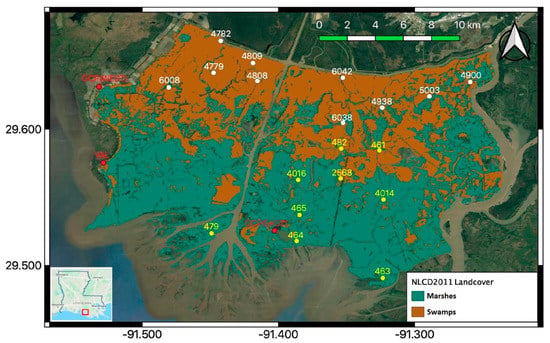
Figure 1.
Land cover from the National Land Cover Database (NLCD2011) showing emergent herbaceous (marshes) and woody (swamps) wetlands within the study area, located within the Atchafalaya basin of coastal Louisiana, USA. The location of the Coastwide Reference Monitoring System (CRMS) stations are shown as white and yellow dots (white dots: swamp, yellow dots: fresh marsh). Red dots show the locations of the ground control points (GCPs) and validation point (VAL). The inset at bottom left shows the location of the study area in Louisiana. (Background Map from Google [26]).
The CRMS design implements a multiple reference approach by using aspects of hydrogeomorphic functional assessments and probabilistic sampling [25]. The measurements include surface water gauges, vegetation type, wetland type, among others. More than 300 stations are spread out along the Louisiana coastline.
Figure 1 shows the location of the CRMS stations, with IDs, over the study area. The wetland type and available date range of the hourly gauge data are listed in Table 1 for 19 CRMS stations [27]. The CRMS data include the wetland type as either fresh marsh or swamp. The water level is recorded hourly, and a wetland elevation value is provided in CRMS dataset. To ensure wetland elevation represented a wide area near the CRMS stations, we estimated averaged DEM over 30 square meters around each CRMS station for local wetland elevation using the United States Geological Survey (USGS) Digital Elevation Model (DEM) [28,29,30]. Given that the CRMS gauges indicate water level in small channels rather than that in the unchannelized wetlands, we use both wetland elevation references to identify whether a wetland is inundated. Disregarding sites located in floating marshes, which do not have elevations in the CRMS database, the USGS DEM gives similar elevation ranges for swamps and freshwater marshes. In Louisiana, the wet season is generally from April to September and the dry season from October to March. October is the driest month, while May is the wettest. In our study, non-inundated wetlands are identified using the USGS DEM. The starting date of CRMS water level records differs, with a few cases providing only partial record during our study period.

Table 1.
In situ measurements from the Coastwide Reference Monitoring System (CRMS) & the USGS DEM.
We observed that the wetland type for each CRMS station is consistent with the land cover types from the NLCD. Note that “swamp” is the name of the landcover class in the CRMS data and it falls in the class of “woody wetland” in the NLCD. Similarly, “fresh marsh” in the CRMS data falls in the class of “herbaceous wetlands” in the NLCD.
3. Satellite Data and Data Processing
In this section, we describe the processing of interferometric data from PALSAR using the InSAR Scientific Computing Environment (ISCE) and using ancillary information from radar backscatter and MODIS to characterize the contribution of radar backscattering mechanisms and plant structure, respectively.
3.1. Phased Array Type L-Band Synthetic Aperture Radar (PALSAR)
PALSAR was active during 2006 to 2011. Stripmap (SM) data are used in this study and they provide polarization options of single-pol (FBS), dual-pol (FBD), or quad-pol (PLR). With full polarization products, the full polarimetry allows us to study the scattering mechanisms using polarimetric decompositions. Table 2 lists the PALSAR images used in this study. It includes SM3 mode data of level 1.0 and SM2 mode data of level 1.1 acquired through the Alaska Satellite Facility Distributed Active Archive Center (ASF DAAC) [31]. All images are from ascending orbits. SM3 stands for fine beam mode with a spatial resolution of 9.1 m 5.3 m (range azimuth) and coverage of 70 km 70 km. The SM3 images we use are acquired from the same frame whose polarization is either single-polarization (HH) or dual-polarization (HH and HV). The first letter stands for the polarization of the transmitted electromagnetic wave and the second letter is for the receiving polarization. SM2 stands for high-sensitive mode with a resolution of 5.1 m 4.3 m and coverage of 40–50 km 70 km. The two full polarimetry images listed in Table 2 are the only ones in PLR mode covering the study area. They are not included in the interferometric processing but are used to study microwave scattering mechanisms through polarimetric decomposition (Section 4.2.2).

Table 2.
ALOS/PALSAR Data.
3.2. InSAR Processing
Here we consider interferometry using a single monostatic SAR acquiring successive images of the same land surface with similar viewing geometry, an imaging mode known as repeat-pass (or zero-baseline) interferometry [13]. The separation in time between the two acquisitions is referred to as the temporal baseline. For consistency, we selected the 17 pairs listed in Table 3 with a 46-day temporal baseline (the minimum temporal baseline for PALSAR). We only consider HH pairs because water level change is accentuated through double-bounce scattering [11,14,32,33].

Table 3.
InSAR pairs with HH-polarization.
An ideal zero-baseline repeat orbit is rarely achieved. The perpendicular baseline (Table 3) is the physical separation, perpendicular to the line-of-sight, between the location of PALSAR as it acquired the first and second images. We evaluate its impact on measured InSAR phase change from the topography-related errors using [13]:
Comparing the USGS Lidar-based DEM [28,29,30] and the Shuttle Radar Topography Mission digital elevation model (SRTM DEM) [34], which we also use to process the InSAR data, we find that = 1.5 m (standard deviation) over both swamps and marshes. Other parameters except the perpendicular baseline () are assumed to be the same for each pair including the slant range distance () of 940 km and incidence angle () of 38 degrees. The largest estimated error () due to the non-zero perpendicular baseline is 0.62 cm, which is significantly smaller than the field-measured range of water level change (~110 cm).
We process the SAR data using ISCE, developed at the Jet Propulsion Laboratory [22]. ISCE is currently in active development and has evolved from its predecessor, Repeat Orbit Interferometry PACkage (ROI PAC). It is capable of processing SAR data from various spaceborne and airborne sensors. ISCE Ver. 2.1.0 distributed by the Western North America Interferometric SAR Consortium (WInSAR), is used for this study. ISCE runs through a series of computations to co-register images, remove expected topographic phase, unwrap measured phase, and geocode the InSAR products. A detailed description of processing steps can be found in WInSAR’s tutorials [35]. The direct outputs used in this study are described below.
3.2.1. Interferometric Coherence
The major quantity in radar interferometry is the ensembled complex product, from a pair of SAR images. Both and are complex scattering amplitudes. The subscripted numbers denote the acquisitions from different passes. The angular brackets denote the ensemble averaging (e.g., spatial averaging). This complex product has an unnormalized magnitude term with the phase term varying within 0 to . Normalizing the magnitude of gives the interferometric coherence as:
Both and in our study are of HH-polarization. The ensembled average is over a multi-looking window of 5 pixels in azimuth and 2 pixels in range. ISCE provides both unfiltered and filtered coherence. We use the unfiltered coherence to maximize the dynamic range over time and more easily observe seasonal changes.
A general expression of observed coherence can be written to include potential decorrelation sources:
Geometric decorrelation, , results from changes in the viewing geometry between the time of SAR acquisitions. This includes changes in looking angle and non-parallel orbits in repeated visiting. Thermal decorrelation, , can be determined by the signal-to-noise ratio (SNR) of the radar system. Volumetric decorrelation, , decreases as the perpendicular baseline or vegetation height increases. Temporal decorrelation, , results from the motion of scatterers and the change of scattering properties such as permittivity [36]. Vegetation experiences different magnitudes of decorrelation over time. There are decorrelation models for trees and pasture [37,38]. In our study, temporal decorrelation is the most significant one with its magnitude varying throughout the year. The decorrelation effects caused by changes in dielectric properties and configuration of plant leaves and size are expected to vary within seasons due to changes in weather and vegetation phenology.
3.2.2. Interferometric Phase: Unwrapping and Calibration
The phase term of is known as the interferometric phase difference, or simply InSAR phase. It is confined within . However, the physical changes which cause the observed phase differences are not bounded, such that a large water level change can result in an observed phase difference greater than . This is a mathematically ‘wrapped’ condition of the complex number. If the physical displacement causing the phase change is equal to more than half of the wavelength in the radar line-of-sight (LoS) direction, it is necessary to consider phase unwrapping.
Using ISCE [22], we initially obtain the interferogram output representing the wrapped phase, within , which contains phase biases due to atmospheric effects such as microwave propagation delays. In ISCE, we choose SNAPHU [39] to unwrap the InSAR phase and select a set of ground control points (GCP) that are fixed non-moving targets to estimate the phase bias. Corner reflectors are not installed as control points (GCPs) within the Wax Lake wetlands, and therefore, we need to select fixed GCPs or ones with known vertical displacements [14,16,32]. We elect to use fixed man-made structures as GCPs to calibrate the InSAR phase and use vertically moving GCPs (i.e., water level stations) for validation. The calibration GCPs are selected based on two criteria: First, the physical structures at the GCP location should be unchanged from 2007 to 2010. Second, and most important, the coherence at the GCP location must satisfy a minimum threshold value of 0.85. Given these constraints, the number of valid GCPs are very limited within this study area.
Figure 2 shows the processing flow diagram starting with a pair of SAR images. We process them to form the interferogram using ISCE. Based on the phase observed at the GCP(WEST), we correct each interferogram. This bias corrected interferogram serves as the updated input for ISCE to unwrap the phase. After unwrapping, ISCE generates both the unwrapped interferogram and connected component indices. While the phase is spatially unwrapped for the entire interferogram, the exact phase at the GCPs may not be zero. The GCP phase correction, therefore, has to be performed again, this time within each valid connected component (next sub-section).
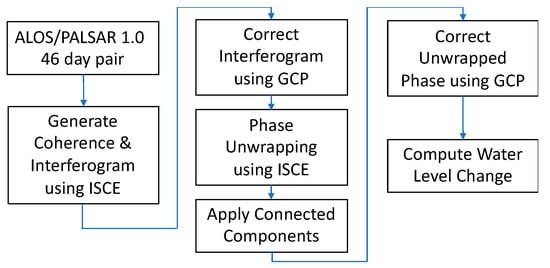
Figure 2.
Flow diagram of InSAR processing, phase correction, and water level change retrieval (ISCE stands for InSAR Scientific Computing Environment).
3.2.3. Connected Component
The SNAPHU program also generates a map of the connected components describing connected interferogram pixels that exhibit sufficient coherence. The low coherence pixels that may occur for example in rivers separate the interferogram into discrete components. The phase unwrapping is performed independently within each connected component, and thus, may result in different unwrapping cycles. The connected component output from ISCE is an index map with the same size as the unwrapped interferogram. The connected component maps are applied in phase correction described in Section 4.2.1.
3.3. PolSAR Processing
We use a polarimetric decomposition to understand how contributions of the various microwave scattering mechanisms (i.e., volume, double-bounce, and surface scattering) may impact InSAR retrieval of water level change. We decompose them using the non-negative eigenvalue decomposition (NNED) [40]. Figure 3 illustrates these mechanisms for both marshes and swamps. Volume scattering comes from the emergent vegetation canopy for which the surface scattering from water surface is negligible. The double-bounce scattering mechanism provides the means to estimate water level change. The presence of tree trunks in swamps increases double bounce and volume scattering in swamps. We use the NNED [40] to perform the polarimetric decomposition via the PolSARpro v6.0 (Biomass Edition) Toolbox. The software contains a collection of well-known algorithms and tools to explore polarimetric techniques for scientific developments [41].
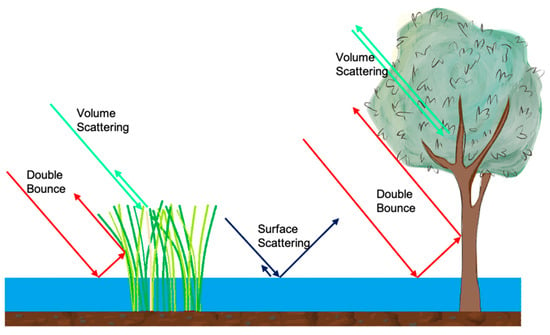
Figure 3.
Scattering mechanisms in marshes (left) and swamps (right). These include volume scattering, double-bounce scattering, and surface scattering. The surface scattering is mostly specular scattering that backscatters away from the radar, due to the smooth, flat water surface (except small ripples and waves).
3.4. Moderate Resolution Imaging Spectroradiometer (MODIS)
MODIS offers abundant products from various spectral bands. We use the Normalized Difference Vegetation Index (NDVI) to characterize vegetation trends in coverage. NDVI is derived from atmospherically corrected reflectance in the red and near-infrared wavebands [42]. It effectively characterizes the global range of vegetation cover. MODIS/NDVI is distributed through the online Earth Explorer, courtesy of the NASA EOSDIS Land Processes Distributed Active Archive Center (LP DAAC), USGS/Earth Resources Observation and Science (EROS) Center, Sioux Falls, South Dakota. The NDVI data, MOD13Q1 v006, has a 16-day revisiting time with a spatial resolution of 250 meters [43].
4. Results and Discussion
4.1. Interferometric Coherence and Vegetation Cover
Figure 4 shows a calendar of HH-coherence maps from 2007 to 2010. The period of 17 images is listed in Table 3. Open water surfaces are excluded with the wetland map. The observed seasonal trend over the wetlands shows high coherence in the winter (November to February) and low coherence in the summer (May to September). The spatial pattern of coherence, which highlights the south marshes and northern swamps (Figure 1), is more pronounced during the spring (March to June) than during the summer and winter months. This may be explained by the impact of vegetation growing quickly during the spring.
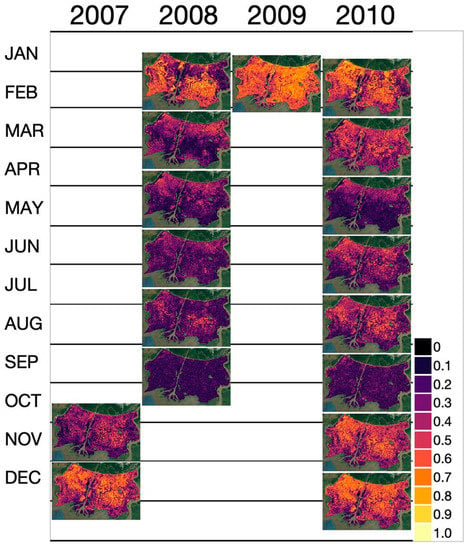
Figure 4.
The calendar of 46-day HH-coherence maps from PALSAR during 2007 and 2010. Refer to the Table 3 for the acquisition time of each pair. (Background Map from Google [26]).
The observed seasonal trend in coherence hints at changes in vegetation structure. Figure 5 shows the NDVI, a proxy to vegetation cover, from 2007 to 2010. NDVI exhibits seasonal trends across the entire landscape with values between 0.3 and 0.8. Over the Wax Lake Delta (WLD), NDVI is poorly resolved due to inundation of the delta islands and the coarse resolution, 250 m, of the MODIS NDVI data. Figure 6 shows the seasonal trends of HH coherence, NDVI, and water level height extracted at the location of the CRMS stations listed in Table 1. We separate the curves for swamps and marshes. While it is known that temporal decorrelation increases with time between radar acquisitions (i.e., temporal baseline) [11,20,44], the consistent use of a 46-day temporal baseline indicates the observed decorrelation is due to physical changes in the imaged scene as both vegetation and water level changed.
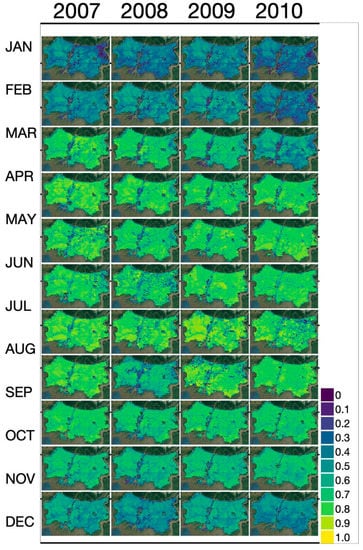
Figure 5.
The calendar of NDVI maps from MODIS during 2007 and 2010. (Background Map from Google [26]).
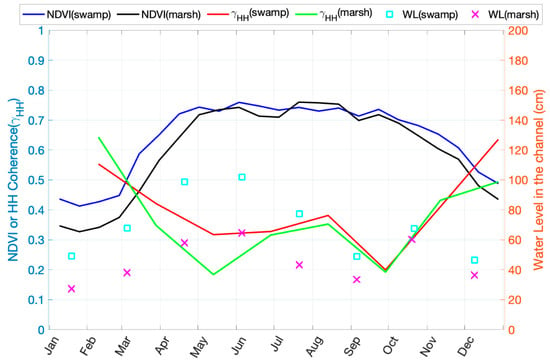
Figure 6.
Seasonal trends of HH-coherence, NDVI, and water level in the channel for both swamps and marshes extracted at CRMS station locations. The curves come from the average of available data during 2007 and 2010.
We observe an inverse correlation between HH-coherence and NDVI for both swamps and marshes. HH-coherence is higher during seasons with lower NDVI values, and vice versa, similar to the relationship previously observed at C-band [18]. Our results show that coherence reaches its lowest values during periods of peak growth where the NDVI is elevated. The impact of temporal decorrelation is known to increase with plant volume (e.g., over forests [45,46], and grasses [38]) with the distribution of the greater number of vegetation microwave scatterers (stems, branches, leaves, etc.) more likely to change between two SAR acquisitions. Changes in plant structure within 46 days can be significant for annual plants, especially for marshes. We can also distinguish the dry and wet seasons from the water level. For example, during the drier season occurring around October to December, the difference between swamps and marshes is small. During the wet season of April to June, higher water levels increase the amount of double-bounce scattering, with the coherence in swamps being higher than in marshes. However, during the drier season, lower water level brings uncertainty as to whether a wetland is inundated or not, when the wetland elevation (Table 1) may be higher than the water level recorded in the distributary channel. Nonetheless, non-inundated wetlands effectively produce high coherence during the dry season when both images are acquired during inundation. If one image is acquired during inundated conditions and the other during drier conditions (e.g., first pair in 2008), there is significant decorrelation.
4.2. Interferometric Phase Difference and Water Level Change
Changes in water level can be correlated to the InSAR phase change of the double-bounce scattering using:
in which the sub-indices, 1 and 2, stand for the first and second acquisitions; is the wavenumber, about 26.4 rad/m at L-band; is the line-of-sight (LoS) look angl,. while is the water level.
The subtraction order of the water level follows the convention of the time harmonics, , for both transmitting and receiving waves. Since the interferogram is used to infer spatial variation, this is also known as differential InSAR (D-InSAR). Section 4.2.1 describes how we process before retrieving the water level change, .
Figure 7 shows one interferogram example: pair 2008.3.1~2008.4.16. The color represents the wrapped interferometric phase while the brightness shows the magnitude of coherence. The phase is relative and wrapped. To apply the phase difference for water level change retrieval using Equation (4) requires further processing including phase unwrapping and phase correction. However, from Figure 7 we already observe a significant InSAR phase response ranging from the Gulf Intracoastal Waterway with coherence decreasing significantly (darker in Figure 7) in marshes. Thus, we expect that the water level change retrieval may not work in marshes.

Figure 7.
HH-interferogram from InSAR pair of 2008.3.1~2008.4.16. The image brightness stands for the coherence magnitude and the color corresponds to the wrapped InSAR phase between to , which indicates water level change gradients generally run perpendicular to the GIWW.
4.2.1. Interferogram Calibration
We could only find 8 pixels (pixel size of ~26 m 30 m) that satisfy our GCP criteria (from location unchanged from 2007 to 2010 and coherence above 0.85) within three locations as shown in Figure 8. All the selected pixels occur at locations with large tanks. There is 1 pixel found in Figure 8a, 3 pixels found in Figure 8b, and 4 pixels found in Figure 8c. Their locations on the larger map can be found in Figure 1. For Figure 8b,c, the phase of different pixels from the same location is similar. We average them and use a single phase to represent these two locations respectively. While there are not enough GCPs to generate a spatially varying phase correction surface, we will show that applying a constant bias correction within each connected component suffices to obtain accurate estimates of water level change. We choose the GCP from Figure 8a for the eastern part of the study area and that of Figure 8b for the western part to correct the independent connected components. The third GCP (Figure 8c), which is closer to Figure 8b, is used, in addition to the CRMS stations themselves, to validate the results.

Figure 8.
Google Map images during December 2010 around locations with high coherence; (a) GCP (EAST) [47], (b) GCP (WEST) [48], (c) GCP(VAL) [49]. Refer to Figure 1 for the locations of these points in the Wax Lake wetlands.
Figure 9 shows four distinct types of connected component maps we observe out of the 17 connected component maps (one for each unwrapped interferogram). Each component is shown in a different color. These are the components used independently during phase unwrapping by the SNAPHU algorithm. Within each component, the unwrapped phase is spatially correlated. The valid connected components have coherence above the threshold estimated by SNAPHU, about 0.2 from our results. Rivers and wetlands with low coherence are excluded. Also, the Wax Lake Delta (WLD) is mostly excluded because it is generally below the coherence threshold.
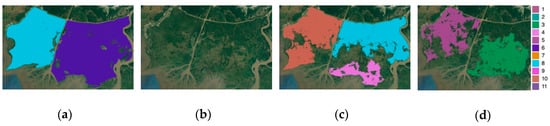
Figure 9.
Examples of connected component maps. (a) One at west and one at east (2010.1.20~2010.3.7). (b) No valid components (2008.9.1~2008.10.17). (c) One at west; one at northeast, adjacent to the west component; one at southeast, not adjacent to other components (2008.3.1~2008.4.16). (d) One at west; one at southeast, not adjacent to other components (2008.7.17~2008.9.1). The coverage for (a~d) is the same as Figure 1. Colors are used to distinguish different connected components only. (Background Map from Google [26]).
Figure 9a shows the component covering both sides of the Wax Lake Outlet and encompassing the GCP(WEST) and GCP(EAST). The pair from 2008.9.1~2008.10.17 shown in Figure 9b exhibit no valid components. In Figure 9c, parts of the west side component are missing due to low coherence areas, however, it still covers the GCP(WEST). For the east, there are two separate components and the GCP(EAST) is within the south one. There is no valid GCP for the north component. Figure 9d is similar to Figure 9c except there is no north component for the east side. In each case, we use the phase of the GCP within a component to correct the entire component. For areas without valid component coverage (i.e., low coherence), we disregard these areas. We only make an exception for the northeast component in Figure 9c, as we assume a progressive correction across the Wax Lake Outlet, using the GCP(WEST). Without losing generality, the water level change should be similar on both sides of the river. We then consider the phase difference between the two sides of river from the unwrapped interferogram together with the phase at GCP(WEST) to correct the north component on the eastern side of the river. The progressive correction starts from the GCP(WEST), then the west component, and finally the component across the river, resulting in a smooth and consistent water level change map.
We convert the unwrapped and bias-corrected interferograms to water level change maps using Equation (4). Our results are independently validated using both the GCP(VAL) and the in situ CRMS data. The average unwrapped phase at the location of the GCP(VAL) in Figure 8c, from the 14 valid pairs, corresponds to a vertical displacement of 1 cm, which is much smaller than the water level change RMSE of 7.53 cm (Section 4.2.3). It is also small compared to the observed range of water level change, which varies between -50cm and 60cm. This confirms the choices of GCP are reliable. The validation using in situ water level change at the locations of the CRMS stations is described in Section 4.2.3.
4.2.2. Scattering Decomposition
We hypothesize that the dominant scattering mechanisms are different for swamps and marshes and test our hypothesis with a polarimetric decomposition. The non-negative eigenvalue decomposition (NNED) provides the fractional power from three scattering mechanisms, double bounce (), volume scattering (), and surface scattering (). There are two available polarimetric scenes from November 2009 and April 2011 as shown in Figure 10. The sum of the three fractional powers is equal to one. The wetlands at both times, 2009.11.13 and 2011.4.3, are flooded at all the covered CRMS stations. The double-bounce fraction, which enables measurement of water level change, is dominant for the northern regions of the wetlands but is small for the southern area (Figure 10a,d). The volume and surface scattering fractions are distributed more uniformly over the southern area. In April, volume and surface scattering contribute to the signal in the north, but they are insignificant in November in the north. Comparing these results with the landcover map in Figure 1, we observe that the double-bounce scattering dominates the signal in the swamps. In contrast, the signal from marshes is not dominated by double-bounce scattering, which may cause inaccurate InSAR-retrieval of water level change in these areas.
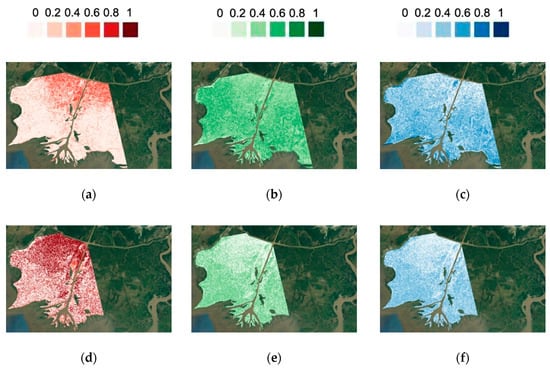
Figure 10.
Double bounce (), volume (), and surface scattering () from non-negative eigenvalue decomposition (NNED) decomposition: (a) 2011.4.3), (b) (2011.4.3), (c) 2011.4.3), (d) (2009.11.13), (e) (2009.11.13), and (f) (2009.11.13). (Background Map from Google [26]).
4.2.3. Validation at CRMS Stations
Figure 11 shows a plot of in situ water level data with other data such as coherence and NDVI at a CRMS station. The yellow bar shows the 46-day InSAR pair period and the red marker shows the water level at the time of the InSAR acquisition. In situ data was unavailable for some stations early 2008 and the middle of 2009 (Figure 11). The wetland elevation is shown as the black line in the plot and is used to identify whether the wetland is inundated or not. The CRMS gauges are set in the distributary channels, so the wetland elevation could be either higher or lower than the recorded water level. In those cases, the water level change retrieval using Equation (4) is not applicable.
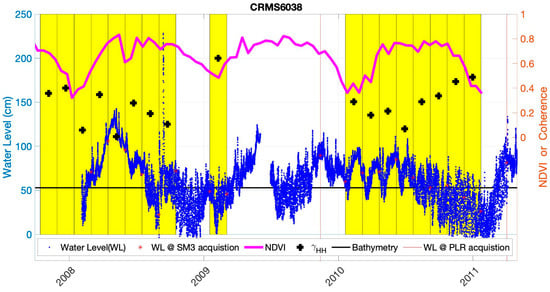
Figure 11.
Time-series water level and NDVI at CRMS6038 during the study period. Water levels extracted during SAR acquisition are marked. Each yellow bar corresponds to the period of one InSAR pair. The coherence is marked in the middle of each pair. The wetland elevation from USGS DEM is plotted as a horizontal black line and is used as a reference for comparison with the CRMS water level in the channel, shown as blue dots. Water level data was not recorded in early 2008 and the middle of 2009.
Overall, we have 10 swamp sites and 9 marsh sites to validate 17 InSAR pairs. Figure 12 shows the overall scatter plots at CRMS stations for swamps and marshes, respectively. We exclude invalid points with no in situ water level measurement and low coherence points with coherence less than 0.2. For swamp sites, there are 85 invalid points and 19 low coherence points. For marsh sites, there are 81 invalid points and 23 low coherence points. Besides invalid and low coherence points, the rest are shown in Figure 12. The retrievals at CRMS swamp stations are highly correlated to in situ measurements, while retrievals at marsh stations are insensitive to water level changes.
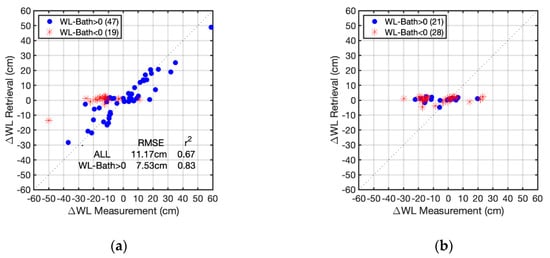
Figure 12.
Total scatter plots of water level change retrieval from (a) swamp CRMS stations, (b) marsh CRMS stations. Bath stands for the wetland elevation from USGS DEM around each CRMS station. WL stands for water level.
During the wet season, the water level is generally high, and most wetlands are inundated through hydrologic connectivity between the channels and the unchannelized wetlands. In Table 1, we listed the wetland elevation that is used to separate the validation data points into two classes: above (i.e., inundated) or below (non-inundated) the wetland elevation. Note that using the wetland elevation to determine if the wetland is inundated is a fair assumption but is not an absolute threshold because there is spatial variability in topography, such as levees, that may prevent connectivity. For the swamp, there are 66 valid points in total, but 19 of them are below the wetland elevation. These 19 points include one extreme outlier, at the leftmost in Figure 12a, and 18 others scattered within a horizontal strip of retrieved water level differences around 0 cm. The insensitivity of these 18 points to water level changes in channels highlights when Equation (4) fails, i.e., when the wetland is not inundated. Besides these 19 points, the other 47 points scatter mostly along the 1:1 line. We calculate the error and r2 in two ways, including all valid points and including only points with water level greater than the wetland elevation, which we expect to be flooded. The flooded points show RMSE of 7.53 cm and r2 of 0.83. If we include non-inundated points, the RMSE increases nearly 50% to 11.17 cm and the r2 drops to 0.67. There are fewer valid points for marsh sites because the coherence is usually lower and the range of water levels is also lower. The points above wetland elevation still do not show the correlation between the retrieved and measured water level change, which we attribute to the volume scattering mechanism dominating the signal. In comparison, from Figure 10a,d, we observe strong dominance of double-bounce scattering in swamps that leads to an accurate retrieval of water level change (Figure 12a). The overall validated range of water level changes at the swamp sites varies between −50 cm and 60 cm, which is a range of 110 cm. The validation results—with RMSE values corresponding to about half of one wrapping cycle and the range of 110 cm corresponding to seven phase wrapping cycles—demonstrate the robustness of the phase unwrapping procedure.
For validation within swamp sites, we further look at where the non-inundated sites are distributed using single InSAR-retrieval sets plots shown in Figure 13. InSAR pairs 1, 2, 3, and 8 do not produce valid points for validation (pair index enumerated in Table 3). Non-inundated points in pairs 7, 9, 10, 14, 16, and 17 suggest these pairs are during lower water level conditions and the wetland may be dry especially for pairs 7, 16, and 17. For the periods with higher water level, the validation sites are close to the 1:1 line, such as pairs 4, 5, and 13. The contrast between the validation of high and low water levels suggests that caution is required to apply this technique to retrieve water level change in the low river discharge season. Pair 6 (2008.6.1~2008.7.17) shows larger error close to 25 cm. The period of pair 6 is about the time NDVI reaches its seasonal maximum and reversely the coherence hits its seasonal minimum, as shown in Figure 4. Although this period is during high water levels, the overall lower coherence may contribute to the larger errors for these points. With a shorter temporal baseline, an increased coherence will improve water level change retrieval through the growth season. We expect the future NISAR mission, which will collect 12-day temporal baseline data, will offer better coherence with more reliable InSAR retrievals.
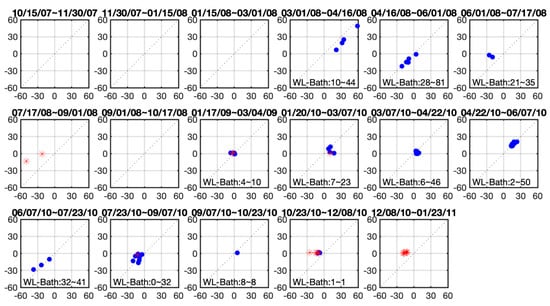
Figure 13.
Water level change retrieval by InSAR pair as listed in Table 3. (blue dots: water level above the wetland elevation; red dots: water level below the wetland elevation) (WL stands for water level and Bath stands for the wetland elevation from USGS DEM. The numerical range in each plot if any is for blue dots only.) (No valid points for InSAR pairs 1, 2, 3, and 8) (Horizontal axis: in situ measurement in cm; Vertical axis: retrieval in cm) (pair index enumerated in Table 3).
Figure 14 shows scatter plots for each swamp CRMS station. Each site in Figure 14 except CRMS4809 has both high and low water surface elevation estimates available for validation. The data shows that most non-inundated points behave similarly in each subplot, remaining around zero water level with no sensitivity between InSAR phase and the actual water level change. The remaining points, shown in blue, show good agreement with in situ measurements.
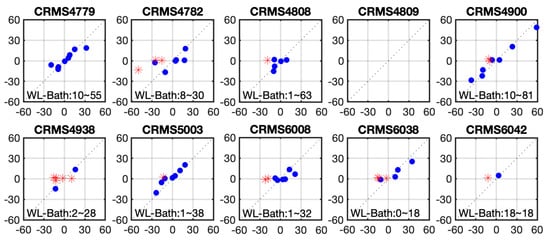
Figure 14.
Water level change () retrieval at swamp CRMS stations listed in Table 1 (WL stands for water level and Bath stands for the wetland elevation from USGS DEM. The numerical range in each plot if any is for blue dots only.) (Horizontal axis: Measurement in cm; Vertical axis: Retrieval in cm).
Since the successful retrievals are only obtained over swamps, we apply the mask of swamps from Figure 1 to the retrieved water level change map. Figure 15 shows the calendar of all pairs. Note that in each map, the coverage of the retrieved water level is different because each InSAR pair has different connected components. From Figure 13, we know that InSAR pairs 1, 2, 3, and 8 do not contain valid points for validation, and pairs 7 and 17 only have non-inundated points for validation. For the other 11 pairs, there is at least one point when the site is inundated that is available for validation.
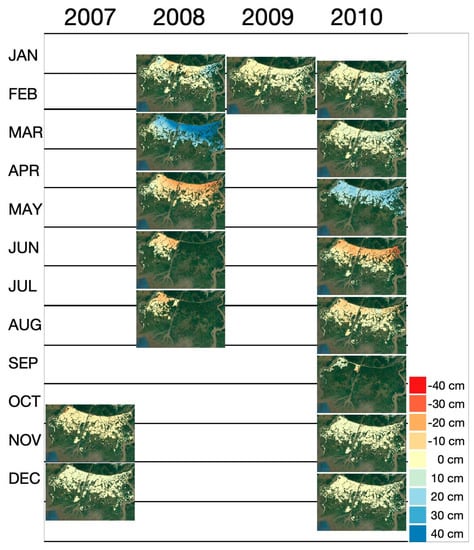
Figure 15.
The calendar of retrieved water level change maps over the swamps (also within valid connected component) at Wax Lake during 2008 and 2010. The missing area for east Wax Lake in June and August 2008, is due to a lacking GCP for phase correction. (Background Map from Google [26]).
Among these maps, we observe gradual changes in water surface level emanating from the Gulf Intracoastal Waterway toward wetlands (e.g., Figure 15 March and May in 2008). In some InSAR pairs, the northeast corner has larger water level change compared to other areas, which may result from the strong influence of the nearby Atchafalaya river. Interestingly, many of the retrievals indicate a strong N-S water surface gradient, suggesting a high degree of water connectivity between the Gulf Intracoastal Waterway and the swamps, a conclusion supported by prior field observations [50].
4.2.4. River Discharge Influence at swamps
The water surface level is influenced by two sources. One source is the tide, which varies quickly on a daily basis. The second source is the river discharge, which varies at seasonal scales. We decompose the contribution from these two sources using the water level measured by a USGS water-level gauge at Calumet in the Wax Lake Outlet river. As an example, the water level between 2008.3.1 and 2008.4.16 is shown in Figure 16, corresponding to the time when InSAR pair 4 is acquired. The water level difference between and is given by
The 90-day lowpass curve in Figure 16 represents the water level,, caused only by changes in river discharge, because the 90-day averaging window is large enough to smooth out any tidal variation. The water level difference due to river discharge can therefore be estimated as
The difference between and gives the tidal contribution, , of the water level difference, or
Based on and , we calculate the percentage of the water level change due to the river discharge contribution using
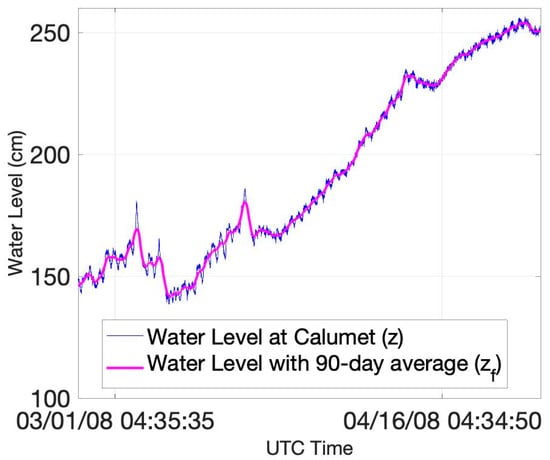
Figure 16.
Time series water level height (fast-changing) and estimated flooding height (slow-changing) at the Calumet water level gauge (USGS 07381590). The time period covers two PALSAR acquisitions, 2008.3.1 and 2008.4.16.
Table 4 shows the discharge contribution for the time period represented by 8 InSAR pairs in Figure 15. The percentage of the water level change that is attributed to river discharge over these time periods ranges from 72% to 99%, indicating river discharge is the main source of water level change in wetlands. The swamps in Wax Lake are over 6.4km seaward of Calumet. The dominance of river discharge supports the water level change pattern observed in Figure 15. As an example, a closer view of the water level change map estimated from the pair 2008.3.1–2008.4.16 is shown in Figure 17. We observe a 70 cm increase in water level at Calumet based on the gauge data and a similar increase over the swamps based on the InSAR estimation.

Table 4.
Estimation of River Discharge Contribution from Water Level at Calumet.
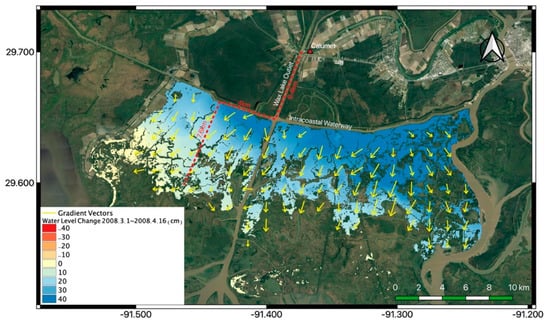
Figure 17.
The gradient for water level change map estimated from the pair 2008.3.1 to 2008.4.16, over swamps. The arrows are the inferred flow direction parallel to the steepest water-level change gradient. The red dashed lines are an example of the covered distance of flooding from Calumet, 18 km. (Background Map from Google [26]).
Based on the retrieved water level change maps, we plot the direction of the gradient of the water surface level change. It is shown that the gradients are generally perpendicular to the Gulf Intracoastal Waterway (GIWW), aligned with the north-south direction (Figure 15 and Figure 17). The river input from the north or from the neighboring Atchafalaya must first distribute the water to the GIWW, and from there it flows out into the wetlands. The pattern appears to reflect a wave of increased amount of water moving into the wetlands from the GIWW when the water level change is positive (e.g., Figure 17), and reduced amount of water moving into the wetlands from the GIWW when the river discharge is falling. The scenario is unusual because in natural systems, floodplain connectivity is typically associated with a seaward directed river channel. However, in the highly engineered Wax Lake wetlands, it appears that the swamps are better connected hydrologically with the GIWW than the Wax Lake Outlet.
To better illustrate this connectivity, we estimate the mean gradient of the water level change over the swamps in the north-south direction (Figure 18). Results show that time periods with significant water level gradients over the wetlands estimated from InSAR correlate with time periods of significant water surface change in the main river channels, , as measured at the Calumet gauge. Figure 18 reveals a clear positive correlation between the river discharge-induced water level change as measured at Calumet and the water level gradient over swamps as measured by InSAR, supporting the idea of a high degree of hydrologic connectivity. Moreover, the time periods where we visually observe the strongest N-S gradients in Figure 15 are times of the most significant water level changes at Calumet, as shown by the red markers in Figure 18.
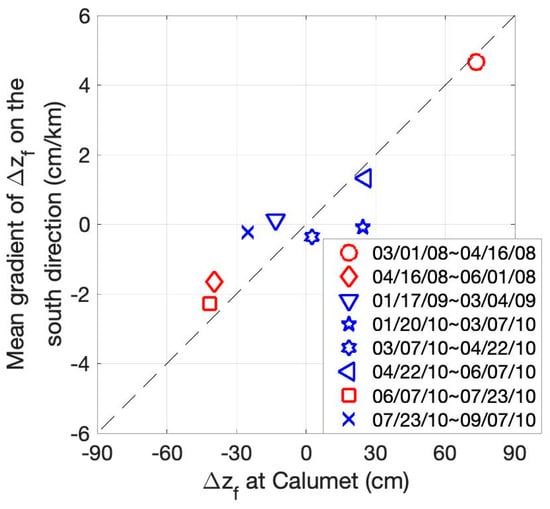
Figure 18.
The projection on the south direction of the mean gradient of water level change retrieval over swamps, , plotted against the water level change at Calumet. Red markers show InSAR pairs where we observe significant patterns in Figure 15.
5. Conclusions
In this paper, we evaluated the capabilities of spaceborne L-band InSAR to retrieve water surface level change in wetlands against two important features of wetlands: vegetation structure and water level. This study is designed in preparation for the upcoming NASA-ISRO SAR mission (NISAR) mission that will generate a global InSAR dataset every 12-days, enabling monitoring of water levels in wetlands. However, there is currently no assessment of capabilities of L-band SAR across seasons. Using time-series data from JAXA’s PALSAR, we demonstrated that L-band InSAR can measure water level changes across seasons, even with a long 46-day temporal baseline. Interestingly, the time-series enabled observation of a large-scale overflow of water from the Gulf Intracoastal Water Way (GIWW) to the wetlands, supporting field observations [50].
While InSAR retrievals have previously been done using in situ measurements of water level change [14,16,31], we demonstrate that as few as two GCPs may be sufficient for robust calibration of InSAR retrievals of water level change, facilitating application of this technique to global wetlands. The PALSAR-estimates of water surface elevation change are validated with in situ measurements, in addition to a third fixed GCP. Using the lidar-derived USGS DEM [28,29,30], we identify whether the wetland is inundated or not during the SAR image acquisitions. We validate 47 points acquired during inundation of swamps and 21 inundated data points in marshes.
Double-bounce microwave scattering improves performance of the water level change retrieval. In the swamps, which exhibit large double-bounce scattering signal, the water level change retrieval performed well with RMSE of 7.53 cm and r2 of 0.83, within the full range of observations from −50 cm to 60 cm. In contrast, the signal from marshes, which is shown through polarimetric decomposition to be dominated by volume scattering, exhibits no correlation between retrieved and in situ water level change. This suggests that a pre-assessment of the dominant scattering mechanism within the study area is recommended to identify where the InSAR retrieval algorithm is likely to work.
We show, using 17 HH-coherence maps ranging from 2007 to 2010, that seasonal trends in L-band InSAR coherence are opposite to NDVI, a proxy of vegetation cover. The temporal decorrelation is significant in the summer and is minor in the winter. In the winter, the combined impact of low absolute water levels and low herbaceous vegetation cover may enhance or reduce the InSAR coherence depending on whether the wetland is inundated or not during acquisition of both SAR images.
The forthcoming NISAR, planned to launch in 2022, will collect L-band data globally with a repeat-pass period of 12 days. This temporal baseline promises improved coherence and higher spatial and temporal resolutions than the data used in this study. Thus, it is expected that NISAR will outperform the results presented in this study. In addition, the shorter revisit period of NISAR will provide denser time series than currently available data. ALOS/PALSAR-2 time-series data, with a 14-day temporal baseline, may bridge the gap with NISAR and should be examined when they become available in the study area. The methods described in this paper can contribute to allowing for more frequent and consistent monitoring of coastal wetlands, globally.
Author Contributions
All four authors devised the study. The SAR processing was done by T.-H.L. The data processing, the generation and analysis of results were performed by T.-H.L., M.S., and M.D. The hydrologic connection to the results was analyzed and interpreted by T.-H.L., M.S. and M.P.L., T.-H.L. generated the figures and all four authors contributed nearly equally in writing the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
The research was supported by the Terrestrial Ecology Program at National Aeronautics and Space Administration (NASA).
Acknowledgments
This work was performed at the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration (NASA), and supported by NASA’s Terrestrial Ecology Program. Authors acknowledge the help from, National Aeronautics and Space Administration (NASA), Jet Propulsion Laboratory (JPL), the Japan Aerospace Exploration Agency (JAXA), the Alaska Satellite Facility (ASF) and the U.S. Geological Survey (USGS) including providing access to the satellite images, wetlands gauge station information, and suggestion for data processing. The leading author would like to thank Charlie, Daniel, Tom, Jessica, and Talib for useful discussions, as well as the anonymous reviewers for their constructive comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- United States, Environmental Protection Agency, Office of Wetlands and Watersheds. America’s Wetlands: Our Vital Link between Land and Water; U.S. Environmental Protection Agency, Office of Water, Office of Wetlands, Oceans, and Watersheds: Washington, DC, USA, 1995.
- Syvitski, J.P.M.; Kettner, A.J.; Overeem, I.; Hutton, E.W.H.; Hannon, M.T.; Brakenridge, G.R.; Day, J.; Vörösmarty, C.; Saito, Y.; Giosan, L.; et al. Sinking deltas due to human activities. Nat. Geosci. 2009, 2, 681–686. [Google Scholar] [CrossRef]
- Giosan, L.; Syvitski, J.; Constantinescu, S.; Day, J. Climate change: Protect the world’s deltas. Nature 2014, 516, 31–33. [Google Scholar] [CrossRef]
- Twilley, R.R.; Bentley, S.; Chen, Q.; Edmonds, D.A.; Hagen, S.C.; Lam, N.S.-N.; Willson, C.S.; Xu, K.; Braud, D.; Peele, R.H.; et al. Co-evolution of wetland landscapes, flooding, and human settlement in the Mississippi River Delta Plain. Sustain. Sci. 2016, 11, 711–731. [Google Scholar] [CrossRef]
- Syvitski, J. Deltas at risk. Sustain. Sci. 2008, 3, 23–32. [Google Scholar] [CrossRef]
- Couvillion, B.R.; Barras, J.A.; Steyer, G.D.; Sleavin, W.; Fischer, M.; Beck, H.; Trahan, N.; Griffin, B.; Heckman, D. Land Area Change in Coastal Louisiana from 1932 to 2010; Scientific Investigations Map 3164, scale 1:265,000; USGS Publication: Reston, VA, USA, 2011. [CrossRef]
- Couvillion, B.R.; Fischer, M.; Beck, H.J.; Sleavin, W.J. Spatial Configuration Trends in Coastal Louisiana from 1985 to 2010. Wetlands 2016, 36, 347–359. [Google Scholar] [CrossRef]
- Sasser, C.E.; Visser, J.; Mouton, E.; Linscombe, J.; Hartley, S.B. Vegetation Types in Coastal Louisiana in 2013; Scientific Investigations Map 3290, 1 sheet, scale 1:550,000; USGS Publication: Reston, VA, USA, 2014. [CrossRef]
- Steyer, G.D.; Sasser, C.E.; Visser, J.M.; Swenson, E.M.; Nyman, J.A.; Raynie, R.C. A Proposed Coast-Wide Reference Monitoring System for Evaluating Wetland Restoration Trajectories in Louisiana. Environ. Monit. Assess. 2003, 81, 107–117. [Google Scholar] [CrossRef]
- Hiatt, M.; Snedden, G.A.; Day, J.W.; Rohli, R.V.; Nyman, J.A.; Lane, R.; Sharp, L.A. Drivers and impacts of water level fluctuations in the Mississippi River delta: Implications for delta restoration. Estuar. Coast. Shelf Sci. 2019, 224, 117–137. [Google Scholar] [CrossRef]
- Lu, Z.; Kwoun, O.-I. Radarsat-1 and ERS InSAR Analysis Over Southeastern Coastal Louisiana: Implications for Mapping Water-Level Changes Beneath Swamp Forests. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2167–2184. [Google Scholar] [CrossRef]
- Hess, L.L.; Melack, J.M.; Simonett, D.S. Radar detection of flooding beneath the forest canopy: A review. Int. J. Remote Sens. 1990, 11, 1313–1325. [Google Scholar] [CrossRef]
- Cloude, S.R. Polarisation: Applications in Remote Sensing; Oxford U. Press: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Wdowinski, S.; Kim, S.-W.; Amelung, F.; Dixon, T.; Miralles-Wilhelm, F.; Sonenshein, R. Space-based detection of wetlands’ surface water level changes from L-band SAR interferometry. Remote Sens. Environ. 2008, 112, 681–696. [Google Scholar] [CrossRef]
- Mohammadimanesh, F.; Salehi, B.; Mahdianpari, M.; Brisco, B.; Motagh, M. Wetland Water Level Monitoring Using Interferometric Synthetic Aperture Radar (InSAR): A Review. Can. J. Remote Sens. 2018, 44, 247–262. [Google Scholar] [CrossRef]
- Hong, S.-H.; Wdowinski, S. Multitemporal Multitrack Monitoring of Wetland Water Levels in the Florida Everglades Using ALOS PALSAR Data With Interferometric Processing. IEEE Geosci. Remote Sens. Lett. 2013, 11, 1355–1359. [Google Scholar] [CrossRef]
- Oliver-Cabrera, T.; Wdowinski, S. InSAR-Based Mapping of Tidal Inundation Extent and Amplitude in Louisiana Coastal Wetlands. Remote Sens. 2016, 8, 393. [Google Scholar] [CrossRef]
- Brisco, B.; Ahern, F.; Murnaghan, K.; White, L.; Canisus, F.; Lancaster, P. Seasonal Change in Wetland Coherence as an Aid to Wetland Monitoring. Remote Sens. 2017, 9, 158. [Google Scholar] [CrossRef]
- Lu, Z.; Crane, M.; Kwoun, O.-I.; Wells, C.; Swarzenski, C.; Rykhus, R. C-band radar observes water level change in swamp forests. Eos Trans. Am. Geophys. Union 2005, 86, 141. [Google Scholar] [CrossRef]
- Kim, S.-W.; Wdowinski, S.; Amelung, F.; Dixon, T.; Won, J.-S. Interferometric Coherence Analysis of the Everglades Wetlands, South Florida. IEEE Trans. Geosci. Remote Sens. 2013, 51, 5210–5224. [Google Scholar] [CrossRef]
- Jet Propulsion Laboratory. NASA-ISRO SAR (NISAR) Mission Science Users’ Handbook; National Aeronautics and Space Administration (NASA): Pasadena, CA, USA, 2019.
- Rosen, P.A.; Gurrola, E.M.; Sacco, G.F.; Zebker, H. The InSAR scientific computing environment. In Proceedings of the EUSAR 2012, 9th European Conference on Synthetic Aperture Radar, Nuremberg, Germany, 23–26 April 2012. [Google Scholar]
- Kim, J.-W.; Lu, Z.; Lee, H.; Shum, C.K.; Swarzenski, C.M.; Doyle, T.W.; Baek, S.-H. Integrated analysis of PALSAR/Radarsat-1 InSAR and ENVISAT altimeter data for mapping of absolute water level changes in Louisiana wetlands. Remote Sens. Environ. 2009, 113, 2356–2365. [Google Scholar] [CrossRef]
- Homer, C.G.; Fry, J.A.; Barnes, C. The National Land Cover Database; US Geological Survey: Reston, VA, USA, 2012.
- Steyer, G.D. Coastwide Reference Monitoring System (CRMS); US Geological Survey: Reston, VA, USA, 2010.
- Google. (n.d.) [Google Maps, Wax Lake, LA]. Available online: https://goo.gl/maps/UeX3XBQESjck1dmG8 (accessed on 20 June 2020).
- Coastal Protection and Restoration Authority (CPRA) of Louisiana. 2007–2011. Coastwide Reference Monitoring System-Wetlands Monitoring Data. Retrieved from Coastal Information Management System (CIMS) Database. Available online: http://cims.coastal.louisiana.gov (accessed on 2 February 2017).
- Dataset: U.S. Geological Survey. USGS NED 1/3 arc-second n30w091 1 × 1 degree ArcGrid 2016; U.S. Geological Survey: Reston, VA, USA, 2016.
- Dataset: U.S. Geological Survey. USGS NED 1/3 arc-second n30w092 1 × 1 degree ArcGrid 2016; U.S. Geological Survey: Reston, VA, USA, 2016.
- Archuleta, C.-A.M.; Constance, E.W.; Arundel, S.T.; Lowe, A.J.; Mantey, K.S.; Phillips, L.A. The National Map Seamless Digital Elevation Model Specifications; US Geological Survey: Reston, VA, USA, 2017; Volume 11, Chapter 9; p. 39. [CrossRef]
- ALOS PALSAR. L1.0 2007–2011. Accessed through ASF DAAC. Available online: http://www.asf.alaska.edu (accessed on 19 October 2018).
- Hong, S.-H.; Wdowinski, S.; Kim, S.-W.; Won, J.-S. Multi-temporal monitoring of wetland water levels in the Florida Everglades using interferometric synthetic aperture radar (InSAR). Remote Sens. Environ. 2010, 114, 2436–2447. [Google Scholar] [CrossRef]
- Alsdorf, D.E.; Melack, J.M.; Dunne, T.; Mertes, L.A.K.; Hess, L.L.; Smith, L.C. Interferometric radar measurements of water level changes on the Amazon flood plain. Nature 2000, 404, 174–177. [Google Scholar] [CrossRef]
- Mukul, M.; Srivastava, V.; Jade, S.; Mukul, M. Uncertainties in the Shuttle Radar Topography Mission (SRTM) Heights: Insights from the Indian Himalaya and Peninsula. Sci. Rep. 2017, 7, 41672. [Google Scholar] [CrossRef]
- The Western North America InSAR (WInSAR) Consortium. Available online: https://winsar.unavco.org/ (accessed on 21 July 2020).
- Rosen, P.; Hensley, S.; Joughin, I.; Li, F.; Madsen, S.; Rodriguez, E.; Goldstein, R. Synthetic aperture radar interferometry. Proc. IEEE 2000, 88, 333–382. [Google Scholar] [CrossRef]
- Simard, M.; Denbina, M. An Assessment of Temporal Decorrelation Compensation Methods for Forest Canopy Height Estimation Using Airborne L-Band Same-Day Repeat-Pass Polarimetric SAR Interferometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 95–111. [Google Scholar] [CrossRef]
- Morishita, Y.; Hanssen, R.F. Temporal Decorrelation in L-, C-, and X-band Satellite Radar Interferometry for Pasture on Drained Peat Soils. IEEE Trans. Geosci. Remote Sens. 2014, 53, 1096–1104. [Google Scholar] [CrossRef]
- Chen, C.W.; Zebker, H.A. Two-dimensional phase unwrapping with use of statistical models for cost functions in nonlinear optimization. J. Opt. Soc. Am. A 2001, 18, 338–351. [Google Scholar] [CrossRef]
- Van Zyl, J.J.; Arii, M.; Kim, Y. Model-Based Decomposition of Polarimetric SAR Covariance Matrices Constrained for Nonnegative Eigenvalues. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3452–3459. [Google Scholar] [CrossRef]
- Pottier, E.; Ferro-Famil, L.; Allain, S.; Cloude, S.; Hajnsek, I.; Papathanassiou, K.; Moreira, A.; Williams, M.; Minchella, A.; LaValle, M.; et al. Overview of the PolSARpro V4.0 software: The open source toolbox for polarimetric and interferometric polarimetric SAR data processing. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Didan, K. MOD13Q1 MODIS/Terra Vegetation Indices 16-Day L3 Global 250m SIN Grid V006; NASA EOSDIS LP DAAC: Sioux Falls, SD, USA, 2015. [CrossRef]
- Mohammadimanesh, F.; Salehi, B.; Mahdianpari, M.; Brisco, B.; Motagh, M. Multi-temporal, multi-frequency, and multi-polarization coherence and SAR backscatter analysis of wetlands. ISPRS J. Photogramm. Remote Sens. 2018, 142, 78–93. [Google Scholar] [CrossRef]
- Pinto, N.; Simard, M.; Dubayah, R. Using InSAR Coherence to Map Stand Age in a Boreal Forest. Remote Sens. 2012, 5, 42–56. [Google Scholar] [CrossRef]
- Simard, M.; Hensley, S.; LaValle, M.; Dubayah, R.; Pinto, N.; Hofton, M. An Empirical Assessment of Temporal Decorrelation Using the Uninhabited Aerial Vehicle Synthetic Aperture Radar over Forested Landscapes. Remote Sens. 2012, 4, 975–986. [Google Scholar] [CrossRef]
- Google. (n.d.) [Google Maps, Belle Isle, LA]. Available online: https://goo.gl/maps/MHwYjwsjNCUrrA5U6 (accessed on 20 June 2020).
- Google. (n.d.) [Google Maps, Lake Palourde St, Franklin, LA]. Available online: https://goo.gl/maps/xJZxmJXsWmuVUuvw7 (accessed on 20 June 2020).
- Google. (n.d.) [Google Maps, Mobil Oil Ln Franklin, LA]. Available online: https://goo.gl/maps/oPhRwhL7c7MFS8pU6 (accessed on 20 June 2020).
- Swarzenski, C.M. Surface-water hydrology of the Gulf Intracoastal Waterway in South-Central Louisiana, 1996–99; US Geological Survey: Reston, VA, USA, 2003.
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).