Delineation of Tree Patches in a Mangrove-Marsh Transition Zone by Watershed Segmentation of Aerial Photographs
Abstract
1. Introduction
- Generating a binary grayscale image;
- Delineating markers.
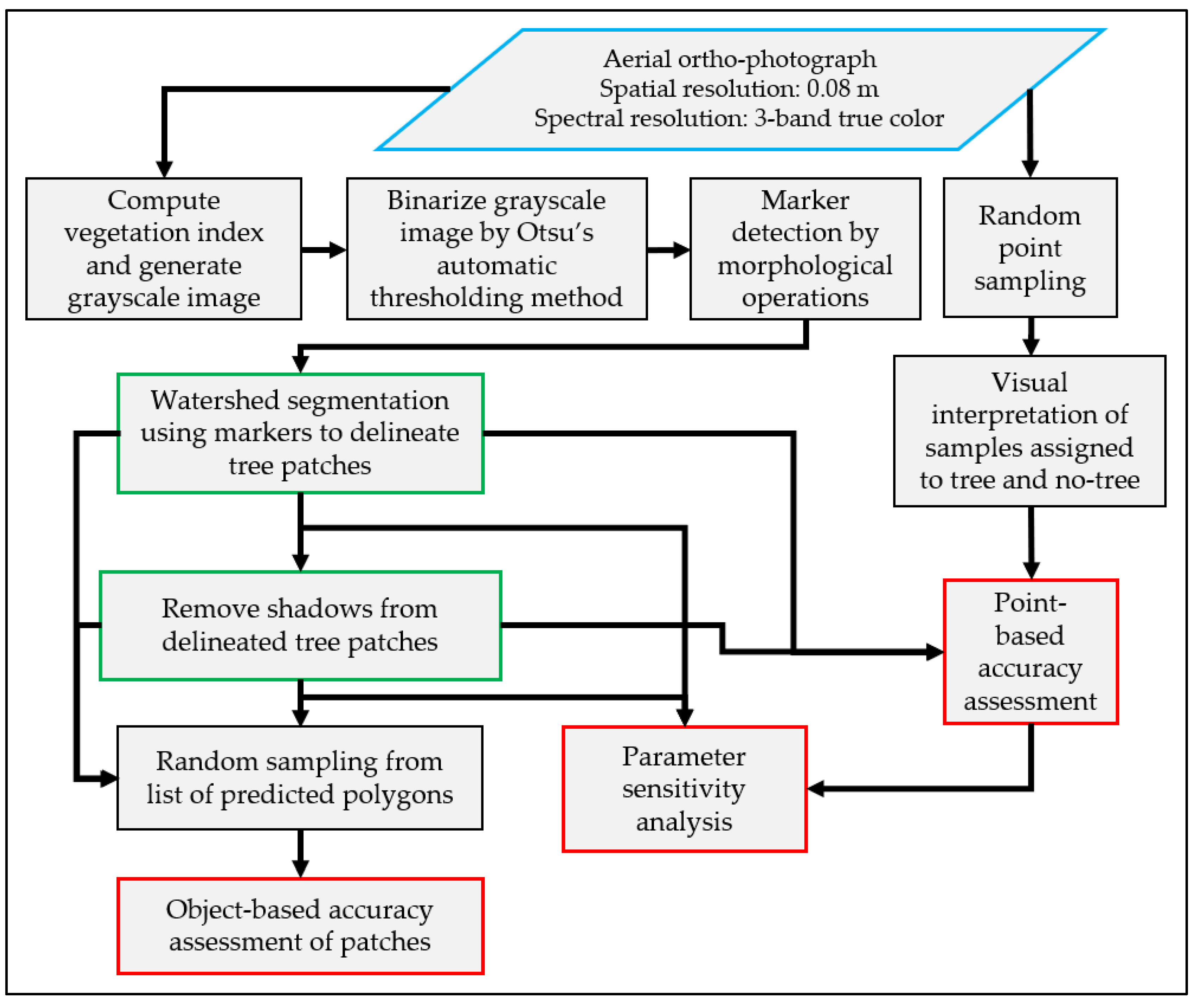
2. Materials and Methods
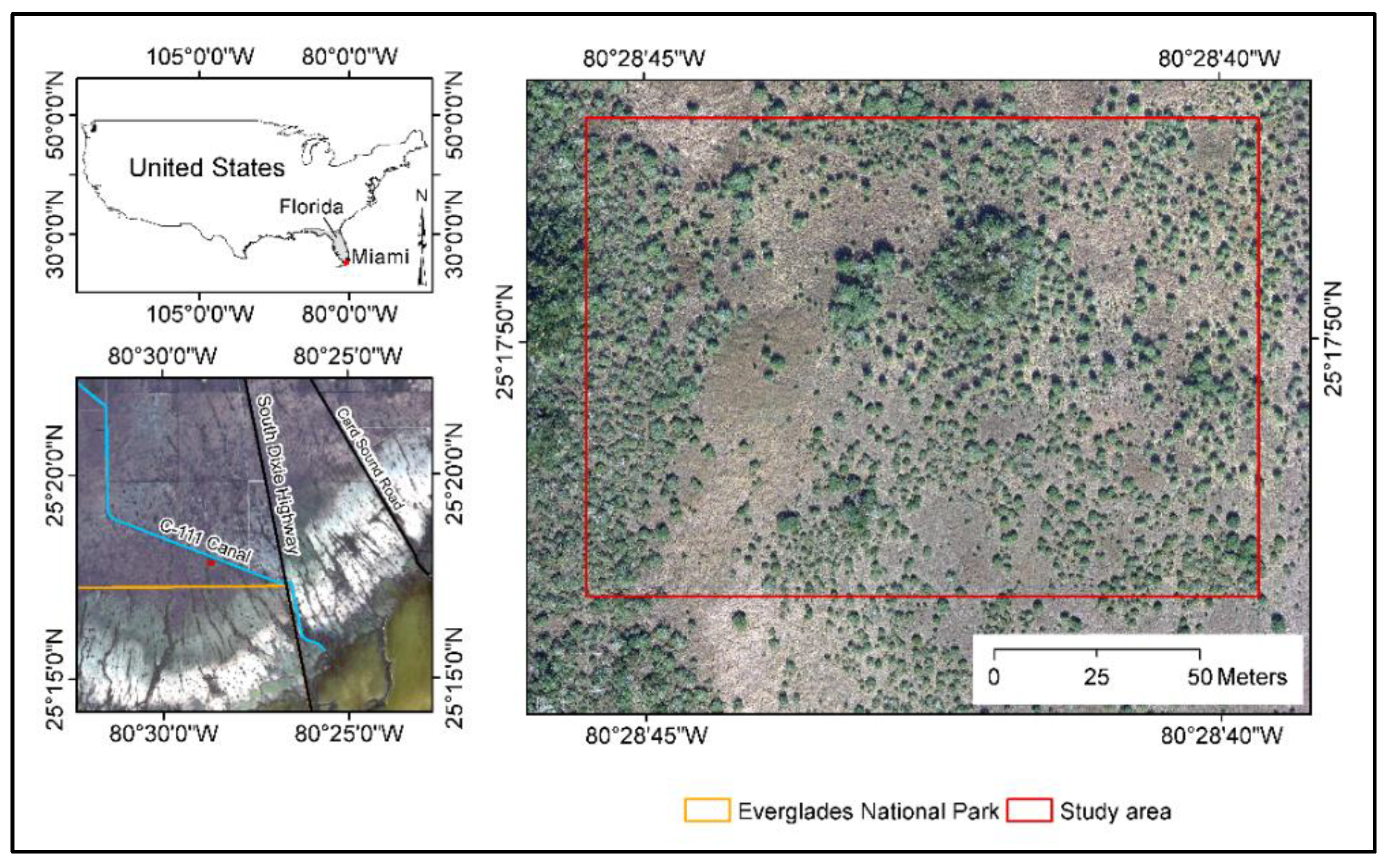
2.1. Study Area and Image Acquisition
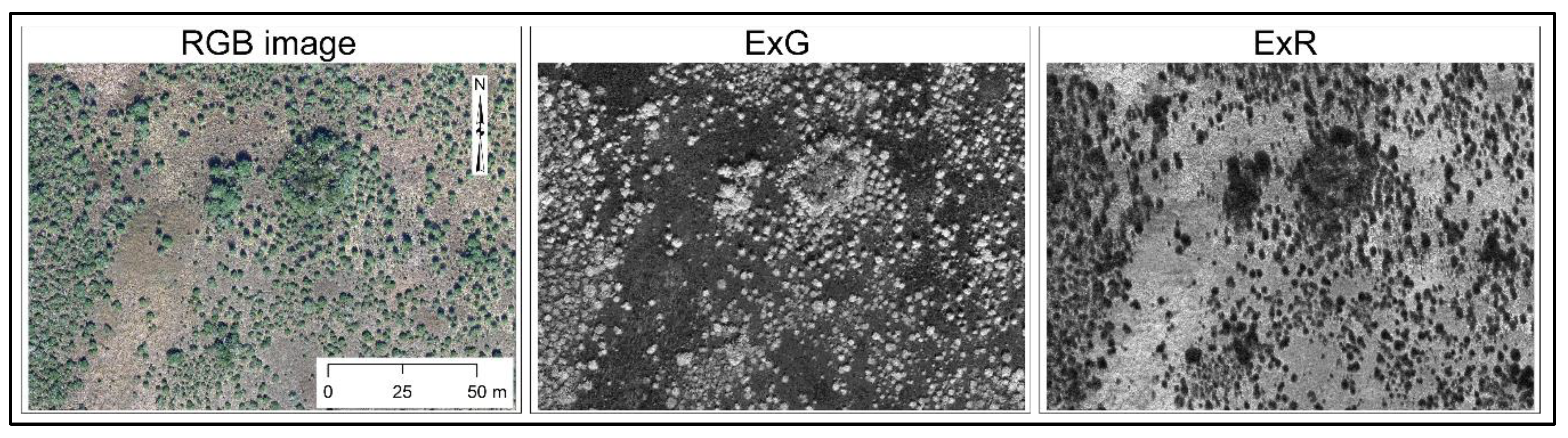
2.2. Vegetation Indices
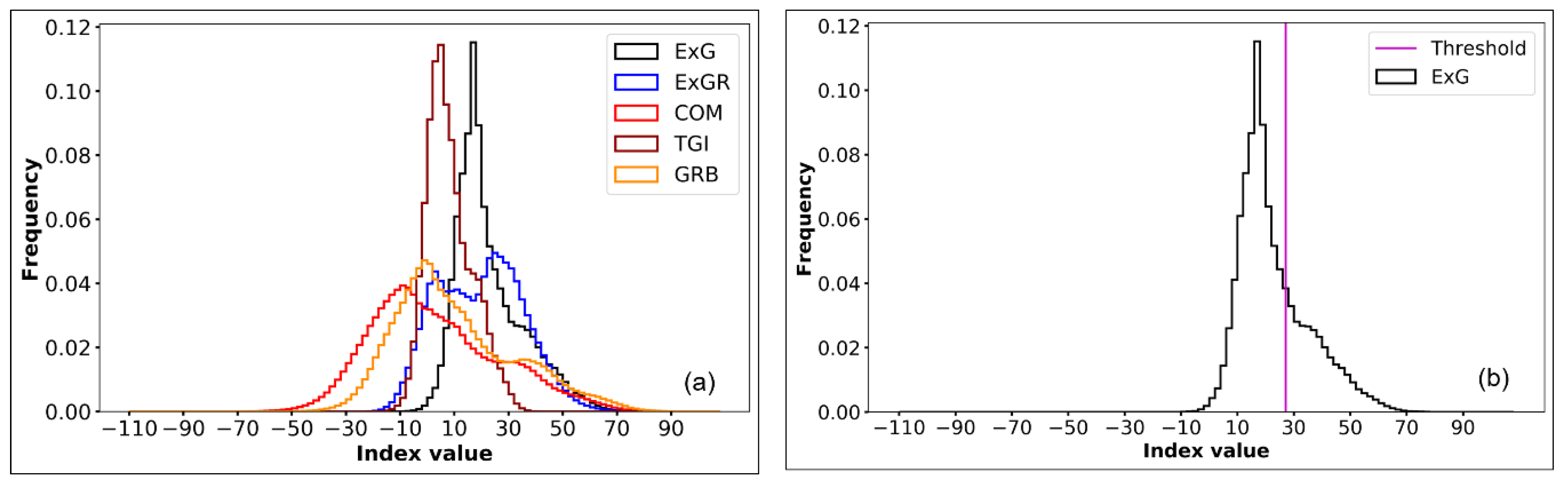
2.3. Otsu’s Thresholding Method
2.4. Marker Detection and Watershed Segmentation
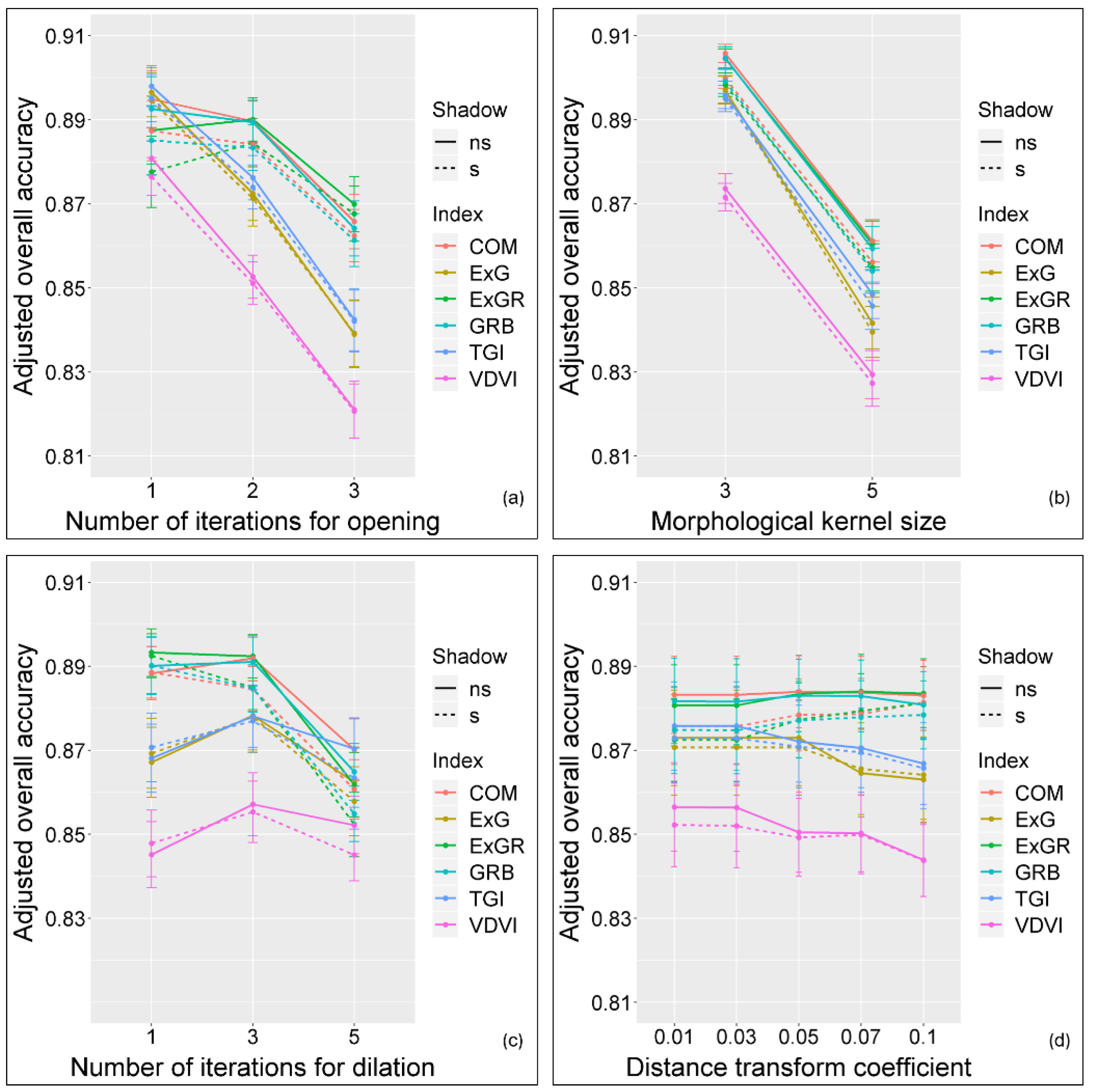
- Opening morphological transformations that conduct erosions followed by dilations were applied to remove noise from patch boundaries and break up tree patches with thin connections [56]. Since we were interested in removing small and isolated noisy pixels from patch boundaries, we chose the frequently used square kernel shape because it is computationally efficient and effective. We used several opening iterations with varying square kernel sizes to determine their effect on marker delineation and watershed segmentation.
- Unequivocal tree patch regions were identified by applying a distance transform followed by thresholding to the opening image generated in Step 1 (Figure 6b). The distance transform calculated the distances between the pixels inside a tree patch and the nearest background (marsh matrix) pixels. Euclidean distance was computed and the threshold was determined using the percentage of the maximum distance value in the image [57]. The optimum unequivocal tree patch image was generated by distance thresholding. This step ensured that the core portions of tree patches were identified.
- A dilation was employed to expand tree patches in the opening image to include indeterminate regions (Figure 6c). Since tree patch boundaries were located in indeterminate regions between the outside boundaries of unequivocal patches and the outside boundaries of expanded tree patches (Figure 6c), consecutive dilations were conducted to ensure expanded tree patches were large enough to contain true patch boundaries. A number of consecutive dilations were tested to determine the effect of dilations on marker delineation and watershed segmentation.
- Indeterminate regions were identified by subtracting the unequivocal patch image generated in Step 2 from the expanded patch image generated in Step 3 (Figure 6c).
- Then, the marker image was generated by labeling connected regions in the unequivocal patch image with increasing integers from 1 to N and labeling the indeterminate regions as zero in the expanded patch image (Figure 6c).
- Finally, watershed segmentation was executed on the color image utilizing the delineated markers to derive tree patch boundaries.
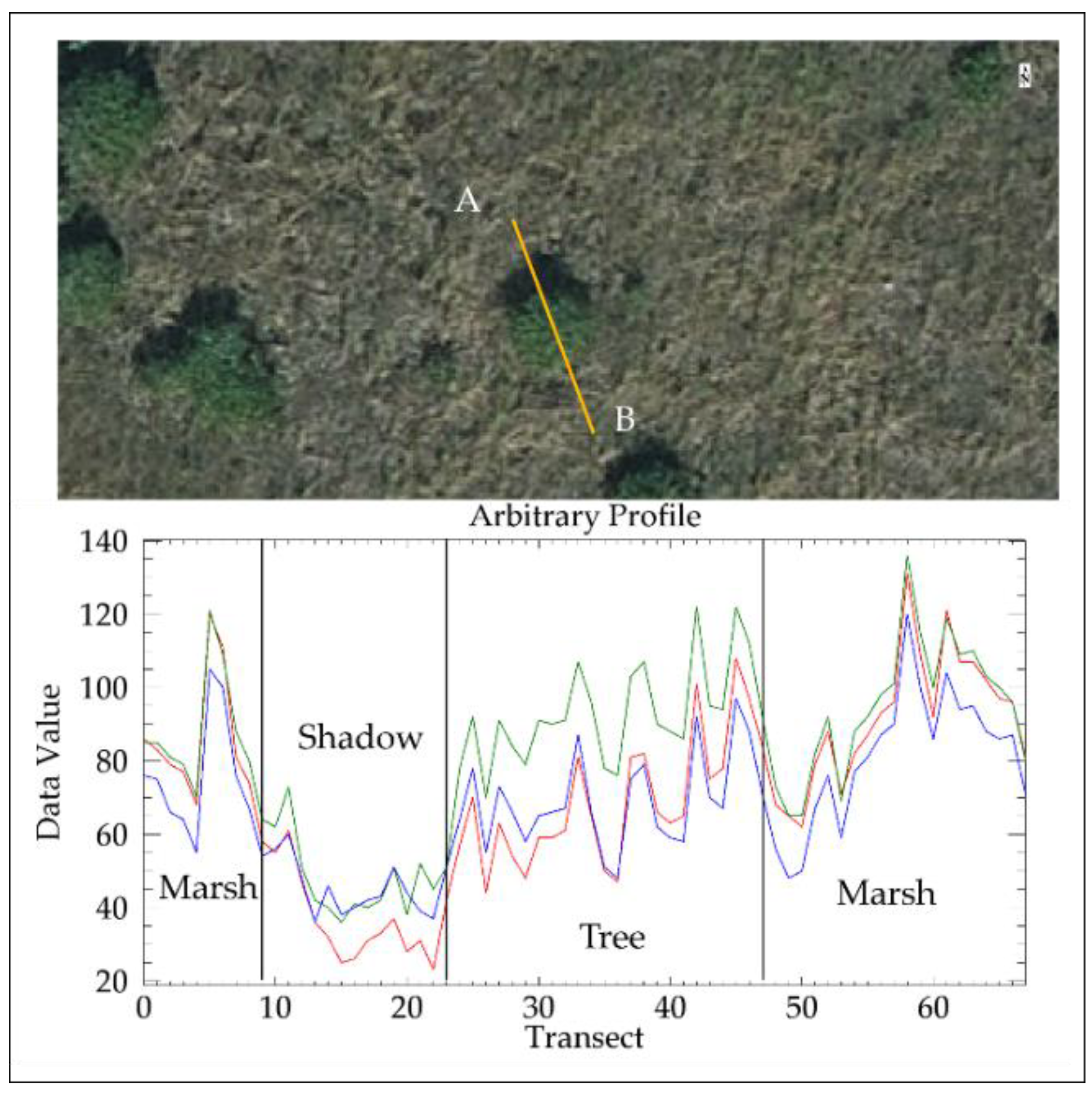
2.5. Removal of Shadows
- A mean RGB (mRGB) index image was calculated by summing intensity values from all the bands and dividing by three. A mask image of same size as the mRGB index was created, where values from the mRGB index image was kept at 0 if mRGB values were less than the first percentile, and 1 if mRGB was equal to or greater than the first percentile.
- The shadows were removed by multiplying the patch mask and the original image.
- Isolated pixels in the shadow-removed image were eliminated by applying a morphological closing operation using a kernel of 4 pixels.
- The morphologically filtered image was labeled for connected components and small objects were removed by using a size threshold of 4 pixels to generate the final shadow-removed patches.
2.6. Parameter Sensitivity
2.7. Tree-Cover Estimation from Random Samples and Tree Detection Accuracy
2.8. Object-Based Overlap Accuracy Assessment
3. Results
3.1. Parameter Sensitivity Analysis
3.2. Tree-Cover Area Estimation and Tree Detection Analysis
3.3. Object-Based Overlap Analysis
4. Discussion
4.1. Feasibility of the Method
4.2. Comparison with Other Studies
4.3. Future Work and Challenges
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mohd, O.; Suryanna, N.; Sahib Sahibuddin, S.; Faizal Abdollah, M.; Rahayu Selamat, S. Thresholding and Fuzzy Rule-Based Classification Approaches in Handling Mangrove Forest Mixed Pixel Problems Associated with in QuickBird Remote Sensing Image Analysis. Int. J. Agric. For. 2012, 2, 300–306. [Google Scholar] [CrossRef]
- Kuenzer, C.; Bluemel, A.; Gebhardt, S.; Quoc, T.V.; Dech, S. Remote Sensing of Mangrove Ecosystems: A Review. Remote Sens. 2011, 3, 878–928. [Google Scholar] [CrossRef]
- Ewel, K.C.; Twilley, R.R.; Ong, J.E. Different Kinds of Mangrove Forests Provide Different Goods and Services. Glob. Ecol. Biogeogr. Lett. 1998, 7, 83–94. [Google Scholar] [CrossRef]
- Costanza, R.; d’Arge, R.; de Groot, R.; Farber, S.; Grasso, M.; Hannon, B.; Limburg, K.; Naeem, S.; O’Neill, R.V.; Paruelo, J.; et al. The Total Value of the World’s Ecosystem Services and Natural Capital. Nature 1996, 387, 253–260. [Google Scholar] [CrossRef]
- Zhang, K.; Liu, H.; Li, Y.; Xu, H.; Shen, J.; Rhome, J.; Smith, T.J., III. The role of mangroves in attenuating storm surges. Estuar. Coast. Shelf Sci. 2012, 102, 11–23. [Google Scholar] [CrossRef]
- Gilman, E.L.; Ellison, J.; Duke, N.C.; Field, C. Threats to mangroves from climate change and adaptation options: A review. Aquat. Bot. 2008, 89, 237–250. [Google Scholar] [CrossRef]
- Alongi, D.M. The Impact of Climate Change on Mangrove Forests. Curr. Clim. Chang. Rep. 2015, 1, 30–39. [Google Scholar] [CrossRef]
- Ross, M.S.; Meeder, J.F.; Sah, J.P.; Ruiz, P.L.; Telesnicki, G.J. The Southeast Saline Everglades revisited: 50 years of coastal vegetation change. J. Veg. Sci. 2000, 11, 101–112. [Google Scholar] [CrossRef]
- Rogers, K.; Saintilan, N.; Heijnis, H. Mangrove encroachment of salt marsh in Western Port Bay, Victoria: The role of sedimentation, subsidence, and sea level rise. Estuaries 2005, 28, 551–559. [Google Scholar] [CrossRef]
- Yao, Q.; Liu, K.B. Dynamics of marsh-mangrove ecotone since the mid-Holocene: A palynological study of mangrove encroachment and sea level rise in the Shark River Estuary, Florida. PLoS ONE 2017, 12, e0173670. [Google Scholar] [CrossRef]
- Rodriguez, W.; Feller, I.C.; Cavanaugh, K.C. Spatio-temporal changes of a mangrove–saltmarsh ecotone in the northeastern coast of Florida, USA. Glob. Ecol. Conserv. 2016, 7, 245–261. [Google Scholar] [CrossRef]
- Saintilan, N.; Williams, R.J. Mangrove transgression into saltmarsh environments in south-east Australia. Glob. Ecol. Biogeogr. 1999, 8, 117–124. [Google Scholar] [CrossRef]
- Rosenzweig, C.; Karoly, D.; Vicarelli, M.; Neofotis, P.; Wu, Q.; Casassa, G.; Menzel, A.; Root, T.L.; Estrella, N.; Seguin, B.; et al. Attributing physical and biological impacts to anthropogenic climate change. Nature 2008, 453, 353. [Google Scholar] [CrossRef]
- Ke, Y.; Quackenbush, L.J. A comparison of three methods for automatic tree crown detection and delineation from high spatial resolution imagery. Int. J. Remote Sens. 2011, 32, 3625–3647. [Google Scholar] [CrossRef]
- Giri, C.; Ochieng, E.; Tieszen, L.L.; Zhu, Z.; Singh, A.; Loveland, T.; Masek, J.; Duke, N. Status and distribution of mangrove forests of the world using earth observation satellite data. Glob. Ecol. Biogeogr. 2011, 20, 154–159. [Google Scholar] [CrossRef]
- Thomas, N.; Bunting, P.; Lucas, R.; Hardy, A.; Rosenqvist, A.; Fatoyinbo, T. Mapping mangrove extent and change: A globally applicable approach. Remote Sens. 2018, 10, 1466. [Google Scholar] [CrossRef]
- Zhang, K.; Thapa, B.; Ross, M.; Gann, D. Remote sensing of seasonal changes and disturbances in mangrove forest: A case study from South Florida. Ecosphere 2016, 7, e01366. [Google Scholar] [CrossRef]
- Simard, M.; Zhang, K.; Rivera-monroy, V.H.; Ross, M.S.; Ruiz, P.L.; Castañeda-moya, E.; Twilley, R.R.; Rodriguez, E. Mapping Height and Biomass of Mangrove Forests in Everglades National Park with SRTM Elevation Data. Photogramm. Eng. Remote Sens. 2006, 72, 299–311. [Google Scholar] [CrossRef]
- Feliciano, E.A.; Wdowinski, S.; Potts, M.D.; Lee, S.K.; Fatoyinbo, T.E. Estimating mangrove canopy height and above-ground biomass in the Everglades National Park with airborne LiDAR and TanDEM-X data. Remote Sens. 2017, 9, 702. [Google Scholar] [CrossRef]
- Giri, C.P.; Long, J. Mangrove reemergence in the northernmost range limit of eastern Florida. Proc. Natl. Acad. Sci. USA 2014, 111, E1447–E1448. [Google Scholar] [CrossRef]
- USGS. Looking for an Old Aerial Photograph; Fact Sheet; Series Number 127-96; U.S. Geological Survey: Reston, VA, USA, 1997.
- Freeman, M.; Stow, D.; Roberts, D. Object-based Image Mapping of Conifer Tree Mortality in San Diego County based on Multitemporal Aerial Ortho-imagery. Photogramm. Eng. Remote Sens. 2016, 82, 571–580. [Google Scholar] [CrossRef]
- Rutchey, K.; Vilchek, L. Air photointerpretation and satellite imagery analysis techniques for mapping cattail coverage in a northern Everglades impoundment. Photogramm. Eng. Remote Sens. 1999, 65, 185–191. [Google Scholar]
- Kataoka, T.; Kaneko, T.; Okamoto, H.; Hata, S. Crop growth estimation system using machine vision. In Proceedings of the 2003 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM 2003), Kobe, Japan, 20–24 July 2003; Volume 2, pp. 1079–1083. [Google Scholar]
- Meyer, G.E.; Neto, J.C. Verification of color vegetation indices for automated crop imaging applications. Comput. Electron. Agric. 2008, 63, 282–293. [Google Scholar] [CrossRef]
- Ponti, M.P. Segmentation of low-cost remote sensing images combining vegetation indices and mean shift. IEEE Geosci. Remote Sens. Lett. 2013, 10, 67–70. [Google Scholar] [CrossRef]
- Yang, W.; Wang, S.; Zhao, X.; Zhang, J.; Feng, J. Greenness identification based on HSV decision tree. Inf. Process. Agric. 2015, 2, 149–160. [Google Scholar] [CrossRef]
- Xiaoqin, W.; Miaomiao, W.; Shaoqiang, W.; Yundong, W. Extraction of vegetation information from visible unmanned aerial vehicle images. Trans. Chin. Soc. Agric. Eng. 2015, 31, 152–159. [Google Scholar]
- Kazmi, W.; Garcia-Ruiz, F.J.; Nielsen, J.; Rasmussen, J.; Jørgen Andersen, H. Detecting creeping thistle in sugar beet fields using vegetation indices. Comput. Electron. Agric. 2015, 112, 10–19. [Google Scholar] [CrossRef]
- Hamuda, E.; Glavin, M.; Jones, E. A survey of image processing techniques for plant extraction and segmentation in the field. Comput. Electron. Agric. 2016, 125, 184–199. [Google Scholar] [CrossRef]
- Woebbecke, D.M.; Meyer, G.E.; Von Bargen, K.; Mortensen, D.A. Color Indices for Weed Identification Under Various Soil, Residue, and Lighting Conditions. Trans. ASAE 1995, 38, 259–269. [Google Scholar] [CrossRef]
- Meyer, G.E.; Hindman, T.W.; Laksmi, K. Machine Vision Detection Parameters for Plant Species Identification. In Precision Agriculture and Biological Quality; SPIE Proceedings: Bellingham, WA, USA, 1999; Volume 3543, pp. 327–336. [Google Scholar]
- Hague, T.; Tillett, N.D.; Wheeler, H. Automated Crop and Weed Monitoring in Widely Spaced Cereals. Precis. Agric. 2006, 7, 21–32. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Stark, R.; Rundquist, D. Novel algorithms for remote estimation of vegetation fraction. Pap. Nat. Resour. 2002, 149, 76–87. [Google Scholar] [CrossRef]
- Woebbecke, D.M.; Meyer, G.E.; Von Bargen, K.; Mortensen, D.A. Plant Species Identification, Size, and Enumeration Using Machine Vision Techniques on Near-Binary Images. In Optics in Agriculture and Forestry; DeShazer, J.A., Meyer, G.E., Eds.; SPIE: Bellingham, WA, USA, 12 May 1993; Volume 1836, pp. 208–219. [Google Scholar]
- Hunt, E.R.; Daughtry, C.S.T.; Eitel, J.U.H.; Long, D.S. Remote sensing leaf chlorophyll content using a visible band index. Agron. J. 2011, 103, 1090–1099. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man. Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Meyer, G.; Camargo Neto, J.; Jones, D.; Hindman, T. Intensified fuzzy clusters for classifying plant, soil, and residue regions of interest from color images. Comput. Electron. Agric. 2004, 42, 161–180. [Google Scholar] [CrossRef]
- Tian, L.F.; Slaughter, D.C. Environmentally adaptive segmentation algorithm for outdoor image segmentation. Comput. Electron. Agric. 1998, 21, 153–168. [Google Scholar] [CrossRef]
- Guo, W.; Rage, U.K.; Ninomiya, S. Illumination invariant segmentation of vegetation for time series wheat images based on decision tree model. Comput. Electron. Agric. 2013, 96, 58–66. [Google Scholar] [CrossRef]
- Wang, L.; Gong, P.; Biging, G.S. Individual Tree-Crown Delineation and Treetop Detection in High-Spatial-Resolution Aerial Imagery. Photogramm. Eng. Remote Sens. 2004, 70, 351–357. [Google Scholar] [CrossRef]
- Digabel, H.; Lantuejoul, C. Iterative Algorithms. In Proceedings of the Actes du Second Symposium Europeen d’Analyse Quantitative des Microstructures en Sciences des Materiaux, Biologie et Medecine; Chermant, J.-L., Ed.; Riederer: Stuttgart, Germany, 1978; pp. 85–99. [Google Scholar]
- Beucher, S.; Lantuejoul, C. Use of Watersheds in Contour Detection. In Proceedings of the International Workshop on Image Processing CCETT, Rennes, France, 17 September 1979; pp. 2.1–2.12. [Google Scholar]
- Meyer, F.; Beucher, S. Morphological segmentation. J. Vis. Commun. Image Represent. 1990, 1, 21–46. [Google Scholar] [CrossRef]
- Ke, Y.; Quackenbush, L.J. A review of methods for automatic individual tree-crown detection and delineation from passive remote sensing. Int. J. Remote Sens. 2011, 32, 4725–4747. [Google Scholar] [CrossRef]
- Huang, H.; Li, X.; Chen, C. Individual tree crown detection and delineation from very-high-resolution UAV images based on bias field and marker-controlled watershed segmentation algorithms. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2253–2262. [Google Scholar] [CrossRef]
- Jing, L.; Hu, B.; Noland, T.; Li, J. An individual tree crown delineation method based on multi-scale segmentation of imagery. ISPRS J. Photogramm. Remote Sens. 2012, 70, 88–98. [Google Scholar] [CrossRef]
- Lamar, W.R.; McGraw, J.B.; Warner, T.A. Multitemporal censusing of a population of eastern hemlock (Tsuga canadensis L.) from remotely sensed imagery using an automated segmentation and reconciliation procedure. Remote Sens. Environ. 2005, 94, 133–143. [Google Scholar] [CrossRef]
- Yin, D.; Wang, L. Individual mangrove tree measurement using UAV-based LiDAR data: Possibilities and challenges. Remote Sens. Environ. 2019, 223, 34–49. [Google Scholar] [CrossRef]
- MDC Miami-Dade County Aerial Photography Find and Download Application. 2017. Available online: https://gisweb.miamidade.gov/imagerydownload/ (accessed on 6 November 2018).
- ESRI ArcGIS Desktop: Release 10.5; Environmental Systems Research Institute: Redlands, CA, USA, 2016.
- Python Software Foundation Python Language Reference. 2016.
- Bradski, G. The OpenCV Library. Dr. Dobb’s J. Softw. Tools. 2000. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- R Core Team. R: A language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013; ISBN 3-900051-07-0. [Google Scholar]
- Soille, P. Morphological Image Analysis: Principles and Applications, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2004; ISBN 3540429883. (alk. paper). [Google Scholar]
- Borgefors, G. Distance transformations in digital images. Comput. Vision. Graph. Image Process. 1986, 34, 344–371. [Google Scholar] [CrossRef]
- Olofsson, P.; Foodu, G.M.; Martin, H.; Stehman Stephen, V.; Woodcock, C.E.; Wulder, M.A. Good practices for estimating area and assessing accuracy of land change. Remote Sens. Environ. 2014, 148, 42–57. [Google Scholar] [CrossRef]
- Radoux, J.; Bogaert, P. Good Practices for Object-Based Accuracy Assessment. Remote Sens. 2017, 9, 646. [Google Scholar] [CrossRef]
- Olofsson, P.; Foody, G.M.; Stehman, S.V.; Woodcock, C.E. Remote Sensing of Environment Making better use of accuracy data in land change studies: Estimating accuracy and area and quantifying uncertainty using strati fi ed estimation. Remote Sens. Environ. 2013, 129, 122–131. [Google Scholar] [CrossRef]
- Leckie, D.; Gougeon, F.; Hill, D.; Quinn, R.; Armstrong, L.; Shreenan, R. Combined high-density lidar and multispectral imagery for individual tree crown analysis. Can. J. Remote Sens. 2003, 29, 633–649. [Google Scholar] [CrossRef]
- Nagelkirk, R.L.; Dahlin, K.M. Woody cover fractions in African Savannas from landsat and high-resolution imagery. Remote Sens. 2020, 12, 813. [Google Scholar] [CrossRef]
- Huang, C.Y.; Archer, S.R.; McClaran, M.P.; Marsh, S.E. Shrub encroachment into grasslands: End of an era? PeerJ 2018, 2018, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Mitchard, E.T.A.; Saatchi, S.S.; Gerard, F.F.; Lewis, S.L.; Meir, P. Measuring woody encroachment along a forest-savanna boundary in Central Africa. Earth Interact. 2009, 13, 1–29. [Google Scholar] [CrossRef]



| Vegetation Index | Equation | Reference |
|---|---|---|
| Excess Green (ExG) | 2g − r − b | [31] |
| Excess Red (ExR) | 1.4 × r − g | [32] |
| Excess Green minus Excess Red (ExGR) | ExG − ExR | [25] |
| Vegetative Index (VEG) | g/r0.667× b0.333 | [33] |
| Color Index of Vegetation Extraction (CIVE) | 0.441 × r − 0.881 × g + 0.385 × b + 18.78745 | [24] |
| Visible Atmospheric Resistant Index (VARI) | (g − r)/(g + r − b) | [34] |
| Combined Index (COM) | 0.25 × ExG + 0.30 × ExGR + 0.33 × CIVE + 0.12 × VEG | [27] |
| Normalized Difference Index (NDI) | (g − r)/(g + r) | [35] |
| Triangular Greenness Index (TGI) | g − 0.39 × r − 0.61 × b | [36] |
| Visible-band Difference Vegetation Index (VDVI) | (2g − b − r)/(2g + b + r) | [28] |
| Red minus Green (R-G) | r − g | [31] |
| Green minus Blue (G-B) | g − b | [31] |
| Ratio (GB_RG) | (g − b)/(r − g) | [31] |
| GRB | g × r × b | [31] |
| Parameter | Values |
|---|---|
| Number of iterations for opening | {1, 2, 3} |
| Morphological kernel size | {3, 5} |
| Number of iterations for dilation | {1, 3, 5} |
| Distance transform coefficient | {0.01, 0.03, 0.05, 0.07, 0.1} |
| Model | Morphological Kernel Size | Number of Iterations for Opening | Number of Iterations for Dilation | Distance Transform Coefficient |
|---|---|---|---|---|
| GRB_ns | 3 | 1 | 3 | 0.05, 0.07 |
| ExG_s | 3 | 1 | 3 | 0.01, 0.03, 0.05 |
| ExG_ns | 3 | 1 | 3 | 0.01, 0.03, 0.05 |
| GRB_s | 3 | 1 | 1 | 0.05, 0.07, 0.1 |
| COM_ns | 3 | 1 | 3 | 0.01, 0.03, 0.05, 0.07, 0.1 |
| TGI_ns | 3 | 1 | 3 | 0.01, 0.03 |
| TGI_s | 3 | 1 | 3 | 0.01, 0.03 |
| COM_s | 3 | 1 | 1 | 0.05, 0.07, 0.1 |
| ExGR_ns | 3 | 2 | 1 | 0.05, 0.07 |
| ExGR_s | 3 | 2 | 1 | 0.05, 0.07, 0.1 |
| VDVI_ns | 3 | 1 | 3 | 0.01, 0.03 |
| VDVI_s | 3 | 1 | 3 | 0.01, 0.03 |
| Index Name | % Tree Cover | Adjusted User’s Accuracy | Adjusted Producer’s Accuracy | Adjusted Overall Accuracy |
|---|---|---|---|---|
| GRB_ns | 25.8 | 90.1 ± 1.2 | 85.2 ± 1.3 | 93.4 ± 0.5 |
| ExG_s | 27.8 | 87.9 ± 1.3 | 87.4 ± 1.2 | 93.1 ± 0.5 |
| ExG_ns | 26.5 | 89.9 ± 1.2 | 84.6 ± 1.2 | 93.0 ± 0.5 |
| GRB_s | 26.5 | 87.6 ± 1.3 | 85.9 ± 1.3 | 92.9 ± 0.5 |
| R-G_ns | 25.8 | 89.3 ± 1.3 | 84.0 ± 1.3 | 92.9 ± 0.5 |
| COM_ns | 26.5 | 87.3 ± 1.3 | 85.1 ± 1.3 | 92.6 ± 0.5 |
| TGI_ns | 27.9 | 85.9 ± 1.4 | 87.2 ± 1.2 | 92.5 ± 0.5 |
| TGI_s | 26.0 | 88.9 ± 1.3 | 83.2 ± 1.3 | 92.4 ± 0.5 |
| COM_s | 27.3 | 84.8 ± 1.4 | 86.5 ± 1.2 | 92.3 ± 0.5 |
| ExGR_ns | 25.6 | 88.7 ± 1.3 | 82.2 ± 1.3 | 92.2 ± 0.5 |
| ExGR_s | 25.9 | 87.1 ± 1.4 | 82.6 ± 1.3 | 91.9 ± 0.6 |
| VDVI_ns | 25.8 | 86.9 ± 1.4 | 81.1 ± 1.3 | 91.4 ± 0.6 |
| VDVI_s | 27.5 | 82.6 ± 1.5 | 82.9 ± 1.3 | 90.5 ± 0.6 |
| Model (ns-s) | Δ Percent Tree Cover | Δ Adjusted User’s Accuracy | Δ Adjusted Producer’s Accuracy | Δ Adjusted Overall Accuracy |
|---|---|---|---|---|
| COM | −0.76 | 2.53 | −1.47 | 0.32 |
| ExG | −1.32 | 2.07 | −2.78 | −0.10 |
| ExGR | −0.32 | 1.52 | −0.37 | 0.28 |
| GRB | −0.70 | 2.45 | −0.73 | 0.48 |
| R-G | −5.14 | 10.35 | −6.69 | 1.87 |
| TGI | 1.90 | −3.02 | 4.06 | 0.12 |
| VDVI | −1.65 | 4.26 | −1.82 | 0.83 |
| Mean ± SD | −1.14 ± 2.1 | 2.88 ± 3.99 | −1.4 ± 3.2 | 0.54 ± 0.65 |
| Index Image | Omitted Tree Area Sum (m2) | Actual Tree Area Sum (m2) | Committed Mean Tree Area (m2) | Reference Tree Area (m2) | Omitted Tree Area (%) | Actual Tree Area (%) | Committed Mean Tree Area (%) |
|---|---|---|---|---|---|---|---|
| GRB_ns | 24.48 | 181.11 | 29.28 | 205.59 | 11.91 | 88.09 | 16.17 |
| ExG_s | 3.07 | 57.93 | 12.37 | 60.99 | 5.03 | 94.97 | 21.35 |
| Number of Trees in a Polygon Patch | 0 | 1 | 2 | 3 | 9 | 11 |
|---|---|---|---|---|---|---|
| GRB_ns (count) | 3 | 35 | 9 | 1 | 1 | 1 |
| ExG_s (count) | 0 | 49 | 0 | 1 | 0 | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Biswas, H.; Zhang, K.; Ross, M.S.; Gann, D. Delineation of Tree Patches in a Mangrove-Marsh Transition Zone by Watershed Segmentation of Aerial Photographs. Remote Sens. 2020, 12, 2086. https://doi.org/10.3390/rs12132086
Biswas H, Zhang K, Ross MS, Gann D. Delineation of Tree Patches in a Mangrove-Marsh Transition Zone by Watershed Segmentation of Aerial Photographs. Remote Sensing. 2020; 12(13):2086. https://doi.org/10.3390/rs12132086
Chicago/Turabian StyleBiswas, Himadri, Keqi Zhang, Michael S. Ross, and Daniel Gann. 2020. "Delineation of Tree Patches in a Mangrove-Marsh Transition Zone by Watershed Segmentation of Aerial Photographs" Remote Sensing 12, no. 13: 2086. https://doi.org/10.3390/rs12132086
APA StyleBiswas, H., Zhang, K., Ross, M. S., & Gann, D. (2020). Delineation of Tree Patches in a Mangrove-Marsh Transition Zone by Watershed Segmentation of Aerial Photographs. Remote Sensing, 12(13), 2086. https://doi.org/10.3390/rs12132086





