Thematic Classification Accuracy Assessment with Inherently Uncertain Boundaries: An Argument for Center-Weighted Accuracy Assessment Metrics
Abstract
:1. Introduction
- reduce the weight and impact of boundary areas in accuracy assessment metrics;
- support the calculation of a variety of easily interpretable and commonly used accuracy assessment metrics derived from an error matrix;
- allow the calculation of count-based and areas-based assessment metrics, as well as the estimate of population matrices;
- and be generalizable to binary, multiclass, and feature extraction accuracy assessment problems.
2. Background
2.1. Standard Multiclass Remote Sensing Accuracy Assessment Metrics
2.2. Accuracy Assesement of Binary Classifications
2.3. GEOBIA Accuracy Asssessment
2.4. Accuracy Assessment and Pessimisitc Bias
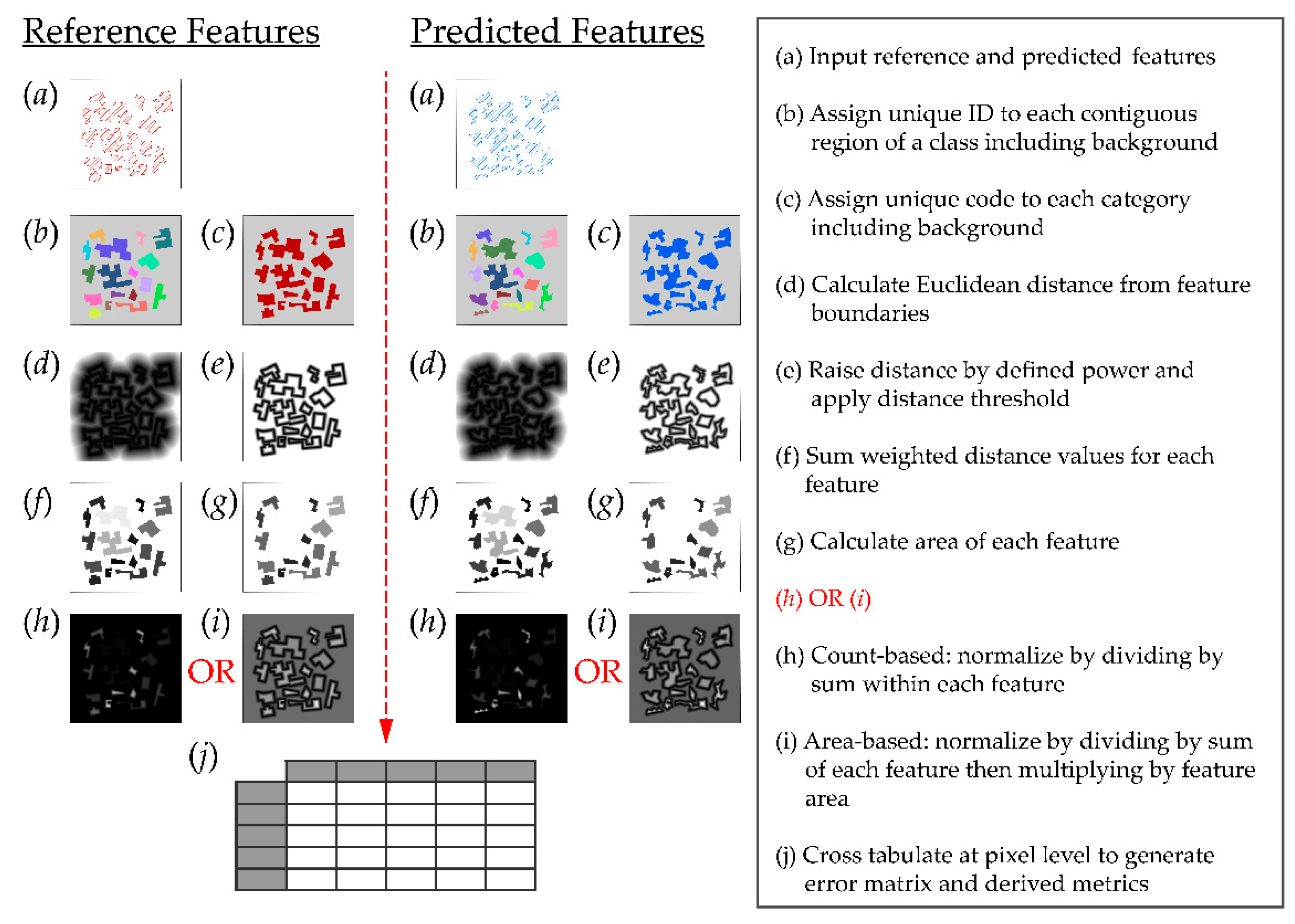
3. Methods
4. Demonstrations and Metric Characteristics
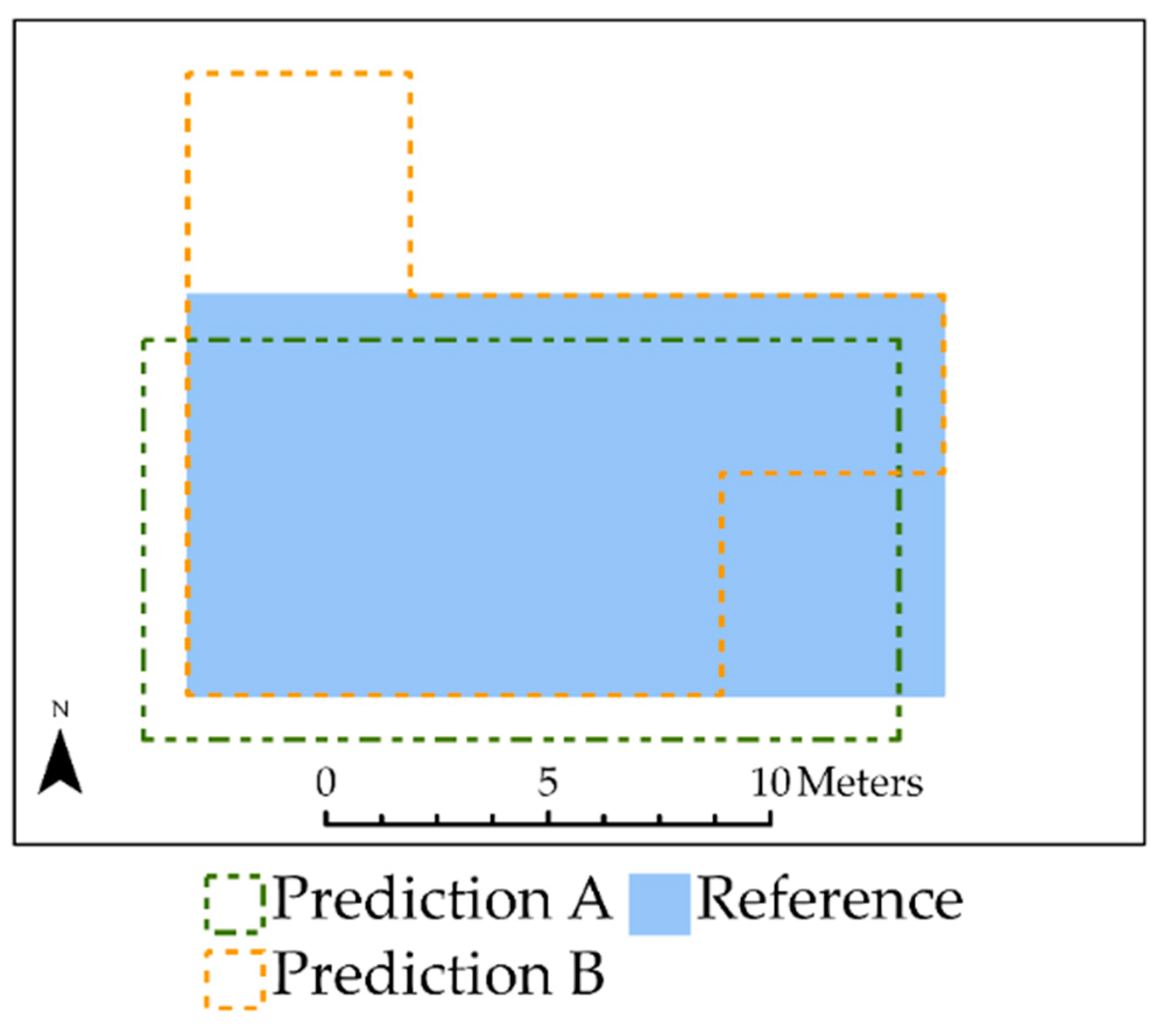
4.1. Example 1: Limitations of Standard Area-Based Accuracy Assessment Compared to Center Weighting
4.2. Example 2: Impact of Over- and Under-Predicting Feature Area
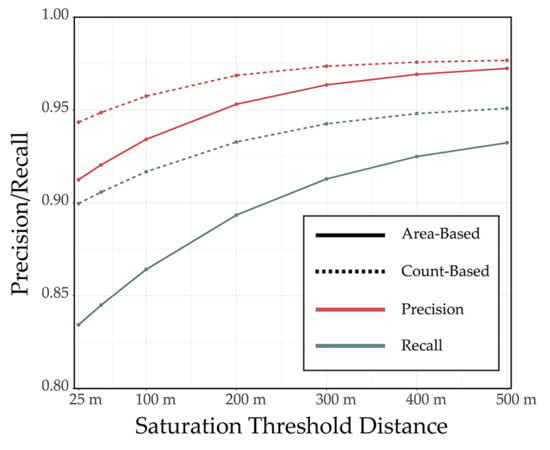
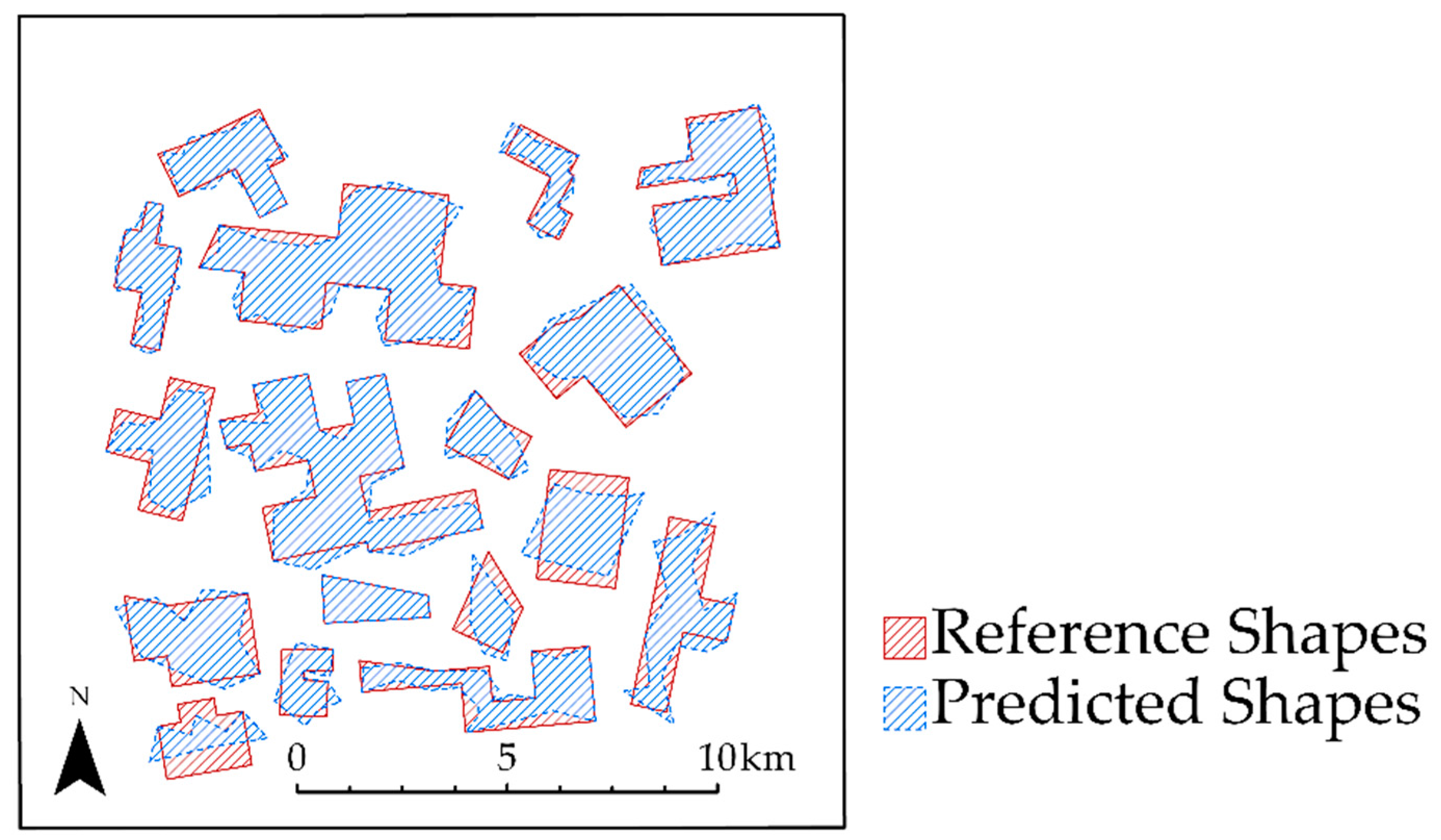
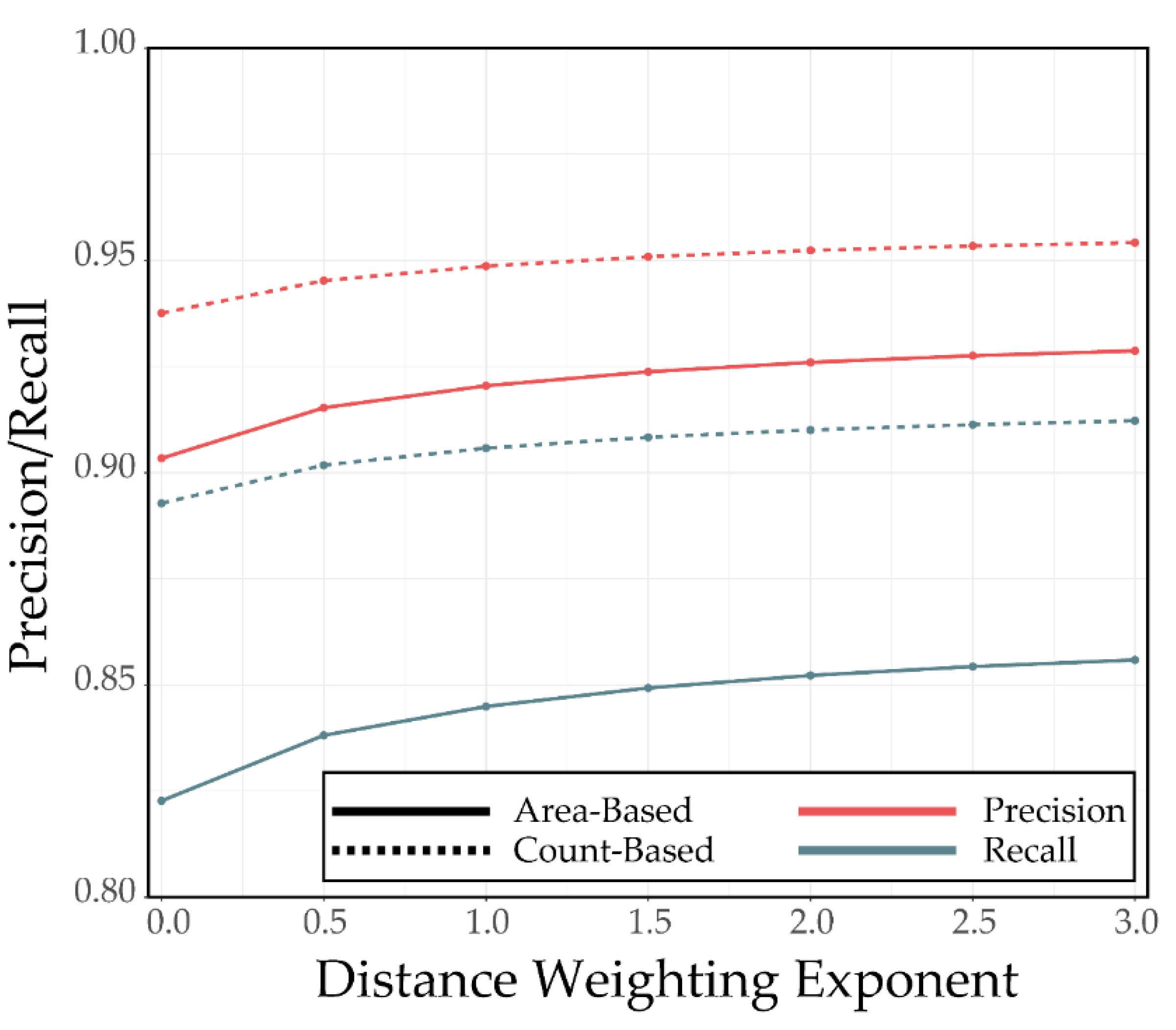
4.3. Example 3: Impact of Distance Weighting Exponent and Saturation Distance for Synthetic Features
4.4. Example 4: Individual Tree Crown Delineation
4.5. Example 5: Results for Assessment of Valley Fill Face Extraction
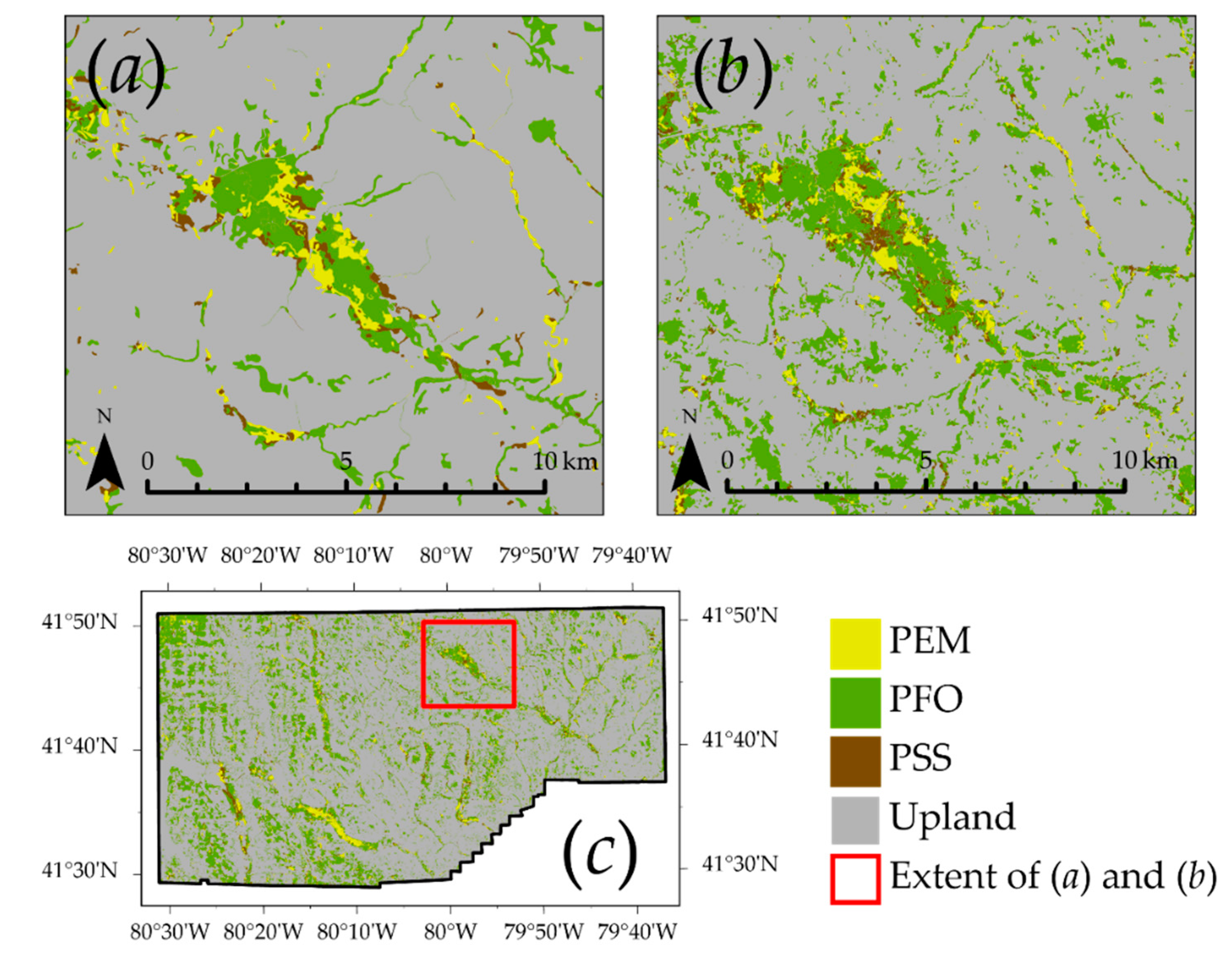
4.6. Example 6: Multiclass and Spatially Contiguous Classification Assessment
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Stehman, S.V.; Foody, G.M. Key issues in rigorous accuracy assessment of land cover products. Remote Sens. Environ. 2019, 231, 111199. [Google Scholar] [CrossRef]
- Stehman, S.V.; Wickham, J.D. Pixels, blocks of pixels, and polygons: Choosing a spatial unit for thematic accuracy assessment. Remote Sens. Environ. 2011, 115, 3044–3055. [Google Scholar] [CrossRef]
- Foody, G.M. Status of land cover classification accuracy assessment. Remote Sens. Environ. 2002, 80, 185–201. [Google Scholar] [CrossRef]
- Foody, G.M. Harshness in image classification accuracy assessment. Int. J. Remote Sens. 2008, 29, 3137–3158. [Google Scholar] [CrossRef] [Green Version]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices, 3rd ed.; CRC Press: London, UK, 2019; ISBN 978-0-429-62935-8. [Google Scholar]
- Congalton, R.G. Accuracy assessment and validation of remotely sensed and other spatial information. Int. J. Wildland Fire 2001, 10, 321–328. [Google Scholar] [CrossRef] [Green Version]
- Foody, G.M. Thematic Map Comparison. Photogramm. Eng. Remote Sens. 2004, 70, 627–633. [Google Scholar] [CrossRef]
- Lawrence, R.L.; Moran, C.J. The AmericaView classification methods accuracy comparison project: A rigorous approach for model selection. Remote Sens. Environ. 2015, 170, 115–120. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of machine-learning classification in remote sensing: An applied review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef] [Green Version]
- Rogan, J.; Franklin, J.; Stow, D.; Miller, J.; Woodcock, C.; Roberts, D. Mapping land-cover modifications over large areas: A comparison of machine learning algorithms. Remote Sens. Environ. 2008, 112, 2272–2283. [Google Scholar] [CrossRef]
- Wright, C.; Gallant, A. Improved wetland remote sensing in Yellowstone National Park using classification trees to combine TM imagery and ancillary environmental data. Remote Sens. Environ. 2007, 107, 582–605. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Strager, M.P. Predicting palustrine wetland probability using random forest machine learning and digital elevation data-derived terrain variables. Photogramm. Eng. Remote Sens. 2016, 82, 437–447. [Google Scholar] [CrossRef]
- Burrough, P.A.; Frank, A. Geographic Objects with Indeterminate Boundaries; CRC Press: London, UK, 1996; ISBN 978-0-7484-0387-5. [Google Scholar]
- Qi, F.; Zhu, A.-X.; Harrower, M.; Burt, J.E. Fuzzy soil mapping based on prototype category theory. Geoderma 2006, 136, 774–787. [Google Scholar] [CrossRef] [Green Version]
- Zhu, A.-X.; Yang, L.; Li, B.; Qin, C.; Pei, T.; Liu, B. Construction of membership functions for predictive soil mapping under fuzzy logic. Geoderma 2010, 155, 164–174. [Google Scholar] [CrossRef]
- Brandtberg, T.; Warner, T.A.; Landenberger, R.E.; McGraw, J.B. Detection and analysis of individual leaf-off tree crowns in small footprint, high sampling density lidar data from the eastern deciduous forest in North America. Remote Sens. Environ. 2003, 85, 290–303. [Google Scholar] [CrossRef]
- Duncanson, L.I.; Cook, B.D.; Hurtt, G.C.; Dubayah, R.O. An efficient, multi-layered crown delineation algorithm for mapping individual tree structure across multiple ecosystems. Remote Sens. Environ. 2014, 154, 378–386. [Google Scholar] [CrossRef]
- Pitkänen, J. Individual tree detection in digital aerial images by combining locally adaptive binarization and local maxima methods. Can. J. For. Res. 2001, 31, 832–844. [Google Scholar] [CrossRef]
- Liebermann, H.; Schuler, J.; Strager, M.; Hentz, A.; Maxwell, A. Using Unmanned Aerial Systems for Deriving Forest Stand Characteristics in Mixed Hardwoods of West Virginia. J. Geospatial Appl. Nat. Resour. 2018, 2, 2. [Google Scholar]
- Stehman, S.V. Sampling designs for accuracy assessment of land cover. Int. J. Remote Sens. 2009, 30, 5243–5272. [Google Scholar] [CrossRef]
- Pontius, R.G.; Millones, M. Death to Kappa: Birth of quantity disagreement and allocation disagreement for accuracy assessment. Int. J. Remote Sens. 2011, 32, 4407–4429. [Google Scholar] [CrossRef]
- Goutte, C.; Gaussier, E. A Probabilistic Interpretation of Precision, Recall and F-Score, with Implication for Evaluation. In Proceedings of the Advances in Information Retrieval; Losada, D.E., Fernández-Luna, J.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 345–359. [Google Scholar]
- Henderson, P.; Ferrari, V. End-to-end training of object class detectors for mean average precision. arXiv 2017, arXiv:1607.03476. Available online: https://arxiv.org/abs/1607.03476 (accessed on 11 June 2020).
- Zhen, Z.; Quackenbush, L.J.; Stehman, S.V.; Zhang, L. Impact of training and validation sample selection on classification accuracy and accuracy assessment when using reference polygons in object-based classification. Int. J. Remote Sens. 2013, 34, 6914–6930. [Google Scholar] [CrossRef]
- MacLean, M.G.; Congalton, D.R.G. Map Accuracy Assessment Issues When Using an Object-Oriented Approach. In Proceedings of the American Society for Photogrammetry and Remote Sensing 2012 Annual Conference, Sacramento, CA, USA, 19–23 March 2012; p. 5. [Google Scholar]
- Clinton, N.; Holt, A.; Scarborough, J.; Yan, L.; Gong, P. Accuracy Assessment Measures for Object-based Image Segmentation Goodness. Photogramm. Eng. Remote Sens. 2010, 76, 289–299. [Google Scholar] [CrossRef]
- Lizarazo, I. Accuracy assessment of object-based image classification: Another STEP. Int. J. Remote Sens. 2014, 35, 6135–6156. [Google Scholar] [CrossRef]
- McGuinness, K.; Keenan, G.; Adamek, T.; O’Connor, N.E. Image Segmentation Evaluation Using an Integrated Framework. In Proceedings of the IET International Conference on Visual Information Engineering, London, UK, 25–27 July 2007; p. 6. [Google Scholar]
- Zhang, Y.J. A survey on evaluation methods for image segmentation. Pattern Recognit. 1996, 29, 1335–1346. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Ming, D.; Zhao, L.; Lv, B.; Zhou, K.; Qing, Y. Review on High Spatial Resolution Remote Sensing Image Segmentation Evaluation. Photogramm. Eng. Remote Sens. 2018, 84, 629–646. [Google Scholar] [CrossRef]
- Costa, H.; Foody, G.M.; Boyd, D.S. Supervised methods of image segmentation accuracy assessment in land cover mapping. Remote Sens. Environ. 2018, 205, 338–351. [Google Scholar] [CrossRef] [Green Version]
- Unnikrishnan, R.; Pantofaru, C.; Hebert, M. Toward Objective Evaluation of Image Segmentation Algorithms. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 929–944. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Fritts, J.E.; Goldman, S.A. Image segmentation evaluation: A survey of unsupervised methods. Comput. Vis. Image Underst. 2008, 110, 260–280. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.J.; Gerbrands, J.J. Objective and quantitative segmentation evaluation and comparison. Signal. Process. 1994, 39, 43–54. [Google Scholar] [CrossRef]
- Yasnoff, W.A.; Mui, J.K.; Bacus, J.W. Error measures for scene segmentation. Pattern Recognit. 1977, 9, 217–231. [Google Scholar] [CrossRef]
- Su, T.; Zhang, S. Local and global evaluation for remote sensing image segmentation. ISPRS J. Photogramm. Remote Sens. 2017, 130, 256–276. [Google Scholar] [CrossRef]
- Vogelmann, J.; Howard, S.; Yang, L.; Larson, C.; Wylie, B.; Driel, N. Completion of the 1990s National Land Cover Data Set for the Conterminous United States From LandSat Thematic Mapper Data and Ancillary Data Sources. Photogramm. Eng. Remote Sens. 2001, 67, 650–655. [Google Scholar] [CrossRef]
- Stehman, S.; Wickham, J.; Smith, J.; Yang, L. Thematic accuracy of the 1992 National Land-Cover Data for the eastern United States: Statistical methodology and regional results. Remote Sens. Environ. 2003, 86, 500–516. [Google Scholar] [CrossRef]
- Fuller, R.; Groom, G.B.; Jones, A.R. The Land Cover Map of Great Britain: An automated classification of Landsat Thematic Mapper data. Photogramm. Eng. Remote Sens. 1994, 60, 553–562. [Google Scholar]
- R: The R Project for Statistical Computing. Available online: https://www.r-project.org/ (accessed on 30 March 2020).
- Hijmans, R.J.; van Etten, J.; Sumner, M.; Cheng, J.; Bevan, A.; Bivand, R.; Busetto, L.; Canty, M.; Forrest, D.; Ghosh, A.; et al. Raster: Geographic Data Analysis and Modeling. 2020. Available online: https://cran.r-project.org/web/packages/raster/index.html (accessed on 11 June 2020).
- Pebesma, E.; Bivand, R.; Racine, E.; Sumner, M.; Cook, I.; Keitt, T.; Lovelace, R.; Wickham, H.; Ooms, J.; Müller, K.; et al. sf: Simple Features for R: Standardized Support for Spatial Vector Data. R J. 2020, 10, 439–446. [Google Scholar] [CrossRef] [Green Version]
- Wickham, H.; François, R.; Henry, L.; Müller, K. RStudio Dplyr: A Grammar of Data Manipulation. 2020. Available online: https://cran.r-project.org/web/packages/dplyr/index.html (accessed on 11 June 2020).
- Kuhn, M. The Caret Package. Available online: https://cran.r-project.org/web/packages/caret/index.html (accessed on 11 June 2020).
- Pontius, R.G.; Santacruz, A. diffeR: Metrics of Difference for Comparing Pairs of Maps or Pairs of Variables. 2019. Available online: https://cran.r-project.org/web/packages/diffeR/index.html (accessed on 11 June 2020).
- Evans, J.S.; Murphy, M.A.; rfUtilities: Random Forests Model. Selection and Performance Evaluation. 2019. Available online: https://cran.r-project.org/web/packages/rfUtilities/index.html (accessed on 11 June 2020).
- EcoHealth Alliance. Ecohealthalliance/Fasterize; EcoHealth Alliance: New York, NY, USA, 2020. [Google Scholar]
- Smith, A.B. Adamlilith/Fasterraster. 2020. Available online: https://github.com/ecohealthalliance/fasterize (accessed on 11 June 2020).
- Python in ArcGIS Pro—ArcPy Get Started. Available online: https://pro.arcgis.com/en/pro-app/arcpy/get-started/installing-python-for-arcgis-pro.htm (accessed on 30 March 2020).
- Welcome to the QGIS Project! Available online: https://qgis.org/en/site/ (accessed on 30 March 2020).
- Welcome to Python.org. Available online: https://www.python.org/ (accessed on 30 March 2020).
- Warner, T.A.; McGraw, J.B.; Landenberger, R. Segmentation and classification of high resolution imagery for mapping individual species in a closed canopy, deciduous forest. Sci. China Ser. E Technol. Sci. 2006, 49, 128–139. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Pourmohammadi, P.; Poyner, J.D. Mapping the Topographic Features of Mining-Related Valley Fills Using Mask R-CNN Deep Learning and Digital Elevation Data. Remote Sens. 2020, 12, 547. [Google Scholar] [CrossRef] [Green Version]
- National Wetlands Inventory. Available online: https://www.fws.gov/wetlands/ (accessed on 31 March 2020).
- Department of Environmental Conservation. Wetland Maps. Available online: https://dec.vermont.gov/watershed/wetlands/maps (accessed on 31 March 2020).
- Baker, B.A.; Warner, T.A.; Conley, J.F.; McNeil, B.E. Does spatial resolution matter? A multi-scale comparison of object-based and pixel-based methods for detecting change associated with gas well drilling operations. Int. J. Remote Sens. 2013, 34, 1633–1651. [Google Scholar] [CrossRef]
- Osco, L.P.; dos Santos de Arruda, M.; Marcato Junior, J.; da Silva, N.B.; Ramos, A.P.M.; Moryia, É.A.S.; Imai, N.N.; Pereira, D.R.; Creste, J.E.; Matsubara, E.T.; et al. A convolutional neural network approach for counting and geolocating citrus-trees in UAV multispectral imagery. ISPRS J. Photogramm. Remote Sens. 2020, 160, 97–106. [Google Scholar] [CrossRef]
- Ammour, N.; Alhichri, H.; Bazi, Y.; Benjdira, B.; Alajlan, N.; Zuair, M. Deep Learning Approach for Car Detection in UAV Imagery. Remote Sens. 2017, 9, 312. [Google Scholar] [CrossRef] [Green Version]
- Moranduzzo, T.; Melgani, F. Automatic Car Counting Method for Unmanned Aerial Vehicle Images. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1635–1647. [Google Scholar] [CrossRef]
- Gopal, S.; Woodcock, C. Theory and methods for accuracy assessment of thematic maps using fuzzy sets. Photogramm. Eng. Remote Sens. 1994, 60, 2. [Google Scholar]
- Binaghi, E.; Brivio, P.A.; Ghezzi, P.; Rampini, A. A fuzzy set-based accuracy assessment of soft classification. Pattern Recognit. Lett. 1999, 20, 935–948. [Google Scholar] [CrossRef]





| Reference Data | UA | ||||
|---|---|---|---|---|---|
| A | B | C | |||
| Classification Result | A | 81 | 9 | 3 | 0.87 |
| B | 7 | 78 | 4 | 0.88 | |
| C | 12 | 13 | 93 | 0.79 | |
| PA | 0.81 | 0.78 | 0.93 | ||
| Reference Data | |||
|---|---|---|---|
| True | False | ||
| Classification Result | True | TP | FP |
| False | FN | TN | |
| Prediction | Distance Weighting Exponent | Distance Threshold | Precision | Recall | Specificity | F1 Score |
|---|---|---|---|---|---|---|
| A | 0 | NA | 0.837 | 0.837 | 0.922 | 0.837 |
| B | 0 | NA | 0.837 | 0.837 | 0.922 | 0.837 |
| A | 1 | 10 m | 0.963 | 0.965 | 0.983 | 0.964 |
| B | 1 | 10 m | 0.871 | 0.876 | 0.938 | 0.873 |
| Size of Classified Feature Relative to Reference Data | Distance Weighting Exponent | Precision | Recall |
|---|---|---|---|
| Larger | 0.0 | 0.445 | 1.000 |
| Larger | 0.5 | 0.542 | 1.000 |
| Larger | 1.0 | 0.611 | 1.000 |
| Larger | 1.5 | 0.663 | 1.000 |
| Larger | 2.0 | 0.703 | 1.000 |
| Larger | 2.5 | 0.735 | 1.000 |
| Larger | 3.0 | 0.761 | 1.000 |
| Smaller | 0.0 | 1.000 | 0.490 |
| Smaller | 0.5 | 1.000 | 0.642 |
| Smaller | 1.0 | 1.000 | 0.750 |
| Smaller | 1.5 | 1.000 | 0.826 |
| Smaller | 2.0 | 1.000 | 0.878 |
| Smaller | 2.5 | 1.000 | 0.914 |
| Smaller | 3.0 | 1.000 | 0.939 |
| Method | Distance Weighting Exponent | Distance Threshold | Precision | Recall | Specificity | F1 Score |
|---|---|---|---|---|---|---|
| Area-Based | 0 | NA | 0.872 | 0.912 | 0.590 | 0.892 |
| Area-Based | 1 | 5 m | 0.925 | 0.949 | 0.758 | 0.937 |
| Count-Based | 0 | NA | 0.883 | 0.969 | NA | 0.924 |
| Count-Based | 1 | 5 m | 0.928 | 0.980 | NA | 0.945 |
| Method | Distance Weight | Distance Threshold | Precision | Recall | Specificity | F1 Score |
|---|---|---|---|---|---|---|
| Area-Based | 0 | 50 m | 0.888 | 0.778 | 0.996 | 0.829 |
| Area-Based | 1 | 50 m | 0.943 | 0.824 | 0.998 | 0.880 |
| Count-Based | 0 | 50 m | 0.919 | 0.844 | NA | 0.880 |
| Count-Based | 1 | 50 m | 0.957 | 0.874 | NA | 0.913 |
| Reference Data | UA | |||||
|---|---|---|---|---|---|---|
| Upland | PEM | PFO | PSS | |||
| Classification Result | Upland | 2,104,233,840 | 37,569,359 | 330,286,054 | 22,279,483 | 0.981 |
| PEM | 8,071,915 | 13,511,700 | 2,841,000 | 4,792,900 | 0.202 | |
| PFO | 24,834,561 | 5,494,000 | 84,684,200 | 5,852,100 | 0.197 | |
| PSS | 8,715,288 | 10,262,200 | 12,249,500 | 10,587,500 | 0.243 | |
| PA | 0.844 | 0.462 | 0.701 | 0.253 | ||
| Reference Data | UA | |||||
|---|---|---|---|---|---|---|
| Upland | PEM | PFO | PSS | |||
| Classification Result | Upland | 2,127,035,350 | 34,638,122 | 314,708,326 | 20,108,600 | 0.986 |
| PEM | 6,653,671 | 14,487,761 | 1,801,477 | 4,969,928 | 0.223 | |
| PFO | 17,879,632 | 5,098,774 | 91,415,185 | 5,513,237 | 0.218 | |
| PSS | 6,613,750 | 10,722,481 | 10,877,585 | 11,237,370 | 0.269 | |
| PA | 0.852 | 0.519 | 0.762 | 0.285 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maxwell, A.E.; Warner, T.A. Thematic Classification Accuracy Assessment with Inherently Uncertain Boundaries: An Argument for Center-Weighted Accuracy Assessment Metrics. Remote Sens. 2020, 12, 1905. https://doi.org/10.3390/rs12121905
Maxwell AE, Warner TA. Thematic Classification Accuracy Assessment with Inherently Uncertain Boundaries: An Argument for Center-Weighted Accuracy Assessment Metrics. Remote Sensing. 2020; 12(12):1905. https://doi.org/10.3390/rs12121905
Chicago/Turabian StyleMaxwell, Aaron E., and Timothy A. Warner. 2020. "Thematic Classification Accuracy Assessment with Inherently Uncertain Boundaries: An Argument for Center-Weighted Accuracy Assessment Metrics" Remote Sensing 12, no. 12: 1905. https://doi.org/10.3390/rs12121905
APA StyleMaxwell, A. E., & Warner, T. A. (2020). Thematic Classification Accuracy Assessment with Inherently Uncertain Boundaries: An Argument for Center-Weighted Accuracy Assessment Metrics. Remote Sensing, 12(12), 1905. https://doi.org/10.3390/rs12121905