Angular-Based Radiometric Slope Correction for Sentinel-1 on Google Earth Engine
Abstract
1. Introduction
2. Method
2.1. Sentinel-1 Data Ingestion into Google Earth Engine
- Apply Orbit file
- Remove thermal noise
- Remove GRD border noise
- Radiometric calibration to
- Range-Doppler terrain correction
2.2. Radiometric Slope Correction
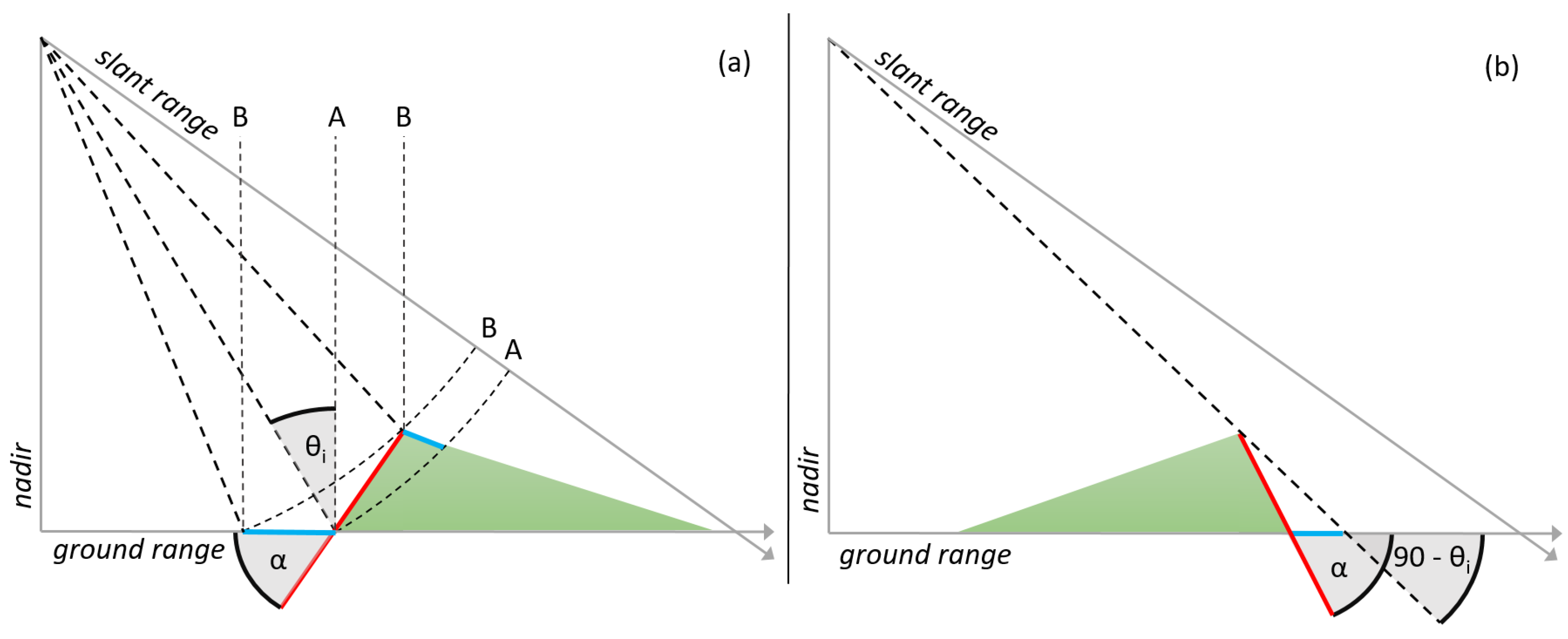
2.2.1. Radar Geometry
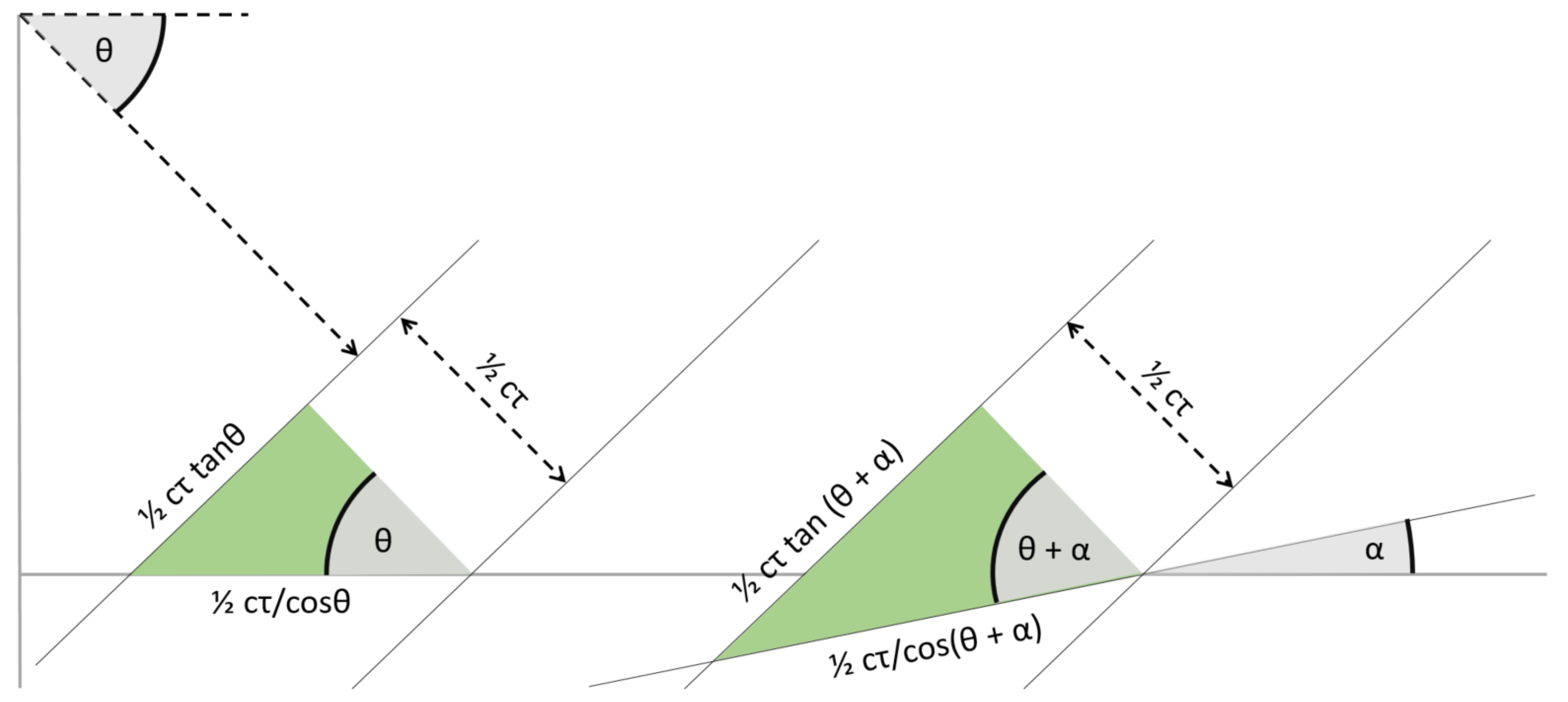
2.2.2. Terrain Geometry
2.2.3. Model Geometry
2.2.4. Reference Models
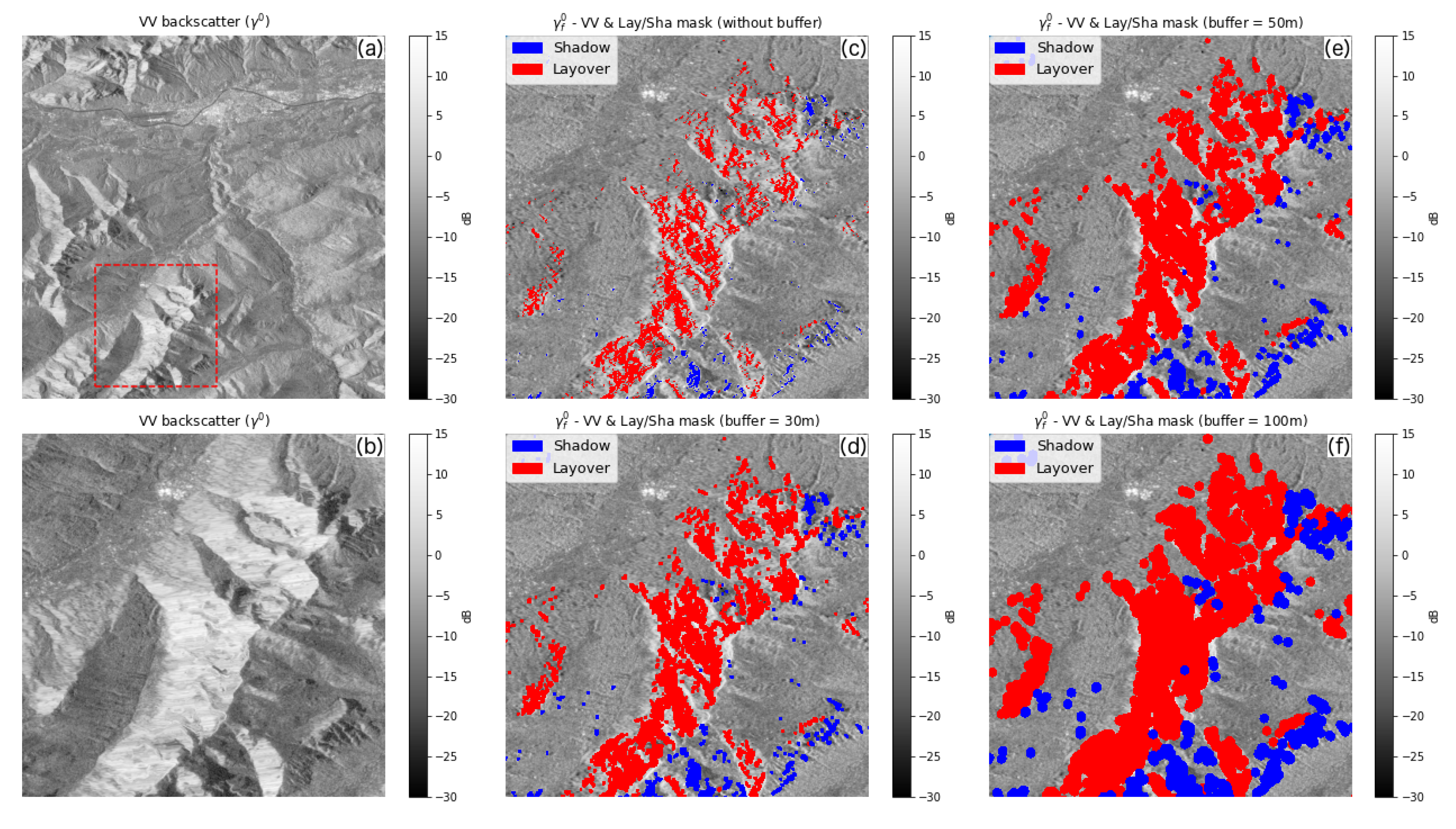
2.3. Layover and Shadow Mask
3. Case Study
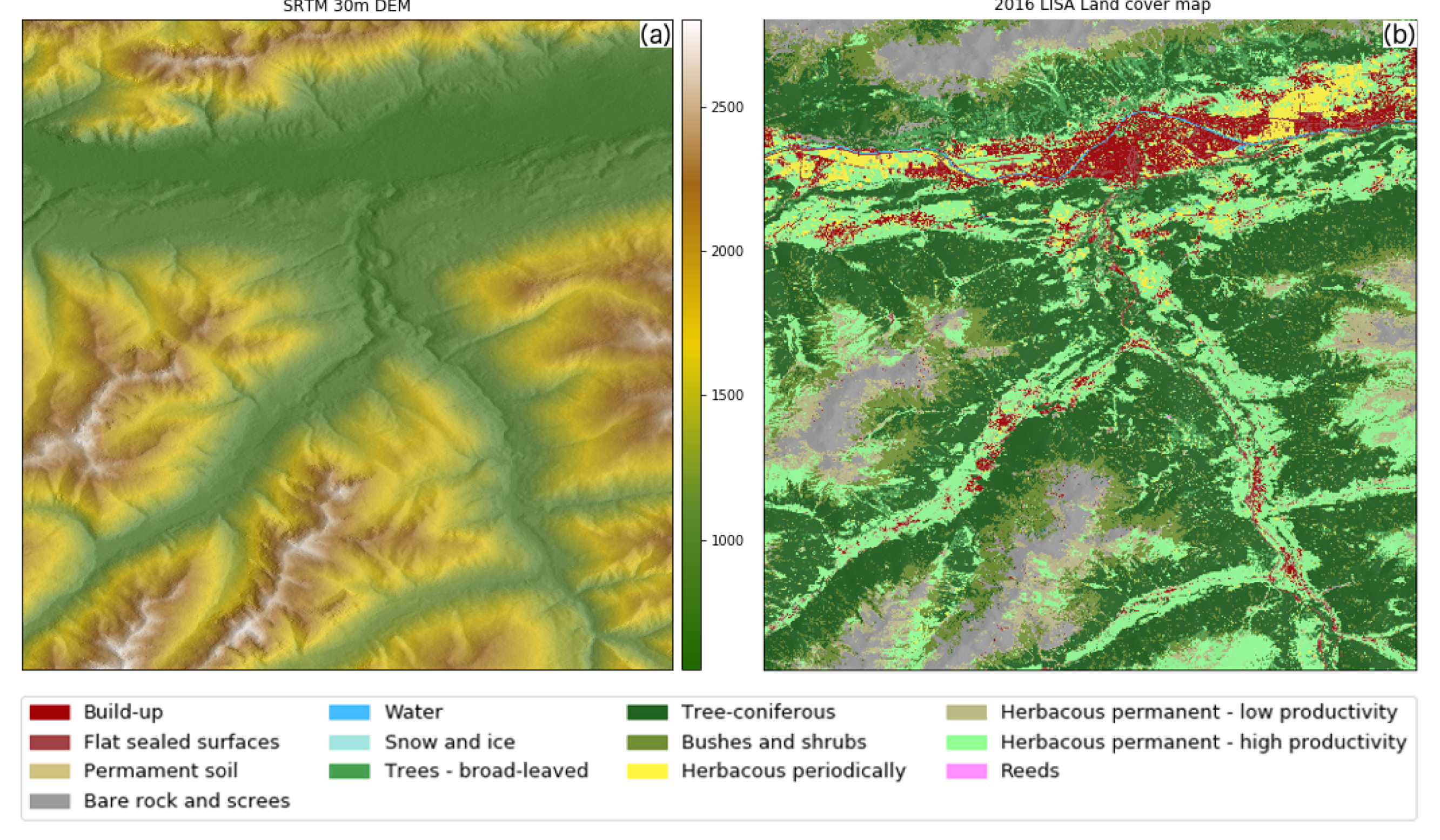
3.1. Study Area and Data
3.2. Evaluation Scheme
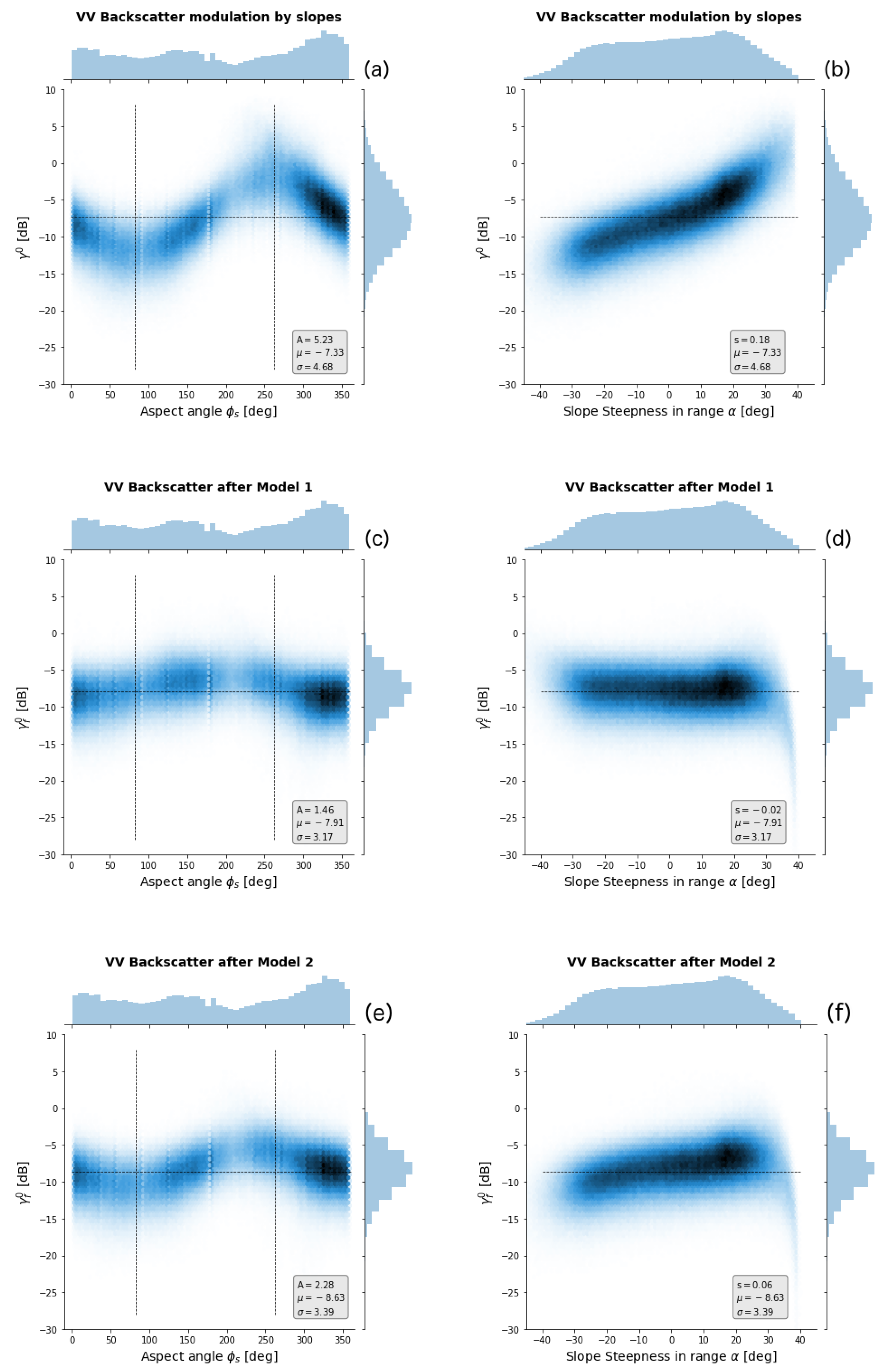
4. Results
5. Discussion
5.1. Earth Engine Module for Slope Correction
5.2. Model Selection
5.3. DEM Selection
5.4. Layover & Shadow Mask
5.5. Drawbacks and Future Perspective
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Reiche, J.; Lucas, R.; Mitchell, A.L.; Verbesselt, J.; Hoekman, D.H.; Haarpaintner, J.; Kellndorfer, J.M.; Rosenqvist, A.; Lehmann, E.A.; Woodcock, C.E.; et al. Combining satellite data for better tropical forest monitoring. Nat. Clim. Chang. 2016, 6, 120–122. [Google Scholar] [CrossRef]
- Google Developers. Sentinel-1 Algorithms. 2020. Available online: https://developers.google.com/earth-engine/sentinel1 (accessed on 17 March 2020).
- Committee on Earth Observation Satellites. Analysis Ready Data For Land. Product Family Specification: Normalised Radar Backscatter, Version 4.1. Available online: http://ceos.org/ard/files/PFS/v4.1/CARD4L_Product_Family_Specification-Normalised_Radar_Backscatter-v4.1.pdf (accessed on 17 March 2020).
- Small, D. Flattening gamma: Radiometric terrain correction for SAR imagery. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3081–3093. [Google Scholar] [CrossRef]
- Hoekman, D.H.; Reiche, J. Multi-model radiometric slope correction of SAR images of complex terrain using a two-stage semi-empiralc approach. Remote Sens. Environ. 2015, 156, 1–10. [Google Scholar] [CrossRef]
- Shimada, M. Ortho-Rectification and Slope Correction of SAR Data Using DEM and Its Accuracy Evaluation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 657–671. [Google Scholar] [CrossRef]
- Frey, O.; Santoro, M.; Werner, C.L.; Wegmüller, U. DEM-based SAR pixel-area estimation for enhanced geocoding refinement and radiometric normalization. IEEE Geosci. Remote Sens. Lett. 2013, 10, 48–52. [Google Scholar] [CrossRef]
- Colesanti, C.; Wasowski, J. Investigating landslides with space-borne Synthetic Aperture Radar (SAR) interferometry. Eng. Geol. 2006, 88, 173–199. [Google Scholar] [CrossRef]
- Kellndorfer, J.M.; Dobson, M.C.; Ulaby, F.T. Geocoding for classification of ERS/JERS-1 SAR composites. Int. Geosci. Remote Sens. Symp. 1996, 4, 2335–2337. [Google Scholar]
- Kropatsch, W.G.; Strobl, D. The Generation of SAR Layover and Shadow Maps from Digital Elevation Models. IEEE Trans. Geosci. Remote Sens. 1990, 28, 98–107. [Google Scholar] [CrossRef]
- European Space Agency. Sentinel-1 Toolbox. 2019. Available online: https://sentinel.esa.int/web/sentinel/toolboxes/sentinel-1 (accessed on 17 March 2020).
- Hoekman, D.H. Radar Remote Sensing Data for Applications in Forestry. Ph.D. Thesis, Technical University Delft, Delft, The Netherlands, 17 October 1990. [Google Scholar]
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.; Floury, N.; Brown, M.; et al. GMES Sentinel-1 mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- Greifeneder, F.; Google Earth Engine Developer Group. Discussion on Derivation of Local Incidence Angle from Sentinel-1. 2018. Available online: https://groups.google.com/forum/#\protect\kern-.1667em\relaxmsg/google-earth-engine-developers/3-q0TEwa-Tk/h3J4havuBAAJ (accessed on 15 May 2020).
- Ulander, L.M. Radiometrie slope correction of synthetic-aperture radar images. IEEE Trans. Geosci. Remote Sens. 1996, 34, 1115–1122. [Google Scholar] [CrossRef]
- Chen, X.; Sun, Q.; Hu, J. Generation of complete SAR geometric distortion maps based on DEM and neighbor gradient algorithm. Appl. Sci. 2018, 10, 2206. [Google Scholar] [CrossRef]
- Farr, T.; Rosen, P.; Caro, E.; Crippen, R. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45, 1–33. [Google Scholar] [CrossRef]
- GeoVille Information Systems Gmbh. Land Information System Austria. 2017. Available online: https://www.landinformationsystem.at/ (accessed on 17 March 2020).
- Reiche, J.; Verhoeven, R.; Verbesselt, J.; Hamunyela, E.; Wielaard, N.; Herold, M. Characterizing tropical forest cover loss using dense Sentinel-1 data and active fire alerts. Remote Sens. 2018, 10, 777. [Google Scholar] [CrossRef]
- Reiche, J.; Hamunyela, E.; Verbesselt, J.; Hoekman, D.H.; Herold, M. Improving near-real time deforestation monitoring in tropical dry forests by combining dense Sentinel-1 time series with Landsat and ALOS-2 PALSAR-2. Remote Sens. Environ. 2018, 204, 147–161, review. [Google Scholar] [CrossRef]
- Hoekman, D.H.; Vissers, M.A.; Wielaard, N. PALSAR Wide-Area Mapping of Borneo: Methodology and Map Validation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 605–617. [Google Scholar] [CrossRef]
- Google Developers. Datasets Tagged Elevation in Earth Engine. 2020. Available online: https://developers.google.com/earth-engine/datasets/tags/elevation (accessed on 17 March 2020).

| -VV | s-VV | A-VV | -VH | -VH | s-VH | A-VH | ||
|---|---|---|---|---|---|---|---|---|
| Trees—broad-leaved | ||||||||
| Original | −8.584 | 4.433 | 0.176 | 4.469 | −14.144 | 4.208 | 0.160 | 4.024 |
| Model I | −7.900 | 3.276 | −0.013 | 1.398 | −13.460 | 3.250 | −0.029 | 1.308 |
| Model II | −8.947 | 3.519 | 0.074 | 2.272 | −14.507 | 3.390 | 0.058 | 1.845 |
| Tree—coniferous | ||||||||
| Original | −7.332 | 4.679 | 0.181 | 5.232 | −12.973 | 4.426 | 0.168 | 4.824 |
| Model I | −7.908 | 3.172 | −0.020 | 1.461 | −13.550 | 3.144 | −0.034 | 1.404 |
| Model II | −8.630 | 3.393 | 0.057 | 2.283 | −14.272 | 3.252 | 0.044 | 1.892 |
| Herbaceous permanent— | ||||||||
| high productivity | ||||||||
| Original | −10.225 | 3.889 | 0.167 | 2.970 | −16.107 | 3.635 | 0.138 | 2.463 |
| Model I | −10.149 | 3.104 | −0.020 | 0.888 | −16.031 | 3.153 | −0.049 | 1.111 |
| Model II | −10.636 | 3.199 | 0.060 | 1.337 | −16.518 | 3.115 | 0.030 | 0.958 |
| Herbaceous periodically | ||||||||
| Original | −8.753 | 3.310 | 0.152 | 1.022 | −15.354 | 3.223 | 0.130 | 0.814 |
| Model I | −8.622 | 3.131 | −0.024 | 0.686 | −15.223 | 3.101 | −0.046 | 0.490 |
| Model II | −8.785 | 3.187 | 0.065 | 0.632 | −15.386 | 3.107 | 0.043 | 0.306 |
| Bushes and shrubs | ||||||||
| Original | −8.313 | 5.793 | 0.196 | 6.252 | −13.944 | 5.238 | 0.171 | 5.442 |
| Model I | −8.828 | 4.027 | −0.020 | 1.597 | −14.458 | 3.953 | −0.046 | 1.686 |
| Model II | −9.905 | 4.280 | 0.067 | 2.734 | −15.536 | 3.975 | 0.042 | 1.995 |
| Bare rock and scree | ||||||||
| Original | −6.946 | 7.556 | 0.219 | 8.448 | −13.456 | 6.956 | 0.189 | 7.293 |
| Model I | −6.825 | 5.760 | −0.013 | 2.005 | −13.334 | 5.684 | −0.043 | 1.761 |
| Model II | −8.737 | 6.261 | 0.089 | 4.253 | −15.247 | 5.872 | 0.060 | 3.140 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vollrath, A.; Mullissa, A.; Reiche, J. Angular-Based Radiometric Slope Correction for Sentinel-1 on Google Earth Engine. Remote Sens. 2020, 12, 1867. https://doi.org/10.3390/rs12111867
Vollrath A, Mullissa A, Reiche J. Angular-Based Radiometric Slope Correction for Sentinel-1 on Google Earth Engine. Remote Sensing. 2020; 12(11):1867. https://doi.org/10.3390/rs12111867
Chicago/Turabian StyleVollrath, Andreas, Adugna Mullissa, and Johannes Reiche. 2020. "Angular-Based Radiometric Slope Correction for Sentinel-1 on Google Earth Engine" Remote Sensing 12, no. 11: 1867. https://doi.org/10.3390/rs12111867
APA StyleVollrath, A., Mullissa, A., & Reiche, J. (2020). Angular-Based Radiometric Slope Correction for Sentinel-1 on Google Earth Engine. Remote Sensing, 12(11), 1867. https://doi.org/10.3390/rs12111867






