Satellite-Based Monitoring and Modeling of Ground Movements Caused by Water Rebound
Abstract
1. Introduction
- To analyze the time-dependent vertical ground movements related to the groundwater rebound after mine closure;
- To estimate the termination of ground uplift due to groundwater rebound with the support of PSInSAR observation;
- To develop an algorithm based on complex geological, hydrological, and PSInSAR observation data to assess residual groundwater-rebound-related vertical ground movements in post-mining areas.
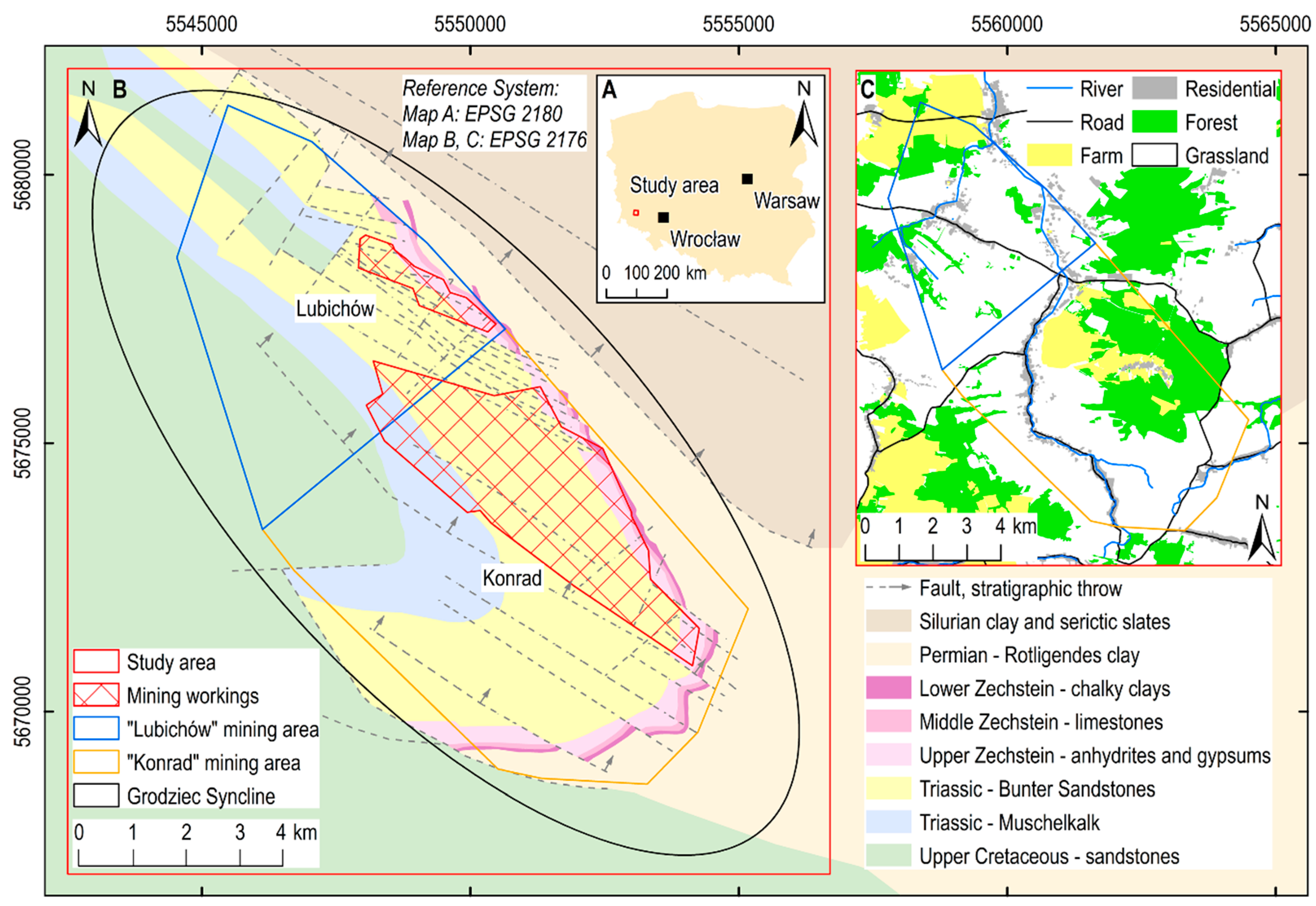
2. Study Area
2.1. Geological and Hydrogeological Constraints
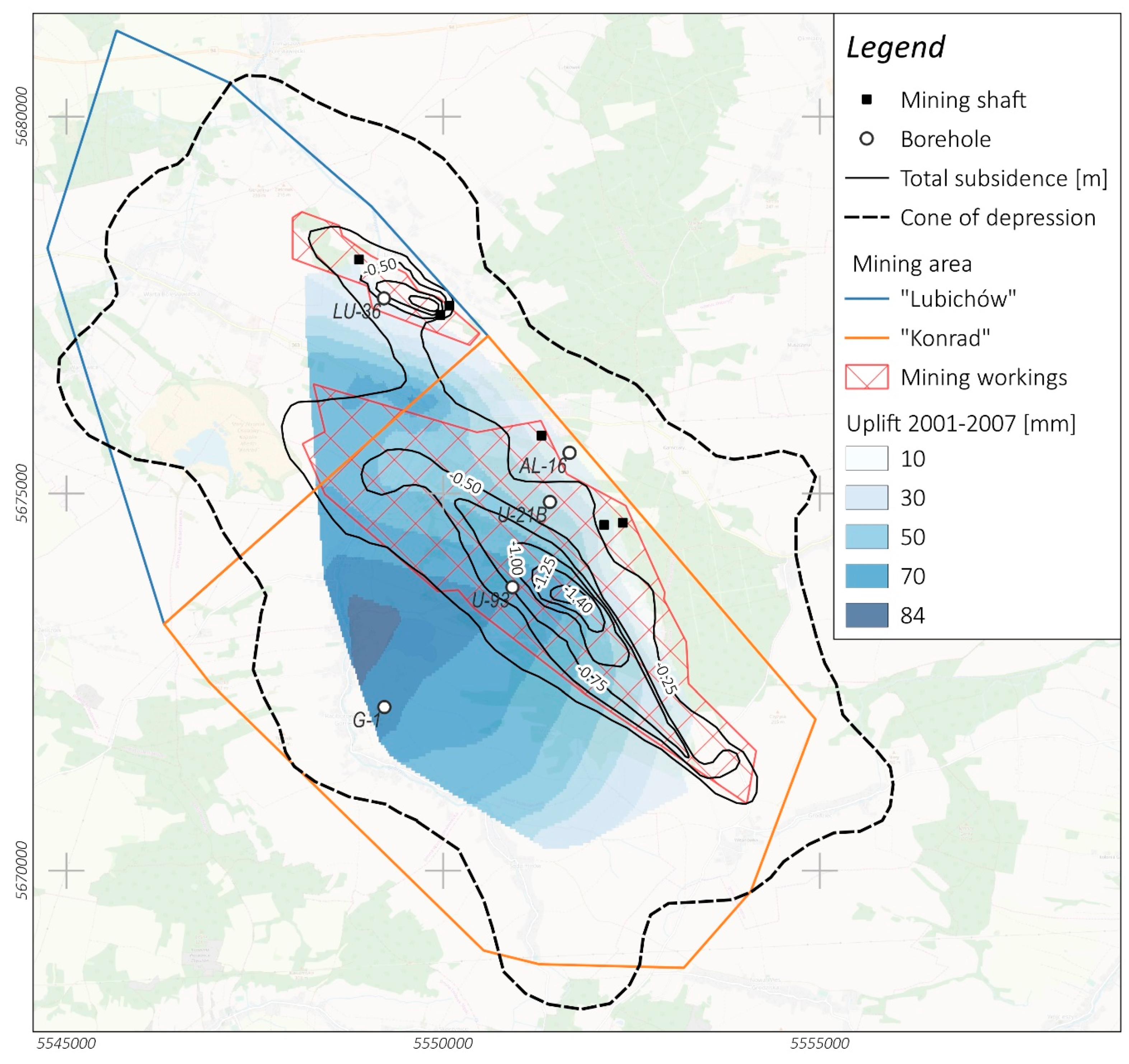
2.2. Impact of Mining Exploitation on the Terrain Surface
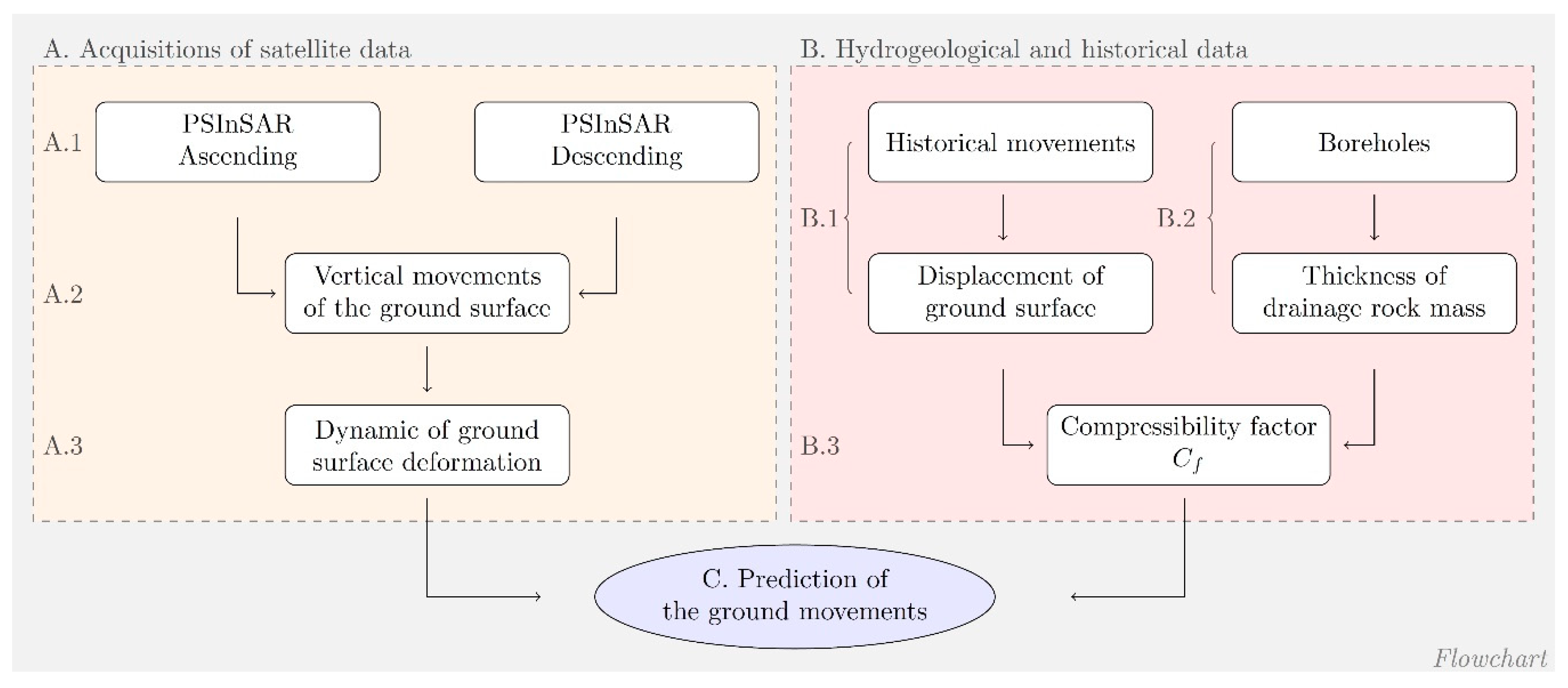
3. Research Methodology
3.1. The PSInSAR Image Processing Methodology
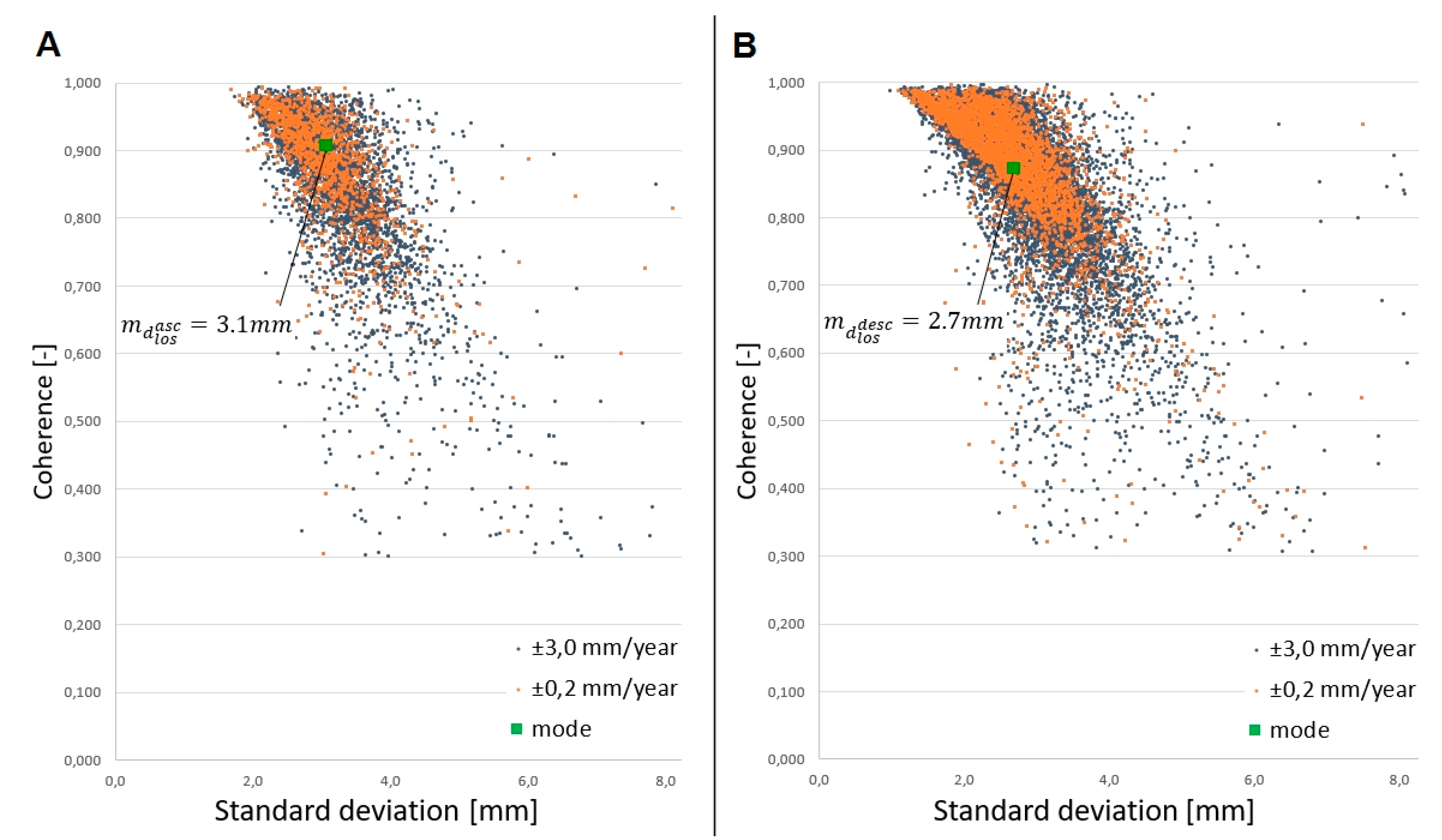
3.2. PSInSAR Processing Accuracy
3.3. Modeling of the Rock Matrix Volume Change
4. Results and Discussion
4.1. Vertical Ground Movement Velocity Observed by PSInSAR
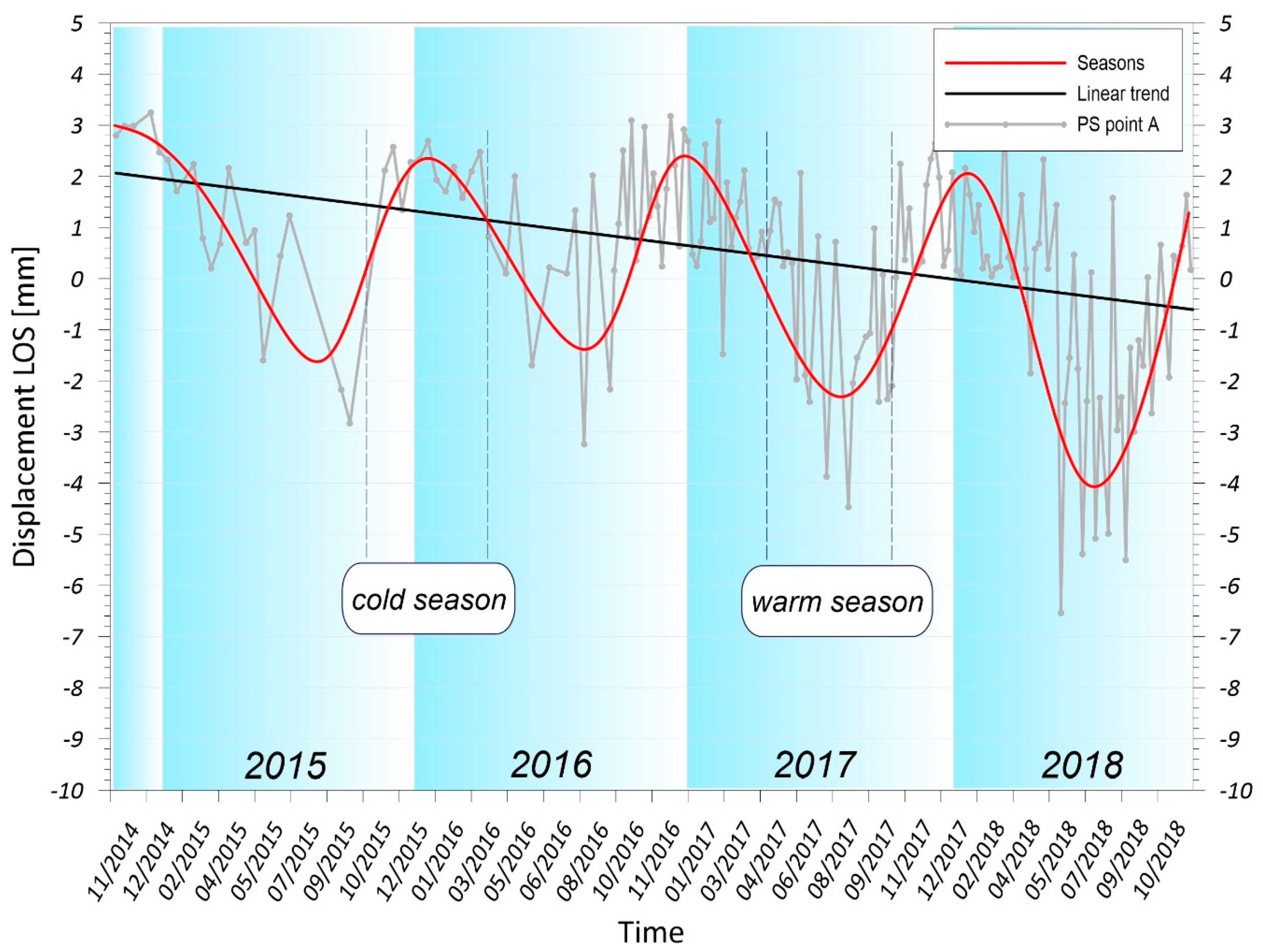
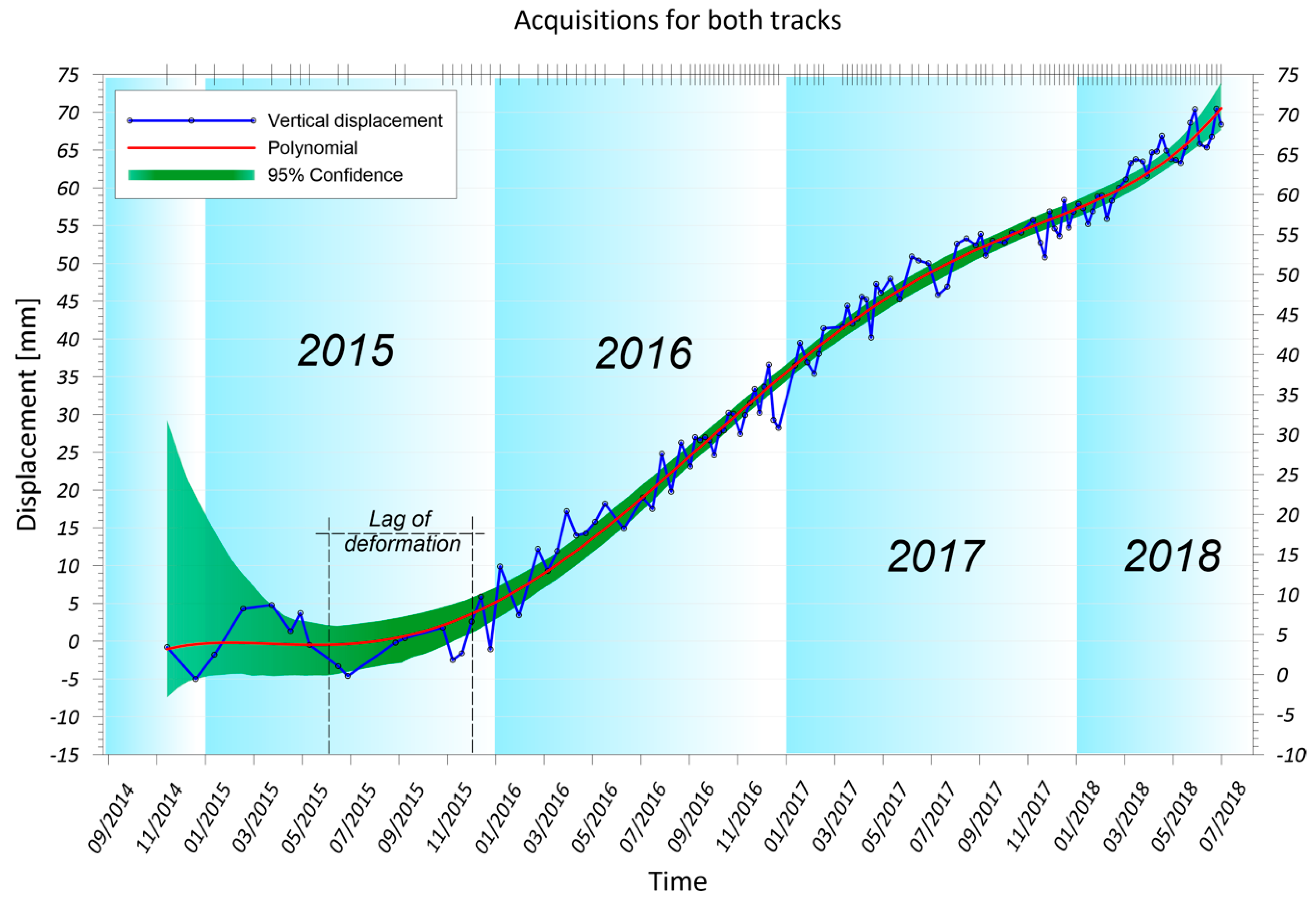
4.2. Dynamics of the Ground Movements
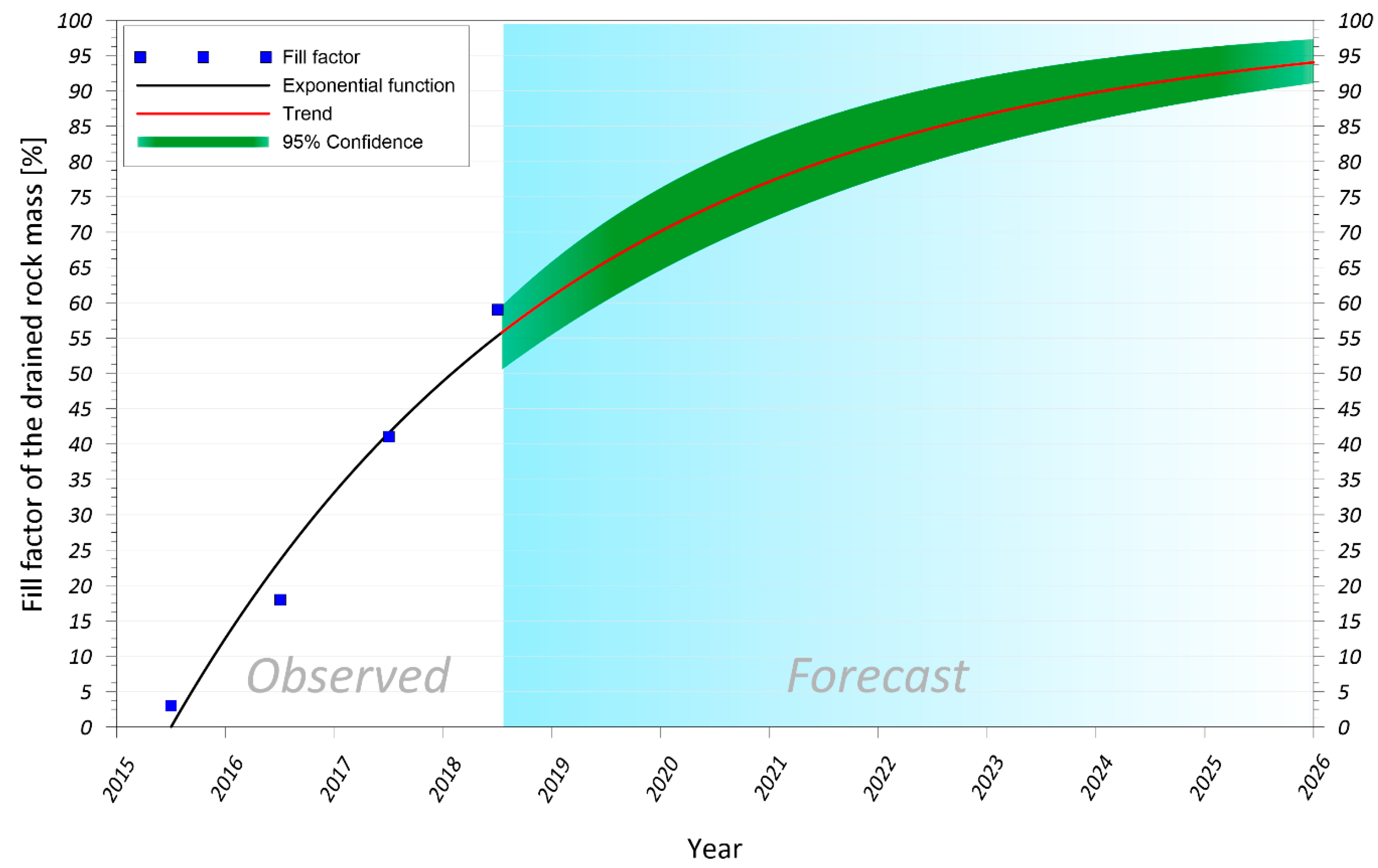
4.3. Spatio-Temporal Evolution of Groundwater Recharge from Vertical Ground Movements
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Brown, T.J.; Idoine, N.E.; Raycraft, E.R.; Shaw, R.A.; Hobbs, S.F.; Everett, P.; Deady, E.A.; Bide, T. World Mineral Production 2012–2016; British Geological Survey: Nottingham, UK, 2018. [Google Scholar] [CrossRef]
- Islam, M.; Hayashi, D.; Kamruzzaman, A. Finite Element Modeling of Stress Distributions and Problems for Multi-Slice Longwall Mining in Bangladesh, with Special Reference to the Barapukuria Coal Mine. Int. J. Coal Geol. 2009, 78, 91–109. [Google Scholar] [CrossRef]
- Whittaker, B.N.; Reddish, D.J. Subsidence: Occurrence, Prediction, and Control; Elsevier: Amsterdam, The Netherlands, 1989. [Google Scholar]
- Terzaghi, K.; Mesri, G.; Peck, R. Soil Mechanics in Engineering Practice/Karl Terzaghi, Ralph B Peck, Gholamreza Mesri, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1996; ISBN 978-0-471-08658-1. [Google Scholar]
- Younger, P.; Adams, R. Predicting Mine Water Rebound: Progress Reports; Environment Agency R&D Technical Report W179: Bristol, UK, 1999; 108p. [Google Scholar]
- Bukowski, P. Water Hazard Assessment in Active Shafts in Upper Silesian Coal Basin Mines. Mine Water Environ. 2011, 30, 302–311. [Google Scholar] [CrossRef]
- Gui, H.; Song, X.; Lin, M. Water-Inrush Mechanism Research Mining above Karst Confined Aquifer and Applications in North China Coalmines. Arab. J. Geosci. 2017, 10, 1–9. [Google Scholar] [CrossRef]
- Fan, G.; Zhang, S.; Zhang, D.; Zhang, C.; Chen, M.; Li, Q. An Index of Aquiclude Destabilization for Mining-Induced Roof Water Inrush Forecasting: A Case Study. Water 2019, 11, 2170. [Google Scholar] [CrossRef]
- Yin, H.; Zhao, H.; Xie, D.; Sang, S.; Shi, Y.; Tian, M. Mechanism of Mine Water Inrush from Overlying Porous Aquifer in Quaternary: A Case Study in Xinhe Coal Mine of Shandong Province, China. Arab. J. Geosci. 2019, 12. [Google Scholar] [CrossRef]
- Wolkersdorfer, C. Water Management at Abandoned Flooded Underground Mines: Fundamentals, Tracer Tests, Modelling, Water Treatment; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Nichols, T.C. Rebound, Its Nature and Effect on Engineering Works. Q. J. Eng. Geol. 1980, 13, 133–152. [Google Scholar] [CrossRef]
- Bekendam, R.F.; Pottgens, J.J. Ground Movements over the Coal Mines of Southern Limburg, the Netherlands, and Their Relation to Rising Mine Waters. Subsid. Proc. Int. Symp. Hague 1995, 234, 3–12. [Google Scholar] [CrossRef]
- Caro Cuenca, M.; Hanssen, R.F. Subsidence and Uplift at Wassenberg, Germany Due to Coal Mining Using Persistent Scatterer Interferometry. In Proceedings of the 13th FIG International Symposium on Deformation Measurements and Analysis, Lisbon, Portugal, 12–15 May 2008; pp. 1–9. [Google Scholar]
- Caro Cuenca, M.; Hooper, A.J.; Hanssen, R.F. Surface Deformation Induced by Water Influx in the Abandoned Coal Mines in Limburg, The Netherlands Observed by Satellite Radar Interferometry. J. Appl. Geophys. 2013, 88, 1–11. [Google Scholar] [CrossRef]
- Bateson, L.; Cigna, F.; Boon, D.; Sowter, A. The Application of the Intermittent SBAS (ISBAS) InSAR Method to the South Wales Coalfield, UK. Int. J. Appl. Earth Obs. Geoinf. 2015, 34, 249–257. [Google Scholar] [CrossRef]
- Samsonov, S.; D’Oreye, N.; Smets, B. Ground Deformation Associated with Post-Mining Activity at the French-German Border Revealed by Novel InSAR Time Series Method. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 142–154. [Google Scholar] [CrossRef]
- Vervoort, A.; Declercq, P.Y. Surface Movement above Old Coal Longwalls after Mine Closure. Int. J. Min. Sci. Technol. 2017, 27, 481–490. [Google Scholar] [CrossRef]
- Blachowski, J.; Kopec, A.; Milczarek, W.; Owczarz, K. Evolution of Secondary Deformations Captured by Satellite Radar Interferometry: Case Study of an Abandoned Coal Basin in SW Poland. Sustainability 2019, 11, 884. [Google Scholar] [CrossRef]
- Svigkas, N.; Papoutsis, I.; Constantinos, L.; Tsangaratos, P.; Kiratzi, A.; Kontoes, C.H. Land Subsidence Rebound Detected via Multi-Temporal InSAR and Ground Truth Data in Kalochori and Sindos Regions, Northern Greece. Eng. Geol. 2016, 209, 175–186. [Google Scholar] [CrossRef]
- Chen, C.T.; Hu, J.C.; Lu, C.Y.; Lee, J.C.; Chan, Y.C. Thirty-Year Land Elevation Change from Subsidence to Uplift Following the Termination of Groundwater Pumping and Its Geological Implications in the Metropolitan Taipei Basin, Northern Taiwan. Eng. Geol. 2007, 95, 30–47. [Google Scholar] [CrossRef]
- Ishitsuka, K.; Fukushima, Y.; Tsuji, T.; Yamada, Y.; Matsuoka, T.; Giao, P.H. Natural Surface Rebound of the Bangkok Plain and Aquifer Characterization by Persistent Scatterer Interferometry. Geochem. Geophys. Geosyst. 2014, 15, 965–974. [Google Scholar] [CrossRef]
- Galloway, D.L.; Hoffmann, J. The Application of Satellite Differential SAR Interferometry-Derived Ground Displacements in Hydrogeology. Hydrogeol. J. 2007, 15, 133–154. [Google Scholar] [CrossRef]
- Strozzi, T.; Delaloye, R.; Poffet, D.; Hansmann, J.; Loew, S. Surface Subsidence and Uplift above a Headrace Tunnel in Metamorphic Basement Rocks of the Swiss Alps as Detected by Satellite SAR Interferometry. Remote Sens. Environ. 2011, 115, 1353–1360. [Google Scholar] [CrossRef]
- Zhao, C.; Liu, C.; Zhang, Q.; Lu, Z.; Yang, C. Deformation of Linfen-Yuncheng Basin (China) and Its Mechanisms Revealed by Π-RATE InSAR Technique. Remote Sens. Environ. 2018, 218, 221–230. [Google Scholar] [CrossRef]
- Malinowska, A.A.; Witkowski, W.T.; Hejmanowski, R.; Chang, L.; van Leijen, F.J.; Hanssen, R.F. Sinkhole Occurrence Monitoring Over Shallow Abandoned Coal Mines with Satellite-Based Persistent Scatterer Interferometry. Eng. Geol. 2019, 262, 105336. [Google Scholar] [CrossRef]
- Pawluszek-Filipiak, K.; Borkowski, A. Integration of DInSAR and SBAS Techniques to Determine Mining-Related Deformations Using Sentinel-1 Data: The Case Study of Rydultowy Mine in Poland. Remote Sens. 2020, 12, 242. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry, Data Interpretation and Error Analysis; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent Scatterers in SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Hooper, A.; Bekaert, D.; Spaans, K.; Arikan, M. Recent Advances in SAR Interferometry Time Series Analysis for Measuring Crustal Deformation. In Tectonophysics; Elsevier: Amsterdam, The Netherlands, 2012; pp. 1–13. [Google Scholar] [CrossRef]
- Hooper, A.; Zebker, H.; Segall, P.; Kampes, B. A New Method for Measuring Deformation on Volcanoes and Other Natural Terrains Using InSAR Persistent Scatterers. Geophys. Res. Lett. 2004, 31, 1–5. [Google Scholar] [CrossRef]
- Crosetto, M.; Monserrat, O.; Cuevas-González, M.; Devanthéry, N.; Crippa, B. Persistent Scatterer Interferometry: A Review. ISPRS J. Photogramm. Remote Sens. 2016, 115, 78–89. [Google Scholar] [CrossRef]
- Kisielewski, F. Polish Geological Institute—National Research Institute. Available online: https://www.pgi.gov.pl/ (accessed on 14 March 2020).
- Oszczepalski, S.; Speczik, S.; Zieliński, K.; Chmielewski, A. The Kupferschiefer Deposits and Prospects in SW Poland: Past, Present and Future. Minerals 2019, 9, 592. [Google Scholar] [CrossRef]
- Wilk, Z.; Bocheńska, T. Hydrogeology of Polish Mineral Deposit and Mining Water Problems, 2nd ed.; AGH Uczelniane Wydawnictwa Naukowo-Dydaktyczne: Cracow, Poland, 2003. [Google Scholar]
- Downorowicz, S. Hydrogeological Problems of Copper Ore Mining, Mine Water Inflow Rates. Rudy Met. 2005, No. 3, 126–130. [Google Scholar]
- Głowacki, T. Prediction of Vertical Displacements on “KONRAD” Mining Ground in Iwiny (SW Poland). Min. Sci. 2010, 128, 50–51. [Google Scholar]
- Milczarek, W.; Głowacki, T. Secondary Surface Deformations of Former Mining Areas. Min. Sci. 2013, 20, 39–55. [Google Scholar] [CrossRef]
- Sousa, J.J.; Hooper, A.J.; Hanssen, R.F.; Bastos, L.C.; Ruiz, A.M. Persistent Scatterer InSAR: A Comparison of Methodologies Based on a Model of Temporal Deformation vs. Spatial Correlation Selection Criteria. Remote Sens. Environ. 2011, 115, 2652–2663. [Google Scholar] [CrossRef]
- Samieie-Esfahany, S.; Hanssen, R.F.; Thienen-visser, K.; Muntendam-bos, A. On the Effect of Horizontal Deformation on InSAR Subsidence Estimates. Proc. Fringe Work. 2010, 2009, 1–7. [Google Scholar]
- Foumelis, M.; Blasco, J.M.D.; Desnos, Y.L.; Engdahl, M.; Fernández, D.; Veci, L.; Lu, J.; Wong, C. ESA SNAP—Stamps Integrated Processing for Sentinel-1 Persistent Scatterer Interferometry. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 22–27 July 2018; pp. 1364–1367. [Google Scholar] [CrossRef]
- Freeze, R.A.; Cherry, A.J. Groundwater; Prentice-Hall: Englewood Cliffs, NJ, USA, 1979. [Google Scholar]
- Bonì, R.; Cigna, F.; Bricker, S.; Meisina, C.; McCormack, H. Characterisation of Hydraulic Head Changes and Aquifer Properties in the London Basin Using Persistent Scatterer Interferometry Ground Motion Data. J. Hydrol. 2016, 540, 835–849. [Google Scholar] [CrossRef]
- Bonì, R.; Meisina, C.; Cigna, F.; Herrera, G.; Notti, D.; Bricker, S.; McCormack, H.; Tomás, R.; Béjar-Pizarro, M.; Mulas, J.; et al. Exploitation of Satellite A-DInSAR Time Series for Detection, Characterization and Modelling of Land Subsidence. Geosciences 2017, 7, 25. [Google Scholar] [CrossRef]
- Sroka, A.; Hejmanowski, R. Subsidence Prediction Caused by the Oil and Gas Development. In Proceedings of the 3rd IAG/12th FIG Symposium, Baden, Germany, 22–24 May 2006. [Google Scholar]
| Geometry | Track | Master Acquisition | Timespan | Perpendicular Baseline (m) | No. of Interferograms |
|---|---|---|---|---|---|
| Ascending | 73 | 22/03/2017 | 15/11/2014–27/07/2018 | −101–+113 | 145 |
| Descending | 22 | 25/03/2017 | 06/12/2014–30/07/2018 | −148–+89 | 154 |
| Borehole | Thickness of the Drained Rock Mass (m) | Observed Land Uplift (mm) | Compressibility Factor Cf (Dimensionless) |
|---|---|---|---|
| G-1 | 111.5 | 73 | 6.55 × 10−4 |
| U-93 | 131.0 | 66 | 5.04 × 10−4 |
| U-21B | 56.8 | 32 | 5.63 × 10−4 |
| Al-16 | 24.0 | 12 | 5.00 × 10−4 |
| Borehole | Thickness of the Drained Rock Mass (m) | Observed Land Uplift (mm) | Refill Fraction of the Drained Rock Mass (m) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2015 | 2016 | 2017 | 2018 | ∑ | 2015 | 2016 | 2017 | 2018 | ∑ | ||
| LU-36 | 215 | 3 | 18 | 28 | 21 | 70 | 5 | 32 | 50 | 38 | 126 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malinowska, A.A.; Witkowski, W.T.; Guzy, A.; Hejmanowski, R. Satellite-Based Monitoring and Modeling of Ground Movements Caused by Water Rebound. Remote Sens. 2020, 12, 1786. https://doi.org/10.3390/rs12111786
Malinowska AA, Witkowski WT, Guzy A, Hejmanowski R. Satellite-Based Monitoring and Modeling of Ground Movements Caused by Water Rebound. Remote Sensing. 2020; 12(11):1786. https://doi.org/10.3390/rs12111786
Chicago/Turabian StyleMalinowska, Agnieszka A., Wojciech T. Witkowski, Artur Guzy, and Ryszard Hejmanowski. 2020. "Satellite-Based Monitoring and Modeling of Ground Movements Caused by Water Rebound" Remote Sensing 12, no. 11: 1786. https://doi.org/10.3390/rs12111786
APA StyleMalinowska, A. A., Witkowski, W. T., Guzy, A., & Hejmanowski, R. (2020). Satellite-Based Monitoring and Modeling of Ground Movements Caused by Water Rebound. Remote Sensing, 12(11), 1786. https://doi.org/10.3390/rs12111786








