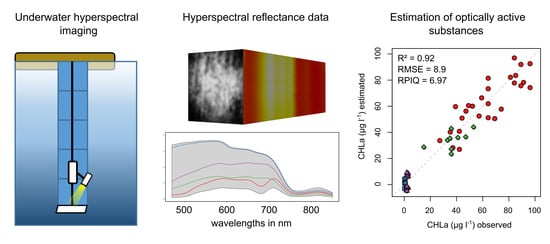
Underwater Use of a Hyperspectral Camera to Estimate Optically Active Substances in the Water Column of Freshwater Lakes
Abstract
1. Introduction
2. Materials and Methods
2.1. Hyperspectral Snapshot Camera
2.2. Laboratory Experiment
2.3. Field Campaign
2.4. CHLa and CDOM Reference Analysis
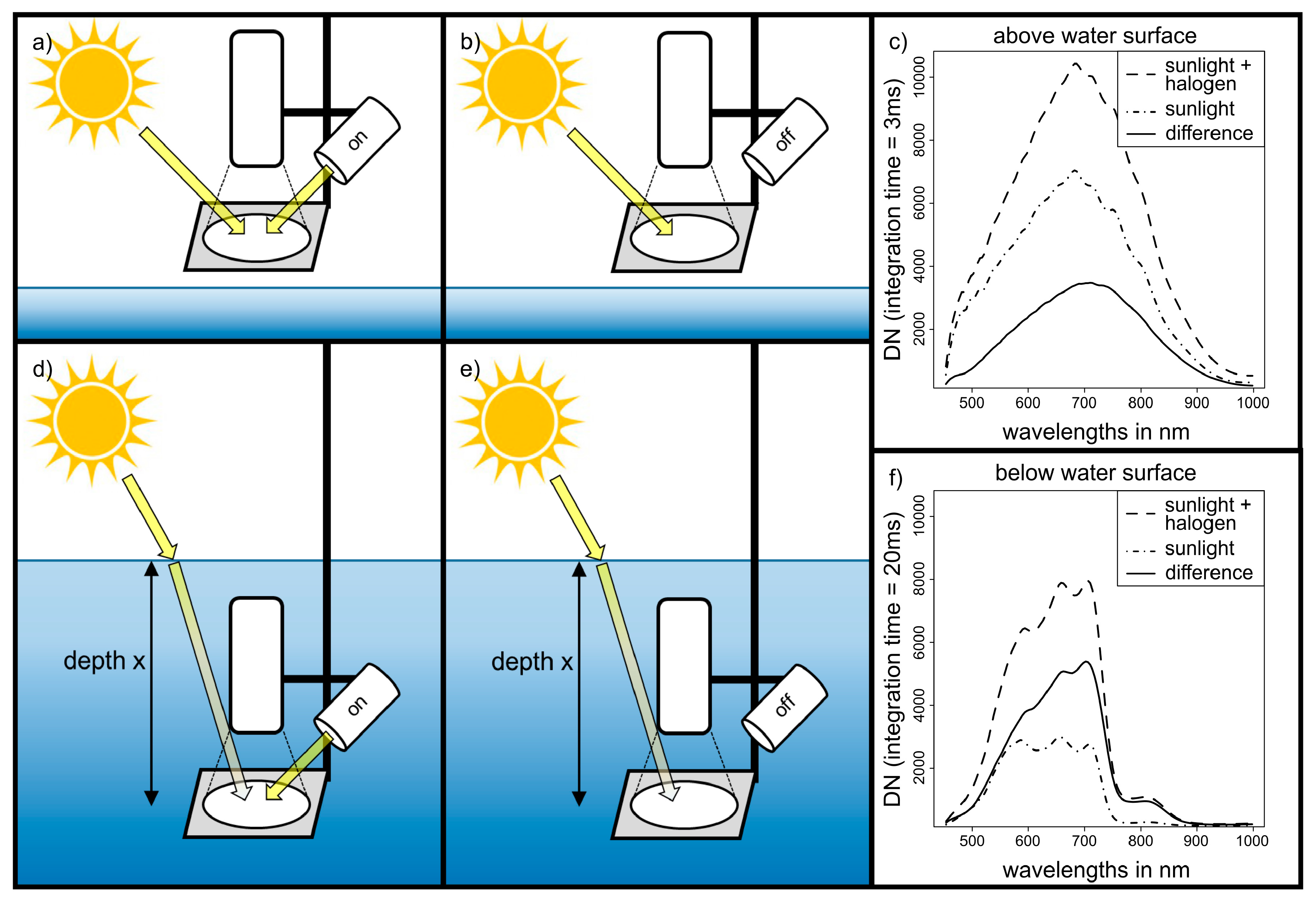
2.5. Hyperspectral Image Acquisition and Processing
2.6. Predictive Modeling of CHLa and CDOM
3. Results and Discussion
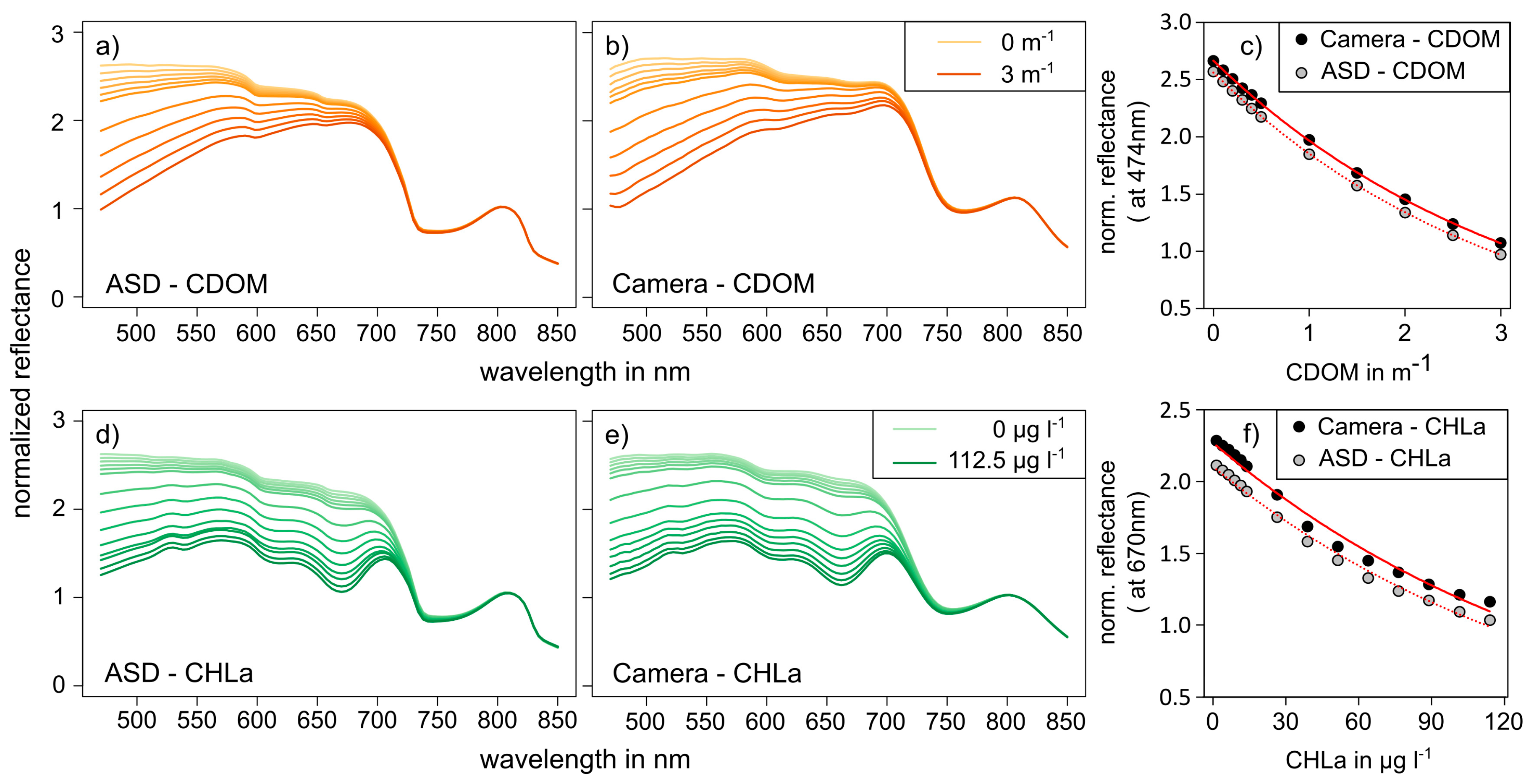
3.1. Laboratory Experiment
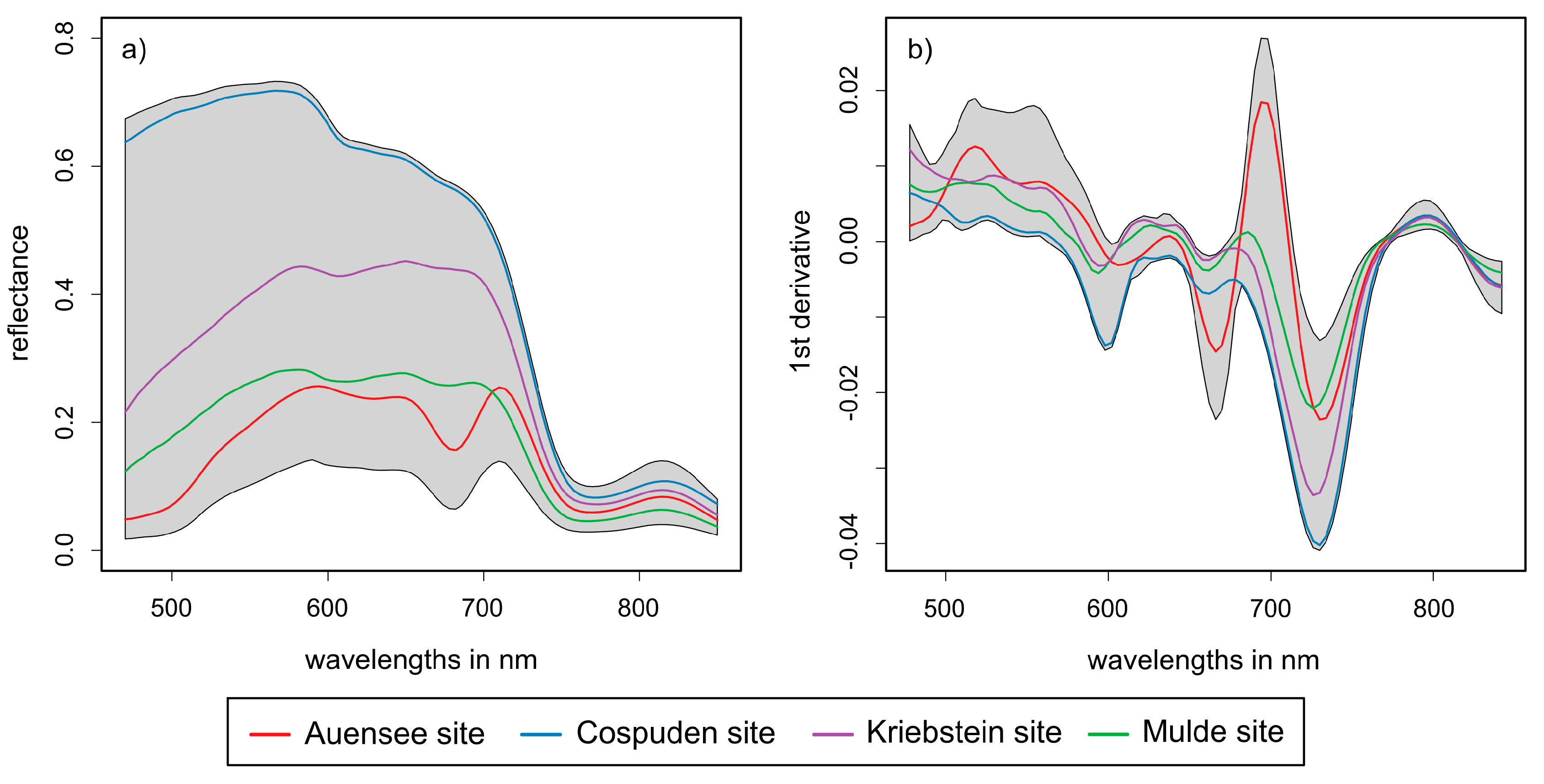
3.2. Water Quality Characteristics of the Investigated Lakes
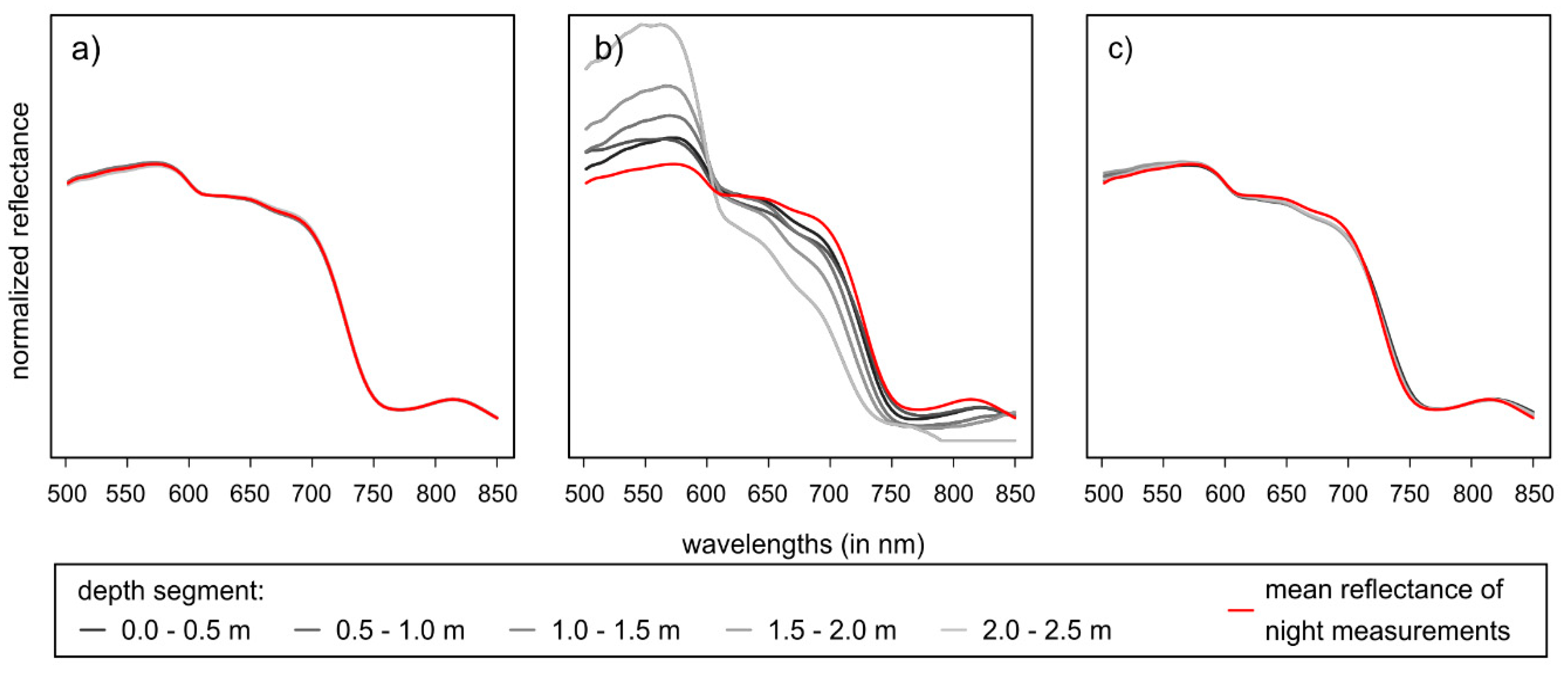
3.3. Validation of Ambient Light Compensation
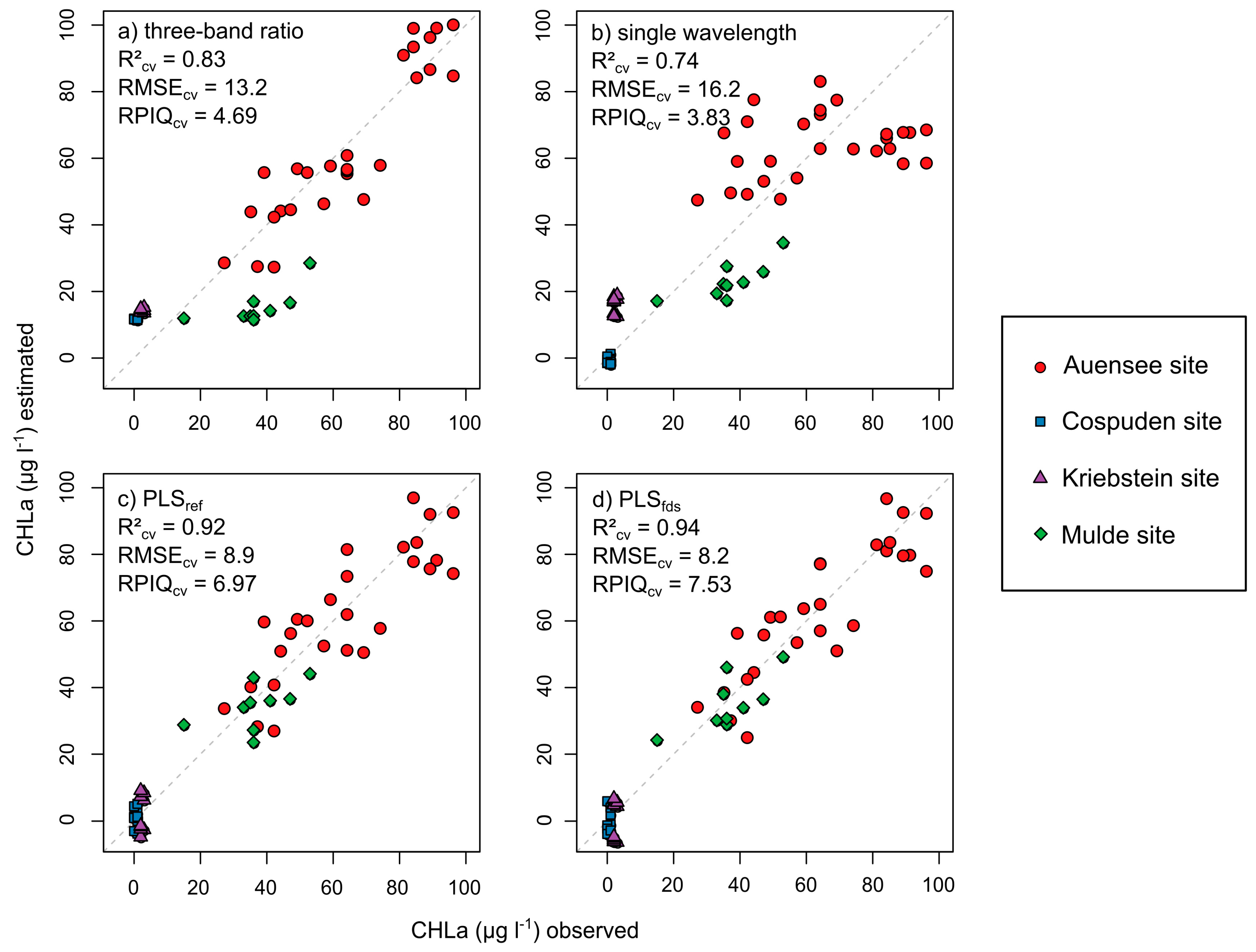
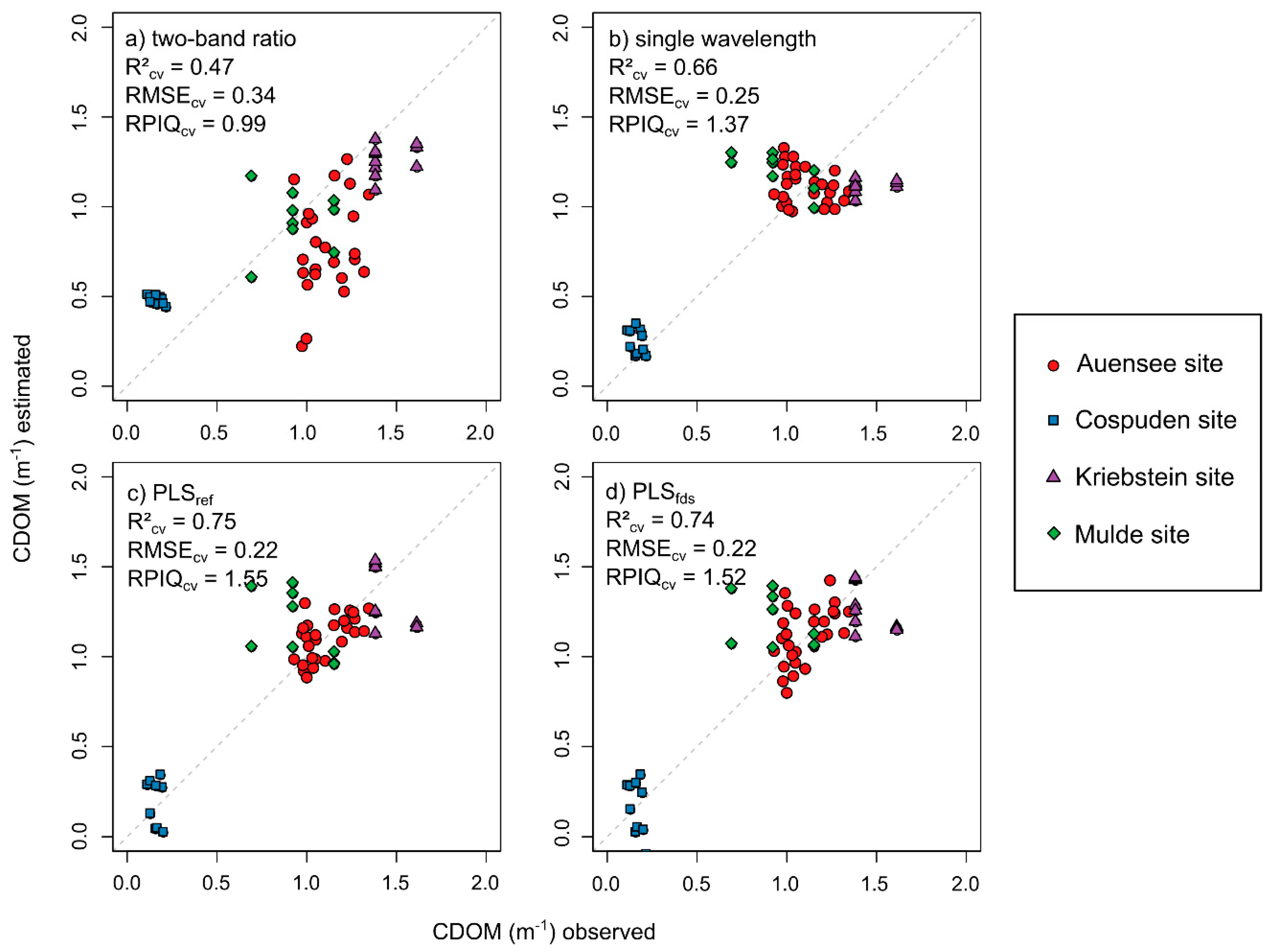
3.4. Predictive Modeling of CHLa and CDOM
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Aylward, B.; Bandyopadhyay, J.; Belausteguigotia, J.-C.; Börkey, P.; Cassar, A.; Meadors, L.; Saade, L.; Siebentritt, M.; Stein, R.; Tognetti, S.; et al. Freshwater ecosystem services. In Millenium Ecosystem Assessment: Ecosystems and Human Well-Being: Policy Responses; Chopra, K., Leemans, R., Kumar, P., Simons, H., Eds.; Island Press: Washington, DC, USA, 2005; pp. 213–255. [Google Scholar]
- Schallenberg, M.; de Winton, M.D.; Verburg, P.; Kelly, D.J.; Hamill, K.D.; Hamilton, D.P. Ecosystem services of lakes. In Ecosystem Services in New Zealand–Conditions and Trends; Dymond, J.R., Ed.; Whenua Press: Lincoln, New Zealand, 2013; pp. 203–225. [Google Scholar]
- Carpenter, S.R.; Stanley, E.H.; Zanden, M.J.V. State of the World’s Freshwater Ecosystems: Physical, Chemical, and Biological Changes. Annu. Rev. Environ. Resour. 2011, 36, 75–99. [Google Scholar] [CrossRef]
- Dörnhöfer, K.; Oppelt, N. Remote sensing for lake research and monitoring – Recent advances. Ecol. Indic. 2016, 64, 105–122. [Google Scholar] [CrossRef]
- Gholizadeh, M.H.; Melesse, A.; Reddi, L.N. A Comprehensive Review on Water Quality Parameters Estimation Using Remote Sensing Techniques. Sensors 2016, 16, 1298. [Google Scholar] [CrossRef]
- Odermatt, D.; Gitelson, A.; Brando, V.; Schaepman, M.E. Review of constituent retrieval in optically deep and complex waters from satellite imagery. Remote Sens. Environ. 2012, 118, 116–126. [Google Scholar] [CrossRef]
- Giardino, C.; Brando, V.; Gege, P.; Pinnel, N.; Hochberg, E.; Knaeps, E.; Reusen, I.; Doerffer, R.; Bresciani, M.; Braga, F.; et al. Imaging Spectrometry of Inland and Coastal Waters: State of the Art, Achievements and Perspectives. Surv. Geophys. 2018, 40, 401–429. [Google Scholar] [CrossRef]
- Matthews, M. A current review of empirical procedures of remote sensing in inland and near-coastal transitional waters. Int. J. Remote Sens. 2011, 32, 6855–6899. [Google Scholar] [CrossRef]
- Palmer, S.; Kutser, T.; Hunter, P.D. Remote sensing of inland waters: Challenges, progress and future directions. Remote Sens. Environ. 2015, 157, 1–8. [Google Scholar] [CrossRef]
- Matthews, M.; Bernard, S. Characterizing the Absorption Properties for Remote Sensing of Three Small Optically-Diverse South African Reservoirs. Remote Sens. 2013, 5, 4370–4404. [Google Scholar] [CrossRef]
- Bernardo, N.; Watanabe, F.; Rodrigues, T.; Alcantara, E. Atmospheric correction issues for retrieving total suspended matter concentrations in inland waters using OLI/Landsat-8 image. Adv. Space Res. 2017, 59, 2335–2348. [Google Scholar] [CrossRef]
- Moses, W.J.; Sterckx, S.; Montes, M.J.; Keukelaere, L.D.; Knaeps, E. Atmospheric correction for inland waters. In Bio-Optical Modeling and Remote Sensing of Inland Waters, 1st ed.; Deepak, M., Ogashawara, I., Gitelson, A., Eds.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 69–100. [Google Scholar]
- Mouw, C.B.; Greb, S.; Aurin, D.; Digiacomo, P.M.; Lee, Z.; Twardowski, M.; Binding, C.; Hu, C.; Ma, R.; Moore, T.; et al. Aquatic color radiometry remote sensing of coastal and inland waters: Challenges and recommendations for future satellite missions. Remote Sens. Environ. 2015, 160, 15–30. [Google Scholar] [CrossRef]
- Sterckx, S.; Knaeps, E.; Ruddick, K. Detection and correction of adjacency effects in hyperspectral airborne data of coastal and inland waters: The use of the near infrared similarity spectrum. Int. J. Remote Sens. 2011, 32, 6479–6505. [Google Scholar] [CrossRef]
- Kutser, T.; Metsamaa, L.; Dekker, A. Influence of the vertical distribution of cyanobacteria in the water column on the remote sensing signal. Estuar. Coast. Shelf Sci. 2008, 78, 649–654. [Google Scholar] [CrossRef]
- Pitarch, J.; Odermatt, D.; Kawka, M.; Wüest, A. Retrieval of vertical particle concentration profiles by optical remote sensing: A model study. Opt. Express 2014, 22, A947–A959. [Google Scholar] [CrossRef] [PubMed]
- Xue, K.; Zhang, Y.; Duan, H.; Ma, R.; Loiselle, S.A.; Zhang, M. A Remote Sensing Approach to Estimate Vertical Profile Classes of Phytoplankton in a Eutrophic Lake. Remote Sens. 2015, 7, 14403–14427. [Google Scholar] [CrossRef]
- Xue, K.; Zhang, Y.; Ma, R.; Duan, H. An approach to correct the effects of phytoplankton vertical nonuniform distribution on remote sensing reflectance of cyanobacterial bloom waters. Limnol. Oceanogr. Methods 2017, 15, 302–319. [Google Scholar] [CrossRef]
- Leach, T.H.; Beisner, B.; Carey, C.C.; Pernica, P.; Rose, K.C.; Huot, Y.; Brentrup, J.A.; Domaizon, I.; Grossart, H.-P.; Ibelings, B.W.; et al. Patterns and drivers of deep chlorophyll maxima structure in 100 lakes: The relative importance of light and thermal stratification. Limnol. Oceanogr. 2017, 63, 628–646. [Google Scholar] [CrossRef]
- Duan, W.; He, B.; Chen, Y.; Zou, S.; Wang, Y.; Nover, D.; Chen, W.; Yang, G. Identification of long-term trends and seasonality in high-frequency water quality data from the Yangtze River basin, China. PLoS ONE 2018, 13. [Google Scholar] [CrossRef]
- Keller, S.; Maier, P.M.; Riese, F.; Norra, S.; Holbach, A.; Börsig, N.; Wilhelms, A.; Moldaenke, C.; Zaake, A.; Hinz, S. Hyperspectral Data and Machine Learning for Estimating CDOM, Chlorophyll a, Diatoms, Green Algae and Turbidity. Int. J. Environ. Res. Public Heal. 2018, 15, 1881. [Google Scholar] [CrossRef]
- Kwon, Y.S.; Pyo, J.; Duan, H.; Cho, K.H.; Park, Y.; Kwon, Y.-H. Drone-based hyperspectral remote sensing of cyanobacteria using vertical cumulative pigment concentration in a deep reservoir. Remote Sens. Environ. 2020, 236, 111517. [Google Scholar] [CrossRef]
- Greb, S.; Odermatt, D.; Schaeffer, B.A.; Spyrakos, E.; Wang, M. Complementarity of in situ and satellite measurements. In Earth Observations in Support of Global Water Quality Monitoring; Greb, S., Dekker, A., Binding, C., Eds.; IOCCG: Dartmouth, NS, Canada, 2018; pp. 29–42. [Google Scholar]
- Kutser, T.; Paavel, B.; Verpoorter, C.; Ligi, M.; Soomets, T.; Toming, K.; Casal, G. Remote Sensing of Black Lakes and Using 810 nm Reflectance Peak for Retrieving Water Quality Parameters of Optically Complex Waters. Remote Sens. 2016, 8, 497. [Google Scholar] [CrossRef]
- Pyo, J.; Ligaray, M.V.; Kwon, Y.; Ahn, M.-H.; Kim, K.; Lee, H.; Kang, T.; Cho, S.B.; Park, Y.; Cho, K.H. High-Spatial Resolution Monitoring of Phycocyanin and Chlorophyll-a Using Airborne Hyperspectral Imagery. Remote Sens. 2018, 10, 1180. [Google Scholar] [CrossRef]
- Abd-Elrahman, A.; Croxton, M.; Pande-Chettri, R.; Toor, G.S.; Smith, S.E.; Hill, J. In situ estimation of water quality parameters in freshwater aquaculture ponds using hyperspectral imaging system. ISPRS J. Photogramm. Remote Sens. 2011, 66, 463–472. [Google Scholar] [CrossRef]
- Wagner, A.; Hilgert, S.; Kattenborn, T.; Fuchs, S. Proximal VIS-NIR spectrometry to retrieve substance concentrations in surface waters using partial least squares modelling. Water Supply 2018, 19, 1204–1211. [Google Scholar] [CrossRef]
- Jung, A.; Vohland, M.; Thiele-Bruhn, S. Use of A Portable Camera for Proximal Soil Sensing with Hyperspectral Image Data. Remote Sens. 2015, 7, 11434–11448. [Google Scholar] [CrossRef]
- Mobley, C.D. Estimation of the remote-sensing reflectance from above-surface measurements. Appl. Opt. 1999, 38, 7442–7455. [Google Scholar] [CrossRef]
- Dunker, S.; Nadrowski, K.; Jakob, T.; Kasprzak, P.; Becker, A.; Langner, U.; Kunath, C.; Harpole, S.; Wilhelm, C. Assessing in situ dominance pattern of phytoplankton classes by dominance analysis as a proxy for realized niches. Harmful Algae 2016, 58, 74–84. [Google Scholar] [CrossRef]
- Abel, A.; Michael, A.; Zartl, A.; Werner, F. Impact of erosion-transported overburden dump materials on water quality in Lake Cospuden evolved from a former open cast lignite mine south of Leipzig, Germany. Environ. Earth Sci. 2000, 39, 683–688. [Google Scholar] [CrossRef]
- ISO 10260. Water Quality—Measurement of Biochemical Parameters—Spectrometric Determination of the Chlorophyll-A Concentration; International Organization for Standardization: Geneva, Switzerland, 1992. [Google Scholar]
- Mannino, A.; Novak, M.G.; Nelson, N.B.; Belz, M.; Berthon, J.-F.; Blough, N.V.; Boss, E.; Bricaud, A.; Chaves, J.; del Castillo, C.; et al. Measurement protocol of absorption by chromophoric dissolved organic matter (CDOM) and other dissolved materials (DRAFT). In Inherent Optical Property Measurements and Protocols: Absorption Coefficient; Mannino, A., Novak, M.G., Eds.; IOCCG: Dartmouth, NS, Canada, 2019; pp. 22–27. [Google Scholar]
- Gitelson, A.A.; Gritz, Y.; Merzlyak, M.N. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef]
- Han, L.; Rundquist, D.C. Comparison of NIR/RED ratio and first derivative of reflectance in estimating algal-chlorophyll concentration: A case study in a turbid reservoir. Remote Sens. Environ. 1997, 62, 253–261. [Google Scholar] [CrossRef]
- Ficek, D.; Zapadka, T.; Dera, J. Remote sensing reflectance of Pomeranian lakes and the Baltic. Oceanologia 2011, 53, 959–970. [Google Scholar] [CrossRef]
- Zhu, W.; Yu, Q.; Tian, Y.; Becker, B.L.; Zheng, T.; Carrick, H.J. An assessment of remote sensing algorithms for colored dissolved organic matter in complex freshwater environments. Remote Sens. Environ. 2014, 140, 766–778. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Ali, K.A.; Ortiz, J.D. Multivariate approach for chlorophyll-a and suspended matter retrievals in Case II type waters using hyperspectral data. Hydrol. Sci. J. 2015, 61, 200–213. [Google Scholar] [CrossRef]
- Ryan, K.; Ali, K. Application of a partial least-squares regression model to retrieve chlorophyll-a concentrations in coastal waters using hyper-spectral data. Ocean Sci. J. 2016, 51, 209–221. [Google Scholar] [CrossRef]
- Song, K.; Li, L.; Tedesco, L.; Li, S.; Duan, H.; Liu, D.; Hall, B.; Du, J.; Li, Z.; Shi, K.; et al. Remote estimation of chlorophyll-a in turbid inland waters: Three-band model versus GA-PLS model. Remote Sens. Environ. 2013, 136, 342–357. [Google Scholar] [CrossRef]
- Wang, Z.; Kawamura, K.; Sakuno, Y.; Fan, X.; Gong, Z.; Lim, J. Retrieval of Chlorophyll-a and Total Suspended Solids Using Iterative Stepwise Elimination Partial Least Squares (ISE-PLS) Regression Based on Field Hyperspectral Measurements in Irrigation Ponds in Higashihiroshima, Japan. Remote Sens. 2017, 9, 264. [Google Scholar] [CrossRef]
- Helms, J.; Stubbins, A.; Ritchie, J.D.; Minor, E.C.; Kieber, D.J.; Mopper, K. Absorption spectral slopes and slope ratios as indicators of molecular weight, source, and photobleaching of chromophoric dissolved organic matter. Limnol. Oceanogr. 2008, 53, 955–969. [Google Scholar] [CrossRef]
- Strömbeck, N.; Pierson, D. The effects of variability in the inherent optical properties on estimations of chlorophyll a by remote sensing in Swedish freshwaters. Sci. Total Environ. 2001, 268, 123–137. [Google Scholar] [CrossRef]
- Twardowski, M.S.; Boss, E.; Sullivan, J.M.; Donaghay, P.L. Modeling the spectral shape of absorption by chromophoric dissolved organic matter. Mar. Chem. 2004, 89, 69–88. [Google Scholar] [CrossRef]
- Defoin-Platel, M.; Chami, M. How ambiguous is the inverse problem of ocean color in coastal waters? J. Geophys. Res. Space Phys. 2007, 112, 843. [Google Scholar] [CrossRef]
- Brezonik, P.L.; Olmanson, L.G.; Finlay, J.C.; Bauer, M.E. Factors affecting the measurement of CDOM by remote sensing of optically complex inland waters. Remote Sens. Environ. 2015, 157, 199–215. [Google Scholar] [CrossRef]
- Duan, H.; Ma, R.; Xu, J.; Zhang, Y.; Zhang, B. Comparison of different semi-empirical algorithms to estimate chlorophyll-a concentration in inland lake water. Environ. Monit. Assess. 2009, 170, 231–244. [Google Scholar] [CrossRef] [PubMed]
- Cheng, C.; Wei, Y.; Sun, X.; Zhou, Y. Estimation of Chlorophyll-a Concentration in Turbid Lake Using Spectral Smoothing and Derivative Analysis. Int. J. Environ. Res. Public Heal. 2013, 10, 2979–2994. [Google Scholar] [CrossRef] [PubMed]
- Shao, T.; Song, K.; Du, J.; Zhao, Y.; Liu, Z.; Zhang, B. Retrieval of CDOM and DOC Using In Situ Hyperspectral Data: A Case Study for Potable Waters in Northeast China. J. Indian Soc. Remote Sens. 2015, 44, 77–89. [Google Scholar] [CrossRef]
- Babin, M.; Stramski, D.; Ferrari, G.M.; Claustre, H.; Bricaud, A.; Obolensky, G.; Hoepffner, N. Variations in the light absorption coefficients of phytoplankton, nonalgal particles, and dissolved organic matter in coastal waters around Europe. J. Geophys. Res. Space Phys. 2003, 108, 3211. [Google Scholar] [CrossRef]
- Nouchi, V.; Odermatt, D.; Wüest, A.; Bouffard, D. Effects of non-uniform vertical constituent profiles on remote sensing reflectance of oligo- to mesotrophic lakes. Eur. J. Remote Sens. 2018, 51, 808–821. [Google Scholar] [CrossRef]
- Göritz, A.; Berger, S.A.; Gege, P.; Grossart, H.-P.; Nejstgaard, J.C.; Riedel, S.; Röttgers, R.; Utschig, C. Retrieval of Water Constituents from Hyperspectral In-Situ Measurements under Variable Cloud Cover—A Case Study at Lake Stechlin (Germany). Remote Sens. 2018, 10, 181. [Google Scholar] [CrossRef]
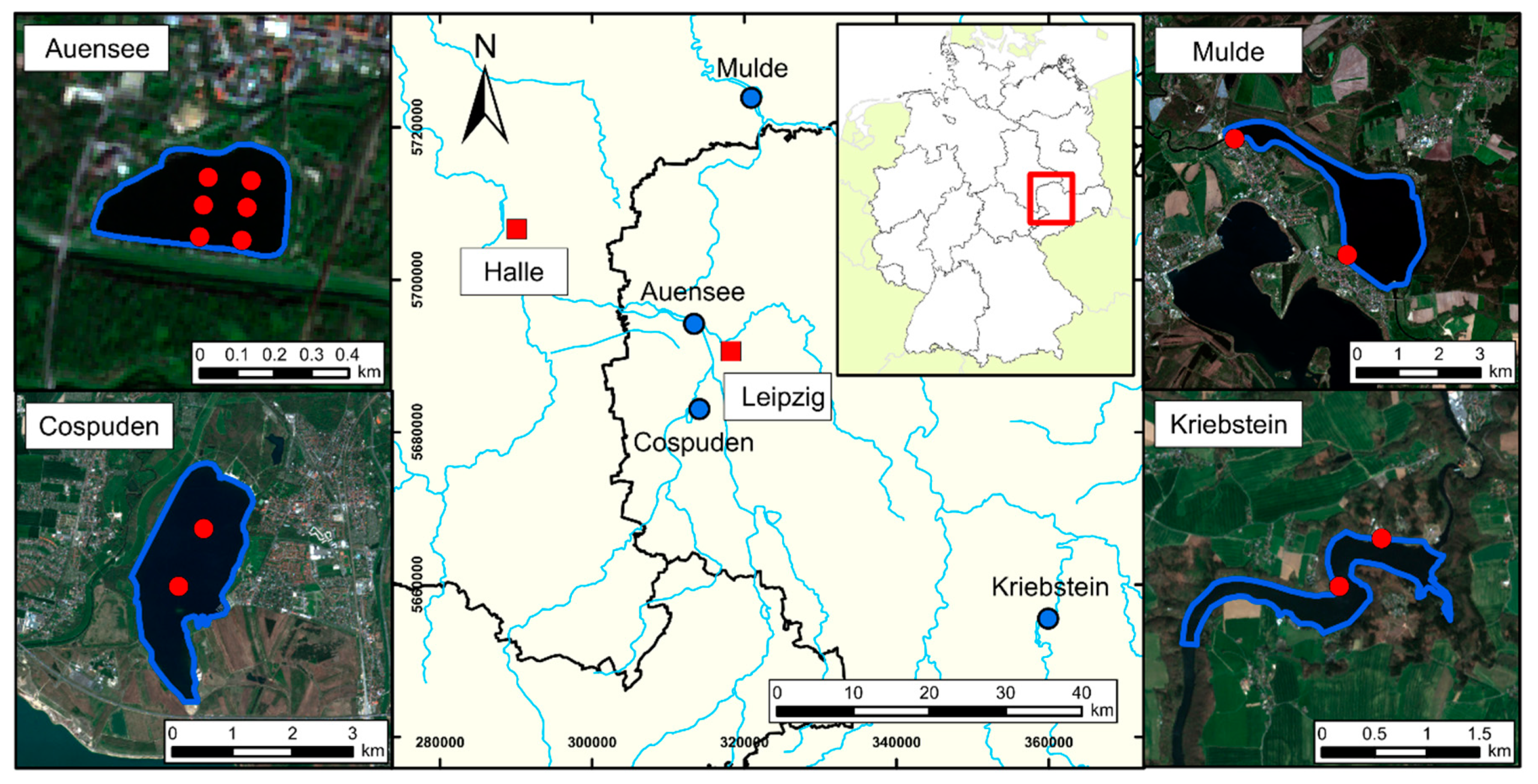


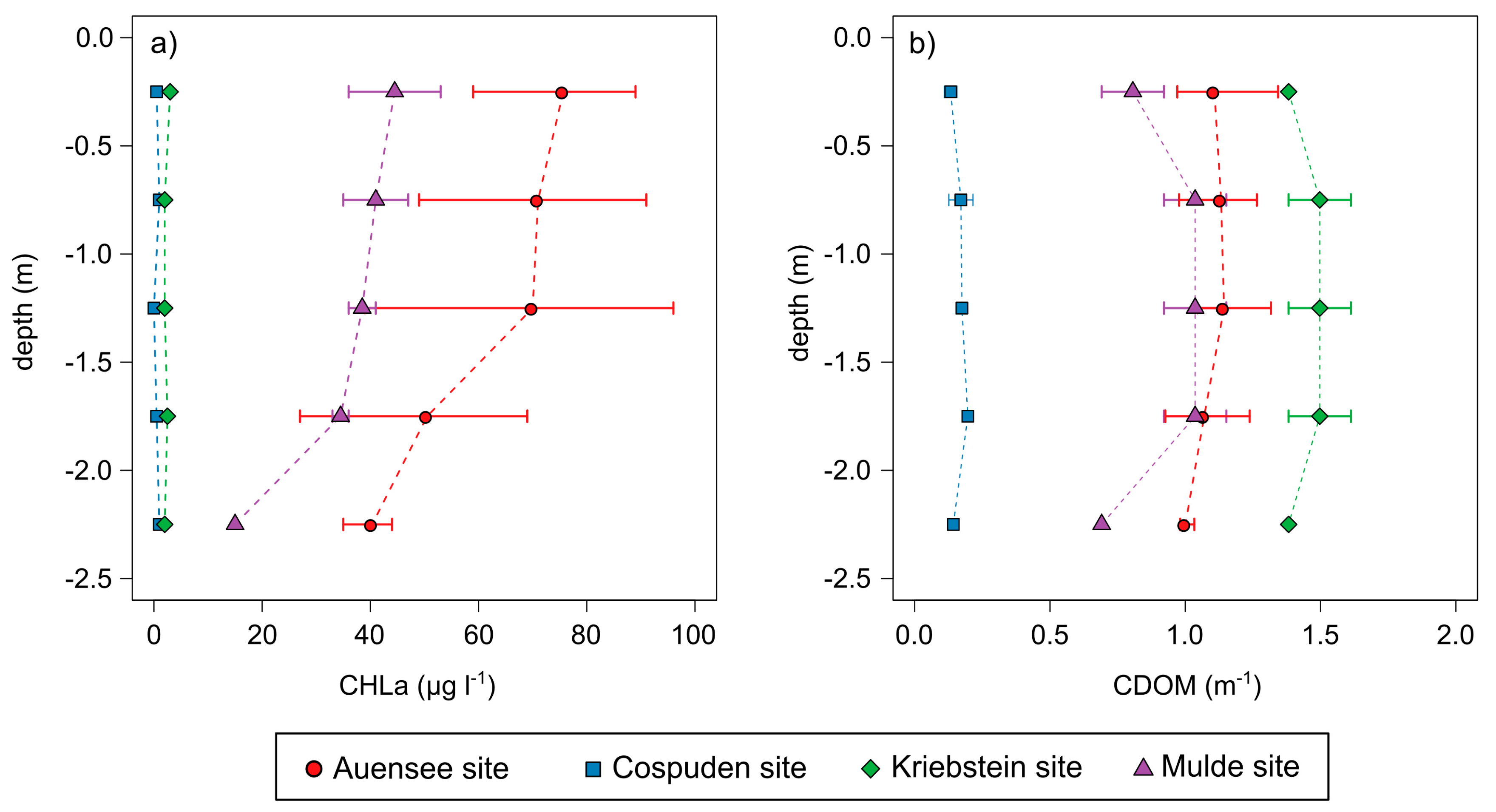
| Site | Area (ha) | Trophic State Index | Type | Secchi Depth * (m) | Number of Sampling Points | Number of Sampling Units |
|---|---|---|---|---|---|---|
| Auensee | 12 | Eutrophic/hypereutrophic | Former gravel pit | 0.40–0.65 | 6 | 27 |
| Cospuden | 436 | Oligotrophic | Former open cast mine | 6.00–6.05 | 2 | 10 |
| Kriebstein | 132 | Oligotrophic | Reservoir | 2.35–2.45 | 2 | 10 |
| Mulde | 630 | Mesoeutrophic | Reservoir | 1.25–1.30 | 2 | 9 |
| OAS | Site | n | Min | Q1 | Q2 | Q3 | Max | Mean | sd |
|---|---|---|---|---|---|---|---|---|---|
| CHLa | all | 56 | 0 | 2 | 37 | 64 | 96 | 37.2 | 32.2 |
| Auensee | 27 | 27 | 46 | 64 | 84 | 96 | 63.9 | 20.9 | |
| Cospuden | 10 | 0 | 0 | 1 | 1 | 1 | 0.6 | 0.5 | |
| Kriebstein | 10 | 2 | 2 | 2 | 3 | 3 | 2.3 | 0.5 | |
| Mulde | 9 | 15 | 35 | 36 | 41 | 53 | 36.9 | 10.5 | |
| CDOM | all | 56 | 0.1 | 0.9 | 1.0 | 1.3 | 1.6 | 0.97 | 0.43 |
| Auensee | 27 | 0.9 | 1.0 | 1.0 | 1.2 | 1.3 | 1.10 | 0.12 | |
| Cospuden | 10 | 0.1 | 0.1 | 0.2 | 0.2 | 0.2 | 0.16 | 0.03 | |
| Kriebstein | 10 | 1.4 | 1.4 | 1.4 | 1.6 | 1.6 | 1.45 | 0.11 | |
| Mulde | 9 | 0.7 | 0.9 | 0.9 | 1.2 | 1.2 | 0.95 | 0.18 |
| Site | Three-Band Ratio | Single Wavelength | PLSref | PLSfds |
|---|---|---|---|---|
| Auensee (63.9) * | 9.52 | 19.86 | 11.24 | 10.29 |
| Cospuden (0.6) * | 11.04 | 1.72 | 2.69 | 3.46 |
| Kriebstein (2.3) * | 12.07 | 13.78 | 5.17 | 5.98 |
| Mulde (36.9) * | 22.78 | 15.23 | 8.72 | 7.13 |
| Site | Two-Band Ratio | Single Wavelength | PLSref | PLSfds |
|---|---|---|---|---|
| Auensee (1.10) * | 0.42 | 0.18 | 0.11 | 0.15 |
| Cospuden (0.16) * | 0.32 | 0.12 | 0.17 | 0.16 |
| Kriebstein (1.45) * | 0.22 | 0.35 | 0.27 | 0.27 |
| Mulde (0.95) * | 0.23 | 0.36 | 0.38 | 0.36 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seidel, M.; Hutengs, C.; Oertel, F.; Schwefel, D.; Jung, A.; Vohland, M. Underwater Use of a Hyperspectral Camera to Estimate Optically Active Substances in the Water Column of Freshwater Lakes. Remote Sens. 2020, 12, 1745. https://doi.org/10.3390/rs12111745
Seidel M, Hutengs C, Oertel F, Schwefel D, Jung A, Vohland M. Underwater Use of a Hyperspectral Camera to Estimate Optically Active Substances in the Water Column of Freshwater Lakes. Remote Sensing. 2020; 12(11):1745. https://doi.org/10.3390/rs12111745
Chicago/Turabian StyleSeidel, Michael, Christopher Hutengs, Felix Oertel, Daniel Schwefel, András Jung, and Michael Vohland. 2020. "Underwater Use of a Hyperspectral Camera to Estimate Optically Active Substances in the Water Column of Freshwater Lakes" Remote Sensing 12, no. 11: 1745. https://doi.org/10.3390/rs12111745
APA StyleSeidel, M., Hutengs, C., Oertel, F., Schwefel, D., Jung, A., & Vohland, M. (2020). Underwater Use of a Hyperspectral Camera to Estimate Optically Active Substances in the Water Column of Freshwater Lakes. Remote Sensing, 12(11), 1745. https://doi.org/10.3390/rs12111745