Estimating Yields of Household Fields in Rural Subsistence Farming Systems to Study Food Security in Burkina Faso
Abstract
1. Introduction
2. Material and Methods
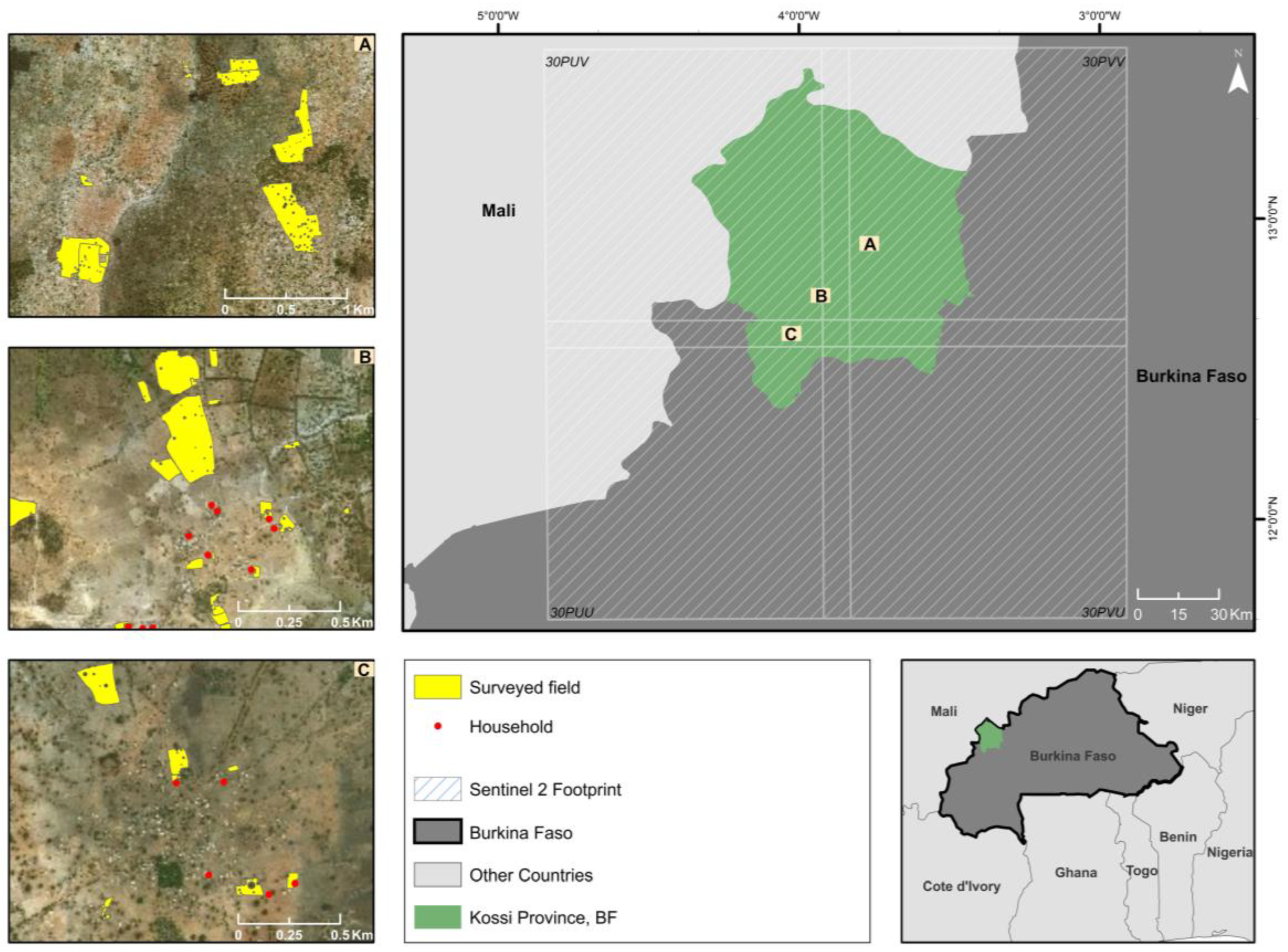
2.1. Study Area
2.2. Data
2.2.1. Field Data
2.2.2. Field Sampling Approach
2.2.3. Harvest Measurements
2.2.4. Remote Sensing Data
| Normalized Difference Vegetation Index | [55] | (1) | |
| Normalized Difference Red Edge Index | [56] | (2) | |
| Normalized Difference Water Index | [53] | (3) |
2.3. Modelling Methodology
2.3.1. Model Parametrization
2.3.2. Model Validation
3. Results
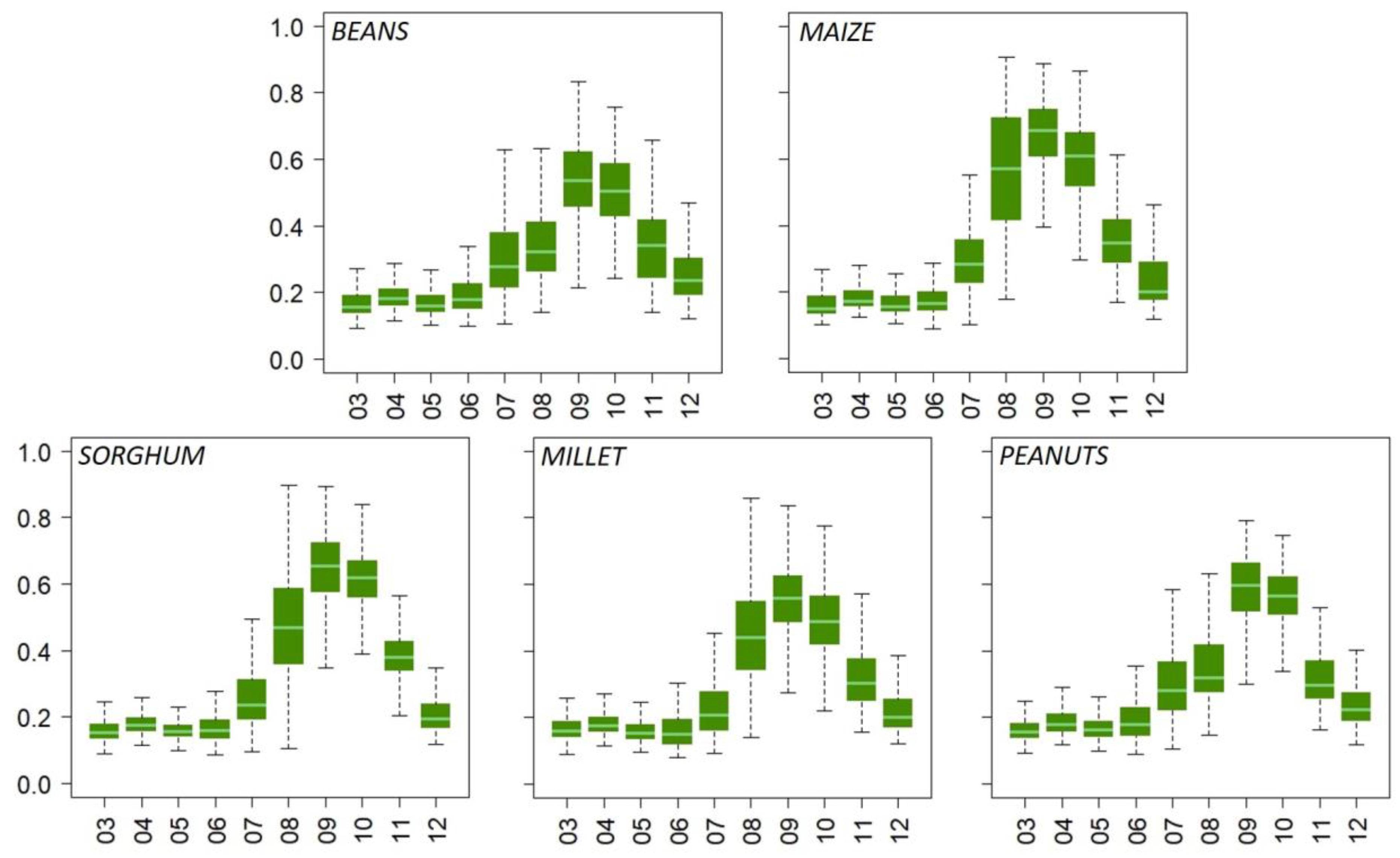
3.1. MLR Requirements
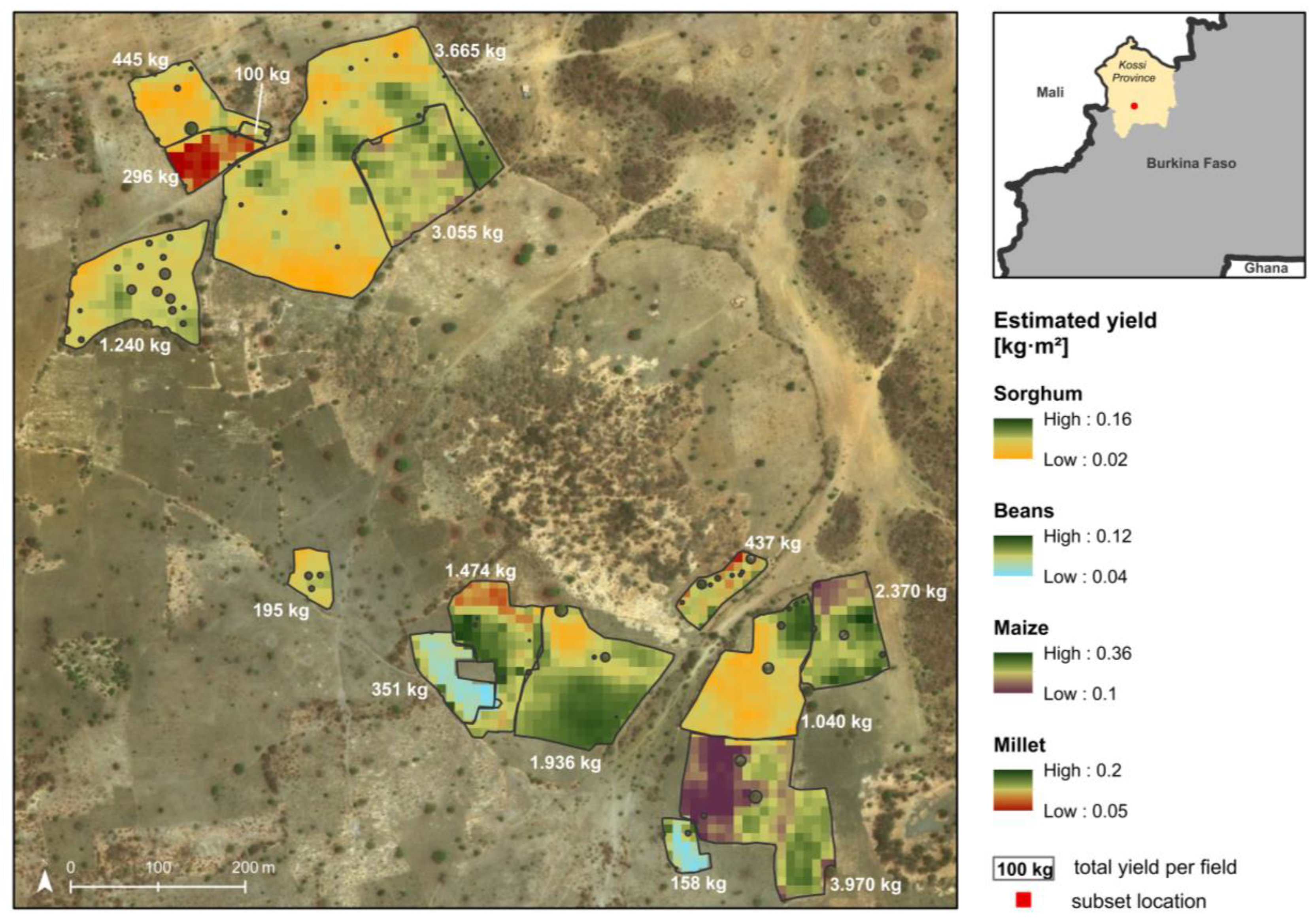
3.2. MLR Model and Yield Estimation
4. Discussion
4.1. Yield Model Results and Limitations
4.2. Linking Smallholder Yield, Child Undernutrition, and Weather Variability
4.3. Potential and Implications for Policymakers and Development Organizations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Myers, S.S.; Smith, M.R.; Guth, S.; Golden, C.D.; Vaitla, B.; Mueller, N.D.; Dangour, A.D.; Huybers, P. Climate Change and Global Food Systems: Potential Impacts on Food Security and Undernutrition. Ann. Rev. Public Health 2017, 38, 259–277. [Google Scholar] [CrossRef]
- Grolleaud, M. Post-harvest Losses: Discovering the full story: Overview of the Phenomenon of Losses During the Post-harvest System. Available online: http://www.fao.org/3/AC301E/AC301e00.htm (accessed on 31 January 2020).
- FAO; IFAD; UNICEF; WFP; WHO. The State of Food Security and Nutrition in the World 2019. Safeguarding against Economic Slowdowns and Downturns; FAO: Rome, Italy, 2019. [Google Scholar]
- Morton, J.F. The impact of climate change on smallholder and subsistence agriculture. Proc. Natl. Acad. Sci. USA 2007, 104, 19680–19685. [Google Scholar] [CrossRef]
- Bégué, A.; Arvor, D.; Bellon, B.; Betbeder, J.; Abelleyra, D.D.; Ferraz, P.D.R.; Lebourgeois, V.; Lelong, C.; Simões, M.R.; Verón, S. Remote Sensing and Cropping Practices: A Review. Remote Sens. 2018, 10, 99. [Google Scholar] [CrossRef]
- Waha, K.; Zipf, B.; Kurukulasuriya, P.; Hassan, R.M. An agricultural survey for more than 9500 African households. Sci. Data 2016, 3, 160020. [Google Scholar] [CrossRef] [PubMed]
- Sorgho, R.; Franke, J.; Simboro, S.; Barteit, S.; Phalkey, R.; Sauerborn, R. Linking Weather Data, Satellite Imagery and Field Observations to Household Food Production and Child Undernutrition: An Exploratory Study in Burkina Faso. Univers. J. Public Health 2017, 5, 256–270. [Google Scholar] [CrossRef][Green Version]
- Longueville, F.D.; Hountondji, Y.-C.; Kindo, I.; Gemenne, F.; Ozer, P. Long-term analysis of rainfall and temperature data in Burkina Faso (1950-2013). Int. J. Climatol. 2016, 36, 4393–4405. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2014. [Google Scholar]
- Belesova, K.; Gornott, C.; Milner, J.; Sié, A.; Sauerborn, R.; Wilkinson, P. Mortality impact of low annual crop yields in a subsistence farming population of Burkina Faso under the current and a 1.5 °C warmer climate in 2100. Sci. Total Environ. 2019, 691, 538–548. [Google Scholar] [CrossRef]
- Hondula, D.M.; Rocklöv, J.; Sankoh, O.A. Past, present, and future climate at select INDEPTH member Health and Demographic Surveillance Systems in Africa and Asia. Glob. Health Action 2012, 5, 74–86. [Google Scholar] [CrossRef] [PubMed]
- Lobell, D.B.; Bänziger, M.; Magorokosho, C.; Vivek, B. Nonlinear heat effects on African maize as evidenced by historical yield trials. Nat. Clim. Chang. 2011, 1, 42–45. [Google Scholar] [CrossRef]
- Rowhani, P.; Lobell, D.B.; Linderman, M.; Ramankutty, N. Climate variability and crop production in Tanzania. Agric. For. Meteorol. 2011, 151, 449–460. [Google Scholar] [CrossRef]
- Kjellstrom, T.; Briggs, D.; Freyberg, C.; Lemke, B.; Otto, M.; Hyatt, O. Heat, Human Performance, and Occupational Health: A Key Issue for the Assessment of Global Climate Change Impacts. Ann. Rev. Public Health 2016, 37, 97–112. [Google Scholar] [CrossRef]
- Sahu, S.; Sett, M.; Kjellstrom, T. Heat exposure, cardiovascular stress and work productivity in rice harvesters in India: Implications for a climate change future. Ind. Health 2013, 51, 424–431. [Google Scholar] [CrossRef]
- Brown, M.E.; Grace, K.; Shively, G.; Johnson, K.B.; Carroll, M. Using satellite remote sensing and household survey data to assess human health and nutrition response to environmental change. Popul. Environ. 2014, 36, 48–72. [Google Scholar] [CrossRef]
- Noromiarilanto, F.; Brinkmann, K.; Faramalala, M.H.; Buerkert, A. Assessment of food self-sufficiency in smallholder farming systems of south-western Madagascar using survey and remote sensing data. Agric. Syst. 2016, 149, 139–149. [Google Scholar] [CrossRef]
- Grace, K.; Brown, M.; McNally, A. Examining the link between food prices and food insecurity: A multi-level analysis of maize price and birthweight in Kenya. Food Policy 2014, 46, 56–65. [Google Scholar] [CrossRef]
- Phalkey, R.K.; Aranda-Jan, C.; Marx, S.; Höfle, B.; Sauerborn, R. Systematic review of current efforts to quantify the impacts of climate change on undernutrition. Proc. Natl. Acad. Sci. USA 2015, 112, E4522–E4529. [Google Scholar] [CrossRef]
- Mank, I.; Vandormael, A.; Traoré, I.; Ouédraogo, A.; Sauerborn, R.; Danquah, I. Dietary habits associated with growth development among children aged <5 years in the Nouna Health and Demographic Surveillance System, Burkina Faso. Nutr. J. (under review).
- Beiersmann, C.; Bountogo, M.; Tiendrébeogo, J.; Louis, V.R.; Gabrysch, S.; Yé, M.; Jahn, A.; Müller, O. Malnutrition in young children of rural Burkina Faso: Comparison of survey data from 1999 with 2009. Trop. Med. Int. Health 2012, 17, 715–721. [Google Scholar] [CrossRef]
- Belesova, K.; Gasparrini, A.; Sié, A.; Sauerborn, R.; Wilkinson, P. Annual Crop-Yield Variation, Child Survival, and Nutrition Among Subsistence Farmers in Burkina Faso. Am. J. Epidemiol. 2018, 187, 242–250. [Google Scholar] [CrossRef]
- Zheng, G.; Moskal, L.M. Retrieving Leaf Area Index (LAI) Using Remote Sensing: Theories, Methods and Sensors. Sensors (Basel) 2009, 9, 2719–2745. [Google Scholar] [CrossRef]
- Tilling, A.K.; O’Leary, G.J.; Ferwerda, J.G.; Jones, S.D.; Fitzgerald, G.J.; Rodriguez, D.; Belford, R. Remote sensing of nitrogen and water stress in wheat. Field Crops Res. 2007, 104, 77–85. [Google Scholar] [CrossRef]
- Lu, D. The potential and challenge of remote sensing-based biomass estimation. Int. J. Remote Sens. 2006, 27, 1297–1328. [Google Scholar] [CrossRef]
- Voss, K.; Franke, J.; Mewes, T.; Menz, G.; Kühbauch, W. Remote Sensing for Precision Crop Protection—A Matter of Scale. In Precision Crop Protection—The Challenge and Use of Heterogeneity; Oerke, E.-C., Gerhards, R., Menz, G., Sikora, R.A., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 101–118. ISBN 978-90-481-9276-2. [Google Scholar]
- Groten, S.M.E. NDVI—Crop monitoring and early yield assessment of Burkina Faso. Int. J. Remote Sens. 1993, 14, 1495–1515. [Google Scholar] [CrossRef]
- Doraiswamy, P.C.; Moulin, S.; Cook, P.W.; Stern, A. Crop Yield Assessment from Remote Sensing. Photogramm. Eng. Remote Sens. 2003, 69, 665–674. [Google Scholar] [CrossRef]
- Bolton, D.K.; Friedl, M.A. Forecasting crop yield using remotely sensed vegetation indices and crop phenology metrics. Agric. For. Meteorol. 2013, 173, 74–84. [Google Scholar] [CrossRef]
- Huang, J.; Gómez-Dans, J.L.; Huang, H.; Ma, H.; Wu, Q.; Lewis, P.E.; Liang, S.; Chen, Z.; Xue, J.-H.; Wu, Y.; et al. Assimilation of remote sensing into crop growth models: Current status and perspectives. Agric.For. Meteorol. 2019, 276–277, 107609. [Google Scholar] [CrossRef]
- Gessner, U.; Machwitz, M.; Esch, T.; Tillack, A.; Naeimi, V.; Kuenzer, C.; Dech, S. Multi-sensor mapping of West African land cover using MODIS, ASAR and TanDEM-X/TerraSAR-X data. Remote Sens. Environ. 2015, 164, 282–297. [Google Scholar] [CrossRef]
- Knauer, K.; Gessner, U.; Fensholt, R.; Forkuor, G.; Kuenzer, C. Monitoring Agricultural Expansion in Burkina Faso over 14 Years with 30 m Resolution Time Series: The Role of Population Growth and Implications for the Environment. Remote Sens. 2017, 9, 132. [Google Scholar] [CrossRef]
- Jin, Z.; Azzari, G.; Burke, M.; Aston, S.; Lobell, D. Mapping Smallholder Yield Heterogeneity at Multiple Scales in Eastern Africa. Remote Sens. 2017, 9, 931. [Google Scholar] [CrossRef]
- Burke, M.; Lobell, D.B. Satellite-based assessment of yield variation and its determinants in smallholder African systems. Proc. Natl. Acad. Sci. USA 2017, 114, 2189–2194. [Google Scholar] [CrossRef]
- Jain, M.; Srivastava, A.; Balwinder, S.; Joon, R.; McDonald, A.; Royal, K.; Lisaius, M.; Lobell, D. Mapping Smallholder Wheat Yields and Sowing Dates Using Micro-Satellite Data. Remote Sens. 2016, 8, 860. [Google Scholar] [CrossRef]
- Lambert, M.-J.; Traoré, P.C.S.; Blaes, X.; Baret, P.; Defourny, P. Estimating smallholder crops production at village level from Sentinel-2 time series in Mali’s cotton belt. Remote Sens. Environ. 2018, 216, 647–657. [Google Scholar] [CrossRef]
- Meroni, M.; Marinho, E.; Sghaier, N.; Verstrate, M.; Leo, O. Remote Sensing Based Yield Estimation in a Stochastic Framework—Case Study of Durum Wheat in Tunisia. Remote Sens. 2013, 5, 539–557. [Google Scholar] [CrossRef]
- Mkhabela, M.S.; Bullock, P.; Raj, S.; Wang, S.; Yang, Y. Crop yield forecasting on the Canadian Prairies using MODIS NDVI data. Agric. For. Meteorol. 2011, 151, 385–393. [Google Scholar] [CrossRef]
- Schwalbert, R.A.; Amado, T.J.C.; Nieto, L.; Varela, S.; Corassa, G.M.; Horbe, T.A.N.; Rice, C.W.; Peralta, N.R.; Ciampitti, I.A. Forecasting maize yield at field scale based on high-resolution satellite imagery. Biosyst. Eng. 2018, 171, 179–192. [Google Scholar] [CrossRef]
- Skakun, S.; Franch, B.; Vermote, E.; Roger, J.-C.; Justice, C.; Masek, J.; Murphy, E. Winter Wheat Yield Assessment Using Landsat 8 and Sentinel-2 Data. In IGARSS 2018—2018 IEEE International Geoscience and Remote Sens. Symposium; IEEE: Valencia, Spain, 2018; pp. 5964–5967. ISBN 978-1-5386-7150-4. [Google Scholar]
- Lambert, M.-J.; Blaes, X.; Traore, P.S.; Defourny, P. Estimate yield at parcel level from S2 time serie in sub-Saharan smallholder farming systems. IEEE 2017, 1–7. [Google Scholar] [CrossRef]
- Shively, G.; Sununtnasuk, C.; Brown, M. Environmental variability and child growth in Nepal. Health Place 2015, 35, 37–51. [Google Scholar] [CrossRef] [PubMed]
- Johnson, K.; Brown, M.E. Environmental risk factors and child nutritional status and survival in a context of climate variability and change. Appl. Geogr. 2014, 54, 209–221. [Google Scholar] [CrossRef]
- Imran, M.; Stein, A.; Zurita-Milla, R. Investigating rural poverty and marginality in Burkina Faso using remote sensing-based products. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 322–334. [Google Scholar] [CrossRef]
- Belesova, K.; Gasparrini, A.; Sié, A.; Sauerborn, R.; Wilkinson, P. Household cereal crop harvest and children’s nutritional status in rural Burkina Faso. Environ. Health 2017, 16, 65. [Google Scholar] [CrossRef]
- Dixon, S.; Holt, J. Livelihood Zoning and Profiling Report: Burkina Faso. A Special Report by the Famine Early Warning Systems Network (FEWS NET); USAID: Washington, DC, USA, 2010.
- Sarr, B.; Atta, S.; Ly, M.; Salack, S.; David, G.A.; Ourback, T.; Subsol, S. Adapting to climate variability and change in smallholder farming communities: A case study from Burkina Faso, Chad and Niger. J. Agric. Ext. Rural Dev. 2015, 7, 16–27. [Google Scholar] [CrossRef]
- Direction de la Prospective et des Statistiques Agricoles et Alimentaires (DPSAA). Rapport General du Module Pluvial. Phase 2°; Ministère de l’Agriculture et de l’Hydraulique: Ouagadougou, Burkina Faso, 2011. [Google Scholar]
- Fermont, A.; Benson, T. Estimating Yield of Food Crops Grown by Smallholder Farmers. A Review in the Uganda Context; IFPRI: Washington, DC, USA; Kampala, Uganda, 2011; p. 01097. [Google Scholar]
- ESA. Sentinel-2-Missions. 2020. Available online: https://sentinels.copernicus.eu/web/sentinel/missions/sentinel-2 (accessed on 13 January 2020).
- Guerini Filho, M.; Kuplich, T.M.; Quadros, F.L.F.D. Estimating natural grassland biomass by vegetation indices using Sentinel 2 remote sensing data. Int. J. Remote Sens. 2020, 41, 2861–2876. [Google Scholar] [CrossRef]
- Kross, A.; McNairn, H.; Lapen, D.; Sunohara, M.; Champagne, C. Assessment of RapidEye vegetation indices for estimation of leaf area index and biomass in corn and soybean crops. Int. J. Appl. Earth Obs. Geoinf. 2015, 34, 235–248. [Google Scholar] [CrossRef]
- Gao, B.-C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. of Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Sharma, L.K.; Bu, H.; Denton, A.; Franzen, D.W. Active-Optical Sensors Using Red NDVI Compared to Red Edge NDVI for Prediction of Corn Grain Yield in North Dakota, U.S.A. Sensors (Basel) 2015, 15, 27832–27853. [Google Scholar] [CrossRef]
- Rouse, J.; Haas, R.; Schell, J.; Deering, D. Monitoring Vegetation Systems in the Great Plains with ERTS. In Proceedings of the Third Earth Resources Technology Satellite-1 Symposium, Washington, DC, USA, 10–14 December 1973. [Google Scholar]
- Barnes, E.; Clarke, T.R.; Richards, S.E.; Colaizzi, P.; Haberland, J.; Kostrzewski, M.; Waller, P.; Choi, C.; Riley, E.; Thompson, T.L. Coincident detection of crop water stress, nitrogen status, and canopy density using ground based multispectral data. In Proceedings of the Fifth International Conference on Precision Agriculture, Bloomington, MN, USA, 16–19 July 2000. [Google Scholar]
- Bastiaanssen, W.G.M.; Ali, S. A new crop yield forecasting model based on satellite measurements applied across the Indus Basin, Pakistan. Agric. Ecosyst. Environ. 2003, 94, 321–340. [Google Scholar] [CrossRef]
- DeGroot, M.H.; Schervish, M.J. Probability and Statistics; Pearson New International, Ed.; Pearson: Harlow, Essex, UK, 2014; ISBN 1292025042. [Google Scholar]
- Chakravarti, I.M.; Laha, R.G.; Roy, J. Handbook of Methods of Applied Statistics; John Wiley & Sons: Hoboken, NJ, USA, 1967; Volume I, pp. 392–394. [Google Scholar]
- Brownlee, J. How to Transform Data to Better Fit the Normal Distribution. 2019. Available online: https://machinelearningmastery.com/how-to-transform-data-to-fit-the-normal-distribution/ (accessed on 13 February 2020).
- Ziegel, E.R.; Rawlings, J.O.; Pantula, S.G.; Dickey, D.A. Applied Regression Analysis: A Research Tool. Technometrics 1999, 41, 82. [Google Scholar] [CrossRef]
- Cohen, I.; Huang, Y.; Chen, J.; Benesty, J. Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 978-3-642-00295-3. [Google Scholar]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.R.G.; Gruber, B.; Lafourcade, B.; Leitão, P.J.; et al. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- Belsley, D.A.; Kuh, K.; Welsch, R.E. Regression diagnostics: Identifying influential data and sources of collinearity. J. Appl. Econ. 1989, 4, 97–99. [Google Scholar] [CrossRef]
- Belsley, D.A. Conditioning Diagnostics. Collinearity and Weak Data in Regression; Wiley: New York, NY, USA, 1991; ISBN 0471528897. [Google Scholar]
- Douglass, D.H.; Clader, B.D.; Christy, J.R.; Michaels, P.J.; Belsley, D.A. Test for harmful collinearity among predictor variables used in modeling global temperature. Clim. Res. 2003, 24, 15–18. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning. With Applications in R; Corrected at 8th printing edition; Springer: New York, NY, USA, 2017; ISBN 9781461471387. [Google Scholar]
- Abdul-Wahab, S.A.; Bakheit, C.S.; Al-Alawi, S.M. Principal component and multiple regression analysis in modelling of ground-level ozone and factors affecting its concentrations. Environ. Model. Softw. 2005, 20, 1263–1271. [Google Scholar] [CrossRef]
- Carfagna, E.; Gallego, F.J. Using Remote Sensing for Agricultural Statistics. Int. Stat. Rev. 2005, 73, 389–404. [Google Scholar] [CrossRef]
- Rasmussen, M.S. Developing simple, operational, consistent NDVI-vegetation models by applying environmental and climatic information. Part II: Crop yield assessment. Int. J. Remote Sens. 1998, 19, 119–139. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Erlbaum: Hillsdale, NJ, USA, 1988; ISBN 1299630081. [Google Scholar]
- Morel, J.; Todoroff, P.; Bégué, A.; Bury, A.; Martiné, J.-F.; Petit, M. Toward a Satellite-Based System of Sugarcane Yield Estimation and Forecasting in Smallholder Farming Conditions: A Case Study on Reunion Island. Remote Sens. 2014, 6, 6620–6635. [Google Scholar] [CrossRef]
- Bauer, J.M.; Mburu, S. Effects of drought on child health in Marsabit District, Northern Kenya. Econ. Hum. Biol. 2017, 24, 74–79. [Google Scholar] [CrossRef] [PubMed]
- Sié, A.; Louis, V.R.; Gbangou, A.; Müller, O.; Niamba, L.; Stieglbauer, G.; Yé, M.; Kouyaté, B.; Sauerborn, R.; Becher, H. The Health and Demographic Surveillance System (HDSS) in Nouna, Burkina Faso, 1993–2007. Glob. Health Action 2010, 3. [Google Scholar] [CrossRef]
- Rembold, F.; Atzberger, C.; Savin, I.; Rojas, O. Using Low Resolution Satellite Imagery for Yield Prediction and Yield Anomaly Detection. Remote Sens. 2013, 5, 1704–1733. [Google Scholar] [CrossRef]
- Nelson, A.D.; Rogers, D.J.; Robinson, T.P. Poverty Mapping in Uganda. Extrapolating Household Expenditure Data Using Environmental Data and Regression Techniques; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 2012; ISBN 9251072116. [Google Scholar]
| Beans | Maize | Sorghum | Millet | Peanuts | |
|---|---|---|---|---|---|
| Predictors Used (from Avail) | 3 (10) | 3 (12) | 4 (14) | 5 (11) | 1 (13) |
| Predictor Months | July, August, October | June, August | March, July, September, November | May, July, September, November | September |
| Correlation Coefficient (R) | 0.74 | 0.68 | 0.66 | 0.63 | 0.35 |
| Coefficient of Determination (R²) | 0.54 | 0.46 | 0.44 | 0.40 | 0.12 |
| Adjusted R² | 0.50 | 0.40 | 0.40 | 0.32 | 0.10 |
| RMSE (kg·25 m−²) | 0.94 | 2.38 | 1.24 | 1.52 | 1.13 |
| Harvest Value Range (kg·25 m−²) | 6.3 | 13.3 | 8.7 | 9 | 4.6 |
| Model Significance | 0.0001 | 0.0004 | 0.000 | 0.0011 | 0.0477 |
| Crop Type | Model Equation |
|---|---|
| Beans | −5.145 + 3.348 × NDVIJul + 6.019 × NDVIAug + 9515 × NDWIOct |
| Maize | 11.666 − 21.440 × NDVIJun + 43.144 × NDWIJun + 9.830 × NDVIAug |
| Sorghum | −0.8368 − 12.3063 × NDWIMar + 5.4679 × NDWIJul + 5.6015 × NDVISep − 4.1599 × NDWINov |
| Millet | 5.260 + 26.152 × NDVIMay + 8.951 × NDWIMay + 5.528 × NDWIJul − 3.599 × NDVISep − 8.258 × NDVINov |
| Beans | Maize | Millet | Sorghum | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | A | B | C | A | B | C | A | B | C | |
| No. Fields | 1 | 1 | 3 | 1 | 1 | 1 | 1 | 1 | 3 | 1 | 3 | 1 |
| Est. total yield (kg) | 454 | 167 | 810 | 417 | 650 | 227 | 771 | 173 | 1665 | 1021 | 1288 | 1167 |
| Mean yield (kg 25 m−²) | 0.1 | 0.07 | 0.13 | 0.23 | 0.21 | 0.25 | 0.10 | 0.05 | 0.12 | 0.08 | 0.07 | 0.10 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karst, I.G.; Mank, I.; Traoré, I.; Sorgho, R.; Stückemann, K.-J.; Simboro, S.; Sié, A.; Franke, J.; Sauerborn, R. Estimating Yields of Household Fields in Rural Subsistence Farming Systems to Study Food Security in Burkina Faso. Remote Sens. 2020, 12, 1717. https://doi.org/10.3390/rs12111717
Karst IG, Mank I, Traoré I, Sorgho R, Stückemann K-J, Simboro S, Sié A, Franke J, Sauerborn R. Estimating Yields of Household Fields in Rural Subsistence Farming Systems to Study Food Security in Burkina Faso. Remote Sensing. 2020; 12(11):1717. https://doi.org/10.3390/rs12111717
Chicago/Turabian StyleKarst, Isabel G., Isabel Mank, Issouf Traoré, Raissa Sorgho, Kim-Jana Stückemann, Séraphin Simboro, Ali Sié, Jonas Franke, and Rainer Sauerborn. 2020. "Estimating Yields of Household Fields in Rural Subsistence Farming Systems to Study Food Security in Burkina Faso" Remote Sensing 12, no. 11: 1717. https://doi.org/10.3390/rs12111717
APA StyleKarst, I. G., Mank, I., Traoré, I., Sorgho, R., Stückemann, K.-J., Simboro, S., Sié, A., Franke, J., & Sauerborn, R. (2020). Estimating Yields of Household Fields in Rural Subsistence Farming Systems to Study Food Security in Burkina Faso. Remote Sensing, 12(11), 1717. https://doi.org/10.3390/rs12111717







