Unseen Land Cover Classification from High-Resolution Orthophotos Using Integration of Zero-Shot Learning and Convolutional Neural Networks
Abstract
:1. Introduction
2. Related Studies
2.1. Zero-Shot Learning (ZSL)
2.2. Transductive or GZSL
2.3. ZSL on Remote Sensing Data
3. Methods
3.1. Theoretical Background
3.1.1. Theory of ZSL
3.1.2. Theory of CNN
3.1.3. KNN Model
3.1.4. Class Embedding
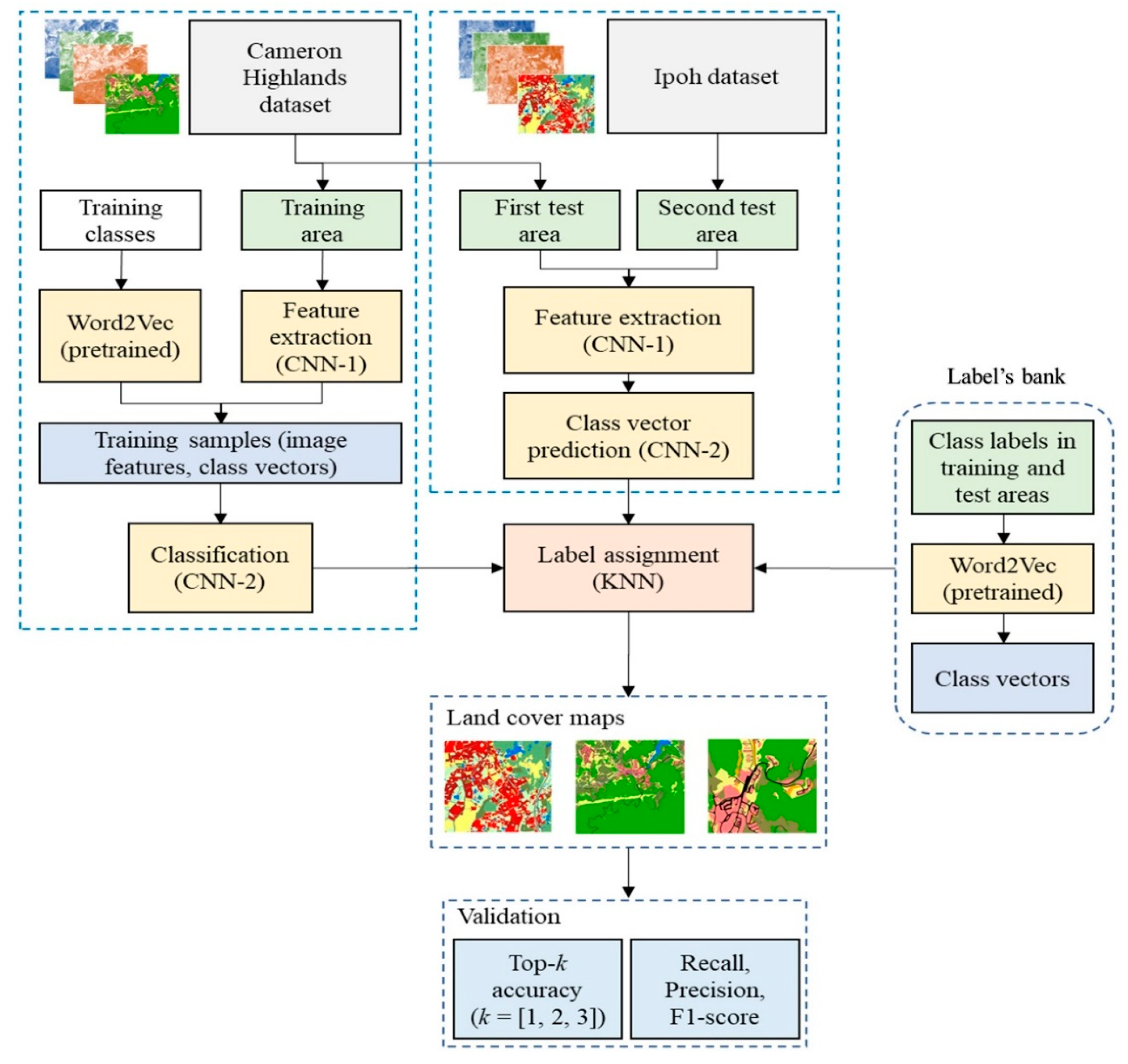
3.2. Overall Workflow
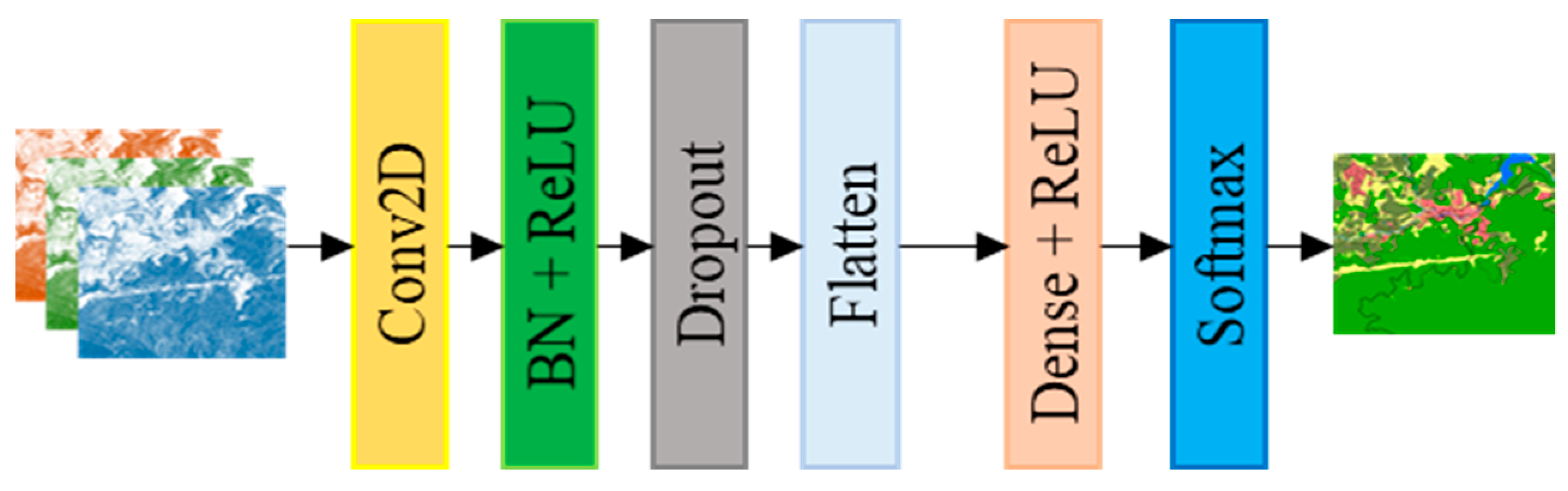
3.3. Details of CNN-1 Used for Image Feature Extraction
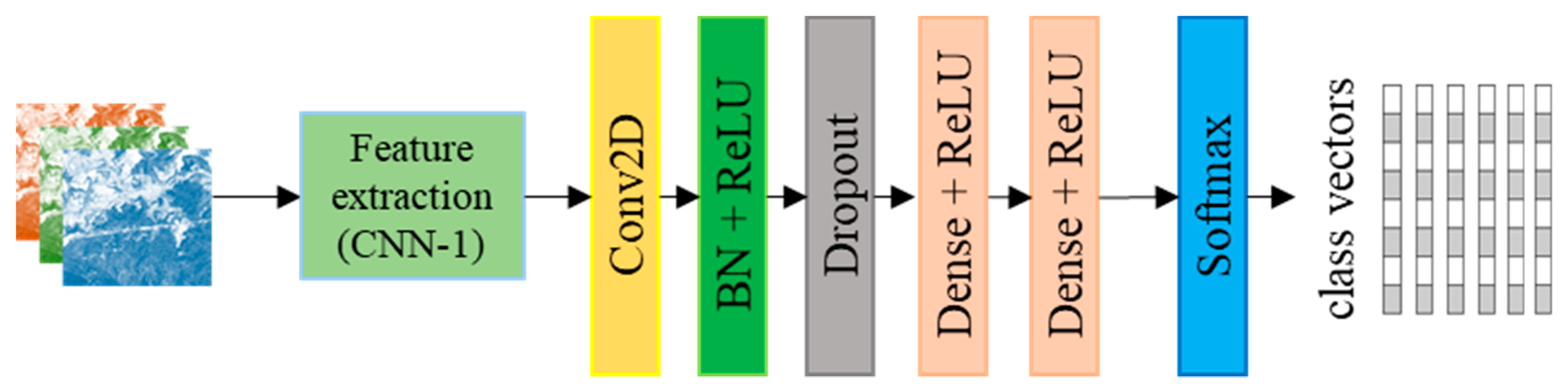
3.4. Details of CNN-2 Used for Class Signature Prediction
3.5. KNN Algorithm for Finding the Nearest Class/Label
3.6. Evaluation Metrics (Precision, Recall and F-measure)
4. Experiments and results
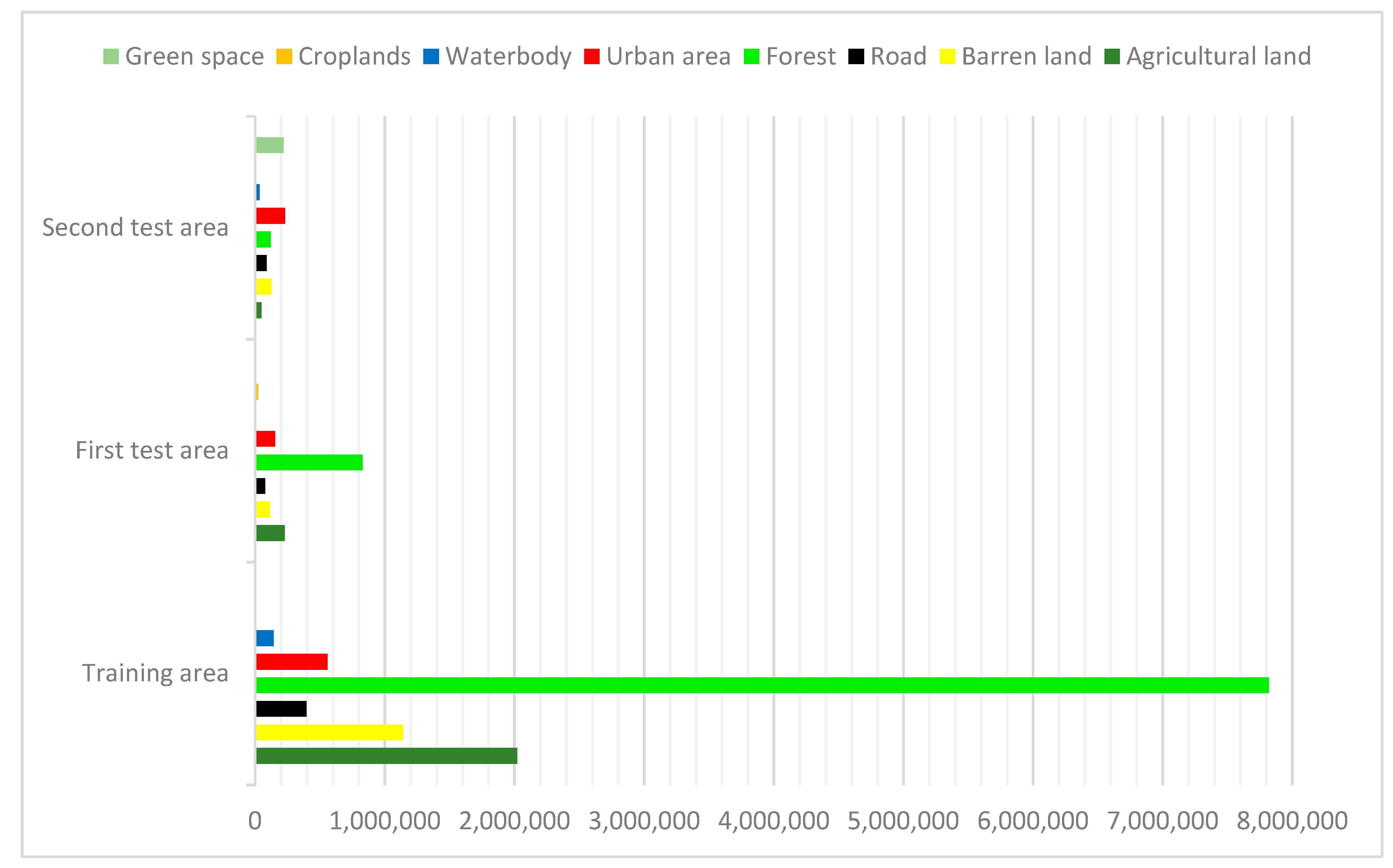
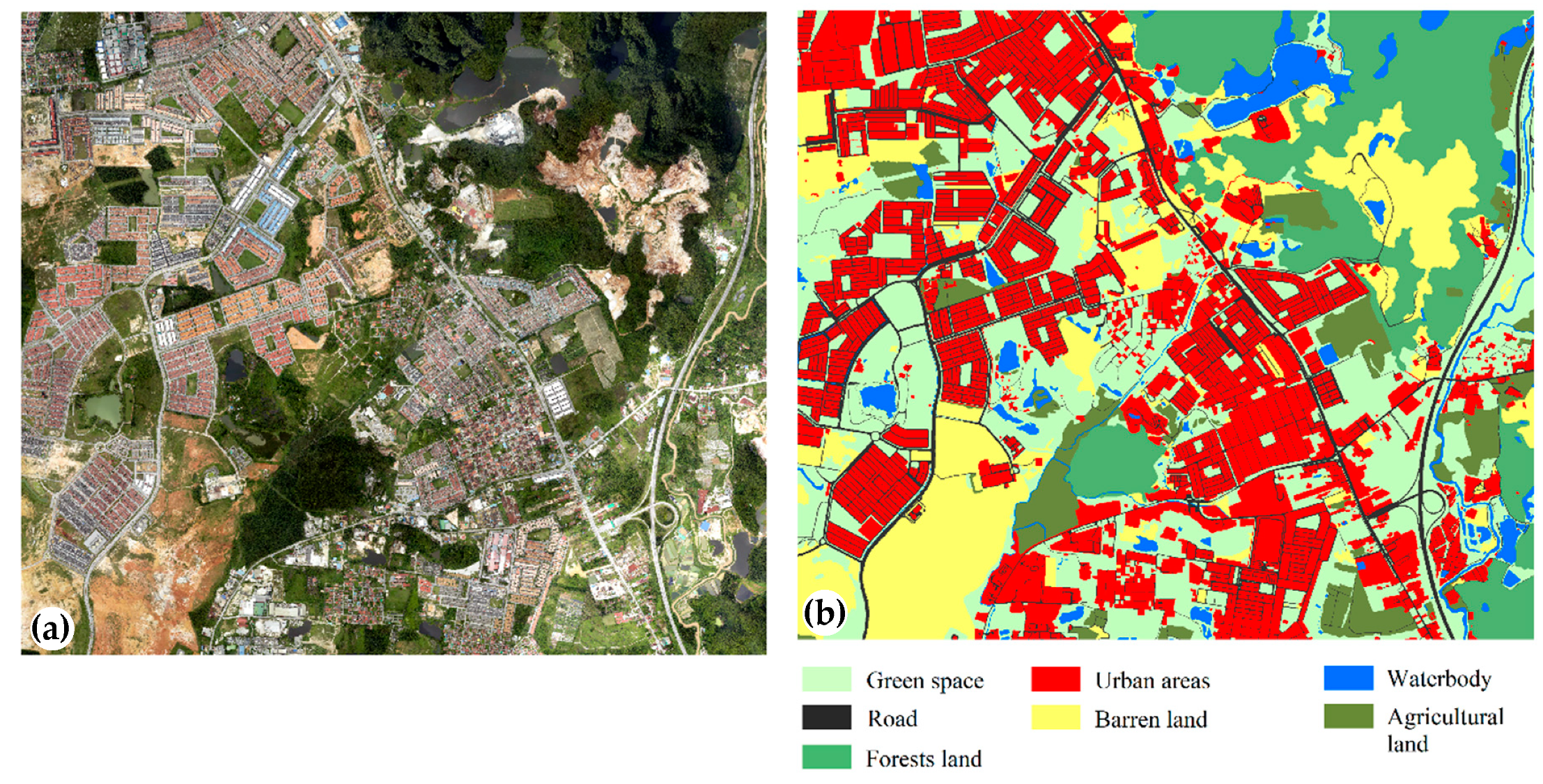
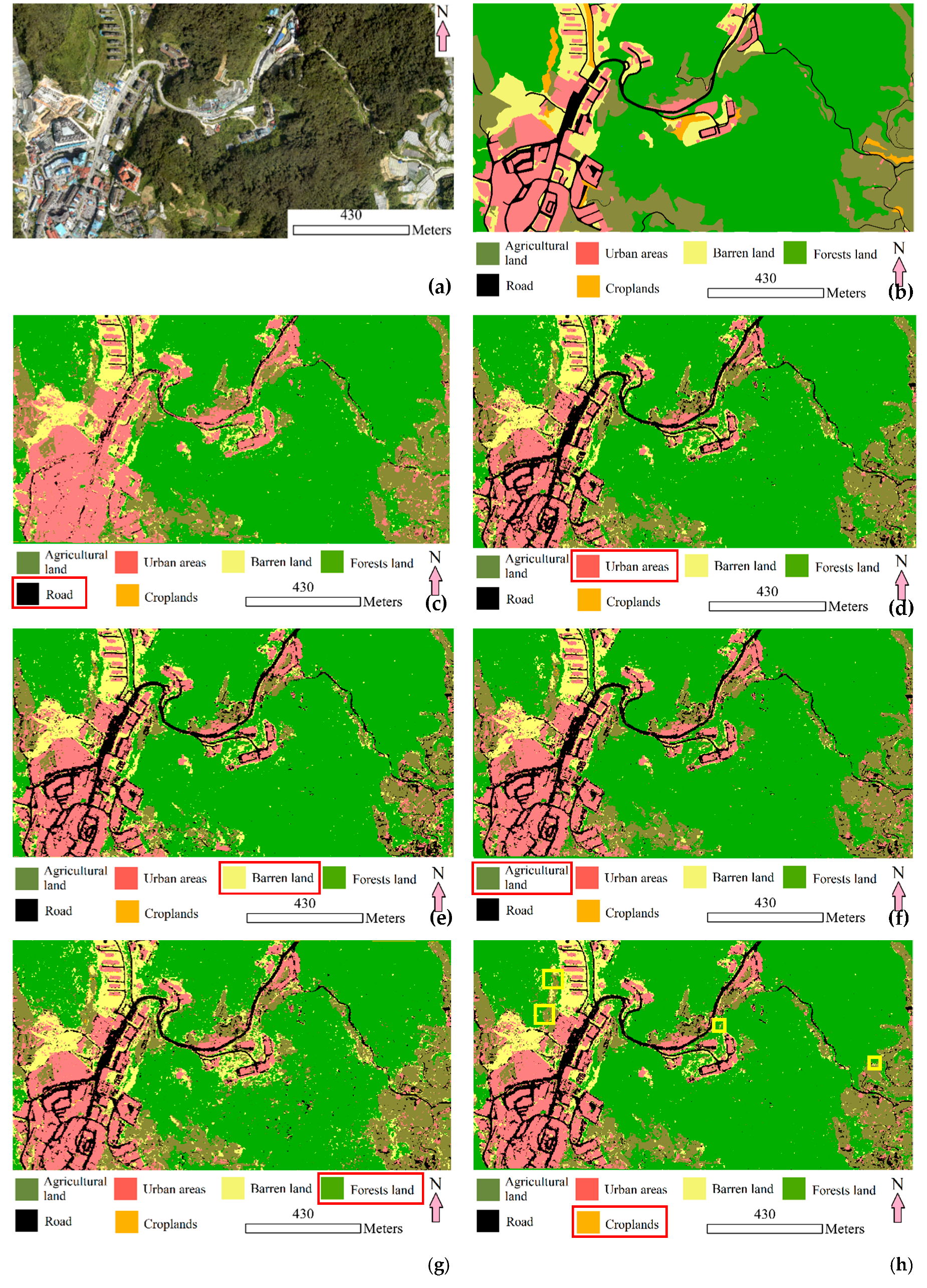
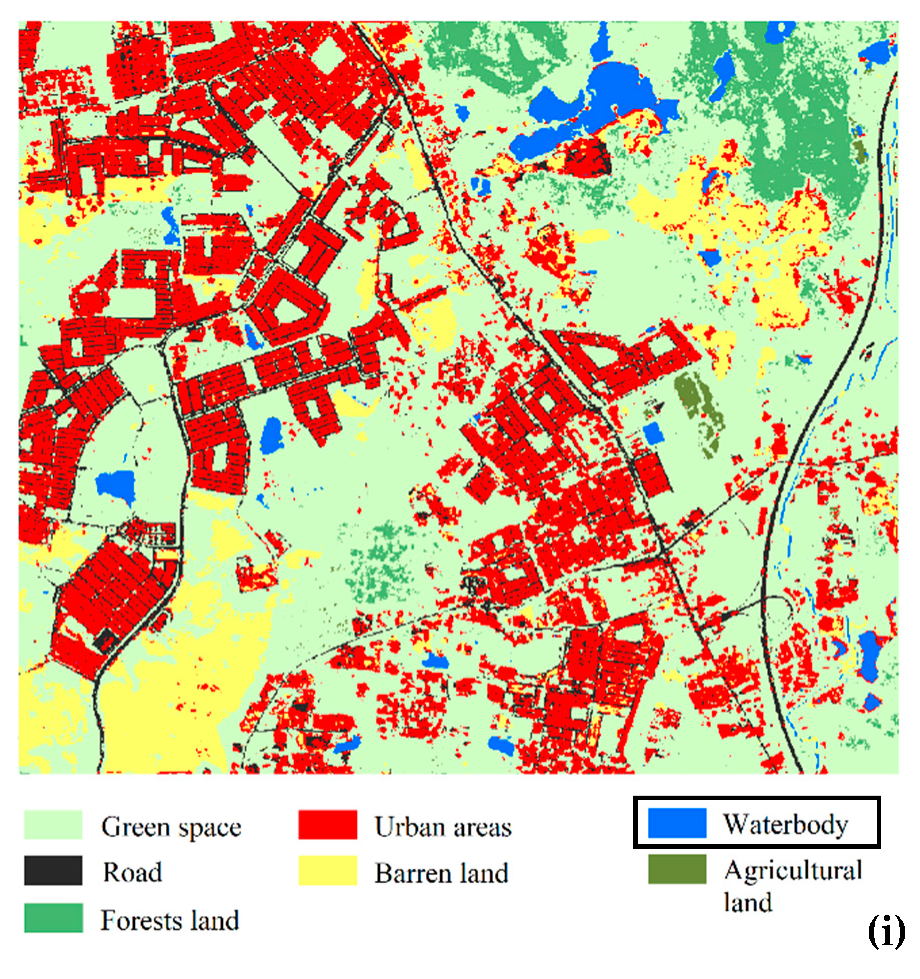
4.1. Datasets
4.2. Results of Feature Extraction (CNN-1)
4.2.1. Impact of Network Architectures
4.2.2. Impact of Filters Size
4.2.3. Impact of Network’s Depth
4.2.4. Impact of Gaussian Noise
4.3. Results of Classification (CNN-2)
4.3.1. Impact of Batch Normalisation
4.3.2. Impact of the Number of Neurons
4.3.3. Impact of Gaussian Noise
4.4. Results of Transferability
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Al-Najjar, H.A.H.; Kalantar, B.; Pradhan, B.; Saeidi, V.; Halin, A.A.; Ueda, N.; Mansor, S. Land cover classification from fused DSM and UAV images using convolutional neural networks. Remote Sens. 2019, 11, 1461. [Google Scholar] [CrossRef] [Green Version]
- Novellino, A.; Jordan, C.; Ager, G.; Bateson, L.; Fleming, C.; Confuorto, P. Geological Disaster Monitoring Based on Sensor Networks; Springer: Singapore, 2019; ISBN 978-981-13-0991-5. [Google Scholar]
- Pradhan, B.; Sezer, E.A.; Gokceoglu, C.; Buchroithner, M.F. Landslide susceptibility mapping by neuro-fuzzy approach in a landslide-prone area (Cameron Highlands, Malaysia). IEEE Trans. Geosci. Remote Sens. 2010, 48, 4164–4177. [Google Scholar] [CrossRef]
- Wang, C.; Myint, S.W.; Wang, Z.; Song, J. Spatio-temporal modeling of the urban heat island in the phoenix metropolitan area : Land use change implications. Remote Sens. 2016, 8, 185. [Google Scholar] [CrossRef] [Green Version]
- Ashby, J.; Moreno-Madriñán, M.J.; Yiannoutsos, C.T.; Stanforth, A. Niche modeling of dengue fever using remotely sensed environmental factors and boosted regression trees. Remote Sens. 2017, 9, 328. [Google Scholar] [CrossRef] [Green Version]
- Lehner, A.; Blaschke, T. A generic classification scheme for urban structure types. Remote Sens. 2019, 11, 173. [Google Scholar] [CrossRef] [Green Version]
- Neuville, R.; Pouliot, J.; Poux, F. 3D Viewpoint management and navigation in urban planning: Application to the exploratory phase. Remote Sens. 2019, 11, 236. [Google Scholar] [CrossRef] [Green Version]
- Cheng, J.; Kustas, W.P. Using very high resolution thermal infrared imagery for more accurate determination of the impact of land cover differences on evapotranspiration in an irrigated agricultural area. Remote Sens. 2019, 11, 613. [Google Scholar] [CrossRef] [Green Version]
- Coops, N.C.; Waring, R.H.; Plowright, A.; Lee, J.; Dilts, T.E. Using remotely-sensed land cover and distribution modeling to estimate tree species migration in the Pacific Northwest Region of North America. Remote Sens. 2016, 8, 65. [Google Scholar] [CrossRef] [Green Version]
- Tehrany, M.S.; Pradhan, B.; Jebuv, M.N. A comparative assessment between object and pixel-based classification approaches for land use/land cover mapping using SPOT 5 imagery. Geocarto Int. 2014, 29, 351–369. [Google Scholar] [CrossRef]
- Rizeei, H.M.; Shafri, H.Z.M.; Mohamoud, M.A.; Pradhan, B.; Kalantar, B. Oil palm counting and age estimation from WorldView-3 imagery and LiDAR data using an integrated OBIA height model and regression analysis. J. Sens. 2018, 2018, 2536327. [Google Scholar] [CrossRef] [Green Version]
- Huete, A.R.; Miura, T.; Gao, X. Land cover conversion and degradation analyses through coupled soil-plant biophysical parameters derived from hyperspectral EO-1 Hyperion. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1268–1276. [Google Scholar] [CrossRef] [Green Version]
- Quan, J.; Wu, C.; Wang, H.; Wang, Z. Structural alignment based zero-shot classification for remote sensing scenes. In Proceedings of the 2018 IEEE International Conference on Electronics and Communication Engineering, ICECE 2018, Xi’an, China, 10–12 December 2018; pp. 17–21. [Google Scholar]
- Li, A.; Lu, Z.; Wang, L.; Xiang, T.; Wen, J.R. Zero-shot scene classification for high spatial resolution remote sensing images. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4157–4167. [Google Scholar] [CrossRef]
- Wang, W.; Zheng, V.W.; Yu, H.; Miao, C. A survey of zero-shot learning: Settings, methods, and applications. ACM Trans. Intell. Syst. Technol. 2019, 10, 1–37. [Google Scholar] [CrossRef]
- Zhang, Z.; Saligrama, V. Zero-shot learning via semantic similarity embedding. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 4166–4174. [Google Scholar]
- Gong, P.; Wang, X.; Cheng, Y.; Fellow, Z.J.W. Zero-shot classification based on multi-task mixed attribute relations and attribute-specific features. IEEE Trans. Cogn. Dev. Syst. 2019, 12, 1-1. [Google Scholar]
- Gaurav, R.; Srivastava, B. Estimating train delays in a large rail network using a zero shot markov model. In Proceedings of the IEEE Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 1221–1226. [Google Scholar]
- Gorbatsevich, V.; Vizilter, Y.; Knyaz, V.; Moiseenko, A. Single-shot semantic matcher for unseen object detection. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2018, 42, 379–384. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Han, L.; Han, L.; Zhu, L. How Well Do Deep Learning-Based Methods for Land Cover Classification and Object Detection Perform on High Resolution Remote Sensing Imagery? Remote Sensing 2020, 12, 417. [Google Scholar] [CrossRef] [Green Version]
- Sumbul, G.; Cinbis, R.G.; Aksoy, S. Multisource region attention network for fine-grained object recognition in remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4929–4937. [Google Scholar] [CrossRef]
- Chen, H.; Luo, Y.; Cao, L.; Zhang, B.; Guo, G.; Wang, C.; Li, J.; Ji, R. Generalized zero-shot vehicle detection in remote sensing imagery via coarse-to-fine framework. In Proceedings of the 28th International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 687–693. [Google Scholar]
- Jia, X.; Khandelwal, A.; Nayak, G.; Gerber, J.; Carlson, K.; West, P.; Kumar, V. Incremental dual-memory LSTM in land cover prediction. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; Part F1296. pp. 867–876. [Google Scholar]
- Gui, R.; Xu, X.; Wang, L.; Yang, R.; Pu, F. A generalized zero-shot learning framework for PolSAR land cover classification. Remote Sens. 2018, 10, 1307. [Google Scholar] [CrossRef] [Green Version]
- Mikolov, T.; Ilya, S.; Kai, C.; Greg, C.; Jeffrey, D. Distributed representations of words and phrases and their compositionality. Adv. Neural Inf. Process. Syst. 2013, 1389–1399. [Google Scholar]
- Lampert, C.H.; Nickisch, H.; Harmeling, S. Attribute-based classification for zero-shot visual object categorizationa. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 453–465. [Google Scholar] [CrossRef]
- Antol, S.; Zitnick, C.L.; Parikh, D. Zero-shot learning via visual abstraction. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; ISBN 9783319105925. [Google Scholar]
- Mensink, T.; Gavves, E.; Snoek, C.G.M. COSTA: Co-occurrence statistics for zero-shot classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2441–2448. [Google Scholar]
- Lu, N.; Sun, Y.; Yun, X. Hybrid Relative attributes based on sparse coding for zero-shot image classification. Math. Probl. Eng. 2019, 2019, 7390327. [Google Scholar] [CrossRef]
- Rusk, N. Computer Vision—ECCV 2016. Part II; Springer: Cham, Switzerland, 2016; Volume 9905, ISBN 978-3-319-46447-3. [Google Scholar]
- Xian, Y.; Lampert, C.H.; Schiele, B.; Akata, Z. Zero-shot learning—A comprehensive evaluation of the good, the bad and the ugly. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 2251–2265. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fu, Y.; Sigal, L. Semi-supervised vocabulary-informed learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5337–5346. [Google Scholar]
- Li, W.; Guo, Q. A new accuracy assessment method for one-class remote sensing classification. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4621–4632. [Google Scholar]
- Liu, P. A survey of remote-sensing big data. Front. Environ. Sci. 2015, 3, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Sameen, M.I.; Pradhan, B.; Aziz, O.S. Classification of very high resolution aerial photos using spectral-spatial convolutional neural networks. J. Sens. 2018, 2018, 7195432. [Google Scholar] [CrossRef] [Green Version]
- Xian, Y.; Akata, Z.; Sharma, G.; Nguyen, Q.; Hein, M.; Schiele, B. Latent embeddings for zero-shot classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 69–77. [Google Scholar]
- Wang, Q.; Chen, K. Zero-shot visual recognition via bidirectional latent embedding. Int. J. Comput. Vis. 2017, 124, 356–383. [Google Scholar] [CrossRef]
- Shi, Y.; Xu, D.; Pan, Y.; Tsang, I.W.; Pan, S. Label embedding with partial heterogeneous contexts. In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI-19), Honolulu, HI, USA, 27 January–1 February 2019; pp. 4926–4933. [Google Scholar]
- Xu, D.; Shi, Y.; Tsang, I.W.; Ong, Y.; Gong, C.; Shen, X. A survey on multi-output learning. IEEE Trans. Neural Netw. Learn. Syst. 2019, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Sumbul, G.; Cinbis, R.G.; Aksoy, S. Fine-grained object recognition and zero-shot learning in remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2018, 56, 770–779. [Google Scholar] [CrossRef] [Green Version]
- Zerrouki, N.; Bouchaffra, D. Pixel-based or object-based: Which approach is more appropriate for remote sensing image classification? In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, San Diego, CA, USA, 5–8 October 2014; pp. 864–869. [Google Scholar]
- Hagiwara, K.; Hayasaka, T.; Toda, N.; Usui, S.; Kuno, K. Upper bound of the expected training error of neural network regression for a Gaussian noise sequence. Neural Networks 2001, 14, 1419–1429. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a Gaussian denoiser: Residual learning of deep CNN for image denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gu, S.; Rigazio, L. Towards deep neural network architectures robust to adversarial examples. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015; pp. 1–9. [Google Scholar]
- Chen, W.; Guang, Y.; Fengjing, Z.; Liu, Y.; Yuan, Y.; Jicheng, Q. Zero-Shot Classification Method for Remote-Sensing Scenes Based on Word Vector Consistent Fusion. Acta Optica Sinica 2019, 39, 0828002. [Google Scholar] [CrossRef]
- Makantasis, K.; Doulamis, A.D.; Doulamis, N.D.; Nikitakis, A. Tensor-based classification models for hyperspectral data analysis. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6884–6898. [Google Scholar] [CrossRef]
- Kossaifi, J.; Lipton, Z.C.; Khanna, A.; Furlanello, T.; Anandkumar, A. Tensor Regression Networks. arXiv 2017, arXiv:1707.08308. [Google Scholar]

| Details of Layers | CNN-1 | CNN-2 |
|---|---|---|
| Duty | Feature extraction | Class signature prediction |
| Kernel size | 3 × 3 | 3x3 |
| Number of filters | 64 | 128 |
| Activation function | ReLU | ReLU |
| Drop out | 0.3 | 0.3 |
| Flatten layers | 1 | None |
| Dense layers | 1 | 2 |
| Size of dense layers | 32 | 64/300 (# attributes) |
| Classifier | Softmax | Softmax |
| Optimiser | Adam (L. Rate = 0.001) | Adam (L. Rate = 0.001) |
| Batch size | 2,048 | 2,048 |
| Iterations | 100 | 100 |
| Model | Metric | Training Area | First Test Area | Second Test Area |
|---|---|---|---|---|
| CNN without Batch Normalisation layer | Recall | 0.780 | 0.748 | 0.733 |
| Precision | 0.927 | 0.885 | 0.826 | |
| F1 | 0.882 | 0.845 | 0.815 | |
| Top-three | 0.947 | 0.897 | 0.924 | |
| Top-two | 0.857 | 0.789 | 0.846 | |
| Top-one | 0.696 | 0.673 | 0.649 | |
| CNN without Pooling layer | Recall | 0.882 | 0.949 | 0.838 |
| Precision | 0.941 | 0.869 | 0.870 | |
| F1 | 0.953 | 0.904 | 0.898 | |
| Top-three | 0.963 | 0.963 | 0.947 | |
| Top-two | 0.892 | 0.911 | 0.886 | |
| Top-one | 0.760 | 0.805 | 0.708 | |
| CNN without Batch normalisation and pooling layers | Recall | 0.834 | 0.807 | 0.777 |
| Precision | 0.936 | 0.860 | 0.844 | |
| F1 | 0.921 | 0.874 | 0.850 | |
| Top-three | 0.957 | 0.905 | 0.938 | |
| Top-two | 0.877 | 0.804 | 0.866 | |
| Top-one | 0.733 | 0.684 | 0.675 | |
| CNN with batch normalisation and pooling layers | Recall | 0.859 | 0.835 | 0.809 |
| Precision | 0.941 | 0.877 | 0.857 | |
| F1 | 0.939 | 0.899 | 0.875 | |
| Top-three | 0.959 | 0.904 | 0.939 | |
| Top-two | 0.882 | 0.812 | 0.875 | |
| Top-one | 0.747 | 0.709 | 0.691 |
| Number of Filters in Conv. Layer | Metric | Training Area | First Test Area | Second Test Area |
|---|---|---|---|---|
| 128 | Recall | 0.896 | 0.853 | 0.764 |
| Precision | 0.946 | 0.854 | 0.881 | |
| F1 | 0.964 | 0.900 | 0.817 | |
| Top-three | 0.966 | 0.889 | 0.931 | |
| Top-two | 0.899 | 0.810 | 0.858 | |
| Top-one | 0.770 | 0.704 | 0.630 | |
| 64 | Recall | 0.882 | 0.949 | 0.838 |
| Precision | 0.941 | 0.869 | 0.870 | |
| F1 | 0.953 | 0.904 | 0.898 | |
| Top-three | 0.963 | 0.963 | 0.947 | |
| Top-two | 0.892 | 0.911 | 0.886 | |
| Top-one | 0.760 | 0.805 | 0.708 | |
| 32 | Recall | 0.871 | 0.931 | 0.810 |
| Precision | 0.941 | 0.963 | 0.858 | |
| F1 | 0.946 | 0.971 | 0.876 | |
| Top-three | 0.962 | 0.959 | 0.940 | |
| Top-two | 0.887 | 0.905 | 0.875 | |
| Top-one | 0.753 | 0.793 | 0.692 |
| Number of Conv. Layers | Metric | Training Area | First Test Area | Second Test Area |
|---|---|---|---|---|
| 1 Conv2D layer | Recall | 0.882 | 0.949 | 0.838 |
| Precision | 0.941 | 0.869 | 0.870 | |
| F1 | 0.953 | 0.904 | 0.898 | |
| Top-three | 0.963 | 0.963 | 0.947 | |
| Top-two | 0.892 | 0.911 | 0.886 | |
| Top-one | 0.760 | 0.805 | 0.708 | |
| 2 Conv2D layers | Recall | 0.805 | 0.882 | 0.705 |
| Precision | 0.939 | 0.971 | 0.824 | |
| F1 | 0.903 | 0.965 | 0.795 | |
| Top-three | 0.948 | 0.951 | 0.913 | |
| Top-two | 0.863 | 0.890 | 0.836 | |
| Top-one | 0.719 | 0.770 | 0.634 | |
| 3 Conv2D layers | Recall | 0.791 | 0.827 | 0.761 |
| Precision | 0.941 | 0.901 | 0.850 | |
| F1 | 0.894 | 0.939 | 0.842 | |
| Top-three | 0.944 | 0.938 | 0.930 | |
| Top-two | 0.860 | 0.870 | 0.855 | |
| Top-one | 0.712 | 0.742 | 0.669 |
| Noise Impact | Metric | Training Area | First Test Area | Second Test Area |
|---|---|---|---|---|
| Without noise | Recall | 0.882 | 0.949 | 0.838 |
| Precision | 0.941 | 0.869 | 0.870 | |
| F1 | 0.953 | 0.904 | 0.898 | |
| Top-three | 0.963 | 0.963 | 0.947 | |
| Top-two | 0.892 | 0.911 | 0.886 | |
| Top-one | 0.760 | 0.805 | 0.708 | |
| With noise | Recall | 0.858 | 0.933 | 0.816 |
| Precision | 0.931 | 0.864 | 0.861 | |
| F1 | 0.934 | 0.893 | 0.881 | |
| Top-three | 0.959 | 0.960 | 0.941 | |
| Top-two | 0.882 | 0.906 | 0.877 | |
| Top-one | 0.742 | 0.795 | 0.695 |
| Unseen Class | F1-Score | Recall | Precision | Top-One | Top-Two | Top-Three |
|---|---|---|---|---|---|---|
| Agricultural land | 0.862 | 0.827 | 0.899 | 0.831 | 0.918 | 0.952 |
| Barren land | 0.842 | 0.809 | 0.877 | 0.813 | 0.914 | 0.952 |
| Urban areas | 0.825 | 0.782 | 0.874 | 0.796 | 0.897 | 0.944 |
| Road | 0.819 | 0.872 | 0.772 | 0.790 | 0.894 | 0.943 |
| Forest lands | 0.803 | 0.750 | 0.863 | 0.775 | 0.884 | 0.938 |
| Croplands | 0.639 | 0.558 | 0.747 | 0.665 | 0.837 | 0.927 |
| Average | 0.798 | 0.766 | 0.838 | 0.778 | 0.890 | 0.942 |
| Unseen Class | F1-Score | Recall | Precision | Top-One | Top-Two | Top-Three |
|---|---|---|---|---|---|---|
| Without batch normalisation | ||||||
| Urban areas | 0.831 | 0.776 | 0.893 | 0.831 | 0.925 | 0.976 |
| Barren land | 0.863 | 0.824 | 0.906 | 0.862 | 0.943 | 0.979 |
| Agricultural land | 0.874 | 0.841 | 0.910 | 0.873 | 0.948 | 0.978 |
| Forest lands | 0.612 | 0.527 | 0.731 | 0.646 | 0.862 | 0.952 |
| Road | 0.829 | 0.774 | 0.893 | 0.830 | 0.924 | 0.975 |
| Water body | 0.830 | 0.775 | 0.893 | 0.830 | 0.924 | 0.975 |
| Mean | 0.806 | 0.752 | 0.871 | 0.812 | 0.921 | 0.972 |
| With batch normalisation | ||||||
| Urban areas | 0.832 | 0.780 | 0.892 | 0.833 | 0.927 | 0.976 |
| Barren land | 0.865 | 0.827 | 0.907 | 0.864 | 0.944 | 0.980 |
| Agricultural land | 0.876 | 0.844 | 0.911 | 0.875 | 0.950 | 0.979 |
| Forest lands | 0.621 | 0.536 | 0.738 | 0.652 | 0.866 | 0.953 |
| Road | 0.832 | 0.780 | 0.892 | 0.833 | 0.927 | 0.976 |
| Water body | 0.832 | 0.780 | 0.892 | 0.832 | 0.926 | 0.975 |
| Mean | 0.809 | 0.757 | 0.872 | 0.814 | 0.923 | 0.973 |
| Unseen Class | F1-Score | Recall | Precision | Top-One | Top-Two | Top-Three |
|---|---|---|---|---|---|---|
| Without batch normalisation | ||||||
| Urban areas | 0.819 | 0.773 | 0.871 | 0.791 | 0.891 | 0.931 |
| Barren land | 0.837 | 0.802 | 0.876 | 0.808 | 0.910 | 0.941 |
| Agricultural land | 0.859 | 0.822 | 0.898 | 0.828 | 0.905 | 0.940 |
| Forest lands | 0.797 | 0.741 | 0.863 | 0.770 | 0.879 | 0.925 |
| Road | 0.814 | 0.765 | 0.870 | 0.786 | 0.889 | 0.931 |
| Croplands | 0.624 | 0.539 | 0.742 | 0.655 | 0.860 | 0.914 |
| Mean | 0.791 | 0.740 | 0.853 | 0.773 | 0.889 | 0.930 |
| With batch normalisation | ||||||
| Urban areas | 0.825 | 0.782 | 0.874 | 0.796 | 0.897 | 0.944 |
| Barren land | 0.842 | 0.809 | 0.877 | 0.813 | 0.914 | 0.952 |
| Agricultural land | 0.862 | 0.827 | 0.899 | 0.831 | 0.918 | 0.952 |
| Forest lands | 0.803 | 0.750 | 0.863 | 0.775 | 0.884 | 0.938 |
| Road | 0.819 | 0.872 | 0.772 | 0.790 | 0.894 | 0.943 |
| Croplands | 0.639 | 0.558 | 0.747 | 0.665 | 0.837 | 0.927 |
| Mean | 0.798 | 0.751 | 0.838 | 0.778 | 0.890 | 0.942 |
| Unseen Class | F1-Score | Recall | Precision | Top-One | Top-Two | Top-Three |
|---|---|---|---|---|---|---|
| Without batch normalisation | ||||||
| Green space | 0.749 | 0.694 | 0.813 | 0.754 | 0.907 | 0.924 |
| Urban areas | 0.729 | 0.679 | 0.787 | 0.737 | 0.903 | 0.928 |
| Barren land | 0.709 | 0.653 | 0.776 | 0.721 | 0.900 | 0.928 |
| Agricultural land | 0.724 | 0.673 | 0.783 | 0.732 | 0.905 | 0.918 |
| Forest lands | 0.713 | 0.656 | 0.781 | 0.723 | 0.894 | 0.905 |
| Road | 0.728 | 0.675 | 0.790 | 0.737 | 0.903 | 0.922 |
| Water body | 0.705 | 0.648 | 0.773 | 0.716 | 0.897 | 0.917 |
| Mean | 0.722 | 0.668 | 0.786 | 0.731 | 0.901 | 0.920 |
| With batch normalisation | ||||||
| Green space | 0.755 | 0.702 | 0.817 | 0.760 | 0.912 | 0.937 |
| Urban areas | 0.737 | 0.688 | 0.792 | 0.744 | 0.908 | 0.921 |
| Barren land | 0.717 | 0.664 | 0.779 | 0.728 | 0.905 | 0.922 |
| Agricultural land | 0.729 | 0.678 | 0.788 | 0.737 | 0.909 | 0.923 |
| Forest lands | 0.721 | 0.664 | 0.787 | 0.730 | 0.900 | 0.918 |
| Road | 0.735 | 0.684 | 0.794 | 0.743 | 0.907 | 0.920 |
| Water body | 0.712 | 0.655 | 0.778 | 0.722 | 0.901 | 0.929 |
| Mean | 0.729 | 0.676 | 0.790 | 0.737 | 0.906 | 0.924 |
| Number of Neurons | Metric | Training Area | First Test Area | Second Test Area |
|---|---|---|---|---|
| 128 | Recall | 0.780 | 0.782 | 0.688 |
| Precision | 0.892 | 0.874 | 0.792 | |
| F1 | 0.832 | 0.825 | 0.737 | |
| Top-three | 0.976 | 0.944 | 0.921 | |
| Top-two | 0.927 | 0.897 | 0.908 | |
| Top-one | 0.833 | 0.796 | 0.744 | |
| 64 | Recall | 0.775 | 0.772 | 0.677 |
| Precision | 0.892 | 0.870 | 0.784 | |
| F1 | 0.829 | 0.818 | 0.727 | |
| Top-three | 0.975 | 0.941 | 0.927 | |
| Top-two | 0.924 | 0.891 | 0.872 | |
| Top-one | 0.829 | 0.790 | 0.735 | |
| 32 | Recall | 0.766 | 0.763 | 0.661 |
| Precision | 0.892 | 0.868 | 0.775 | |
| F1 | 0.824 | 0.812 | 0.714 | |
| Top-three | 0.973 | 0.938 | 0.913 | |
| Top-two | 0.920 | 0.896 | 0.865 | |
| Top-one | 0.826 | 0.814 | 0.724 |
| Metric | Training Area | First Test Area | Second Test Area | |
|---|---|---|---|---|
| Without noise | Recall | 0.780 | 0.782 | 0.688 |
| Precision | 0.892 | 0.874 | 0.792 | |
| F1 | 0.832 | 0.825 | 0.737 | |
| Top-three | 0.976 | 0.944 | 0.921 | |
| Top-two | 0.927 | 0.897 | 0.908 | |
| Top-one | 0.833 | 0.796 | 0.744 | |
| With noise | Recall | 0.762 | 0.779 | 0.679 |
| Precision | 0.873 | 0.882 | 0.785 | |
| F1 | 0.810 | 0.811 | 0.719 | |
| Top-three | 0.957 | 0.929 | 0.901 | |
| Top-two | 0.917 | 0.875 | 0.886 | |
| Top-one | 0.820 | 0.787 | 0.723 |
| Unseen Class | F1-Score | Recall | Precision | Top-One | Top-Two | Top-Three |
|---|---|---|---|---|---|---|
| Green space | 0.755 | 0.702 | 0.817 | 0.760 | 0.912 | 0.937 |
| Urban areas | 0.737 | 0.688 | 0.792 | 0.744 | 0.908 | 0.921 |
| Road | 0.735 | 0.684 | 0.794 | 0.743 | 0.907 | 0.920 |
| Agricultural land | 0.729 | 0.678 | 0.788 | 0.737 | 0.909 | 0.923 |
| Forest lands | 0.721 | 0.664 | 0.787 | 0.730 | 0.900 | 0.918 |
| Barren land | 0.717 | 0.664 | 0.779 | 0.728 | 0.905 | 0.922 |
| Water body | 0.712 | 0.655 | 0.778 | 0.722 | 0.901 | 0.929 |
| Average | 0.729 | 0.676 | 0.790 | 0.737 | 0.906 | 0.924 |
| ZSL Applications On Remote Sensing | Data | Approach | Accuracy | Unseen/Seen Ratio |
|---|---|---|---|---|
| Land cover classification (Current study) | Aerial images | 2 CNNs-based structure | Average: F1-score: 0.798 Precision: 0.838 Recall: 0.766 Top-one: 0.778 Top-two:0.890 Top-three: 0.942 | 1/6 |
| Land cover classification | PolSAR image with 8-meters resolution | Embedding space and latent embedding | Overall: 73% | 1/3–3/3 |
| Object detection | High-resolution satellite image | Label propagation and label refinement | Overall: 58.7% Overall: 70.4% | 5/16 1/7 |
| Street trees detection | Aerial images | CNN-based structure | Average: 14.3% | 16/40 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pradhan, B.; Al-Najjar, H.A.H.; Sameen, M.I.; Tsang, I.; Alamri, A.M. Unseen Land Cover Classification from High-Resolution Orthophotos Using Integration of Zero-Shot Learning and Convolutional Neural Networks. Remote Sens. 2020, 12, 1676. https://doi.org/10.3390/rs12101676
Pradhan B, Al-Najjar HAH, Sameen MI, Tsang I, Alamri AM. Unseen Land Cover Classification from High-Resolution Orthophotos Using Integration of Zero-Shot Learning and Convolutional Neural Networks. Remote Sensing. 2020; 12(10):1676. https://doi.org/10.3390/rs12101676
Chicago/Turabian StylePradhan, Biswajeet, Husam A. H. Al-Najjar, Maher Ibrahim Sameen, Ivor Tsang, and Abdullah M. Alamri. 2020. "Unseen Land Cover Classification from High-Resolution Orthophotos Using Integration of Zero-Shot Learning and Convolutional Neural Networks" Remote Sensing 12, no. 10: 1676. https://doi.org/10.3390/rs12101676
APA StylePradhan, B., Al-Najjar, H. A. H., Sameen, M. I., Tsang, I., & Alamri, A. M. (2020). Unseen Land Cover Classification from High-Resolution Orthophotos Using Integration of Zero-Shot Learning and Convolutional Neural Networks. Remote Sensing, 12(10), 1676. https://doi.org/10.3390/rs12101676








