Beyond Amplitudes: Multi-Trace Coherence Analysis for Ground-Penetrating Radar Data Imaging
Abstract
1. Introduction
2. Material and Methods
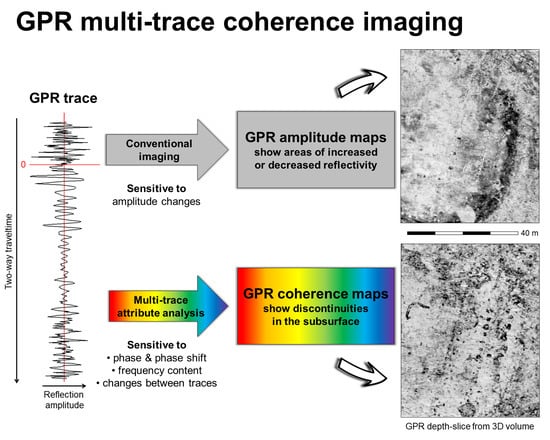
2.1. Seismic Trace Attribute Analysis
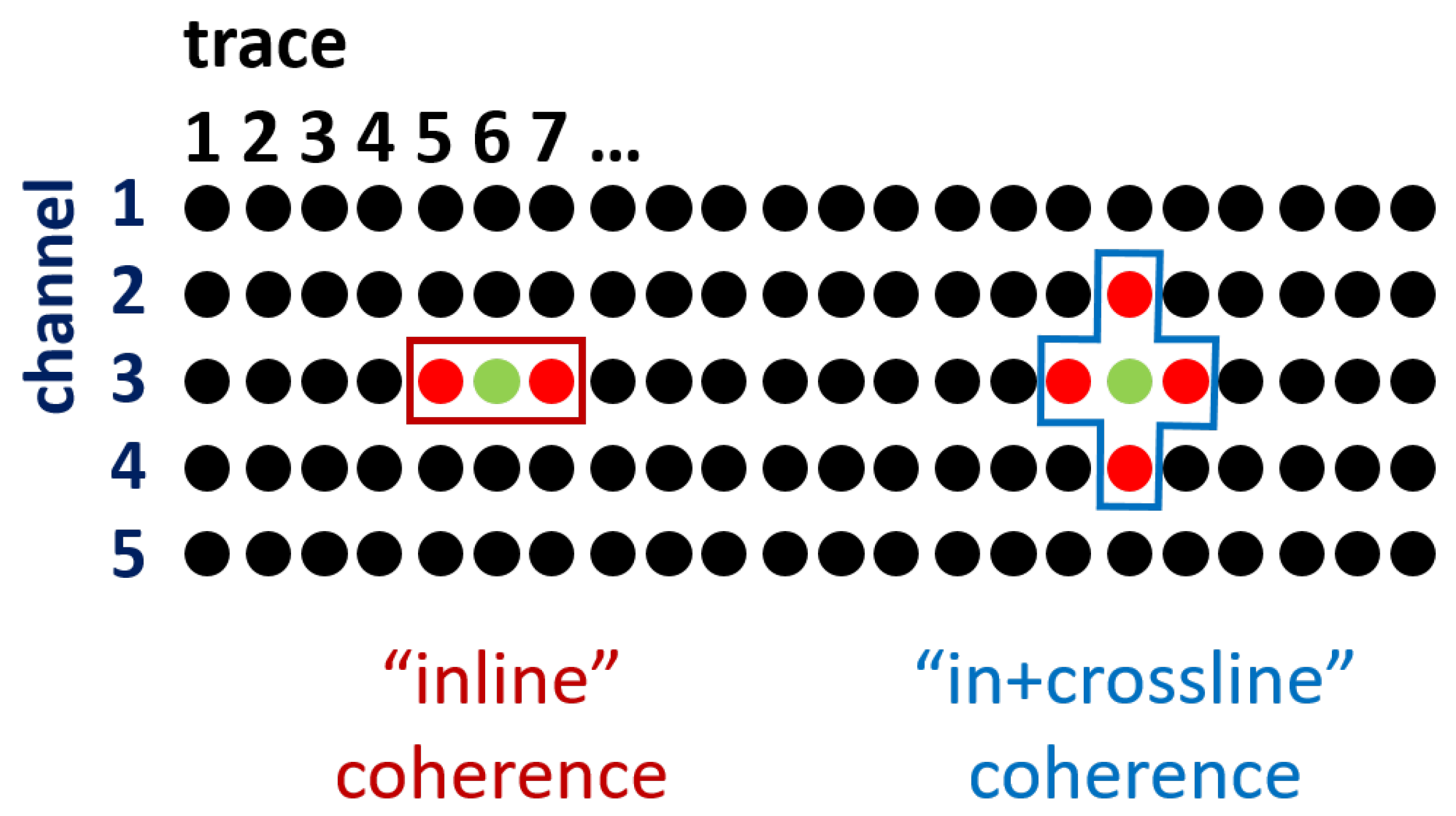
2.2. GPR Coherence and Discontinuity Analysis
 ), the one before and the one after (
), the one before and the one after ( ). Thus, two coherences are computed, and , to determine :
). Thus, two coherences are computed, and , to determine :3. Results—Coherence Imaging Examples
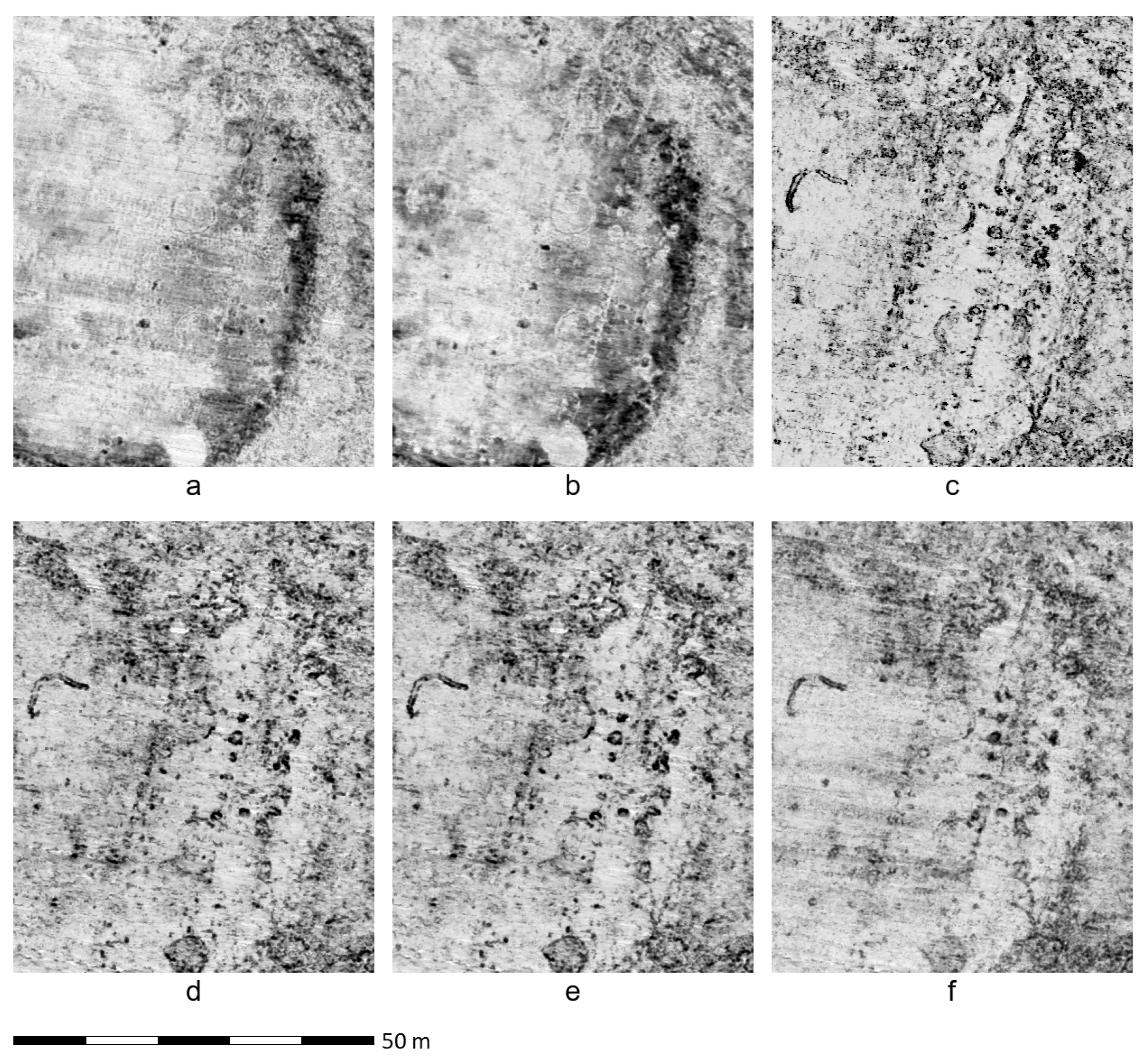
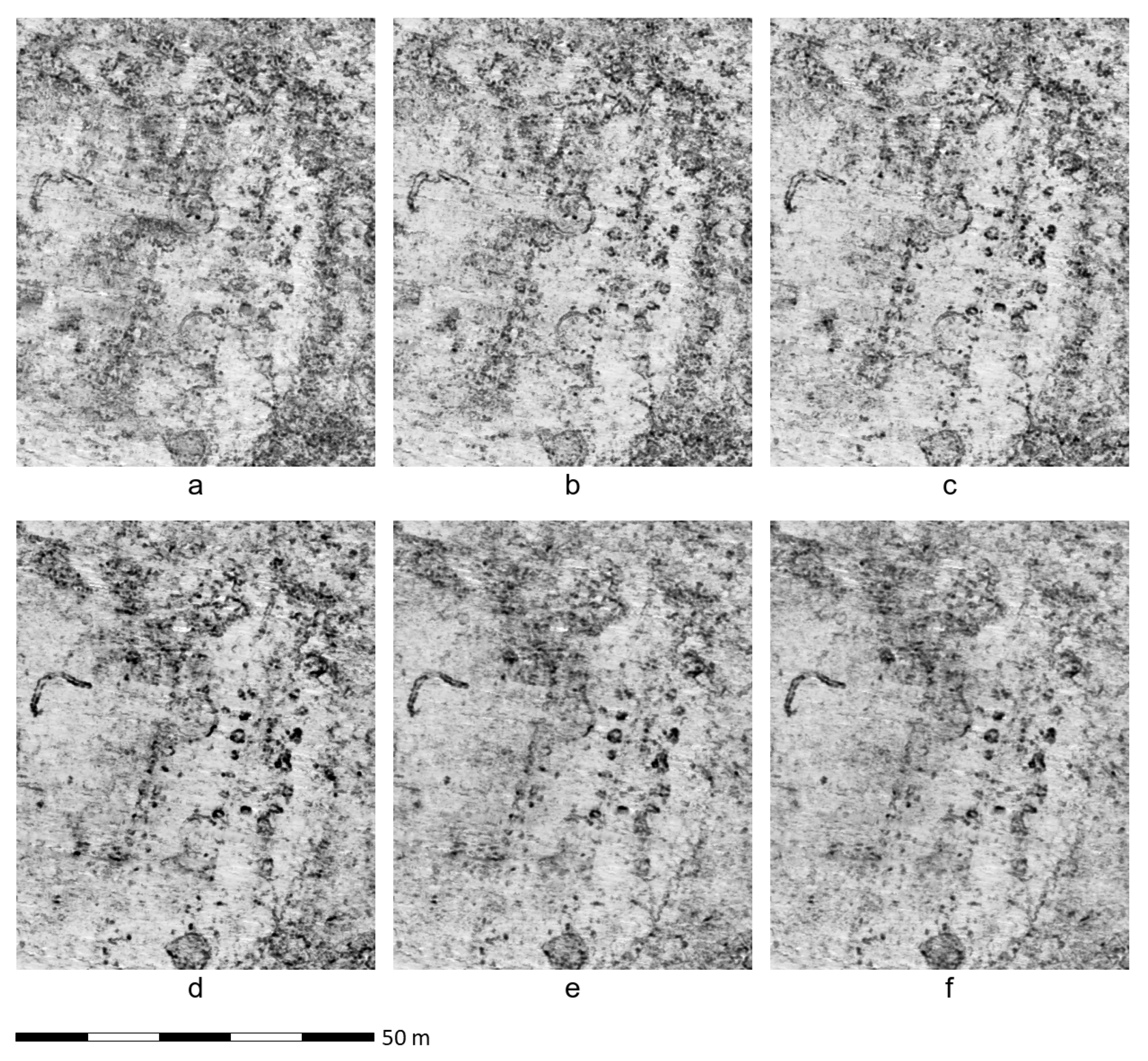
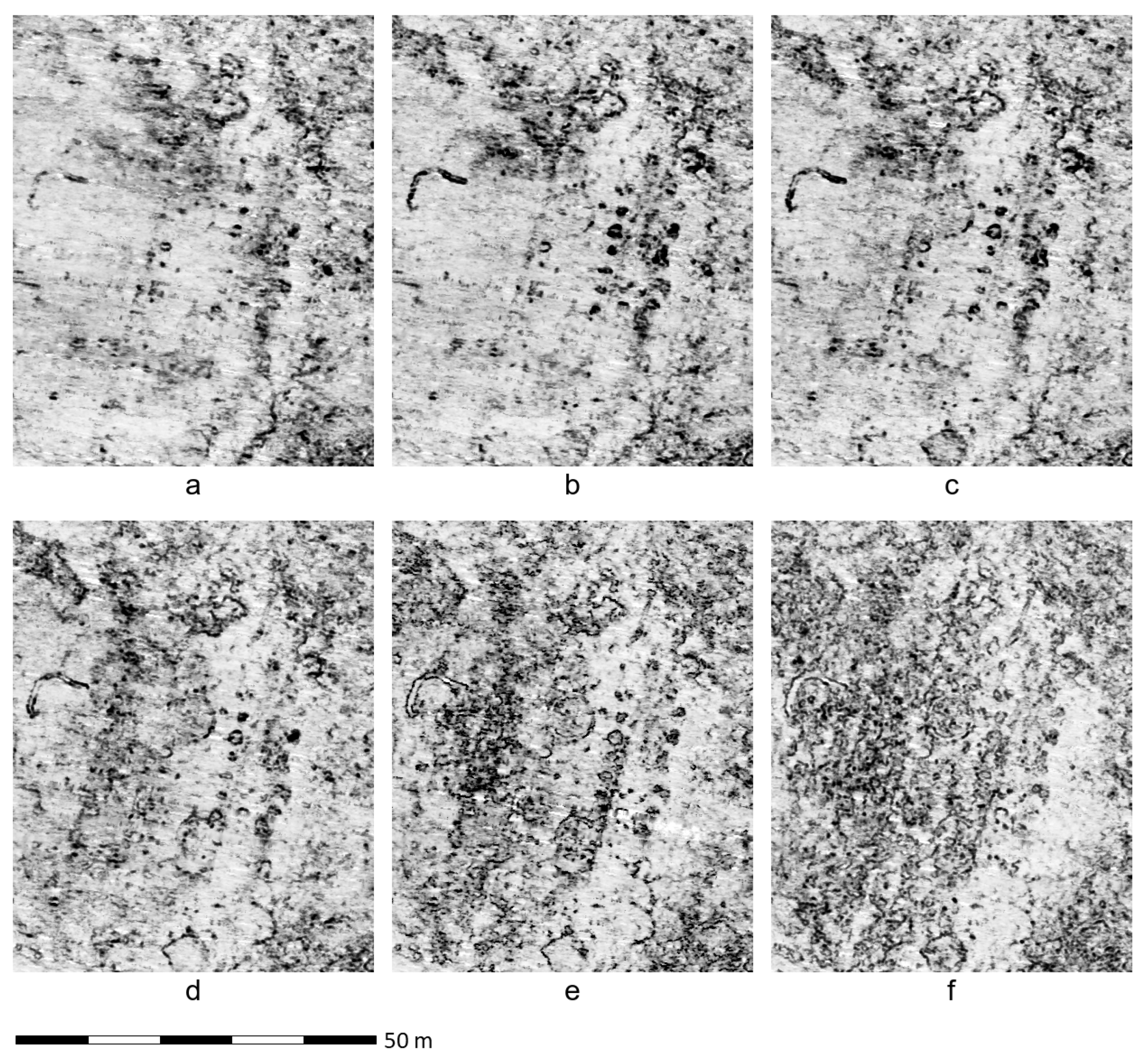
3.1. Rysensten—Denmark
3.2. Stadil Mølleby—Denmark
3.3. Gjellestad Viking Ship Burial
4. Discussion
- is an excellent tool for delineating geological boundaries (faults, lateral stratigraphic contacts, etc.),
- allows accelerated evaluation of large data sets,
- provides quantitative estimate of fault/fracture presence,
- often enhances stratigraphic information that is otherwise difficult to extract,
- algorithms are local—faults that have drag, are poorly migrated, or separate two similar reflectors, or otherwise do not appear locally to be discontinuous, will not show up on coherence volumes”.
5. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AT | Average-Trace |
| LBI ArchPro | Ludwig Boltzmann Institute for Archaeological Prospection and Virtual Archaeology |
| GPR | Ground-Penetrating Radar |
| GST | Gradient Structure Tensor |
References
- Conyers, L. Ground-Penetrating Radar for Archaeology, 3rd ed.; Rowman and Littlefield Publishers, Alta Mira Press: Lanham, MD, USA, 2013. [Google Scholar]
- Leckebusch, J. Ground-penetrating Radar: A Modern Three-dimensional Prospection Method. Archaeol. Prospect. 2003, 10, 213–240. [Google Scholar] [CrossRef]
- Trinks, I.; Hinterleitner, A.; Neubauer, W.; Nau, E.; Löcker, K.; Wallner, M.; Gabler, M.; Filzwieser, R.; Wilding, J.; Schiel, H.; et al. Large-area high-resolution ground-penetrating radar measurements for archaeological prospection. Archaeol. Prospect. 2018, 25, 171–195. [Google Scholar] [CrossRef]
- Filzwieser, R.; Olesen, L.H.; Neubauer, W.; Trinks, I.; Schlosser Mauritsen, E.; Schneidhofer, P.; Nau, E.; Gabler, M. Large-scale geophysical archaeological prospection pilot study at Viking Age and medieval sites in west Jutland, Denmark. Archaeol. Prospect. 2017, 24, 373–393. [Google Scholar] [CrossRef]
- Goodman, D.; Nishimura, Y.; Rodgers, J.D. GPR Time Slices in Archaeological Prospection. Archaeol. Prospect. 1995, 2, 85–89. [Google Scholar]
- Daniels, D.J. Ground penetrating radar. In Encyclopedia of RF and Microwave Engineering; Chang, K., Ed.; Wiley-Interscience: Hoboken, NJ, USA, 2005. [Google Scholar]
- Trinks, I.; Johansson, B.; Gustafsson, J.; Emilsson, J.; Friborg, J.; Gustafsson, C.; Nissen, J.; Hinterleitner, A. Efficient, large-scale archaeological prospection using a true three-dimensional ground-penetrating radar array system. Archaeol. Prospect. 2010, 17, 175–186. [Google Scholar] [CrossRef]
- Fisher, S.C.; Stewart, R.R.; Jol, H.M. Ground Penetrating Radar (GPR) Data Enhancement Using Seismic Techniques. J. Environ. Eng. Geophys. 1996, 1, 89–157. [Google Scholar] [CrossRef]
- Chopra, S.; Marfurt, K.J. Seismic attributes—A historical perspective. Geophysics 2005, 70, 3SO–28SO. [Google Scholar] [CrossRef]
- Chopra, S.; Marfurt, K.J. Seismic attributes—A promising aid for geological prediction. CSEG Recorder 2006, 31, 115–126. [Google Scholar]
- Randen, T.; Sønneland, L. Atlas of 3D Seismic Attributes. In Mathematical Methods and Modelling in Hydrocarbon Exploration and Production. Mathematics in Industry; Iske, A., Randen, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Sheriff, R.E. Encyclopedic Dictionary of Applied Geophysics, 4th ed.; Society of Exploration Geophysicists: Houston, TX, USA, 2002. [Google Scholar]
- Eastwood, J. Introduction—The attribute explosion. Lead. Edge 2002, 21, 994–995. [Google Scholar] [CrossRef]
- Taner, M.T.; Koehler, F.; Sheriff, R.E. Complex seismic trace analysis. Geophysics 1979, 44, 1041–1063. [Google Scholar] [CrossRef]
- Tronicke, J.; Böninger, J. GPR attribute analysis: There is more than amplitudes. First Break 2013, 31, 103–108. [Google Scholar]
- Wikipedia Contributors. Seismic Attribute—Wikipedia, The Free Encyclopedia. 2018. Available online: https://en.wikipedia.org/wiki/Seismic_attribute (accessed on 15 May 2020).
- Chopra, S.; Marfurt, K.J. Seismic Attributes for Prospect ID and Reservoir Characterization; SEG/EAGE, 2007. Available online: https://library.seg.org/doi/abs/10.1190/1.9781560801900 (accessed on 15 May 2020).
- Marfurt, K.J. Attribute-Assisted Seismic Processing & Interpretation. Available online: http://mcee.ou.edu/aaspi/index.html (accessed on 15 May 2020).
- Chopra, S. Adding the coherence dimension to 3D seismic data. CSEG Rec. 2001, 26, 5–8. [Google Scholar]
- Nissen, S.; Interpretive Aspects of Seismic Coherence and Related Multi-trace Attributes; Reservoir Characteristics of Morrow/Incised-Valley Fill Plays Workshop & Morrow Incised-Valley Core Workshop. Kansas Geological Surveys, Wichita, Kansas, February 2000. Available online: http://www.kgs.ku.edu/Workshops/IVF2000/nissan-ivf/tocnav1.html (accessed on 15 May 2020).
- Lyatsky, H. The Meaning of Anomaly. Explor. Geophys. 2004, 29, 50–51. [Google Scholar]
- Grasmueck, M. 3-D ground-penetrating radar applied to fracture imaging in gneiss. Geophysics 1996, 61, 1050–1064. [Google Scholar] [CrossRef]
- Henryk, M.; Golebiowski, T. Analysis of GPR Trace Attributes and Spectra for LNAPL Contaminated Ground. In Proceedings of the Near Surface 2006—12th EAGE European Meeting of Environmental and Engineering Geophysics, Helsinki, Finland, 4–6 September 2006. [Google Scholar]
- Böninger, U. Attributes and their potential to analyze and interpret 3D GPR data. Ph.D. Thesis, Potsdam University, Potsdam, Germany, 2010. [Google Scholar]
- Böninger, U.; Tronicke, J. Integrated data analysis at an archaeological site: A case study using 3D GPR, magnetic, and high-resolution topographic data. Geophysics 2010, 75, B169–B176. [Google Scholar] [CrossRef]
- Böninger, U.; Tronicke, J. Improving the interpretability of 3D GPR data using target-specific attributes: Application to tomb-detection. J. Archaeol. Sci. 2010, 37, 360–367. [Google Scholar] [CrossRef]
- Böninger, U.; Tronicke, J. Subsurface Utility Extraction and Characterization: Combining GPR Symmetry and Polarization Attributes. IEEE Trans. Geosci. Remote. Sens. 2012, 50, 736–746. [Google Scholar] [CrossRef]
- Zhao, W.; Forte, E.; Pipan, M.; Tian, G. Ground Penetrating Radar (GPR) attribute analysis for archaeological prospection. J. Appl. Geophys. 2013, 97, 107–117. [Google Scholar] [CrossRef]
- Zhao, W.; Tian, G.; Wang, B.; Forte, E.; Pipan, M.; Lin, J.; Shi, Z.; Li, X. 2D and 3D imaging of a buried prehistoric canoe using GPR attributes: A case study. Near Surf. Geophys. 2013, 11, 457–464. [Google Scholar] [CrossRef]
- Zhao, W.; Forte, E.; Pipan, M. Texture Attribute Analysis of GPR Data for Archaeological Prospection. Pure Appl. Geophys. 2016, 173, 2737–2751. [Google Scholar] [CrossRef]
- Morris, I.; Abdel-Jaber, H.; Glisic, B. Quantitative Attribute Analyses with Ground Penetrating Radar for Infrastructure Assessments and Structural Health Monitoring. Sensors 2019, 19, 1637. [Google Scholar] [CrossRef] [PubMed]
- Kington, J. Semblance, coherence, and other discontinuity attributes. Lead. Edge 2015, 34, 1426–1544. [Google Scholar] [CrossRef]
- Kington, J. Semblance, Coherence, and other Discontinuity Attributes. Available online: https://github.com/seg/tutorials-2015/blob/master/1512_Semblance_coherence_and_discontinuity/Discontinuity_tutorial.ipynb (accessed on 15 May 2020).
- Bahorich, M.; Farmer, S. 3-D seismic discontinuity for faults and stratigraphic features: The coherence cube. Lead. Edge 1995, 14, 1053–1058. [Google Scholar] [CrossRef]
- Marfurt, K.; Kirlin, R.L.; Farmer, S.L.; Bahorich, M.S. 3-D seismic attributes using a semblance-based coherency algorithm. Geophysics 1998, 63, 1150–1165. [Google Scholar] [CrossRef]
- Gersztenkorn, A.; Marfurt, K.J. Eigenstructure-based coherence computations as an aid to 3-D structural and stratigraphic mapping. Geophysics 1999, 64, 1468–1479. [Google Scholar] [CrossRef]
- Marfurt, K.J. Robust estimates of 3D reflector dip and azimuth. Geophysics 2006, 71, 29–40. [Google Scholar] [CrossRef]
- Randen, T.; Monsen, E.; Signer, C.; Abrahamsen, A.; Hansen, J.O.; Sæter, T.; Schlaf, J. Three-dimensional texture attributes for seismic data analysis. In Proceedings of the 70th Annual International Meeting; Expanded Abstracts; SEG: Tulsa, OK, USA, 2000; pp. 668–671. [Google Scholar]
- Filzwieser, R.; Neubauer, W.; Trinks, I.; Olesen, L.; Verhoeven, G.; Mauritsen, E.; Schneidhofer, P.; Nau, E.; Gabler, M. Geofysiske undersøgelser og luftfotoarkæologi i Vestjylland. In Luftfotoarkæologi 2; Olesen, L., Mauritsen, E., Broch, M., Eds.; De Kulturhistoriske Museer i Holstebro Kommune: Copenhagen, Denmark, 2019; pp. 163–177. [Google Scholar]
- Olesen, L.; Mauritsen, E. Luftfotoarkæologi i Danmark; Holstebro Museum: Holstebro, Denmark, 2015; pp. 140–142. [Google Scholar]
- Verhoeven, G.; Nowak, M.; Rebecca, N. Pixel-level image fusion for archaeological interpretative mapping. In Proceedings of the 8th International Congress on Archaeology, Computer Graphics, Cultural Heritage and Innovation ‘ARQUEOLÓGICA 2.0’, Valencia, Spain, 5–7 September 2016; pp. 404–407. [Google Scholar]
- Filzwieser, R.; Olesen, L.; Verhoeven, G.; Mauritsen, E.; Neubauer, W.; Trinks, I.; Nowak, M.; Nowak, R.; Schneidhofer, P.; Nau, E.; et al. Integration of Complementary Archaeological Prospection Data from a Late Iron Age Settlement at Vesterager—Denmark. J. Archaeol. Method Theory 2018, 25, 313–333. [Google Scholar] [CrossRef]
- NIKU. The Gjellestad Ship. Available online: https://www.niku.no/en/prosjekter/jellestadskipet/ (accessed on 15 May 2020).
- Gustavsen, L.; Gjesvold, P.; Gundersen, S.; Hinterleitner, A.; Nau, E.; Paasche, K. Gjellestad—A newly discovered central place in South-East Norway. Antiquity 2020, in press. [Google Scholar]
- SEG Wiki. Coherence. Available online: https://wiki.seg.org/wiki/Coherence (accessed on 15 May 2020).
- Marfurt, K. 3D Seismic Attributes for Prospect Identification and Reservoir Characterization—Introduction; AASPI, University of Oklahoma: Norman, OK, USA, 2016. [Google Scholar]






© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trinks, I.; Hinterleitner, A. Beyond Amplitudes: Multi-Trace Coherence Analysis for Ground-Penetrating Radar Data Imaging. Remote Sens. 2020, 12, 1583. https://doi.org/10.3390/rs12101583
Trinks I, Hinterleitner A. Beyond Amplitudes: Multi-Trace Coherence Analysis for Ground-Penetrating Radar Data Imaging. Remote Sensing. 2020; 12(10):1583. https://doi.org/10.3390/rs12101583
Chicago/Turabian StyleTrinks, Immo, and Alois Hinterleitner. 2020. "Beyond Amplitudes: Multi-Trace Coherence Analysis for Ground-Penetrating Radar Data Imaging" Remote Sensing 12, no. 10: 1583. https://doi.org/10.3390/rs12101583
APA StyleTrinks, I., & Hinterleitner, A. (2020). Beyond Amplitudes: Multi-Trace Coherence Analysis for Ground-Penetrating Radar Data Imaging. Remote Sensing, 12(10), 1583. https://doi.org/10.3390/rs12101583