Predicting Near-Future Built-Settlement Expansion Using Relative Changes in Small Area Populations
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Areas and Data
2.1.1. Built-Settlement Data
2.1.2. Population Data
2.1.3. OpenStreetMap Data
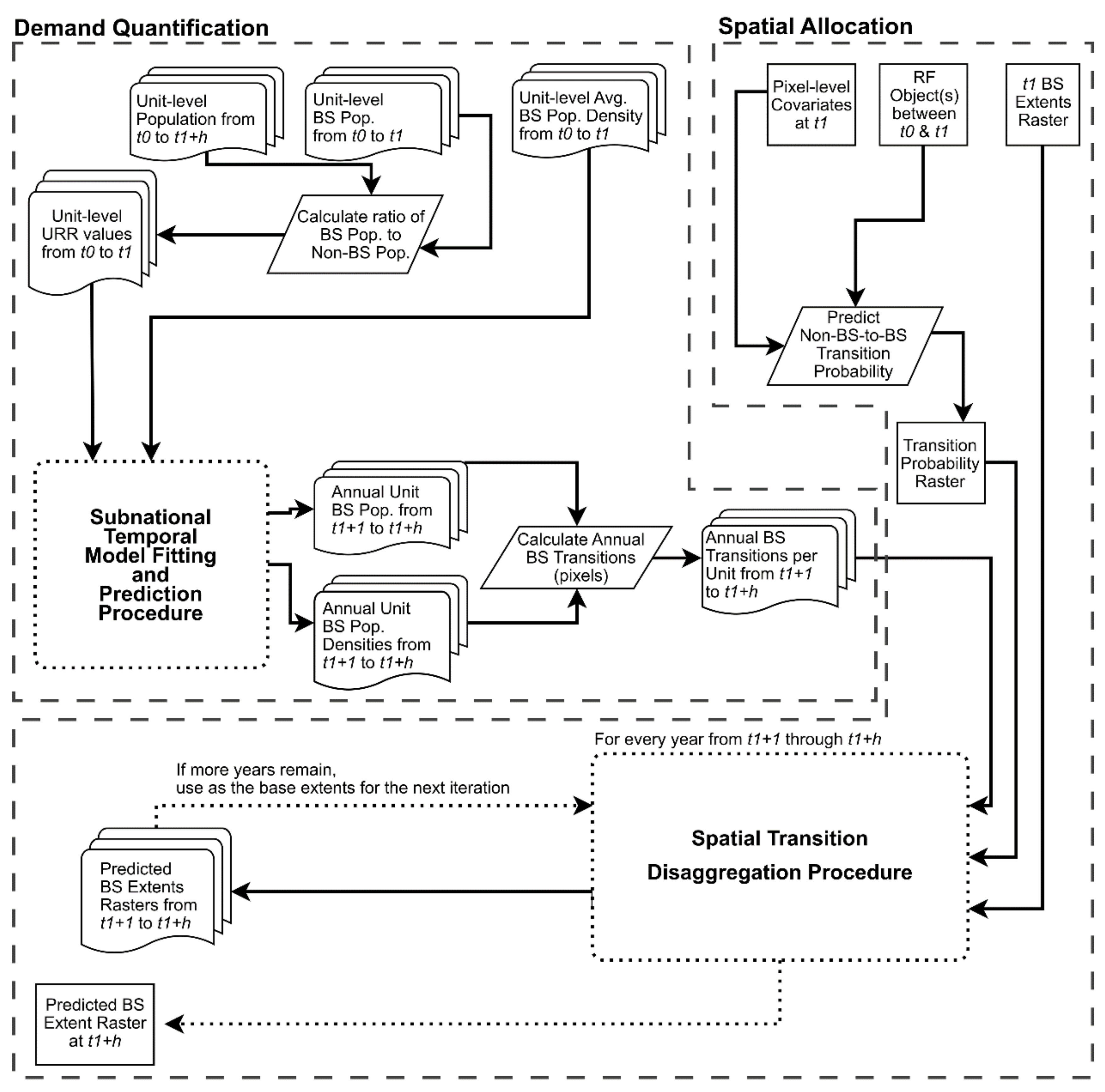
2.2. Built-Settlement Growth Model extrapolation (BSGMe)
2.2.1. Overview
- Create gridded population maps for each year in the input TS, following Stevens et al. [54].
- For all years in the TS, extract the unit-specific population sum that is coincident with the year’s corresponding BS extents and derive the unit-average BS population density
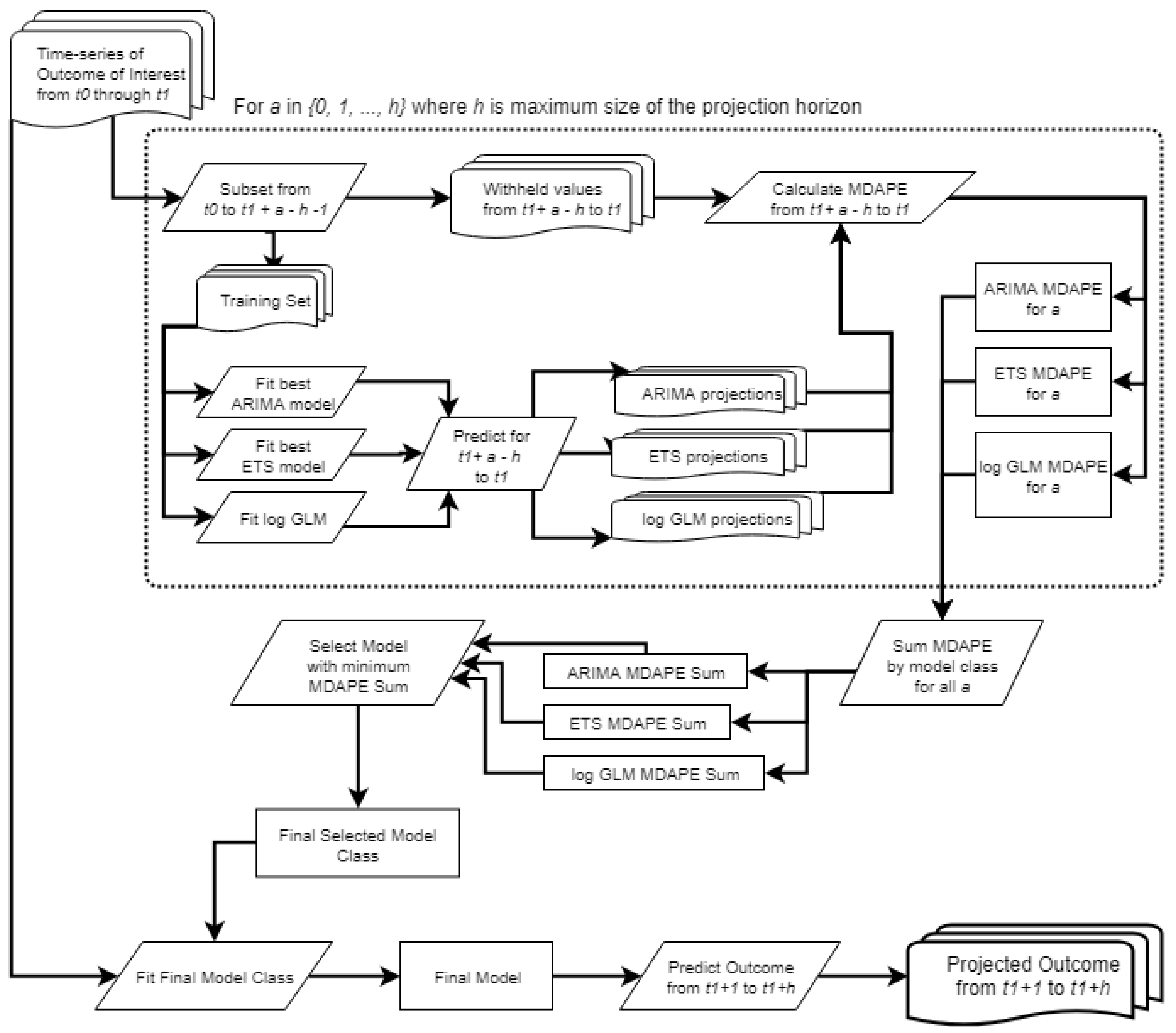
- Independently for each unit, and using a rolling origin validation, select the single best fitting model for BS population and, separately, unit-average BS population density from three classes of models:
- Auto-Regressive Integrated Moving Average (ARIMA),
- Error, Trend, Seasonality (ETS), and
- Generalized Linear Model (GLM) given log-transformed inputs.
- For each unit, use the final selected model for BS population and for unit-average BS population density to predict short-term annual BS population and annual unit-average BS population density starting with year t1+1 and ending with year t1+h, where in this case 1 ≤ h ≤ 5 and represents the projection horizon, in numbers of years.
- Use these estimates to derive the unit-specific annual quantity demand of non-BS-to-BS transitions by dividing the BS population by the BS population density.
- Create a transition probability surface using a Random Forest (RF) based upon the observed transitions between t0 and t1 of the input time-series and covariates corresponding to t0.
- Take the fit relationships between the occurrence of transitions and the predictive covariates, contained in the final RF model, and predict the future non-BS-to-BS transition probability surface using the same covariates, but corresponding to year t1, as the input.
- For each unit and iteratively for all years t1+1 through t1+h, spatially disaggregate the predicted annual unit-level transitions (steps 1–5) using the base transition probability surface (steps 5–6) and, if available, unit-relative weights derived from changes in lights-at-night brightness, similar to Nieves et al. [16].
2.2.2. Demand Quantification
Built-Settlement Population Estimation
Time-Series Model Fitting and Built-Settlement Population Projections
2.2.3. Spatial Allocation
Projecting non-Built-Settlement (BS)-to-BS Transition Probabilities Surface
Annually Adjusting non-BS-to-BS Transition Probabilities
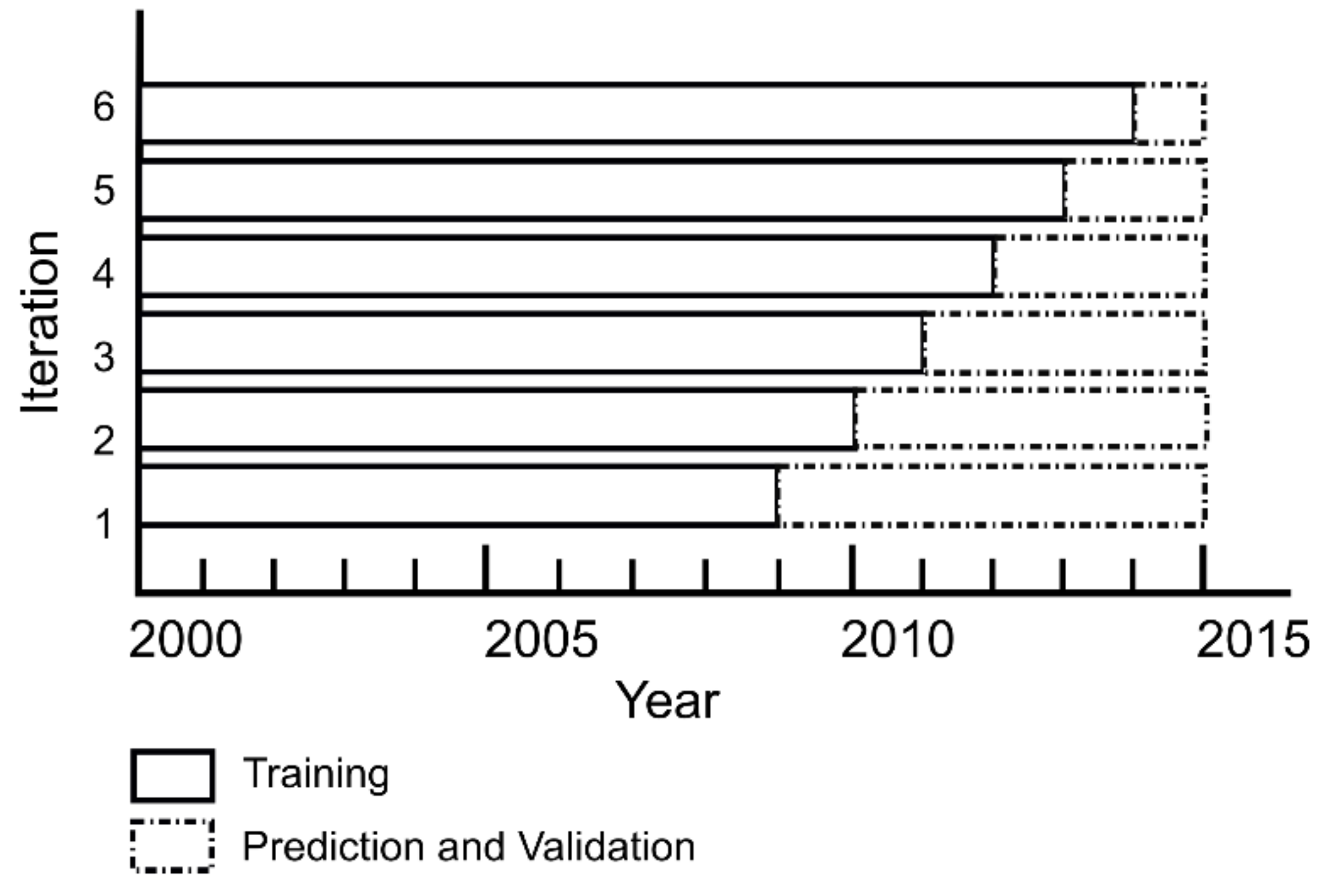
2.3. Analysis
Validation and Comparison Metrics
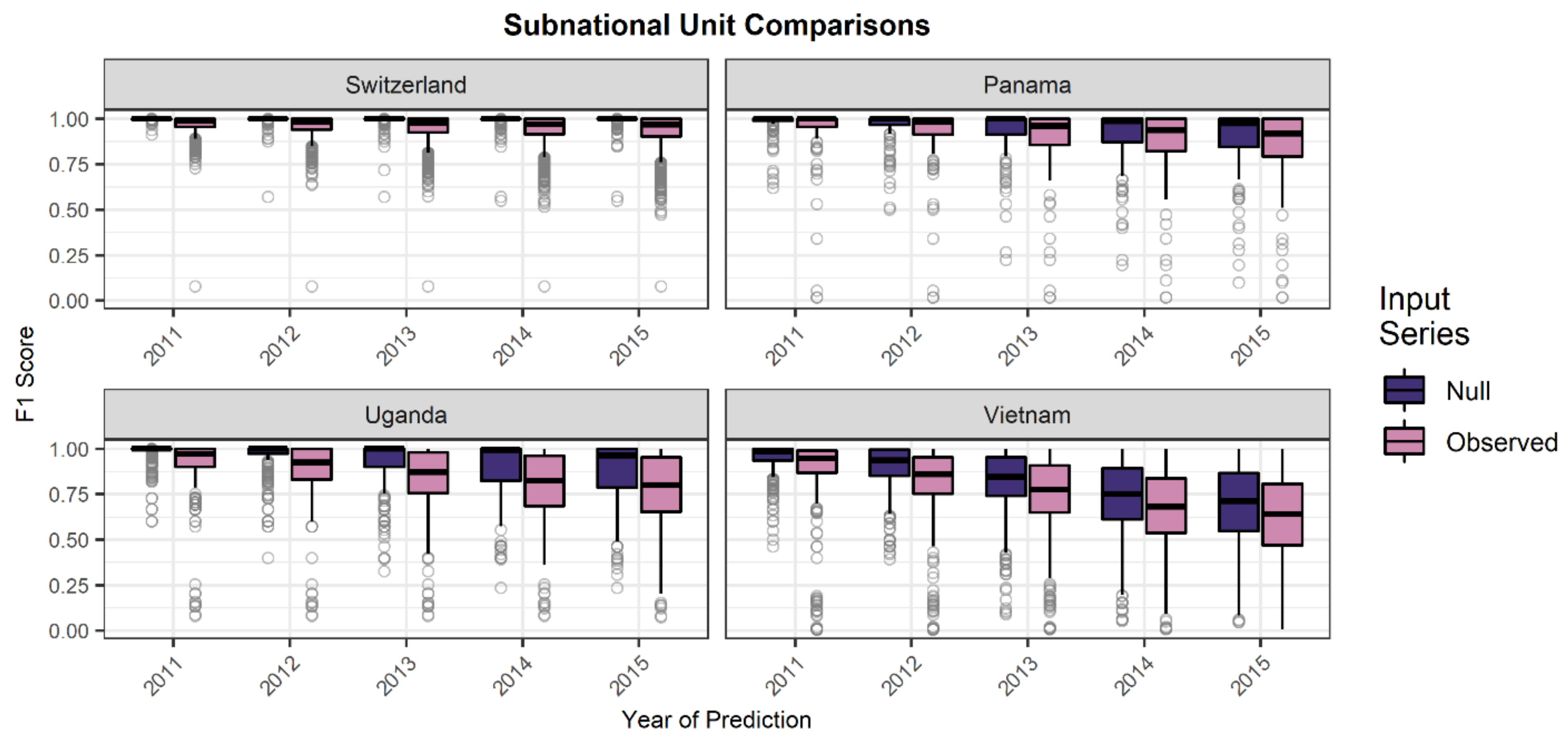
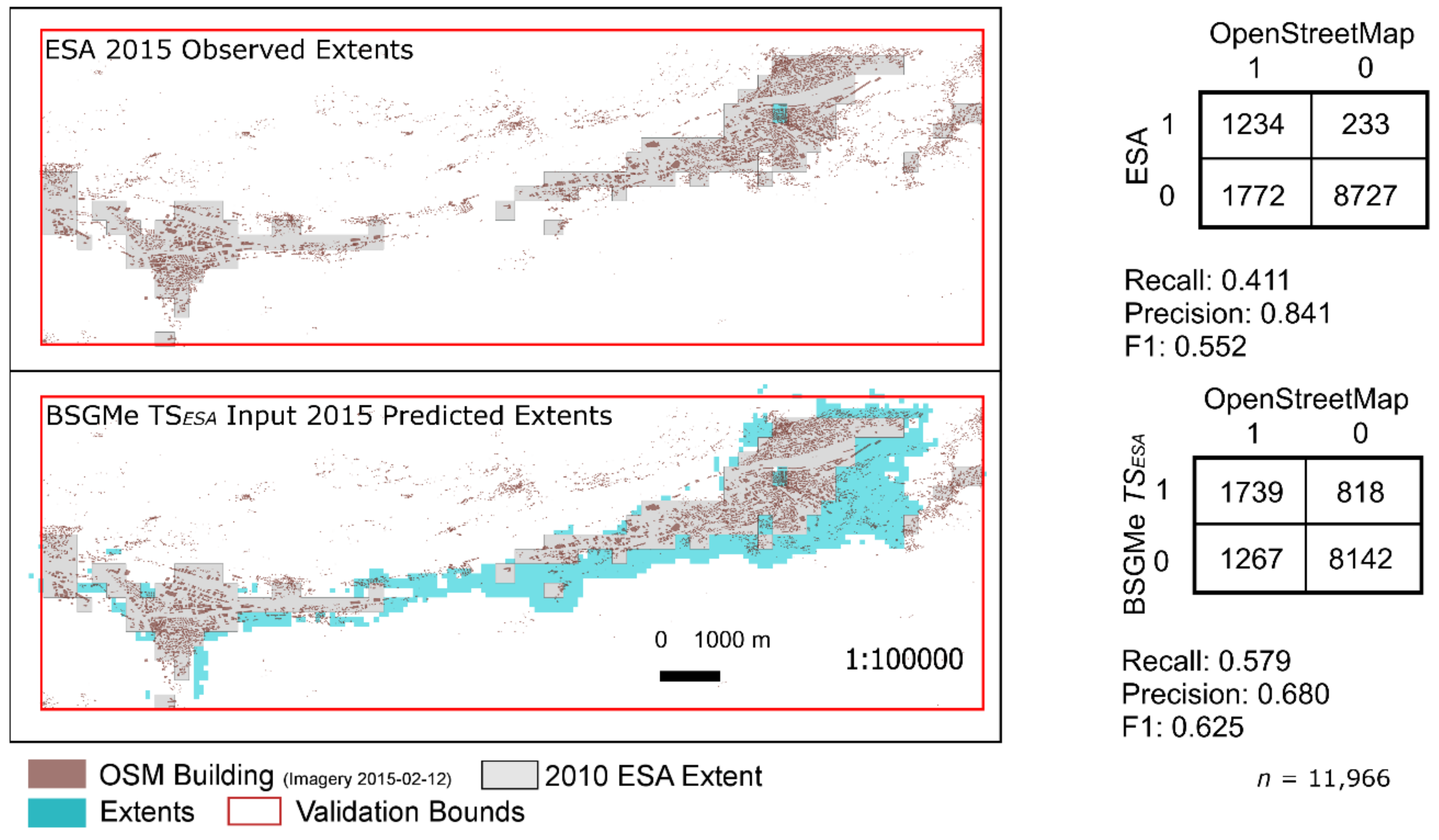
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Covariate | Time Point(s)a | Original Source | Source Resolution |
|---|---|---|---|
| DTE Cultivated landcover | 2000–2010 | ESA CCI Landcover [36] classes 10–30 | 10 arc seconds |
| DTE Woody, Herbaceous, Shrub landcover | 2000–2010 | ESA CCI Landcover [36] classes 40–120 | 10 arc seconds |
| DTE Grassland landcover | 2000–2010 | ESA CCI Landcover [36] class 130 | 10 arc seconds |
| DTE Lichens and Mosses landcover | 2000–2010 | ESA CCI Landcover [36] class 140 | 10 arc seconds |
| DTE Sparse Vegetation landcover | 2000–2010 | ESA CCI Landcover [36] classes 150–153 | 10 arc seconds |
| DTE Aquatic Vegetation landcover | 2000–2010 | ESA CCI Landcover [36] classes 160–180 | 10 arc seconds |
| DTE Bare Areas | 2000–2010 | ESA CCI Landcover [36] class 200 | 10 arc seconds |
| DTE Built-settlement | 2000–2010 | ESA CCI Landcover [36] class 190 | |
| Distance to Inland Water Bodies | 2015, assumed invariant | MERIS-based water bodies [39] | 5 arc seconds |
| Distance to Roads | Downloaded 2017, assumed invariant as temporally specific road data unavailable | OpenStreetMap [44] | Vector |
| Distance to Rivers | Downloaded 2017, assumed invariant | OpenStreetMap [44] | Vector |
| Distance to Coastline | Based upon boundaries of GPWv4, assumed invariant | CIESIN GPWv4 [40] | Vector |
| Slope | 2000, assumed invariant | World Wildlife Fund Void-filled Hydrosheds [37] | 3 arc seconds |
| Elevation | 2000, assumed invariant | World Wildlife Fund Void-filled Hydrosheds [37] | 3 arc seconds |
| DTE: Distance To nearest Edge a Note, for any covariate derived from land cover or built-settlement, only one year-specific covariate was used corresponding to the desired population surface (e.g., for a 2000 population surface only covariates corresponding to 2000, or those assumed temporally invariant, were used as covariates). | |||
References
- United Nations. World Urbanization Prospects: The 2018 Revision; United Nations: New York, NY, USA, 2018. [Google Scholar]
- Ledent, J. Rural-Urban Migration, Urbanization, and Economic Development. Econ. Dev. Cult. Change 1982, 30, 507–538. [Google Scholar] [CrossRef]
- Angel, S.; Parent, J.; Civco, D.L.; Blei, A.M.; Potere, D. The Dimensions of Global Urban Expansion: Estimates and Projections for All Countries, 2000-2050. Prog. Plann. 2011, 75, 53–107. [Google Scholar] [CrossRef]
- Cohen, B. Urban growth in developing countries: A review of current trends and a caution regarding existing forecasting. World Dev. 2004, 32, 23–51. [Google Scholar] [CrossRef]
- Espey, J. Sustainable development will falter without data. Nature 2019, 571, 299. [Google Scholar] [CrossRef] [PubMed]
- Solecki, W.; Seto, K.C.; Marcotullio, P.J. It’s Time for an Urbanization Science. Environ. Sci. Policy Sustain. Dev. 2013, 55, 12–17. [Google Scholar] [CrossRef]
- Scott, G.; Rajabifard, A. Sustainable Development and Geospatial Information: A Strategic Framework for Integrating a Global Policy Agenda into National Geospatial Capabilities. Geo-spatial Inf. Sci. 2017, 20, 59–76. [Google Scholar] [CrossRef]
- United Nations. United Nations Transforming Our World: The 2030 Agenda for Sustainable Development; United Nations: New York, NY, USA, 2016. [Google Scholar]
- United Nations. Economic and Social Council Report of the High-Level Political Forum on Sustainable Development Convened under the Auspices of the Economic and Social Council at its 2016 Session; United Nations: New York, NY, USA, 2016. [Google Scholar]
- Freire, S.; Schiavina, M.; Florczyk, A.J.; MacManus, K.; Pesaresi, M.; Corbane, C.; Borkovska, O.; Mills, J.; Pistolesi, L.; Squires, J.; et al. Enhanced data and methods for improving open and free global population grids: putting ‘leaving no one behind’ into practice. Int. J. Digit. Earth 2018, 1–17. [Google Scholar] [CrossRef]
- Leyk, S.; Gaughan, A.E.; Adamo, S.B.; de Sherbinin, A.; Balk, D.; Freire, S.; Rose, A.; Stevens, F.R.; Blankespoor, B.; Frye, C.; et al. The spatial allocation of population: a review of large-scale gridded population data products and their fitness for use. Earth Syst. Sci. Data 2019, 11, 1385–1409. [Google Scholar] [CrossRef]
- Pesaresi, M.; Guo, H.; Blaes, X.; Ehrlich, D.; Ferri, S.; Gueguen, L.; Halkia, S.; Kauffmann, M.; Kemper, T.; Lu, L.; et al. A Global Human Settlement Layer from Optical HR/VHR Remote Sensing Data: Concept and First Results. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 2102–2131. [Google Scholar] [CrossRef]
- Esch, T.; Marconcini, M.; Felbier, A.; Roth, A.; Heldens, W.; Huber, M.; Schwinger, M.; Taubenbock, H.; Muller, A.; Dech, S. Urban Footprint Processor - Fully Automated Processing Chain Generating Settlement Masks from Global Data of the TanDEM-X Mission. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1617–1621. [Google Scholar] [CrossRef]
- Esch, T.; Bachofer, F.; Heldens, W.; Hirner, A.; Marconcini, M.; Palacios-Lopez, D.; Roth, A.; Üreyen, S.; Zeidler, J.; Dech, S.; et al. Where We Live—A Summary of the Achievements and Planned Evolution of the Global Urban Footprint. Remote Sens. 2018, 10, 895. [Google Scholar] [CrossRef]
- Corbane, C.; Pesaresi, M.; Politis, P.; Syrris, V.; Florczyk, A.J.; Soille, P.; Maffenini, L.; Burger, A.; Vasilev, V.; Rodriguez, D.; et al. Big earth data analytics on Sentinel-1 and Landsat imagery in support to global human settlements mapping. Big Earth Data 2017, 1, 118–144. [Google Scholar] [CrossRef]
- Nieves, J.J.; Sorichetta, A.; Linard, C.; Bondarenko, M.; Steele, J.E.; Stevens, F.R.; Gaughan, A.E.; Carioli, A.; Clarke, D.J.; Esch, T.; et al. Annually modelling built-settlements between remotely-sensed observations using relative changes in subnational populations and lights at night. Comput. Environ. Urban Syst. 2020, 80, 101444. [Google Scholar] [CrossRef] [PubMed]
- Florczyk, A.J.; Melchiorri, M.; Zeidler, J.; Corbane, C.; Schiavina, M.; Freire, S.; Sabo, F.; Politis, P.; Esch, T.; Pesaresi, M. The Generalised Settlement Area: mapping the Earth surface in the vicinity of built-up areas. Int. J. Digit. Earth 2019, 1–16. [Google Scholar] [CrossRef]
- Pesaresi, M.; Ehrlich, D.; Ferri, S.; Florczyk, A.J.; Freire, S.; Halkia, S.; Julea, A.M.; Kemper, T.; Soille, P.; Syrris, V. Operating Procedure for the Production of the Global Human Settlement Layer from Landsat Data of the Epochs 1975, 1990, 2000, and 2014; Publications Office of the European Union: Brussels, Belgium, 2016. [Google Scholar]
- ESA; CCI. European Space Agency Climate Change Initiative Landcover; ESA: Paris, France, 2016. [Google Scholar]
- Facebook Connectivity Lab; Columbia University Center for International Earth Science Information Network (CIESIN). High Resolution Settlement Layer; CIESIN: Palisades, NY, USA, 2016. [Google Scholar]
- Small, C.; Cohen, J.E. Continental physiography, climate, and the global distribution of human population. Curr. Anthropol. 2004, 45, 269–277. [Google Scholar] [CrossRef]
- Small, C.; Elvidge, C.D.; Balk, D.; Montgomery, M. Spatial scaling of stable night lights. Remote Sens. Environ. 2011, 115, 269–280. [Google Scholar] [CrossRef]
- Linard, C.; Gilbert, M.; Snow, R.W.; Noor, A.M.; Tatem, A.J. Population Distribution, Settlement Patterns and Accessibility across Africa in 2010. PLoS One 2012, 7, e31743. [Google Scholar] [CrossRef]
- Seto, K.C.; Fragkias, M.; Guneralp, B.; Reilly, M.K. A Meta-Analysis of Global Urban Land Expansion. PLoS One 2011, 6, e23777. [Google Scholar] [CrossRef]
- Batty, M. Urban Modeling. In International Encyclopedia of Human Geography; Elsevier: Oxford, UK, 2009; pp. 51–58. [Google Scholar]
- Sante, I.; Garcia, A.M.; Miranda, D.; Crecente, R. Cellular Automata Models for the Simulation of Real-world Urban Processes: A Review and Analysis. Landsc. Urban Plan. 2010, 96, 108–122. [Google Scholar] [CrossRef]
- Li, X.; Gong, P. Urban growth models: progress and perspective. Sci. Bull. 2016, 61, 1637–1650. [Google Scholar] [CrossRef]
- Linard, C.; Tatem, A.J.; Gilbert, M. Modelling Spatial Patterns of Urban Growth in Africa. Appl. Geogr. 2013, 44, 23–32. [Google Scholar] [CrossRef] [PubMed]
- Seto, K.C.; Guneralp, B.; Hutyra, L.R. Global Forecasts of Urban Expansion to 2030 and Direct Impacts on Biodiversity and Carbon Pools. Proc. Natl. Acad. Sci. USA 2012, 109, 16083–16088. [Google Scholar] [CrossRef] [PubMed]
- Schneider, A.; Mertes, C.M.; Tatem, A.J.; Tan, B.; Sulla-Menashe, D.; Graves, S.J.; Patel, N.N.; Horton, J.A.; Gaughan, A.E.; Rollo, J.T.; et al. A new urban landscape in East–Southeast Asia, 2000–2010. Environ. Res. Lett. 2015, 10. [Google Scholar] [CrossRef]
- Goldewijk, K.K.; Beusen, A.; Janssen, P. Long-term dynamic modeling of global population and built-up area in a spatially explicit way: HYDE 3.1. The Holocene 2010, 20, 565–573. [Google Scholar] [CrossRef]
- de Koning, G.H.J.; Verburg, P.H.; Veldkamp, A.; Fresco, L.O. Multi-scale modelling of land use change dynamics in Ecuador. Agrcultural Syst. 1999, 61, 77–93. [Google Scholar] [CrossRef]
- Verburg, P.H.; Soepboer, W.; Veldkamp, A.; Limpiada, R.; Espladon, V.; Mastura, S.S.A. Modeling the Spatial Dynamics of Regional Land Use: The CLUE-S Model. Environ. Manage. 2002, 30, 391–405. [Google Scholar] [CrossRef] [PubMed]
- Lloyd, C.T.; Chamberlain, H.; Kerr, D.; Yetman, G.; Pistolesi, L.; Stevens, F.R.; Gaughan, A.E.; Nieves, J.J.; Hornby, G.; MacManus, K.; et al. Global spatio-temporally harmonised datasets for producing high-resolution gridded population distribution datasets. Big Earth Data 2019, 3, 108–139. [Google Scholar] [CrossRef]
- Tobler, W.; Deichmann, U.; Gottsegen, J.; Maloy, K. World Population in a Grid of Spherical Quadrilaterals. Int. J. Popul. Geogr. 1997, 3, 203–225. [Google Scholar] [CrossRef]
- ESA; CCI. European Space Agency Climate Change Initiative Landcover; ESA: Paris, France, 2017. [Google Scholar]
- Lehner, B.; Verdin, K.; Jarvis, A. New Global Hydrography Derived from Spaceborne Elevation Data. Eos, Trans. Am. Geophys. Union 2008, 89, 93–94. [Google Scholar] [CrossRef]
- U.N. Enviroment Programme World Conservation Monitoring Centre; IUCN World Commission on Protected Areas. World Database on Protected Areas; United Nations: New York, NY, USA, 2015. [Google Scholar]
- Lamarche, C.; Santoro, M.; Bontemps, S.; D’Andrimont, R.; Radoux, J.; Giustarini, L.; Brockmann, C.; Wevers, J.; Defourny, P.; Arino, O. Compilation and Validation of SAR and Optical Data Products for a Complete and Global Map of Inland/Ocean Water Tailored to the Climate Modeling Community. Remote Sens. 2017, 9. [Google Scholar] [CrossRef]
- Doxsey-Whitfield, E.; MacManus, K.; Adamo, S.B.; Pistolesi, L.; Squires, J.; Borkovska, O.; Baptista, S.R. Taking advantage of the improved availability of census data: A first look at the Gridded Population of the World, Version 4. Pap. Appl. Geogr. 2015, 1, 226–234. [Google Scholar] [CrossRef]
- Zhang, Q.; Seto, K.C. Mapping urbanization dynamics at regional and global scales using multi-temporal DMSP/OLS nighttime light data. Remote Sens. Environ. 2011, 115, 2320–2329. [Google Scholar] [CrossRef]
- Earth Observation Group NOAA. VIIRS Nighttime Lights - One Month Composites; National Centers for Environmental Information: Asheville, NC, USA, 2016. [Google Scholar]
- Nelson, A. Estimated Travel Time to the Nearest city of 50,000 or More People in Year 2000; Global Environment Monitoring Unit - Joint Research Centre of the European Commission: Ispra, Italy, 2008. [Google Scholar]
- OpenStreetMap. Contributers OpenStreetMap (OSM) Database. 2017. Available online: https://www.openstreetmap.org/ (accessed on 12 May 2020).
- Hijmans, R.J.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. 2005, 25, 1965–1978. [Google Scholar] [CrossRef]
- ESA CCI New Release of the C3S Global Land Cover products for 2016, 2017 and 2018 consistent with the CCI 1992 – 2015 map series. Available online: https://www.esa-landcover-cci.org/?q=node/197 (accessed on 14 November 2019).
- UCL. Geomatics Land Cover CCI Product User Guide Version 2.0; UCL: London, UK, 2017. [Google Scholar]
- Goodchild, M.F. Citizens as sensors: the world of volunteered geography. GeoJournal 2007, 69, 211–221. [Google Scholar] [CrossRef]
- Haklay, M. How good is volunteered geographical information? A comparative study of OpenStreetMap and ordnance survey datasets. Environ. Plan. B Urban Anal. City Sci. 2010, 37, 682–703. [Google Scholar] [CrossRef]
- Neis, P.; Zipf, A. Analyzing the Contributor Activity of a Volunteered Geographic Information Project — The Case of OpenStreetMap. ISPRS Int. J. Geo-Information 2012, 1, 146–165. [Google Scholar] [CrossRef]
- Fan, H.; Zipf, A.; Fu, Q.; Neis, P. Quality assessment for building footprints data on OpenStreetMap. Int. J. Geogr. Inf. Sci. 2014, 28, 700–719. [Google Scholar] [CrossRef]
- Senaratne, H.; Mobasheri, A.; Ali, A.L.; Capineri, C.; Haklay, M. A review of volunteered geographic information quality assessment methods. Int. J. Geogr. Inf. Sci. 2017, 31, 139–167. [Google Scholar] [CrossRef]
- Linard, C.; Tatem, A.J.; Stevens, F.R.; Gaughan, A.E.; Patel, N.N.; Huang, Z. Use of active and passive VGI data for population distribution modelling: experience from the WorldPop project. In Proceedings of the Eighth International Conference on Geographic Information Science, Vienna, Austria, 24–26 September 2014; pp. 1–16. [Google Scholar]
- Stevens, F.R.; Gaughan, A.E.; Linard, C.; Tatem, A.J. Disaggregating Census Data for Population Mapping Using Random Forests with Remotely-sensed Data and Ancillary Data. PLoS One 2015, 10, e0107042. [Google Scholar] [CrossRef]
- Forget, Y.; Linard, C.; Gilbert, M. Supervised Classification of Built-Up Areas in Sub-Saharan African Cities Using Landsat Imagery and OpenStreetMap. Remote Sens. 2018, 10, 1145. [Google Scholar] [CrossRef]
- Grippa, T.; Georganos, S.; Zarougui, S.; Bognounou, P.; Diboulo, E.; Forget, Y.; Lennert, M.; Vanhuysse, S.; Mboga, N.; Wolff, E. Mapping Urban Land Use at Street Block Level Using OpenStreetMap, Remote Sensing Data, and Spatial Metrics. ISPRS Int. J. Geo-Information 2018, 7, 246. [Google Scholar] [CrossRef]
- Weiss, D.J.; Nelson, A.; Gibson, H.S.; Temperley, W.; Peedell, S.; Lieber, A.; Hancher, M.; Poyart, E.; Belchior, S.; Fullman, N.; et al. A global map of travel time to cities to assess inequalities in accessibility in 2015. Nature 2018, 553, 333–336. [Google Scholar] [CrossRef] [PubMed]
- Switzerland Federal Statistical Office STAT-TAB - interaktive Tabellen. Available online: https://www.pxweb.bfs.admin.ch (accessed on 16 August 2019).
- R Core Team. R: A Language and Environment Layer for Statistical Computing; R Core Team: Vienna, Austria, 2016. [Google Scholar]
- Mennis, J.; Hultgren, T. Intelligent dasymetric mapping and its application to areal interpolation. Cartogr. Geogr. Inf. Sci. 2006, 33, 179–194. [Google Scholar] [CrossRef]
- Mennis, J. Generating surface models of population using dasymetric mapping. Prof. Geogr. 2003, 55, 31–42. [Google Scholar]
- Gaughan, A.E.; Stevens, F.R.; Huang, Z.; Nieves, J.J.; Sorichetta, A.; Lai, S.; Ye, X.; Linard, C.; Hornby, G.M.; Hay, S.I.; et al. Spatiotemporal patterns of population in mainland China, 1990 to 2010. Sci. Data 2016, 3. [Google Scholar] [CrossRef] [PubMed]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis: Forecasting and Control, 2nd ed.; Wiley: San Francisco, CA, USA, 1976. [Google Scholar]
- Hyndman, R.J.; Khandakar, Y. Automatic Time Series Forecasting: The forecast package for R. J. Stat. Softw. 2008, 27. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B.; Snyder, R.D.; Grose, S. A state space framework for automatic forecasting using exponential smoothing methods. Int. J. Forecast. 2002, 18, 439–454. [Google Scholar] [CrossRef]
- Pegels, C.C. Exponential Forecasting: Some New Variations. Manage. Sci. 1969, 15, 311–315. [Google Scholar]
- Ord, J.K.; Koehler, A.B.; Snyder, R.D. Estimation and Prediction for a Class of Dynamic Nonlinear Statistical Models. J. Am. Stat. Assoc. 1997, 92. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Booth, H. Stochastic population forecasts using functional data models for mortality, fertility and migration. Int. J. Forecast. 2008, 24, 323–342. [Google Scholar] [CrossRef]
- Fildes, R.; Petropoulos, F. Simple versus complex selection rules for forecasting many time series. J. Bus. Res. 2015, 68, 1692–1703. [Google Scholar] [CrossRef]
- Nelder, J.A.; Wedderburn, R.W.M. Generalized Linear Models. J. R. Stat. Soc. Ser. A 1972, 135, 370–384. [Google Scholar] [CrossRef]
- Shang, H.L. Mortality and life expectancy forecasting for a group of populations in developed countries: A multilevel functional data method. Ann. Appl. Stat. 2016, 10, 1639–1672. [Google Scholar] [CrossRef]
- Tashman, L.J. Out-of-sample tests of forecasting accuracy: an analysis and review. Int. J. Forecast. 2000, 16, 437–450. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Booth, H.; Yasmeen, F. Coherent Mortality Forecasting: The Product-Ratio Method With Functional Time Series Models. Demography 2013, 50, 261–283. [Google Scholar] [CrossRef]
- Makridakis, S.; Hibon, M. The M3-Competition: results, conclusions, and implications. Int. J. Forecast. 2000, 16, 451–476. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Kamusoko, C.; Gamba, J. Simulating Urban Growth Using a Random Forest-Cellular Automata (RF-CA) Model. ISPRS Int. J. Geo-Information 2015, 4, 447–470. [Google Scholar] [CrossRef]
- Tayyebi, A.; Pekin, B.K.; Pijanowski, B.C.; Plourde, J.D.; Doucette, J.S.; Braun, D. Hierarchical modeling of urban growth across the conterminous USA: Developing meso-scale quantity drivers for the Land Transformation Model. J. Land Use Sci. 2013, 8, 422–442. [Google Scholar] [CrossRef]
- Rogan, W.J.; Gladen, B. Estimating prevalence from the results of a screening test. Am. J. Epidemiol. 1978, 107, 71–76. [Google Scholar] [CrossRef]
- Pontius, R.G.; Shusas, E.; McEachern, M. Detecting important categorical land changes while accounting for persistence. Agric. Ecosyst. Environ. 2004, 101, 251–268. [Google Scholar] [CrossRef]
- Google Earth; Maxar Technologies; CNES/Airbus Map Imagery. 2019. Available online: https://earth.google.com/web/ (accessed on 12 May 2020).
- Openshaw, S. The modifiable areal unit problem. Concepts Tech. Mod. Geogr. 1984, 38. [Google Scholar]
- Nagle, N.N.; Buttenfield, B.P.; Leyk, S.; Spielman, S. Dasymetric Modeling and Uncertainty. Ann. Assoc. Am. Geogr. 2014, 104, 80–94. [Google Scholar] [CrossRef] [PubMed]
- Savage, L.J. The Theory of Statistical Decision. J. Am. Stat. Assoc. 1951, 46, 55–67. [Google Scholar] [CrossRef]
- Breiman, L. Statistical Modeling: The Two Cultures. Stat. Sci. 2001, 16, 199–231. [Google Scholar] [CrossRef]
- Shmueli, G. To Explain or Predict. Stat. Sci. 2010, 25, 289–310. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 3, 18–22. [Google Scholar]
- Verburg, P.H.; Overmars, K.P. Combining top-down and bottom-up dynamics in land use modeling: exploring the future of abandoned farmlands in Europe with the Dyna-CLUE model. Landsc. Ecol. 2009, 24, 1167–1181. [Google Scholar] [CrossRef]
- Schaldach, R.; Alcamo, J.; Koch, J.; Kölking, C.; Lapola, D.M.; Schüngel, J.; Priess, J.A. An integrated approach to modelling land-use change on continental and global scales. Environ. Model. Softw. 2011, 26, 1041–1051. [Google Scholar] [CrossRef]
- International Institute of Forecasters M-3 Competition. Available online: https://forecasters.org/resources/time-series-data/m3-competition/ (accessed on 1 December 2019).

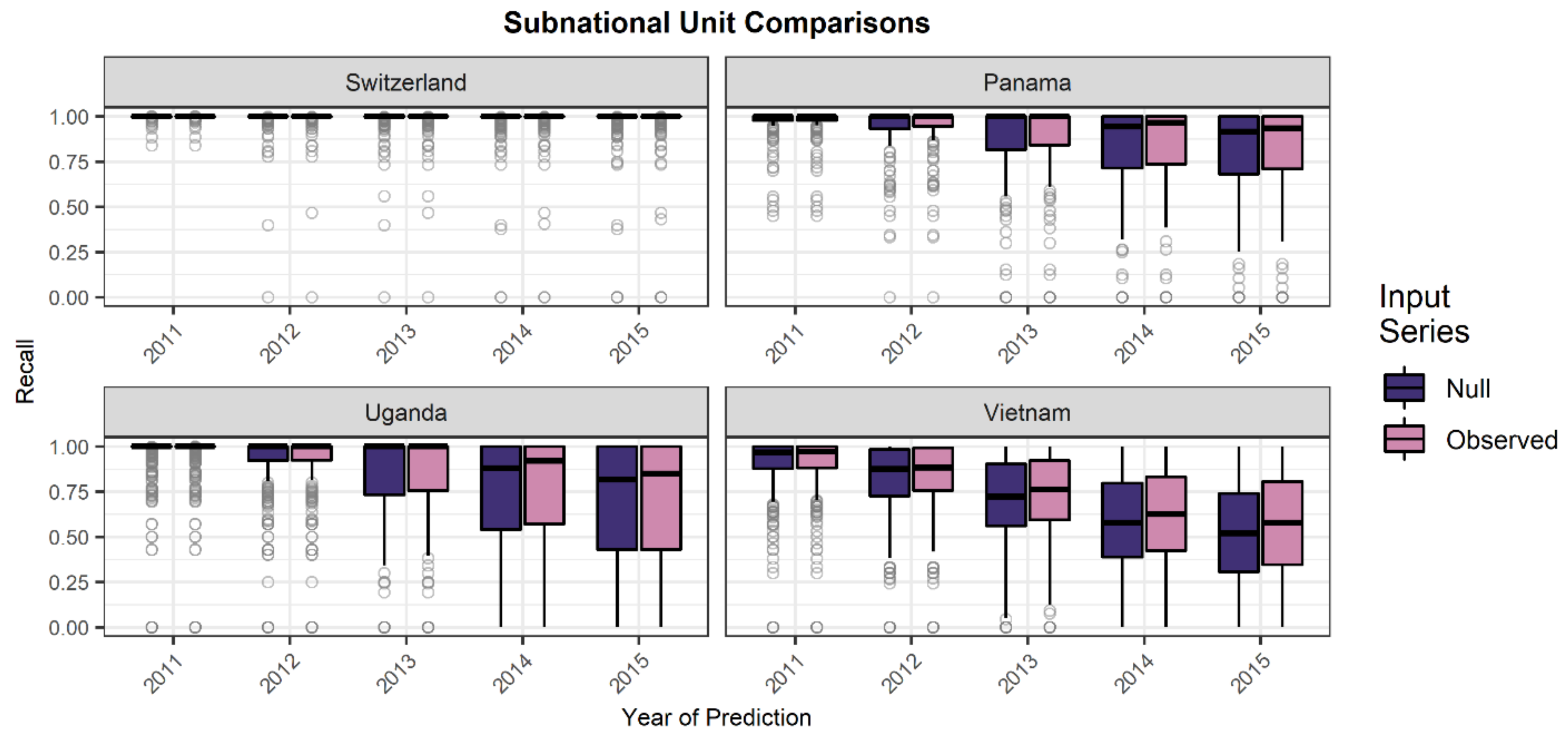
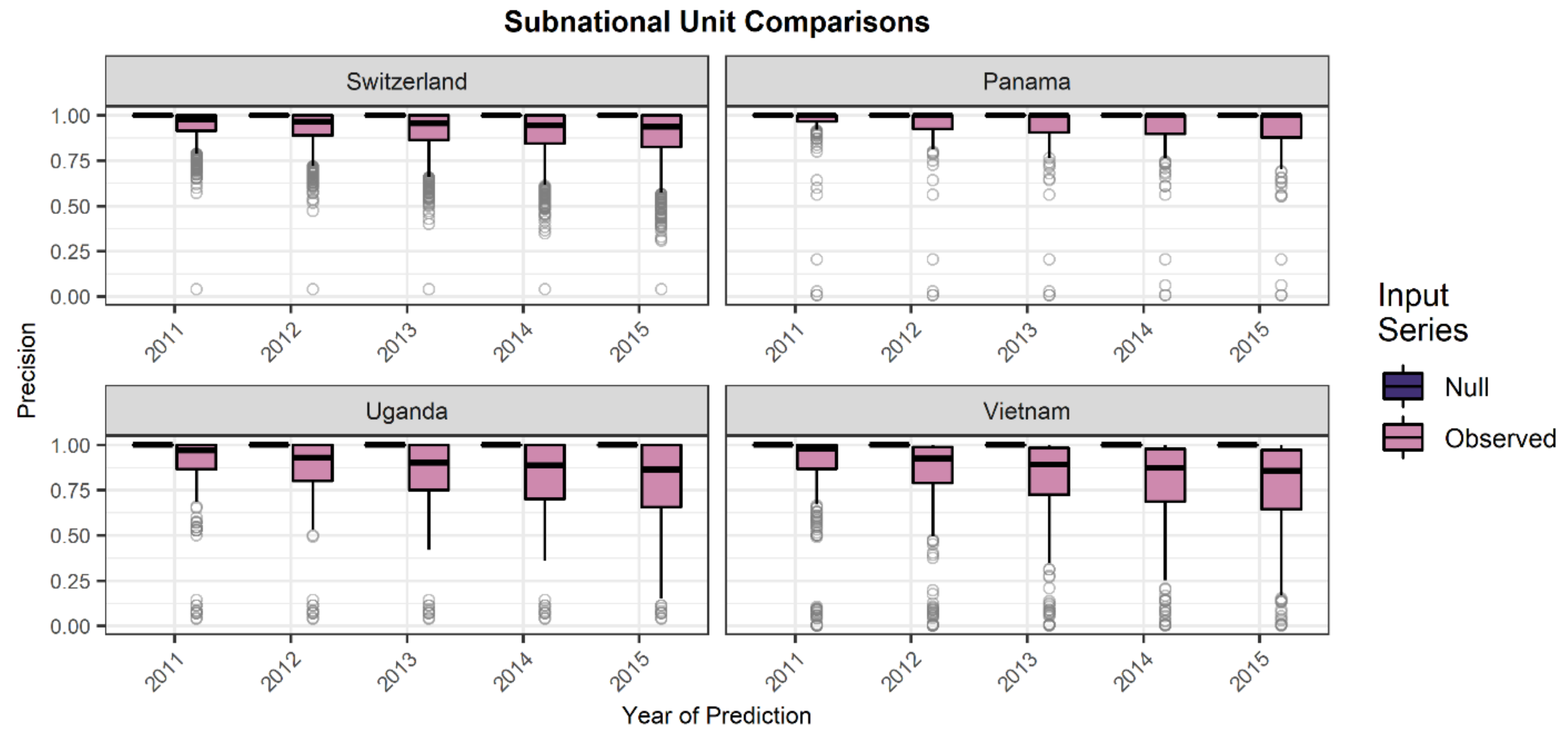
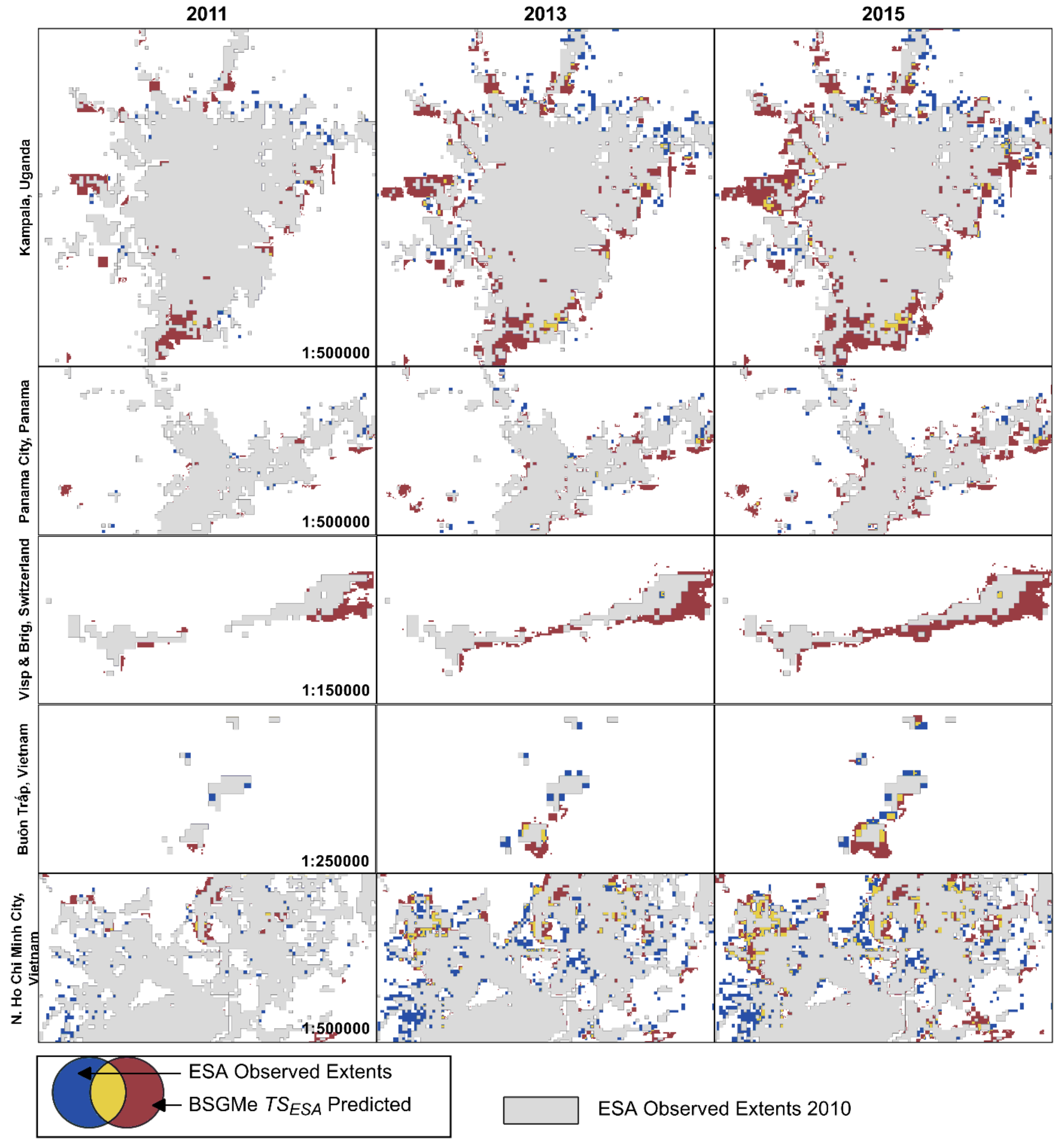
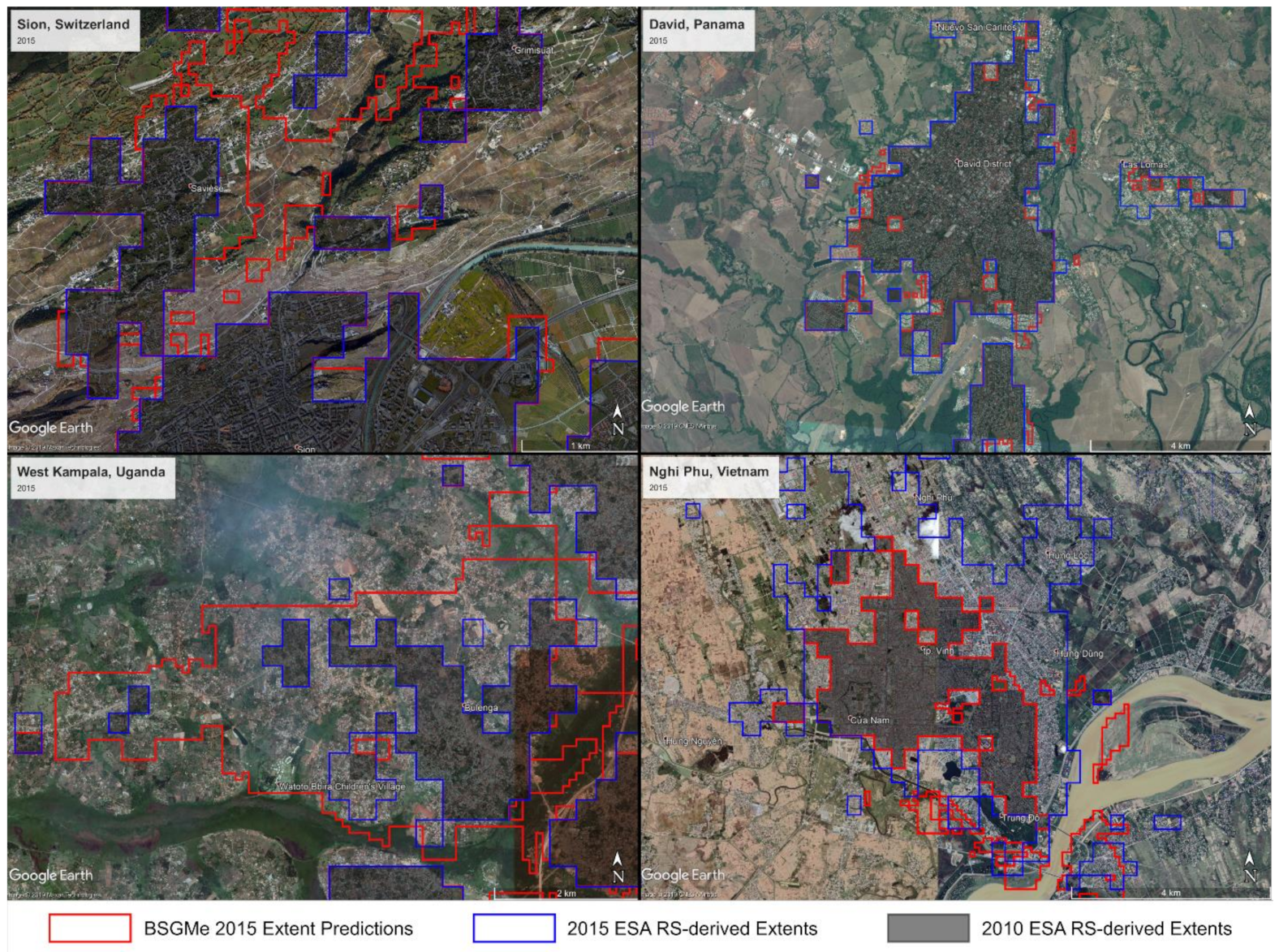
| Country | Average Spatial Resolution a | Period | Initial Non-Built Area (pixels) | Period Transition Prevalence b |
|---|---|---|---|---|
| Panama | 10.9 km | 2000–2010 | 8,901,004 | 0.12 % |
| 2010–2015 | 8,890,339 | 0.75 % | ||
| Switzerland | 3.9 km | 2000–2010 | 6,816,510 | 1.64 % |
| 2010–2015 | 6,704,973 | 0.01 % | ||
| Uganda | 12.2 km | 2000–2010 | 28,231,555 | 0.11 % |
| 2010–2015 | 28,200,084 | 0.04 % | ||
| Vietnam | 21.7 km | 2000–2010 | 40,108,425 | 0.11 % |
| 2010–2015 | 39,990,858 | 0.29 % | ||
| a Average spatial resolution is the square root of the average subnational area, in km, and can be thought of as analogous to pixel resolution with smaller values indicating finer areal data and vice versa [35] b Note: the Switzerland data suffered from disproportionate, relative to manually interpreted 30cm true-color imagery, amounts of growth as indicated by the European Space Agency (ESA) Remote Sensing (RS)-derived extents between 2000–2005 and is thought by Nieves et al. [16] to be due to the 2003–2004 shift from delineating land cover changes at 300m to using imagery to dilenate at 150m, in conjunction with the highly variable terrain in Switzerland compounding classification attempts. | ||||
| Covariate | Description | Use b, d | Time Point(s) | Original Spatial Resolution | DataSource(s) |
|---|---|---|---|---|---|
| Built-settlement b | Binary BS extents | Demand QuantificationSpatial Allocation | 2000–2010 | 10 arc sec | [36] |
| Distance To nearest Edge (DTE) of Built-settlement | Distance to the nearest BS edge | Spatial Allocation c | 2000, 2010 | 10 arc sec | [36] |
| Proportion Built-settlement 1,5,10,15 | Proportion of pixels that are BS within 1,5,10, or 15-pixel radius | Spatial Allocation c | 2000,2010 | 10 arc sec | [36] |
| Elevation | Elevation of terrain | Spatial Allocation c | 2000; Time Invariant | 3 arc sec | [37] |
| Slope | Slope of terrain | Spatial Allocation c | 2000; Time Invariant | 3 arc sec | [37] |
| DTE Protected Areas Category 1 | Distance to the nearest level 1 protected area edge | Spatial Allocation c | 2010 | Vector | [34,38] |
| Water | Areas of water | Restrictive Mask | 5 arc sec | [34,39] | |
| Subnational Population | Annual population by sub-national units | Demand Quantification | 2000–2020 | Vector | [40] |
| Weighted Lights-at-Night (LAN) d | Annual lagged and sub-national unit normalised LAN | Spatial Allocation d | 2000–2016 | 30 arc sec (2000-011)15 arc sec (2012-016) | DMSP [34,41] VIIRS [34,42] |
| Travel Time 50k | Travel time to the nearest city centre containing at least 50,000 people | Spatial Allocation c | 2000 | 30 arc sec | [34,43] |
| ESA CCI Land Cover (LC) Class a | Distance to nearest edge of individual land cover classes | Spatial Allocation c | 2000, 2010 | 10 arc sec | [34,36] |
| Distance to OpenStreetMap (OSM) Rivers | Distance to nearest OSM river feature | Spatial Allocation c | 2017 | Vector | [34,44] |
| Distance to OpenStreetMap (OSM) Roads | Distance to nearest OSM road feature | Spatial Allocation c | 2017 | Vector | [34,44] |
| Average Precipitation | Mean Precipitation | Spatial Allocation c | 1950–2000 | 30 arc sec | [34,45] |
| Average Temperature | Mean temperature | Spatial Allocation c | 1950–2000 | 30 arc sec | [34,45] |
| a Some land cover classes were collapsed prior to calculating distance to edge: 10–30 → 11; 40–120 → 40; 150–153 → 150; 160–180 → 160 (Sorichetta et al>, 2015) b Covariates involved in Demand Quantification were used to determine the demand for non-BS to BS transitions at the subnational unit level for every given year. Covariates involved in Spatial Allocation were either used as predictive covariates in the random forest calculated probabilities of transition (see c) or as a post-random forest year specific weight on those probabilities and the spatial allocation of transitions within each given unit area. Covariates used as restrictive masks prevented transitions from being allocated to these areas. c Used as predictive covariates in the random forest calculated probabilities of transition d See Nieves et al. [16] for details on the construction of weighted LAN | |||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nieves, J.J.; Bondarenko, M.; Sorichetta, A.; Steele, J.E.; Kerr, D.; Carioli, A.; Stevens, F.R.; Gaughan, A.E.; Tatem, A.J. Predicting Near-Future Built-Settlement Expansion Using Relative Changes in Small Area Populations. Remote Sens. 2020, 12, 1545. https://doi.org/10.3390/rs12101545
Nieves JJ, Bondarenko M, Sorichetta A, Steele JE, Kerr D, Carioli A, Stevens FR, Gaughan AE, Tatem AJ. Predicting Near-Future Built-Settlement Expansion Using Relative Changes in Small Area Populations. Remote Sensing. 2020; 12(10):1545. https://doi.org/10.3390/rs12101545
Chicago/Turabian StyleNieves, Jeremiah J., Maksym Bondarenko, Alessandro Sorichetta, Jessica E. Steele, David Kerr, Alessandra Carioli, Forrest R. Stevens, Andrea E. Gaughan, and Andrew J. Tatem. 2020. "Predicting Near-Future Built-Settlement Expansion Using Relative Changes in Small Area Populations" Remote Sensing 12, no. 10: 1545. https://doi.org/10.3390/rs12101545
APA StyleNieves, J. J., Bondarenko, M., Sorichetta, A., Steele, J. E., Kerr, D., Carioli, A., Stevens, F. R., Gaughan, A. E., & Tatem, A. J. (2020). Predicting Near-Future Built-Settlement Expansion Using Relative Changes in Small Area Populations. Remote Sensing, 12(10), 1545. https://doi.org/10.3390/rs12101545







