Development and Validation of a Photo-Based Measurement System to Calculate the Debarking Percentages of Processed Logs
Abstract
1. Introduction
2. Materials and Methods
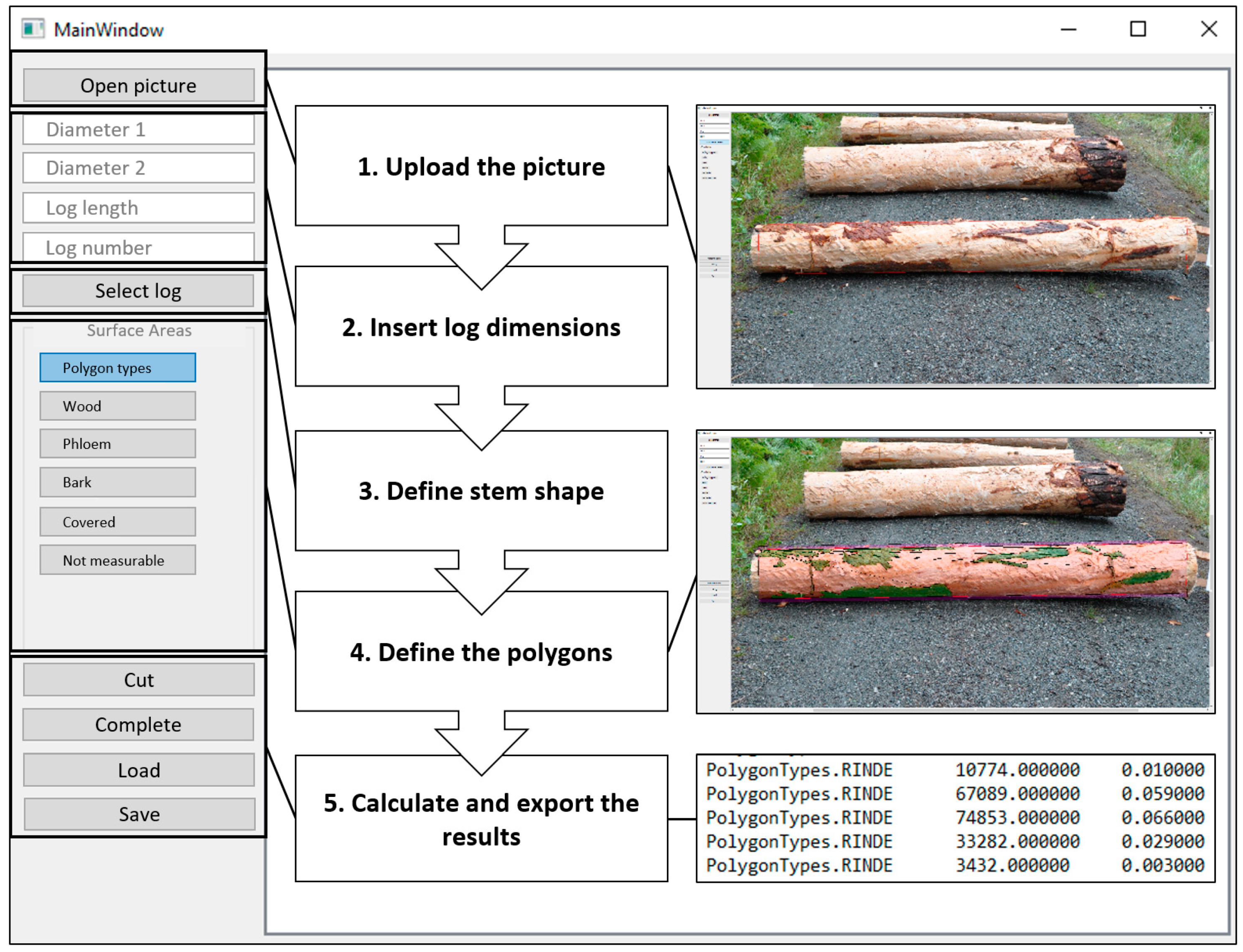
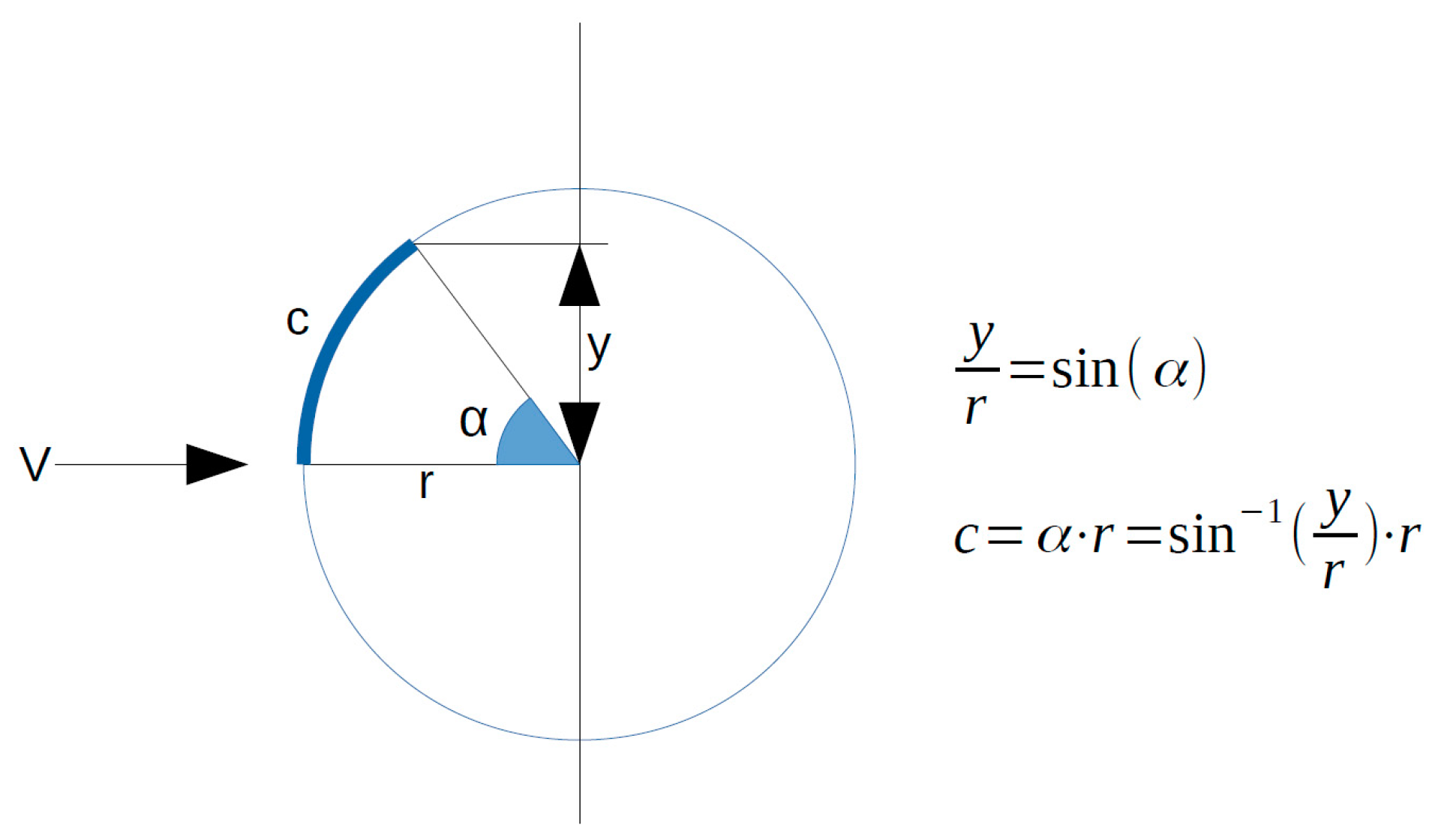
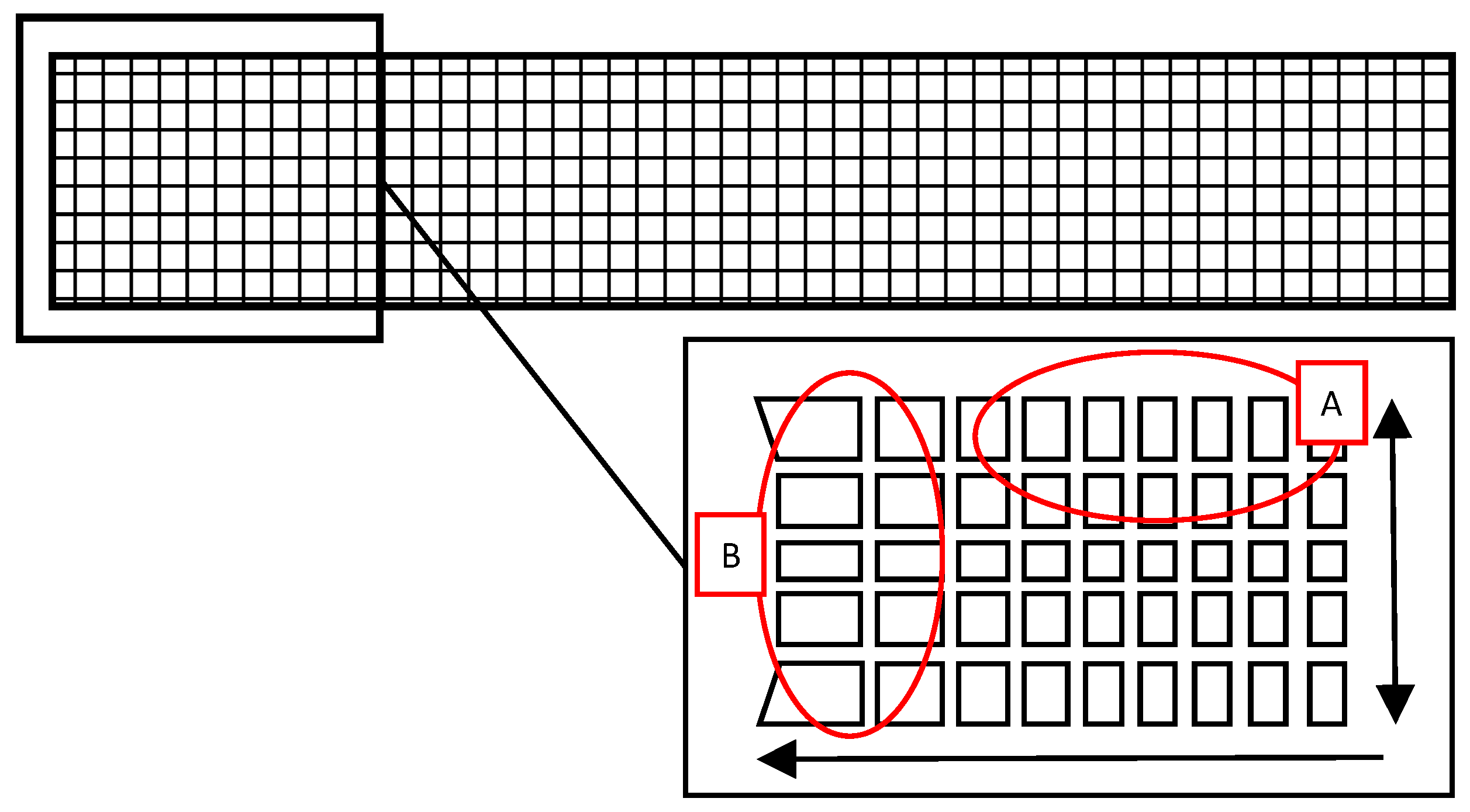
2.1. Development and Programming of the Measurement System Stemsurf
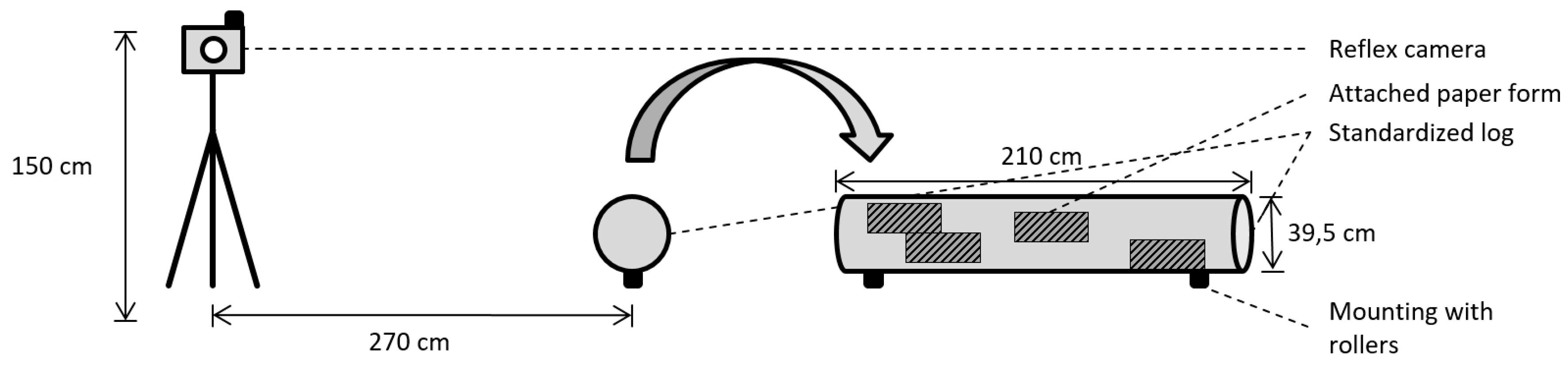
2.2. Precision Validation through Lab Experience
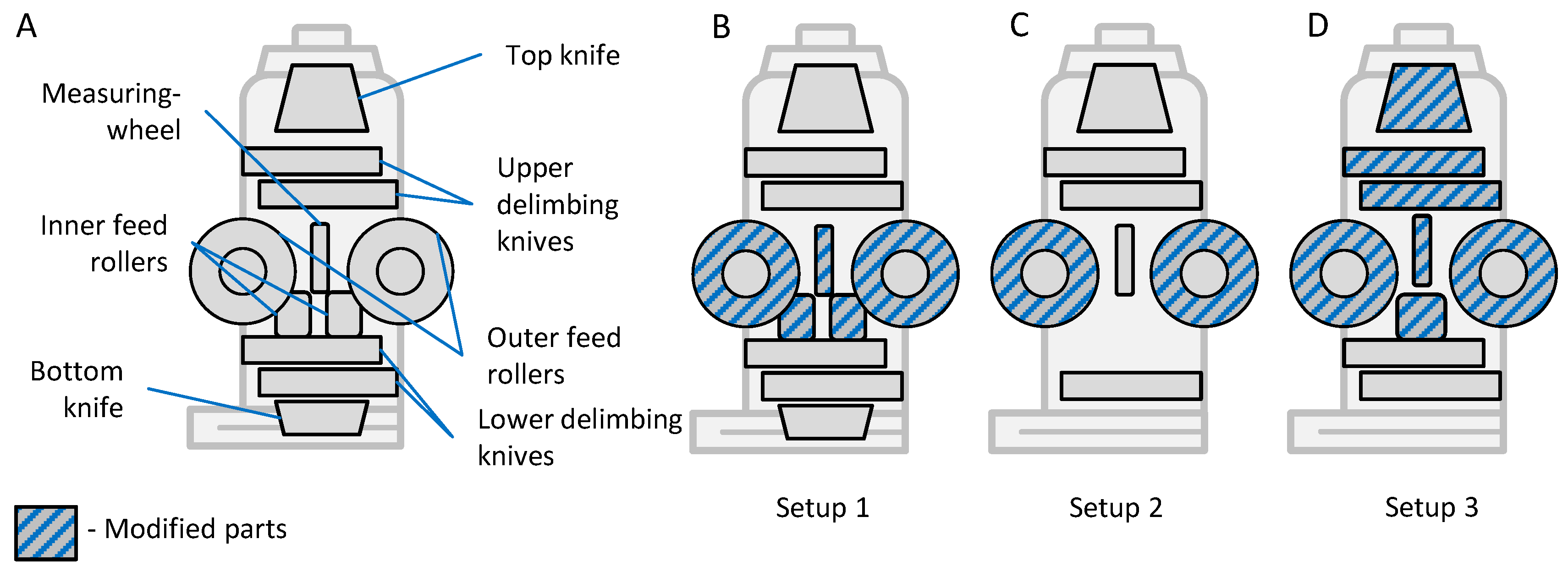
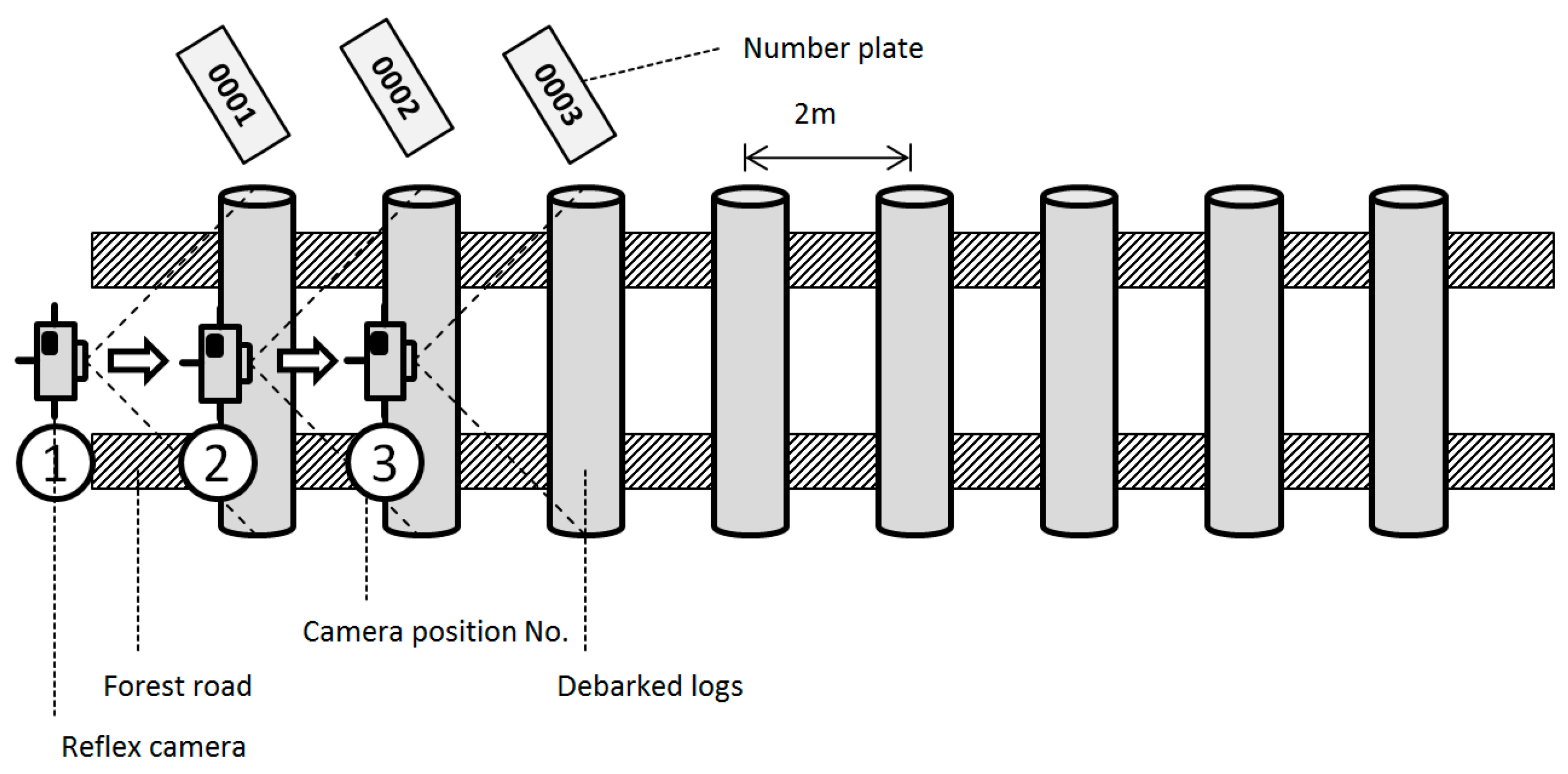
2.3. Field Application
2.4. Time Effort
3. Results
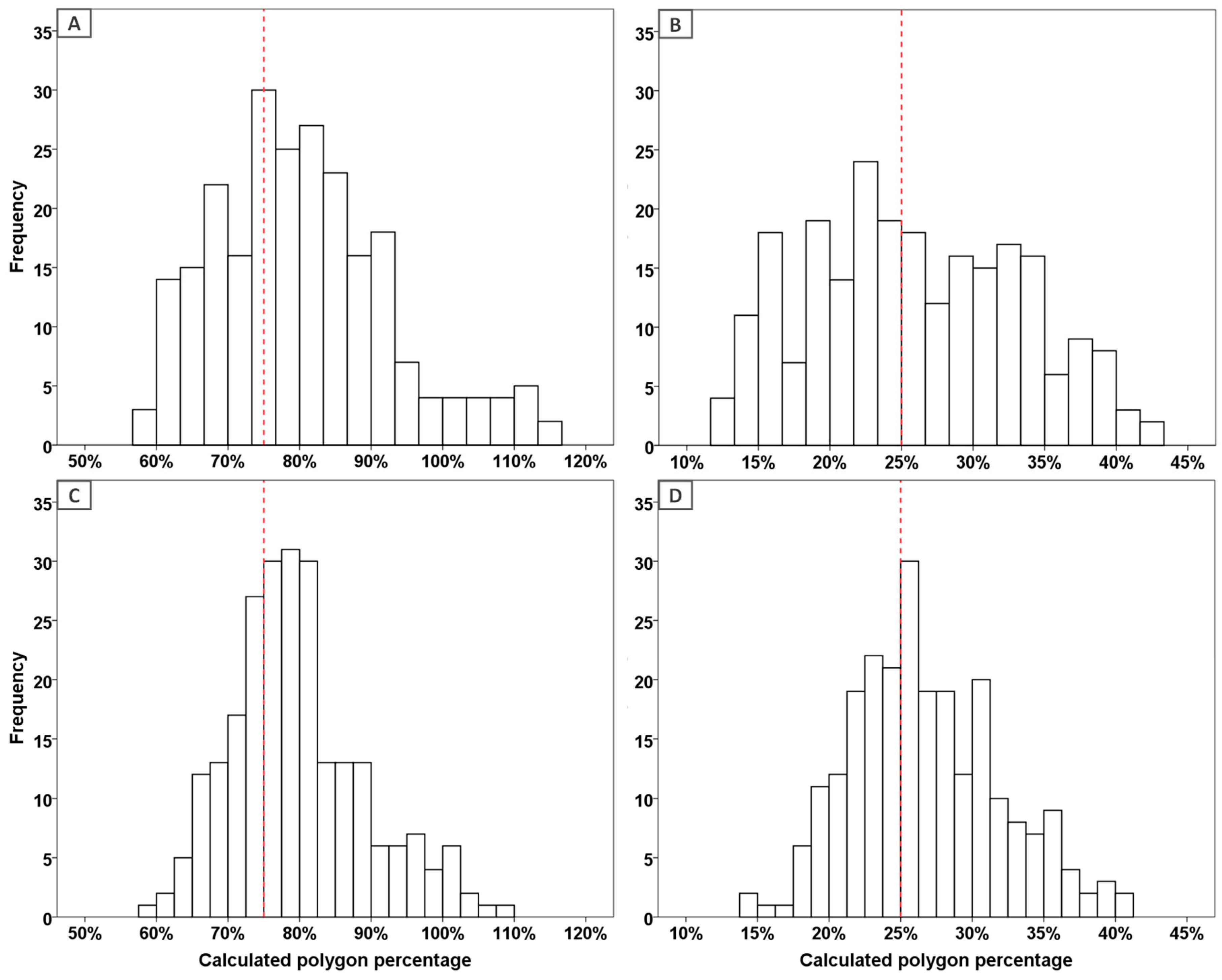
3.1. Performance in Laboratory Settings
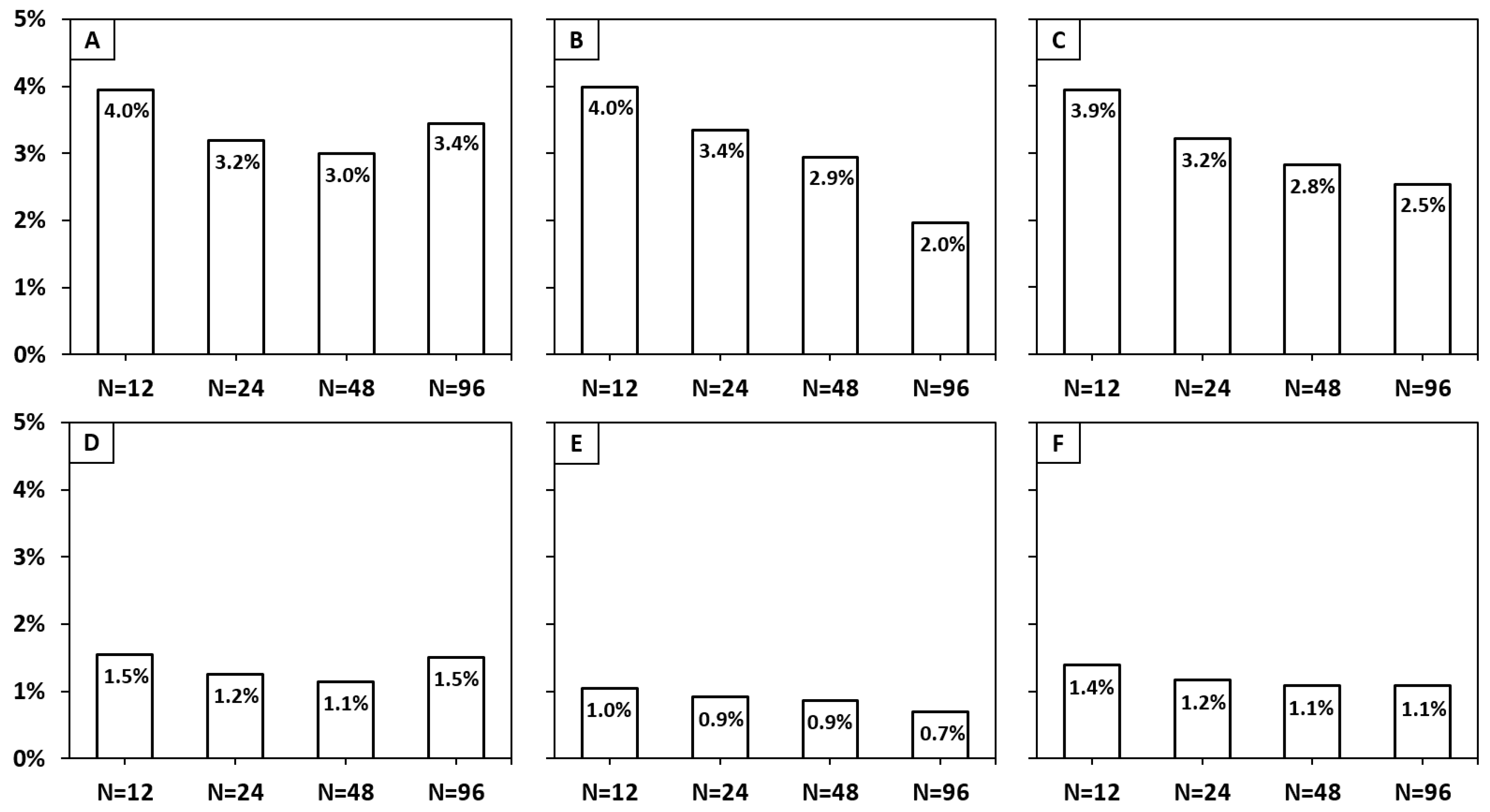
3.1.1. Laboratory Precision Validation—Single Values
3.1.2. Laboratory Precision Validation—Average Values
3.1.3. Laboratory Accuracy Validation—Bias
3.2. Performance in Field Settings
4. Discussion
4.1. Field and Laboratory Test Performance
4.2. Precision and Bias
4.3. Limitations and Areas of Improvements
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping forest canopy height globally with spaceborne lidar. J. Geophys. Res. 2011, 116, G04021. [Google Scholar] [CrossRef]
- Lim, K.; Treitz, P.; Wulder, M.; St-Onge, B.; Flood, M. LiDAR remote sensing of forest structure. Prog. Phys. Geogr. 2003, 27, 88–106. [Google Scholar] [CrossRef]
- Müller, J.; Brandl, R.; Buchner, J.; Pretzsch, H.; Seifert, S.; Strätz, C.; Veith, M.; Fenton, B. From ground to above canopy—Bat activity in mature forests is driven by vegetation density and height. For. Ecol. Manag. 2013, 306, 179–184. [Google Scholar]
- Bayer, D.; Seifert, S.; Pretzsch, H. Structural crown properties of Norway spruce (Picea abies [L.] Karst.) and European beech (Fagus sylvatica [L.]) in mixed versus pure stands revealed by terrestrial laser scanning. Trees 2013, 27, 1035–1047. [Google Scholar] [CrossRef]
- Boudreau, J.; Nelson, R.F.; Margolis, H.A.; Beaudoin, A.; Guindon, L.; Kimes, D.S. Regional aboveground forest biomass using airborne and spaceborne LiDAR in Québec. Remote Sens. Environ. 2008, 112, 3876–3890. [Google Scholar] [CrossRef]
- Kunneke, A.; van Aardt, J.; Roberts, W.; Seifert, T. Localisation of Biomass Potentials. In Bioenergy from Wood: Sustainable Production in the Tropics; Seifert, T., Ed.; Springer: Dordrecht, the Netherlands, 2014; pp. 11–41. [Google Scholar]
- Hilker, T.; van Leeuwen, M.; Coops, N.C.; Wulder, M.A.; Newnham, G.J.; Jupp, D.L.B.; Culvenor, D.S. Comparing canopy metrics derived from terrestrial and airborne laser scanning in a Douglas-fir dominated forest stand. Trees 2010, 24, 819–832. [Google Scholar] [CrossRef]
- Moorthy, I.; Miller, J.R.; Hu, B.; Chen, J.; Li, Q. Retrieving crown leaf area index from an individual tree using ground based lidar data. Can. J. For. Res. 2008, 34, 320–332. [Google Scholar]
- Strahler, A.H.; Jupp, D.L.B.; Woodcock, C.E.; Schaaf, C.B. Retrieval of forest structural parameters using a ground based lidar instrument. Can. J. For. Res. 2008, 34, 426–440. [Google Scholar] [CrossRef]
- Bao, Y.; Ni, W.; Wang, D.; Yue, C.; He, H.; Verbeeck, H. Effects of tree trunks on estimation of clumping index and LAI from HemiView and Terrestrial LiDAR. Forests 2018, 9, 144. [Google Scholar] [CrossRef]
- Hopkinson, C.; Chasmer, L.; Young-Pow, C.; Treitz, P. Assessing forest metrics with a ground-based scanning lidar. Can. J. For. Res. 2004, 34, 573–583. [Google Scholar] [CrossRef]
- Henning, J.; Radtke, P. Detailed stem measurements of standing trees from ground-based scanning Lidar. For. Sci. 2006, 52, 67–80. [Google Scholar]
- Watt, P.J.; Donoghue, D.N.M. Measuring forest structure with terrestrial laser scanning. Int. J. Remote Sens. 2005, 26, 1437–1446. [Google Scholar] [CrossRef]
- Maas, H.G.; Bienert, A.; Scheller, S.; Keane, E. Automatic forest inventory parameter determination from terrestrial laser scanner data. Int. J. Remote Sens. 2008, 29, 1579–1593. [Google Scholar] [CrossRef]
- Yu, X.; Liang, X.; Hyyppä, J.; Kankare, V.; Vastaranta, M.; Holopainen, M. Stem biomass estimation based on stem reconstruction from terrestrial laser scanning point clouds. Remote Sens. Lett. 2013, 4, 344–353. [Google Scholar] [CrossRef]
- Spriggs, R.; Coomes, D.; Jones, T.; Caspersen, J.; Vanderwel, M. (2017): An Alternative Approach to Using LiDAR Remote Sensing Data to Predict Stem Diameter Distributions across a Temperate Forest Landscape. Remote Sens. 2017, 9, 944. [Google Scholar] [CrossRef]
- Fang, R.; Strimbu, B.M. Stem Measurements and Taper Modeling Using Photogrammetric Point Clouds. Remote Sens. 2017, 9, 716. [Google Scholar] [CrossRef]
- Yan, Y.; Xia, M.; Fan, S.; Zhan, M.; Guan, F. Detecting the competition between Moso bamboos and broad-leaved trees in mixed forests using a terrestrial laser scanner. Forests 2018, 9, 520. [Google Scholar] [CrossRef]
- Labelle, E.R.; Heppelmann, J.B.; Borchert, H. Application of Terrestrial Laser Scanner to Evaluate the Influence of Root Collar Geometry on Stump Height after Mechanized Forest Operations. Forests 2018, 9, 709. [Google Scholar] [CrossRef]
- Schad, K.C.; Schmoldt, D.L.; Ross, R.J. Nondestructive Methods for Detecting Defects in Softwood Logs; USDA Forest Service Research Paper FPL-RP-546; USDA: Washington, DC, USA, 1996; 13p.
- Fonseca, M.A. The Measurement of Roundwood: Methodologies and Conversion Rations; CABI Publishing: Wallingford, Oxfordshire, UK, 2005; 269p. [Google Scholar]
- Colin, F.; Laborie, M.P.; Fortin, M. Wood properties: Future needs, measurement and modelling. Ann. For. Sci. 2015, 72, 665–670. [Google Scholar] [CrossRef][Green Version]
- Hodges, D.G.; Anderson, W.C.; McMillin, C.W. The economic potential of CT scanners for hardwood sawmills. For. Prod. J. 1990, 40, 65–69. [Google Scholar]
- Rais, A.; Ursella, E.; Vicario, E.; Giudiceandrea, F. The use of the first industrial X-ray CT scanner increases the lumber recovery value: Case study on visually strength-graded Douglas-fir timber. Ann. For. Sci. 2017, 74, 9. [Google Scholar]
- Gjerdrum, P. Sawlog scaling accuracy before and after barking, and the importance for sawn timber recovery – A case study. Wood Mater. Sci. Eng. 2012, 7, 120–125. [Google Scholar] [CrossRef]
- Weidenhiller, A.; Denzler, J.K. On the suitability of colour and texture analysis for detecting the presence of bark on a log. Comput. Electr. Agric. 2014, 106, 42–48. [Google Scholar] [CrossRef]
- Roth, A.; Kennel, E.; Knoke, T.; Matthes, U. Line intercept sampling: An efficient method for sampling of coarse woody debris? Eur. J. For. Res. 2003, 122, 318–336. [Google Scholar]
- Murphy, G.E.; Pilkerton, S.J. Seasonal Impacts of Bark Loss on Simulated Payloads, Bark Delivery, and Transport Costs for Freshly Harvested Logs. For. Prod. J. 2011, 61, 71–76. [Google Scholar] [CrossRef]
- Weisstein, E.W. Point-Line Distance--2-Dimensional. Available online: http://mathworld.wolfram.com/Point-LineDistance2-Dimensional.html (accessed on 29 April 2019).
- Baumgartner, R.; Brüchert, F.; Staudenmaier, J.; Sauter, U.-H. Bark measurements with x-ray technology. In Proceedings of the COST E 53 Conference – Quality Control for Wood and Wood Products, Warsaw, Poland, 15–17 October 2007; 4p. [Google Scholar]
- Thomas, L.; Shaffer, C.A.; Mili, L.; Thomas, E. Automated detection of severe surface defects on barked hardwood logs. For. Prod. J. 2007, 57, 50–56. [Google Scholar]
| Setup 1 | Setup 2 | Setup 3 | |
|---|---|---|---|
| Harvester | John Deere 1270 E | Timberpro 620E | Ponsse ScorpionKing |
| Harvesting head | John Deere H480C | LogMax 7000c | Ponsse H7 |
| Polygon | Test Series | Sample Size | Mean (%) | Standard Deviation (%) | Range (%) | Minimum (%) | Maximum (%) |
|---|---|---|---|---|---|---|---|
| Wood | Rectangular | 240 | 80.5 | 12.8 | 66.8 | 56.8 | 123.6 |
| Round | 240 | 79.6 | 9.4 | 47.8 | 59.9 | 107.7 | |
| Bark | Rectangular | 240 | 25.8 | 7.6 | 34.8 | 8.4 | 43.2 |
| Round | 240 | 26.7 | 5.2 | 26.5 | 14.3 | 40.8 |
| Polygon | Test Series | Sample Size (%) | Standard Deviation (%) | Range (%) | Minimum (%) | Maximum (%) | Deviation Range * (%) |
|---|---|---|---|---|---|---|---|
| Wood | Rectangular | 12 | 3.95 | 17.4 | 74.7 | 92.1 | −0.3–17.1 |
| Round | 12 | 3.98 | 14.5 | 75.3 | 89.9 | 0.3–14.9 | |
| Rectangular | 24 | 3.19 | 9.9 | 76.2 | 86.0 | 1.2–11.0 | |
| Round | 24 | 3.35 | 10.0 | 75.8 | 85.8 | 0.8–10.8 | |
| Rectangular | 48 | 3.00 | 8.0 | 76.3 | 84.2 | 1.3–9.2 | |
| Round | 48 | 2.94 | 6.1 | 77.3 | 83.4 | 2.3–8.4 | |
| Rectangular | 96 | 3.44 | 6.2 | 76.3 | 82.4 | 1.3–7.4 | |
| Round | 96 | 1.97 | 3.9 | 77.4 | 81.3 | 2.4–6.1 | |
| Bark | Rectangular | 12 | 1.54 | 5.5 | 23.7 | 29.2 | −1.3–4.2 |
| Round | 12 | 1.05 | 3.5 | 25.8 | 29.2 | 0.8–4.2 | |
| Rectangular | 24 | 1.25 | 3.8 | 24.3 | 28.1 | −0.7–3.1 | |
| Round | 24 | 0.91 | 3.2 | 25.8 | 29.0 | 0.8–4.0 | |
| Rectangular | 48 | 1.14 | 2.8 | 25.0 | 27.8 | 0–2.8 | |
| Round | 48 | 0.87 | 2.1 | 26.1 | 28.3 | 1.1–3.3 | |
| Rectangular | 96 | 1.50 | 2.6 | 25.2 | 27.8 | 0.2–2.8 | |
| Round | 96 | 0.69 | 1.2 | 26.1 | 27.3 | 1.1–2.3 |
| Polygon | Test Series | E (Θ) (%) | θ (%) | E(Θ) – θ (%) | CorrE(Θ) − θ (%) |
|---|---|---|---|---|---|
| Wood | Rectangular | 80.5 | 75 | 5.5 | 7.3 |
| Round | 79.6 | 75 | 4.6 | 6.1 | |
| Bark | Rectangular | 25.8 | 25 | 0.8 | 3.2 |
| Round | 26.7 | 25 | 1.7 | 6.8 |
| Field Tests | S1 Summer I (%) | S1 Winter (%) | S1 Summer II (%) | S2 Winter (%) | S3 Winter (%) | S2 Summer (%) | S3 Summer (%) |
|---|---|---|---|---|---|---|---|
| Debarking percentage | 84.1 | 53.8 | 89.9 | 34.8 | 83.4 | 73.1 | 83.8 |
| Corrected debarking percentage * | 85.1 | 56.9 | 90.6 | 39.2 | 84.5 | 74.9 | 84.9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heppelmann, J.B.; Labelle, E.R.; Seifert, T.; Seifert, S.; Wittkopf, S. Development and Validation of a Photo-Based Measurement System to Calculate the Debarking Percentages of Processed Logs. Remote Sens. 2019, 11, 1133. https://doi.org/10.3390/rs11091133
Heppelmann JB, Labelle ER, Seifert T, Seifert S, Wittkopf S. Development and Validation of a Photo-Based Measurement System to Calculate the Debarking Percentages of Processed Logs. Remote Sensing. 2019; 11(9):1133. https://doi.org/10.3390/rs11091133
Chicago/Turabian StyleHeppelmann, Joachim B., Eric R. Labelle, Thomas Seifert, Stefan Seifert, and Stefan Wittkopf. 2019. "Development and Validation of a Photo-Based Measurement System to Calculate the Debarking Percentages of Processed Logs" Remote Sensing 11, no. 9: 1133. https://doi.org/10.3390/rs11091133
APA StyleHeppelmann, J. B., Labelle, E. R., Seifert, T., Seifert, S., & Wittkopf, S. (2019). Development and Validation of a Photo-Based Measurement System to Calculate the Debarking Percentages of Processed Logs. Remote Sensing, 11(9), 1133. https://doi.org/10.3390/rs11091133





