Hybrid Grasshopper Optimization Algorithm and Differential Evolution for Multilevel Satellite Image Segmentation
Abstract
1. Introduction
- Propose an efficient satellite image segmentation method.
- Apply the hybrid algorithm of GOA and DE to the multilevel thresholding domain.
- Introduce an alternative hybrid model for a meta-heuristic algorithm.
2. Grasshopper Optimization Algorithm
| Algorithm 1 Pseudocode of grasshopper optimization algorithm for optimization problem |
| 1. Begin 2. Initialize a randomly distributed population in the search space; 3. Initialize the best search agent ; 4. while 5. Evaluate using Equation (3); 6. for 7. Calculate the objective value of each grasshopper ; 8. Update the best search agent ; 9. Normalize the distance between grasshoppers in [1,4]; 10. Update the position of grasshopper using Equation (2); 11. Correct the position of the current grasshopper if it is beyond the border; 12. end for 13. end while 14. return , which represents the optimal position of optimization; 15. End |
3. Multilevel Thresholding
4. Proposed Methodology
4.1. Differential Evolution
4.1.1. Mutation
4.1.2. Crossover
4.1.3. Selection
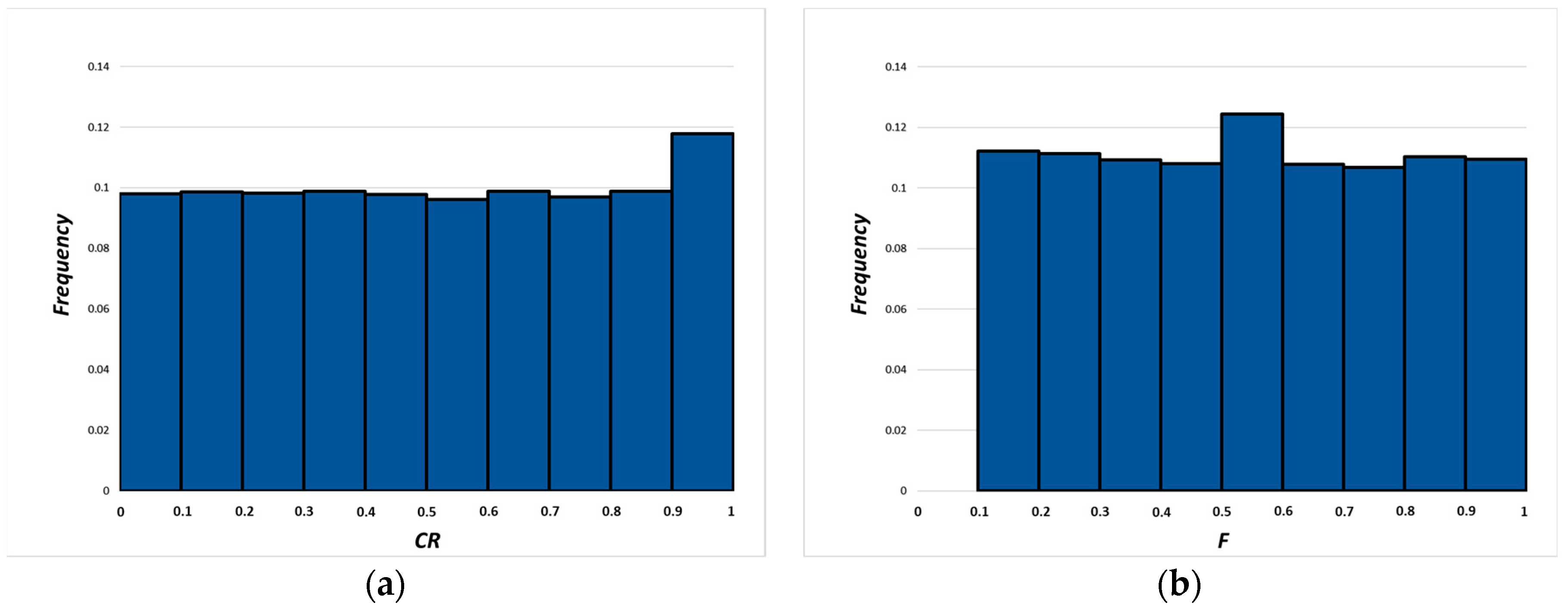
4.2. Self-Adapting Differential Evolution (jDE)
| Algorithm 2 Pseudocode of jDE algorithm for an optimization problem |
| 1. Begin 2. Initialize a randomly distributed population in the search space; 3. Initialize the best search agent ; 4. while 5. for 6. Calculate the objective value of each search agent ; 7. Update the best search agent ; 8. Evaluate the control parameters and of each search agent using Equations (8)–(9); 9. Mutation: Generate a mutant individual using Equation (5), and then check the position; 10. Crossover: Choose the trial individual from current individual and mutant individual using Equation (6); 11. Selection: Select the better individual that will be preserved for the next generation using Equation (7); 12. end for 13. end while 14. return , which represents the optimal position of optimization; 15. End |
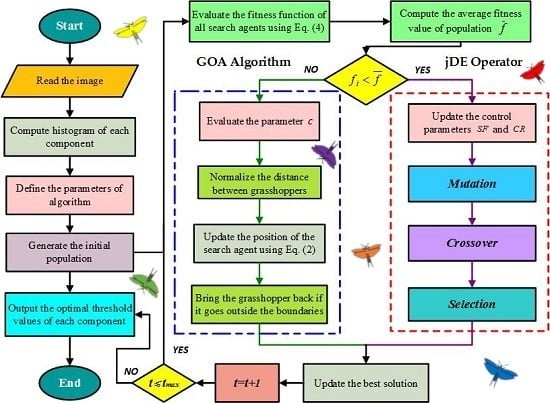
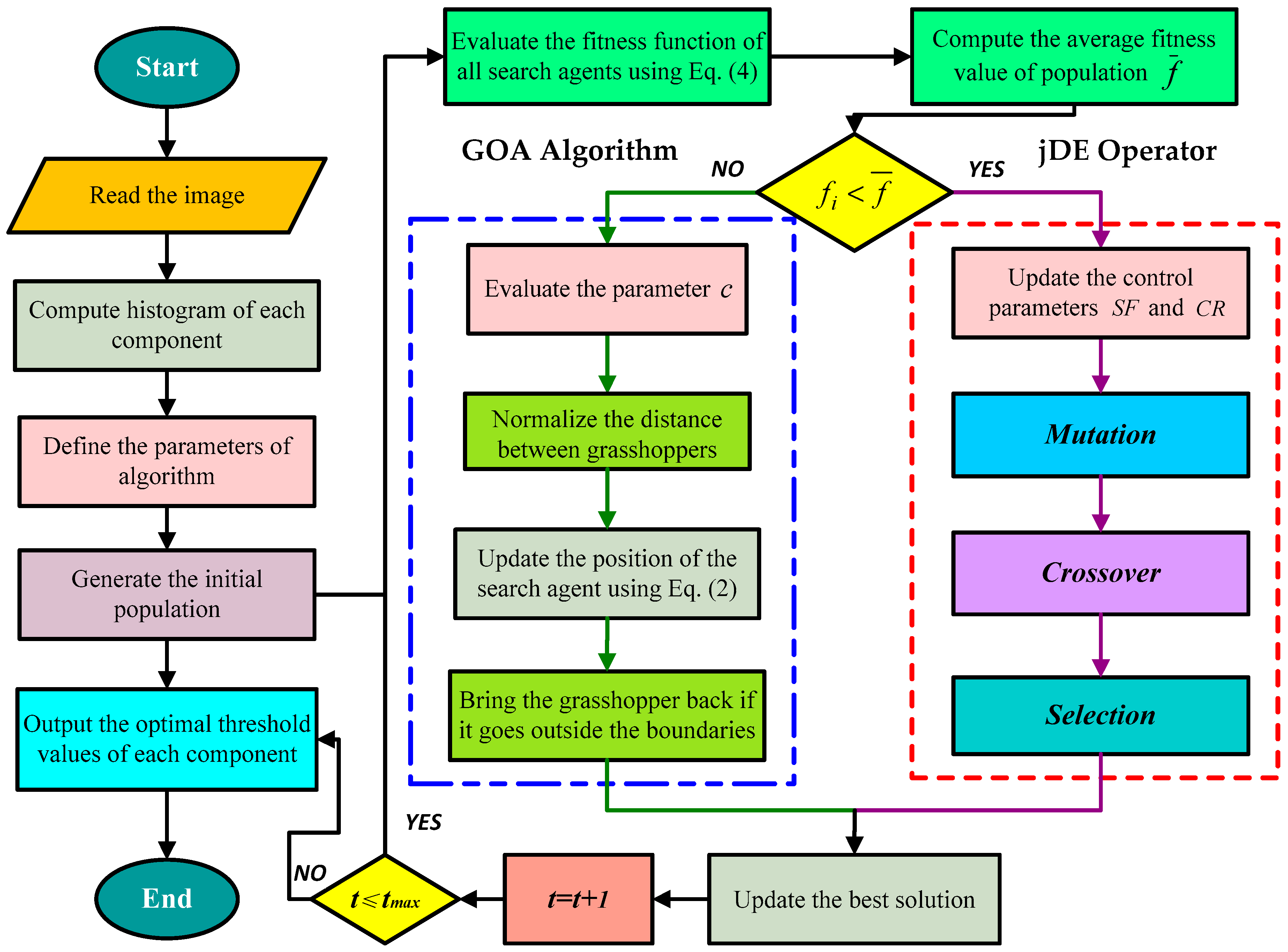
4.3. Hybrid Algorithm of GOA and jDE (GOA–jDE)
| Algorithm 3 Pseudocode of GOA–jDE-based multilevel satellite image thresholding |
| Input: The given satellite image. Output: Segmentation thresholds. 1. Read the given color satellite image; 2. Extract the histogram of each color component (R, G, and B); 3. Initialize a randomly distributed population in the search space; 4. Initialize the best search agent ; 5. Initialize the fitness values of the grasshoppers ; 6. Set population size and maximum number of iterations ; 7. Set the dimensions of the optimization problem , namely the number of thresholds; 8. while (termination condition is not met ) 9. Check the boundary and evaluate the fitness value of each grasshopper using Equation (4); 10. Update the location and fitness value of best search agent if there is a better one; 11. Evaluate the parameter using Equation (3); 12. Calculate the average fitness value of the population; 13. for (each grasshopper )) 14. if () % GOA Algorithm 15. Update the position of grasshopper using Equation (2); 16. else % jDE Operator 17. Evaluate and of each search agent using Equations (8)–(9); 18. Mutation, Crossover, and Selection using Equations (5)–(7). 19. end if 20. end for 21. end while |
| Fitness function (Minimum Cross entropy) |
| Input: Histogram of a color component, and segmentation thresholds . Output: Fitness function value . 1. The histogram is divided into parts by thresholds; 2. Calculate the proportion of pixels in each gray level to the total based on the histogram; 3. Compute the zero-moment and first-moment on partial range of the image histogram; 4. Calculate the minimum cross entropy of each part ; 5. The sum of the entropies of all parts represents the fitness function value; 6. ; |
4.4. Computational Complexity
5. Experimental Results and Discussion
5.1. Experimental Setup
5.2. Performance Measures
5.3. Experimental Series 1: Comparison of Satellite Image Thresholding Methods Based on MCE
5.3.1. Results and Discussions
5.3.2. Statistical Tests
5.4. Experimental Series 2: Performance on Other Objective Functions
5.5. Experimental Series 3: Further Evaluation on SIPI Image Database
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hinojosa, S.; Dhal, K.G.; Elaziz, M.A.; Oliva, D.; Cuevas, E. Entropy-based imagery segmentation for breast histology using the stochastic fractal search. Neurocomputing 2018, 321, 201–215. [Google Scholar] [CrossRef]
- Elaziz, M.A.; Oliva, D.; Ewees, A.A.; Xiong, S. Multi-level thresholding-based grey scale image segmentation using multi-objective multi-verse optimizer. Expert Syst. Appl. 2019, 125, 112–129. [Google Scholar] [CrossRef]
- Lee, S.H.; Koo, H.I.; Cho, N.I. Image segmentation algorithms based on the machine learning of features. Pattern Recognit. Lett. 2010, 31, 2325–2336. [Google Scholar] [CrossRef]
- Chen, W.; Yue, H.; Wang, J.; Wu, X. An improved edge detection algorithm for depth map inpainting. Opt. Lasers Eng. 2014, 55, 69–77. [Google Scholar] [CrossRef]
- Qian, P.; Zhao, K.; Jiang, Y.; Su, K.; Deng, Z.; Wang, S.; Muzic, R.F. Knowledge-leveraged transfer fuzzy C-Means for texture image segmentation with self-adaptive cluster prototype matching. Knowl. Based Syst. 2017, 130, 33–50. [Google Scholar] [CrossRef]
- Qureshi, M.N.; Ahamad, M.V. An improved method for image segmentation using K-means clustering with neutrosophic Logic. Procedia Comput. Sci. 2018, 132, 534–540. [Google Scholar] [CrossRef]
- Xu, G.; Li, X.; Lei, B.; Lv, K. Unsupervised color image segmentation with color-alone feature using region growing pulse coupled neural network. Neurocomputing 2018, 306, 1–16. [Google Scholar] [CrossRef]
- Hinojosa, S.; Avalos, O.; Oliva, D.; Cuevas, E.; Pajares, G.; Zaldivar, D.; Gálvez, J. Unassisted thresholding based on multi-objective evolutionary algorithms. Knowl. Based Syst. 2018, 159, 221–232. [Google Scholar] [CrossRef]
- Oliva, D.; Cuevas, E.; Pajares, G.; Zaldivar, D.; Osuna, V. A Multilevel Thresholding algorithm using electromagnetism optimization. Neurocomputing 2014, 139, 357–381. [Google Scholar] [CrossRef]
- Sambandam, R.K.; Jayaraman, S. Self-adaptive dragonfly based optimal thresholding for multilevel segmentation of digital images. J. King Saud Univ. Comput. Inf. Sci. 2018, 30, 449–461. [Google Scholar] [CrossRef]
- Li, C.H.; Lee, C.K. Minimum cross entropy thresholding. Pattern Recognit. 1993, 26, 617–625. [Google Scholar] [CrossRef]
- Sarkar, S.; Das, S.; Chaudhuri, S.S. A multilevel color image thresholding scheme based on minimum cross entropy and differential evolution. Pattern Recognit. Lett. 2015, 54, 27–35. [Google Scholar] [CrossRef]
- Pare, S.; Kumar, A.; Bajaj, V.; Singh, G.K. An efficient method for multilevel color image thresholding using cuckoo search algorithm based on minimum cross entropy. Appl. Soft Comput. 2017, 61, 570–592. [Google Scholar] [CrossRef]
- Oliva, D.; Hinojosa, S.; Cuevas, E.; Pajares, G.; Avalos, O.; Gálvez, J. Cross entropy based thresholding for magnetic resonance brain images using crow search algorithm. Expert Syst. Appl. 2017, 79, 164–180. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Piscataway, NJ, USA, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Global Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Yang, X. A new metaheuristic bat-inspired algorithm. Comput. Knowl. Technol. 2010, 284, 65–74. [Google Scholar]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Applic. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Mirjalili, S. Grey wolf optimizer. Adv. Eng. Software 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Suresh, S.; Lal, S. Multilevel thresholding based on chaotic darwinian particle swarm optimization for segmentation of satellite images. Appl. Soft Comput. 2017, 55, 503–522. [Google Scholar] [CrossRef]
- Mlakar, U.; Potočnik, B.; Brest, J. A hybrid differential evolution for optimal multilevel image thresholding. Expert Syst. Appl. 2016, 65, 221–232. [Google Scholar] [CrossRef]
- Satapathy, S.C.; Raja, N.S.M.; Rajinikanth, V.; Ashour, A.S.; Dey, N. Multi-level image thresholding using Otsu and chaotic bat algorithm. Expert Syst. Appl. 2018, 29, 1285–1307. [Google Scholar] [CrossRef]
- Díaz-Cortés, M.; Ortega-Sánchez, N.; Hinojosa, S.; Oliva, D.; Cuevas, E.; Rojas, R.; Demin, A. A multi-level thresholding method for breast thermograms analysis using dragonfly algorithm. Infrared Phys. Technol. 2018, 93, 346–361. [Google Scholar] [CrossRef]
- Khairuzzaman, A.K.M.; Chaudhury, S. Multilevel thresholding using grey wolf optimizer for image segmentation. Expert Syst. Appl. 2017, 86, 64–76. [Google Scholar] [CrossRef]
- Aziz, M.A.E.; Ewees, A.A.; Hassanien, A.E. Whale optimization algorithm and moth-flame optimization for multilevel thresholding image segmentation. Expert Syst. Appl. 2017, 83, 242–256. [Google Scholar] [CrossRef]
- Pare, S.; Bhandari, A.K.; Kumar, A.; Singh, G.K. A new technique for multilevel color image thresholding based on modified fuzzy entropy and Lévy flight firefly algorithm. Comput. Electr. Eng. 2018, 70, 476–495. [Google Scholar] [CrossRef]
- Jia, H.; Peng, X.; Song, W.; Lang, C.; Xing, Z.; Sun, K. Multiverse optimization algorithm based on lévy flight improvement for multithreshold color image segmentation. IEEE Access 2019, 7, 32805–32844. [Google Scholar] [CrossRef]
- Ouadfel, S.; Taleb-Ahmed, A. Social spiders optimization and flower pollination algorithm for multilevel image thresholding: A performance study. Expert Syst. Appl. 2016, 55, 566–584. [Google Scholar] [CrossRef]
- Gill, H.S.; Khehra, B.S.; Singh, A.; Kaur, L. Teaching-learning-based optimization algorithm to minimize cross entropy for selecting multilevel threshold values. Egypt. Inform. J. 2019, 20, 11–25. [Google Scholar] [CrossRef]
- Beevi, S.; Nair, M.S.; Bindu, G.R. Automatic segmentation of cell nuclei using Krill Herd optimization based multi-thresholding and localized active contour model. Biocybern. Biomed. Eng. 2016, 36, 584–596. [Google Scholar] [CrossRef]
- Kotte, S.; Pullakura, R.K.; Injeti, S.K. Optimal multilevel thresholding selection for brain MRI image segmentation based on adaptive wind driven optimization. Measurement 2018, 130, 340–361. [Google Scholar] [CrossRef]
- He, L.; Huang, S. Modified firefly algorithm based multilevel thresholding for color image segmentation. Neurocomputing 2017, 240, 152–174. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper optimisation algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef]
- Luo, J.; Chen, H.; Zhang, Q.; Xu, Y.; Huang, H.; Zhao, X.A. An improved grasshopper optimization algorithm with application to financial stress prediction. Appl. Math. Modell. 2018, 64, 654–668. [Google Scholar] [CrossRef]
- Mafarja, M.; Aljarah, I.; Faris, H.; Hammouri, A.I.; Al-Zoubi, A.M.; Mirjalili, S. Binary grasshopper optimisation algorithm approaches for feature selection problems. Expert Syst. Appl. 2019, 117, 267–286. [Google Scholar] [CrossRef]
- Zhang, X.; Miao, Q.; Zhang, H.; Wang, L. A parameter-adaptive VMD method based on grasshopper optimization algorithm to analyze vibration signals from rotating machinery. Mech. Syst. Sig. Process. 2018, 108, 58–72. [Google Scholar] [CrossRef]
- Fathy, A. Recent meta-heuristic grasshopper optimization algorithm for optimal reconfiguration of partially shaded PV array. Solar Energy 2018, 171, 638–651. [Google Scholar] [CrossRef]
- Ewees, A.A.; Elaziz, M.A.; Houssein, E.H. Improved grasshopper optimization algorithm using opposition-based learning. Expert Syst. Appl. 2018, 112, 156–172. [Google Scholar] [CrossRef]
- Wu, J.; Wang, H.; Li, N.; Yao, P.; Huang, Y.; Su, Z.; Yu, Y. Distributed trajectory optimization for multiple solar-powered UAVs target tracking in urban environment by adaptive grasshopper optimization algorithm. Aerosp. Sci. Technol. 2017, 70, 497–510. [Google Scholar] [CrossRef]
- Jadon, S.S.; Tiwari, R.; Sharma, H.; Bansal, J.C. Hybrid artificial bee colony algorithm with differential evolution. Appl. Soft Comput. 2017, 58, 11–24. [Google Scholar] [CrossRef]
- Dash, J.; Dam, B.; Swain, R. Design of multipurpose digital FIR double-band filter using hybrid firefly differential evolution algorithm. Appl. Soft Comput. 2017, 59, 529–545. [Google Scholar] [CrossRef]
- Xiong, G.; Zhang, J.; Yuan, X.; Shi, D.; He, Y.; Yao, G. Parameter extraction of solar photovoltaic models by means of a hybrid differential evolution with whale optimization algorithm. Solar Energy 2018, 176, 742–761. [Google Scholar] [CrossRef]
- Ewees, A.A.; Elaziz, M.A.; Oliva, D. Image segmentation via multilevel thresholding using hybrid optimization algorithms. J. Electr. Imaging 2018, 27. [Google Scholar] [CrossRef]
- Bhandari, A.K.; Kumar, A.; Singh, G.K. Tsallis entropy based multilevel thresholding for colored satellite image segmentation using evolutionary algorithms. Expert Syst. Appl. 2015, 42, 8707–8730. [Google Scholar] [CrossRef]
- Mafarja, M.; Aljarah, I.; Heidari, A.A.; Hammouri, A.I.; Faris, H.; Al-Zoubi, A.M.; Mirjalili, S. Evolutionary population dynamics and grasshopper optimization approaches for feature selection problems. Knowl. Based Syst. 2018, 145, 25–45. [Google Scholar] [CrossRef]
- Ibrahim, R.A.; Elaziz, M.A.; Lu, S. Chaotic opposition-based grey-wolf optimization algorithm based on differential evolution and disruption operator for global optimization. Expert Syst. Appl. 2018, 108, 1–27. [Google Scholar] [CrossRef]
- Yüzgeç, U.; Eser, M. Chaotic based differential evolution algorithm for optimization of baker’s yeast drying process. Egypt. Inform. J. 2018, 19, 151–163. [Google Scholar] [CrossRef]
- Lin, Q.; Zhu, Q.; Huang, P.; Chen, J.; Ming, Z.; Yu, J. A novel hybrid multi-objective immune algorithm with adaptive differential evolution. Comput. Oper. Res. 2015, 62, 95–111. [Google Scholar] [CrossRef]
- Brest, J.; Greiner, S.; Boskovic, B.; Mernik, M.; Zumer, V. Self-adapting control parameters in differential evolution: A comparative study on numerical benchmark problems. IEEE Trans. Evol. Comput. 2006, 10, 646–657. [Google Scholar] [CrossRef]
- Elaziz, M.A.; Xiong, S.; Jayasena, K.P.N.; Li, L. Task scheduling in cloud computing based on hybrid moth search algorithm and differential evolution. Knowl. Based Syst. 2019, 169, 39–52. [Google Scholar] [CrossRef]
- Zhao, F.; Xue, F.; Zhang, Y.; Ma, W.; Zhang, C.; Song, H. A hybrid algorithm based on self-adaptive gravitational search algorithm and differential evolution. Expert Syst. Appl. 2018, 113, 515–530. [Google Scholar]
- Zhao, F.; Xue, F.; Shao, Z.; Wang, J.; Zhang, C. A hybrid optimization algorithm based on chaotic differential evolution and estimation of distribution. Comput. Appl. Math. 2017, 36, 433–458. [Google Scholar] [CrossRef]
- Xu, L.; Jia, H.; Lang, C.; Peng, X.; Sun, K. A novel method for multilevel color image segmentation based on dragonfly algorithm and differential evolution. IEEE Access 2019, 7, 19502–19538. [Google Scholar] [CrossRef]
- Landsat Imagery Courtesy of NASA Goddard Space Flight Center and U.S. Geological Survey. Available online: https://landsat.visibleearth.nasa.gov/index.php?&p=1 (accessed on 7 October 2018).
- Liang, H.; Jia, H.; Xing, Z.; Ma, J.; Peng, X. Modified grasshopper algorithm-based multilevel thresholding for color image segmentation. IEEE Access 2019, 7, 11258–11295. [Google Scholar] [CrossRef]
- Bhandari, A.K. A novel beta differential evolution algorithm-based fast multilevel thresholding for color image segmentation. Neural Comput. Appl. 2018, 1–31. [Google Scholar] [CrossRef]
- Bhandari, A.K.; Kumar, A.; Singh, G.K. Modified artificial bee colony based computationally efficient multilevel thresholding for satellite image segmentation using Kapur’s, Otsu and Tsallis functions. Expert Syst. Appl. 2015, 42, 1573–1601. [Google Scholar] [CrossRef]
- Kotte, S.; Kumar, P.R.; Injeti, S.K. An efficient approach for optimal multilevel thresholding selection for gray scale images based on improved differential search algorithm. Ain Shams Eng. J. 2018, 9, 1043–1067. [Google Scholar] [CrossRef]
- The USC-SIPI Image Database. Available online: http://sipi.usc.edu/database/ (accessed on 9 April 2019).
- Lang, C.; Jia, H. Kapur’s entropy for color image segmentation based on a hybrid whale optimization algorithm. Entropy 2019, 21, 318. [Google Scholar] [CrossRef]
- Shen, L.; Fan, C.; Huang, X. Multi-level image thresholding using modified flower pollination algorithm. IEEE Access 2018, 6, 30508–30519. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Mou, X.; Zhang, D. FSIM: A feature similarity index for image quality assessment. IEEE Trans. Image Process. 2011, 20, 2378–2386. [Google Scholar] [CrossRef] [PubMed]
- Frank, W. Individual comparisons of grouped data by ranking methods. J. Econ. Entomol. 1946, 39, 269–270. [Google Scholar]
- Friedman, M. The use of ranks to avoid the assumption of normality implicit in the analysis of variance. J. Am. Stat. Assoc. 1937, 32, 676–701. [Google Scholar] [CrossRef]
- Albuquerque, M.P.D.; Esquef, I.A.; Mello, A.R.G.; Albuquerque, M.P.D. Image thresholding using Tsallis entropy. Pattern Recognit. Lett. 2004, 25, 1059–1065. [Google Scholar] [CrossRef]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Mousavirad, S.J.; Ebrahimpour-Komleh, H. Multilevel image thresholding using entropy of histogram and recently developed population-based metaheuristic algorithms. Evol. Intel. 2017, 10, 45–75. [Google Scholar] [CrossRef]
- Jia, H.; Peng, X.; Song, W.; Oliva, D.; Lang, C.; Yao, L. Masi entropy for satellite color image segmentation using tournament-based lévy multiverse optimization algorithm. Remote Sens. 2019, 11, 942. [Google Scholar] [CrossRef]
- The Berkeley Segmentation Dataset and Benchmark. Available online: https://www2.eecs.berkeley.edu/Research/Projects/CS/vision/grouping/segbench/ (accessed on 11 July 2018).
- Jia, H.; Peng, X.; Song, W.; Lang, C.; Xing, Z.; Sun, K. Hybrid multiverse optimization algorithm with gravitational search algorithm for multithreshold color image segmentation. IEEE Access 2019, 7, 44903–44927. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. Evolut. Comput. IEEE Trans. 1997, 1, 67–82. [Google Scholar] [CrossRef]


| 14.0625 | 13.75 | 16.6875 | 9.75 | 11.75 | |
| 7.0625 | 13.4375 | 9.8125 | 13 | 12.6875 | |
| 15.6875 | 16.6875 | 14.3125 | 15.1875 | 17.0625 | |
| 13.8125 | 13.8125 | 14.5 | 12.6875 | 9.5 | |
| 15.875 | 9 | 3 | 14.875 | 17 |
| Image Number | Explanation |
|---|---|
| 1. | The Aïr Mountains dispersed across the Sahara Desert in northern Niger. |
| 2. | Glacier cover in the mountainous region of northwestern Venezuela. |
| 3. | Dukan Lake in the Zagros Mountains, the largest lake in Iraqi Kurdistan. |
| 4. | Candeleros rock containing quite a menagerie of fossilized fauna. |
| 5. | The waters of Foxe Basin, which have been choked with sea ice for most of the year. |
| 6. | The Port of Busan at the southeastern tip of the Korean Peninsula, which has been a trading hub since at least the 15th century. |
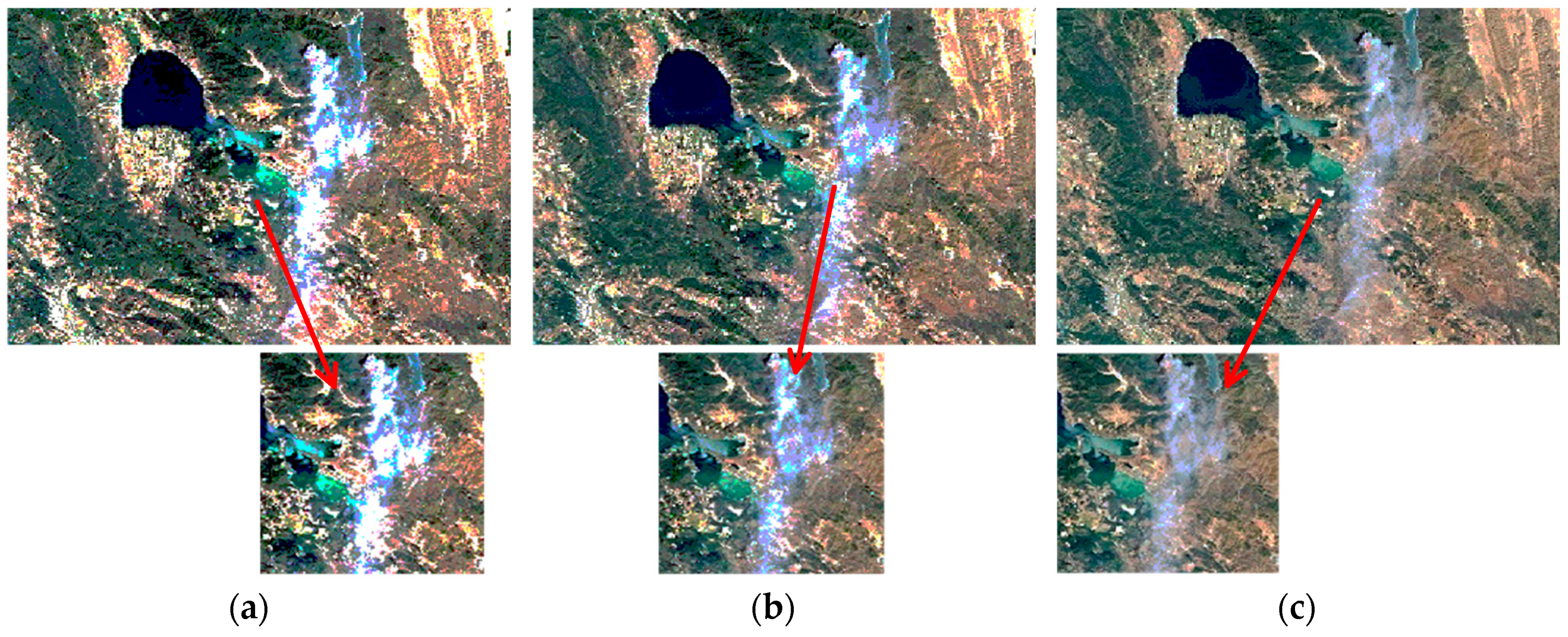
| 7. | A fire in Northern California during the summer of 2018. |
| 8. | The Ebro Delta, located more than 200 kilometers (120 miles) southwest of Barcelona. |
| No. | Algorithm | Parameter Setting | Year | Reference |
|---|---|---|---|---|
| 1. | GOA–jDE | — | — | |
| 2. | GOA | 2017 | [33] | |
| 3. | DE | 1997 | [16] | |
| 4. | MGOA | 2019 | [55] | |
| 5. | hjDE | 2016 | [21] | |
| 6. | BDE | 2018 | [56] | |
| 7. | BA | 2010 | [17] | |
| 8. | PSO | 1995 | [15] | |
| 9. | MABC | 2015 | [57] | |
| 10. | IDSA | — | 2018 | [58] |
| 11. | CS | 2017 | [13] |
| No. | Measures | Formulation | Remark | Reference |
|---|---|---|---|---|
| 1. | Average Fitness Function Value | Indicates the center value of sample data. | [46] | |
| 2. | Standard Deviation (STD) | Reflects the degree of dispersion in a dataset. A lower value shows better performance. | [46] | |
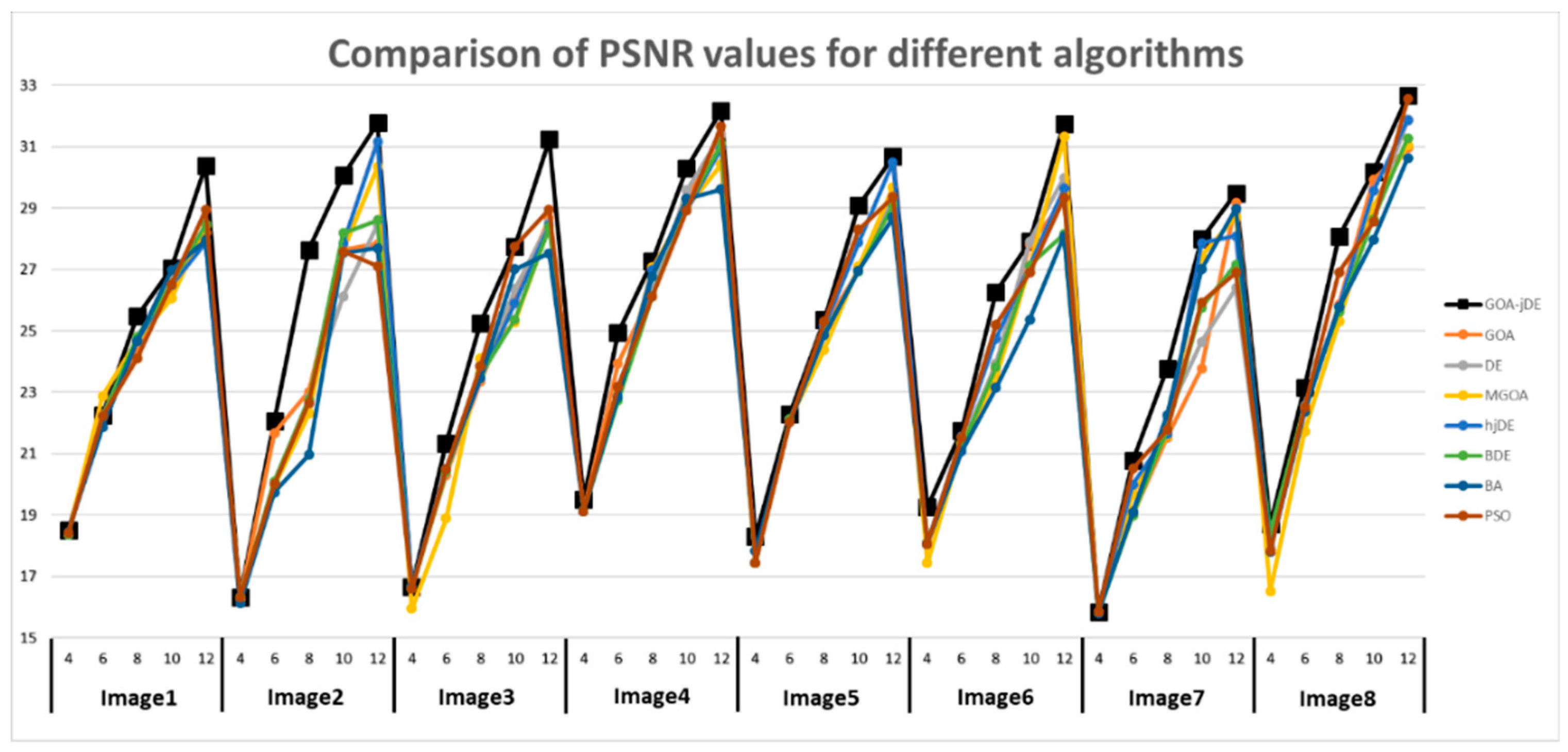
| 3. | Peak Signal to Noise Ratio (PSNR) | The ratio of the maximum possible power of the signal to the destructive noise power. | [60] | |
| 4. | Mean Squared Error (MSE) | Computes the difference between the predicted value. | [60] | |
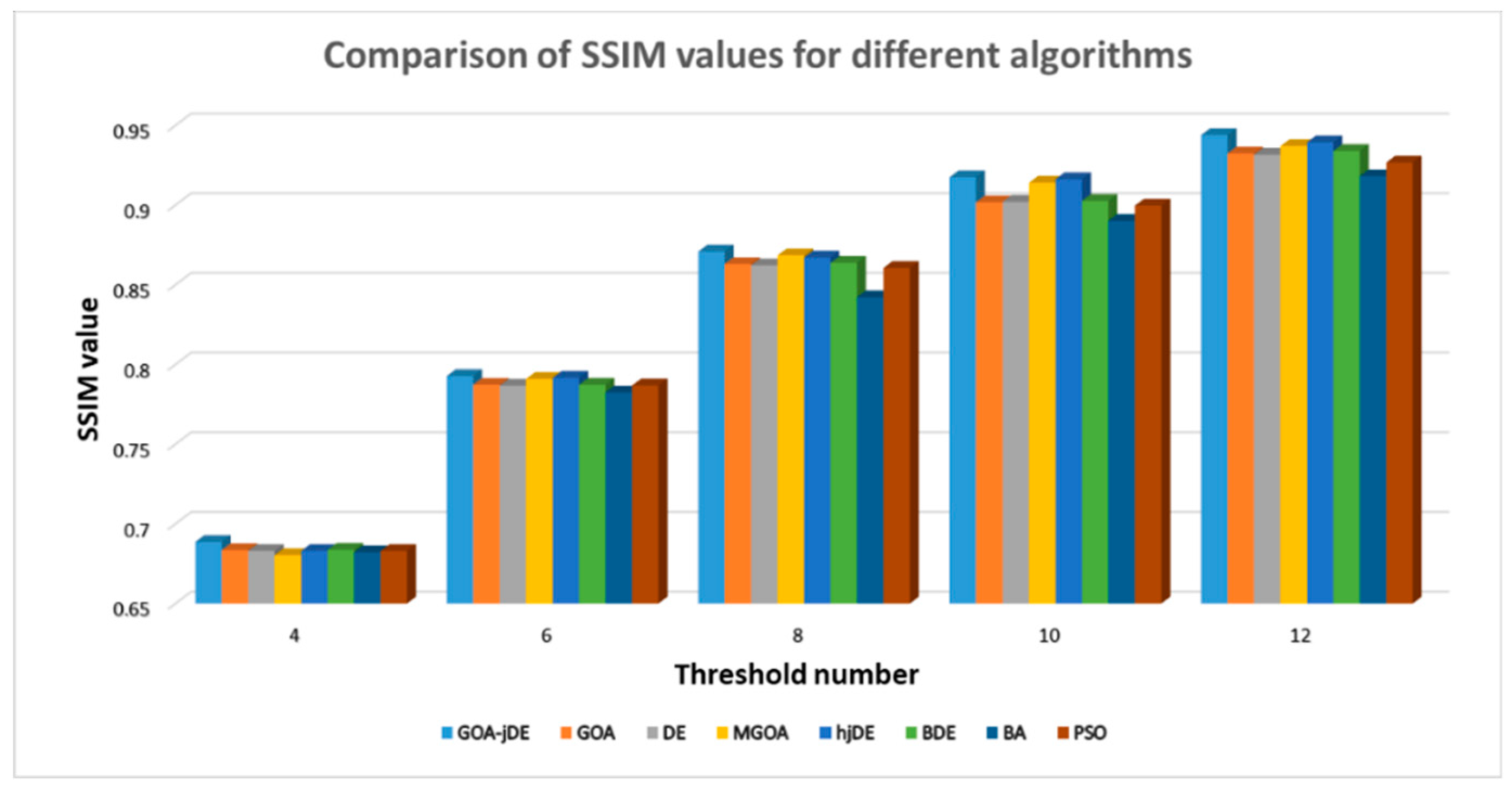
| 5. | Structural Similarity Index (SSIM) | Defines the similarity between the original image and the segmented image. | [61] | |
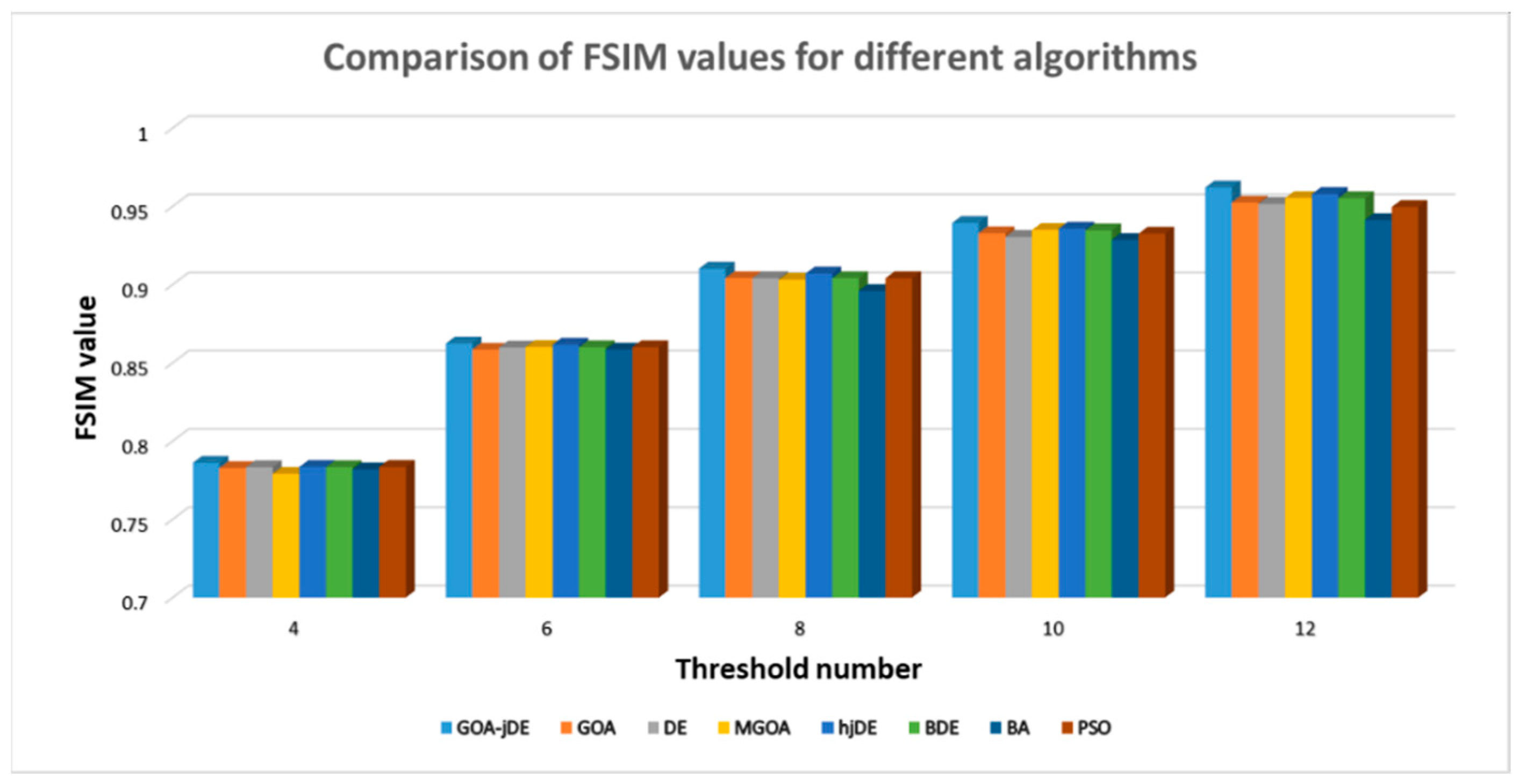
| 6. | Feature Similarity Index (FSIM) | Reflects the similarity of feature structure, the maximum value is 1. | [62] | |
| 7. | Average Computation Time | Indicates the operating efficiency of each method. | [14] | |
| 8. | Wilcoxon’s Rank Sum Test | Whether there is a significant difference between two algorithms. | [63] | |
| 9. | Friedman Test | Detects significant differences between the behaviors of two or more algorithms. | [64] |
| Images | K | GOA–jDE | GOA | DE | MGOA | hjDE | BDE | BA | PSO |
|---|---|---|---|---|---|---|---|---|---|
| Image1 | 4 | −701.0136 | −700.9701 | −701.0136 | −701.0136 | −701.0136 | −701.0136 | −701.0132 | −701.0136 |
| 6 | −701.2706 | −701.2705 | −701.2705 | −701.2705 | −701.2706 | −701.2704 | −701.2267 | −701.2702 | |
| 8 | −701.3808 | −701.3829 | −701.3803 | −701.3806 | −701.3807 | −701.3807 | −701.3152 | −701.3782 | |
| 10 | −701.4401 | −701.4371 | −701.4395 | −701.4389 | −701.4392 | −701.439 | −701.3746 | −701.4042 | |
| 12 | −701.4753 | −701.473 | −701.4737 | −701.4736 | −701.4751 | −701.4749 | −701.3678 | −701.4573 | |
| Image2 | 4 | −370.8833 | −370.8833 | −370.8833 | −370.8833 | −370.8833 | −370.8833 | −370.7795 | −370.8833 |
| 6 | −371.1958 | −371.1958 | −371.1959 | −371.1958 | −371.1959 | −371.1959 | −371.045 | −371.1898 | |
| 8 | −371.3386 | −371.3108 | −371.3372 | −371.3209 | −371.3385 | −371.3381 | −371.2998 | −371.2486 | |
| 10 | −371.4126 | −371.3998 | −371.4082 | −371.3839 | −371.4124 | −371.4115 | −371.2348 | −371.3697 | |
| 12 | −371.457 | −371.4345 | −371.4507 | −371.4395 | −371.4569 | −371.4558 | −371.3314 | −371.3988 | |
| Image3 | 4 | −645.6498 | −645.6498 | −645.6498 | −645.6498 | −645.6498 | −645.6498 | −645.646 | −645.6498 |
| 6 | −646.008 | −645.9872 | −646.008 | −646.008 | −646.008 | −646.0079 | −645.98 | −646.0059 | |
| 8 | −646.1744 | −646.1662 | −646.1735 | −646.1743 | −646.1742 | −646.1741 | −646.066 | −646.1298 | |
| 10 | −646.261 | −646.2592 | −646.2597 | −646.2605 | −646.2603 | −646.2582 | −646.1845 | −646.235 | |
| 12 | −646.3107 | −646.2853 | −646.3092 | −646.3039 | −646.3077 | −646.3098 | −646.2148 | −646.2988 | |
| Image4 | 4 | −474.0258 | −474.0258 | −474.0257 | −474.0258 | −474.0258 | −474.0254 | −474.0241 | −474.0257 |
| 6 | −474.3694 | −474.3683 | −474.3691 | −474.3694 | −474.3694 | −474.3693 | −474.3543 | −474.3685 | |
| 8 | −474.526 | −474.5238 | −474.5229 | −474.5259 | −474.5251 | −474.5257 | −474.3738 | −474.5036 | |
| 10 | −474.6101 | −474.6052 | −474.6082 | −474.6068 | −474.6088 | −474.6082 | −474.4214 | −474.5932 | |
| 12 | −474.6598 | −474.6508 | −474.6569 | −474.6563 | −474.6596 | −474.6585 | −474.5078 | −474.6356 | |
| Image5 | 4 | −498.1325 | −498.1325 | −498.1325 | −498.1325 | −498.1325 | −498.1325 | −498.1271 | −498.1325 |
| 6 | −498.5083 | −498.4884 | −498.5083 | −498.5083 | −498.5082 | −498.4757 | −498.4172 | −498.5078 | |
| 8 | −498.6791 | −498.6698 | −498.6783 | −498.6784 | −498.6791 | −498.679 | −498.5085 | −498.6742 | |
| 10 | −498.774 | −498.7722 | −498.7672 | −498.7733 | −498.7731 | −498.7736 | −498.6267 | −498.734 | |
| 12 | −498.8269 | −498.8226 | −498.8201 | −498.826 | −498.8248 | −498.826 | −498.7248 | −498.8073 | |
| Image6 | 4 | −306.5464 | −306.5464 | −306.5463 | −306.5464 | −306.5464 | −306.5461 | −306.5389 | −306.5463 |
| 6 | −306.9244 | −306.9237 | −306.9244 | −306.9244 | −306.9244 | −306.9231 | −306.8676 | −306.8951 | |
| 8 | −307.0986 | −307.0977 | −307.0981 | −307.0985 | −307.0985 | −307.0985 | −306.8234 | −307.0793 | |
| 10 | −307.1962 | −307.187 | −307.1699 | −307.1871 | −307.1961 | −307.1912 | −307.0848 | −307.1482 | |
| 12 | −307.2547 | −307.2322 | −307.2507 | −307.2423 | −307.252 | −307.2517 | −307.0775 | −307.2106 | |
| Image7 | 4 | −480.5483 | −480.5483 | −480.5483 | −480.5483 | −480.5483 | −480.5483 | −480.5475 | −480.548 |
| 6 | −480.8448 | −480.8428 | −480.8441 | −480.8448 | −480.8448 | −480.8448 | −480.7985 | −480.8158 | |
| 8 | −480.974 | −480.9729 | −480.9725 | −480.9735 | −480.9733 | −480.9725 | −480.83 | −480.9581 | |
| 10 | −481.041 | −481.0396 | −481.0402 | −481.04 | −481.0408 | −481.0407 | −480.9169 | −481.0313 | |
| 12 | −481.0802 | −481.0699 | −481.0776 | −481.0723 | −481.0796 | −481.0771 | −480.9164 | −481.0549 | |
| Image8 | 4 | −411.1164 | −411.1164 | −411.1164 | −411.1164 | −411.1164 | −411.1164 | −411.1118 | −411.1164 |
| 6 | −411.4617 | −411.4605 | −411.4616 | −411.4616 | −411.4616 | −411.4611 | −411.308 | −411.4607 | |
| 8 | −411.6287 | −411.6273 | −411.6285 | −411.6284 | −411.6286 | −411.6231 | −411.5499 | −411.5935 | |
| 10 | −411.7136 | −411.7007 | −411.7105 | −411.7043 | −411.7119 | −411.7131 | −411.6203 | −411.6984 | |
| 12 | −411.7664 | −411.7632 | −411.7641 | −411.758 | −411.7662 | −411.7653 | −411.6613 | −411.7395 |
| Images | GOA–jDE | GOA | DE | MGOA | hjDE | BDE | BA | PSO |
|---|---|---|---|---|---|---|---|---|
| 1 | 6.67 | 0 | 0 | 0 | 0 | 0 | 3.33 | 0 |
| 2 | 100 | 0 | 10 | 86.67 | 0 | 0 | 36.67 | 13.33 |
| 3 | 83.33 | 26.67 | 20 | 40 | 0 | 23.33 | 0 | 10 |
| 4 | 100 | 100 | 100 | 96.67 | 100 | 93.33 | 100 | 90 |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 100 | 60 | 36.67 | 53.33 | 30 | 70 | 86.67 | 40 |
| 7 | 73.33 | 0 | 3.33 | 40 | 0 | 6.67 | 13.33 | 0 |
| 8 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| K | GOA–jDE | GOA | DE | MGOA | hjDE | BDE | BA | PSO |
|---|---|---|---|---|---|---|---|---|
| 4 | 1.744575 | 3.339125 | 1.132188 | 3.338625 | 1.632425 | 1.50965 | 1.3265 | 1.081413 |
| 6 | 1.814575 | 3.407225 | 1.225213 | 3.467038 | 1.734113 | 1.701825 | 1.5425 | 1.1903 |
| 8 | 2.027638 | 3.493013 | 1.31005 | 3.492675 | 1.987663 | 1.876263 | 1.885988 | 1.321688 |
| 10 | 2.258513 | 3.567325 | 1.446075 | 3.58 | 2.248538 | 2.023563 | 2.240663 | 1.454863 |
| 12 | 2.558875 | 3.860313 | 1.5924 | 3.750038 | 2.380238 | 2.263163 | 2.813125 | 1.56585 |
| Comparison | p-Value |
|---|---|
| GOA–jDE vs. GOA | 0.0197 |
| GOA–jDE vs. DE | 2.7461 × 10−4 |
| GOA–jDE vs. MGOA | 2.3012 × 10−5 |
| GOA–jDE vs. hjDE | 8.7216 × 10−4 |
| GOA–jDE vs. BDE | 1.6063 × 10−9 |
| GOA–jDE vs. BA | 3.9766 × 10−7 |
| GOA–jDE vs. PSO | 5.0219 × 10−8 |
| K | Average Rank | |||||||
|---|---|---|---|---|---|---|---|---|
| GOA-jDE | GOA | DE | MGOA | hjDE | BDE | BA | PSO | |
| 4 | 2 | 5.4625 | 3.6 | 4.55 | 4.075 | 4.9 | 6.4125 | 5 |
| 6 | 1.475 | 5.425 | 4.1 | 4.3375 | 3.75 | 4.9625 | 6.7625 | 5.1875 |
| 8 | 1.0625 | 4.6125 | 4.4125 | 4.475 | 4.325 | 4.725 | 6.9625 | 5.425 |
| 10 | 1.05 | 4.8625 | 4.8125 | 4.6375 | 3.7625 | 4.2125 | 6.9625 | 5.7 |
| 12 | 1 | 5.0375 | 4.2375 | 4.5875 | 3.725 | 4.3875 | 7.5125 | 5.5125 |
| K | Chi-Square Value | p-Value |
|---|---|---|
| 4 | 101.901 | 4.36751 × 10−19 |
| 6 | 114.919 | 8.73960 × 10−22 |
| 8 | 126.529 | 3.33534 × 10−24 |
| 10 | 135.448 | 4.56229 × 10−26 |
| 12 | 155.666 | 2.61739 × 10−30 |
| Images | K | Tsallis | Otsu | MCE | |||
|---|---|---|---|---|---|---|---|
| GOA–jDE | MABC | GOA–jDE | IDSA | GOA–jDE | CS | ||
| Image1 | 20 | 65.6992 | 63.9303 | 2536.0239 | 2533.7508 | −701.5320 | −701.5321 |
| 25 | 72.0775 | 69.8990 | 2538.4352 | 2537.4078 | −701.5441 | −701.5440 | |
| 30 | 78.0006 | 74.2769 | 2540.1262 | 2539.0127 | −701.5516 | −701.5513 | |
| Image2 | 20 | 65.1949 | 63.3661 | 1380.4683 | 1378.9008 | −371.5264 | −371.5240 |
| 25 | 71.4121 | 69.0462 | 1382.6497 | 1382.0753 | −371.5386 | −371.5390 | |
| 30 | 77.1012 | 73.8485 | 1383.9328 | 1383.0637 | −371.5467 | −371.5457 | |
| Image3 | 20 | 66.3283 | 64.7228 | 2267.4996 | 2265.5258 | −646.3892 | −646.3875 |
| 25 | 73.0784 | 70.6841 | 2270.3662 | 2269.1050 | −646.4058 | −646.4052 | |
| 30 | 78.9913 | 74.9226 | 2272.1397 | 2270.5508 | −646.4160 | −646.4150 | |
| Image4 | 20 | 67.2077 | 65.8090 | 1654.2822 | 1652.9518 | −474.7376 | −474.7383 |
| 25 | 74.0556 | 71.2441 | 1656.8361 | 1655.9701 | −474.7543 | −474.7542 | |
| 30 | 80.2195 | 75.7998 | 1658.3974 | 1657.8302 | −474.7638 | −474.7638 | |
| Image5 | 20 | 67.1305 | 65.6002 | 5516.8189 | 5515.3632 | −498.9233 | −498.9223 |
| 25 | 74.3413 | 71.3003 | 5519.9728 | 5519.1290 | −498.9440 | −498.9433 | |
| 30 | 79.8769 | 75.9055 | 5521.8659 | 5521.0078 | −498.9556 | −498.9552 | |
| Image6 | 20 | 66.7823 | 65.4021 | 3210.8833 | 3209.5405 | −307.3492 | −307.3459 |
| 25 | 74.1973 | 71.5457 | 3213.7465 | 3212.8257 | −307.3670 | −307.3685 | |
| 30 | 79.4842 | 75.5905 | 3215.0132 | 3214.2657 | −307.3798 | −307.3795 | |
| Image7 | 20 | 65.5192 | 63.8334 | 1803.2208 | 1801.3177 | −481.1434 | −481.1416 |
| 25 | 72.4605 | 68.99 | 1805.3468 | 1803.8873 | −481.1571 | −481.1556 | |
| 30 | 77.5298 | 74.1611 | 1806.9075 | 1806.2681 | −481.1634 | −481.1624 | |
| Image8 | 20 | 66.8490 | 65.1504 | 2355.6389 | 2354.3242 | −411.8501 | −411.8497 |
| 25 | 73.6971 | 71.5997 | 2358.1153 | 2356.7401 | −411.8686 | −411.8674 | |
| 30 | 78.9075 | 75.0792 | 2359.6548 | 2358.5339 | −411.8757 | −411.8768 | |
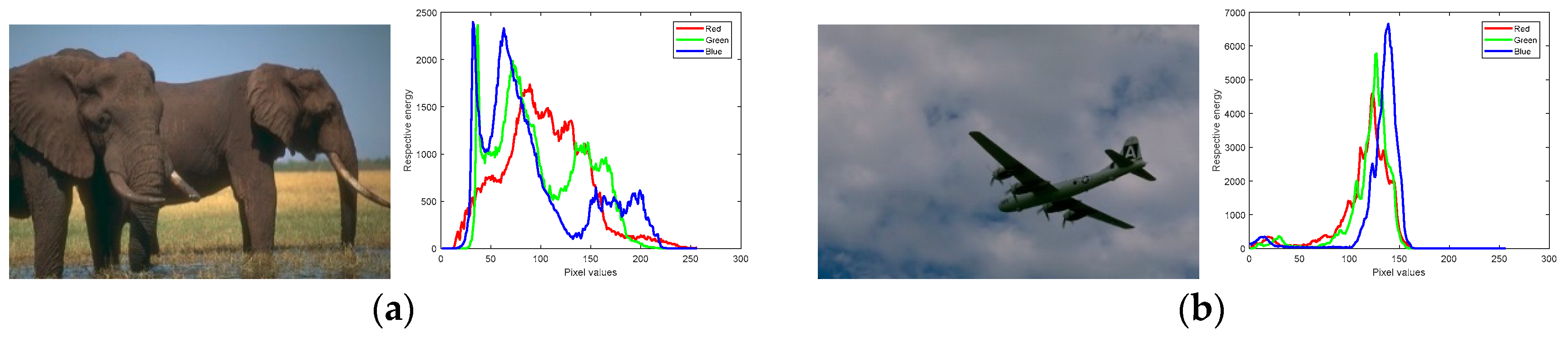
| Elephant | 20 | 62.1191 | 60.7010 | 2009.5697 | 2008.3336 | −457.3469 | −457.3467 |
| 25 | 67.8767 | 66.4680 | 2011.4073 | 2010.5957 | −457.3577 | −457.3569 | |
| 30 | 72.9363 | 69.5792 | 2012.2340 | 2011.6498 | −457.3633 | −457.3631 | |
| Plane | 20 | 52.1894 | 52.1762 | 706.7254 | 706.6974 | −587.0459 | −587.0450 |
| 25 | 55.6713 | 55.8603 | 707.6530 | 707.4842 | −587.0525 | −587.0503 | |
| 30 | 58.7978 | 58.3922 | 707.8326 | 708.1450 | −587.0541 | −587.0538 | |
| K | Average Rank | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| GOA–jDE–MCE | MGOA–MCE | hjDE–MCE | BDE–MCE | BA–MCE | PSO–MCE | CS–MCE | IDSA–Otsu | MABC–Tsallis | |
| 20 | 3.1754 | 4.4781 | 5.5833 | 6.3070 | 5.6974 | 4.9693 | 4.9167 | 3.9430 | 5.9298 |
| 25 | 2.7368 | 4.9342 | 5.0746 | 6.5219 | 6.4342 | 4.1535 | 4.8640 | 4.2588 | 6.0219 |
| 30 | 1.3421 | 4.6886 | 4.5526 | 5.9254 | 7.4386 | 5.1798 | 4.6316 | 4.5175 | 6.7237 |
| Overall | 2.4181 | 4.7003 | 5.0702 | 6.2515 | 6.5234 | 4.7675 | 4.8041 | 4.2398 | 6.2251 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, H.; Lang, C.; Oliva, D.; Song, W.; Peng, X. Hybrid Grasshopper Optimization Algorithm and Differential Evolution for Multilevel Satellite Image Segmentation. Remote Sens. 2019, 11, 1134. https://doi.org/10.3390/rs11091134
Jia H, Lang C, Oliva D, Song W, Peng X. Hybrid Grasshopper Optimization Algorithm and Differential Evolution for Multilevel Satellite Image Segmentation. Remote Sensing. 2019; 11(9):1134. https://doi.org/10.3390/rs11091134
Chicago/Turabian StyleJia, Heming, Chunbo Lang, Diego Oliva, Wenlong Song, and Xiaoxu Peng. 2019. "Hybrid Grasshopper Optimization Algorithm and Differential Evolution for Multilevel Satellite Image Segmentation" Remote Sensing 11, no. 9: 1134. https://doi.org/10.3390/rs11091134
APA StyleJia, H., Lang, C., Oliva, D., Song, W., & Peng, X. (2019). Hybrid Grasshopper Optimization Algorithm and Differential Evolution for Multilevel Satellite Image Segmentation. Remote Sensing, 11(9), 1134. https://doi.org/10.3390/rs11091134