1. Introduction
The Ice, Cloud, and land Elevation Satellite-2 (ICESat-2) that was successfully launched on 15 September 2018, is equipped with the Advanced Topographic Laser Altimeter System (ATLAS), and the main payload of the system is the micro-pulse photon-counting system [
1]. Therefore, the system is expected to provide a reliable estimation of carbon storage [
2]. Unlike the Geoscience Laser Altimeter System (GLAS) on the Ice, Cloud, and land Elevation Satellite-1 (ICESat-1), the ATLAS laser emission mode has six beams grouped in three beam pairs, each of which is composed of two different beam energies to increase system dynamic range. Each beam pair is composed of a strong beam and a weak beam, where the energy ratio of a strong beam to a weak beam is 4:1, and the right-pointed beam and left-pointed beam of each pair denote a strong beam and a weak beam, respectively [
1]. The laser emission frequency of the ATLAS laser is 10 kHz. By combining the satellite orbit and laser emission angle of the ICESat-2, it can be estimated that the diameter of the ATLAS spot on the surface is about 17 m at a 0.7 m center-to-center spacing along the track [
2,
3]. The center-to-center spacing along the ATLAS track is narrower than that along the GLAS track. This characteristic enables the ATLAS to obtain continuous tracking information needed for measuring the carbon storage [
1,
4,
5]. Along with the advantages of high repetition frequency and high sensitivity, a large number of noise photons can also be received by the ATLAS system from solar and the system [
4]. These noise photons can be removed by hardware devices such as range gates; however, due to fixed width characteristics of a range gate, the noise photons cannot be eliminated in the range gate [
6]. Therefore, effective noise filtering is essential to retrieve signal photons from noise photons.
With the aim to improve the ICESat-2 noise filtering algorithm, different noise filtering algorithms have been tested on the airborne Sigma Space’s Single Photon Lidar (SPL), Multiple Altimeter Beam Experimental Lidar (MABEL), Slope Imaging Multi-polarization Photon-counting Lidar (SIMPL), and MATLAS data released before the ICESat-2 launching [
7,
8,
9,
10]. For instance, Wang et al. [
4] proposed a noise filtering based on the Bayesian method for the MABEL data. Their results showed that the algorithm could effectively distinguish signal photons from noise photons. However, the distribution of noise photons was random and related to the observation target, thus it was difficult to judge the return photon properties accurately based only on the detection probability.
Magruder et al. [
11] proposed three methods, namely the modified Canny Edge Detection (CED), the Probability Distribution Function (PDF)-based signal extraction, and the localized statistical analysis for noise filtering of the photon-counting data. Their results demonstrated that the modified CED algorithm could remove noise from data of the forest area. However, the rasterized data of a signal photon could be lost, which reduced the validity of photon-counting data.
Xia et al. [
12] and Xu [
13] proposed a localized statistics algorithm with a center-pointed laser by using the MABEL data as experimental data. The results showed that the algorithm could effectively eliminate the noise photons. Tang et al. [
14] used the SPL data as experimental data and proposed a new voxel-based spatial filtering method, which could effectively filter noise photons and retain the fine-scale canopy structure details. Nie et al. [
15] proposed an effective noise removal algorithm to filter out noise photons. By using the MATLAS data as experimental data under the conditions of a laser center pointing and a strong beam, they proved that their algorithm could effectively remove noise photons from the photon cloud. However, this algorithm needed to change the threshold parameters of localized statistics artificially according to different photon densities, which significantly reduced its applicability.
Further, the Density Dimension Algorithm (DDA) and Density Based Spatial Clustering of Applications with Noise (DBSCAN) were used as noise filtering algorithms, and they were based on different densities of noise and signal photons [
16,
17,
18,
19,
20]. Herzfeld et al. [
16,
17] proposed a DDA that utilized the Radial Basis Function (RBF) to calculate the weighted density as a form of data aggregation in the photon cloud and considered density as an additional parameter used as an aid in the auto-adaptive threshold determination. The experimental data included SIPML and SPL data. The experimental results showed that the algorithm had an adaptive ability and could effectively filter the noise. Popescu et al. [
18] employed a multi-level noise filtering approach to classify the photons into ground and top of a canopy by using the overlapping moving window based method. The results showed that the algorithm could recognize the background noise and preserve the signal photons of the original data. Zhang et al. [
19] proposed an improved DBSCAN model, whose search area was a modified horizontal ellipse, and the result showed that smoother surfaces resulted in an improved-accuracy ground height estimation. Chen et al. [
20] proposed different elliptical shapes to calculate the distance between the photons and used the MATLAS data at center pointing and a strong beam to evaluate the performance of their algorithm. The results proved that the horizontal-ellipse searching area performed better than the circle and vertical-ellipse searching areas.
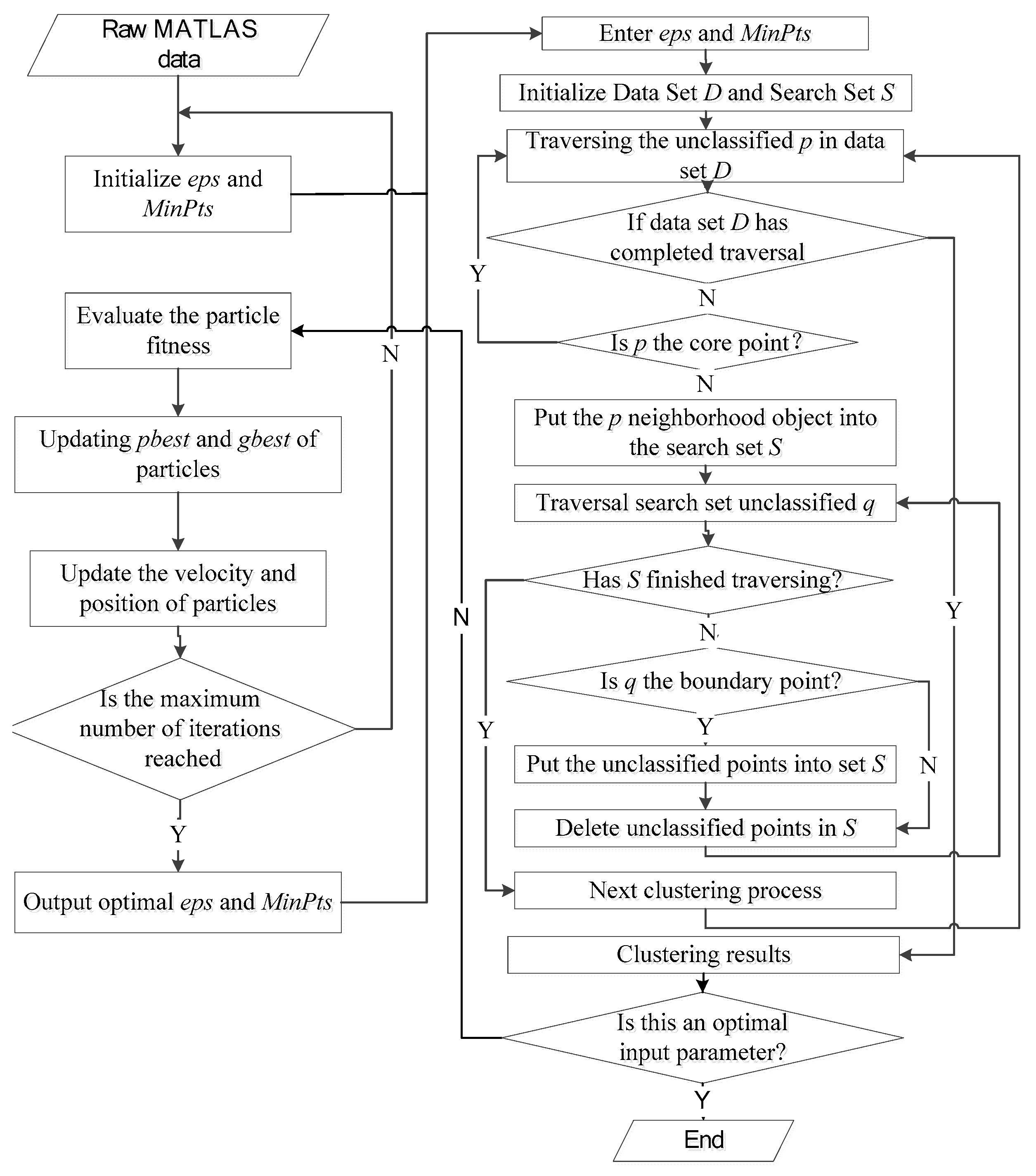
The DBSCAN algorithm was used to extract the signal photon in the noise filtering experiment. The algorithm used two parameters,
eps and
MinPts, to compare the density of data objects. For each data object in each cluster, the number of objects in an
eps-neighborhood with a given radius had to be higher than a threshold
MinPts [
21]. The DBSCAN algorithm could efficiently cluster signal photons without target clusters and was able to discover clusters of an arbitrary shape. In the previous studies on the DBSCAN algorithm improvement, the parallel processing [
22], gridding cells [
23], hierarchical processing [
24], combination with some other clustering algorithms [
25], reduction of searching range [
26], and constraints increasing [
27] were used to improve the clustering accuracy and efficiency of the DBSCAN algorithm. However, the selection of the two chosen parameters (
eps and
MinPts) were not studied profoundly, and these parameters were set mainly by manual selection or based on an empirical formula, but these two methods could have difficulty obtaining the optimal noise filtering parameters for different experimental data. Therefore, the selection of optimal noise filtering parameters for different experimental data is still challenging and represents a research hot spot.
As a representative optimization algorithm in swarm intelligence, the Particle Swarm Optimization (PSO) algorithm has the characteristics of parallel processing and good robustness in selecting optimal parameters [
28,
29,
30,
31,
32]. Besides, it can find the global optimal solution to a problem with a high probability, and its computational efficiency is higher than of the traditional stochastic algorithms. Consequently, it has been used in remote sensing image classification parameter optimization [
28], wind forecasting model optimization [
29], and medical model optimization [
30,
31].
Although the existing noise filtering algorithms can achieve high accuracy on the smooth surface, there are still several challenges. Namely, the noise photons are distributed over a canopy, inside a canopy, and below the ground in a forest region, which seriously affects the accuracy of signal photons extraction, which further influences the accuracy of the noise removal algorithm. At the same time, in the previous research, only strong beam type was considered without considering the laser pointing and intensity, lacking the comprehensive analysis and evaluation of the noise filtering effect. Therefore, a new algorithm for noise photon filtering at different laser pointing types and laser intensities is required.
Aiming to filter out the noise photons, a new photon cloud noise filtering algorithm named the Particle Swarm Optimization Density Based Spatial Clustering of Applications with Noise (PSODBSCAN) is proposed in this paper. The proposed algorithm integrates the global optimization search characteristics of the PSO algorithm and the density search characteristics of the DBSCAN algorithm. Namely, the PSODBSCAN algorithm uses the PSO algorithm to optimize two important parameters of the DBSCAN and then employs the optimized parameters to complete the noise filtering process such that the noise filtering result clearly describes the target height. In this paper, the MATLAS data at different laser pointing types and laser intensities on the same route over the forest region is used as test data to validate the noise filtering performance of the proposed PSODBSCAN algorithm.
The rest of the paper is organized as follows. In
Section 2, the materials and methods are introduced. In
Section 3, the obtained experimental results are provided. In
Section 4, the discussion on the obtained experimental results is presented. Lastly, in
Section 5 the main conclusions and guidelines for our future work are given.
4. Discussion
There is considerable interest in developing an effective noise filtering algorithm needed to conduct an accurate canopy height measurement from the MATLAS data. The proposed PSODBSCAN algorithm addresses some of the drawbacks of the localized statistics algorithm [
12], offering a suitable solution for noise filtering from the MATLAS data.
4.1. Noise Filtering Results at Different Beam Intensities
The mean statistical indicators of the PSODBSCAN algorithm and the localized statistics algorithm at different beam intensities are given in
Table 14.
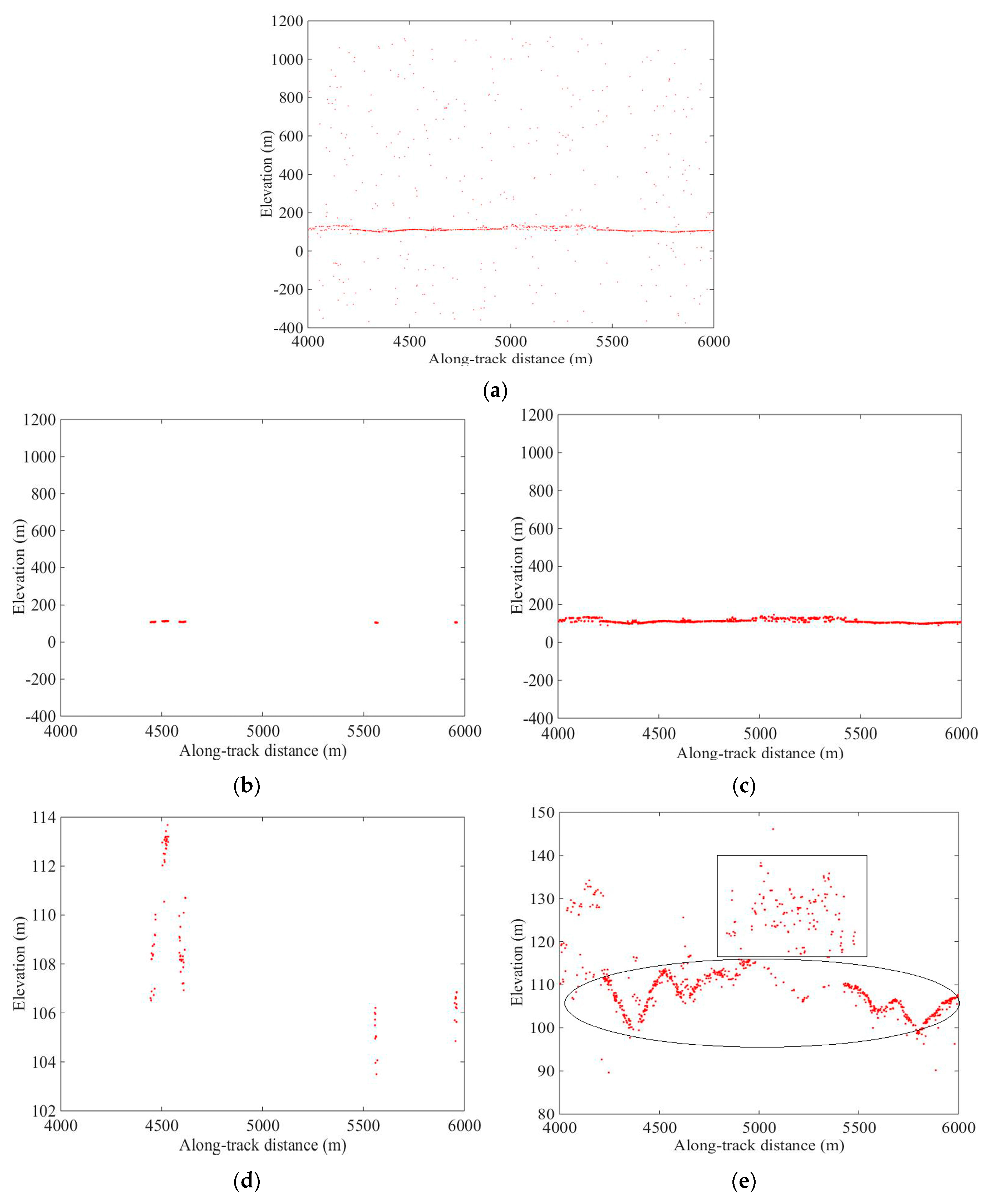
The previous studies suggested that variation in the MATLAS data density, caused by the differences in the photon cloud at studied locations [
15], is an important factor, which should be considered at different laser intensities. In our experiments, the density of signal photons was higher under the strong beam than under the weak laser beam.
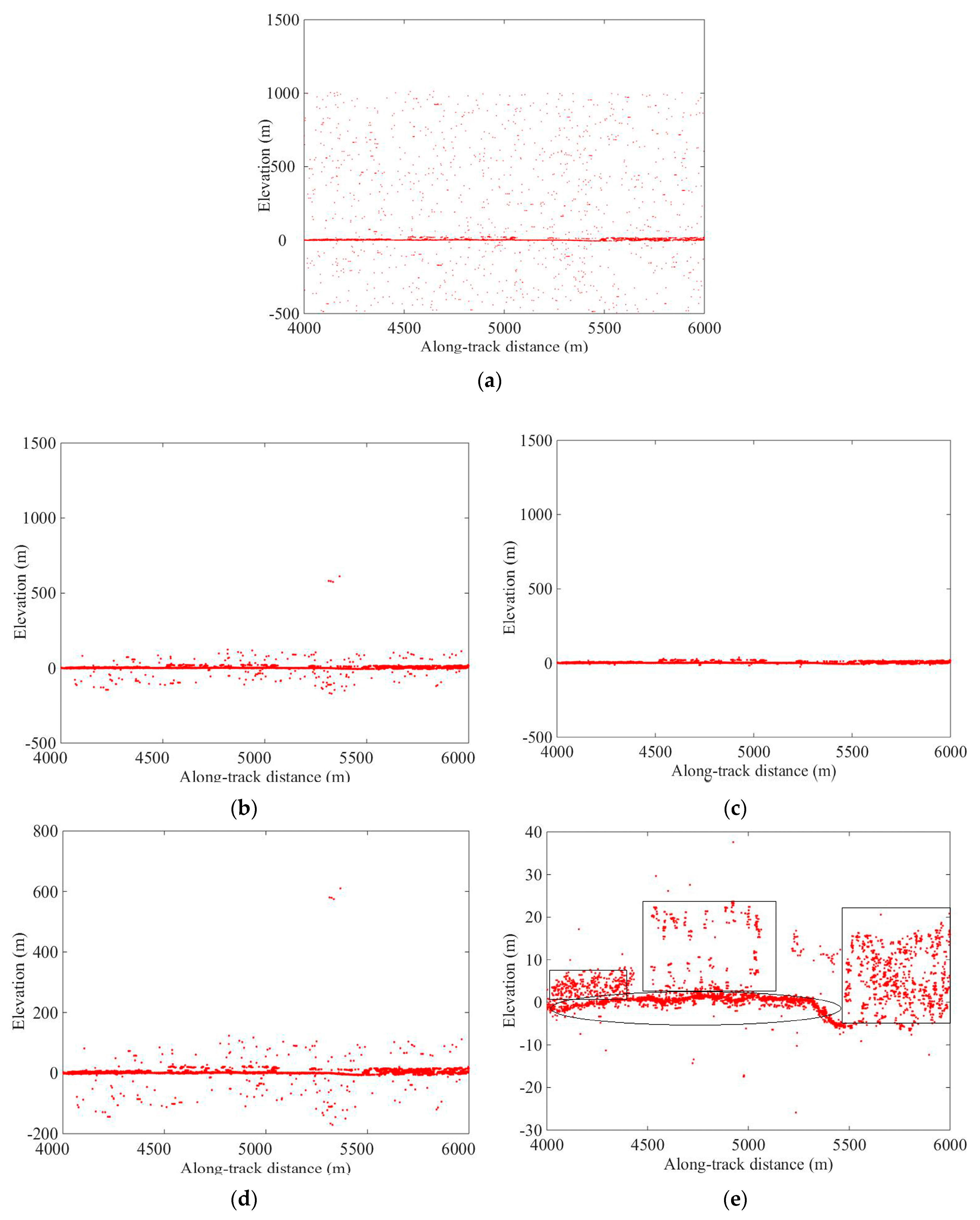
The qualitative analysis results are summarized in
Figure 3,
Figure 4,
Figure 5 and
Figure 6. According to the presented results, under the strong beam, the densities of forest photons and ground photons were particularly discernible, and both noise filtering algorithms could remove the noise photons. However, under the weak laser beam, the densities of forest photons and ground photons could not be clearly described, and only a part of the signal photons was retrieved by the localized statistics algorithm, while the PSODBSCAN algorithm retrieved much more signal photons in studied areas.
The quantitative analysis results are summarized in
Table 14, where it is shown that under the strong beam and weak beam, the PSODBSCAN algorithm achieved the mean
F value of 0.9938 and 0.9599, respectively, while the localized statistics algorithm achieved the mean
F value of 0.9775 and 0.4211, respectively. The mean
F value of the localized statistics algorithm was about 0.42 at different laser intensities, while the mean
F value of the PSODBSCAN algorithm was consistently better than 0.95. Thus, the PSODBSCAN algorithm was more effective than the localized statistics algorithm for the MATLAS photon cloud at all laser intensities, which was due to several reasons. First, the PSODBSCAN algorithm performed better in noise photons filtering (i.e., it achieved higher
R,
P, and
F values) than the localized statistics algorithm because the PSODBSCAN had the characteristics of local search and clusters of arbitrary shapes with a density as a criterion. Therefore, the PSODBSCAN algorithm did not cluster signal photons according to the threshold of a local statistical distance, avoiding the loss of canopy photons and ground photons. Moreover, the localized statistics algorithm eliminated the noise photons using a fixed threshold; thus, errors appeared at a low density where the ground and canopy were difficult to the identify in the photon cloud, especially under the weak laser beam. Second, the localized statistics algorithm needed to adjust the key parameters according to different laser intensity; however, it did not adjust the test parameters manually according to different laser intensity, resulting in the
F value of about 0.20 or even 0 under the weak beam condition. Manual parameter adjustment has been known to affect noise filtering efficiency and accuracy. Although the potential correction methods (e.g., factor adjusting procedures) may help to improve the noise filtering accuracy [
15], the final performance largely depends on manual adjustment of parameters, thus these methods are not suitable to be implemented globally due to their specificity.
Notably, the visual inspection revealed that a part of the signal photons was removed by the localized statistics algorithm (see
Figure 5b, and
Figure 6b and
Table 10 and
Table 13). Besides, the localized statistics algorithm achieved the mean
F value of 0 over the East Coast and West Coast under the weak beam. By analyzing the characteristics of the local statistical algorithm, the obtained results could be explained by the two following facts. Namely, there was a lower density of signal photon in the region, and the distance statistics sum of the signal photons exceeded the threshold of the local statistical algorithm. Therefore, it was difficult to remove the noise photons in the forest and ground regions by the localized statistics algorithm. Moreover, analyzing the test results of the localized statistics algorithm, it was concluded that test parameters affected the noise filtering effect of the localized statistics algorithm. Thus, it was necessary to adjust the algorithm parameters according to a different density of test data. In this work, the parameters were not selected based on test settings but set to the values used in reference [
12]. Both qualitative and quantitative results indicated that the PSODBSCAN algorithm performed better than the localized statistics algorithm, and the PSODBSCAN algorithm did not need manual parameter adjustment to different test data.
Moreover, the noise filtering results of the two algorithms under the strong beam were better than under the weak beam. The signal photon density under the strong beam conditions was higher than under the weak beam conditions, and it could be obviously noticed that ground and canopy photons under the strong beam condition (see
Figure 3 and
Figure 4). Therefore, a higher density of signal photons improved the noise filtering ability of both algorithms.
Overall, the qualitative and quantitative results indicated that the PSODBSCAN algorithm performed better than the localized statistics algorithm in noise photon filtering under both strong beam and weak beam.
4.2. Noise Filtering Results at Different Laser Pointing Types
The mean statistical indicators of the PSODBSCAN algorithm and the localized statistics algorithm at different laser pointing types are given in
Table 15.
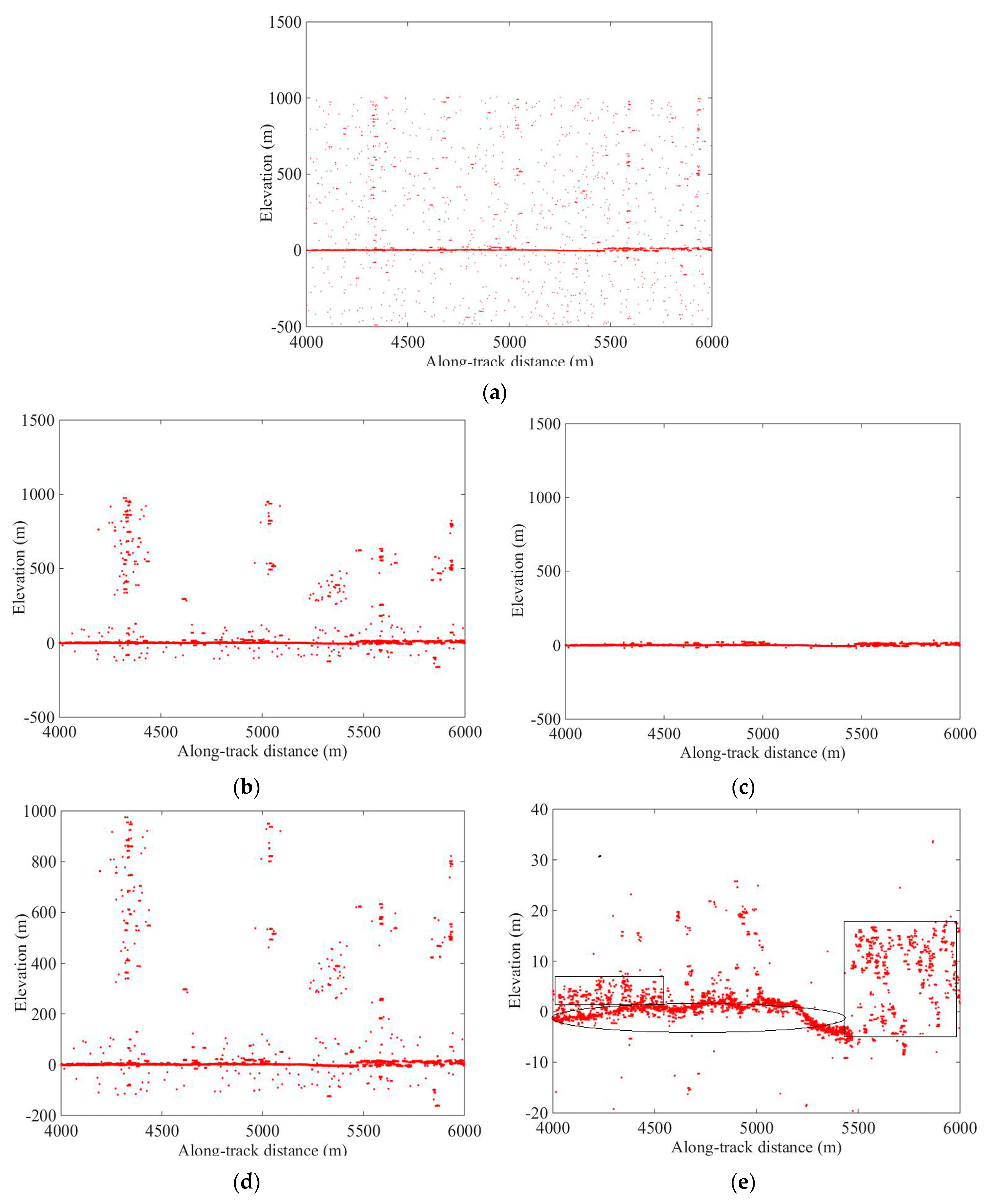
The previous studies suggested that variation in the MATLAS data density, caused by the differences in the photon cloud at studied locations, is an important factor, which should be considered at different laser pointing types. In our experiments, the density of signal photons was higher under the center pointing than under the left pointing. The qualitative analysis results are presented in
Figure 3,
Figure 4,
Figure 5 and
Figure 6. Under the condition of center pointing, the densities of forest photons and ground photons were more obviously discernible than under the left pointing. The visual inspection revealed that a part of the signal photons was removed by the localized statistics algorithm under the left pointing, while the PSODBSCAN algorithm obtained more signal photons in those areas (see
Figure 4 and
Figure 6).
The quantitative analysis results are summarized in
Table 15. Based on these results, under the center pointing and left pointing, the PSODBSCAN algorithm achieved a mean F value of 0.9844 and 0.9654, respectively, and the localized statistics algorithm achieved a mean F value of 0.7110 and 0.6818, respectively. The mean
F value of the localized statistics algorithm was about 0.68, while the mean
F value of the PSODBSCAN algorithm was higher than 0.96. The comparison results indicated that the PSODBSCAN algorithm was more effective than the localized statistics algorithm for the MATLAS photon cloud at different beam pointing types, which was due to several reasons. First, the PSODBSCAN algorithm achieved consistently better accuracy in noise photon filtering (i.e., it achieved higher
R,
P, and
F values) than the localized statistics algorithm. The main reason for this was that the localized statistics algorithm resulted in a loss of canopy photons and ground photons due to the fixed threshold, while the PSODBSCAN algorithm identified the noise cluster based on the signal photon density. Therefore, the localized statistics algorithm failed to remove the noise at a lower density where the ground and canopy were difficult to identify in the photon cloud (left pointing). Second, the localized statistics algorithm should have adjusted the key parameters according to different test data; however, it did not adjust all the test parameters according to different laser pointing data, resulting in the
F value of about 0.19 or even 0 under the left pointing. As it is well known, the manual parameter adjustment affects the noise filtering efficiency and accuracy; therefore, it was necessary to combine the PSO algorithm with the photon cloud noise filtering algorithm to determine the optimal parameters for the given test data.
Moreover, the noise filtering results of the two algorithms were better under laser center pointing than under laser left pointing. By analyzing the photon cloud data under different laser pointing, it is obviously discernible that the ground and canopy photons under center pointing. Hence, a higher density of signal photons improved the noise filtering ability of both algorithms.
In summary, both qualitative and quantitative results indicated that the PSODBSCAN algorithm performed better than the localized statistics algorithm in noise photon filtering under both center and left pointing.
4.3. Noise Removal Results of Different Algorithms
The mean statistical indicators of noise filtering algorithms are given in
Table 16.
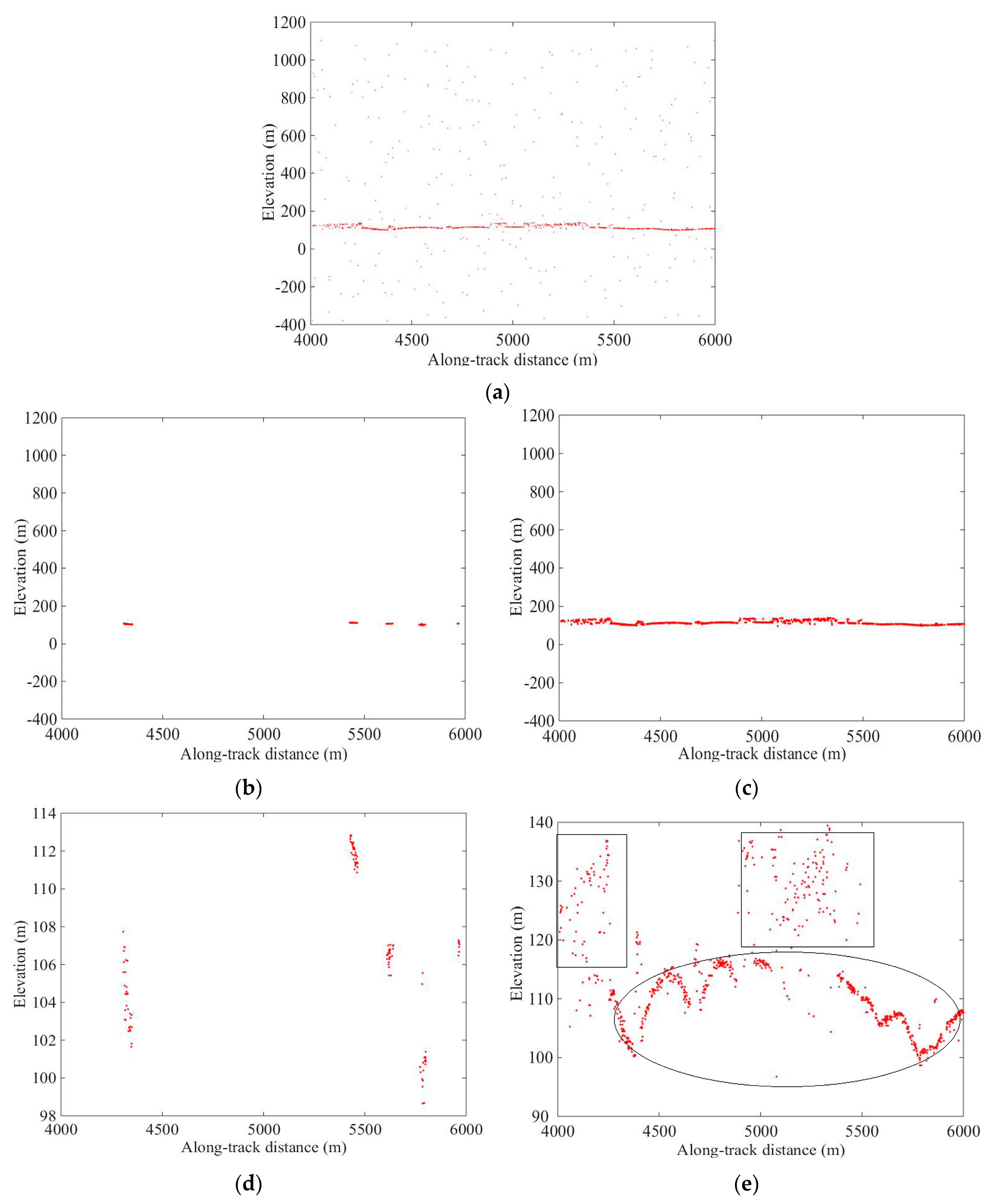
The noise filtering experiments were conducted at different laser pointing and different beam types. The qualitative analysis results are shown in
Figure 3,
Figure 4,
Figure 5 and
Figure 6. The visual analysis showed that the results of the PSODBSCAN algorithm contained fewer noise photon than that of the localized statistics algorithm. Thus, the PSODBSCAN algorithm described the coverage of canopy vegetation and the change in the ground more clearly, especially in the case of strong beam and center pointing (see
Figure 3).
The quantitative analysis results are summarized in
Table 16. In the noise filtering experiments, the PSODBSCAN algorithm achieved the mean
R,
P, and
F values of 0.9994, 0.9560, and 0.9759, respectively, and the localized statistics algorithm achieved the mean
R,
P, and
F values of 0.6802, 0.8016, and 0.6978, respectively. In fact, the localized statistics algorithm had a large variation range of
F value (
F was 0.99 under the center pointing and strong beam, and it was 0 under the left pointing and weak beam). Such results indicated that the localized statistics algorithm was greatly affected by the change in the photon density. Correspondingly, the localized statistics algorithm obtained high noise filtering accuracy under the high signal photon density, but it failed in the photon cloud noise filtering test at the low signal photon density. On the contrary, the PSODBSCAN algorithm consistently maintained a high noise filtering accuracy without manual parameters adjustment.
In general, both qualitative and quantitative evaluation results showed that the PSODBSCAN algorithm performed better in noise photon filtering than the localized statistics algorithm. This can be explained by the two following reasons. First, the PSODBSCAN algorithm clustered signal photons by using photon density rather than by using a certain threshold. Second, under different experimental conditions, by using manual adjustment of the noise filtering algorithm parameters it was difficult to obtain an optimal filtering effect. Therefore, the parameter adjustment was very critical in the noise filtering experiment. At the same time, it was proven that the PSODBSCAN algorithm achieved high noise filtering accuracy without manual parameters adjustment.
Ultimately, the result proved that the noise filtering effect of both algorithms depended on the photon density of the MATLAS data because the MATLAS technology is still in the airborne simulation stage. Based on the obtained results, the localized statistics algorithm can be useful for rapid noise photon filtering achieving a moderate accuracy, but this algorithm results in loss of signal photons at a low density of photon cloud. Thus, it can be used for rapid noise filtering at a high density of signal photons (e.g., strong beam and center pointing) but it requires a clear threshold for classification of noise and signal photons. Moreover, in the applications involving the MATLAS data, the PSODBSCAN algorithm represents a more convenient solution because it can largely retain the ground and canopy details achieving a much higher noise filtering accuracy at different laser pointing and beam types, which is extremely valuable in an automatic method. Accordingly, due to the proven usefulness for photon cloud processing of the proposed algorithm, it can be successfully implemented over the studied locations.