Accurate Measurement of Tropical Forest Canopy Heights and Aboveground Carbon Using Structure From Motion
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site
2.2. Photographic and LiDAR surveys
2.3. Calculating the Correction
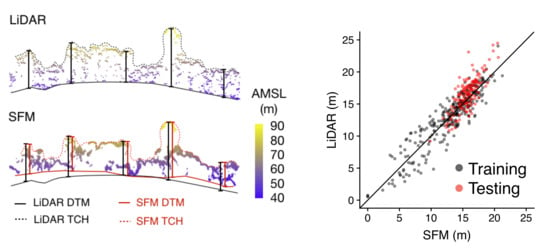
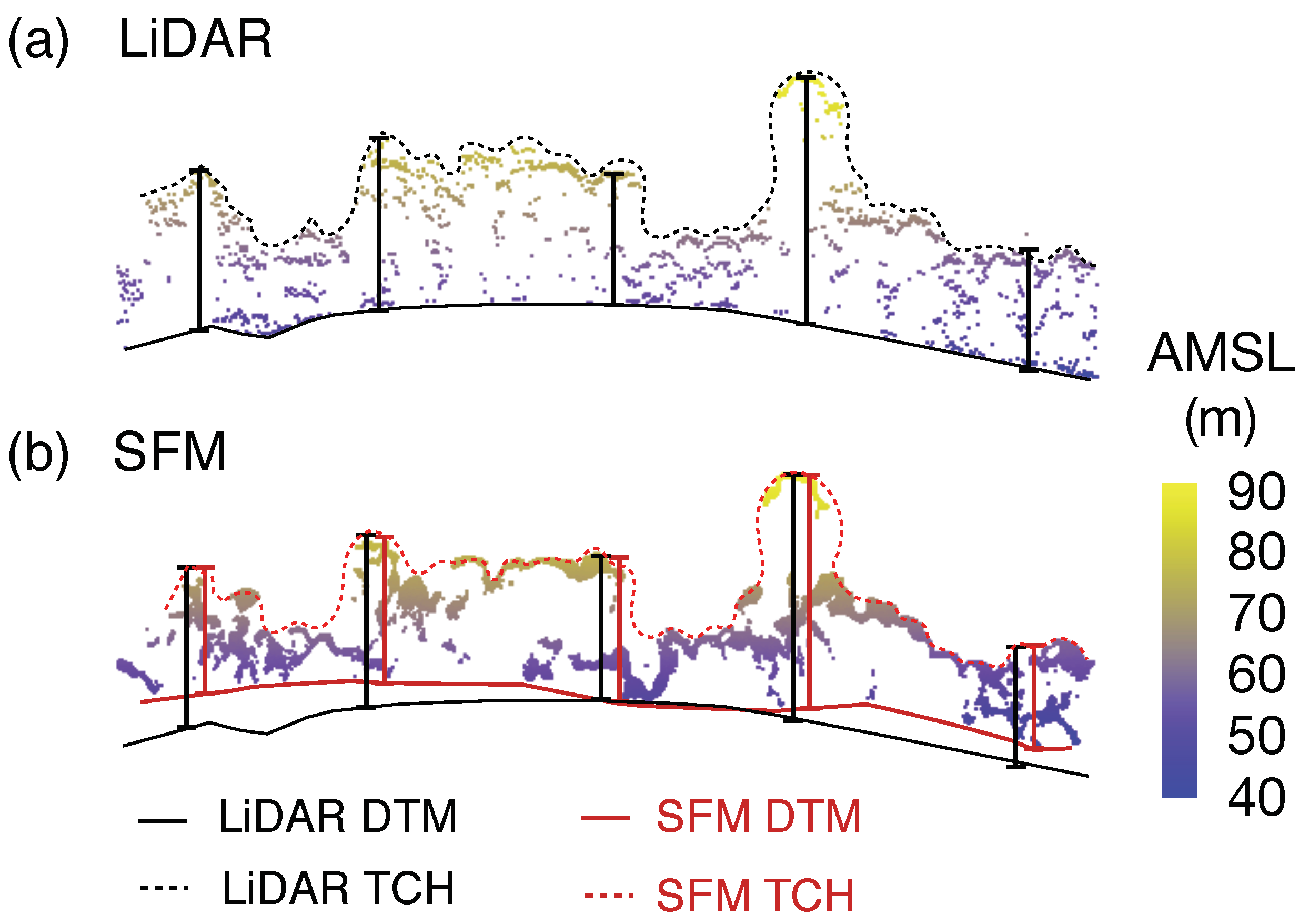
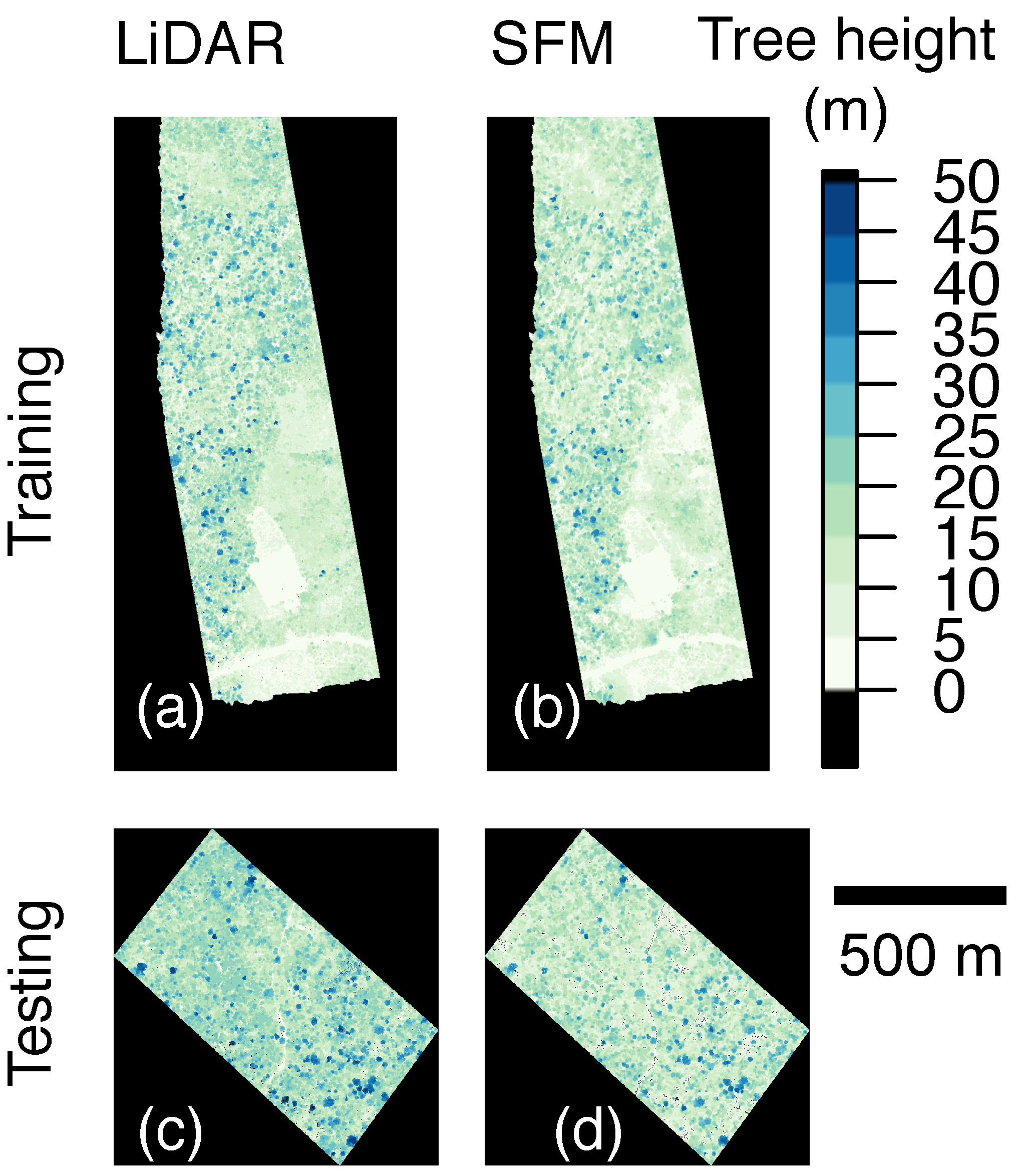
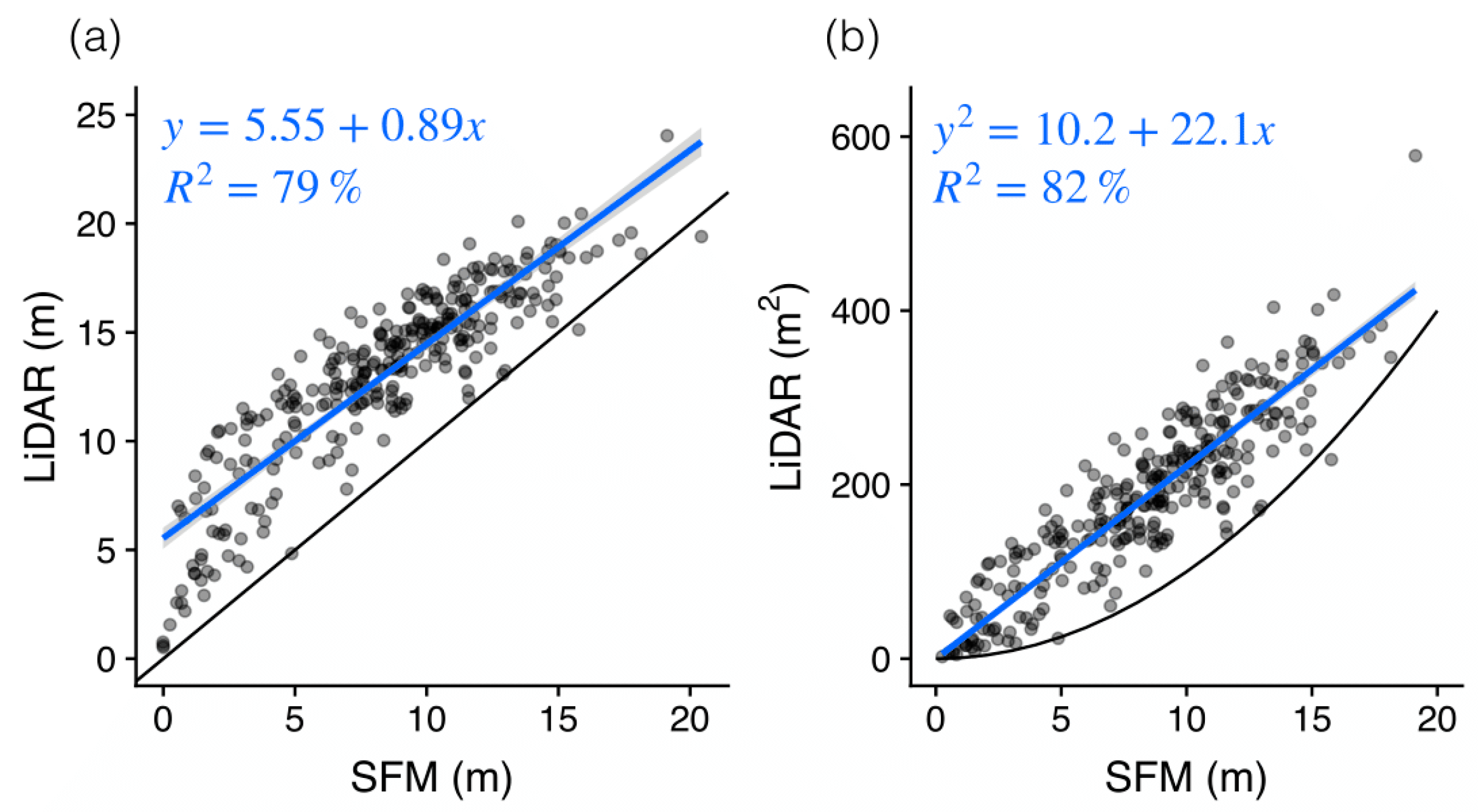
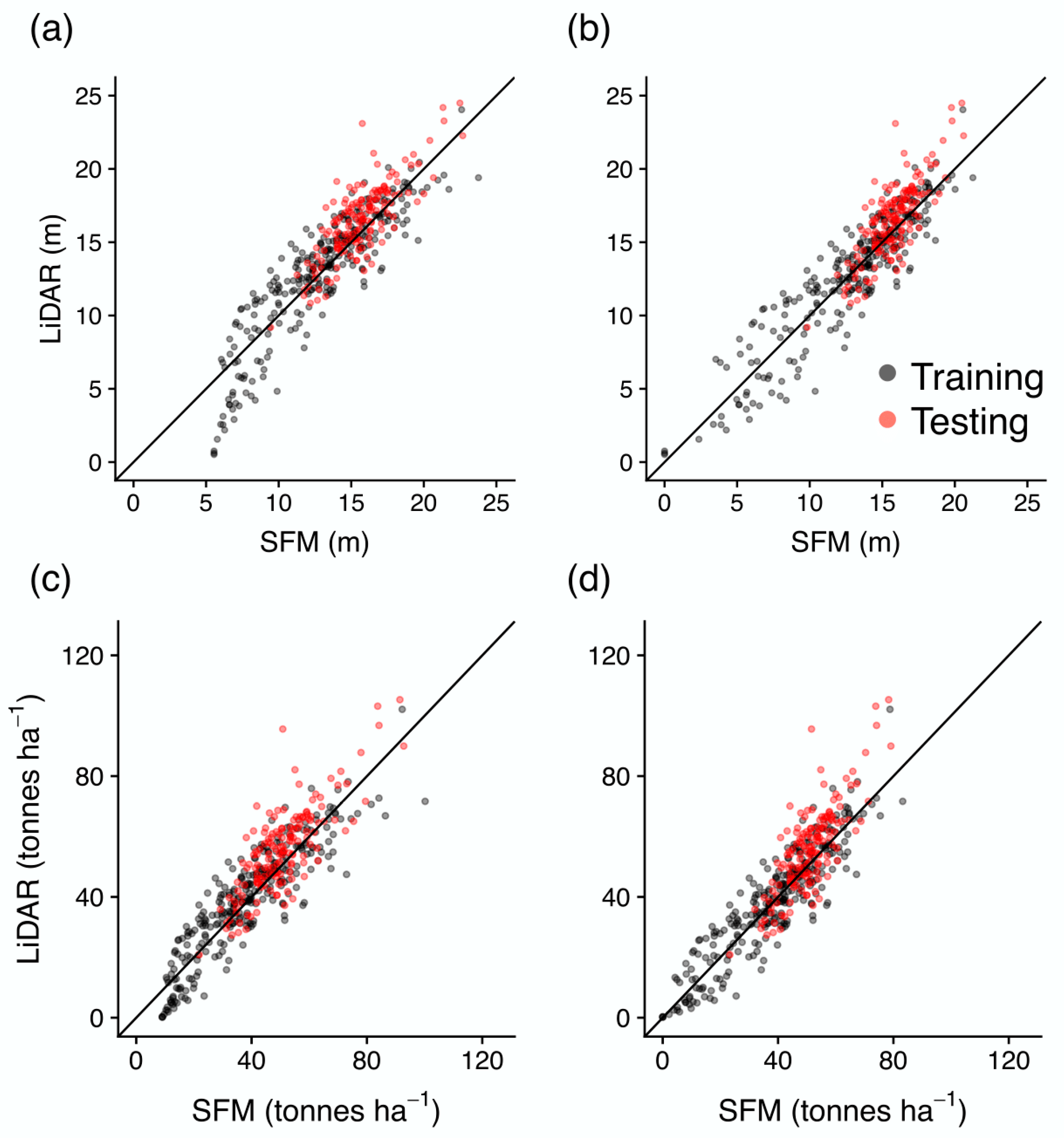
3. Results
Developing the Tree Height Correction Model
4. Discussion
4.1. Improved Accuracy of SfM Measurements
4.2. Application in Other Forest Types
4.3. The Value of Ground Control Points
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| UAV | Unmanned aerial vehicle |
| LiDAR | Light detection and ranging |
| SfM | Structure from Motion |
| DTM | Digital terrain model |
| CHM | Canopy height model |
| GCP | Ground control point |
| RMSE | Root mean square error |
References
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-resolution global maps of 21st-century forest cover change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef]
- van Leeuwen, M.; Nieuwenhuis, M. Retrieval of forest structural parameters using LiDAR remote sensing. Eur. J. For. Res. 2010, 129, 749–770. [Google Scholar] [CrossRef]
- Asner, G.P.; Martin, R.E.; Knapp, D.E.; Tupayachi, R.; Anderson, C.B.; Sinca, F.; Vaughn, N.R.; Llactayo, W. Airborne laser-guided imaging spectroscopy to map forest trait diversity and guide conservation. Science 2017, 355, 385–389. [Google Scholar] [CrossRef]
- Cordell, S.; Questad, E.J.; Asner, G.P.; Kinney, K.M.; Thaxton, J.M.; Uowolo, A.; Brooks, S.; Chynoweth, M.W. Remote sensing for restoration planning: How the big picture can inform stakeholders. Restor. Ecol. 2016. [Google Scholar] [CrossRef]
- Laestadius, L.S.; Maginnis, S.; Minnemeyer, S.; Potapov, P.; Saint-Laurent, C.; Sizer, N. Mapping opportunities for forest landscape restoration. Unasylva 2012, 62, 47–48. [Google Scholar]
- Chazdon, R.L. Beyond deforestation: Restoring forests and ecosystem services on degraded lands. Science 2008, 320, 1458–1460. [Google Scholar] [CrossRef] [PubMed]
- Poorter, L.; Bongers, F.; Aide, T.M.; Almeyda Zambrano, A.M.; Balvanera, P.; Becknell, J.M.; Boukili, V.; Brancalion, P.H.S.; Broadbent, E.N.; Chazdon, R.L.; et al. Biomass resilience of Neotropical secondary forests. Nature 2016, 530, 211–214. [Google Scholar] [CrossRef] [PubMed]
- Peña-Claros, M.; Fredericksen, T.; Alarcón, A.; Blate, G.; Choque, U.; Leaño, C.; Licona, J.; Mostacedo, B.; Pariona, W.; Villegas, Z.; et al. Beyond reduced-impact logging: Silvicultural treatments to increase growth rates of tropical trees. For. Ecol. Manag. 2008, 256, 1458–1467. [Google Scholar] [CrossRef]
- Palma, A.C.; Laurance, S.G. A review of the use of direct seeding and seedling plantings in restoration: What do we know and where should we go? Appl. Veg. Sci. 2015, 18, 561–568. [Google Scholar] [CrossRef]
- Swinfield, T.; Afriandi, R.; Antoni, F.; Harrison, R.D. Accelerating tropical forest restoration through the selective removal of pioneer species. For. Ecol. Manag. 2016, 381, 209–216. [Google Scholar] [CrossRef]
- Dubayah, R.O.; Drake, J.B. Lidar Remote Sensing for Forestry Applications. J. For. 2000, 98, 44–46. [Google Scholar] [CrossRef]
- Asner, G.P.; Mascaro, J. Mapping tropical forest carbon: Calibrating plot estimates to a simple LiDAR metric. Remote Sens. Environ. 2014, 140, 614–624. [Google Scholar] [CrossRef]
- Lim, K.; Treitz, P.; Wulder, M.; St-Onge, B.; Flood, M. LiDAR remote sensing of forest structure. Prog. Phys. Geogr. 2003, 27, 88–106. [Google Scholar] [CrossRef]
- Jucker, T.; Asner, G.P.; Dalponte, M.; Brodrick, P.; Philipson, C.D.; Vaughn, N.; Brelsford, C.; Burslem, D.F.R.P.; Deere, N.J.; Ewers, R.M.; et al. A regional model for estimating the aboveground carbon density of Borneo’s tropical forests from airborne laser scanning. arXiv, 2017; arXiv:1705.09242. [Google Scholar]
- Duncanson, L.; Dubayah, R.; Cook, B.; Rosette, J.; Parker, G. The importance of spatial detail: Assessing the utility of individual crown information and scaling approaches for lidar-based biomass density estimation. Remote Sens. Environ. 2015, 168, 102–112. [Google Scholar] [CrossRef]
- Coomes, D.A.; Dalponte, M.; Jucker, T.; Asner, G.P.; Banin, L.F.; Burslem, D.F.; Lewis, S.L.; Nilus, R.; Phillips, O.L.; Phua, M.H.; et al. Area-based vs. tree-centric approaches to mapping forest carbon in Southeast Asian forests from airborne laser scanning data. Remote Sens. Environ. 2017, 194, 77–88. [Google Scholar] [CrossRef]
- Koh, L.P.; Wich, S.A. Dawn of Drone Ecology: Low-Cost Autonomous Aerial Vehicles for Conservation. Trop. Conserv. Sci. 2012, 5, 121–132. [Google Scholar] [CrossRef]
- Sutherland, W.J.; Bardsley, S.; Clout, M.; Depledge, M.H.; Dicks, L.V.; Fellman, L.; Fleishman, E.; Gibbons, D.W.; Keim, B.; Lickorish, F.; et al. A horizon scan of global conservation issues for 2013. Trends Ecol. Evol. 2013, 28, 16–22. [Google Scholar] [CrossRef] [PubMed]
- Anderson, K.; Gaston, K.J. Lightweight unmanned aerial vehicles will revolutionize spatial ecology. Front. Ecol. Environ. 2013, 11, 138–146. [Google Scholar] [CrossRef]
- Lisein, J.; Pierrot-Deseilligny, M.; Bonnet, S.; Lejeune, P. A Photogrammetric Workflow for the Creation of a Forest Canopy Height Model from Small Unmanned Aerial System Imagery. Forests 2013, 4, 922–944. [Google Scholar] [CrossRef]
- Tomasi, C.; Kanade, T. Shape and Motion from Image Streams: A Factorization Method—2. Point Features in 3D Motion. Int. J. Comput. Vis. 1991, 9, 137–154. [Google Scholar] [CrossRef]
- Dandois, J.; Baker, M.; Olano, M.; Parker, G.; Ellis, E. What is the Point? Evaluating the Structure, Color, and Semantic Traits of Computer Vision Point Clouds of Vegetation. Remote Sens. 2017, 9, 355. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.; Diaz-Varela, R.; Angileri, V.; Loudjani, P. Tree height quantification using very high resolution imagery acquired from an unmanned aerial vehicle (UAV) and automatic 3D photo-reconstruction methods. Eur. J. Agron. 2014, 55, 89–99. [Google Scholar] [CrossRef]
- Meng, X.; Currit, N.; Zhao, K. Ground Filtering Algorithms for Airborne LiDAR Data: A Review of Critical Issues. Remote Sens. 2010, 2, 833–860. [Google Scholar] [CrossRef]
- Dandois, J.P.; Ellis, E.C. High spatial resolution three-dimensional mapping of vegetation spectral dynamics using computer vision. Remote Sens. Environ. 2013, 136, 259–276. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Malenovský, Z.; Turner, D.; Vopěnka, P. Assessment of Forest Structure Using Two UAV Techniques: A Comparison of Airborne Laser Scanning and Structure from Motion (SfM) Point Clouds. Forests 2016, 7, 62. [Google Scholar] [CrossRef]
- Dandois, J.; Olano, M.; Ellis, E. Optimal Altitude, Overlap, and Weather Conditions for Computer Vision UAV Estimates of Forest Structure. Remote Sens. 2015, 7, 13895–13920. [Google Scholar] [CrossRef]
- Zahawi, R.A.; Dandois, J.P.; Holl, K.D.; Nadwodny, D.; Reid, J.L.; Ellis, E.C. Using lightweight unmanned aerial vehicles to monitor tropical forest recovery. Biol. Conserv. 2015, 186, 287–295. [Google Scholar] [CrossRef]
- Larjavaara, M.; Muller-Landau, H.C. Measuring tree height: A quantitative comparison of two common field methods in a moist tropical forest. Methods Ecol. Evol. 2013, 4, 793–801. [Google Scholar] [CrossRef]
- Li, D.; Gu, X.; Pang, Y.; Chen, B.; Liu, L.; Li, D.; Gu, X.; Pang, Y.; Chen, B.; Liu, L. Estimation of Forest Aboveground Biomass and Leaf Area Index Based on Digital Aerial Photograph Data in Northeast China. Forests 2018, 9, 275. [Google Scholar] [CrossRef]
- Geman, S.; Bienenstock, E.; Doursat, R. Neural Networks and the Bias/Variance Dilemma. Neural Comput. 1992, 4, 1–58. [Google Scholar] [CrossRef]
- Jucker, T.; Caspersen, J.; Chave, J.; Antin, C.; Barbier, N.; Bongers, F.; Dalponte, M.; van Ewijk, K.Y.; Forrester, D.I.; Haeni, M.; et al. Allometric equations for integrating remote sensing imagery into forest monitoring programmes. Glob. Chang. Biol. 2017, 23, 177–190. [Google Scholar] [CrossRef] [PubMed]
- Lasky, J.R.; Uriarte, M.; Boukili, V.K.; Erickson, D.L.; John Kress, W.; Chazdon, R.L. The relationship between tree biodiversity and biomass dynamics changes with tropical forest succession. Ecol. Lett. 2014, 17, 1158–1167. [Google Scholar] [CrossRef] [PubMed]
- Vaglio Laurin, G.; Puletti, N.; Chen, Q.; Corona, P.; Papale, D.; Valentini, R. Above ground biomass and tree species richness estimation with airborne lidar in tropical Ghana forests. Int. J. Appl. Earth Observ. Geoinf. 2016, 52, 371–379. [Google Scholar] [CrossRef]
- Harrison, R.D.; Swinfield, T. Restoration of logged humid tropical forests: An experimental programme at Harapan Rainforest, Indonesia. Trop. Conserv. Sci. 2015, 888, 4–16. [Google Scholar] [CrossRef]
- Isenburg, M. LAStools, “Efficient LiDAR Processing Software”. 2014. Available online: https://www.uleth.ca/node/2177 (accessed on 16 April 2019).
- Khosravipour, A.; Skidmore, A.K.; Isenburg, M.; Wang, T.; Hussin, Y.A. Generating Pit-free Canopy Height Models from Airborne Lidar. Photogramm. Eng. Remote Sens. 2014, 80, 863–872. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, J.; Lian, J.; Fan, Z.; Ouyang, X.; Ye, W. Seeing the forest from drones: Testing the potential of lightweight drones as a tool for long-term forest monitoring. Biol. Conserv. 2016, 198, 60–69. [Google Scholar] [CrossRef]
- Messinger, M.; Asner, G.; Silman, M. Rapid Assessments of Amazon Forest Structure and Biomass Using Small Unmanned Aerial Systems. Remote Sens. 2016, 8, 615. [Google Scholar] [CrossRef]
- Ota, T.; Ogawa, M.; Shimizu, K.; Kajisa, T.; Mizoue, N.; Yoshida, S.; Takao, G.; Hirata, Y.; Furuya, N.; Sano, T.; et al. Aboveground Biomass Estimation Using Structure from Motion Approach with Aerial Photographs in a Seasonal Tropical Forest. Forests 2015, 6, 3882–3898. [Google Scholar] [CrossRef]
- Jensen, J.; Mathews, A.; Jensen, J.L.R.; Mathews, A.J. Assessment of Image-Based Point Cloud Products to Generate a Bare Earth Surface and Estimate Canopy Heights in a Woodland Ecosystem. Remote Sens. 2016, 8, 50. [Google Scholar] [CrossRef]
- Guariguata, M.R.; Ostertag, R. Neotropical secondary forest succession: Changes in structural and functional characteristics. For. Ecol. Manag. 2001, 148, 185–206. [Google Scholar] [CrossRef]
- Roşca, S.; Suomalainen, J.; Bartholomeus, H.; Herold, M. Comparing terrestrial laser scanning and unmanned aerial vehicle structure from motion to assess top of canopy structure in tropical forests. Interface Focus 2018, 8, 20170038. [Google Scholar] [CrossRef]
- Viljanen, N.; Honkavaara, E.; Näsi, R.; Hakala, T.; Niemeläinen, O.; Kaivosoja, J.; Viljanen, N.; Honkavaara, E.; Näsi, R.; Hakala, T.; et al. A Novel Machine Learning Method for Estimating Biomass of Grass Swards Using a Photogrammetric Canopy Height Model, Images and Vegetation Indices Captured by a Drone. Agriculture 2018, 8, 70. [Google Scholar] [CrossRef]
- Alonzo, M.; Andersen, H.E.; Morton, D.; Cook, B.; Alonzo, M.; Andersen, H.E.; Morton, D.C.; Cook, B.D. Quantifying Boreal Forest Structure and Composition Using UAV Structure from Motion. Forests 2018, 9, 119. [Google Scholar] [CrossRef]
- Iizuka, K.; Yonehara, T.; Itoh, M.; Kosugi, Y.; Iizuka, K.; Yonehara, T.; Itoh, M.; Kosugi, Y. Estimating Tree Height and Diameter at Breast Height (DBH) from Digital Surface Models and Orthophotos Obtained with an Unmanned Aerial System for a Japanese Cypress (Chamaecyparis obtusa) Forest. Remote Sens. 2017, 10, 13. [Google Scholar] [CrossRef]
- Roussel, J.R.; Caspersen, J.; Béland, M.; Thomas, S.; Achim, A. Removing bias from LiDAR-based estimates of canopy height: Accounting for the effects of pulse density and footprint size. Remote Sens. Environ. 2017, 198, 1–16. [Google Scholar] [CrossRef]
- Nouwakpo, S.K.; Weltz, M.A.; McGwire, K. Assessing the performance of structure-from-motion photogrammetry and terrestrial LiDAR for reconstructing soil surface microtopography of naturally vegetated plots. Earth Surf. Process. Landf. 2016, 41, 308–322. [Google Scholar] [CrossRef]
- De Souza, C.H.W.; Lamparelli, R.A.C.; Rocha, J.V.; Magalhães, P.S.G. Height estimation of sugarcane using an unmanned aerial system (UAS) based on structure from motion (SfM) point clouds. Int. J. Remote Sens. 2017, 38, 2218–2230. [Google Scholar] [CrossRef]
- Forsmoo, J.; Anderson, K.; Macleod, C.J.A.; Wilkinson, M.E.; Brazier, R. Drone-based structure-from-motion photogrammetry captures grassland sward height variability. J. Appl. Ecol. 2018, 55, 2587–2599. [Google Scholar] [CrossRef]
- Doughty, C.E.; Goulden, M.L. Seasonal patterns of tropical forest leaf area index and CO2 exchange. J. Geophys. Res. Biogeosci. 2008, 113. [Google Scholar] [CrossRef]
- Tonkin, T.; Midgley, N.; Tonkin, T.N.; Midgley, N.G. Ground-Control Networks for Image Based Surface Reconstruction: An Investigation of Optimum Survey Designs Using UAV Derived Imagery and Structure-from-Motion Photogrammetry. Remote Sens. 2016, 8, 786. [Google Scholar] [CrossRef]
- Chen, Q.; Vaglio Laurin, G.; Battles, J.J.; Saah, D. Integration of airborne lidar and vegetation types derived from aerial photography for mapping aboveground live biomass. Remote Sens. Environ. 2012, 121, 108–117. [Google Scholar] [CrossRef]
- Chudley, T.R.; Christoffersen, P.; Doyle, S.H.; Abellan, A.; Snooke, N. High accuracy UAV photogrammetry of ice sheet dynamics with no ground control. Cryosphere Discuss. 2018, 1–22. [Google Scholar] [CrossRef]
- St-Onge, B.A.; Achaichia, N. Measuring forest canopy height using a combination of lidar and aerial photography data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2001, 34, 121–138. [Google Scholar]
- Wallace, L.; Lucieer, A.; Watson, C.; Turner, D. Development of a UAV-LiDAR System with Application to Forest Inventory. Remote Sens. 2012, 4, 1519–1543. [Google Scholar] [CrossRef]
- Schneider, F.D.; Kükenbrink, D.; Schaepman, M.E.; Schimel, D.S.; Morsdorf, F. Quantifying 3D structure and occlusion in dense tropical and temperate forests using close-range LiDAR. Agric. For. Meteorol. 2019, 268, 249–257. [Google Scholar] [CrossRef]
- Qi, W.; Dubayah, R.O. Combining Tandem-X InSAR and simulated GEDI lidar observations for forest structure mapping. Remote Sens. Environ. 2016, 187, 253–266. [Google Scholar] [CrossRef]
- James, M.; Robson, S. Sequential digital elevation models of active lava flows from ground-based stereo time-lapse imagery. ISPRS J. Photogramm. Remote Sens. 2014, 97, 160–170. [Google Scholar] [CrossRef]
| Canopy Height Model | Canopy Height (m) | |||||
| Mean | s.d. | RMSE | Bias | |||
| LiDAR | 16.6 | 2.83 | - | - | - | |
| SfM | 11.4 | 2.63 | 0.67 | 5.45 | −5.20 | |
| Model 1 | 15.7 | 2.34 | 0.67 | 1.85 | −0.89 | |
| Model 2 | 15.8 | 1.80 | 0.66 | 1.90 | −0.84 | |
| Model 3 | 15.9 | 1.93 | 0.65 | 1.85 | −0.69 | |
| Model 4 | 15.7 | 1.81 | 0.64 | 1.96 | −0.90 | |
| Model 5 | 15.9 | 1.53 | 0.68 | 1.91 | −0.69 | |
| Model 6 | 15.8 | 1.96 | 0.67 | 1.84 | −0.81 | |
| Model 1 no GCPs | 15.6 | 2.43 | 0.51 | 2.25 | −1.02 | |
| Model 2 no GCPs | 15.7 | 1.88 | 0.51 | 2.20 | −0.95 | |
| Canopy Height Model | Above-Ground Carbon Density (Tonnes) | Total AGCD (tonnes) | ||||
| Mean | s.d. | RMSE | Bias | |||
| LiDAR | 56.3 | 16.1 | - | - | - | 8332 |
| SfM | 30.7 | 12.0 | 0.68 | 27.2 | −25.6 | 4537 |
| Model 1 | 51.2 | 12.9 | 0.68 | 10.4 | −5.07 | 7582 |
| Model 2 | 51.3 | 9.7 | 0.67 | 11.1 | −5.04 | 7586 |
| Model 3 | 52.1 | 10.4 | 0.64 | 10.8 | −4.22 | 7707 |
| Model 4 | 50.9 | 9.6 | 0.64 | 11.5 | −5.35 | 7504 |
| Model 5 | 52.0 | 8.2 | 0.68 | 11.2 | −4.34 | 7690 |
| Model 6 | 51.5 | 10.7 | 0.68 | 10.5 | −4.83 | 7717 |
| Model 1 no GCPs | 50.6 | 13.4 | 0.53 | 12.5 | −5.71 | 7487 |
| Model 2 no GCPs | 50.7 | 10.1 | 0.52 | 12.5 | −5.60 | 7502 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Swinfield, T.; Lindsell, J.A.; Williams, J.V.; Harrison, R.D.; Agustiono; Habibi; Gemita, E.; Schönlieb, C.B.; Coomes, D.A. Accurate Measurement of Tropical Forest Canopy Heights and Aboveground Carbon Using Structure From Motion. Remote Sens. 2019, 11, 928. https://doi.org/10.3390/rs11080928
Swinfield T, Lindsell JA, Williams JV, Harrison RD, Agustiono, Habibi, Gemita E, Schönlieb CB, Coomes DA. Accurate Measurement of Tropical Forest Canopy Heights and Aboveground Carbon Using Structure From Motion. Remote Sensing. 2019; 11(8):928. https://doi.org/10.3390/rs11080928
Chicago/Turabian StyleSwinfield, Tom, Jeremy A. Lindsell, Jonathan V. Williams, Rhett D. Harrison, Agustiono, Habibi, Elva Gemita, Carola B. Schönlieb, and David A. Coomes. 2019. "Accurate Measurement of Tropical Forest Canopy Heights and Aboveground Carbon Using Structure From Motion" Remote Sensing 11, no. 8: 928. https://doi.org/10.3390/rs11080928
APA StyleSwinfield, T., Lindsell, J. A., Williams, J. V., Harrison, R. D., Agustiono, Habibi, Gemita, E., Schönlieb, C. B., & Coomes, D. A. (2019). Accurate Measurement of Tropical Forest Canopy Heights and Aboveground Carbon Using Structure From Motion. Remote Sensing, 11(8), 928. https://doi.org/10.3390/rs11080928