Assimilation of SMOS Sea Surface Salinity in the Regional Ocean Model for South China Sea
Abstract
1. Introduction
2. SMOS Salinity Observations Preprocessing Based on GRNN
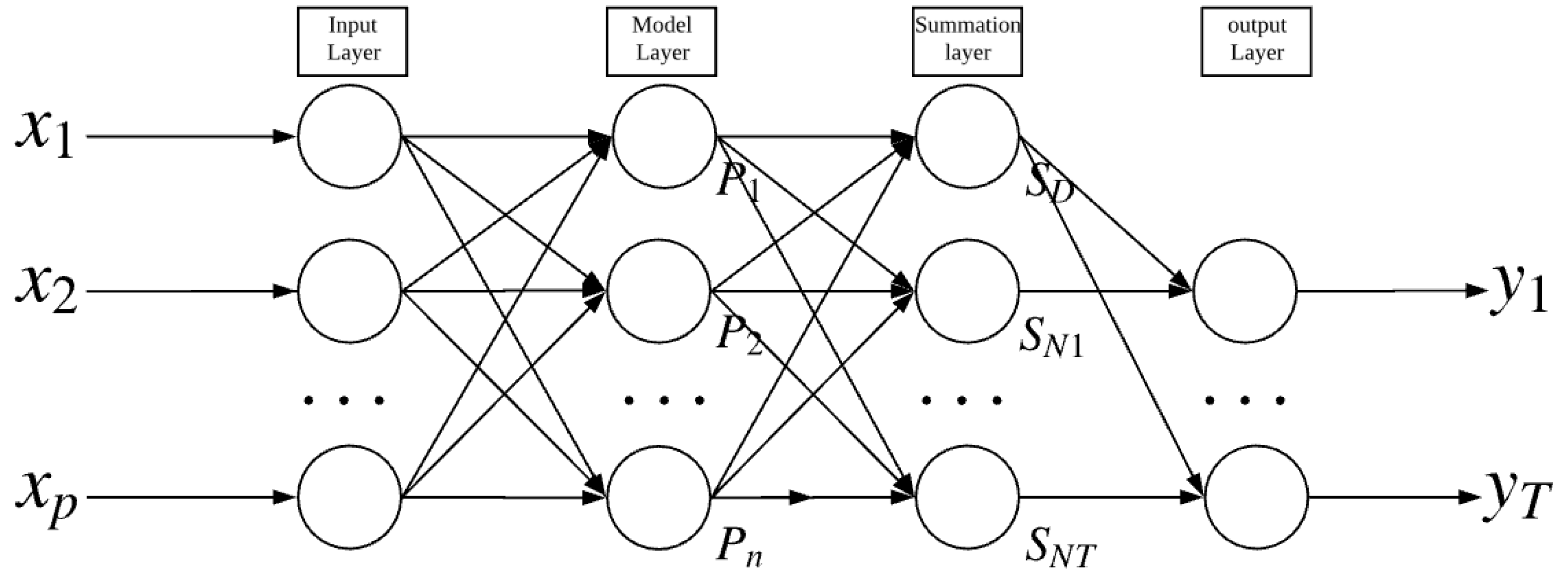
2.1. The Theory and Structure of GRNN
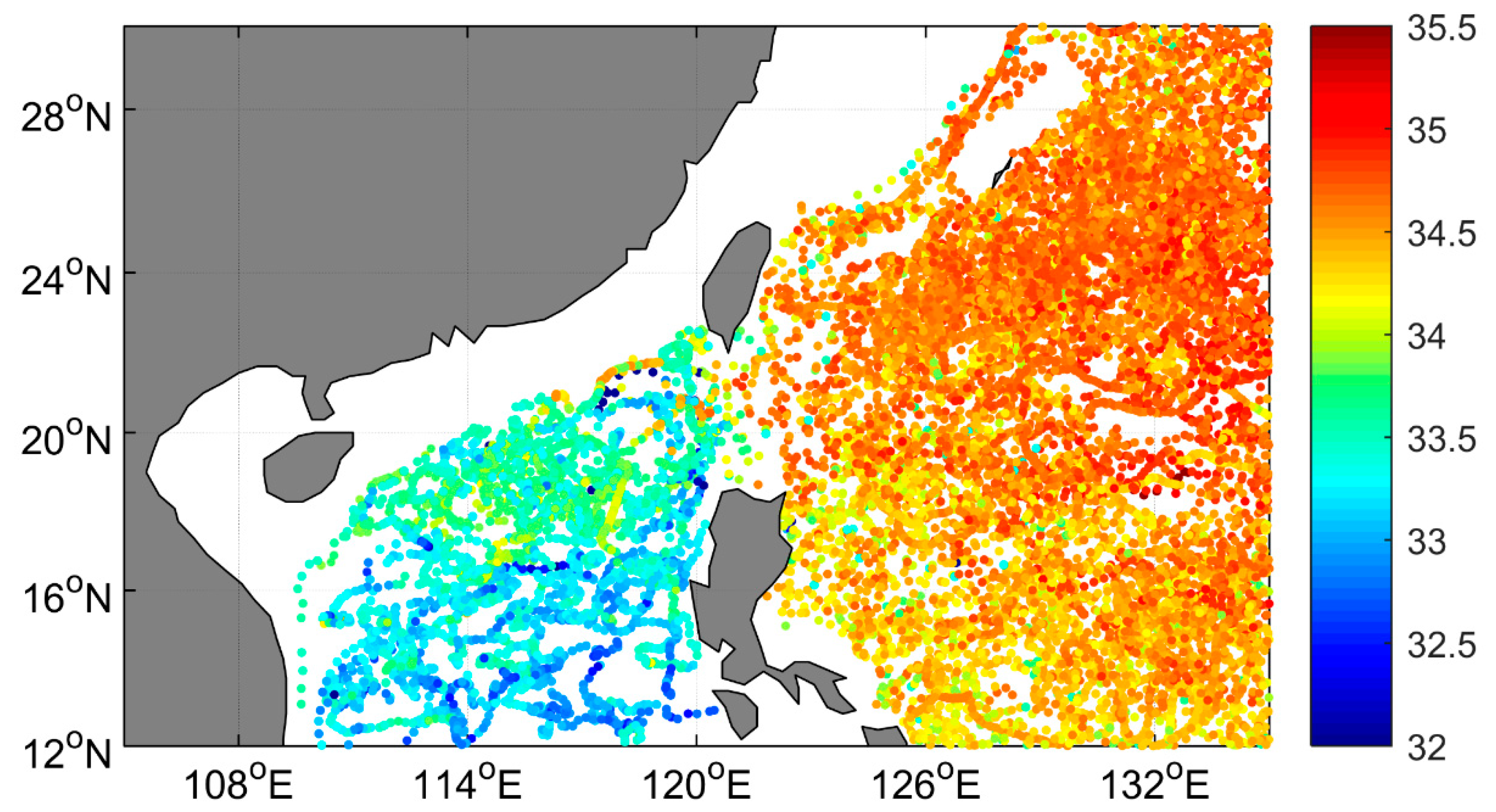
2.2. Data Description
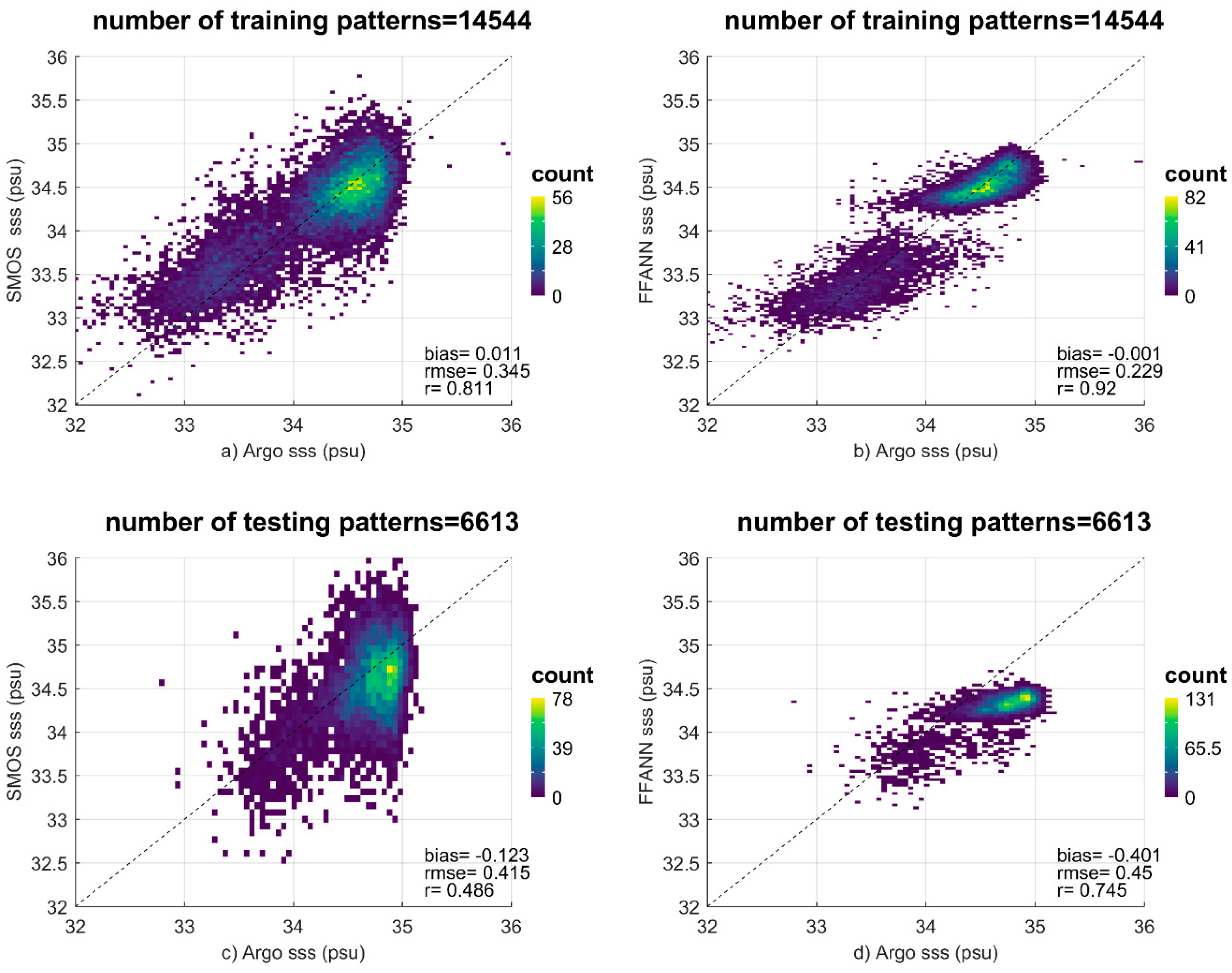
2.3. Neural Network Construction and Model tTraining
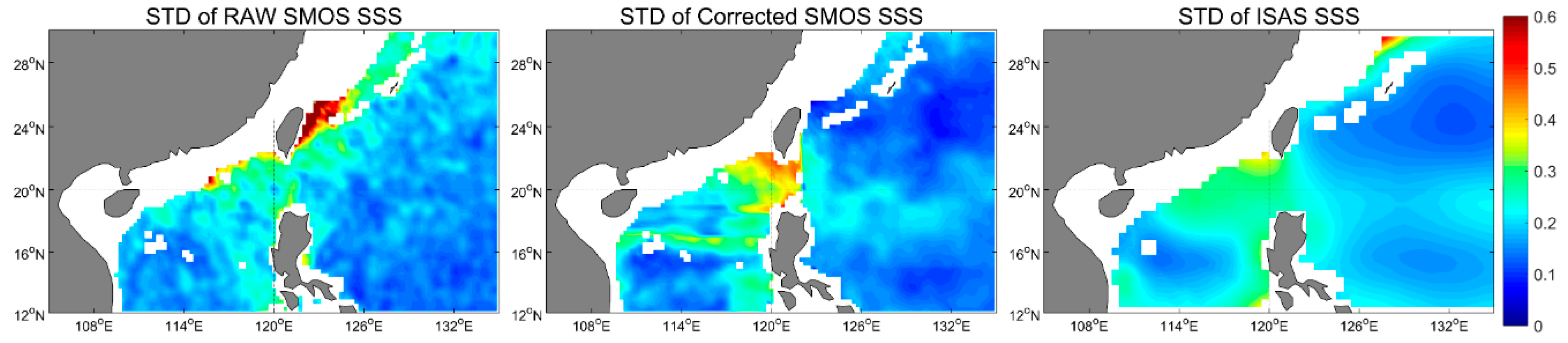
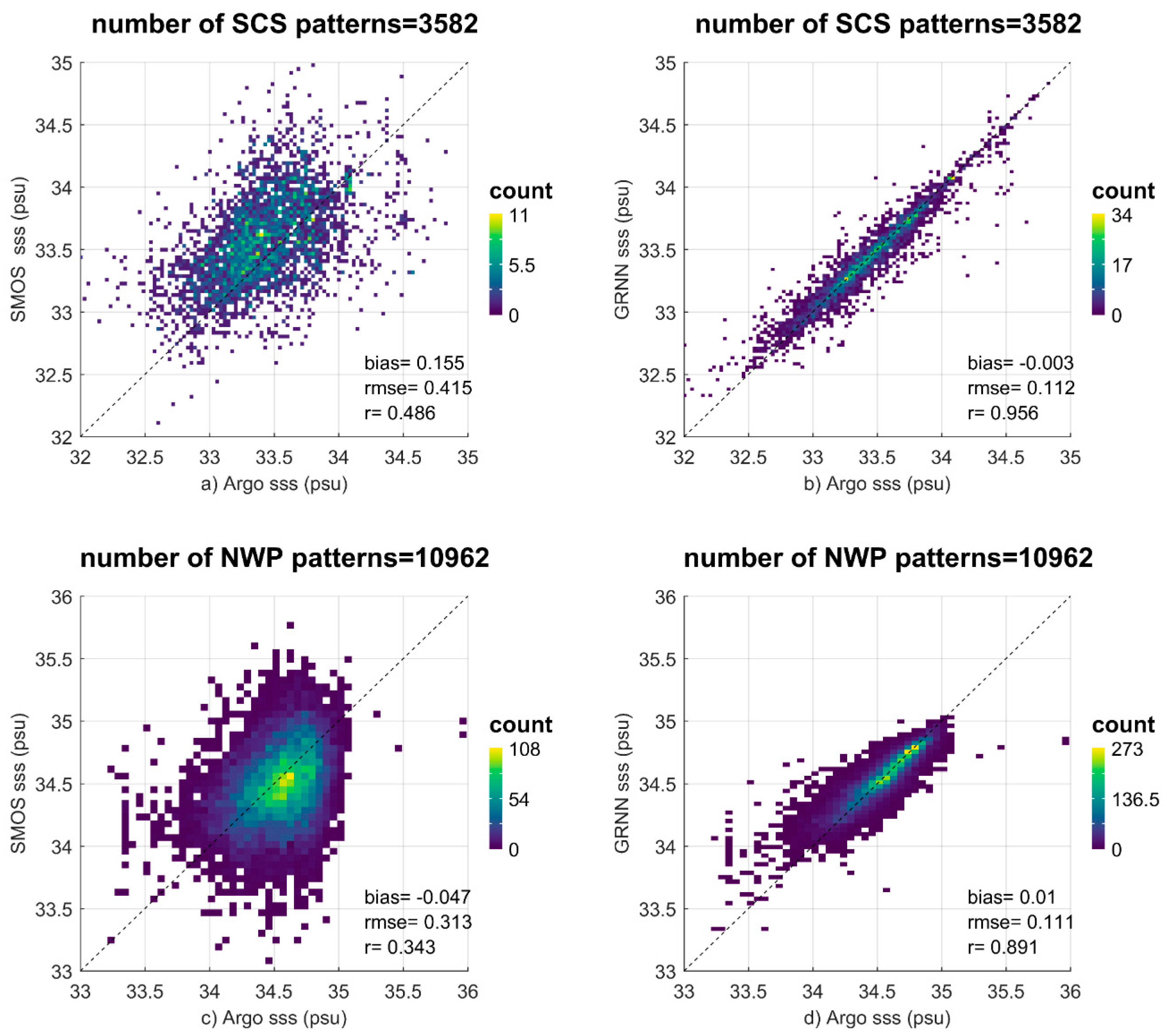
2.4. Analysis of the GRNN Correction Results
3. Assimilation of Corrected SSS in the Regional Ocean Modeling System (ROMS) 4DVAR System
3.1. The Regional Ocean Modeling System (ROMS) Ocean Model and 4DVAR
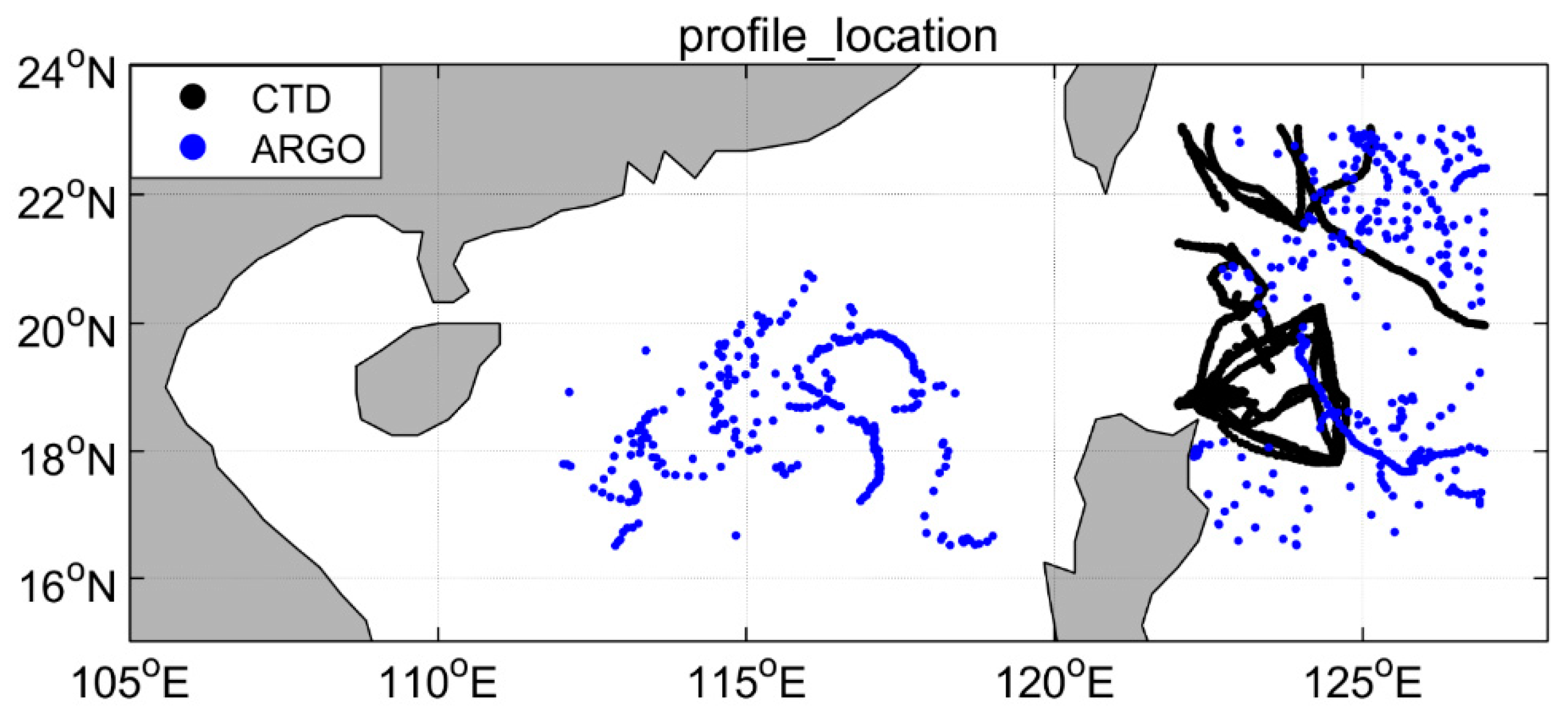
3.2. Data Used for the Assimilation
3.3. Experimental Setup
4. Assimilation Results
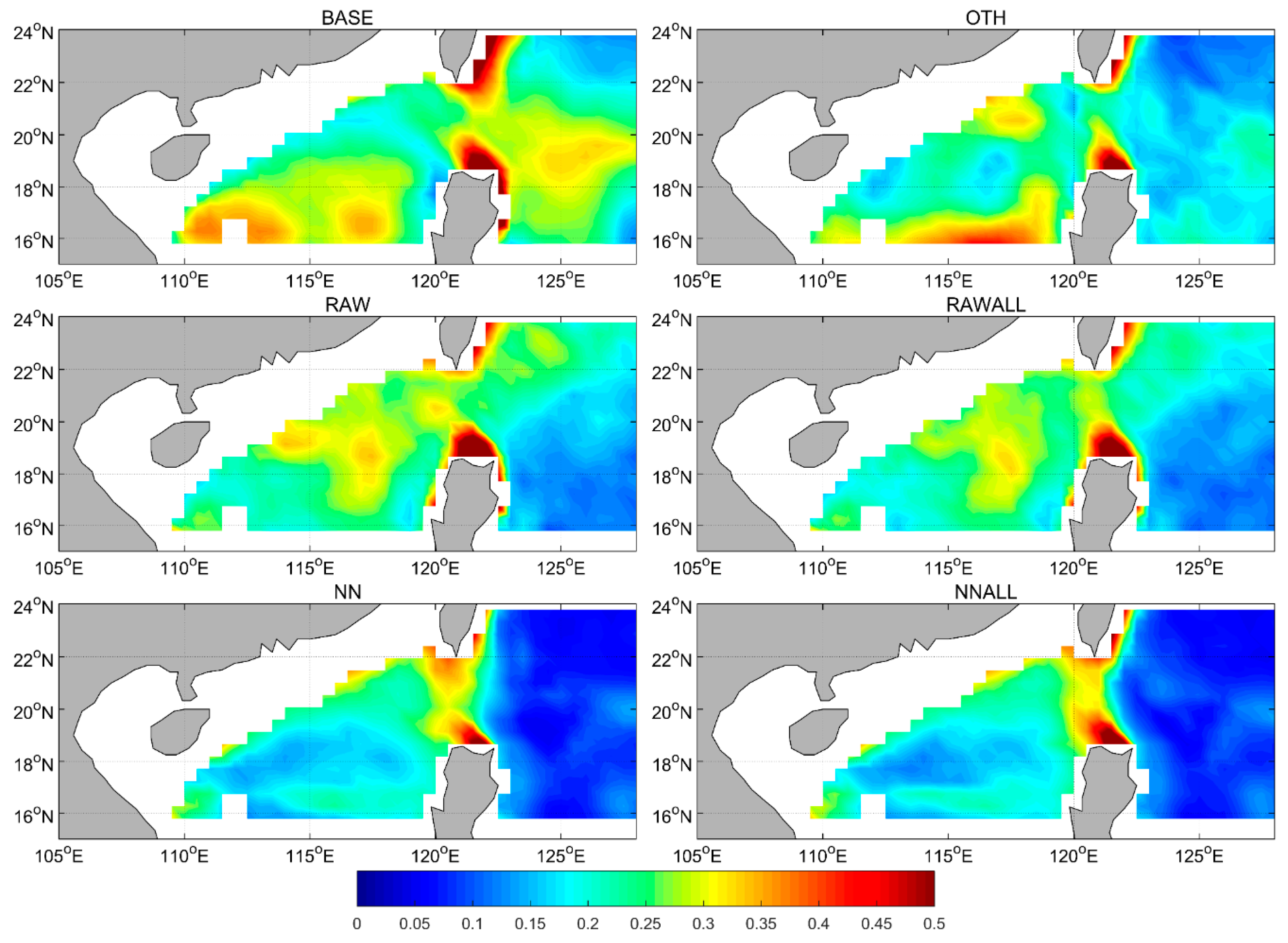
4.1. SSS Analysis
4.2. Subsurface Salinity Analysis
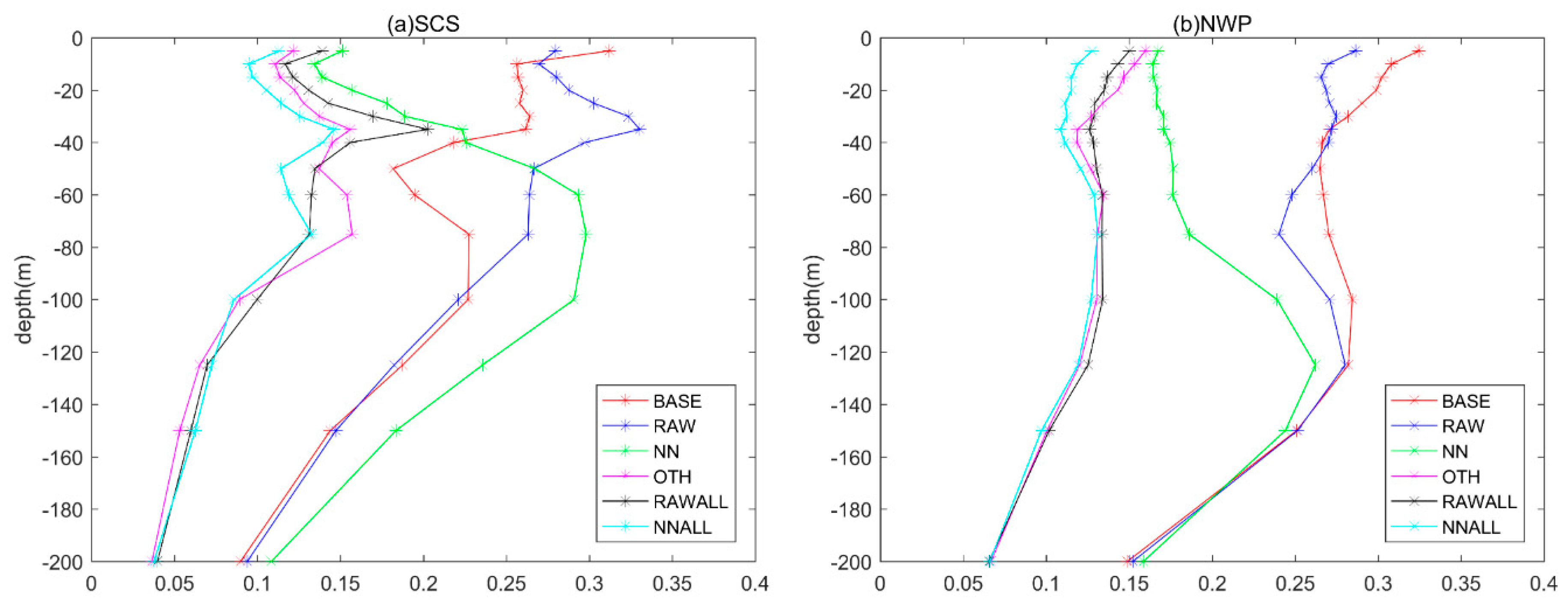
4.2.1. Salinity Profile
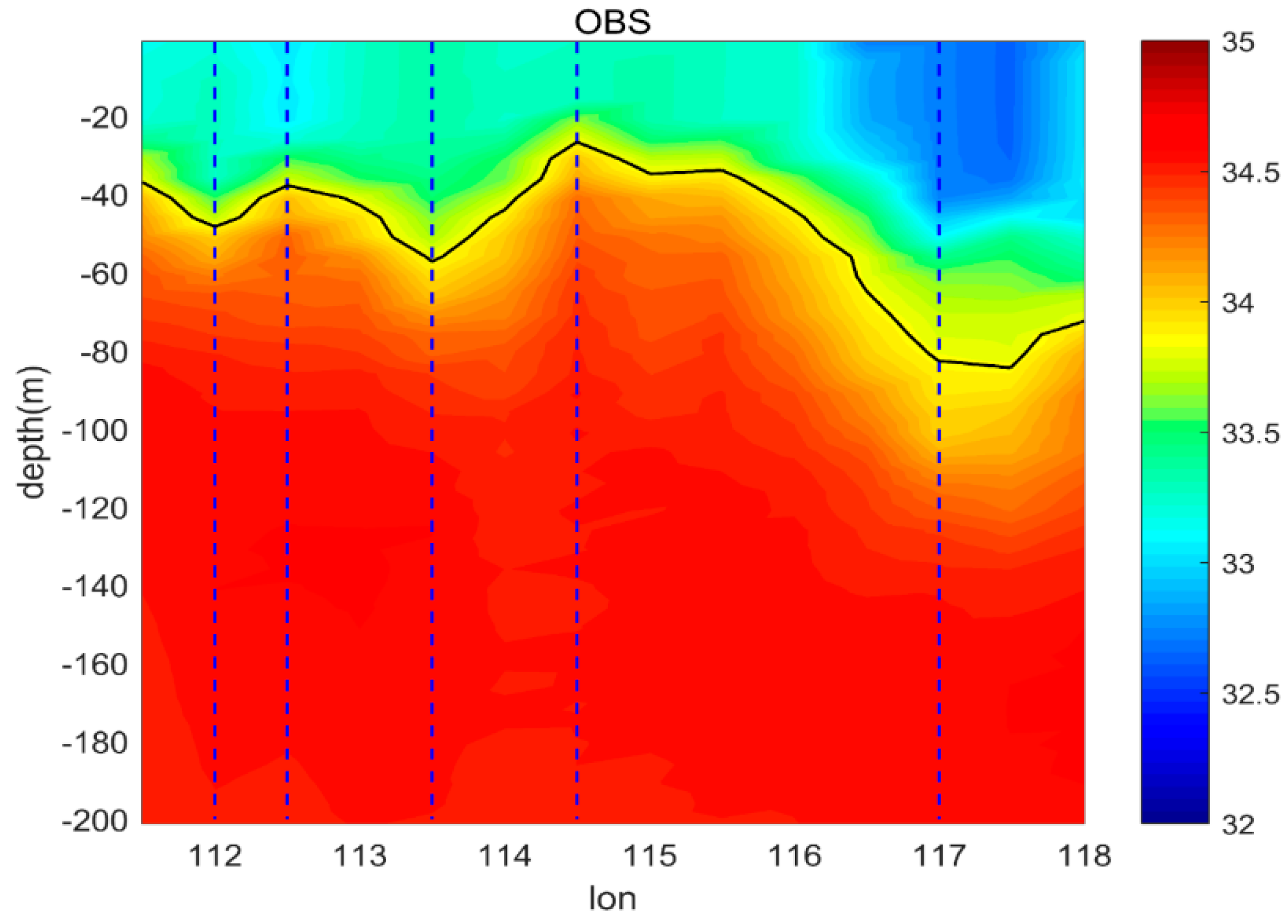
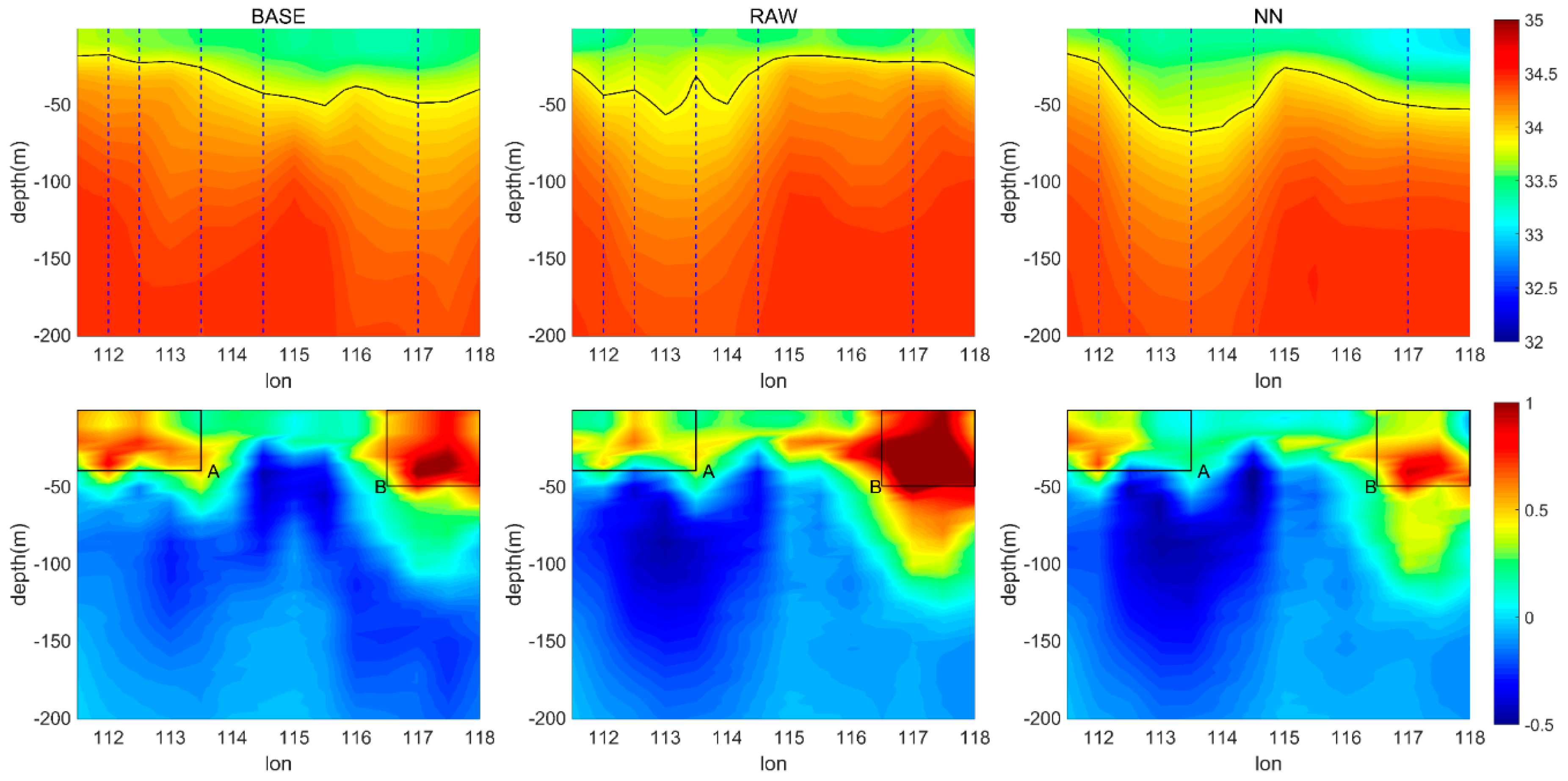
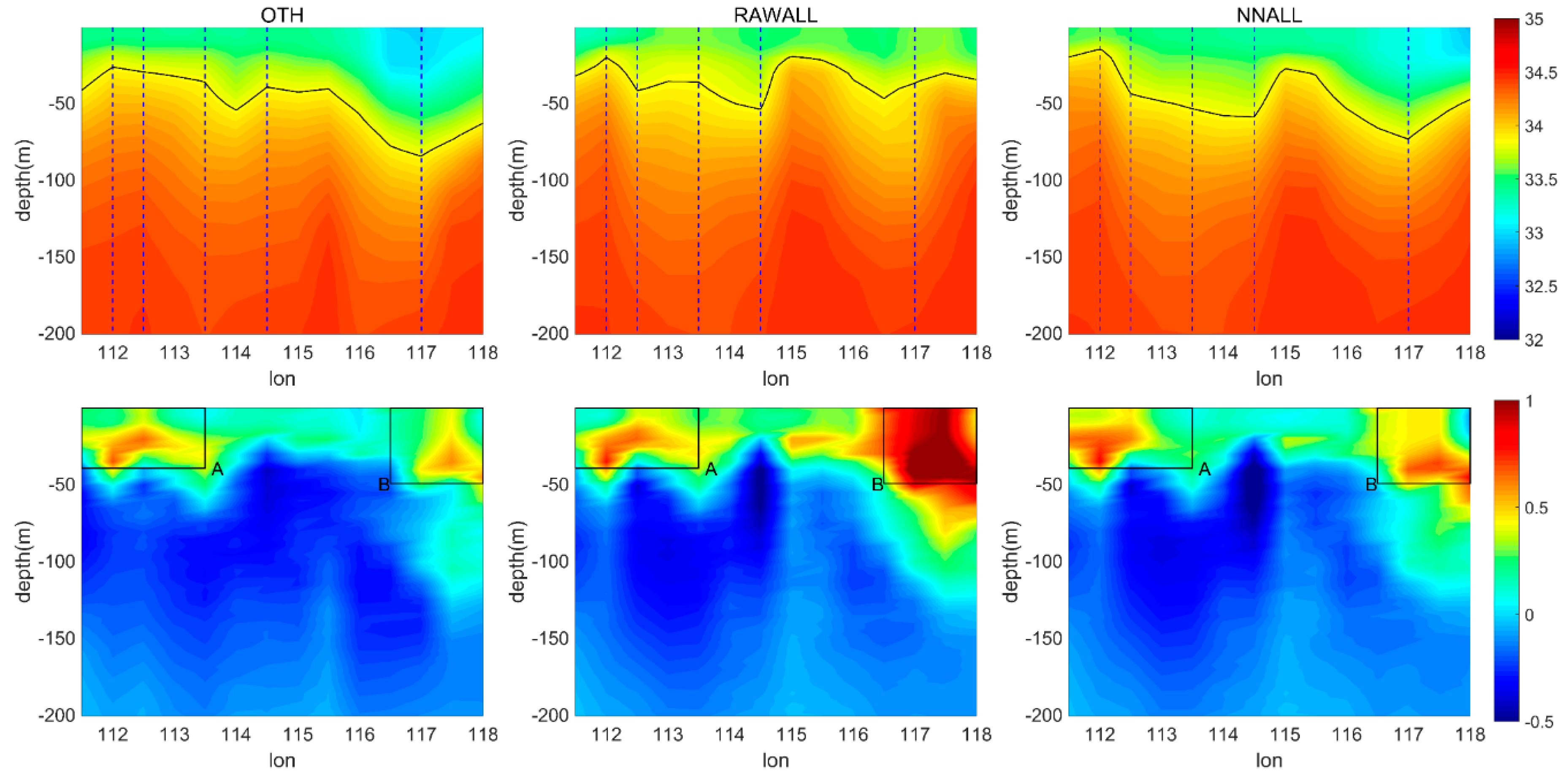
4.2.2. Salinity Section
5. Discussion
6. Conclusions
- (a)
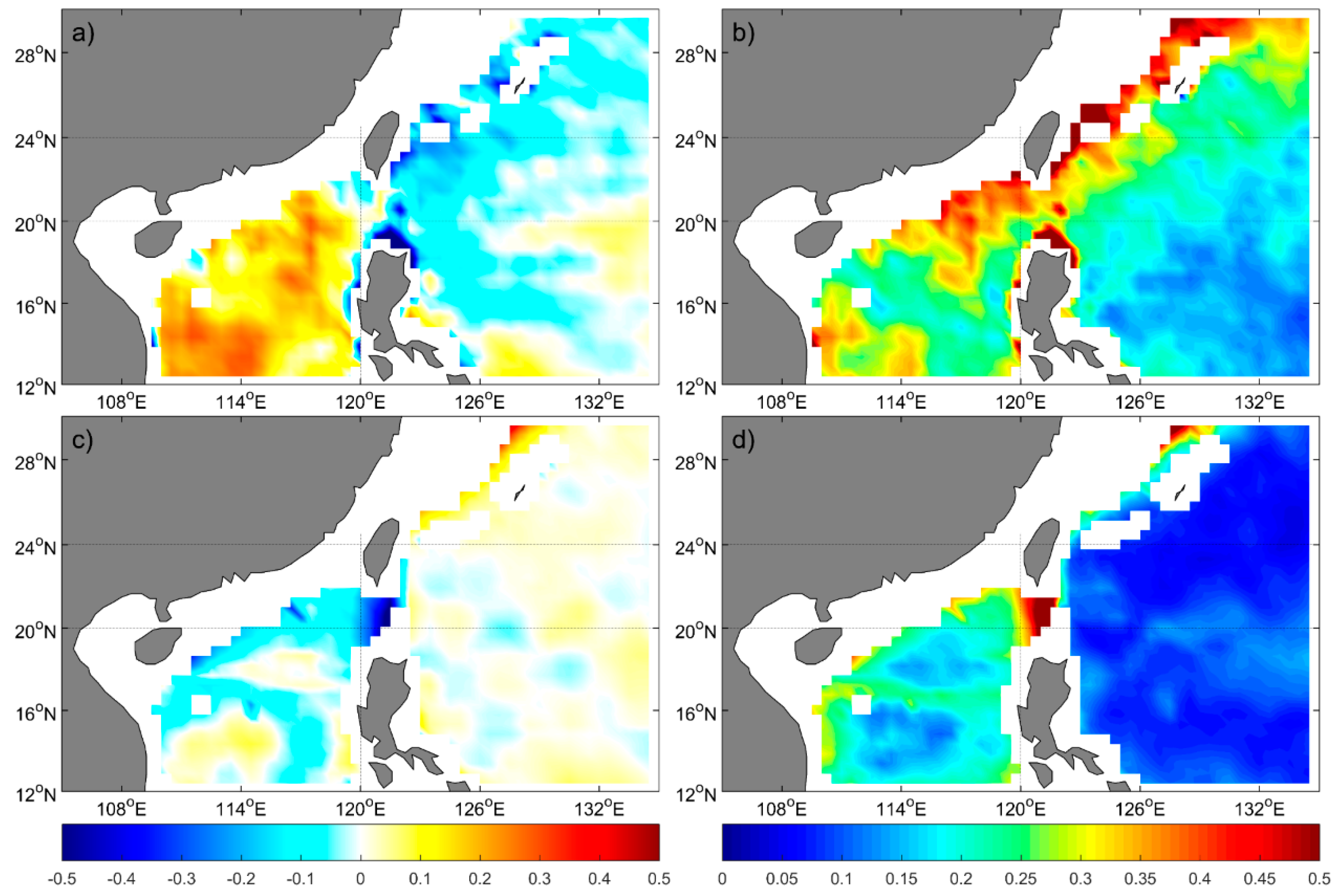
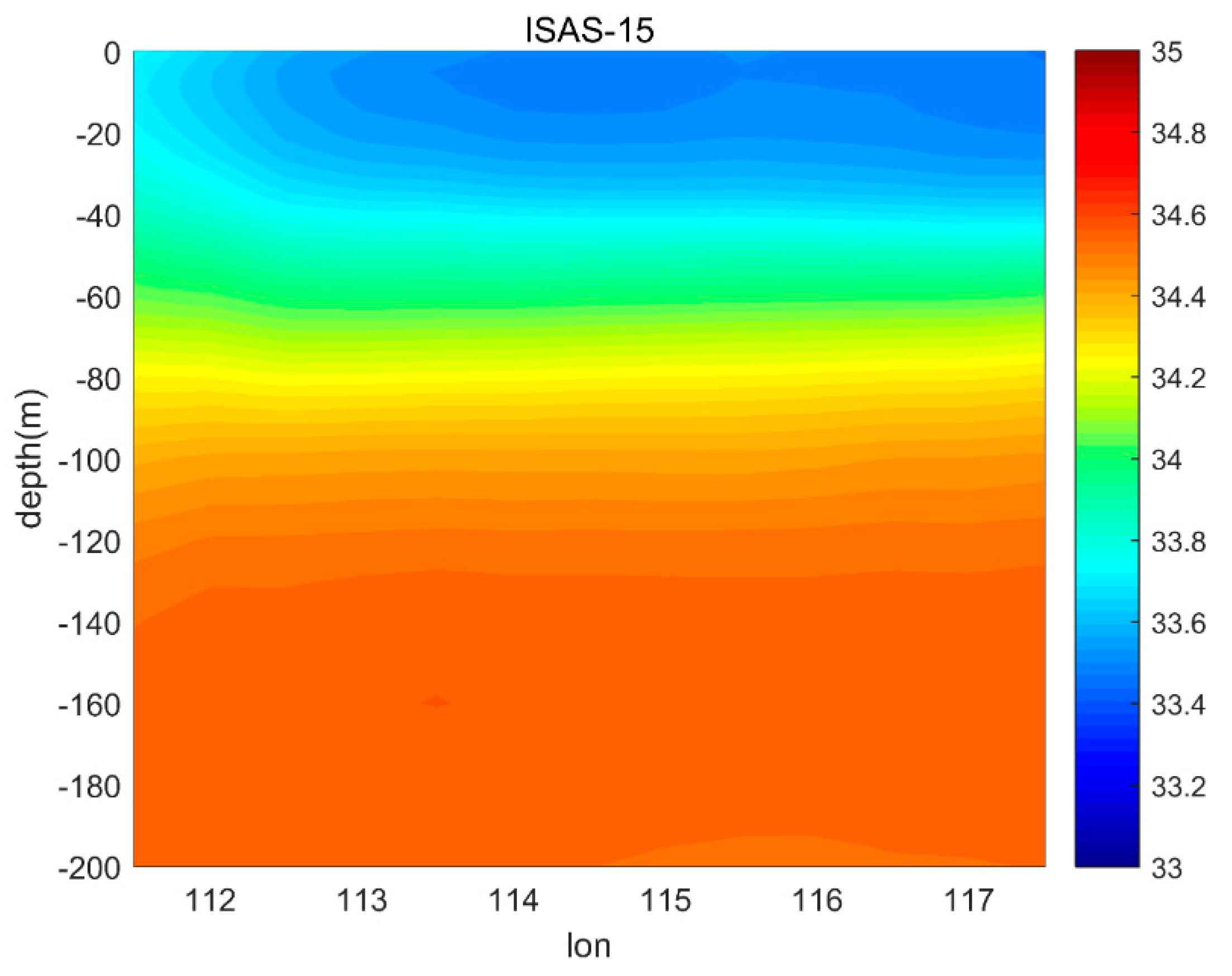
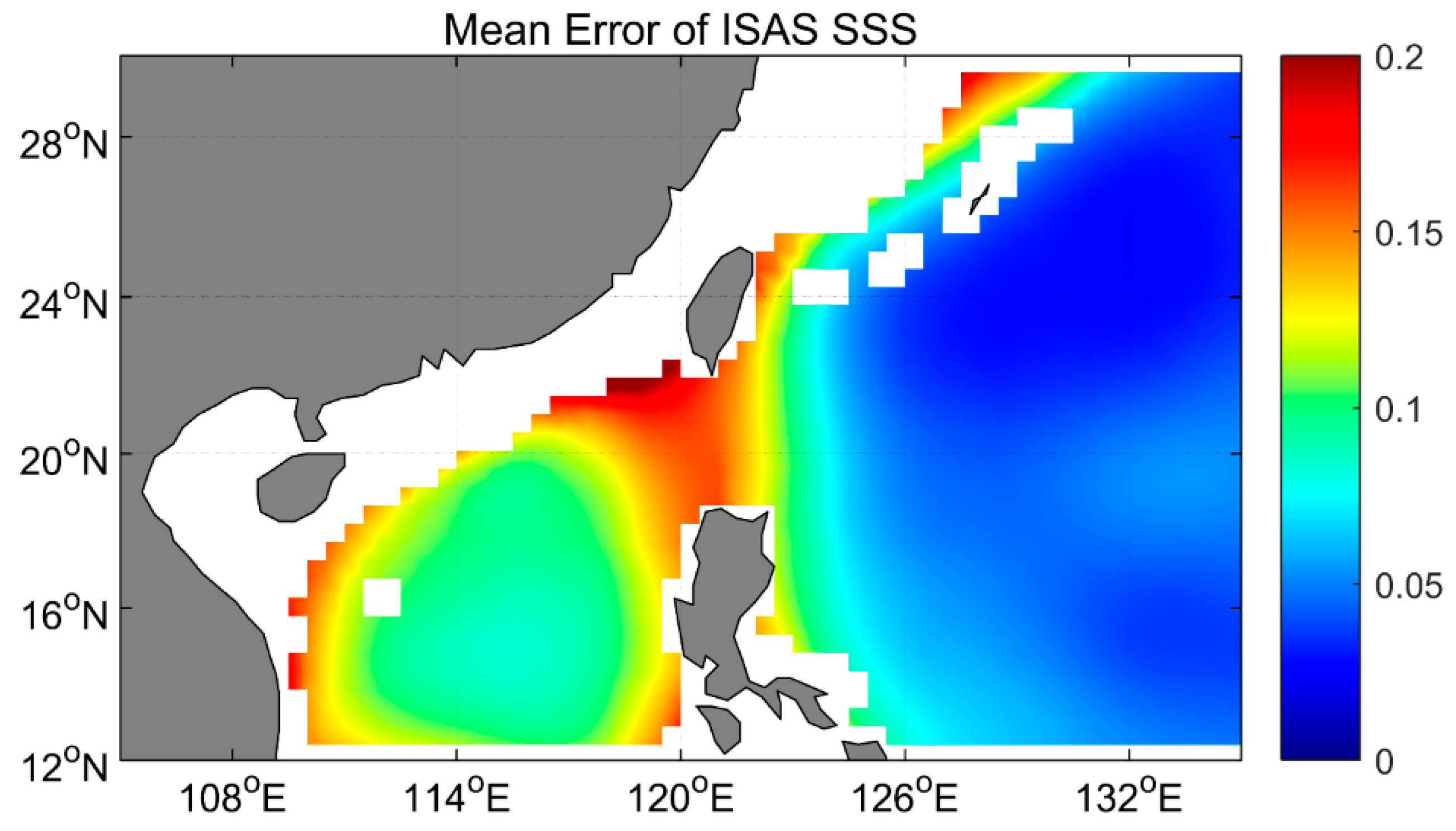
- Compared with Argo floats data, in addition to the northwestern Pacific, the errors in SSS product have also been reduced significantly in the northern SCS after being corrected by GRNN. The bias and RMSE are reduced to the order of 0.01 PSU and 0.1 PSU. The mean bias and RMSE compared with ISAS-15 SSS for the period of 2012–2014 are reduced and the variability of the corrected SSS maintains the same order as SSS of the ISAS dataset.
- (b)
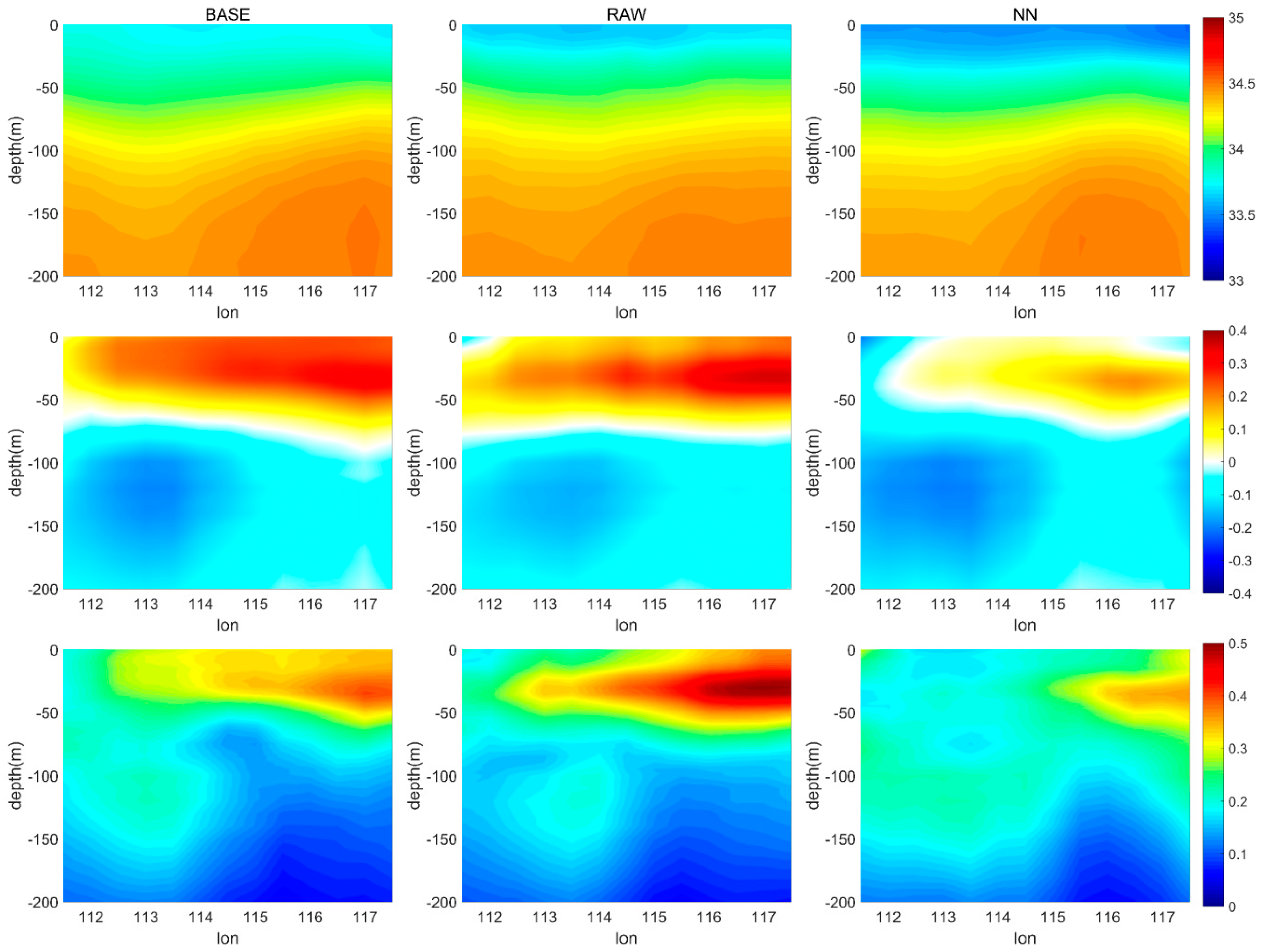
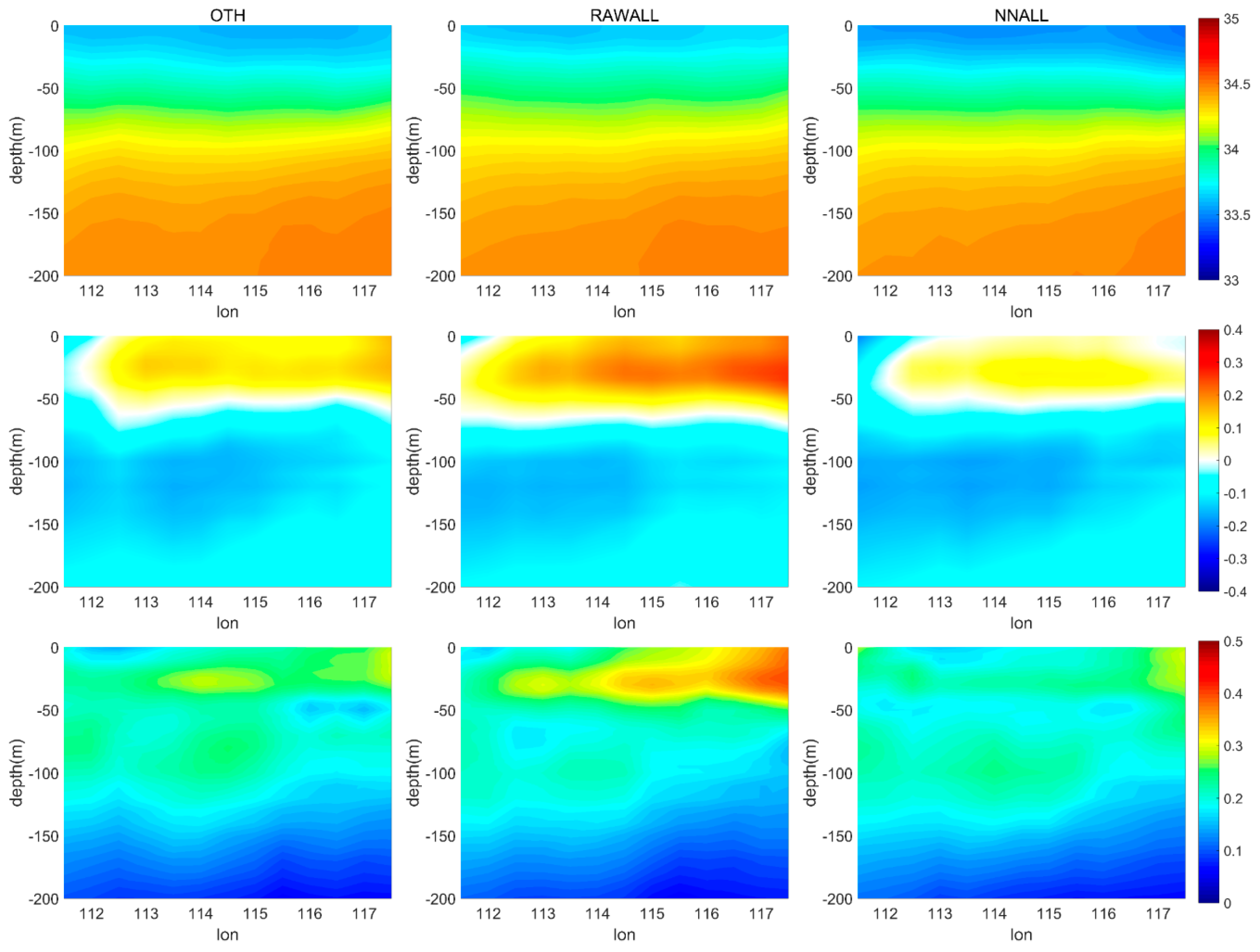
- T/S profiles assimilation can yield a positive impact on northwestern Pacific SSS simulations, but only slightly influences northern SCS SSS, while the assimilation of both raw SSS and GRNN corrected SSS yields improvements on model SSS. The largest improvements are shown in experiments with GRNN corrected SSS assimilation (EX3 and EX6), proving the importance of GRNN for SSS correction.
- (c)
- Comparing the experimental results with EN4 profiles shows that the assimilation of corrected SSS also improved the salinity fields simulation in the mixed layer, except for horizontal improvements on sea surface. Below the mixed layer, T/S profiles data are more important than SSS data. The influence depths of SSS assimilation are shallower in the northern SCS than in the northwestern Pacific, which indicates that the corrected SSS should be assimilated with T/S profiles data to obtain a better estimation of ocean states in coastal regions. However, after long-term assimilation, the improvements generated by corrected SSS assimilation are better than those from traditional observations’ assimilations in most areas of the 18°N section in the SCS.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Derber, J.; Rosati, A. A global oceanic data assimilation system. J. Phys. Oceanogr. 1989, 19, 1333–1347. [Google Scholar] [CrossRef]
- Clancy, R.M.; Phoebus, P.A.; Pollak, K.D. An operational global-scale ocean thermal analysis system. J. Atmos. Ocean. Technol. 1990, 7, 233–254. [Google Scholar] [CrossRef]
- Meyers, G.; Phillips, H.; Smith, N.; Sprintall, J. Space and time scales for optimal interpolation of temperature—Tropical Pacific Ocean. Prog. Oceanogr. 1991, 28, 189–218. [Google Scholar] [CrossRef]
- Shu, Y.; Zhu, J.; Wang, D.; Yan, C.; Xiao, X. Performance of four sea surface temperature assimilation schemes in the South China Sea. Cont. Shelf Res. 2009, 29, 1489–1501. [Google Scholar] [CrossRef]
- Cooper, N.S. The effect of salinity on tropical ocean models. J. Phys. Oceanogr. 1988, 18, 697–707. [Google Scholar] [CrossRef]
- Murtugudde, R.; Busalacchi, A.J. Salinity effects in a tropical ocean model. J. Geophys. Res. Oceans 1998, 103, 3283–3300. [Google Scholar] [CrossRef]
- Roemmich, D.; Gilson, J. The 2004–2008 mean and annual cycle of temperature, salinity, and steric height in the global ocean from the Argo Program. Prog. Oceanogr. 2009, 82, 81–100. [Google Scholar] [CrossRef]
- Han, G.; Zhu, J.; Zhou, G. Salinity estimation using the T-S relation in the context of variational data assimilation. J. Geophys. Res. Oceans 2004, 109, C03018. [Google Scholar] [CrossRef]
- Zhu, J.; Zhou, G.; Yan, C.; Fu, W.; You, X. A three-dimensional variational ocean data assimilation system: Scheme and preliminary results. Sci. China Ser. D Earth Sci. 2006, 49, 1212–1222. [Google Scholar] [CrossRef]
- Durack, P.J.; Wijffels, S.E. Fifty-year trends in global ocean salinities and their relationship to broad-scale warming. J. Clim. 2010, 23, 4342–4362. [Google Scholar] [CrossRef]
- Freeland, H.; Roemmich, D.; Garzoli, S.; Le Traon, P.Y.; Ravichandran, M.; Riser, S.; Thierry, V.; Wijffels, S.; Belbéoch, M.; Gould, J. Argo-a decade of progress. In Proceedings of the OceanObs’ 09: Sustained Ocean Observations and Information for Society, Venice, Italy, 21–25 September 2009; Volume 2. [Google Scholar]
- Hackert, E.; Ballabrera-Poy, J.; Busalacchi, A.J.; Zhang, R.H.; Murtugudde, R. Impact of sea surface salinity assimilation on coupled forecasts in the tropical Pacific. J. Geophys. Res. Oceans 2011, 116, C05009. [Google Scholar] [CrossRef]
- Hackert, E.; Busalacchi, A.J.; Ballabrera-Poy, J. Impact of Aquarius sea surface salinity observations on coupled forecasts for the tropical Indo-Pacific Ocean. J. Geophys. Res. Oceans 2014, 119, 4045–4067. [Google Scholar] [CrossRef]
- Chakraborty, A.; Sharma, R.; Kumar, R.; Basu, S. A SEEK filter assimilation of sea surface salinity from Aquarius in an OGCM: Implication for surface dynamics and thermohaline structure. J. Geophys. Res. Oceans 2014, 119, 4777–4796. [Google Scholar] [CrossRef]
- Vernieres, G.; Kovach, R.; Keppenne, C.; Akella, S.; Brucker, L.; Dinnat, E. The impact of the assimilation of Aquarius sea surface salinity data in the GEOS ocean data assimilation system. J. Geophys. Res. Oceans 2014, 119, 6974–6987. [Google Scholar] [CrossRef]
- Lu, Z.; Cheng, L.; Zhu, J.; Lin, R. The complementary role of SMOS sea surface salinity observation for estimating global ocean salinity state. J. Geophys. Res. Oceans 2016, 121, 3672–3691. [Google Scholar] [CrossRef]
- Köhl, A.; Sena Martins, M.; Stammer, D. Impact of assimilating surface salinity from SMOS on ocean circulation estimates. J. Geophys. Res. Oceans 2014, 119, 5449–5464. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.-J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS mission: New tool for monitoring key elements ofthe global water cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef]
- Boutin, J.; Martin, N.; Yin, X.; Font, J.; Reul, N.; Spurgeon, P. First assessment of SMOS data over open ocean: Part II, sea surface alinity. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1662–1675. [Google Scholar] [CrossRef]
- Vinogradova, N.T.; Ponte, R.M.; Fukumori, I.; Wang, O. Estimating satellite salinity errors for assimilation of Aquarius and SMOS data into climate models. J. Geophys. Res. Oceans 2014, 119, 4732–4744. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, G.; Qian, C.; Jiang, H. Assessment of two SMOS sea surface salinity level 3 products against Argo upper salinity measurements. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1434–1438. [Google Scholar] [CrossRef]
- Olmedo, E.; Martínez, J.; Turiel, A.; Ballabrera-Poy, J.; Portabella, M. Debiased non-Bayesian retrieval: A novel approach to SMOS Sea Surface Salinity. Remote Sens. Environ. 2017, 193, 103–126. [Google Scholar] [CrossRef]
- Ammar, A.; Labroue, S.; Obligis, E.; Mejia, C.; Thiria, S.; Crepon, M. Sea surface salinity retrieval throughout a SMOS half-orbit using neural networks. In Proceedings of the 2006 IEEE MicroRad, SanJuan, Puerto Rico, 28 February–3 March 2006; pp. 103–108. [Google Scholar]
- Gao, S.; Tian, J.; Wang, F.; Bai, Y.; Gao, W.; Yang, S. The study of GRNN for wind speed forecasting based on Markov Chain. In Proceedings of the International Conference on Modelling, Simulation and Applied Mathematics (MSAM 2015), Phuket, Thailand, 23–24 August 2015; pp. 285–288. [Google Scholar]
- Zhou, K.; Yu, D.; Lin, Z.; Cao, B.; Wang, Z.; Guo, S. Anode effect prediction of aluminum electrolysis using GRNN. In Proceedings of the 2015 Chinese Automation Congress (CAC), Wuhan, China, 27–29 November 2015; pp. 853–858. [Google Scholar]
- Carval, T.; Keeley, B.; Takatsuki, Y.; Yoshida, T.; Loch, S.; Schmid, C.; Goldsmith, R.; Wong, A.; McCreadie, R.; Thresher, A.; et al. ARGO Data Management: 2012. Argo User’s Manual v2.4. IFREMER Reference cor-do/dti-mut/02-084. Available online: http://www.argodatamgt.org/content/download/12096/80327/file/argo-dm-user-manual.pdf (accessed on 9 September 2014).
- Reynolds, R.W.; Smith, T.M.; Liu, C.; Chelton, D.B.; Casey, K.S.; Schlax, M.G. Daily high-resolution-blended analyses for sea surface temperature. J. Clim. 2007, 20, 5473–5496. [Google Scholar] [CrossRef]
- Nicolas, K.; Annaig, P.; Fabienne, G. ISAS-SSS: In Situ Sea Surface Salinity Gridded Fields. SEANOE: 2018. Available online: https://doi.org/10.17882/55600 (accessed on 1 June 2018).
- Gaillard, F.; Reynaud, T.; Thierry, V.; Kolodziejczyk, N.; von Schuckmann, K. In-situ based reanalysis of the global ocean temperature and salinity with ISAS: Variability of the heat content and steric height. J. Clim. 2016, 29, 1305–1323. [Google Scholar] [CrossRef]
- Bao, S.; Zhang, R.; Wang, H.; Yan, H.; Yu, Y.; Chen, J. Salinity Profile Estimation in the Pacific Ocean from Satellite Surface Salinity Observations. J. Atmos. Ocean. Technol. 2019, 36, 53–68. [Google Scholar] [CrossRef]
- Boutin, J.; Waldteufel, P.; Martin, N.; Caudal, G.; Dinnat, E. Surface salinity retrieved from SMOS measurements over the global ocean: Imprecisions due to sea surface roughness and temperature uncertainties. J. Atmos. Ocean. Technol. 2004, 21, 1432–1447. [Google Scholar] [CrossRef]
- Anderson, J.E.; Riser, S.C. Near-surface variability of temperature and salinity in the near-tropical ocean: Observations from profiling floats. J. Geophys. Res. Oceans 2014, 119, 7433–7448. [Google Scholar] [CrossRef]
- Shchepetkin, A.F.; McWilliams, J.C. A method for computing horizontal pressure-gradient force in an oceanic model with a nonaligned vertical coordinate. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Shchepetkin, A.F.; McWilliams, J.C. The Regional Ocean Modeling System: A split-explicit, free-surface, topography following coordinates ocean model. Ocean Model. 2005, 9, 347–404. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Atlas, R.; Hoffman, R.N.; Ardizzone, J.; Leidner, S.M.; Jusem, J.C.; Smith, D.K.; Gombos, D. A cross-calibrated, multiplatform ocean surface wind velocity product for meteorological and oceanographic applications. Bull. Am. Meteorol. Soc. 2011, 92, 157–174. [Google Scholar] [CrossRef]
- Carton, J.A.; Chepurin, G.A.; Chen, L. SODA3: A new ocean climate reanalysis. J. Clim. 2018, 31, 6967–6983. [Google Scholar] [CrossRef]
- Moore, A.M.; Arango, H.G.; Broquet, G.; Powell, B.S.; Weaver, A.T.; Zavala-Garay, J. The Regional Ocean Modeling System (ROMS) 4-dimensional variational data assimilation systems: Part I–System overview and formulation. Prog. Oceanogr. 2011, 91, 34–49. [Google Scholar] [CrossRef]
- Moore, A.M.; Arango, H.G.; Broquet, G.; Edwards, C.; Veneziani, M.; Powell, B.; Foley, D.; Doyle, J.D.; Costa, D.; Robinson, P.; et al. The Regional Ocean Modeling System (ROMS) 4-dimensional variational data assimilation systems: Part II–performance and application to the California Current System. Prog. Oceanogr. 2011, 91, 50–73. [Google Scholar] [CrossRef]
- Courtier, P.; Thépaut, J.N.; Hollingsworth, A. A strategy for operational implementation of 4D-Var, using an incremental approach. Q. J. R. Meteorol. Soc. 1994, 120, 1367–1387. [Google Scholar] [CrossRef]
- Weaver, A.T.; Vialard, J.; Anderson, D.L.T. Three-and four-dimensional variational assimilation with a general circulation model of the tropical Pacific Ocean. Part I: Formulation, internal diagnostics, and consistency checks. Mon. Weather Rev. 2003, 131, 1360–1378. [Google Scholar] [CrossRef]
- Good, S.A.; Martin, M.J.; Rayner, N.A. EN4: Quality controlled ocean temperature and salinity profiles and monthly objective analyses with uncertainty estimates. J. Geophys. Res. Oceans 2013, 118, 6704–6716. [Google Scholar] [CrossRef]
- You, Y.; Chern, C.S.; Yang, Y.; Liu, C.T.; Liu, K.K.; Pai, S.C. The South China Sea, a cul-de-sac of North Pacific intermediate water. J. Oceanogr. 2005, 61, 509–527. [Google Scholar] [CrossRef]
- Qu, T.; Mitsudera, H.; Yamagata, T. Intrusion of the north Pacific waters into the South China Sea. J. Geophys. Res. Oceans 2000, 105, 6415–6424. [Google Scholar] [CrossRef]
- Liu, Q.; Jia, Y.; Liu, P.; Wang, Q.; Chu, P.C. Seasonal and intra-seasonal thermocline variability in the central South China Sea. Geophys. Res. Lett. 2001, 28, 4467–4470. [Google Scholar] [CrossRef]
- Zeng, X. A Reanalysis Dataset of the South China Sea and Its Application in the Study of Mesoscale Eddies; South China Sea Institute of Oceanology Chinese Academy of Science: Guangzhou, China, 2015. [Google Scholar]
- Henocq, C.; Boutin, J.; Reverdin, G.; Petitcolin, F.; Arnault, S.; Lattes, P. Vertical variability of near-surface salinity in the tropics: Consequences for L-band radiometer calibration and validation. J. Atmos. Ocean. Technol. 2010, 27, 192–209. [Google Scholar] [CrossRef]
- Boutin, J.; Martin, N.; Reverdin, G.; Yin, X.; Gaillard, F. Sea surface freshening inferred from SMOS and ARGO salinity: Impact of rain. Ocean Sci. 2013, 9, 183–192. [Google Scholar] [CrossRef]
| Variable | Horizontal Resolution | Temporal Resolution | Source |
|---|---|---|---|
| Heat flux | 0.75° × 0.75° | 6 h | ERA-interim [35] |
| Freshwater flux | 0.75° × 0.75° | 6 h | ERA-interim |
| Wind stresses | 0.25° × 0.25° | 6 h | [36] |
| Boundary conditions | – | – | [37] |
| Experiments | Experiments Name | Data Assimilated |
|---|---|---|
| EX1 | BASE | None |
| EX2 | RAW | Raw SMOS SSS |
| EX3 | NN | Corrected SMOS SSS |
| EX4 | OTH | SSH, SST, T/S profile |
| EX5 | RAWALL | Raw SMOS SSS, SSH, SST, T/S profile |
| EX6 | NNALL | Corrected SMOS SSS, SSH, SST, T/S profile |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mu, Z.; Zhang, W.; Wang, P.; Wang, H.; Yang, X. Assimilation of SMOS Sea Surface Salinity in the Regional Ocean Model for South China Sea. Remote Sens. 2019, 11, 919. https://doi.org/10.3390/rs11080919
Mu Z, Zhang W, Wang P, Wang H, Yang X. Assimilation of SMOS Sea Surface Salinity in the Regional Ocean Model for South China Sea. Remote Sensing. 2019; 11(8):919. https://doi.org/10.3390/rs11080919
Chicago/Turabian StyleMu, Ziyao, Weimin Zhang, Pinqiang Wang, Huizan Wang, and Xiaofeng Yang. 2019. "Assimilation of SMOS Sea Surface Salinity in the Regional Ocean Model for South China Sea" Remote Sensing 11, no. 8: 919. https://doi.org/10.3390/rs11080919
APA StyleMu, Z., Zhang, W., Wang, P., Wang, H., & Yang, X. (2019). Assimilation of SMOS Sea Surface Salinity in the Regional Ocean Model for South China Sea. Remote Sensing, 11(8), 919. https://doi.org/10.3390/rs11080919






