A Data-Driven Approach to Classifying Wave Breaking in Infrared Imagery
Abstract
1. Introduction
2. Materials and Methods
2.1. Field Site and Instrumentation
2.2. Model for Discrete Classification of Breaker Type
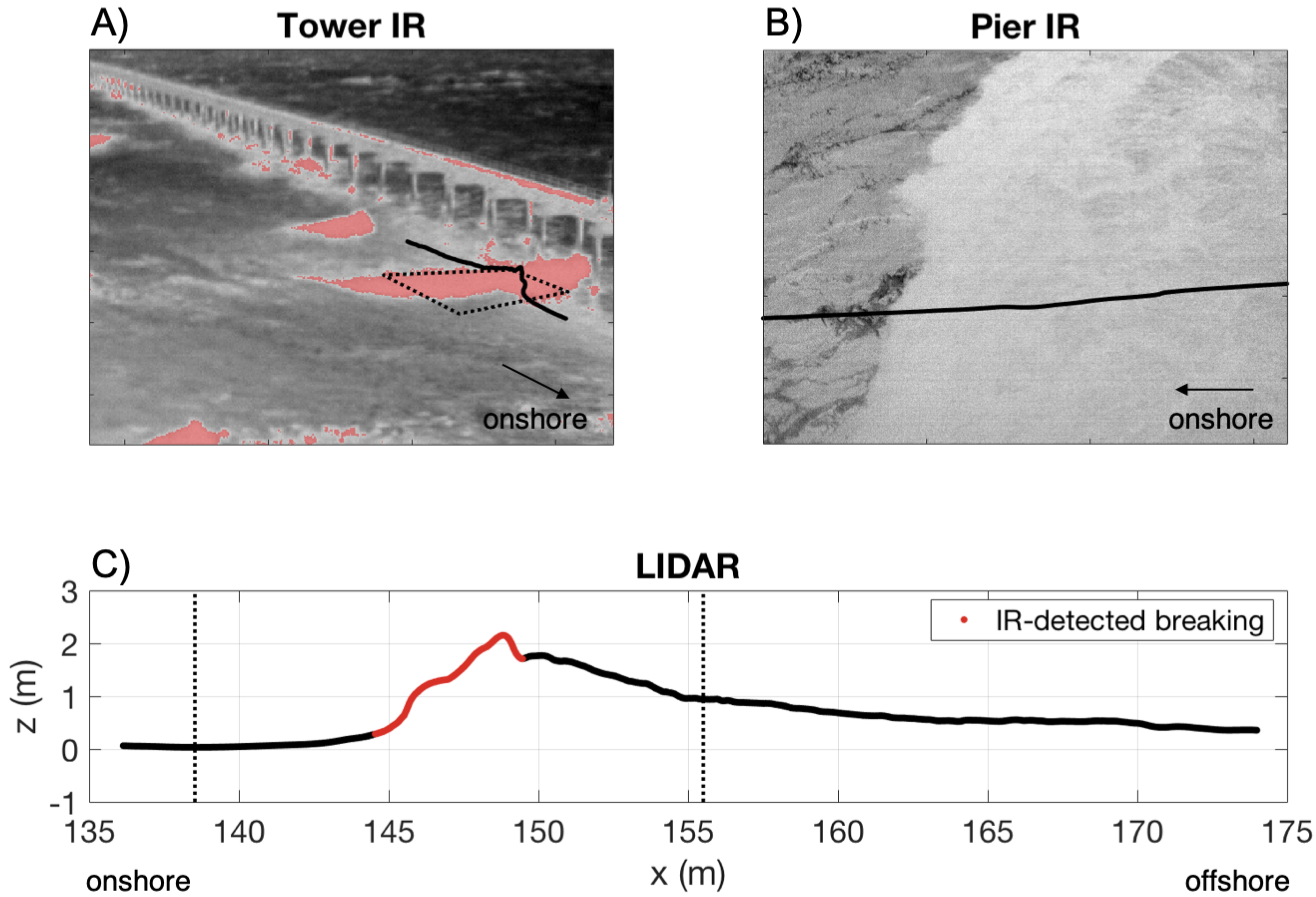
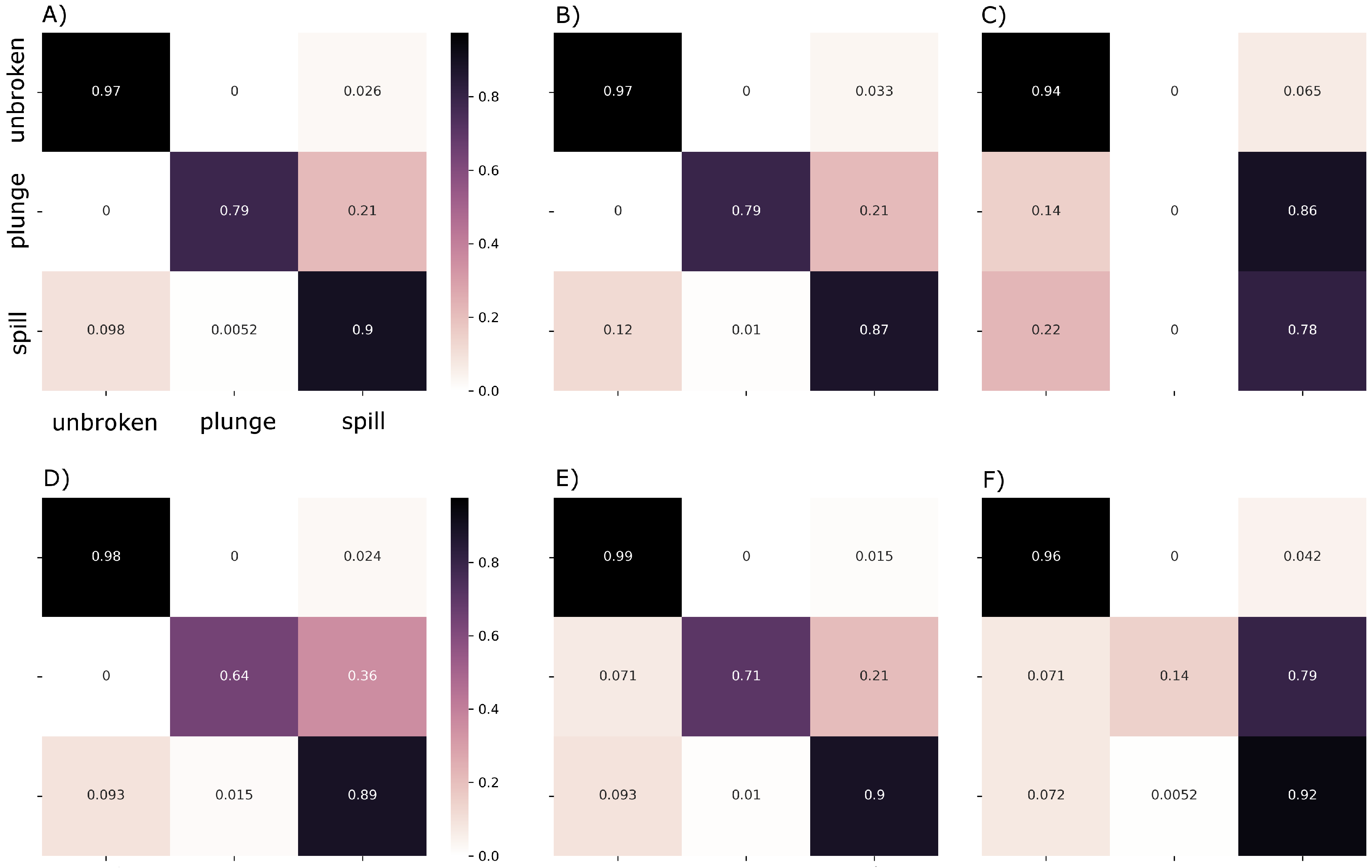
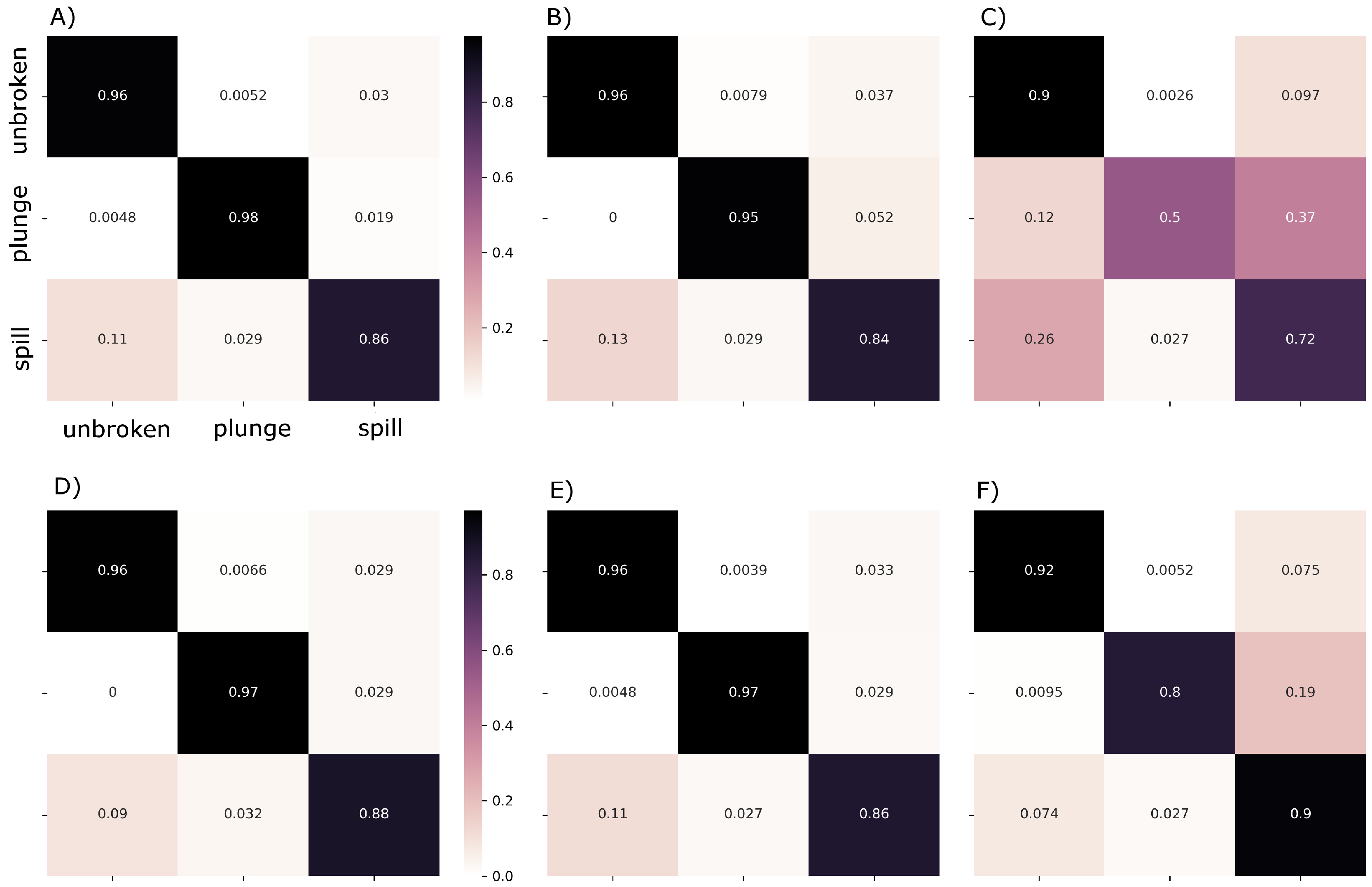
3. Results
4. Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- MacMahan, J.H.; Thornton, E.B.; Reniers, A.J. Rip current review. Coast. Eng. 2006, 53, 191–208. [Google Scholar] [CrossRef]
- Defeo, O.; McLachlan, A.; Schoeman, D.S.; Schlacher, T.A.; Dugan, J.; Jones, A.; Lastra, M.; Scapini, F. Threats to sandy beach ecosystems: A review. Estuar. Coast. Shelf S 2009, 81, 1–12. [Google Scholar] [CrossRef]
- Thornton, E.B.; Guza, R. Transformation of wave height distribution. J. Geophys. Res. Oceans 1983, 88, 5925–5938. [Google Scholar] [CrossRef]
- Duncan, J. An experimental investigation of breaking waves produced by a towed hydrofoil. Proc. R. Soc. Lond. A 1981, 377, 331–348. [Google Scholar] [CrossRef]
- Banner, M.; Peregrine, D. Wave breaking in deep water. Annu. Rev. Fluid Mech. 1993, 25, 373–397. [Google Scholar] [CrossRef]
- Filipot, J.F.; Ardhuin, F.; Babanin, A.V. A unified deep-to-shallow water wave-breaking probability parameterization. J. Geophys. Res. Oceans 2010, 115. [Google Scholar] [CrossRef]
- Basco, D.R. A qualitative description of wave breaking. J. Waterw. Port Coast. 1985, 111, 171–188. [Google Scholar] [CrossRef]
- Iafrati, A. Energy dissipation mechanisms in wave breaking processes: Spilling and highly aerated plunging breaking events. J. Geophys. Res. Oceans 2011, 116. [Google Scholar] [CrossRef]
- Jessup, A.; Zappa, C.; Loewen, M.; Hesany, V. Infrared remote sensing of breaking waves. Nature 1997, 385, 52. [Google Scholar] [CrossRef]
- Jessup, A.; Zappa, C.J.; Yeh, H. Defining and quantifying microscale wave breaking with infrared imagery. J. Geophys. Res. Oceans 1997, 102, 23145–23153. [Google Scholar] [CrossRef]
- Carini, R.J.; Chickadel, C.C.; Jessup, A.T.; Thomson, J. Estimating wave energy dissipation in the surf zone using thermal infrared imagery. J. Geophys. Res. Oceans 2015, 120, 3937–3957. [Google Scholar] [CrossRef]
- Watanabe, Y.; Mori, N. Infrared measurements of surface renewal and subsurface vortices in nearshore breaking waves. J. Geophys. Res. Oceans 2008, 113, C07015. [Google Scholar] [CrossRef]
- Huang, Z.C.; Hwang, K.S. Measurements of surface thermal structure, kinematics, and turbulence of a large-scale solitary breaking wave using infrared imaging techniques. Coast. Eng. 2015, 96, 132–147. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning; MIT Press: Cambridge, UK, 2016; Volume 1. [Google Scholar]
- Holman, R.; Haller, M.C. Remote sensing of the nearshore. Annu. Rev. Mar. Sci. 2013, 5, 95–113. [Google Scholar] [CrossRef]
- Baldock, T.E.; Moura, T.; Power, H.E. Video-Based Remote Sensing of Surf Zone Conditions. IEEE Potentials 2017, 36, 35–41. [Google Scholar] [CrossRef]
- Stringari, C.; Harris, D.; Power, H. A novel machine learning algorithm for tracking remotely sensed waves in the surf zone. Coast. Eng. 2019, 147, 149–158. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. In Proceedings of the 25th International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv, 2014; arXiv:1409.1556. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv, 2017; arXiv:1704.04861. [Google Scholar]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; Chen, T. Recent advances in convolutional neural networks. Pattern Recogn. 2017, 77, 354–377. [Google Scholar] [CrossRef]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. ImageNet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Buscombe, D.; Ritchie, A. Landscape classification with deep neural networks. Geosciences 2018, 8, 244. [Google Scholar] [CrossRef]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. Imagenet large scale visual recognition challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. MobileNetV2: Inverted Residuals and Linear Bottlenecks. arXiv, 2018; arXiv:1801.04381. [Google Scholar]
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1251–1258. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A.A. Inception-v4, Inception-ResNet and the impact of residual connections on learning. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 4278–4284. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. Tensorflow: Large-scale machine learning on heterogeneous distributed systems. arXiv, 2016; arXiv:1603.04467. [Google Scholar]
- Murphy, K. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, UK, 2012. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef]
- Zhou, B.; Khosla, A.; Lapedriza, A.; Oliva, A.; Torralba, A. Learning deep features for discriminative localization. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2921–2929. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Fu, G.; Liu, C.; Zhou, R.; Sun, T.; Zhang, Q. Classification for high resolution remote sensing imagery using a fully convolutional network. Remote Sens. 2017, 9, 498. [Google Scholar] [CrossRef]

| Model | Rank-1 Score | F1 Score | ||
|---|---|---|---|---|
| Unbroken | Plunging | Spilling | ||
| MobilenetV2 | 0.95 (0.94) | 0.97 (0.96) | 0.85 (0.95) | 0.90 (0.89) |
| Xception | 0.94 (0.92) | 0.96 (0.95) | 0.81 (0.93) | 0.88 (0.86) |
| Resnet-50 | 0.87 (0.78) | 0.92 (0.87) | 0.0 (0.6) | 0.76 (0.68) |
| InceptionV3 | 0.95 (0.94) | 0.97 (0.96) | 0.69 (0.95) | 0.9 (0.9) |
| Inception-ResnetV2 | 0.96 (0.93) | 0.98 (0.95) | 0.77 (0.95) | 0.92 (0.89) |
| VGG19 | 0.93 (0.90) | 0.96 (0.94) | 0.24 (0.86) | 0.88 (0.83) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buscombe, D.; Carini, R.J. A Data-Driven Approach to Classifying Wave Breaking in Infrared Imagery. Remote Sens. 2019, 11, 859. https://doi.org/10.3390/rs11070859
Buscombe D, Carini RJ. A Data-Driven Approach to Classifying Wave Breaking in Infrared Imagery. Remote Sensing. 2019; 11(7):859. https://doi.org/10.3390/rs11070859
Chicago/Turabian StyleBuscombe, Daniel, and Roxanne J. Carini. 2019. "A Data-Driven Approach to Classifying Wave Breaking in Infrared Imagery" Remote Sensing 11, no. 7: 859. https://doi.org/10.3390/rs11070859
APA StyleBuscombe, D., & Carini, R. J. (2019). A Data-Driven Approach to Classifying Wave Breaking in Infrared Imagery. Remote Sensing, 11(7), 859. https://doi.org/10.3390/rs11070859





