Classification of 3D Digital Heritage
Abstract
1. Introduction
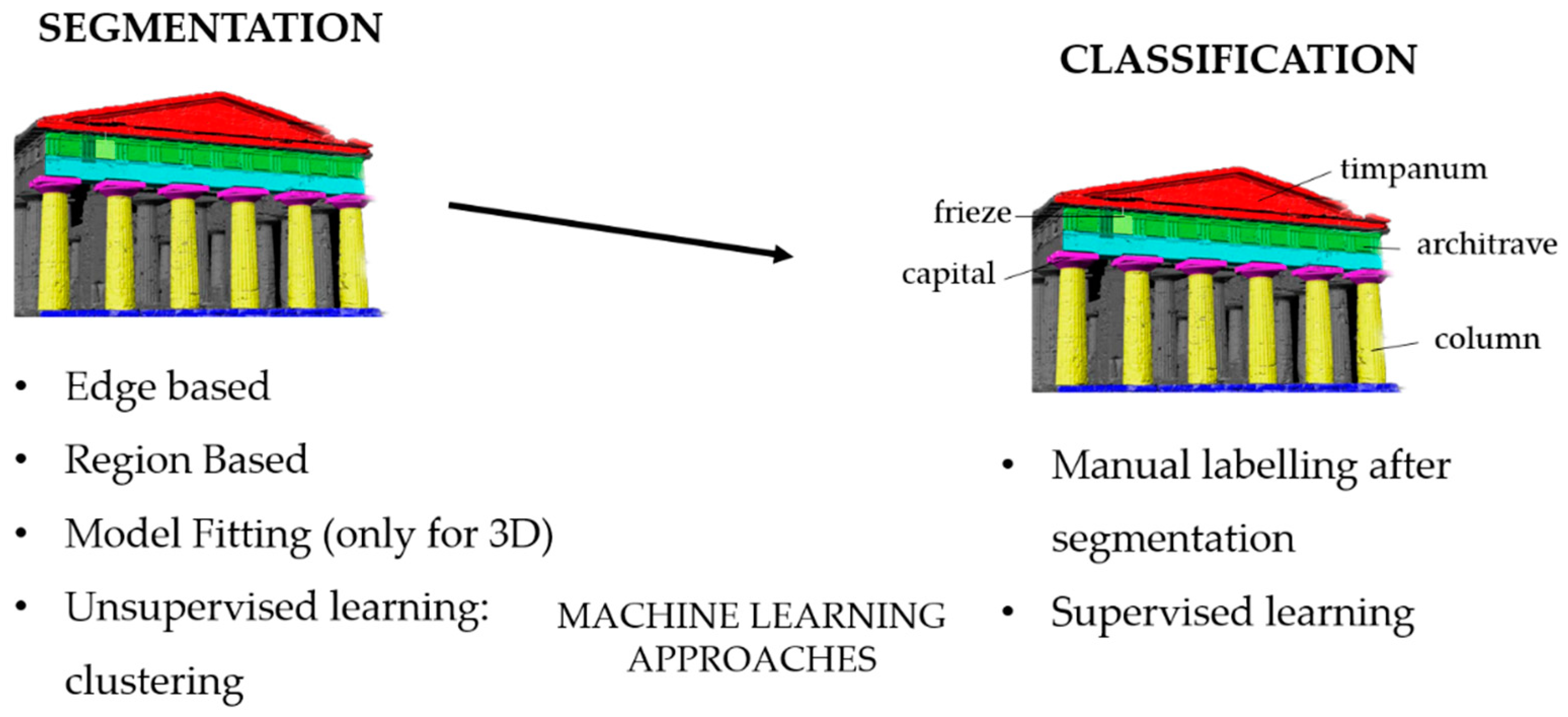
2. State of the Art: 2D/3D Segmentation and Classification Techniques
2.1. Segmentation Methods
2.2. Machine Learning for Data Segmentation and Classification
- A supervised approach is where semantic categories are learned from a dataset of annotated data and the trained model is used to provide a semantic classification of the entire dataset. If for the aforementioned methods the classification is a step after the segmentation, when using supervised machine learning methods, the class labeling procedure is planned before to segment the model. Random forest [62], described in detail at Section 4.2, is one of the most used supervised learning algorithms for classification problem [63,64].
- An unsupervised approach is where the data are automatically partitioned into segments based on a user-provided parameterization of the algorithm. No annotations are requested but the outcome might not be aligned with the user’s intention. Clustering is a type of unsupervised machine learning that aims to find homogeneous subgroups such that objects in the same group (clusters) are more similar to each other than those in other groups. K-Means is a clustering algorithm that divides observations into k clusters using features. Since we can dictate the number of clusters, it can be easily used in classification where we divide data into clusters that can be equal to or more than the number of classes. The original K-means algorithm presented by MacQueen et al. [65] has been then largely exploited for image and point clouds by various researchers [66,67,68,69,70].
- An interactive approach is where the user is actively involved in the segmentation/classification loop by guiding the extraction of segments via feedback signals. This requires a large effort from the user side but it could adapt and improve the segmentation result based on the user’s feedback.
3. Segmentation and Classification in Cultural Heritage
4. Project’s Methodology
- Create and optimize models, orthoimages (for 2.5D geometries) and UV maps (for 3D geometries) (Figure 6a–c).
- Segment the orthoimage or the UV map following different approaches tailored to the case study (clustering, random forest) (Figure 6d-e).
- Project the 2D classification results onto the 3D object space by back-projection and collinearity model (Figure 6f).
4.1. Image Preparation
- Planar objects (e.g. walls, Section 5.1): The object orthophoto is created and the procedure classifies and finally re-maps the information onto the 3D geometry.
- Regular objects (e.g. building or other 3D structures with certain level of complexity fit into this category, Section 5.2): Instead of creating various orthoimages from different points of view, unwrapped texture (UV maps) are generated and classified. To generate a good texture image to be classified, we followed these steps:
- Remeshing: Beneficial to improve the quality of the mesh and to simplify the next steps.
- Unwrapping: UV maps are generated using Blender, adjusting and optimizing seam lines and overlap (Figure 6c) to facilitate the subsequent analysis with machine learning strategies. This correction is made commanding the UV unwrapper to cut the mesh along edges chosen in accordance with the shape of the case study [90].
- Texture mapping: The created UV map is then textured (Figure 6d) using the original textured polygonal model (as vertex color or with external texture). This way the radiometric quality is not compromised despite the remeshing phase.
- Complex objects (e.g.; monuments or statue, Section 5.3): When objects are too complex for a good unwrap, the classification is done directly on the texture generates as output during the 3D modeling procedure.
4.2. Supervised Learning Classification
4.3. Unsupervised Learning Classification
4.4. Evaluation Method
5. Test Objects and Classification Results
- The Pecile’s wall of Villa Adriana in Tivoli: it is a 60 m L × 9 m H wall (Figure 7a) with holes on its top meant for the beams of a roof. The digital model of the wall was classified to identify the different categories of opus (roman building techniques), distinguishing original and restored parts.
- Part of a renaissance portico located in the city center of Bologna: It spans ca. 8 m L × 13 m H × 5 m D (Figure 7b). The classification aimed to identify principal parts and architectural elements;
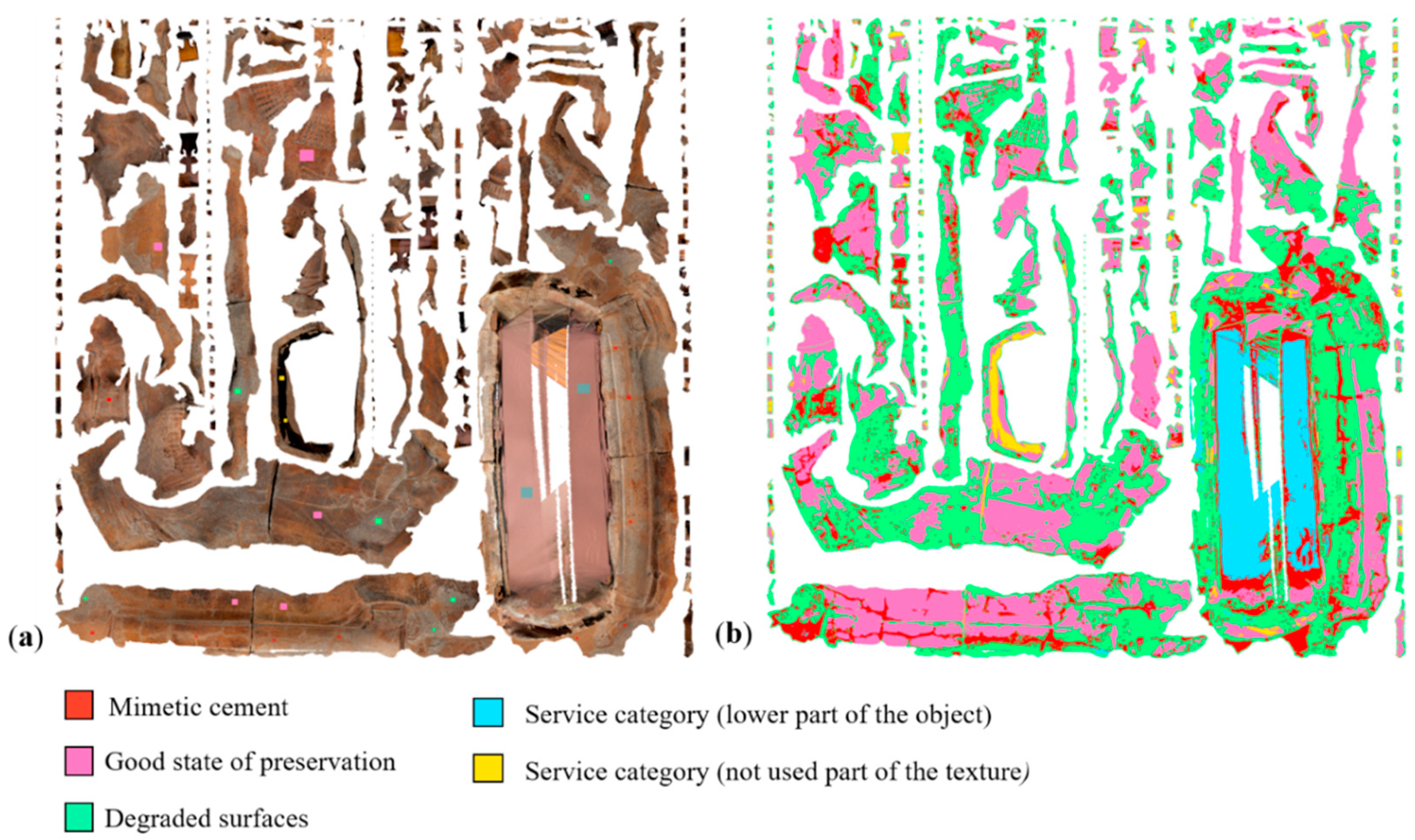
- The Sarcophagus of the Spouses (Figure 7c): It is a late 6th century BC Etruscan anthropoid sarcophagus, 1.14 m high by 1.9 m wide, made of terracotta, which was once brightly painted [97]. The classification aimed at identifying surface anomalies (such as fractures and decays) and quantifying the percentage of mimetic cement used to assemble the sarcophagus.
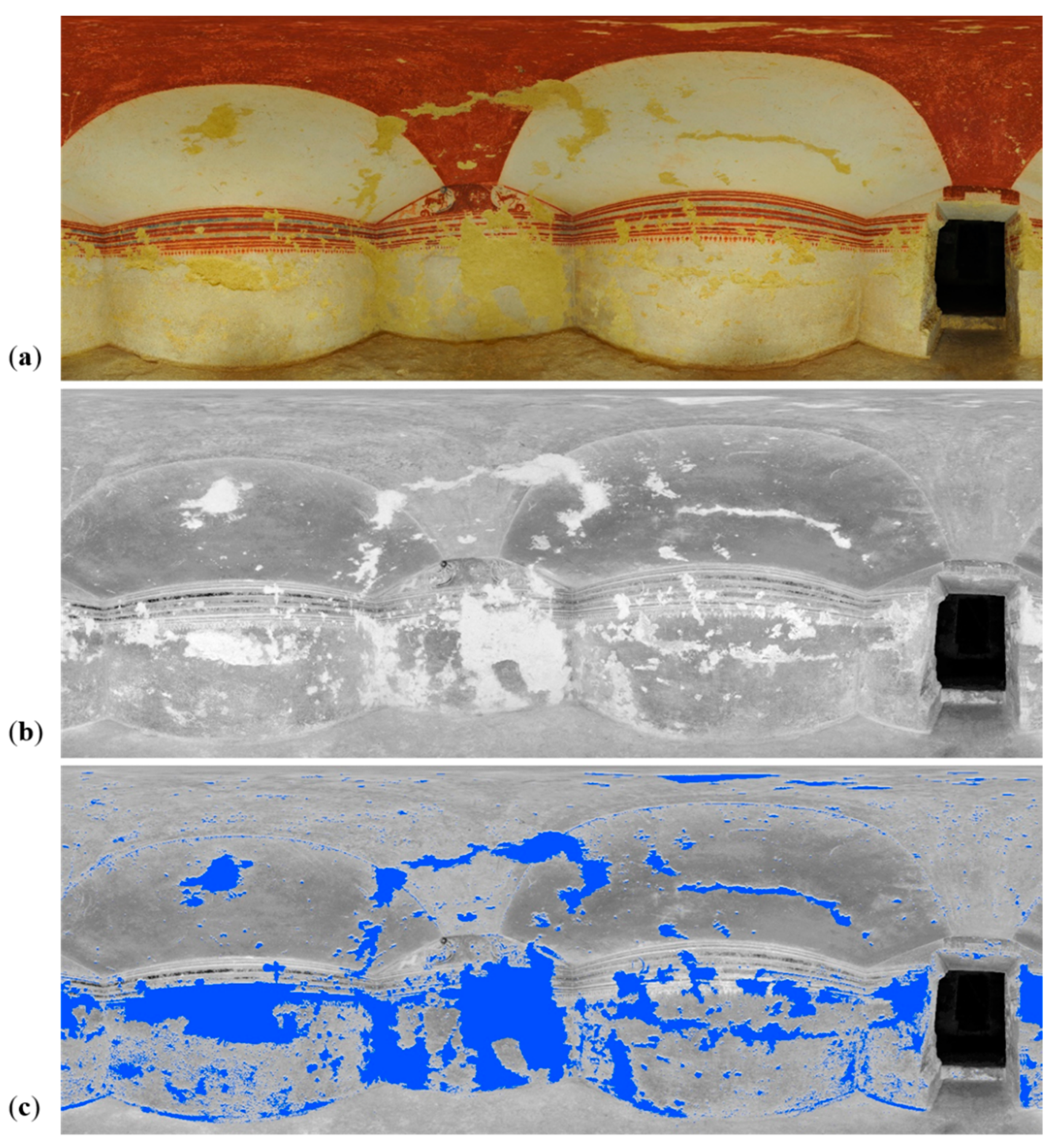
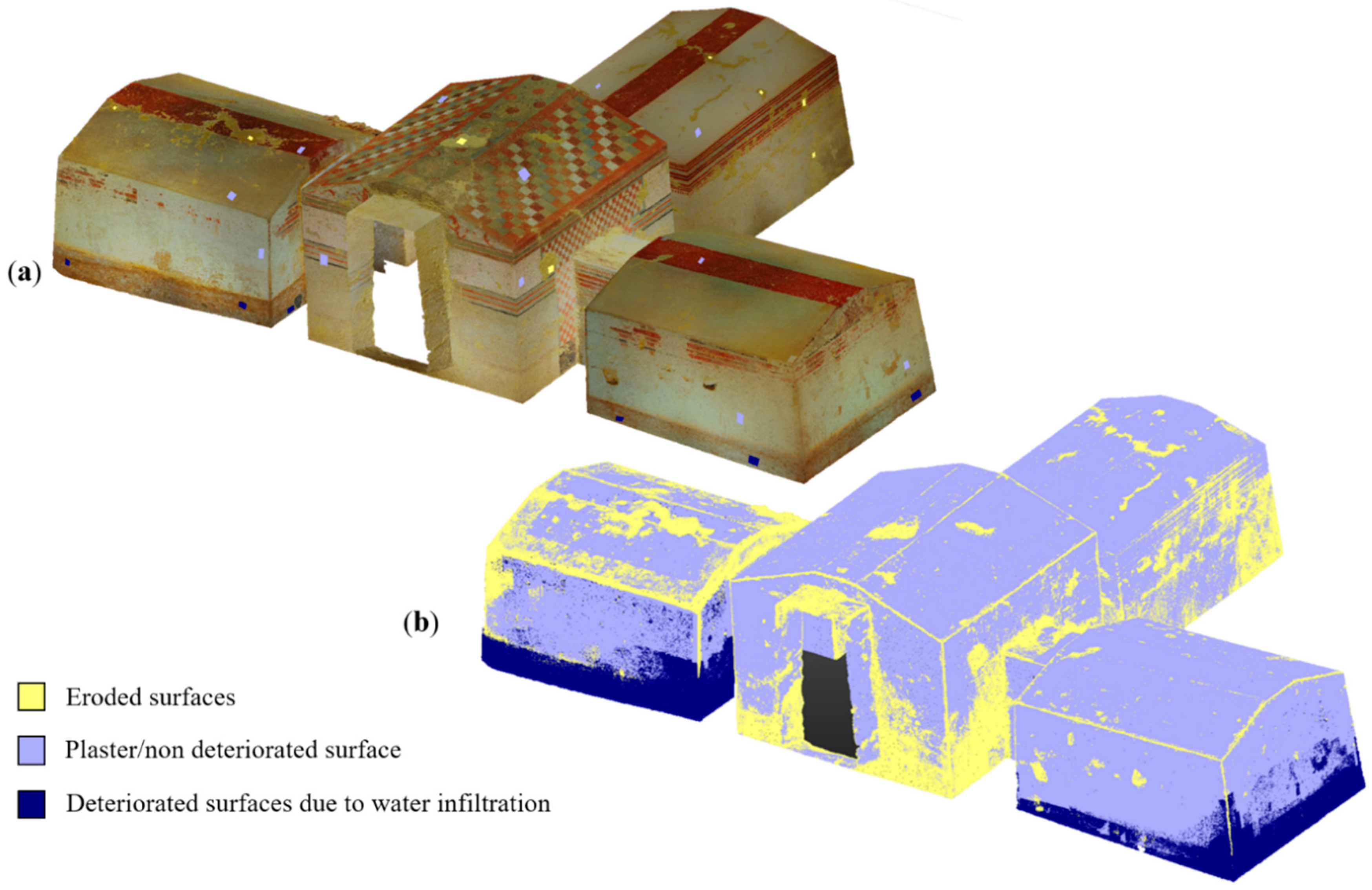
- The Bartoccini’s Tomb in Tarquinia (Figure 7d): the tomb, excavated in the hard sand in the 4th century, has four rooms—a central one (ca. 5 m × 4 m) and three later rooms (ca. 3 m × 3 m)—all connected through small corridors. The height of the tomb rooms does not exceed 3 m and it is all painted with a reddish color and various figures. The aim was to automatically identify the still painted areas on the wall and the deteriorated parts.
5.1. The Pecile’s Wall
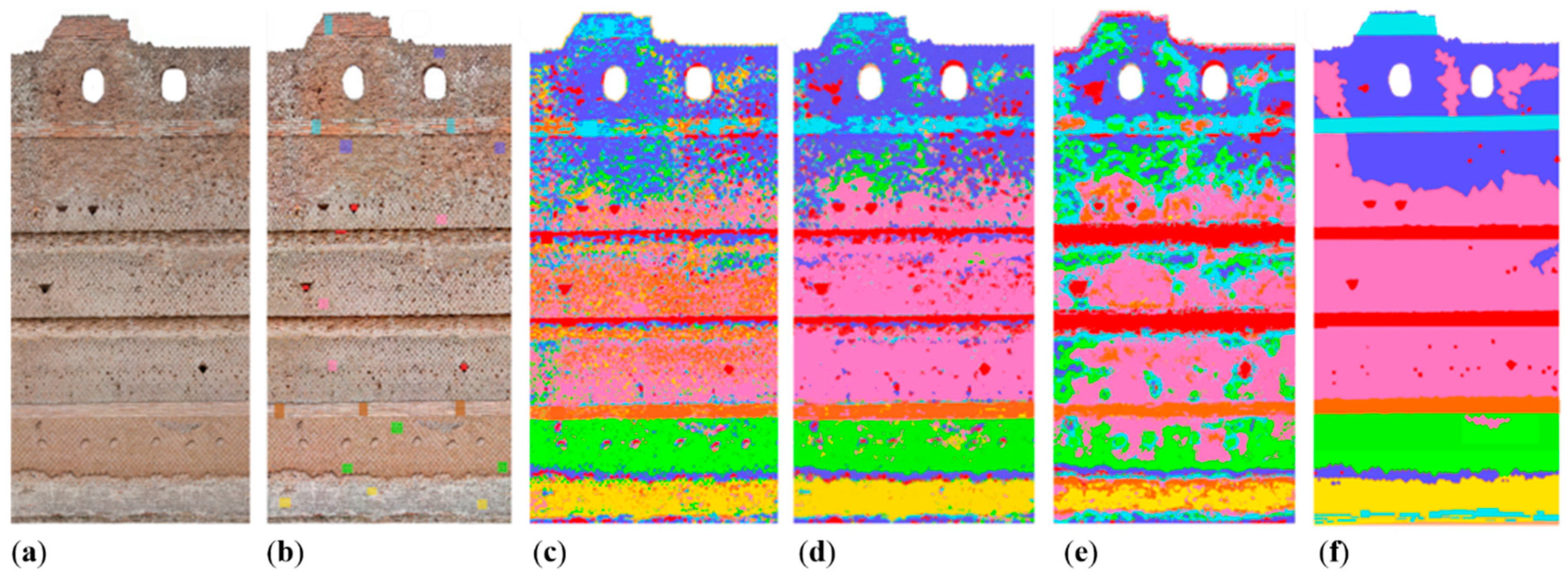
5.2. Bologna’s Porticoes
- different architectural elements;
- diverse materials (bricks vs. stones vs. marble); and
- categories of decay (cracks vs. humidity vs. swelling).
5.2.1. Classification of 2D Data
5.2.2 Classification of 3D Data
5.3 The Etruscan Sarcophagus of the Spouses
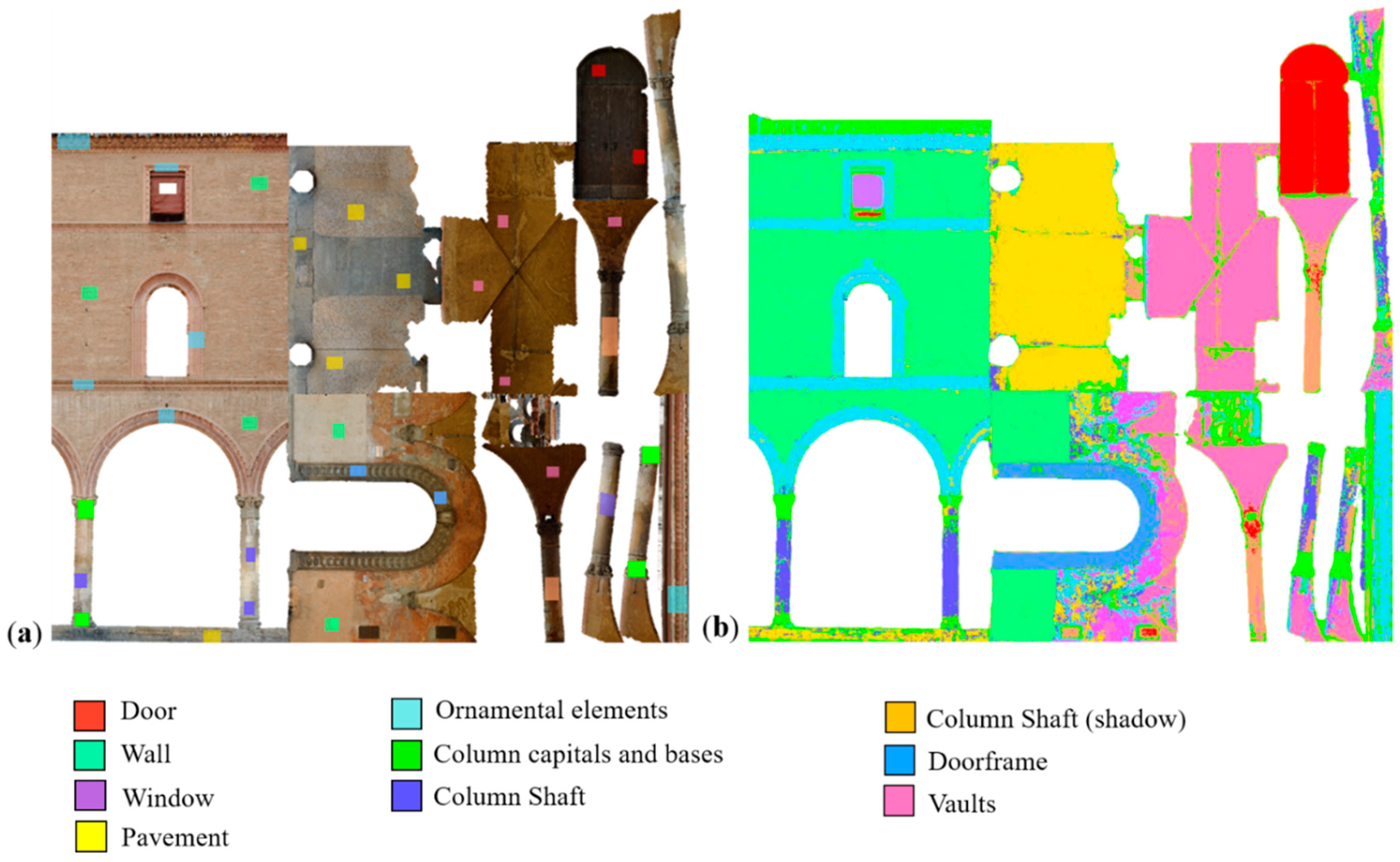
5.4. The Etruscan Bartoccini’s Tomb in Tarquinia, Italy
5.4.1. Classification of 2D Data
5.4.2. Classification of 3D data
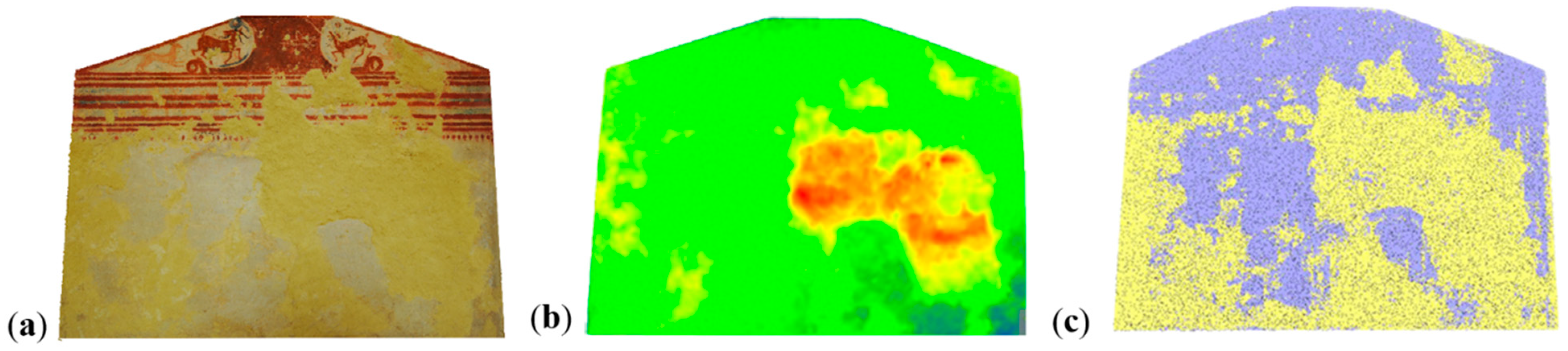
5.4.3. Quantification Analyses
6. Conclusions and Future Works
- shorter time to classify objects with respect to manual methods (Table 1);
- over-segmentation results useful for restoration purposes to detect small cracks or deteriorated parts;
- replicability of the training set for buildings of the same historical period or with similar construction material (e.g. roman walls);
- visualization of classification results onto 3D models from different points of view, using unwrapped textures;
- possibility to compute absolute and relative areas of each class (Table 3), useful for analysis and restoration purposes; and
- applicability of the pipeline to different kinds of heritage buildings, monuments or any other kind of 3D models.
- Difficult identification of the classes of analysis case by case (e.g. problems with the drainpipes classified as columns): the choice of the right classes during the training phase becomes fundamental.
- Misinterpretation of the shadows can introduce errors in the classification: the use of different color spaces from the classic RGB one, e.g. HSV and Lab, makes the lighting differences less problematic during the segmentation phase.
- Over-segmentation results in many classes, commonly useless in semantic analysis: this implies the need to make the regions more uniform in a post processing phase.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Saygi, G.; Remondino, F. Management of architectural heritage information in BIM and GIS: State-of-the-art and future perspectives. Int. J. Herit. Digit. Era 2013, 2, 695–713. [Google Scholar] [CrossRef]
- Hackel, T.; Wegner, J.D.; Schindler, K. Fast semantic segmentation of 3D point clouds with strongly varying density. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 3, 177–184. [Google Scholar] [CrossRef]
- Weinmann, M.; Weinmann, M. Geospatial Computer Vision Based on Multi-Modal Data—How Valuable Is Shape Information for the Extraction of Semantic Information? Remote Sens. 2017, 10, 2. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic graph CNN for learning on point clouds. arXiv, 2018; arXiv:1801.07829. [Google Scholar]
- Macher, H.; Landes, T.; Grussenmeyer, P. Point clouds segmentation as base for as-built BIM creation. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 2, 191. [Google Scholar] [CrossRef]
- Barsanti, S.G.; Guidi, G.; De Luca, L. Segmentation of 3D Models for Cultural Heritage Structural Analysis–Some Critical Issues. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 4, 115. [Google Scholar] [CrossRef]
- Maturana, D.; Scherer, S. Voxnet: A 3D convolutional neural network for real-time object recognition. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 922–928. [Google Scholar]
- Wang, L.; Zhang, Y.; Wang, J. Map-Based Localization Method for Autonomous Vehicles Using 3D-LIDAR. IFAC-PapersOnLine 2017, 50, 276–281. [Google Scholar]
- Xu, S.; Vosselman, G.; Oude Elberink, S. Multiple-entity based classification of airborne laser scanning data in urban areas. ISPRS J. Photogramm. Remote Sens. 2014, 88, 1–15. [Google Scholar] [CrossRef]
- Corso, J.; Roca, J.; Buill, F. Geometric analysis on stone façades with terrestrial laser scanner technology. Geosciences 2017, 7, 103. [Google Scholar] [CrossRef]
- Cheng, G.; Han, J. A survey on object detection in optical remote sensing images. ISPRS J. Photogramm. Remote Sens. 2016, 117, 11–28. [Google Scholar] [CrossRef]
- Shen, D.; Wu, G.; Suk, H.I. Deep learning in medical image analysis. Annu. Rev. Biomed. Eng. 2017, 19, 221–248. [Google Scholar] [CrossRef]
- Li, H.; Shen, C. Reading car license plates using deep convolutional neural networks and LSTMs. arXiv, 2016; arXiv:1601.05610. [Google Scholar]
- Li, C.; Shirahama, K.; Grzegorzek, M. Application of content-based image analysis to environmental microorganism classification. Biocybern. Biomed. Eng. 2015, 35, 10–21. [Google Scholar] [CrossRef]
- Dubey, S.R.; Dixit, P.; Singh, N.; Gupta, J.P. Infected fruit part detection using K-means clustering segmentation technique. Ijimai 2013, 2, 65–72. [Google Scholar] [CrossRef][Green Version]
- Llamas, J.; Lerones, P.M.; Medina, R.; Zalama, E.; Gómez-García-Bermejo, J. Classification of architectural heritage images using deep learning techniques. Appl. Sci. 2017, 7, 992. [Google Scholar] [CrossRef]
- Grilli, E.; Menna, F.; Remondino, F. A review of point clouds segmentation and classification algorithms. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 339–344. [Google Scholar] [CrossRef]
- Weinmann, M. Reconstruction and Analysis of 3D Scenes: From Irregularly Distributed 3D Points to Object Classes; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Stathopoulou, E.K.; Remondino, F. Semantic photogrammetry: boosting image-based 3D reconstruction with semantic labeling. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 422, 685–690. [Google Scholar] [CrossRef]
- Yuheng, S.; Hao, Y. Image Segmentation Algorithms Overview. arXiv, 2017; arXiv:1707.02051. [Google Scholar]
- Al-Amri, S.S.; Kalyankar, N.V.; Khamitkar, S.D. Image segmentation by using edge detection. Int. J. Comput. Sci. Eng. 2010, 2, 804–807. [Google Scholar]
- Kaur, J.; Agrawal, S.; Vig, R. A comparative analysis of thresholding and edge detection segmentation techniques. Int. J. Comput. Appl. 2012, 39, 29–34. [Google Scholar] [CrossRef]
- Schoenemann, T.; Kahl, F.; Cremers, D. Curvature regularity for region-based image segmentation and inpainting: A linear programming relaxation. In Proceedings of the International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 17–23. [Google Scholar]
- Chitade, A.Z.; Katiyar, S.K. Colour based image segmentation using k-means clustering. Int. J. Eng. Sci. Technol. 2010, 2, 5319–5325. [Google Scholar]
- Saraswathi, S.; Allirani, A. Survey on image segmentation via clustering. In Proceedings of the 2013 International Conference on Information Communication and Embedded Systems (ICICES), Chennai, India, 21–22 February 2013; pp. 331–335. [Google Scholar]
- Fiorillo, F.; Fernández-Palacios, B.J.; Remondino, F.; Barba, S. 3D Surveying and modelling of the Archaeological Area of Paestum, Italy. Virtual Archaeol. Rev. 2013, 4, 55–60. [Google Scholar] [CrossRef]
- Naik, D.; Shah, P. A review on image segmentation clustering algorithms. Int. J. Comput. Sci. Inf. Technol. 2014, 5, 3289–3293. [Google Scholar]
- Rabbani, T.; Van Den Heuvel, F.; Vosselmann, G. Segmentation of point clouds using smoothness constraint. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2006, 36, 248–253. [Google Scholar]
- Bhanu, B.; Lee, S.; Ho, C.C.; Henderson, T. Range data processing: Representation of surfaces by edges. In Proceedings of the 8th International Conference on Pattern Recognition, Paris, France, 27–31 October 1986; pp. 236–238. [Google Scholar]
- Sappa, A.D.; Devy, M. Fast range image segmentation by an edge detection strategy. In Proceedings of the IEEE 3rd 3D Digital Imaging and Modeling, Quebec City, QC, Canada, 28 May–1 June 2001; pp. 292–299. [Google Scholar]
- Wani, M.A.; Arabnia, H.R. Parallel edge-region-based segmentation algorithm targeted at reconfigurable multiring network. J. Supercomput. 2003, 25, 43–62. [Google Scholar] [CrossRef]
- Castillo, E.; Liang, J.; Zhao, H. Point cloud segmentation and denoising via constrained nonlinear least squares normal estimates. In Innovations for Shape Analysis; Springer: Berlin/Heidelberg, Germany, 2013; pp. 283–299. [Google Scholar]
- Jagannathan, A.; Miller, E.L. Three-dimensional surface mesh segmentation using curvedness-based region growing approach. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 2195–2204. [Google Scholar] [CrossRef]
- Besl, P.J.; Jain, R.C. Segmentation through variable order surface fitting. IEEE Trans. Pattern Anal. Mach. Intell. 1988, 10, 167–192. [Google Scholar] [CrossRef]
- Vosselman, M.G.; Gorte, B.G.H.; Sithole, G.; Rabbani, T. Recognising structure in laser scanning point clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 46, 33–38. [Google Scholar]
- Belton, D.; Lichti, D.D. Classification and segmentation of terrestrial laser scanner point clouds using local variance information. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2006, 36, 44–49. [Google Scholar]
- Klasing, K.; Althoff, D.; Wollherr, D.; Buss, M. Comparison of surface normal estimation methods for range sensing applications. In Proceedings of the IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3206–3211. [Google Scholar]
- Xiao, J.; Zhang, J.; Adler, B.; Zhang, H.; Zhang, J. Three-dimensional point cloud plane segmentation in both structured and unstructured environments. Robot. Auton. Syst. 2013, 61, 1641–1652. [Google Scholar] [CrossRef]
- Vo, A.V.; Truong-Hong, L.; Laefer, D.F.; Bertolotto, M. Octree-based region growing for point cloud segmentation. ISPRS J. Photogramm. Remote Sens. 2015, 104, 88–100. [Google Scholar] [CrossRef]
- Liu, Y.; Xiong, Y. Automatic segmentation of unorga-nized noisy point clouds based on the gaussian map. Comput. Aided Des. 2008, 40, 576–594. [Google Scholar] [CrossRef]
- Vieira, M.; Shimada, K. Surface mesh segmentation and smooth surface extraction through region growing. Comput. Aided Geom. Des. 2005, 22, 771–792. [Google Scholar] [CrossRef]
- Ballard, D.H. Generalizing the Hough transform to detect arbitrary shapes. Pattern Recognit. 1991, 13, 183–194. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Poux, F.; Hallot, P.; Neuville, R.; Billen, R. Smart point cloud: Definition and remaining challenge. In Proceedings of the 11th 3D Geoinfo Conference, Athens, Greece, 20–21 October 2016. [Google Scholar]
- Barnea, S.; Filin, S. Segmentation of terrestrial laser scanning data using geometry and image information. ISPRS J. Photogramm. Remote Sens. 2013, 76, 33–48. [Google Scholar] [CrossRef]
- 2D Semantic labelling. Available online: http://www2.isprs.org/commissions/comm3/wg4/semantic-labeling.html (accessed on 28 March 2019).
- Deepglobe. Available online: http://deepglobe.org/challenge.html (accessed on 28 March 2019).
- Mapping challenge. Available online: https://www.crowdai.org/challenges/mapping-challenge (accessed on 28 March 2019).
- Large-Scale Semantic 3D Reconstruction. Available online: https://www.grss-ieee.org/community/technical-committees/data-fusion/data-fusion-contest/ (accessed on 28 March 2019).
- Large-Scale Point Cloud Classification Benchmark. Available online: http://www.semantic3d.net/ (accessed on 28 March 2019).
- KITTI Vision Benchmark Suite. Available online: http://www.cvlibs.net/datasets/kitti/ (accessed on 28 March 2019).
- Semantic, instance-wise, dense pixel annotations of 30 classes. Available online: https://www.cityscapes-dataset.com/ (accessed on 28 March 2019).
- Noh, H.; Hong, S.; Han, B. Learning deconvolution network for semantic segmentation. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1520–1528. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Garcia-Garcia, A.; Orts-Escolano, S.; Oprea, S.; Villena-Martinez, V.; Garcia-Rodriguez, J. A review on deep learning techniques applied to semantic segmentation. arXiv, 2017; arXiv:1704.06857. [Google Scholar]
- Perez, L.; Wang, J. The effectiveness of data augmentation in image classification using deep learning. arXiv, 2017; arXiv:1712.04621. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 834–848. [Google Scholar] [CrossRef]
- Guo, B.; Huang, X.; Zhang, F.; Sohn, G. Classification of airborne laser scanning data using JointBoost. ISPRS J. Photogramm. Remote Sens. 2014, 92, 124–136. [Google Scholar] [CrossRef]
- Niemeyer, J.; Rottensteiner, F.; Soergel, U. Contextual classification of LiDAR data and building object detection in urban areas. ISPRS J. Photogramm. Remote Sens. 2014, 87, 152–165. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3D classification and segmentation. In Proceedings of the Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; Volume 1, p. 4. [Google Scholar]
- Weinmann, M.; Schmidt, A.; Mallet, C.; Hinz, S.; Rottensteiner, F.; Jutzi, B. Contextual classification of point cloud data by exploiting individual 3D neighbourhoods. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 2, 271–278. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Bassier, M.; Van Genechten, B.; Vergauwen, M. Classification of sensor independent point cloud data of building objects using random forests. J. Build. Eng. 2019, 21, 468–477. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, June 1967. [Google Scholar]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Burney, S.A.; Tariq, H. K-means cluster analysis for image segmentation. Int. J. Comput. Appl. 2014, 96. [Google Scholar] [CrossRef]
- Dhanachandra, N.; Manglem, K.; Chanu, Y.J. Image segmentation using K-means clustering algorithm and subtractive clustering algorithm. Procedia Comput. Sci. 2015, 54, 764–771. [Google Scholar] [CrossRef]
- Zhang, C.; Mao, B. 3D Building Models Segmentation Based on K-means++ Cluster Analysis. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 42. [Google Scholar] [CrossRef]
- Hétroy-Wheeler, F.; Casella, E.; Boltcheva, D. Segmentation of tree seedling point clouds into elementary units. Int. J. Remote Sens. 2016, 37, 2881–2907. [Google Scholar] [CrossRef]
- Guo, Y.; Bennamoun, M.; Sohel, F.; Lu, M.; Wan, J.; Kwok, N.M. A comprehensive performance evaluation of 3D local feature descriptors. Int. J. Comput. Vis. 2016, 116, 66–89. [Google Scholar] [CrossRef]
- Georganos, S.; Grippa, T.; Vanhuysse, S.; Lennert, M.; Shimoni, M.; Kalogirou, S.; Wolff, E. Less is more: Optimizing classification performance through feature selection in a very-high-resolution remote sensing object-based urban application. GISci. Remote Sens. 2018, 55, 221–242. [Google Scholar] [CrossRef]
- Weinmann, M.; Jutzi, B.; Mallet, C. Feature relevance assessment for the semantic interpretation of 3D point cloud data. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 5, W2. [Google Scholar] [CrossRef]
- Aijazi, A.K.; Serna, A.; Marcotegui, B.; Checchin, P.; Trassoudaine, L. Segmentation and Classification of 3D Urban Point Clouds: Comparison and Combination of Two Approaches. In Field and Service Robotics; Springer: Cham, Switzerland, 2016; pp. 201–216. [Google Scholar]
- Mathias, M.; Martinovic, A.; Weissenberg, J.; Haegler, S.; Van Gool, L. Automatic architectural style recognition. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2011, 3816, 171–176. [Google Scholar] [CrossRef]
- Oses, N.; Dornaika, F.; Moujahid, A. Image-based delineation and classification of built heritage masonry. Remote Sens. 2014, 6, 1863–1889. [Google Scholar] [CrossRef]
- Shalunts, G.; Haxhimusa, Y.; Sablatnig, R. Architectural style classification of building facade windows. In Proceedings of the International Symposium on Visual Computing, Las Vegas, NV, USA, 26–28 September 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 280–289. [Google Scholar]
- Zhang, L.; Song, M.; Liu, X.; Sun, L.; Chen, C.; Bu, J. Recognizing architecture styles by hierarchical sparse coding of blocklets. Inf. Sci. 2014, 254, 141–154. [Google Scholar] [CrossRef]
- Chu, W.T.; Tsai, M.H. Visual pattern discovery for architecture image classification and product image search. In Proceedings of the 2nd ACM International Conference on Multimedia Retrieval, Hong Kong, China, 5–8 June 2012; p. 27. [Google Scholar]
- Llamas, J.; Lerones, P.M.; Zalama, E.; Gómez-García-Bermejo, J. Applying deep learning techniques to cultural heritage images within the INCEPTION project. In Proceedings of the Euro-Mediterranean Conference, Nicosia, Cyprus, 31 October–5 November 2016; Springer: Cham, Switzerland, 2016; pp. 25–32. [Google Scholar]
- Manferdini, A.M.; Remondino, F.; Baldissini, S.; Gaiani, M.; Benedetti, B. 3D modeling and semantic classification of archaeological finds for management and visualization in 3D archaeological databases. In Proceedings of the International Conference on Virtual Systems and MultiMedia (VSMM), Limassol, Cyprus, 20–25 October 2008; pp. 221–228. [Google Scholar]
- Poux, F.; Neuville, R.; Hallot, P.; Billen, R. Point cloud classification of tesserae from terrestrial laser data combined with dense image matching for archaeological information extraction. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 4, 203–211. [Google Scholar] [CrossRef]
- De Luca, L.; Buglio, D.L. Geometry vs. Semantics: Open issues on 3D reconstruction of architectural elements. In 3D Research Challenges in Cultural Heritage; Springer: Berlin/Heidelberg, Germany, 2014; pp. 36–49. [Google Scholar]
- Stefani, C.; Busayarat, C.; Lombardo, J.; Luca, L.D.; Véron, P. A web platform for the consultation of spatialized and semantically enriched iconographic sources on cultural heritage buildings. J. Comput. Cult. Herit. 2013, 6, 13. [Google Scholar] [CrossRef]
- Apollonio, F.I.; Basilissi, V.; Callieri, M.; Dellepiane, M.; Gaiani, M.; Ponchio, F.; Rizzo, F.; Rubino, A.R.; Scopigno, R. A 3D-centered information system for the documentation of a complex restoration intervention. J. Cult. Herit. 2018, 29, 89–99. [Google Scholar] [CrossRef]
- Campanaro, D.M.; Landeschi, G.; Dell’Unto, N.; Touati, A.M.L. 3D GIS for cultural heritage restoration: A ‘white box’workflow. J. Cult. Herit. 2016, 18, 321–332. [Google Scholar] [CrossRef]
- Sithole, G. Detection of bricks in a masonry wall. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, XXXVII, 1–6. [Google Scholar]
- Riveiro, B.; Lourenço, P.B.; Oliveira, D.V.; González-Jorge, H.; Arias, P. Automatic Morphologic Analysis of Quasi-Periodic Masonry Walls from LiDAR. Comput.-Aided Civ. Infrastruct. Eng. 2016, 31, 305–319. [Google Scholar] [CrossRef]
- Messaoudi, T.; Véron, P.; Halin, G.; De Luca, L. An ontological model for the reality-based 3D annotation of heritage building conservation state. J. Cult. Herit. 2018, 29, 100–112. [Google Scholar] [CrossRef]
- Cipriani, L.; Fantini, F. Digitalization culture vs. archaeological visualization: Integration of pipelines and open issues. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 195. [Google Scholar] [CrossRef]
- Bora, D.J.; Gupta, A.K. A new approach towards clustering based color image segmentation. Int. J. Comput. Appl. 2014, 107, 23–30. [Google Scholar]
- Jurio, A.; Pagola, M.; Galar, M.; Lopez-Molina, C.; Paternain, D. A comparison study of different color spaces in clustering based image segmentation. In Proceedings of the International Conference on Information Processing and Management of Uncertainty in Knowledge-Based Systems, Dortmund, Germany, 28 June–2 July 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 532–541. [Google Scholar]
- Sural, S.; Qian, G.; Pramanik, S. Segmentation and histogram generation using the HSV color space for image retrieval. In Proceedings of the 2002 International Conference on Image Processing, Rochester, NY, USA, 22–25 September 2002; Volume 2, p. II. [Google Scholar]
- Witten, I.H.; Frank, E.; Hall, M.A.; Pal, C.J. Data Mining: Practical Machine Learning Tools and Techniques; Morgan Kaufmann: Burlington, MA, USA, 2016. [Google Scholar]
- Image processing package Imagej. Available online: http://imagej.net/Fiji (accessed on 25 March 2019).
- Imagej K-means plugin. Available online: http://ij-plugins.sourceforge.net/plugins/segmentation/k-means.html (accessed on 25 March 2019).
- Kleiner, F.S. A History of Roman Art; Cengage Learning: Boston, MA, USA, 2016. [Google Scholar]
- Remondino, F.; Gaiani, M.; Apollonio, F.; Ballabeni, A.; Ballabeni, M.; Morabito, D. 3D documentation of 40 kilometers of historical porticoes-the challenge. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41. [Google Scholar] [CrossRef]
- Giraudot, S.; Lafarge, F. Classification. In CGAL User and Reference Manual, 4.14 ed; CGAL Editorial Board, 2019. [Google Scholar]
- ETHZ Random Forest code. Available online: www.prs.igp.ethz.ch/research/Source_code_and_datasets.html (accessed on 25 March 2019).
- Menna, F.; Nocerino, E.; Remondino, F.; Dellepiane, M.; Callieri, M.; Scopigno, R. 3D digitization of an heritage masterpiece-a critical analysis on quality assessment. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41. [Google Scholar] [CrossRef]
- Jiménez Fernández-Palacios, B.; Rizzi, A.; Remondino, F. Etruscans in 3D—Surveying and 3D modeling for a better access and understanding of heritage. Virtual Archaeol. Rev. 2013, 4, 85–89. [Google Scholar] [CrossRef]












| Classifier | Overall Accuracy | Time |
|---|---|---|
| j48 | 0.44 | 22 s |
| Random Tree | 0.46 | 15 s |
| RepTREE | 0.47 | 33 s |
| LogitBoost | 0.52 | 20 s |
| Random Forest | 0.57 | 23 s |
| Fast Random Forest | 0.70 | 120 s |
 | Precision | Recall | F1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TRUE LABEL | Undercut/holes |  | 0.64 | 0.01 | 0 | 0.07 | 0.08 | 0.02 | 0.13 | 0.56 | 0.67 | 0.6 |
| Restored Opus latericium | 0.2 | 0.73 | 0.02 | 0.02 | 0.18 | 0.01 | 0 | 0.85 | 0.63 | 0.72 | ||
| Plaster wall | 0.02 | 0.03 | 0.75 | 0.04 | 0.12 | 0.02 | 0.03 | 0.91 | 0.74 | 0.82 | ||
| Old Opus latericium | 0.08 | 0.02 | 0.01 | 0.43 | 0.2 | 0.05 | 0.21 | 0.56 | 0.43 | 0.49 | ||
| Opus reticulatum grey | 0.06 | 0.05 | 0.01 | 0.08 | 0.66 | 0.05 | 0.08 | 0.47 | 0.67 | 0.55 | ||
| Restored Opus reticulatum | 0.02 | 0.01 | 0.01 | 0.01 | 0.07 | 0.83 | 0.06 | 0.77 | 0.82 | 0.8 | ||
| Old Opus reticulatum | 0.15 | 0.01 | 0.02 | 0.12 | 0.08 | 0.09 | 0.52 | 0.5 | 0.52 | 0.51 | ||
| PREDICTED LABEL | ||||||||||||
| Classifier | % Eroded Surfaces | Area/Volume | Time for Elaborations | |
|---|---|---|---|---|
| 2D Manual classification |  | 58% | 2,8 m2 | 30 min |
| 2D Unsupervised clustering |  | 49% | 2,4 m2 | 5 min |
| 3D Supervised segmentation |  | 56% | 2,7 m2 | 10 min |
| Depth map |  | 40% | 1,96 m2 / 0,1m3 | 10 min |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grilli, E.; Remondino, F. Classification of 3D Digital Heritage. Remote Sens. 2019, 11, 847. https://doi.org/10.3390/rs11070847
Grilli E, Remondino F. Classification of 3D Digital Heritage. Remote Sensing. 2019; 11(7):847. https://doi.org/10.3390/rs11070847
Chicago/Turabian StyleGrilli, Eleonora, and Fabio Remondino. 2019. "Classification of 3D Digital Heritage" Remote Sensing 11, no. 7: 847. https://doi.org/10.3390/rs11070847
APA StyleGrilli, E., & Remondino, F. (2019). Classification of 3D Digital Heritage. Remote Sensing, 11(7), 847. https://doi.org/10.3390/rs11070847







