Time Series High-Resolution Land Surface Albedo Estimation Based on the Ensemble Kalman Filter Algorithm
Abstract
:1. Introduction
2. Study Areas and Data
2.1. Study Areas
2.2. Ground Verification Data
2.3. Landsat Satellite Data
2.4. MCD43A3 BRDF/Albedo Product
3. Methods
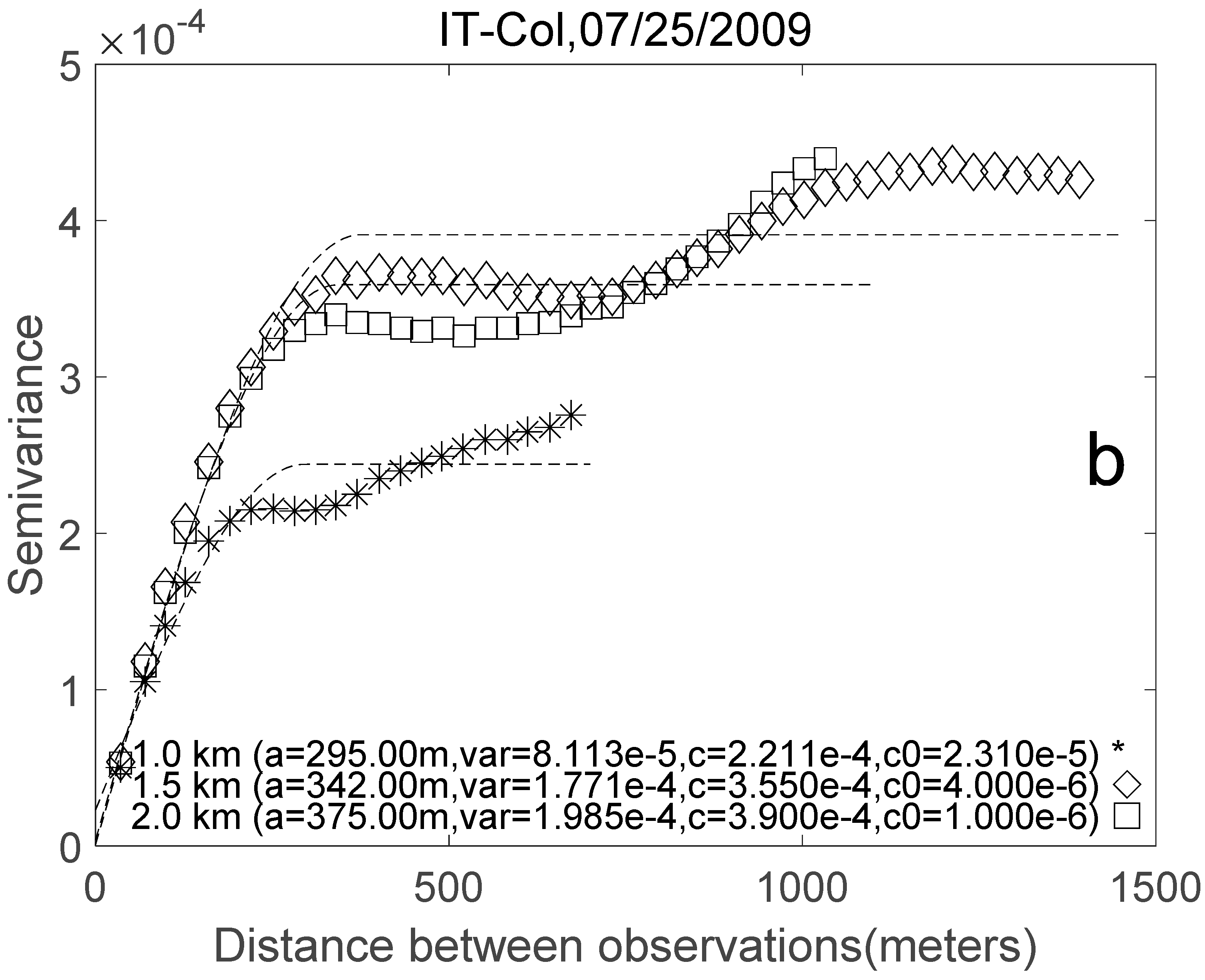
3.1. Validation Site Land Surface Heterogeneity
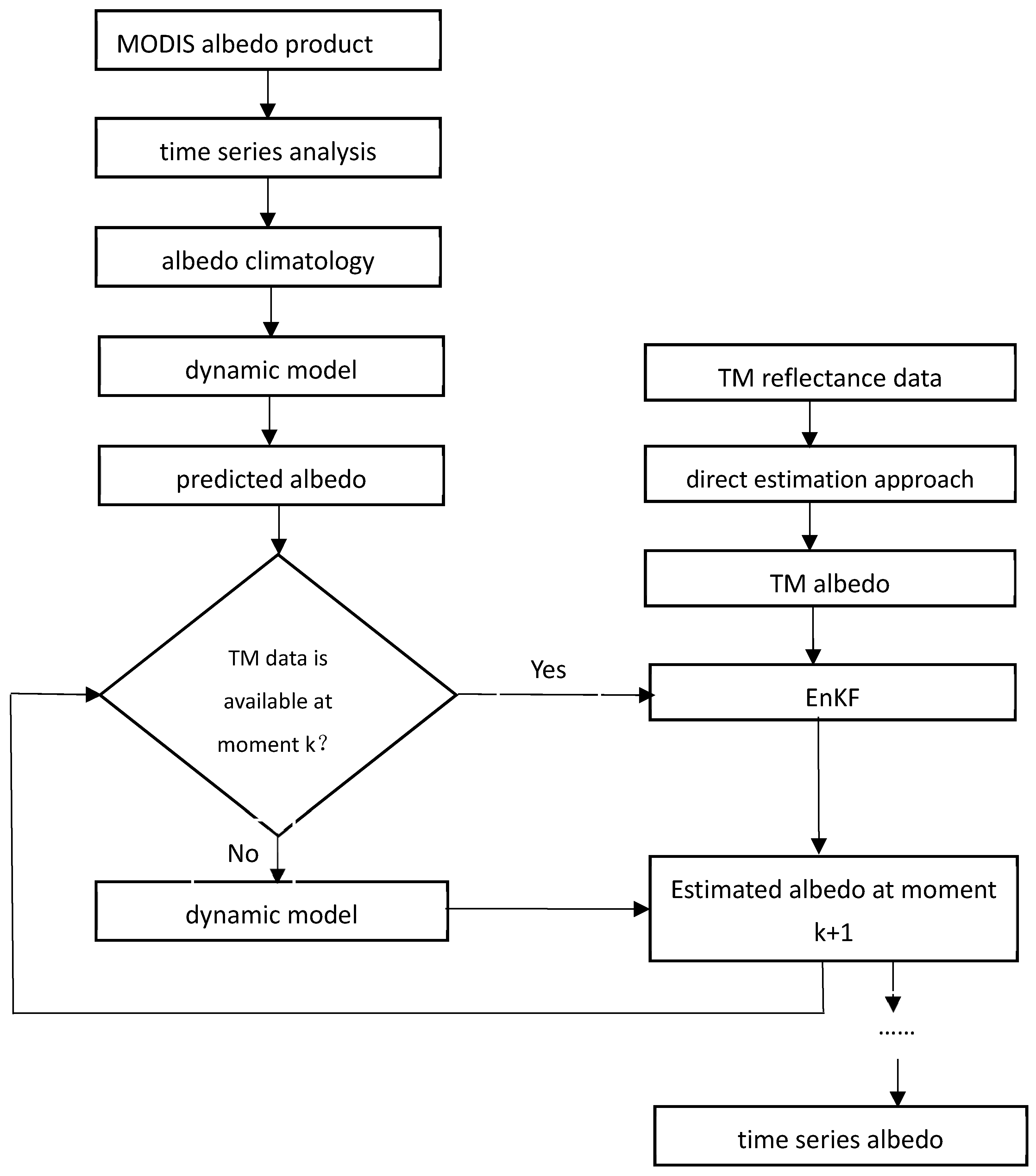
3.2. Albedo Dynamic Model Construction
3.3. High-Resolution Albedo Estimation
3.4. Ensemble Kalman Filter
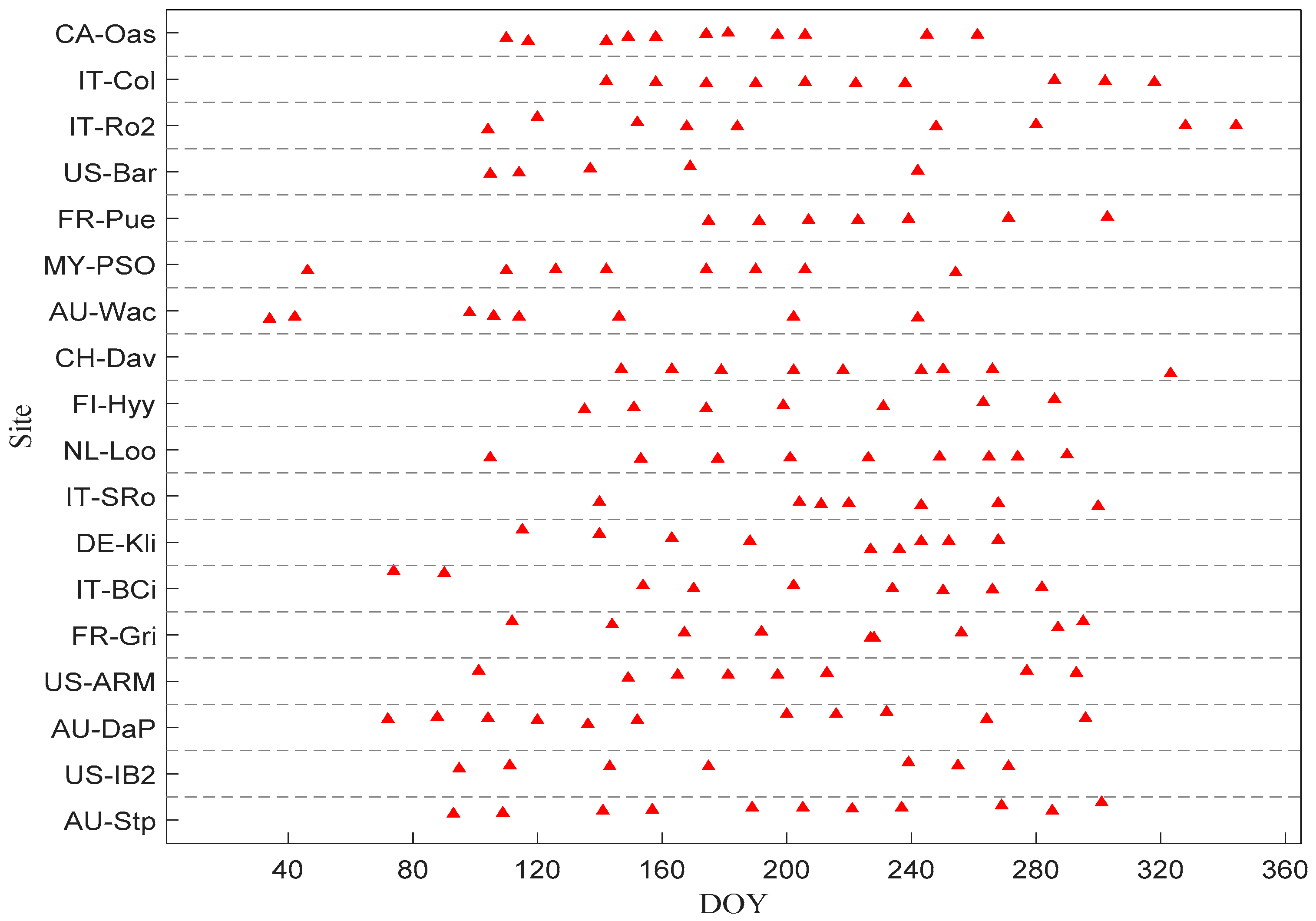
3.5. Validation
4. Results
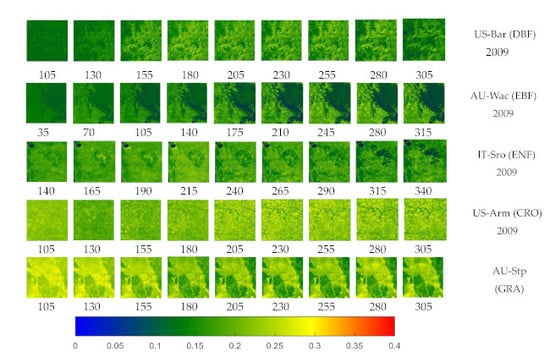
4.1. Land Surface Heterogeneity at FluxNet Sites
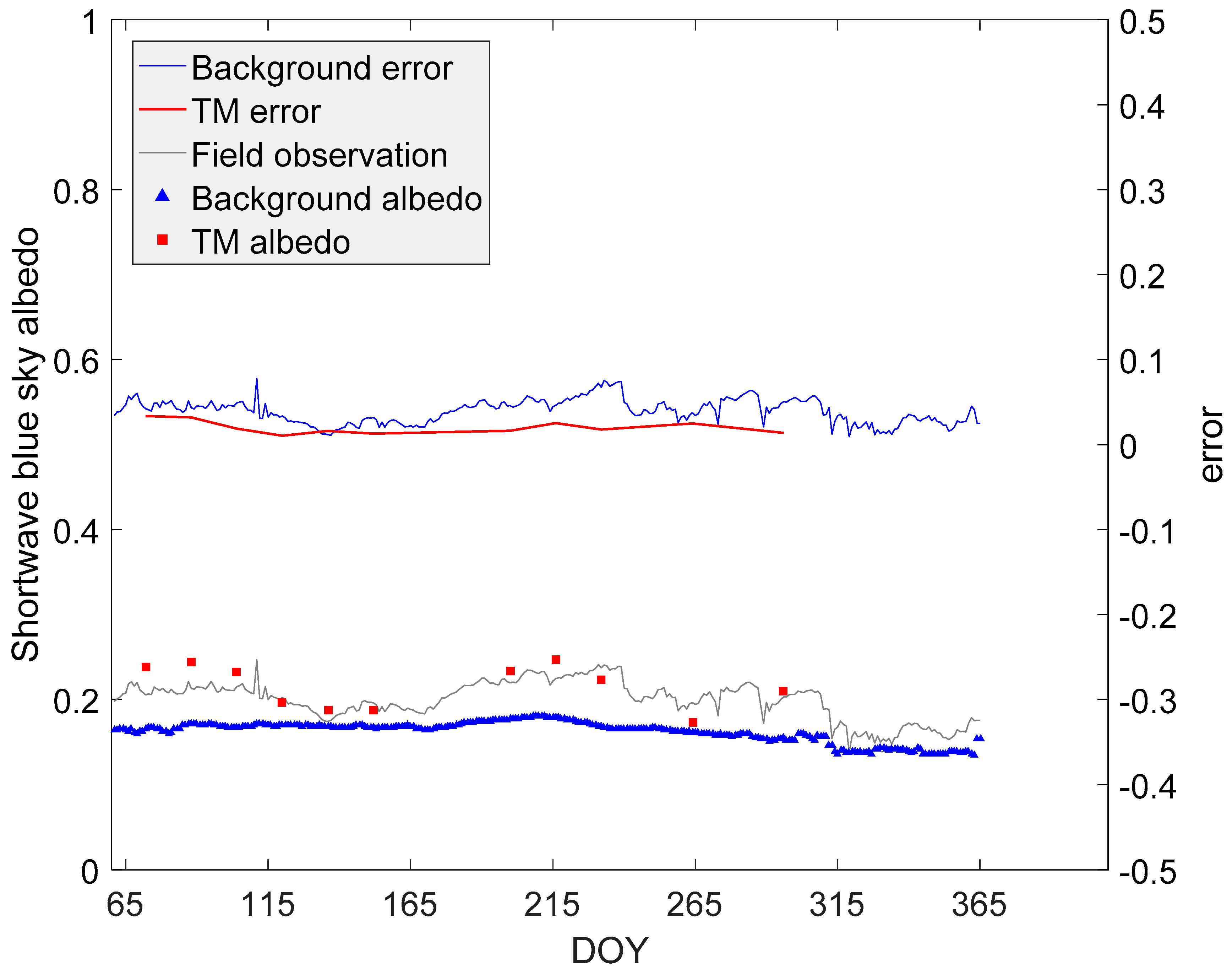
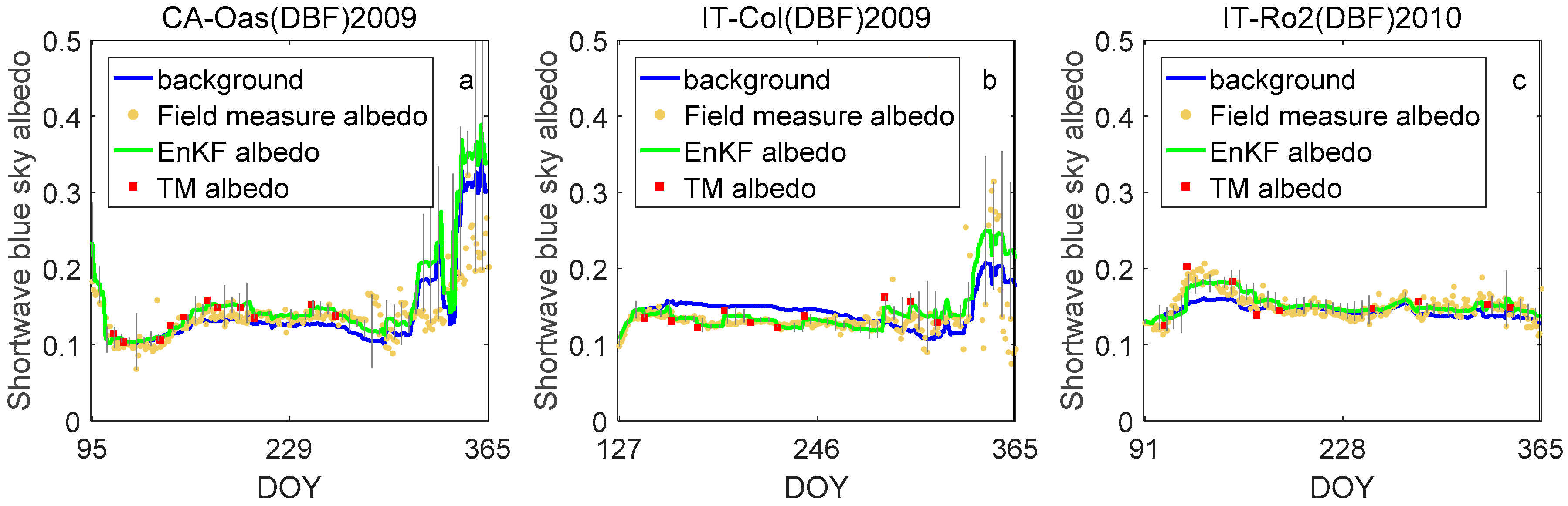
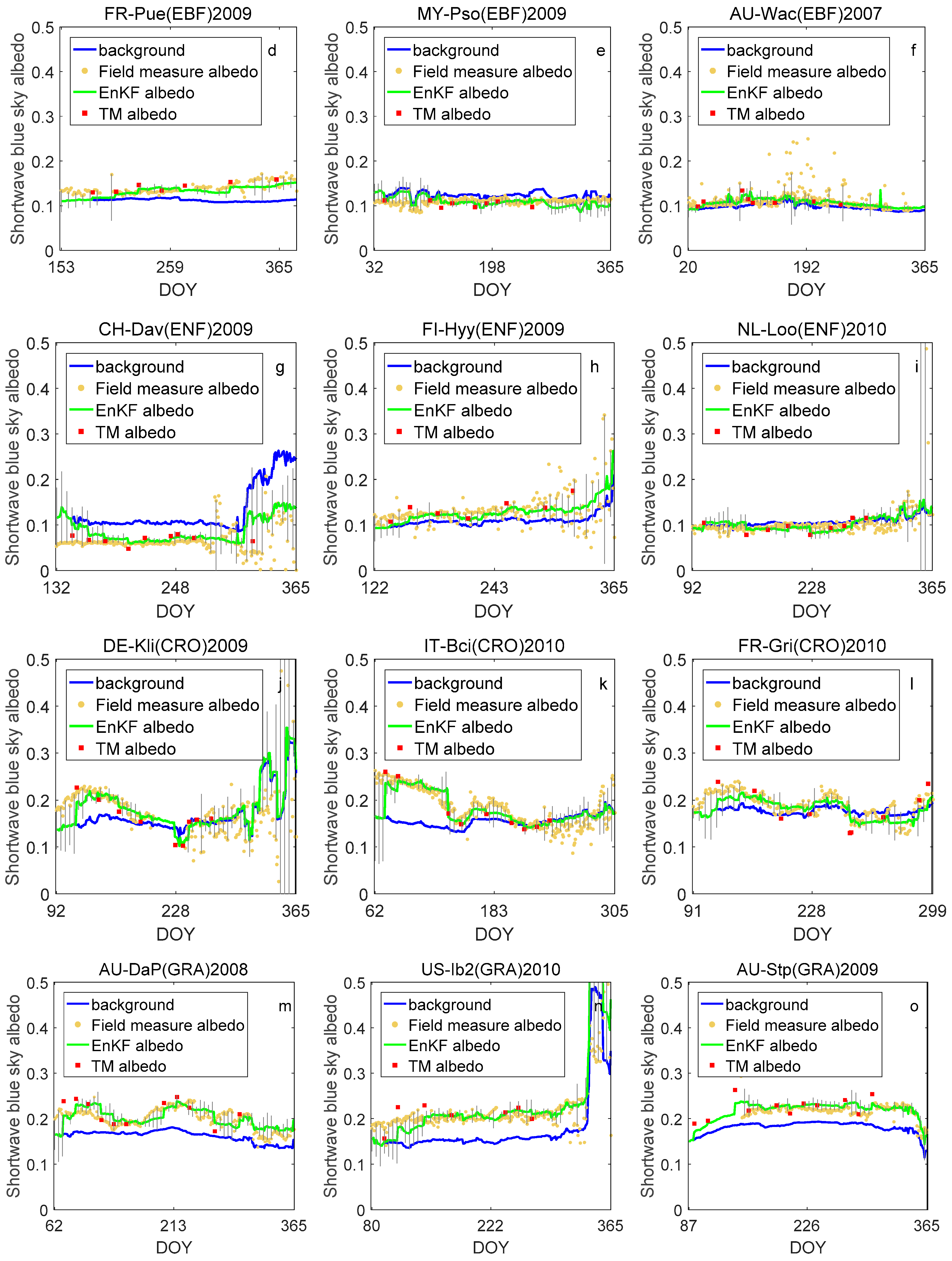
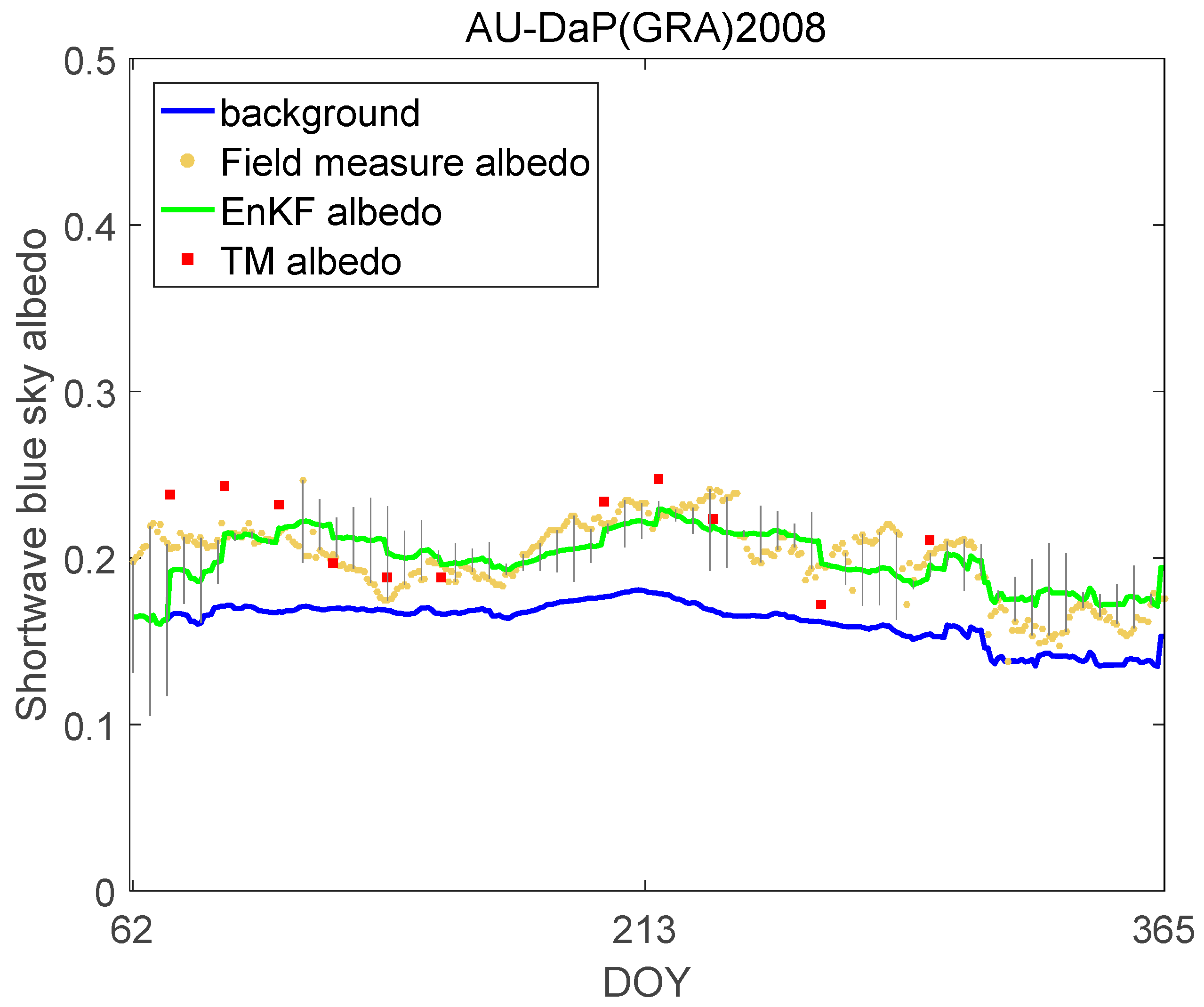
4.2. Estimating and Verifying Single-Point Time Series Albedo
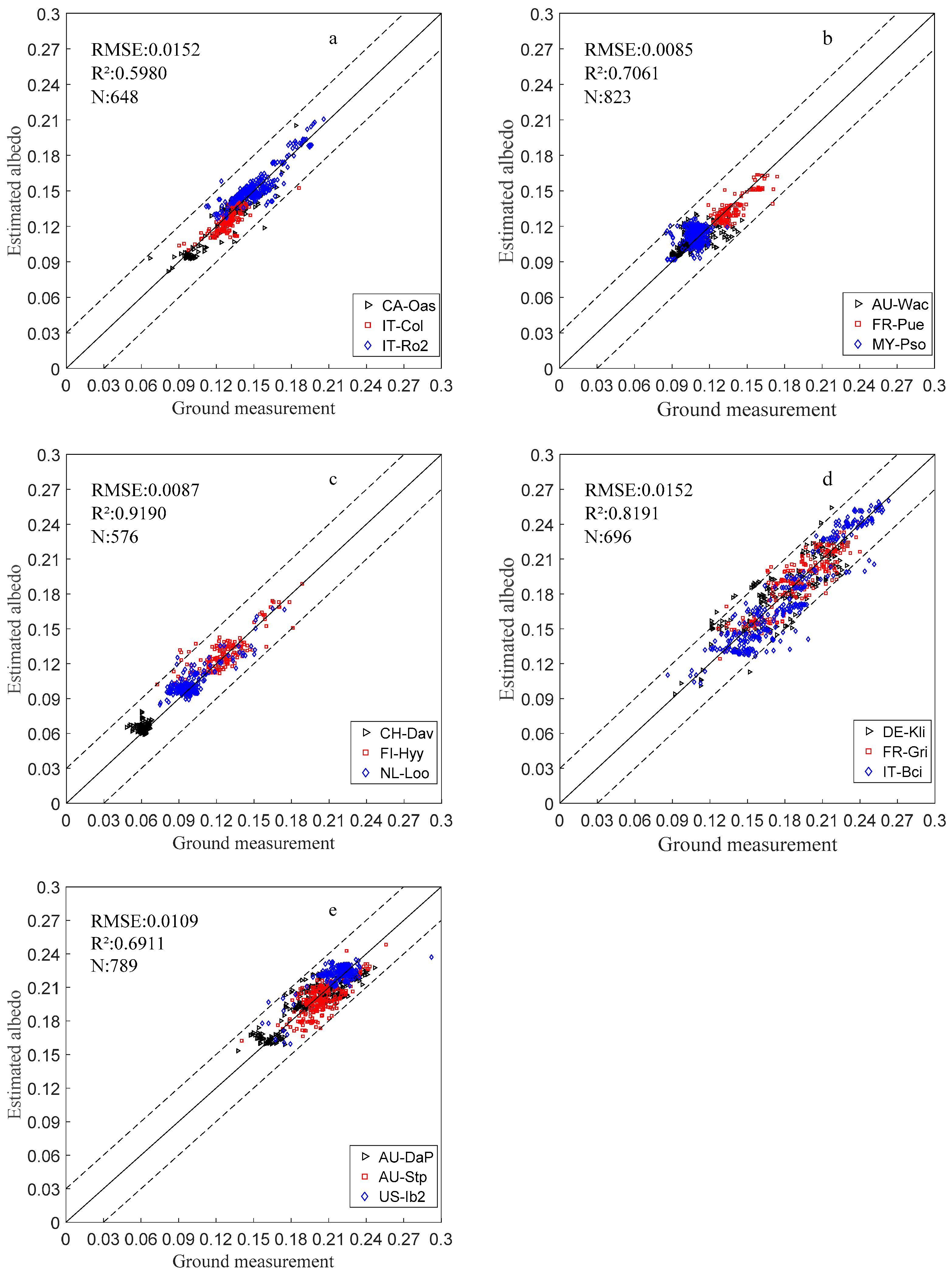
4.3. Regional Timing Albedo Estimation and Verification
5. Discussion
5.1. Accuracy of the Albedo Background
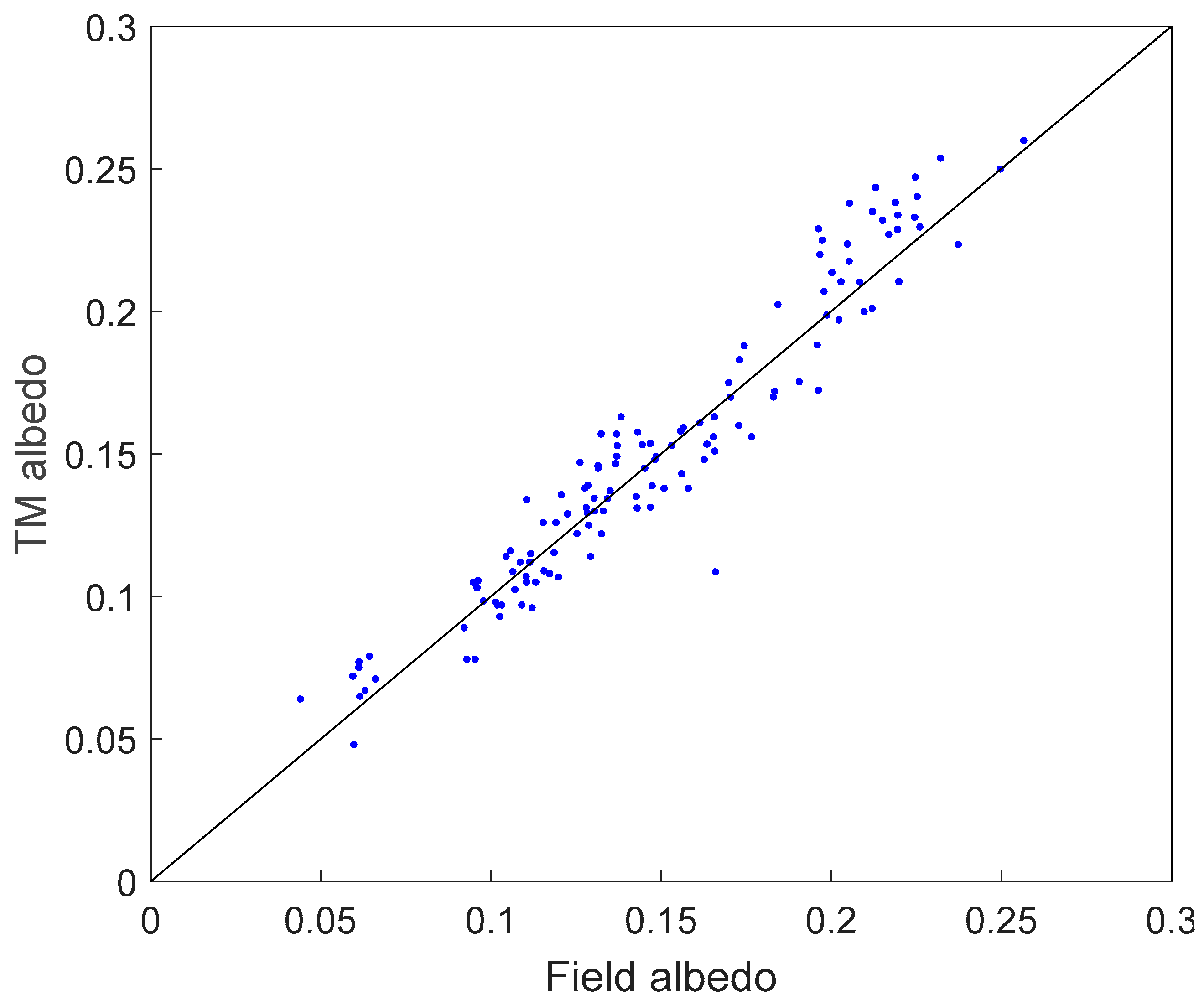
5.2. Errors Induced by TM Albedo Estimation
5.3. Error Setting in the Data Assimilation Algorithm
5.4. Capability of Capturing Abrupt Variations in Land Surface Albedo
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dickinson, R.E. Land surface processes and climate surface albedos and energy-balance. Adv. Geophys. 1983, 25, 305–353. [Google Scholar]
- Ollinger, S.V.; Richardson, A.D.; Martin, M.E.; Hollinger, D.Y.; Frolking, S.E.; Reich, P.B.; Plourde, L.C.; Katul, G.G.; Munger, J.W.; Oren, R. Canopy nitrogen, carbon assimilation, and albedo in temperate and boreal forests: Functional relations and potential climate feedbacks. Proc. Natl. Acad. Sci. USA 2008, 105, 19336–19341. [Google Scholar] [CrossRef] [PubMed]
- Amut, A.; Lu, G.; Yuan, Z. Spatial distributions of surface albedo from satellite data in arid oasis. Proc. SPIE Int. Soc. Opt. Eng. 2007, 6679, 66791V–66796V. [Google Scholar]
- Csiszar, I.; Gutman, G. Mapping global land surface albedo from NOAA AVHRR. J. Geophys. Res. Atmos. 1999, 104, 6215–6228. [Google Scholar] [CrossRef]
- Strugnell, N.C.; Lucht, W.; Schaaf, C. A global albedo data set derived from AVHRR data for use in climate simulations. Geophys. Res. Lett. 2001, 28, 191–194. [Google Scholar] [CrossRef]
- Strugnell, N.C.; Lucht, W. An algorithm to infer continental-scale albedo from AVHRR data, land cover class, and field observations of typical BRDFs. J. Clim. 1999, 14, 1360–1376. [Google Scholar] [CrossRef]
- Li, Z.; Garand, L. Estimation of surface albedo from space: A parameterization for global application. J. Geophys. Res. Atmos. 1994, 99, 8335–8350. [Google Scholar] [CrossRef]
- Lucht, W.; Schaaf, C.B.; Strahler, A.H. An algorithm for the retrieval of albedo from space using semiempirical BRDF models. IEEE Trans. Geosci. Remote Sens. 2002, 38, 977–998. [Google Scholar] [CrossRef]
- Diner, D.J.; Beckert, J.C.; Reilly, T.H.; Bruegge, C.J.; Conel, J.E.; Kahn, R.A.; Martonchik, J.V.; Ackerman, T.P.; Davies, R.; Gerstl, S.A.W. Multi-angle Imaging Spectro Radiometer (MISR) instrument description and experiment overview. IEEE Trans. Geosci. Remote Sens. 2007, 98, 1072–1087. [Google Scholar]
- Leroy, M.; Deuzé, J.L.; Bréon, F.M.; Hautecoeur, O.; Herman, M.; Buriez, J.C.; Tanré, D.; Bouffiès, S.; Chazette, P.; Roujean, J.L. Retrieval of atmospheric properties and surface bidirectional reflectances over land from POLDER/ADEOS. J. Geophys. Res. Atmos. 1997, 102, 17023–17037. [Google Scholar] [CrossRef]
- Hautecœur, O.; Leroy, M.M. Surface bidirectional reflectance distribution function observed at global scale by POLDER/ADEOS. Geophys. Res. Lett. 1998, 25, 4197–4200. [Google Scholar] [CrossRef]
- Hautecoeur, O.; Roujean, J.L. Validation of POLDER surface albedo products based on a review of other satellites and climate databases. In Proceedings of the IEEE International Geoscience & Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007. [Google Scholar]
- Pinty, B.; Roveda, F.; Verstraete, M.M.; Gobron, N.; Govaerts, Y.; Martonchik, J.V.; Diner, D.J.; Kahn, R.A. Surface albedo retrieval from Meteosat: 1. Theory. J. Geophys. Res. Atmos. 2000, 105, 18113–18134. [Google Scholar] [CrossRef]
- Liang, S.; Zhao, X.; Liu, S.; Yuan, W.; Cheng, X.; Xiao, Z.; Zhang, X.; Liu, Q.; Cheng, J.; Tang, H. A long-term Global LAnd Surface Satellite (GLASS) data-set for environmental studies. Int. J. Digit. Earth 2013, 6, 5–33. [Google Scholar] [CrossRef]
- Barnes, C.A.; Roy, D.P. Radiative forcing over the conterminous United States due to contemporary land cover land use albedo change. Geophys. Res. Lett. 2009, 35, 148–161. [Google Scholar] [CrossRef]
- Liang, S. Narrowband to broadband conversions of land surface albedo I: Algorithms. Remote Sens. Environ. 2001, 76, 213–238. [Google Scholar] [CrossRef]
- Tao, H.; Liang, S.; Wang, D.; Chen, X.; Song, D.X.; Bo, J. Land surface albedo estimation from Chinese HJ satellite data based on the direct estimation approach. Remote Sens. 2015, 7, 5495–5510. [Google Scholar]
- He, T.; Liang, S.; Wang, D.; Cao, Y.; Gao, F.; Yu, Y.; Feng, M. Evaluating land surface albedo estimation from Landsat MSS, TM, ETM +, and OLI data based on the unified direct estimation approach. Remote Sens. Environ. 2018, 204, 181–196. [Google Scholar] [CrossRef]
- Shuai, Y.; Masek, J.G. An algorithm for the retrieval of 30-m snow-free albedo from Landsat surface reflectance and MODIS BRDF. Remote Sens. Environ. 2011, 115, 2204–2216. [Google Scholar] [CrossRef]
- Zhang, K.; Zhou, H.; Wang, J.; Xue, H. Estimation and validation of high temporal and spatial resolution albedo. J. Remote Sens. 2014, 18, 497–517. [Google Scholar]
- Lü, H.; Yu, Z.; Zhu, Y.; Drake, S.; Hao, Z.; Sudicky, E.A. Dual state-parameter estimation of root zone soil moisture by optimal parameter estimation and extended Kalman filter data assimilation. Adv. Water Res. 2011, 34, 395–406. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, S.; Shen, S. Assimilating remote sensing information with crop model using Ensemble Kalman Filter for improving LAI monitoring and yield estimation. Ecol. Modell. 2013, 270, 30–42. [Google Scholar] [CrossRef]
- Li, X.; Xiao, Z.; Wang, J.; Song, J. Simultaneous estimation of LAI and dynamic model parameters using dual EnKF from time series MODIS data. In Proceedings of the International Conference on Multimedia Technology, Ningbo, China, 29–31 October 2010. [Google Scholar]
- Zhou, H.; Chen, P.; Wang, J.; Liang, S.; Guo, L.; Zhang, K. A data-based mechanistic assimilation method to estimate time series LAI. In Proceedings of the Geoscience and Remote Sensing Symposium, Melbourne, Australia, 21–26 July 2013. [Google Scholar]
- Shi, C.X.; Xie, Z.H.; Hui, Q.; Liang, M.L.; Yang, X.C. China land soil moisture EnKF data assimilation based on satellite remote sensing data. Sci. China Earth Sci. 2011, 54, 1430–1440. [Google Scholar] [CrossRef]
- Jin, H.; Wang, J.; Xiao, Z.; Fu, Z. Leaf area index estimation from MODIS data using the ensemble Kalman smoother method. In Proceedings of the IEEE International Geoscience & Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010. [Google Scholar]
- Xu, J.; Shu, H. Assimilating MODIS-based albedo and snow cover fraction into the Common Land Model to improve snow depth simulation with direct insertion and deterministic ensemble Kalman filter methods. J. Geophys. Res. Atmos. 2015, 119, 10, 684–610, 701. [Google Scholar] [CrossRef]
- Chander, G.; Helder, D.L.; Markham, B.L.; Dewald, J.D.; Kaita, E.; Thome, K.J.; Micijevic, E.; Ruggles, T.A. Landsat-5 TM reflective-band absolute radiometric calibration. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2747–2760. [Google Scholar] [CrossRef]
- Roujean, J.L.; Leroy, M.; Deschamps, P.Y. A bidirectional reflectance model of the Earth’s surface for the correction of remote sensing data. J. Geophys. Res. Atmos. 1992, 97, 20455–20468. [Google Scholar] [CrossRef]
- Schaaf, C.B.; Gao, F.; Strahler, A.H.; Lucht, W.; Li, X.; Tsang, T.; Strugnell, N.C.; Zhang, X.; Jin, Y.; Muller, J.P. First operational BRDF, albedo nadir reflectance products from MODIS. Remote Sens. Environ. 2002, 83, 135–148. [Google Scholar] [CrossRef]
- Svacina, N.A.; Duguay, C.R.; King, J.M.L. Modelled and satellite-derived surface albedo of lake ice—Part II: Evaluation of MODIS albedo products. Hydrol. Processes 2014, 28, 4562–4572. [Google Scholar] [CrossRef]
- Privette, J.L.; Mukelabai, M.; Zhang, H.; Schaaf, C.B. Characterization of MODIS land albedo (MOD43) accuracy with atmospheric conditions in Africa. In Proceedings of the IGARSS 2004 IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004. [Google Scholar]
- Zhou, H.; Wang, J.; Liang, S. Design of a novel spectral albedometer for validating the MODerate resolution Imaging Spectroradiometer Spectral Albedo Product. Remote Sens. 2018, 10, 101. [Google Scholar] [CrossRef]
- Salomon, J.G.; Schaaf, C.B.; Strahler, A.H.; Gao, F.; Jin, Y. Validation of the MODIS bidirectional reflectance distribution function and albedo retrievals using combined observations from the aqua and terra platforms. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1555–1565. [Google Scholar] [CrossRef]
- Jin, Y.; Schaaf, C.B.; Woodcock, C.E.; Gao, F.; Li, X.; Strahler, A.H.; Lucht, W.; Liang, S. Consistency of MODIS surface bidirectional reflectance distribution function and albedo retrievals: 2. Validation. J. Geophys. Res. Atmos. 2003, 108, 4159. [Google Scholar] [CrossRef]
- Cescatti, A.; Marcolla, B.; Vannan, S.K.S.; Pan, J.Y.; Román, M.O.; Yang, X.; Ciais, P.; Cook, R.B.; Law, B.E.; Matteucci, G. Intercomparison of MODIS albedo retrievals and in situ measurements across the global FLUXNET network. Remote Sens. Environ. 2012, 121, 323–334. [Google Scholar] [CrossRef]
- Moon, S.K.; Ryu, Y.R.; Lee, D.H.; Kim, J.; Lim, J.H. Quantifying the spatial heterogeneity of the land surface parameters at the two contrasting KoFlux Sites by Semivariogram. J. Agric. For. Meteorol. 2007, 9, 140–148. [Google Scholar] [CrossRef]
- Tittebrand, A. Analysis of the spatial heterogeneity of land surface parameters and energy flux densities. Atmos. Chem. Phys. 2009, 9, 2075–2087. [Google Scholar] [CrossRef]
- Román, M.O.; Schaaf, C.B.; Woodcock, C.E.; Strahler, A.H.; Yang, X.Y.; Braswell, R.H.; Curtis, P.S.; Davis, K.J.; Dragoni, D.; Goulden, M.L. The MODIS (Collection V005) BRDF/albedo product: Assessment of spatial representativeness over forested landscapes. Remote Sens. Environ. 2009, 113, 2476–2498. [Google Scholar] [CrossRef]
- Cooper, S.D.; Barmuta, L.; Sarnelle, O.; Kratz, K.; Diehl, S. Quantifying spatial heterogeneity in streams. J. N. Am. Benthol. Soc. 1997, 16, 174–188. [Google Scholar] [CrossRef]
- Samain, O.; Roujean, J.-L.; Geiger, B. Use of a Kalman filter for the retrieval of surface BRDF coefficients with a time-evolving model based on the ECOCLIMAP land cover classification. Remote Sens. Environ. 2008, 112, 1337–1346. [Google Scholar] [CrossRef]
- Xiao, Z.; Liang, S.; Wang, J.; Jiang, B.; Li, X. Real-time retrieval of Leaf Area Index from MODIS time series data. Remote Sens. Environ. 2011, 115, 97–106. [Google Scholar] [CrossRef]
- Liang, S.; Strahler, A.; Walthall, C. Retrieval of land surface albedo from satellite observations: A simulation study. In Proceedings of the 1998 IEEE International Geoscience and Remote Sensing Symposium IGARSS ′98, Seattle, WA, USA, 6–10 July 1998; Volume 1283, pp. 1286–1288. [Google Scholar]
- Shuai, Y.; Masek, J.G.; Gao, F.; Schaaf, C.B.; He, T. An approach for the long-term 30-m land surface snow-free albedo retrieval from historic Landsat surface reflectance and MODIS-based a priori anisotropy knowledge. Remote Sens. Environ. 2014, 152, 467–479. [Google Scholar] [CrossRef]
- Franch, B.; Vermote, E.; Claverie, M. Intercomparison of Landsat albedo retrieval techniques and evaluation against in situ measurements across the US SURFRAD network. Remote Sens. Environ. 2014, 152, 627–637. [Google Scholar] [CrossRef]
- He, T.; Liang, S. Mapping surface Albedo from the complete landsat archive since the 1980s and its cryospheric application. In Proceedings of the IGARSS 2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018. [Google Scholar]
- Zhou, H.; Hu, N.; He, T.; Liang, S.; Wang, J. High resolution Albedo estimation with Chinese GF-1 WFV data. In Proceedings of the IGARSS 2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018. [Google Scholar]
- Kalman, R.E.; Bucy, R.S. New results in linear filtering and prediction theory. ASME J. Basic Eng. 1961, 83, 95–108. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. ASME J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Angus, J. Forecasting, structural time series and the Kalman filter. J. Oper. Res. Soc. 1991, 34, 496–497. [Google Scholar] [CrossRef]
- Lefferts, E.J.; Markley, F.L.; Shuster, M.D. Kalman Filtering for spacecraft attitude estimation. J. Guid. Control Dynam. 1982, 5, 536–542. [Google Scholar] [CrossRef]
- Yin, X.; Xiao, Z. Optimal integration of MODIS and MISR albedo products. In Proceedings of the International Symposium on Image and Data Fusion, Tengchong, China, 9–11 August 2011. [Google Scholar]
- Sellers, P.J.; Meeson, B.W.; Hall, F.G.; Asrar, G.; Murphy, R.E.; Schiffer, R.A.; Bretherton, F.P.; Dickinson, R.E.; Ellingson, R.G.; Field, C.B. Remote sensing of the land surface for studies of global change: Models—Algorithms—Experiments. Remote Sens. Environ. 1995, 51, 3–26. [Google Scholar] [CrossRef]
- Xiao, Z.; Liang, S.; Wang, J.; Wu, X. Use of an ensemble Kalman filter for real-time inversion of leaf area index from MODIS time series data. In Proceedings of the Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010. [Google Scholar]
- Friedl, M.A.; Mciver, D.K.; Hodges, J.C.F.; Zhang, X.Y.; Muchoney, D.; Strahler, A.H.; Woodcock, C.E.; Gopal, S.; Schneider, A.; Cooper, A. Global land cover mapping from MODIS: Algorithms and early results. Remote Sens. Environ. 2002, 83, 287–302. [Google Scholar] [CrossRef]
- Serbin, S.P.; Ahl, D.E.; Gower, S.T. Spatial and temporal validation of the MODIS LAI and FPAR products across a boreal forest wildfire chronosequence. Remote Sens. Environ. 2013, 133, 71–84. [Google Scholar] [CrossRef]
- Bolten, J.D.; Gupta, M.; Gatebe, C.K.; Ichoku, C.M. Regional land surface hydrology impacts from fire-induced surface Albedo darkening in Northern Sub-Saharan Africa. In Proceedings of the AGU Fall Meeting, San Francisco, CA, USA, 14–18 December 2015. [Google Scholar]


| Site Name | Network | Latitude (°) | Longitude (°) | Land Cover Type | Data Year |
|---|---|---|---|---|---|
| CA-Oas * | FluxNet | 53.6289N | 106.1978W | DBF | 2009 |
| IT-Col * | FluxNet | 41.8494N | 13.5881E | DBF | 2009 |
| IT-Ro2 * | FluxNet | 42.3903N | 11.9209E | DBF | 2010 |
| US-Bar + | AmeriFlux | 44.0646N | 71.2881W | DBF | 2009 |
| FR-Pue * | FluxNet | 43.7414N | 3.5958E | EBF | 2009 |
| MY-Pso * | FluxNet | 2.9730N | 102.3062E | EBF | 2009 |
| AU-Wac *+ | FluxNet | 37.4259S | 145.1878E | EBF | 2007 |
| CH-Dav * | FluxNet | 46.8153N | 9.8559E | ENF | 2009 |
| FI-Hyy * | FluxNet | 61.8474N | 24.2948E | ENF | 2009 |
| NL-Loo * | FluxNet | 52.1666N | 5.7436E | ENF | 2010 |
| IT-Sro + | FluxNet | 43.7279N | 10.2844E | ENF | 2009 |
| DE-Kli * | FluxNet | 50.8931N | 13.5224E | CRO | 2009 |
| IT-Bci * | FluxNet | 40.5238N | 14.9574E | CRO | 2010 |
| FR-Gri * | FluxNet | 48.8442N | 1.9519E | CRO | 2010 |
| US-Arm + | AmeriFlux | 36.6058N | 97.4888W | CRO | 2010 |
| AU-DaP * | FluxNet | 14.0633S | 131.3181E | GRA | 2008 |
| US-Ib2 * | AmeriFlux | 41.8406N | 88.2410W | GRA | 2010 |
| AU-Stp *+ | FluxNet | 17.1507S | 133.3502E | GRA | 2009 |
| Site | TM Overpass Time | 1 km Range | 1.5 km Range | |
|---|---|---|---|---|
| CA-Oas | 10-Aug-09 | 71.00 m | 55.00 m | 5.26% |
| IT-Col | 25-Jul-09 | 295.00 m | 342.00 m | 7.44% |
| IT-Ro2 | 03-Jul-09 | 260.00 m | 129.00 m | 5.38% |
| US-Bar | 17-May-10 | 168.00 m | 353.00 m | 16.87% |
| FR-Pue | 26-Jul-09 | 624.00 m | 332.00 m | 7.8% |
| MY-PSO | 11-Sep-09 | 45.00 m | 644.00 m | 14.38% |
| AU-Wac | 16-Apr-07 | 109.00 m | 112.00 m | 3.40% |
| CH-Dav | 06-Aug-09 | 1453.00 m | 396.00 m | 9.11% |
| FI-Hyy | 31-May-09 | 877.00 m | 155.00 m | 32.46% |
| NL-Loo | 06-Sep-10 | 70.00 m | 34.00 m | 5.33% |
| IT-SRo | 23-Jul-09 | 304.00 m | 641.00 m | 86.38% |
| DE-Kli | 24-Aug-09 | 304.00 m | 193.00 m | 7.25% |
| IT-BCi | 09-Oct-10 | 234.00 m | 182.00 m | 8.94% |
| FR-Gri | 24-May-10 | 114.00 m | 87.00 m | 7.44% |
| US-ARM | 16-Jul-11 | 584.00 m | 393.00 m | 5.53% |
| AU-DaP | 23-Aug-09 | 257.00 m | 422.00 m | 6.74% |
| US-IB2 | 12-Sep-10 | 216.00 m | 243.00 m | 4.30% |
| AU-Stp | 25-Aug-09 | 470.00 m | 341.00 m | 16.77% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Zhou, H.; Wang, C.; Xue, H.; Wang, J.; Wan, H. Time Series High-Resolution Land Surface Albedo Estimation Based on the Ensemble Kalman Filter Algorithm. Remote Sens. 2019, 11, 753. https://doi.org/10.3390/rs11070753
Zhang G, Zhou H, Wang C, Xue H, Wang J, Wan H. Time Series High-Resolution Land Surface Albedo Estimation Based on the Ensemble Kalman Filter Algorithm. Remote Sensing. 2019; 11(7):753. https://doi.org/10.3390/rs11070753
Chicago/Turabian StyleZhang, Guodong, Hongmin Zhou, Changjing Wang, Huazhu Xue, Jindi Wang, and Huawei Wan. 2019. "Time Series High-Resolution Land Surface Albedo Estimation Based on the Ensemble Kalman Filter Algorithm" Remote Sensing 11, no. 7: 753. https://doi.org/10.3390/rs11070753
APA StyleZhang, G., Zhou, H., Wang, C., Xue, H., Wang, J., & Wan, H. (2019). Time Series High-Resolution Land Surface Albedo Estimation Based on the Ensemble Kalman Filter Algorithm. Remote Sensing, 11(7), 753. https://doi.org/10.3390/rs11070753