A Novel Tri-Training Technique for the Semi-Supervised Classification of Hyperspectral Images Based on Regularized Local Discriminant Embedding Feature Extraction
Abstract
1. Introduction
2. Spatial Mean Filtering and Feature Extraction
2.1. Spatial Mean Filtering
2.2. Local Discriminant Embedding (LDE)
2.3. Regularized Local Discriminant Embedding (RLDE)
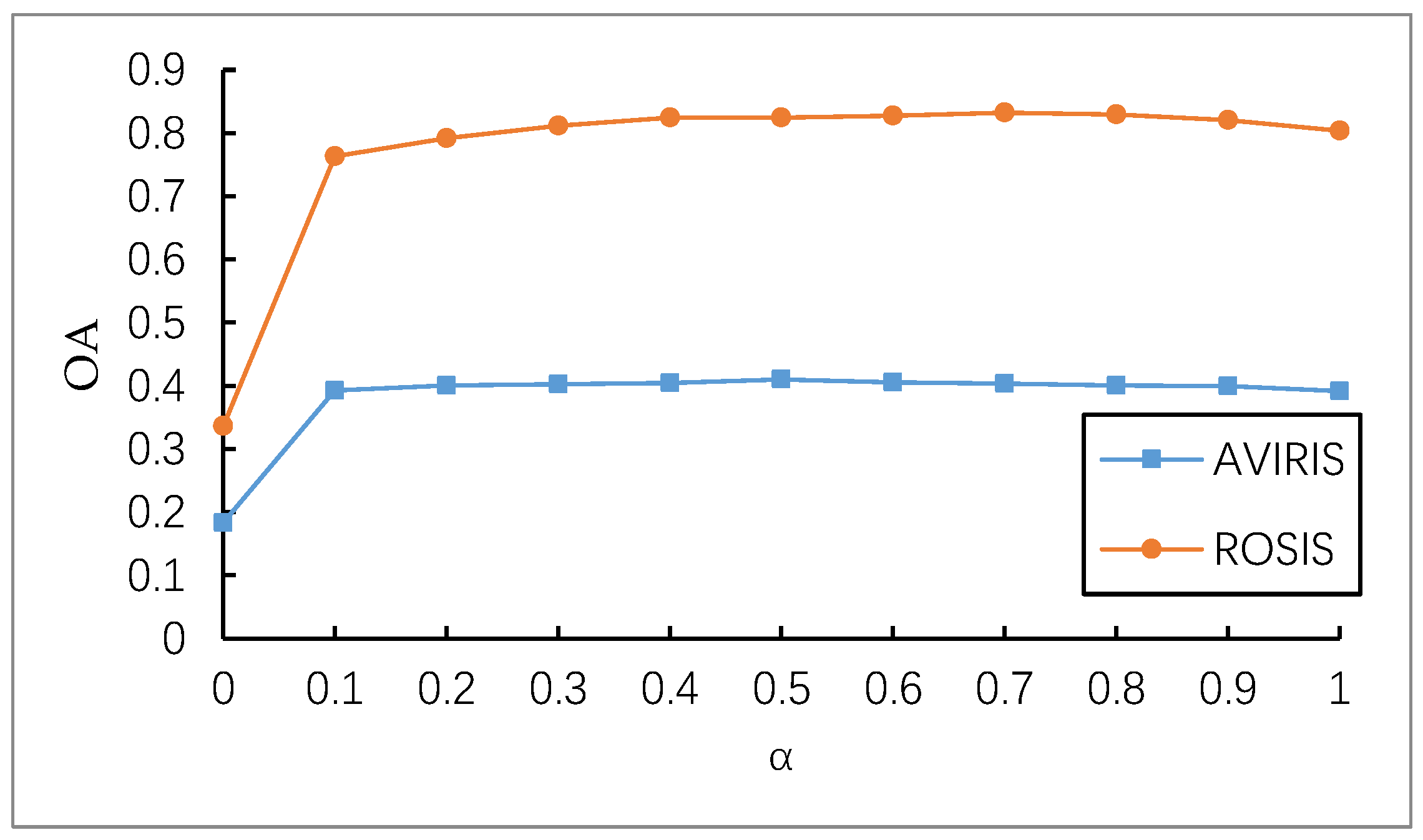
2.4. Cooperative Training Strategy Combining Local Features
- (1)
- A mean filtering process is employed to reduce the noise in the HSI.
- (2)
- The local feature information of training samples is extracted by the RLDE method, and is labeled .
- (3)
- The classifier is trained with , to obtain the predicted classification result .
- (4)
- For the classifier , another two classifiers are selected which agree on the labeling of these samples to build the candidate set .
- (5)
- The active learning method is used to select the most useful and informative samples from the candidate sets and .
- (6)
- The process is terminated if the stopping condition is met; otherwise, go to Step (2).
| Algorithm: RLDE tri-training |
| Input: L: Original labeled sample set U: Unlabeled sample set BT: Breaking ties algorithm MV: Majority voting algorithm Process: L←SMF(L); U←SMF(U) L1←L; L2←L; L3←L Repeat until none of hi(i∈{1,2,3}) changes ←RLDE(); ←RLDE(); ←RLDE() MLR(); KNN(); RF() ←; ←; ← For i ∈ {1,2,3} do ←(i ≠ j ≠ k) ←BT() ; End of for End of repeat OUTPUT: S MV() |
3. Experimental Results and Analysis
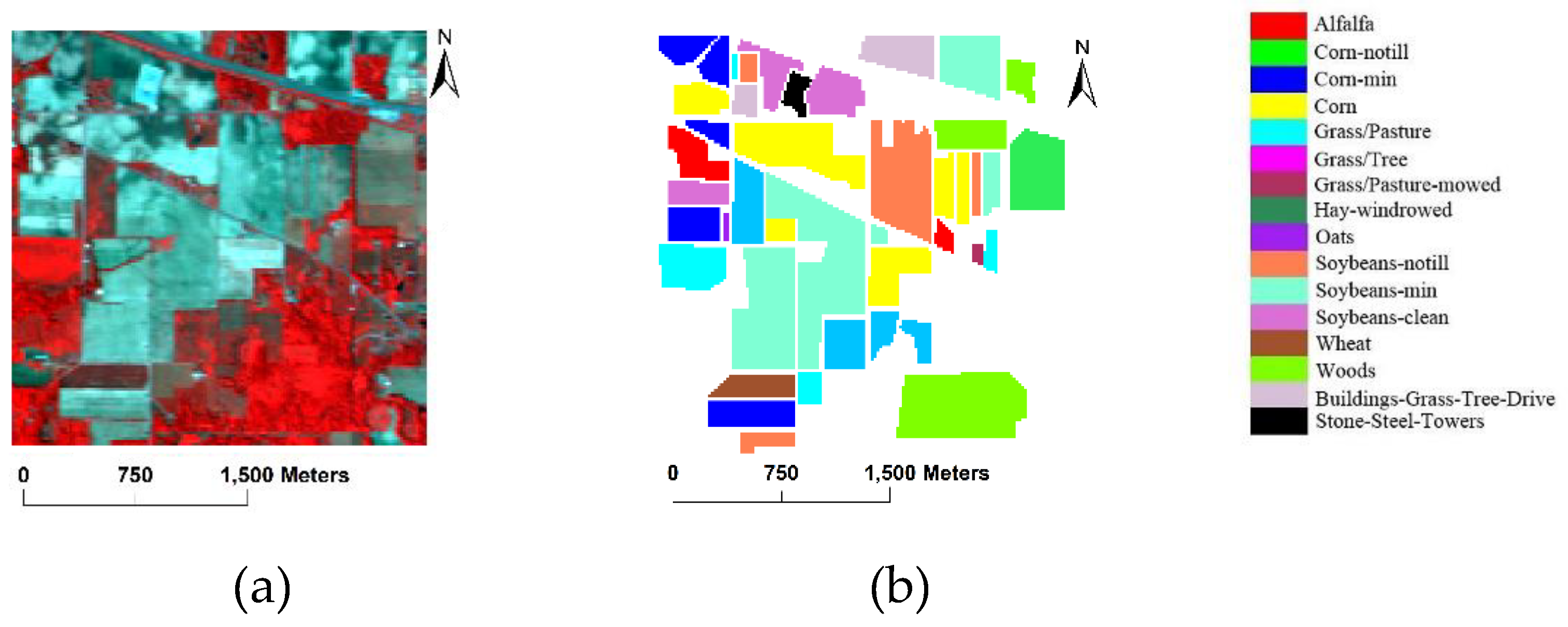
3.1. Data Used in the Experiments
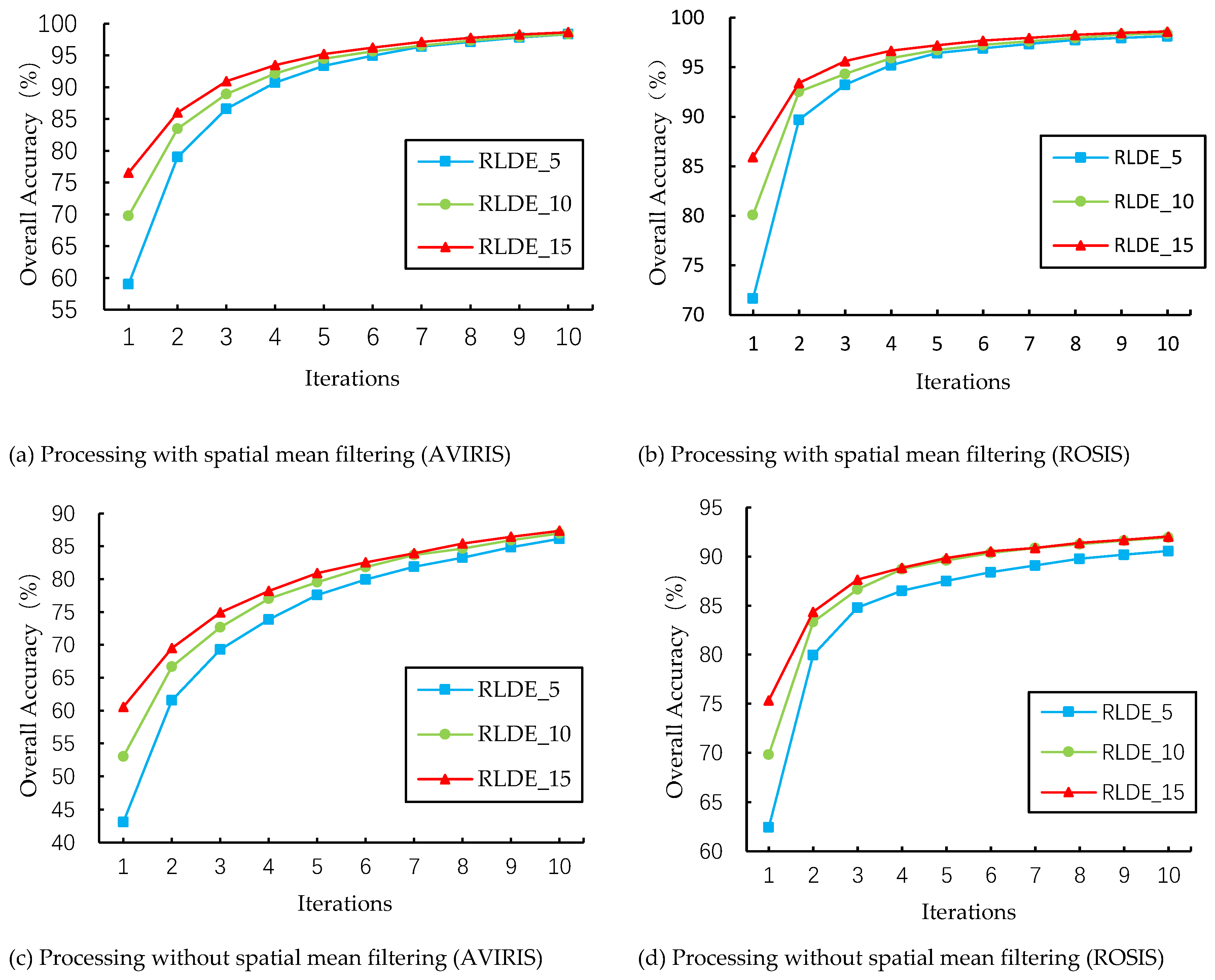
3.2. The Effect of the Spatial Mean Filtering
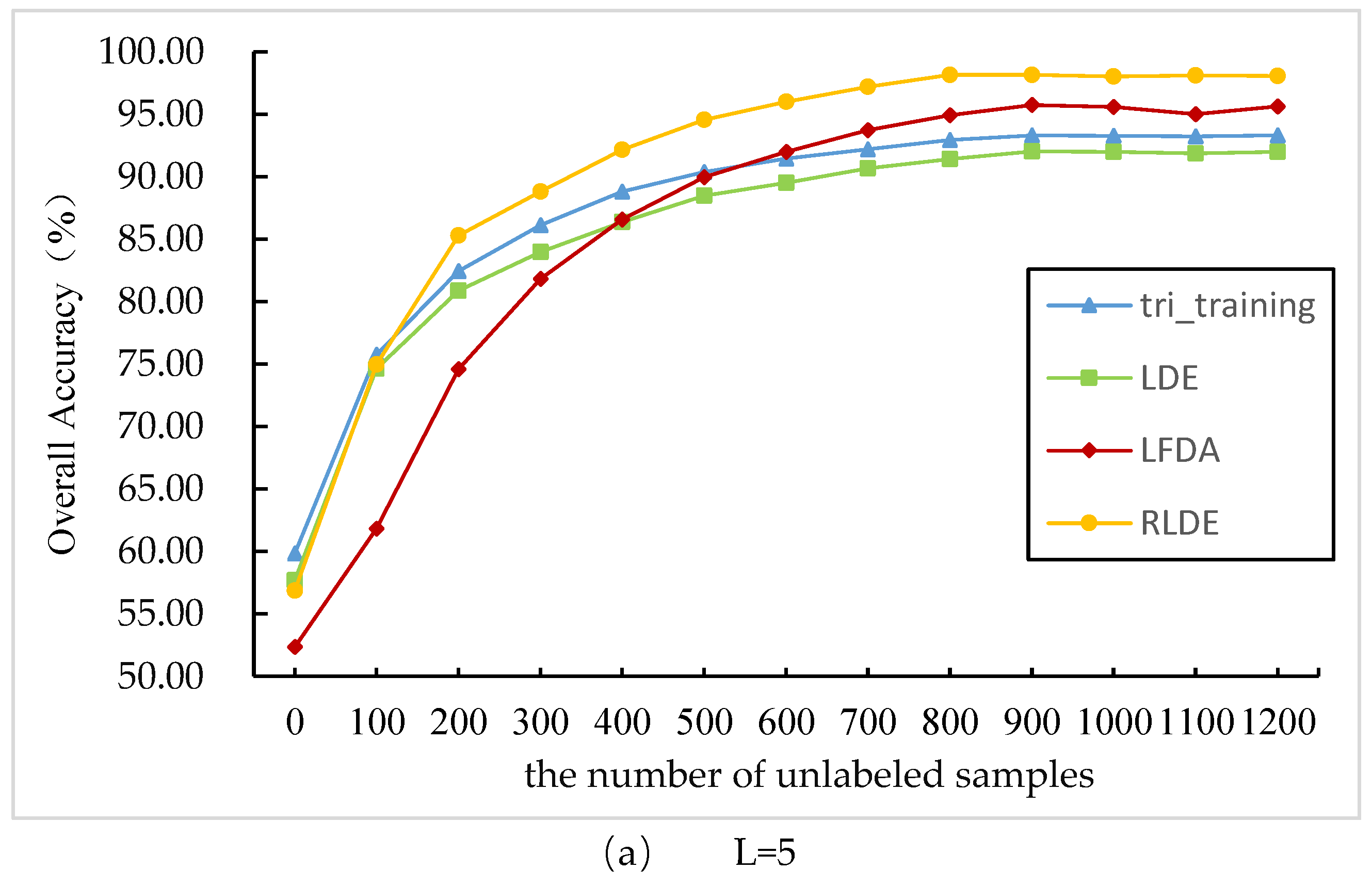
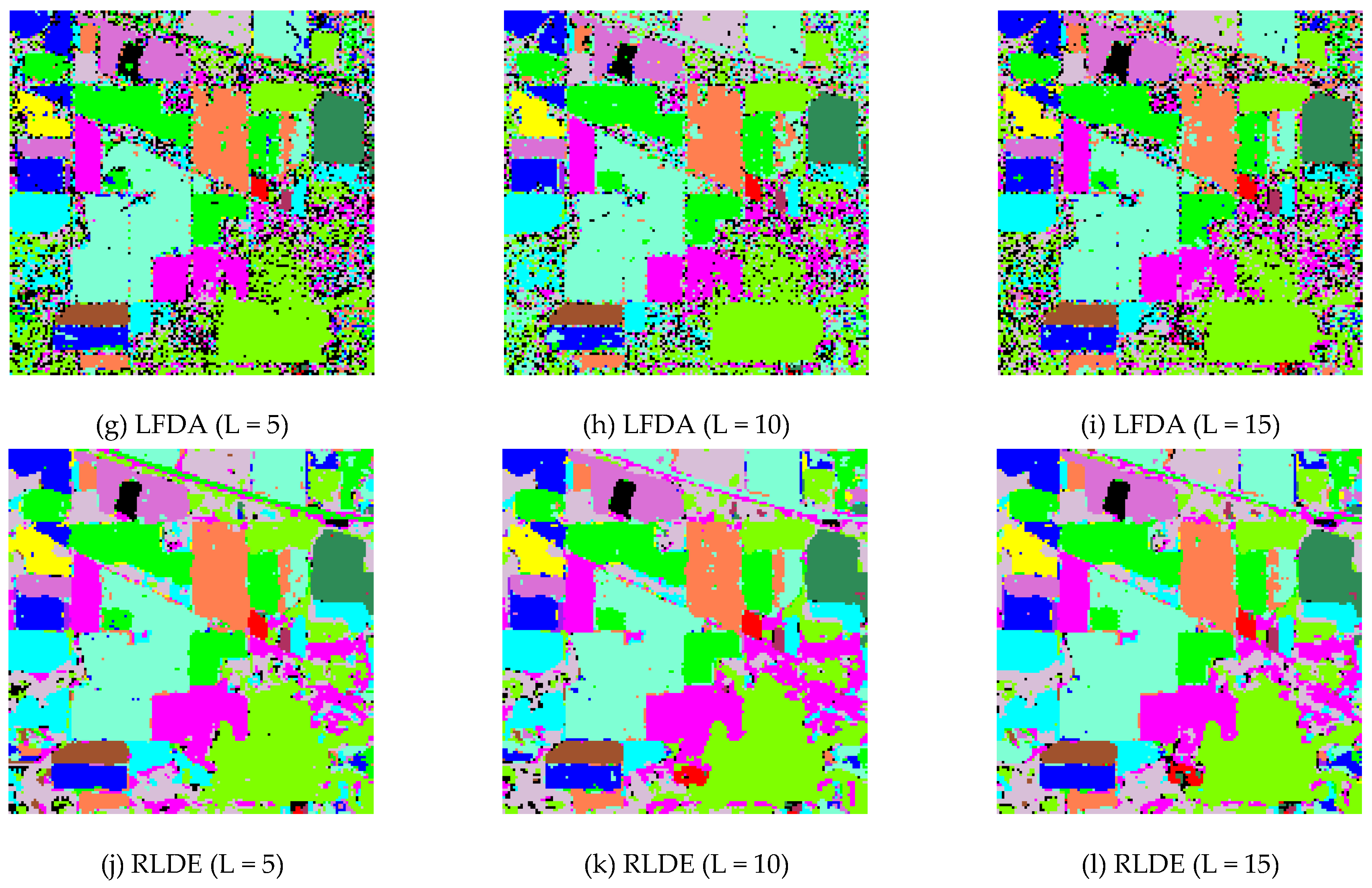
3.3. Comparison between the Different Feature Extraction Methods: AVIRIS Data
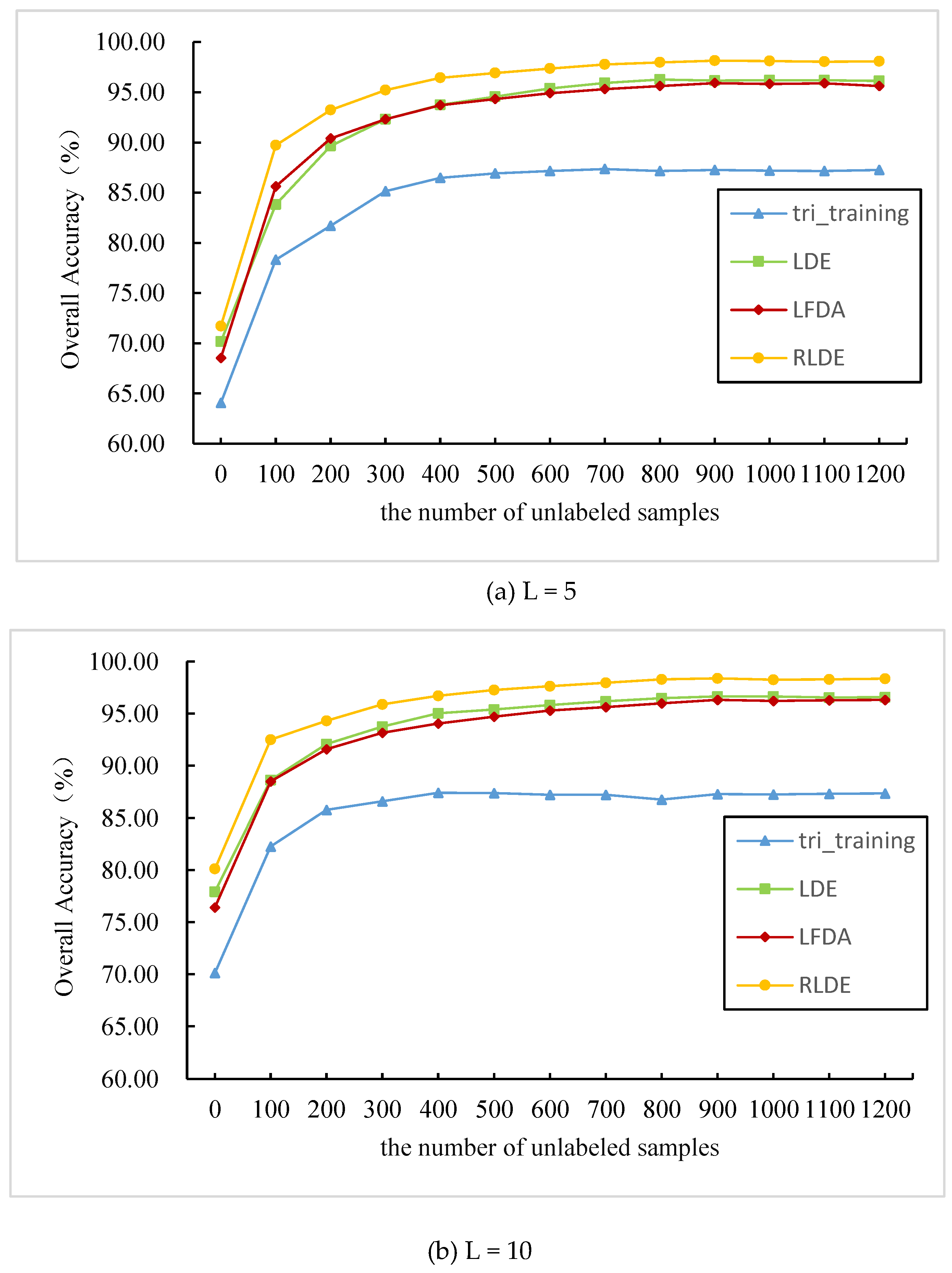
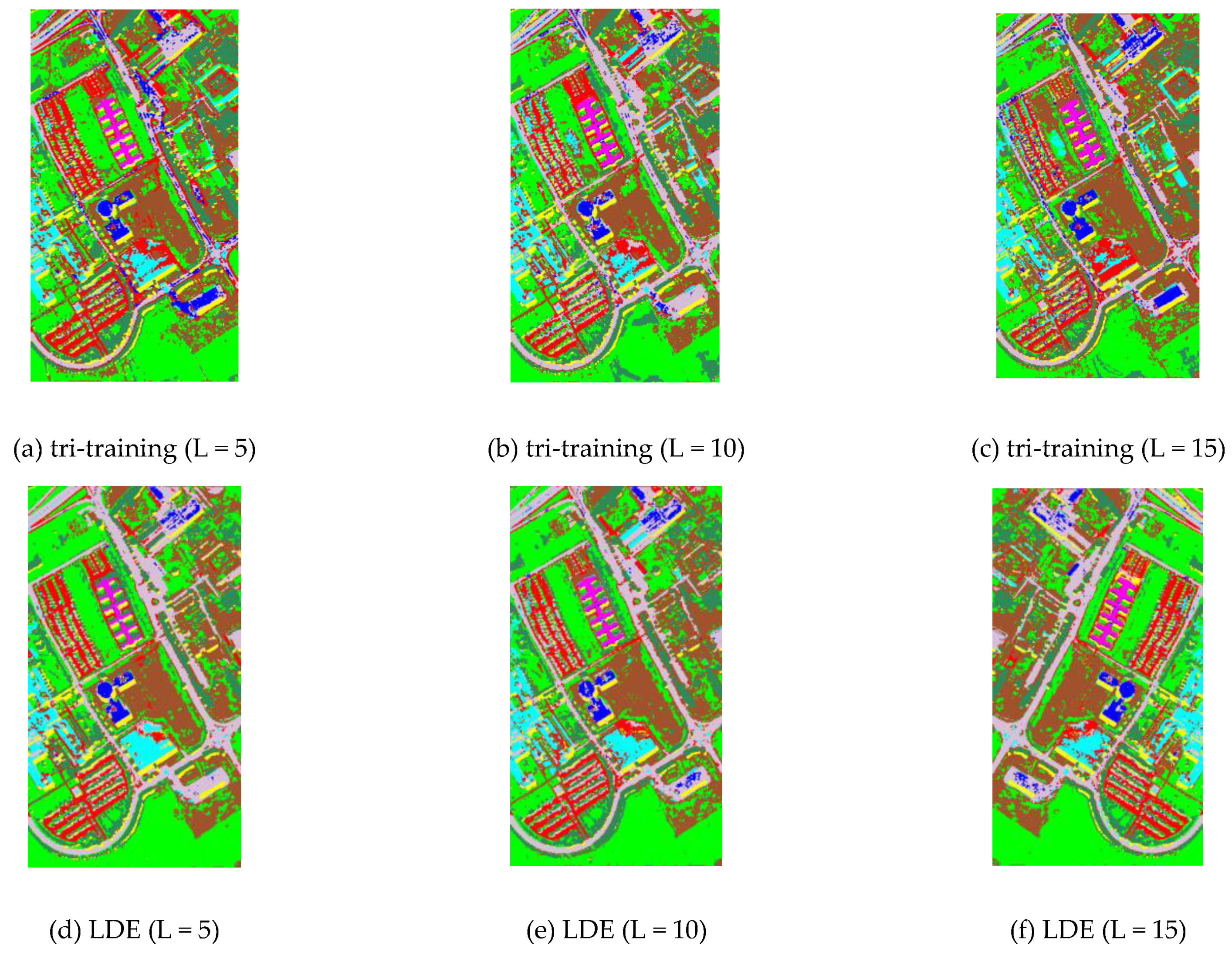
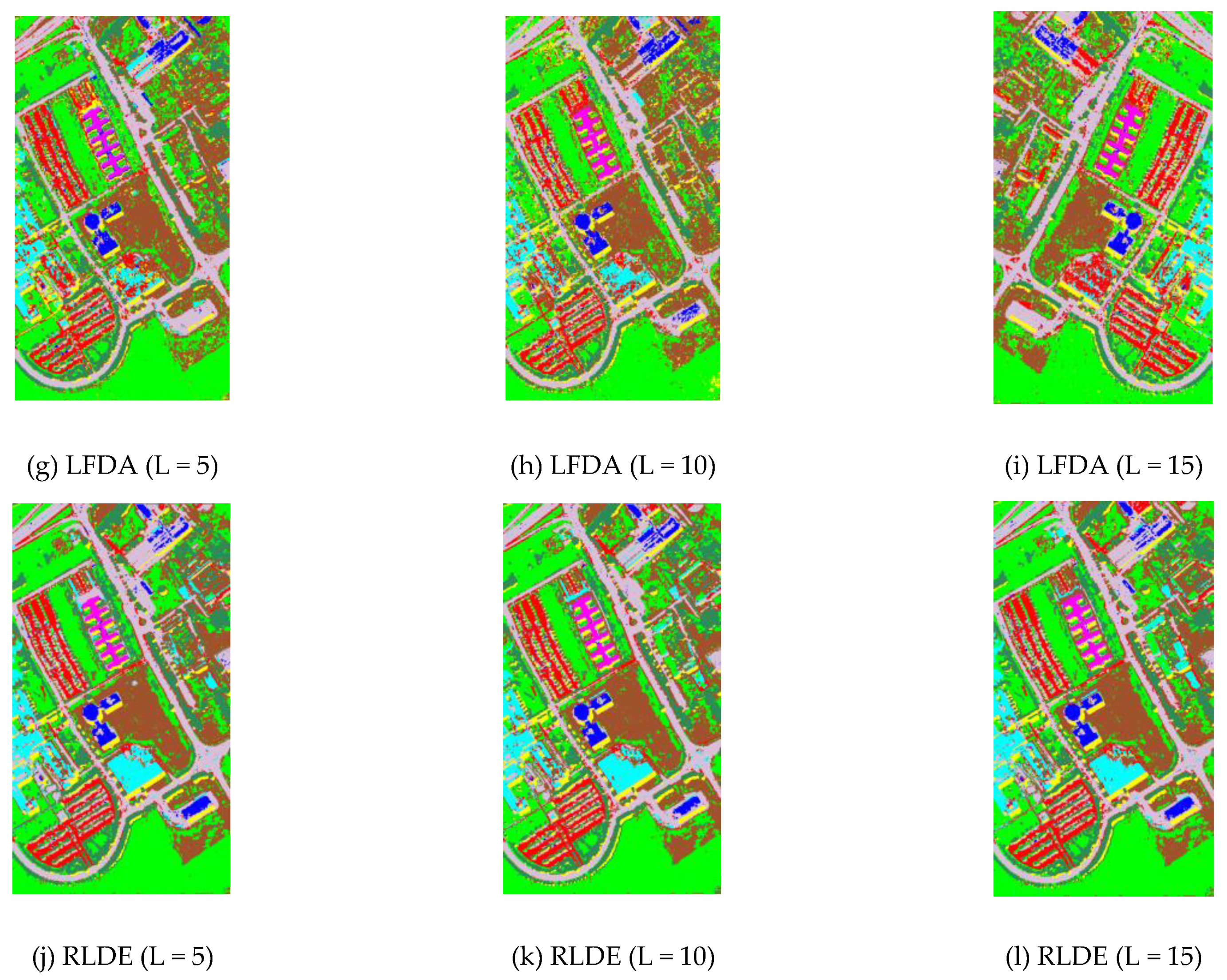
3.4. Comparison between the Different Feature Extraction Methods: ROSIS Data
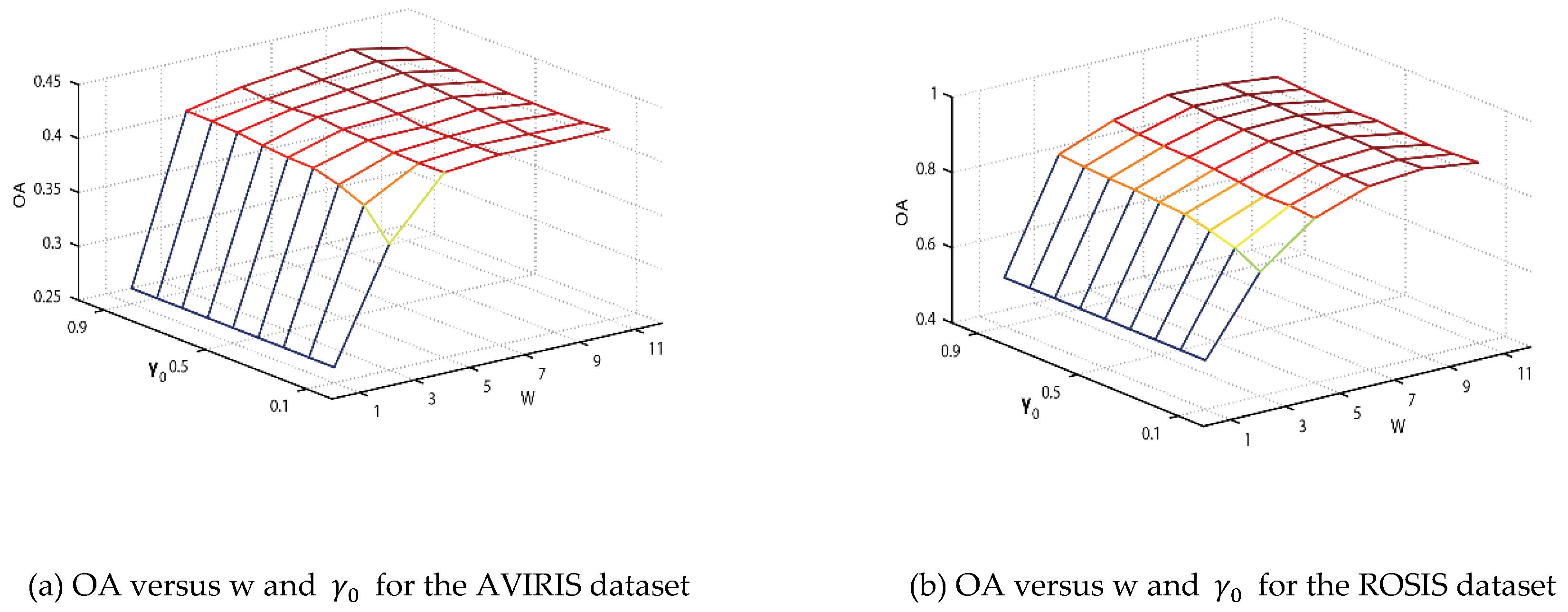
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ben-Dor, E.; Schläpfer, D.; Plaza, A.J.; Malthus, T. Hyperspectral remote sensing. In Airborne Measurements for Environmental Research: Methods and Instruments; Wiley-VCH Verlag & Co. KGaA: Weinheim, Germany, 2013; pp. 1249–1259. [Google Scholar]
- Groves, P.; Tian, L.F.; Bajwa, S.G.; Bajcsy, P. Hyperspectral image data mining for band selection in agricultural applications. Trans. ASAE 2004, 47, 895–907. [Google Scholar]
- Plaza, J.; Pérez, R.; Plaza, A.; Martínez, P.; Valencia, D. Mapping oil spills on sea water using spectral mixture analysis of hyperspectral image data. In Chemical and Biological Standoff Detection III; International Society for Optics and Photonics: Bellingham, WA, USA, 2005; Volume 5995, pp. 79–86. [Google Scholar]
- Iranzad, A. Hyperspectral Mineral Identification Using SVM and SOM; Brock University: St. Catharines, ON, Canada, 2013. [Google Scholar]
- Blum, A.; Mitchell, T. Combining labeled and unlabeled data with co-training. In Proceedings of the Eleventh Conference on Computational Learning Theory, Madisson, WI, USA, 24–26 July 1998; pp. 92–100. [Google Scholar]
- Peng, L.; Hui, Z.; Eom, K.B. Active deep learning for classification of hyperspectral images. IEEE J. Sel. Top. Appl. Earth Observat. Remote Sens. 2017, 10, 712–724. [Google Scholar]
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep convolutional neural networks for hyperspectral image classification. J. Sens. 2015, 2015, 258619. [Google Scholar] [CrossRef]
- Song, J.; Zhang, H.; Li, X.; Gao, L.; Wang, M.; Hong, R. Self-supervised video hashing with hierarchical binary auto-encoder. IEEE Trans. Image Process. A Publ. IEEE Signal Process. Soc. 2018, 27, 3210. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral-spatial classification of hyperspectral imagery with 3d convolutional neural network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef]
- Wang, X.; Gao, L.; Wang, P.; Sun, X.; Liu, X. Two-stream 3d convnet fusion for action recognition in videos with arbitrary size and length. IEEE Trans. Multimed. 2018, 20, 634–644. [Google Scholar] [CrossRef]
- Wang, X.; Gao, L.; Song, J.; Shen, H. Beyond frame-level cnn: Saliency-aware 3d cnn with lstm for video action recognition. IEEE Signal Process. Lett. 2017, 24, 510–514. [Google Scholar] [CrossRef]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Deep recurrent neural networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3639–3655. [Google Scholar] [CrossRef]
- Goldberg, A.B.; Zhu, X.; Singh, A.; Xu, Z.; Nowak, R. Multi-manifold semi-supervised learning. Ynh Lr on Arfal Nllgn & Mahn Larnng 2009, 5, 169–176. [Google Scholar]
- Tan, K.; Zhou, S.; Du, Q. Semisupervised discriminant analysis for hyperspectral imagery with block-sparse graph. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1–5. [Google Scholar]
- Tuia, D.; Ratle, F.; Pacifici, F.; Kanevski, M.F. Active learning methods for remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2218–2232. [Google Scholar] [CrossRef]
- Huang, R.; He, W. Using tri-training to exploit spectral and spatial information for hyperspectral data classification. In Proceedings of the International Conference on Computer Vision in Remote Sensing, Xiamen, China, 16–18 December 2012; pp. 30–33. [Google Scholar]
- Zhou, Z.H.; Li, M. Tri-training: Exploiting unlabeled data using three classifiers. IEEE Trans. Knowl. Data Eng. 2005, 17, 1529–1541. [Google Scholar] [CrossRef]
- Tan, K.; Li, E.; Du, Q.; Du, P. An efficient semi-supervised classification approach for hyperspectral imagery. Isprs J. Photogramm. Remote Sens. 2014, 97, 36–45. [Google Scholar] [CrossRef]
- Nixon, M. Feature Extraction & Image Processing for Computer Vision, 3rd ed.; Academic Press: Cambridge, MA, USA, 2008; pp. 595–599. [Google Scholar]
- Rui, Y.; Huang, T.S.; Chang, S.F. Image retrieval: Current techniques, promising directions, and open issues. J. Vis. Commun. Image Represent. 1999, 10, 39–62. [Google Scholar] [CrossRef]
- Hughes, G.F.; Hughes, G. On the mean accuracy of statistical pattern recognizers. IEEE Trans. Inf. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Pevný, T.; Filler, T.; Bas, P. Using High-Dimensional Image Models to Perform Highly Undetectable Steganography; Springer: Berlin/Heidelberg, Germany, 2010; pp. 161–177. [Google Scholar]
- Yu, L.; Liu, H. Feature selection for high-dimensional data: A fast correlation-based filter solution. In Proceedings of the Twentieth International Conference on Machine Learning, Washington, DC, USA, 21–24 August 2003; pp. 856–863. [Google Scholar]
- Draper, B.A.; Baek, K.; Bartlett, M.S.; Beveridge, J.R. Recognizing faces with pca and ica. Comput. Vis. Image Underst. 2003, 91, 115–137. [Google Scholar] [CrossRef]
- Liu, Z.P. Linear Discriminant Analysis; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006; pp. 2464–2485. [Google Scholar]
- Kukharev, G.; Forczmaski, P.L. Face recognition by means of two-dimensional direct linear discriminant analysis. In Proceedings of the 8th International Conference on Pattern Recognition and Information Processing, Minsk, Belarus, 18–20 May 2005; Volume 280. [Google Scholar]
- Li, H.; Jiang, T.; Zhang, K. Efficient and robust feature extraction by maximum margin criterion. IEEE Trans. Neural Netw. 2006, 17, 157–165. [Google Scholar] [CrossRef]
- Bilgin, G.; Erturk, S.; Yildirim, T. Nonlinear dimension reduction methods and segmentation of hyperspectral images. In Proceedings of the IEEE Signal Processing, Communication and Applications Conference, Aydin, Turkey, 20–22 April 2008; pp. 1–4. [Google Scholar]
- Camps-Valls, G.; Gomez-Chova, L.; Munoz-Mari, J.; Rojo-Alvarez, J.L. Kernel-based framework for multitemporal and multisource remote sensing data classification and change detection. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1822–1835. [Google Scholar] [CrossRef]
- Song, J.; Gao, L.; Nie, F.; Shen, H.; Yan, Y.; Sebe, N. Optimized graph learning with partial tags and multiple features for image and video annotation. IEEE Trans. Image Process. 2016, 25, 4999–5011. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, J.; Zha, H. Adaptive manifold learning. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 253–265. [Google Scholar] [CrossRef]
- Wu, W.; Massart, D.L.; Jong, S.D. The kernel pca algorithms for wide data. Part i: Theory and algorithms. Chemom. Intell. Lab. Syst. 1997, 36, 165–172. [Google Scholar] [CrossRef]
- Mika, S.; Rätsch, G.; Weston, J.; Schölkopf, B.; Müller, K.R. Fisher discriminant analysis with kernels. In Neural Networks for Signal Processing IX: Proceedings of the 1999 IEEE Signal Processing Society Workshop; The Institute of Electrical and Electronics Engineers, Inc.: New York, NY, USA, 1999; pp. 41–48. [Google Scholar]
- Song, J.; Yang, Y.; Li, X.; Huang, Z.; Yang, Y. Robust hashing with local models for approximate similarity search. IEEE Trans. Cybern. 2014, 44, 1225. [Google Scholar] [CrossRef]
- Song, J.; Yang, Y.; Huang, Z.; Shen, H.T.; Luo, J. Effective multiple feature hashing for large-scale near-duplicate video retrieval. IEEE Trans. Multimed. 2013, 15, 1997–2008. [Google Scholar] [CrossRef]
- Tenenbaum, J.B.; De, S.V.; Langford, J.C. A global geometric framework for nonlinear dimensionality reduction. Science 2000, 290, 2319. [Google Scholar] [CrossRef]
- Roweis, S.T.; Saul, L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323. [Google Scholar] [CrossRef]
- He, X.; Cai, D.; Yan, S.; Zhang, H.J. Neighborhood preserving embedding. In Proceedings of the Tenth IEEE International Conference on Computer Vision, Beijing, China, 17–21 October 2005; pp. 1208–1213. [Google Scholar]
- Chen, H.T.; Chang, H.W.; Liu, T.L. Local discriminant embedding and its variants. In Proceedings of the IEEE Computer Society Conference on Computer Vision & Pattern Recognition, San Diego, CA, USA, 20–25 June 2005; pp. 846–853. [Google Scholar]
- Zhou, Y.; Peng, J.; Chen, C.L.P. Dimension reduction using spatial and spectral regularized local discriminant embedding for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1082–1095. [Google Scholar] [CrossRef]
- Liao, W.; Pizurica, A.; Philips, W.; Pi, Y. Feature extraction for hyperspectral images based on semi-supervised local discriminant analysis. IEEE Trans. Geosci. Remote Sens. 2013, 51, 401–404. [Google Scholar]
- Sugiyama, M.; Idé, T.; Nakajima, S.; Sese, J. Semi-Supervised Local Fisher Discriminant Analysis for Dimensionality Reduction; Springer: Berlin/Heidelberg, Germany, 2008; pp. 35–61. [Google Scholar]
- Hua, G.; Brown, M.; Winder, S. Discriminant embedding for local image descriptors. In Proceedings of the IEEE International Conference on Computer Vision, Rio De Janeiro, Brazil, 14–21 October 2007; pp. 1–8. [Google Scholar]
- Wan, M.; Yang, G.; Lai, Z.; Jin, Z. Feature extraction based on fuzzy local discriminant embedding with applications to face recognition. IET Comput. Vis. 2011, 5, 301–308. [Google Scholar] [CrossRef]
- Pang, Y.; Yu, N. Regularized local discrimimant embedding. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Toulouse, France, 14–19 May 2006; p. III. [Google Scholar]
- Tan, K.; Zhu, J.; Du, Q.; Wu, L.; Du, P. A novel tri-training technique for semi-supervised classification of hyperspectral images based on diversity measurement. Remote Sens. 2016, 8, 749. [Google Scholar] [CrossRef]
- Zhang, G.; Jia, X. Feature selection using kernel based local fisher discriminant analysis for hyperspectral image classification. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 1728–1731. [Google Scholar]
- Mei, S.; Ji, J.; Bi, Q.; Hou, J.; Qian, D.; Wei, L. Integrating spectral and spatial information into deep convolutional neural networks for hyperspectral classification. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Beijing, China, 10–15 July 2016. [Google Scholar]
- He, M.; Bo, L.; Chen, H. Multi-scale 3d deep convolutional neural network for hyperspectral image classification. In Proceedings of the IEEE International Conference on Image Processing, Beijing, China, 17–20 September 2017. [Google Scholar]





| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AVIRIS | Non- SMF | 5 | 43.11 | 61.59 | 69.31 | 73.88 | 77.58 | 79.93 | 81.91 | 83.29 | 84.86 | 86.15 |
| 10 | 53.01 | 66.71 | 72.70 | 77.04 | 79.56 | 81.86 | 83.69 | 84.64 | 85.95 | 86.96 | ||
| 15 | 60.57 | 69.52 | 74.92 | 78.21 | 80.91 | 82.56 | 83.94 | 85.44 | 86.45 | 87.35 | ||
| SMF | 5 | 59.01 | 79.01 | 86.60 | 90.75 | 93.36 | 94.98 | 96.37 | 97.13 | 97.83 | 98.34 | |
| 10 | 69.77 | 83.51 | 88.93 | 92.14 | 94.48 | 95.67 | 96.55 | 97.35 | 97.92 | 98.35 | ||
| 15 | 76.54 | 86.00 | 90.96 | 93.47 | 95.23 | 96.21 | 97.14 | 97.79 | 98.30 | 98.65 | ||
| ROSIS | Non- SMF | 5 | 62.45 | 79.98 | 84.83 | 86.53 | 87.51 | 88.43 | 89.10 | 89.78 | 90.19 | 90.58 |
| 10 | 69.83 | 83.35 | 86.68 | 88.72 | 89.61 | 90.36 | 90.87 | 91.27 | 91.63 | 91.94 | ||
| 15 | 75.36 | 84.35 | 87.65 | 88.88 | 89.86 | 90.54 | 90.88 | 91.38 | 91.70 | 92.05 | ||
| SMF | 5 | 71.70 | 89.71 | 93.24 | 95.21 | 96.43 | 96.92 | 97.36 | 97.75 | 97.96 | 98.14 | |
| 10 | 80.11 | 92.52 | 94.33 | 95.91 | 96.73 | 97.27 | 97.63 | 97.96 | 98.29 | 98.39 | ||
| 15 | 85.94 | 93.41 | 95.63 | 96.69 | 97.23 | 97.68 | 97.97 | 98.26 | 98.49 | 98.62 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L = 5 | Tri-training | OA | 59.83 | 75.76 | 82.46 | 86.13 | 88.80 | 90.38 | 91.44 | 92.21 | 92.93 | 93.31 |
| Kappa | 55.41 | 72.38 | 79.96 | 84.15 | 87.21 | 89.01 | 90.23 | 91.11 | 91.93 | 92.36 | ||
| LDE | OA | 57.69 | 74.65 | 80.88 | 83.99 | 86.36 | 88.47 | 89.51 | 90.67 | 91.42 | 92.03 | |
| Kappa | 56.65 | 71.93 | 78.50 | 81.93 | 84.57 | 86.97 | 88.12 | 89.44 | 90.30 | 90.99 | ||
| LFDA | OA | 52.34 | 61.83 | 74.61 | 81.84 | 86.56 | 89.95 | 92.01 | 93.74 | 94.92 | 95.74 | |
| Kappa | 61.09 | 70.80 | 79.20 | 84.25 | 88.23 | 90.97 | 92.56 | 94.08 | 95.02 | 95.67 | ||
| RLDE | OA | 56.86 | 74.96 | 85.29 | 88.82 | 92.14 | 94.56 | 95.99 | 97.19 | 98.16 | 98.16 | |
| Kappa | 52.78 | 71.87 | 83.37 | 87.34 | 91.07 | 93.81 | 95.44 | 96.80 | 97.90 | 97.90 | ||
| L = 10 | Tri-training | OA | 70.07 | 80.29 | 85.21 | 88.17 | 90.07 | 91.47 | 92.49 | 93.25 | 93.81 | 94.00 |
| Kappa | 66.56 | 77.51 | 83.10 | 86.51 | 88.68 | 90.27 | 91.43 | 92.31 | 92.94 | 93.16 | ||
| LDE | OA | 67.93 | 78.95 | 84.48 | 87.06 | 89.22 | 90.46 | 91.37 | 92.04 | 92.54 | 93.09 | |
| Kappa | 67.32 | 77.15 | 82.80 | 85.48 | 87.89 | 89.28 | 90.30 | 91.01 | 91.58 | 92.18 | ||
| LFDA | OA | 57.09 | 70.36 | 79.51 | 85.31 | 88.42 | 91.00 | 93.07 | 94.16 | 95.28 | 96.06 | |
| Kappa | 69.07 | 75.21 | 82.21 | 87.06 | 89.50 | 91.70 | 93.53 | 94.32 | 95.25 | 96.00 | ||
| RLDE | OA | 68.85 | 80.45 | 88.48 | 91.53 | 93.32 | 95.32 | 96.96 | 97.54 | 98.26 | 98.84 | |
| Kappa | 65.59 | 78.11 | 86.95 | 90.41 | 92.42 | 94.67 | 96.53 | 97.20 | 98.02 | 98.68 | ||
| L = 15 | Tri-training | OA | 73.75 | 82.56 | 86.25 | 89.17 | 90.55 | 91.93 | 93.04 | 93.57 | 93.92 | 94.45 |
| Kappa | 70.60 | 80.12 | 84.31 | 87.64 | 89.22 | 90.80 | 92.07 | 92.67 | 93.07 | 93.68 | ||
| LDE | OA | 73.43 | 81.61 | 85.83 | 88.15 | 89.97 | 91.43 | 92.36 | 93.03 | 93.48 | 94.01 | |
| Kappa | 72.68 | 79.82 | 84.21 | 86.70 | 88.66 | 90.29 | 91.32 | 92.07 | 92.59 | 93.21 | ||
| LFDA | OA | 62.32 | 76.62 | 83.36 | 87.31 | 90.11 | 92.17 | 93.62 | 94.85 | 95.74 | 96.50 | |
| Kappa | 68.91 | 80.68 | 85.36 | 88.31 | 90.62 | 92.39 | 93.62 | 94.80 | 95.60 | 96.36 | ||
| RLDE | OA | 71.89 | 82.96 | 89.29 | 92.57 | 94.77 | 96.34 | 97.28 | 98.08 | 98.63 | 98.98 | |
| Kappa | 68.92 | 80.82 | 87.88 | 91.57 | 94.05 | 95.83 | 96.90 | 97.82 | 98.44 | 98.84 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L = 5 | tri-training | OA | 64.05 | 78.30 | 81.71 | 85.13 | 86.47 | 86.91 | 87.16 | 87.35 | 87.14 | 87.26 |
| Kappa | 55.62 | 71.67 | 76.05 | 80.25 | 82.07 | 82.75 | 83.09 | 83.35 | 83.11 | 83.26 | ||
| LDE | OA | 70.15 | 83.80 | 89.63 | 92.29 | 93.72 | 94.56 | 95.37 | 95.92 | 96.26 | 96.16 | |
| Kappa | 62.78 | 78.42 | 86.14 | 89.67 | 91.61 | 92.75 | 93.82 | 94.56 | 95.02 | 94.89 | ||
| LFDA | OA | 68.54 | 85.61 | 90.40 | 92.30 | 93.70 | 94.33 | 94.88 | 95.31 | 95.60 | 95.90 | |
| Kappa | 65.16 | 81.62 | 87.14 | 89.53 | 91.40 | 92.22 | 92.99 | 93.57 | 93.97 | 94.36 | ||
| RLDE | OA | 71.70 | 89.71 | 93.24 | 95.21 | 96.43 | 96.92 | 97.36 | 97.75 | 97.96 | 98.14 | |
| Kappa | 67.16 | 87.22 | 91.24 | 93.68 | 95.22 | 95.84 | 96.41 | 96.93 | 97.21 | 97.44 | ||
| L = 10 | tri-training | OA | 70.12 | 82.27 | 85.78 | 86.59 | 87.42 | 87.39 | 87.23 | 87.22 | 86.75 | 87.30 |
| Kappa | 63.03 | 76.53 | 80.98 | 82.21 | 83.34 | 83.39 | 83.25 | 83.24 | 82.70 | 83.37 | ||
| LDE | OA | 77.92 | 88.64 | 92.10 | 93.76 | 95.03 | 95.40 | 95.84 | 96.19 | 96.50 | 96.66 | |
| Kappa | 72.27 | 84.81 | 89.38 | 91.64 | 93.37 | 93.86 | 94.45 | 94.92 | 95.34 | 95.55 | ||
| LFDA | OA | 76.41 | 88.52 | 91.59 | 93.18 | 94.07 | 94.73 | 95.32 | 95.65 | 95.98 | 96.33 | |
| Kappa | 73.85 | 86.09 | 89.41 | 91.24 | 92.24 | 93.02 | 93.76 | 94.17 | 94.57 | 95.04 | ||
| RLDE | OA | 80.11 | 92.52 | 94.33 | 95.91 | 96.73 | 97.27 | 97.63 | 97.96 | 98.29 | 98.39 | |
| Kappa | 76.45 | 90.38 | 92.53 | 94.51 | 95.58 | 96.30 | 96.78 | 97.21 | 97.66 | 97.80 | ||
| L = 15 | tri-training | OA | 73.58 | 83.70 | 85.85 | 86.70 | 86.64 | 86.62 | 86.84 | 86.89 | 86.75 | 87.26 |
| Kappa | 66.94 | 78.41 | 81.24 | 82.46 | 82.44 | 82.48 | 82.81 | 82.88 | 82.74 | 83.37 | ||
| LDE | OA | 82.54 | 89.98 | 92.71 | 94.20 | 95.02 | 95.58 | 95.81 | 96.21 | 96.45 | 96.66 | |
| Kappa | 77.72 | 86.66 | 90.24 | 92.24 | 93.35 | 94.10 | 94.41 | 94.95 | 95.28 | 95.55 | ||
| LFDA | OA | 81.94 | 90.59 | 92.99 | 94.12 | 94.82 | 95.38 | 95.75 | 96.09 | 96.30 | 96.54 | |
| Kappa | 79.61 | 87.84 | 90.56 | 92.01 | 92.97 | 93.70 | 94.20 | 94.64 | 94.92 | 95.26 | ||
| RLDE | OA | 85.94 | 93.41 | 95.63 | 96.69 | 97.23 | 97.68 | 97.97 | 98.26 | 98.49 | 98.62 | |
| Kappa | 83.61 | 91.45 | 94.21 | 95.56 | 96.25 | 96.85 | 97.22 | 97.62 | 97.94 | 98.10 |
| Training Samples | L = 5 | L = 10 | L = 15 | ||
|---|---|---|---|---|---|
| Feature Extraction Method | |||||
| AVIRIS | LDE | 64.35%(20) | 75.16%(26) | 78.35%(30) | |
| LFDA | 59.72%(30) | 59.48%(30) | 66.90%(24) | ||
| RLDE | 66.54%(12) | 77.23%(10) | 81.20%(11) | ||
| ROSIS | LDE | 70.20%(21) | 77.93%(24) | 82.61%(24) | |
| RLDE | 72.76%(8) | 80.95%(11) | 86.62%(12) | ||
| LFDA | 71.09%(24) | 76.43%(28) | 82.50%(8) | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ou, D.; Tan, K.; Du, Q.; Zhu, J.; Wang, X.; Chen, Y. A Novel Tri-Training Technique for the Semi-Supervised Classification of Hyperspectral Images Based on Regularized Local Discriminant Embedding Feature Extraction. Remote Sens. 2019, 11, 654. https://doi.org/10.3390/rs11060654
Ou D, Tan K, Du Q, Zhu J, Wang X, Chen Y. A Novel Tri-Training Technique for the Semi-Supervised Classification of Hyperspectral Images Based on Regularized Local Discriminant Embedding Feature Extraction. Remote Sensing. 2019; 11(6):654. https://doi.org/10.3390/rs11060654
Chicago/Turabian StyleOu, Depin, Kun Tan, Qian Du, Jishuai Zhu, Xue Wang, and Yu Chen. 2019. "A Novel Tri-Training Technique for the Semi-Supervised Classification of Hyperspectral Images Based on Regularized Local Discriminant Embedding Feature Extraction" Remote Sensing 11, no. 6: 654. https://doi.org/10.3390/rs11060654
APA StyleOu, D., Tan, K., Du, Q., Zhu, J., Wang, X., & Chen, Y. (2019). A Novel Tri-Training Technique for the Semi-Supervised Classification of Hyperspectral Images Based on Regularized Local Discriminant Embedding Feature Extraction. Remote Sensing, 11(6), 654. https://doi.org/10.3390/rs11060654






