Estimation of Tropospheric and Ionospheric Delay in DInSAR Calculations: Case Study of Areas Showing (Natural and Induced) Seismic Activity
Abstract
1. Introduction
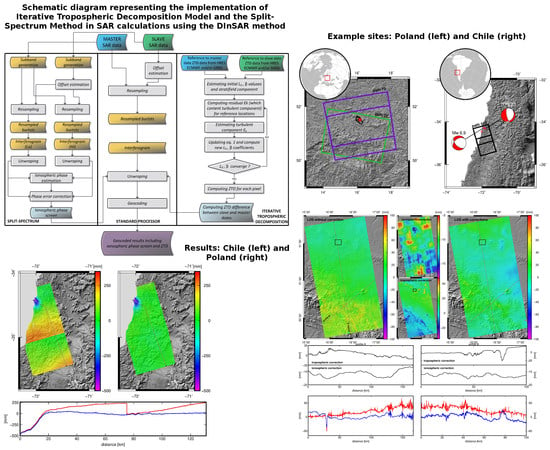
2. Background and Methods
- (I)
- delays due to turbulent mixing in the troposphere. These result from several factors, such as thermal convection, differences in wind speed and direction on different altitudes, friction, and complex weather patterns. Horizontal air currents are the carrier of atmospheric components, including water vapor, which is a significant factor influencing atmospheric signal in SAR images. As the troposphere has a heterogeneous character resulting from local changes, this delay is very difficult to model.
- (II)
- delays resulting from vertical temperature and air-pressure distribution in layers. Each layer has an individual refraction coefficient. The vertical range of atmospheric layers changes in time. For regions that have varied topography, the difference of the vertical distribution of refractions between two image acquisitions causes a phase difference between two image cells having different topographic height.
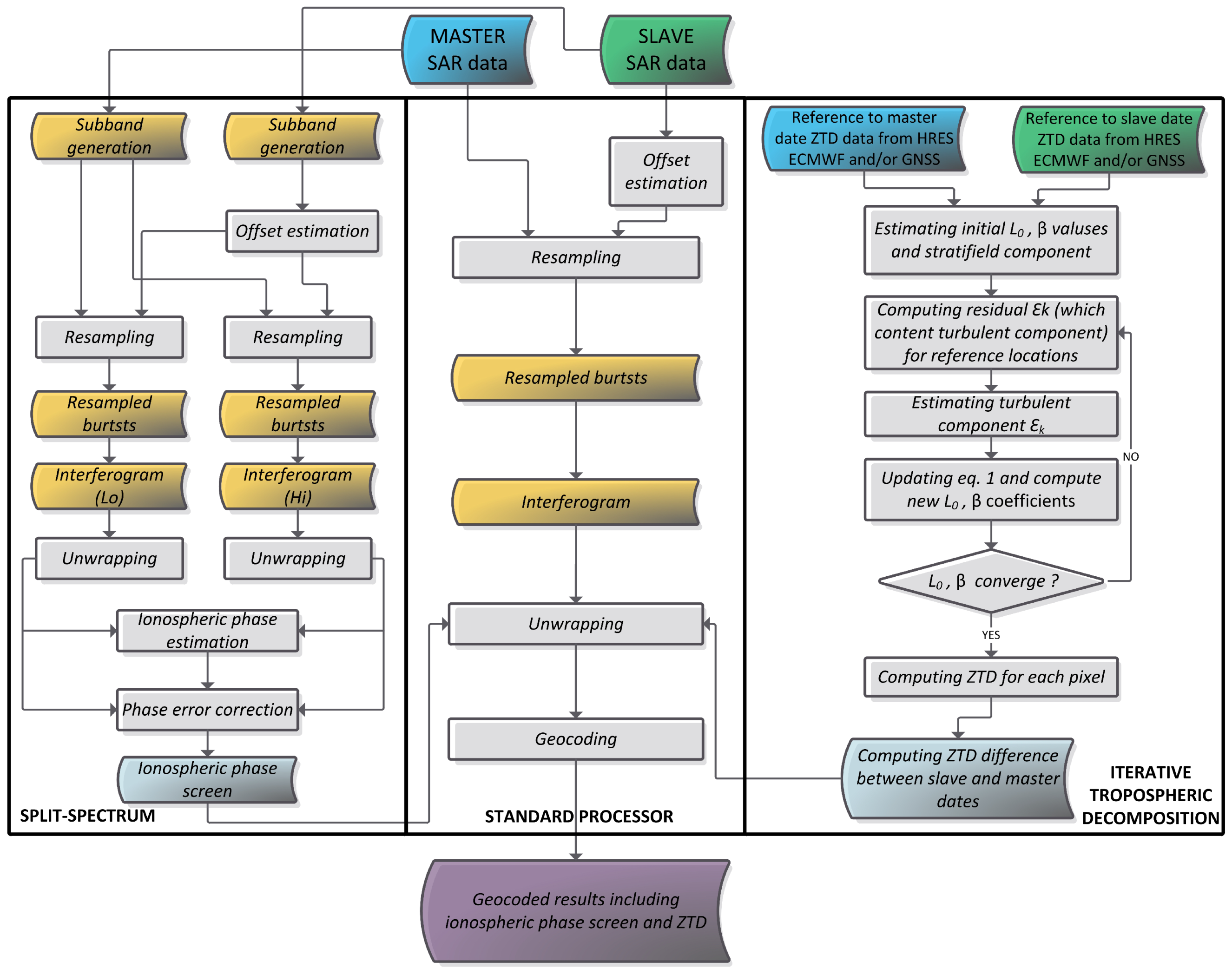
2.1. Tropospheric Delay Correction
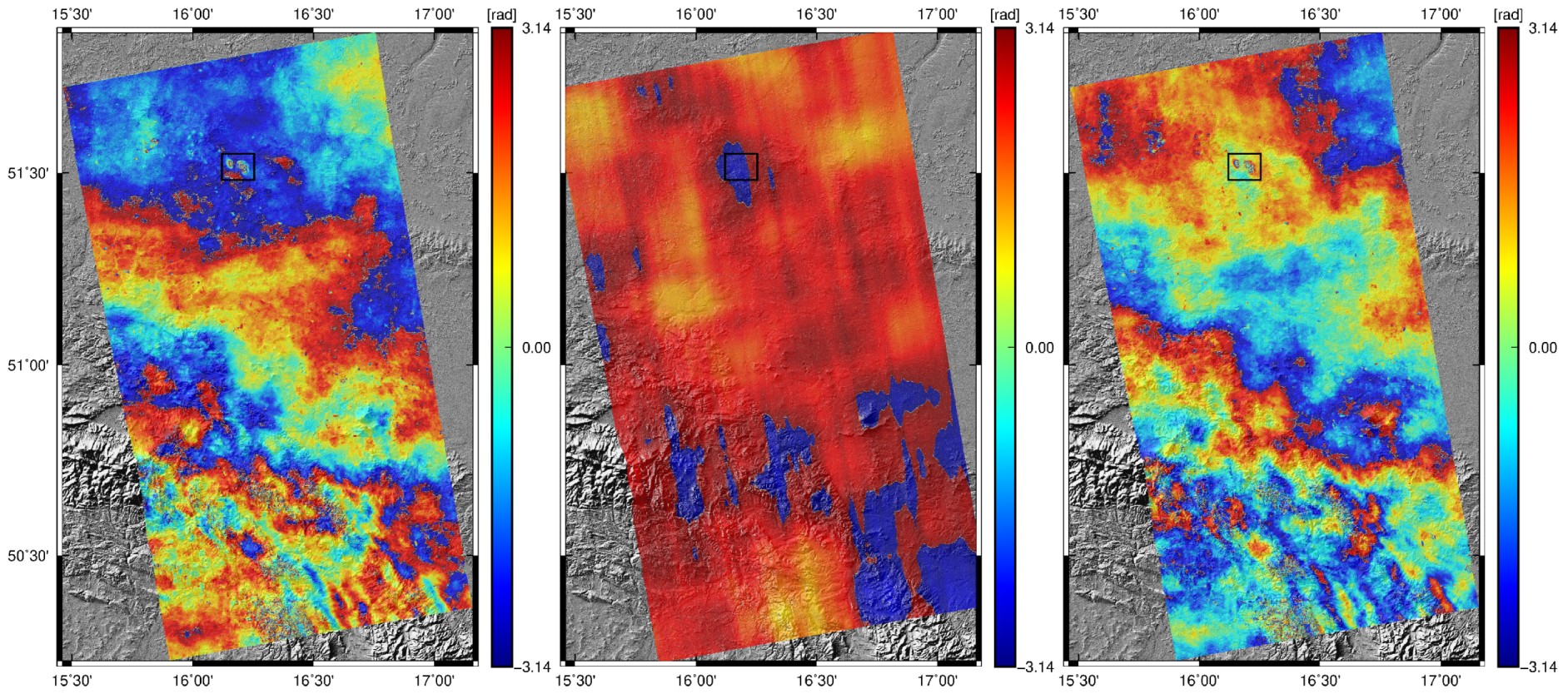
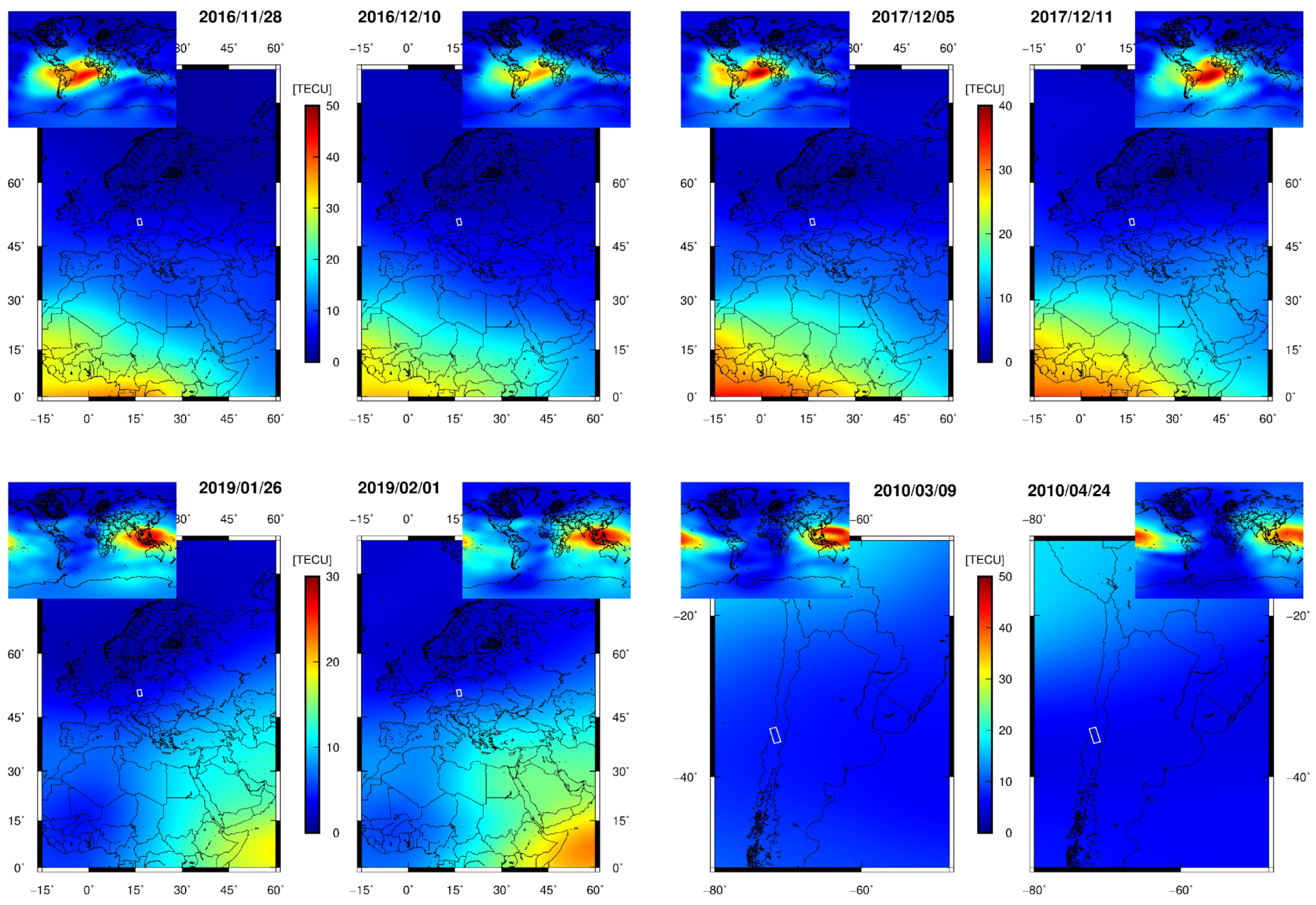
2.2. Ionospheric Delay Correction
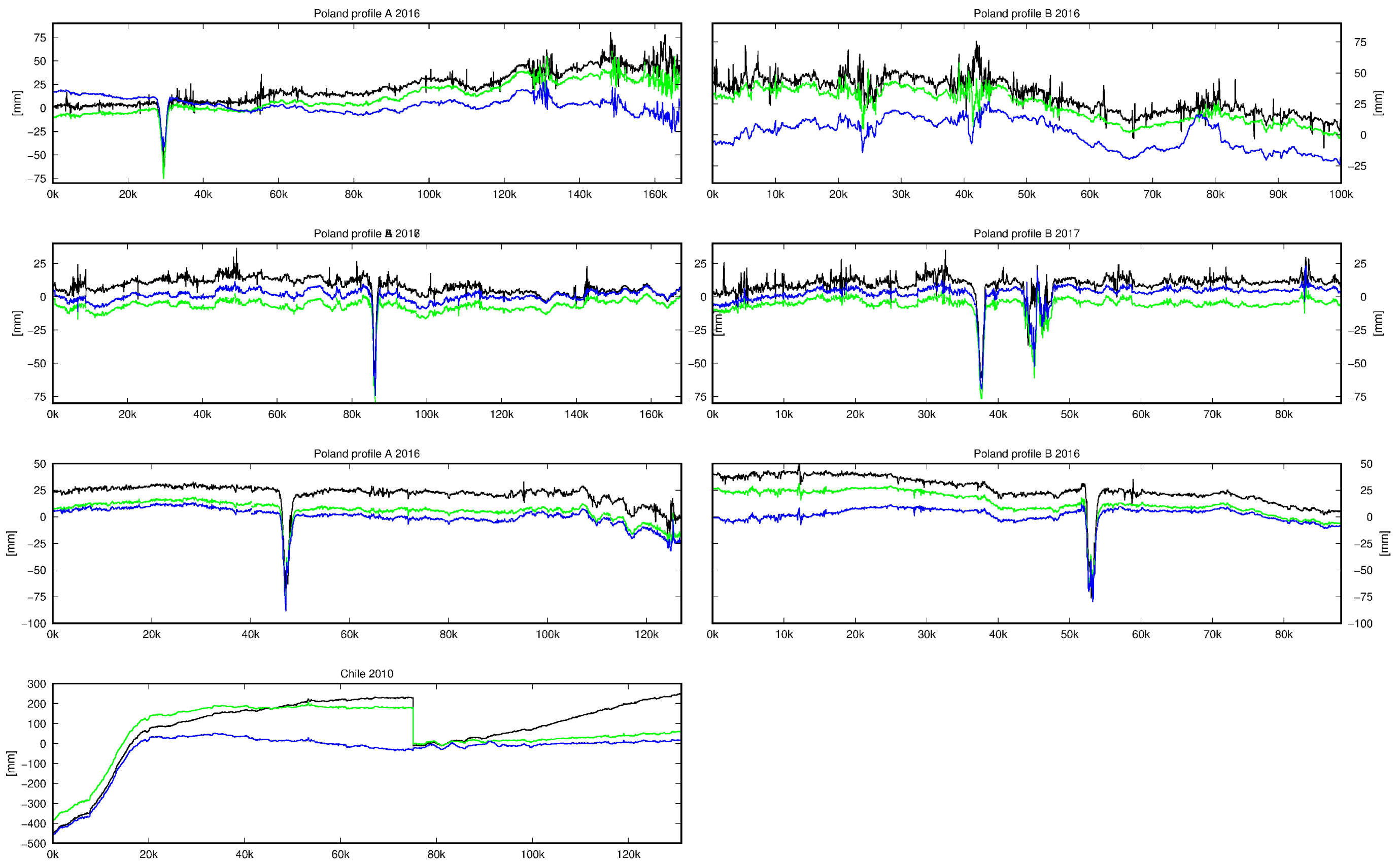
3. Application Examples
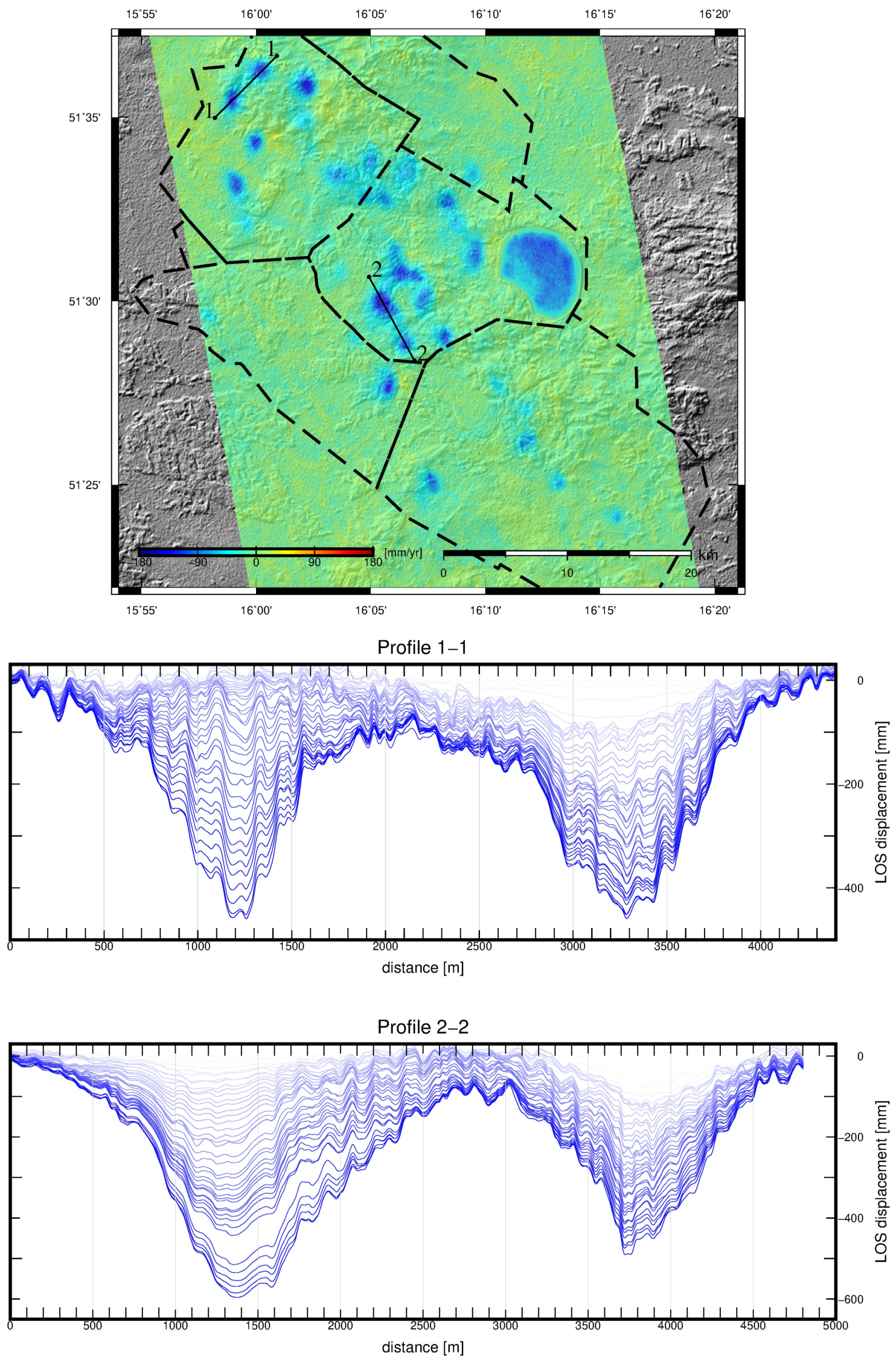
3.1. Legnica-Glogow Copper Belt Area
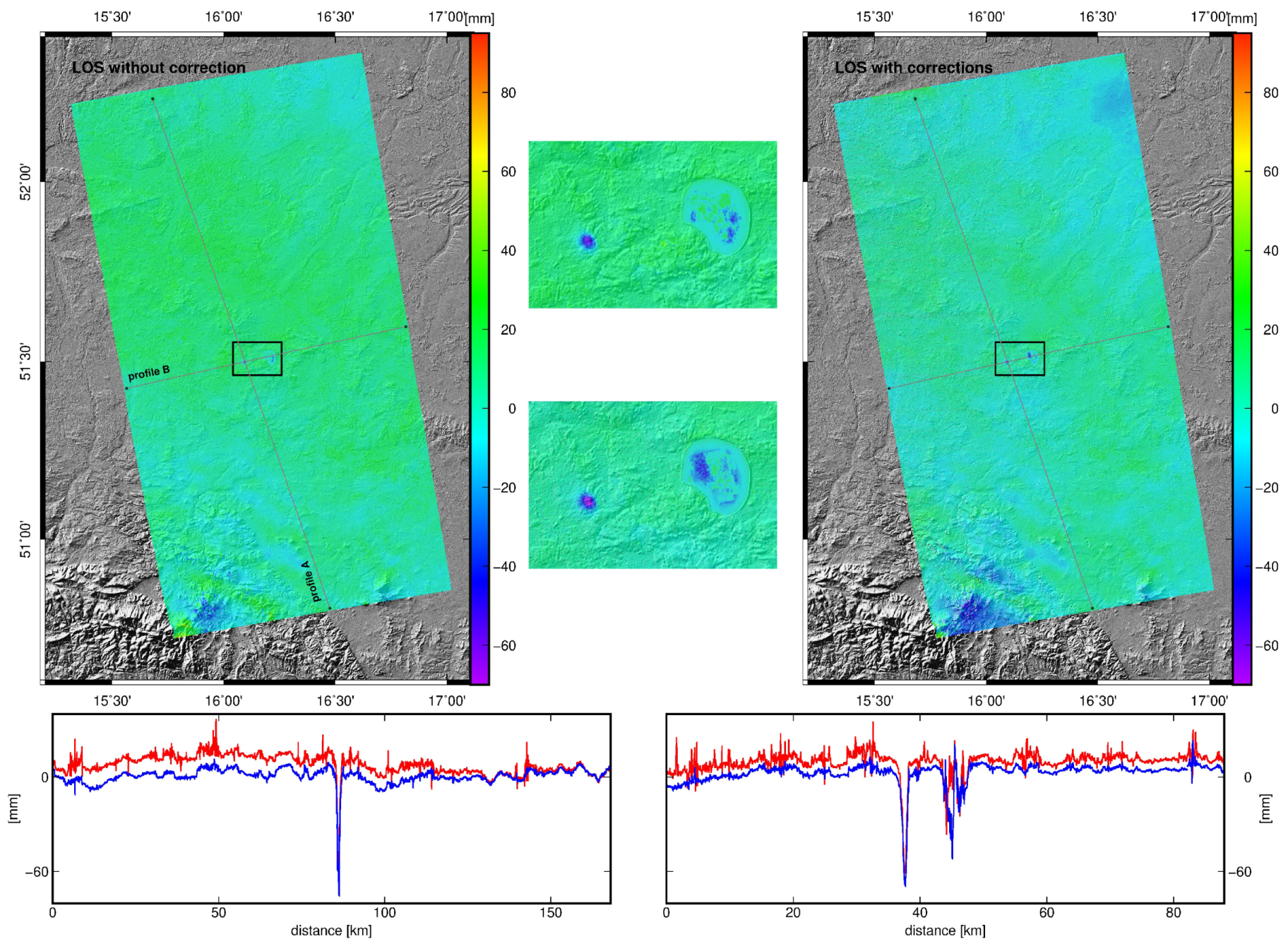
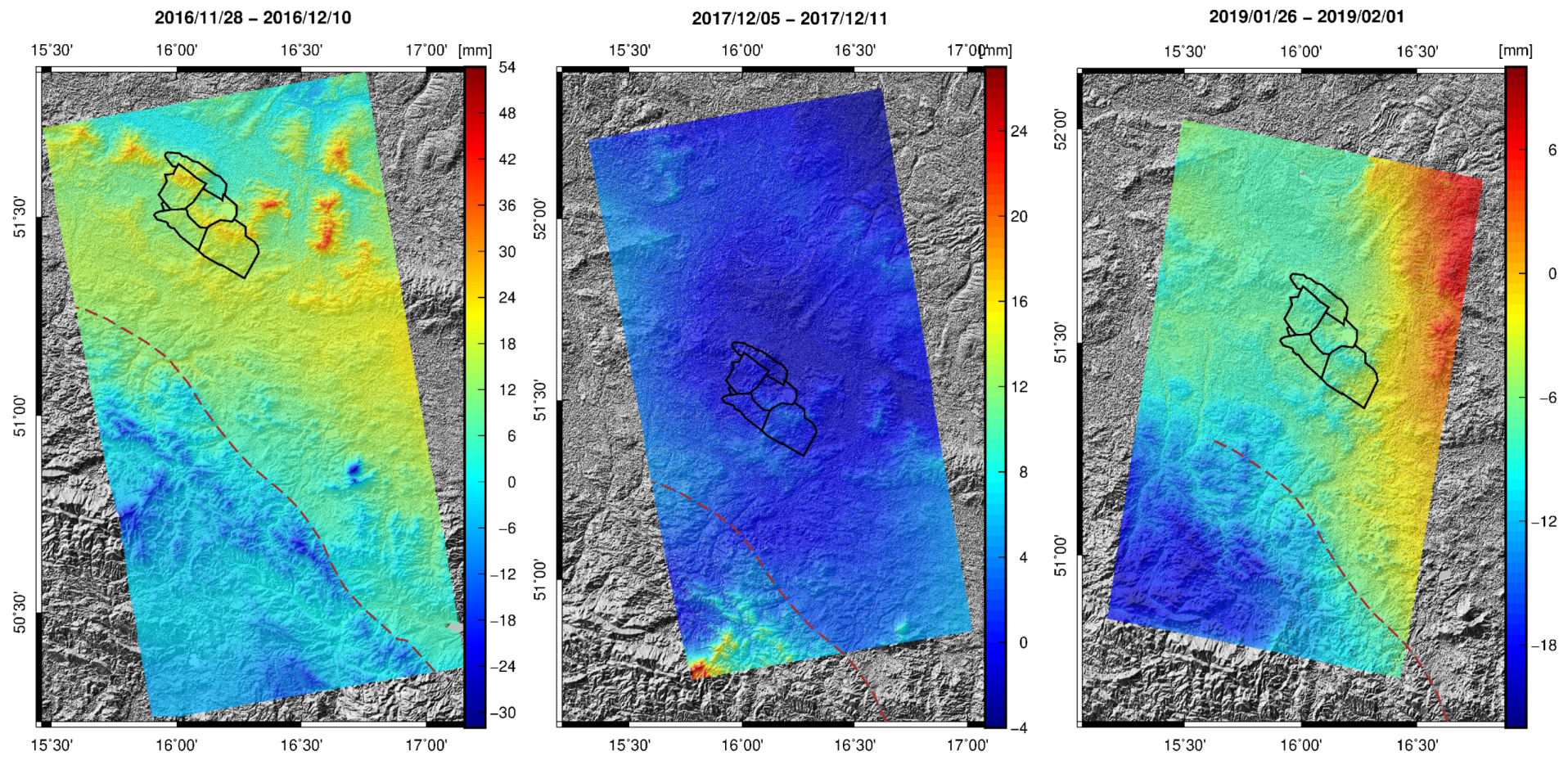
3.2. Induced Tremor on 29 November 2016
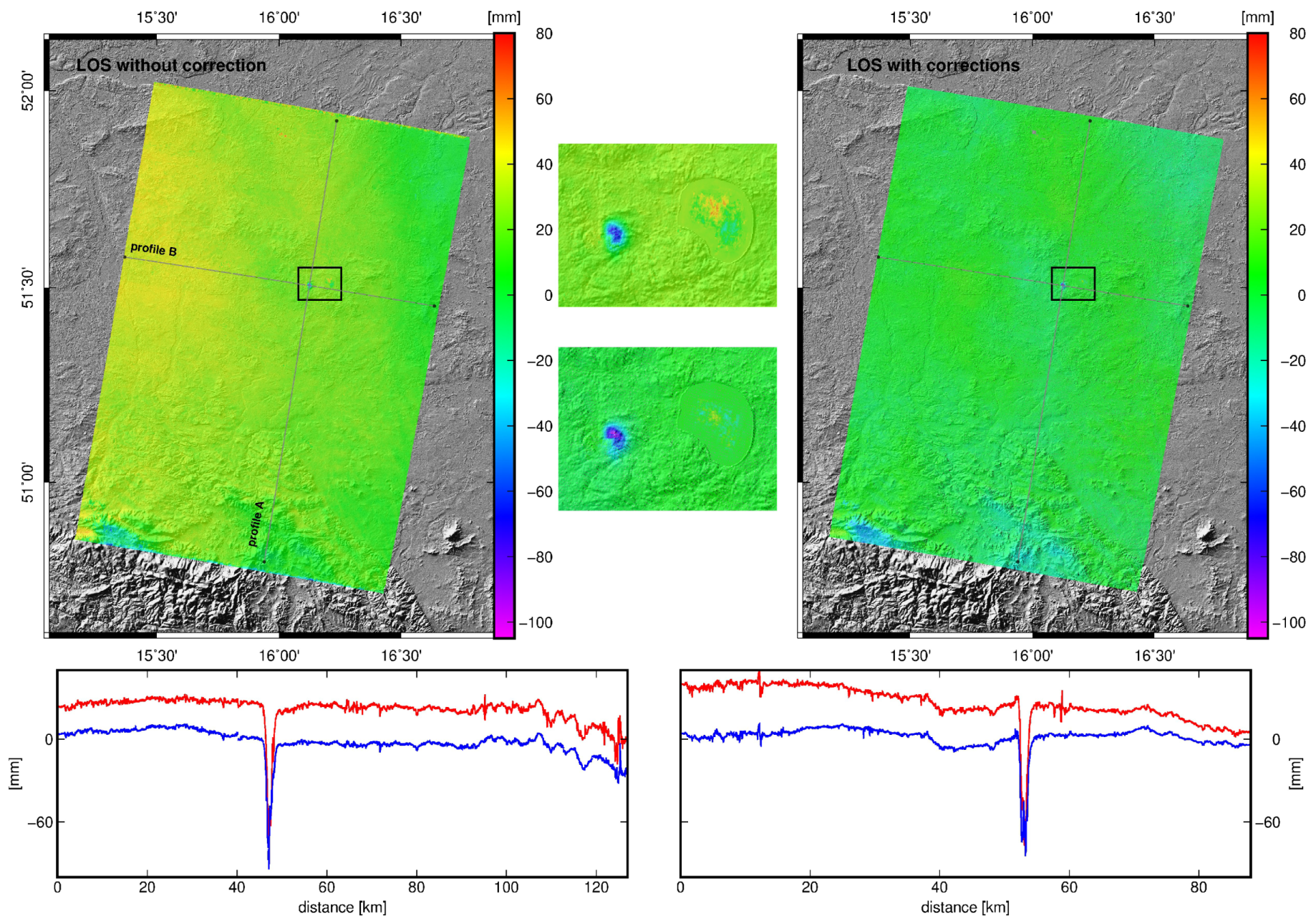
3.3. Induced Tremor on 7 December 2017
3.4. Induced Tremor on 29 January 2019
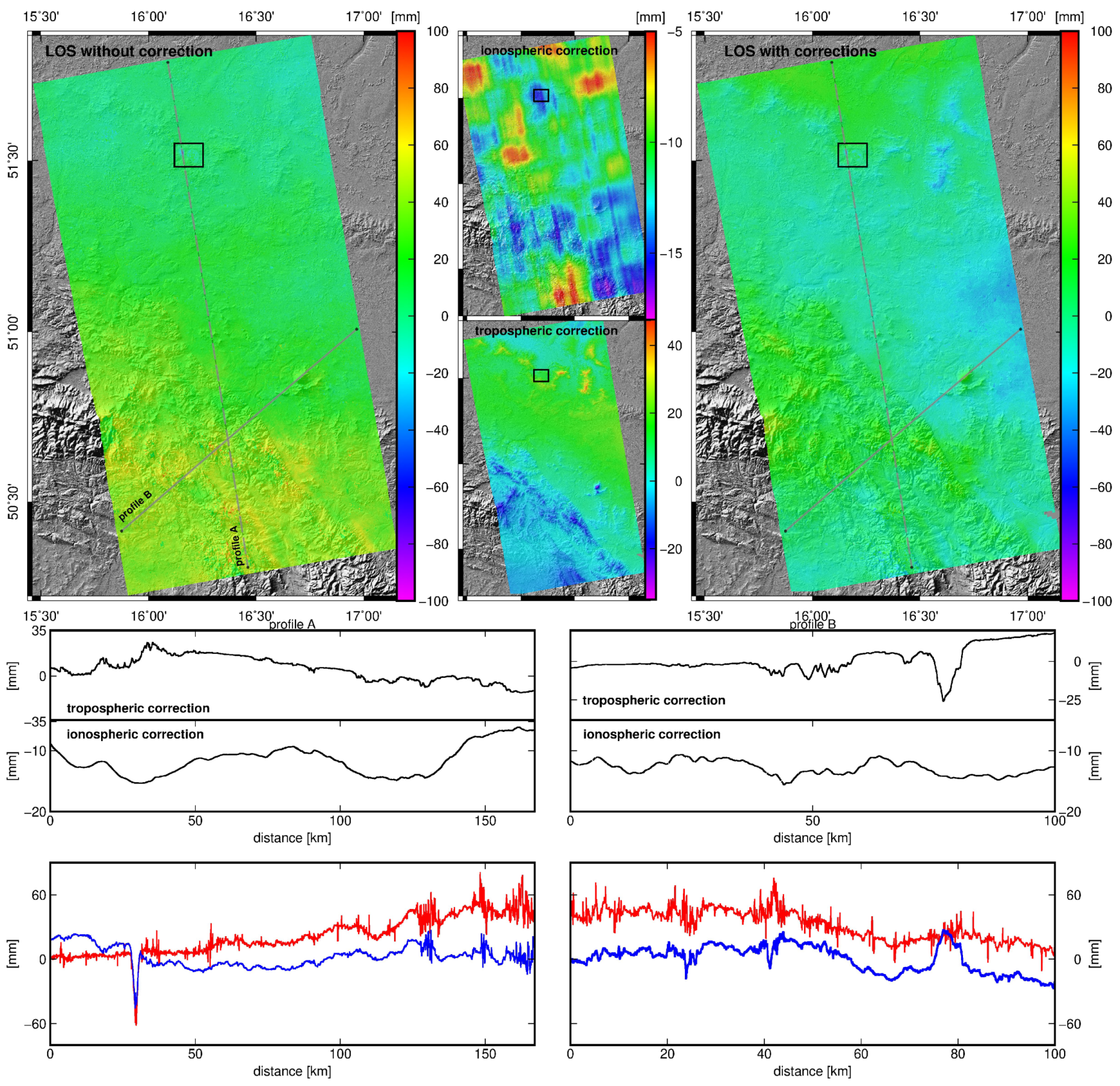
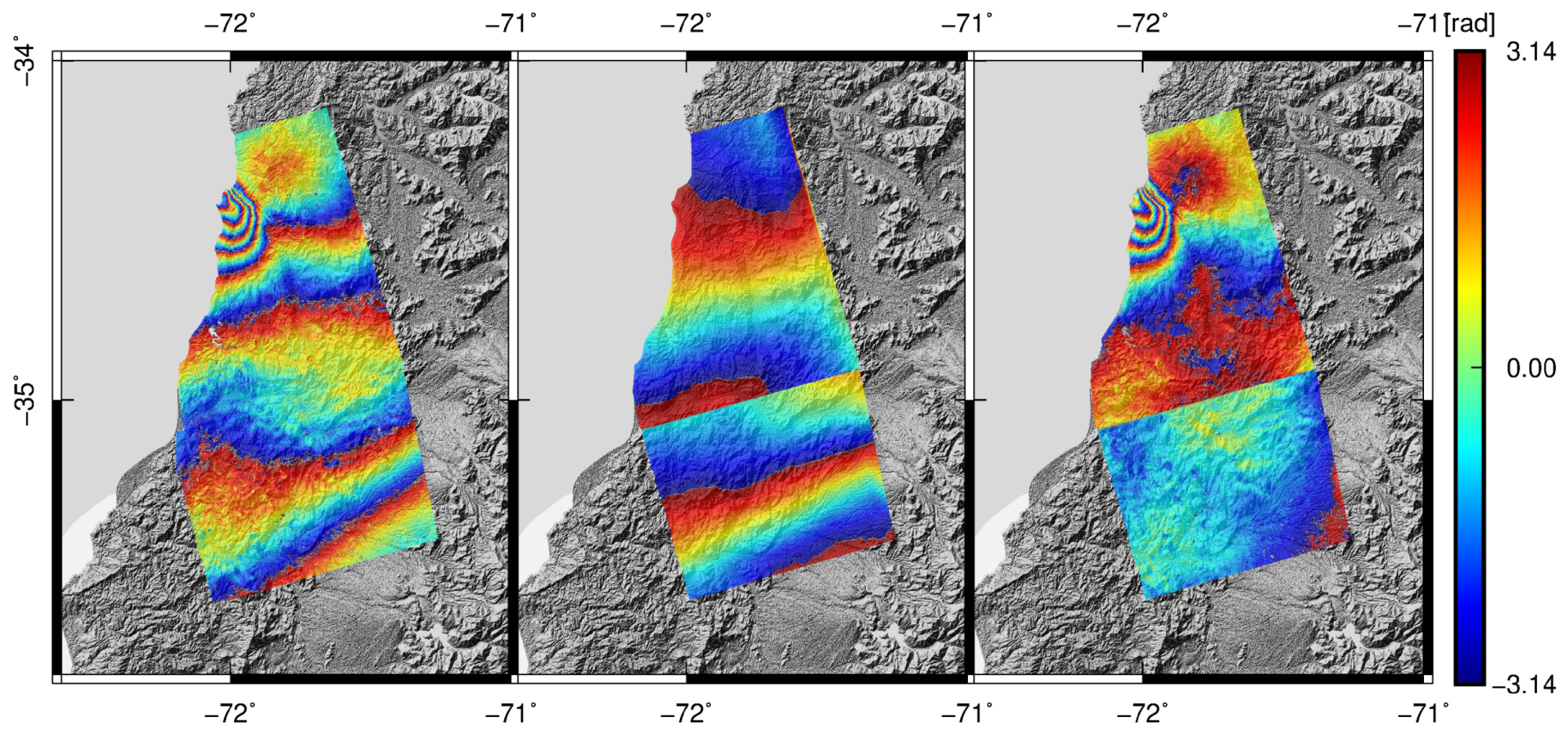
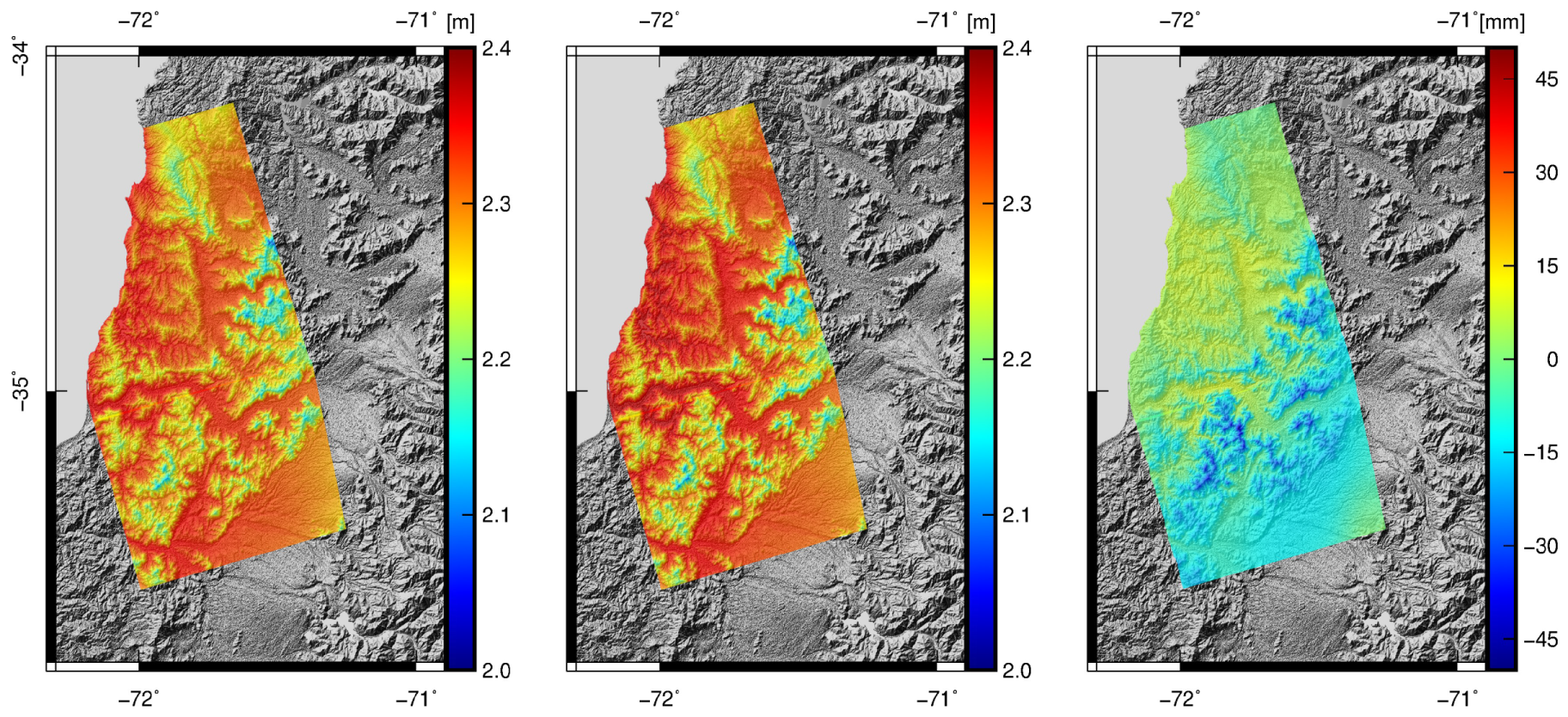
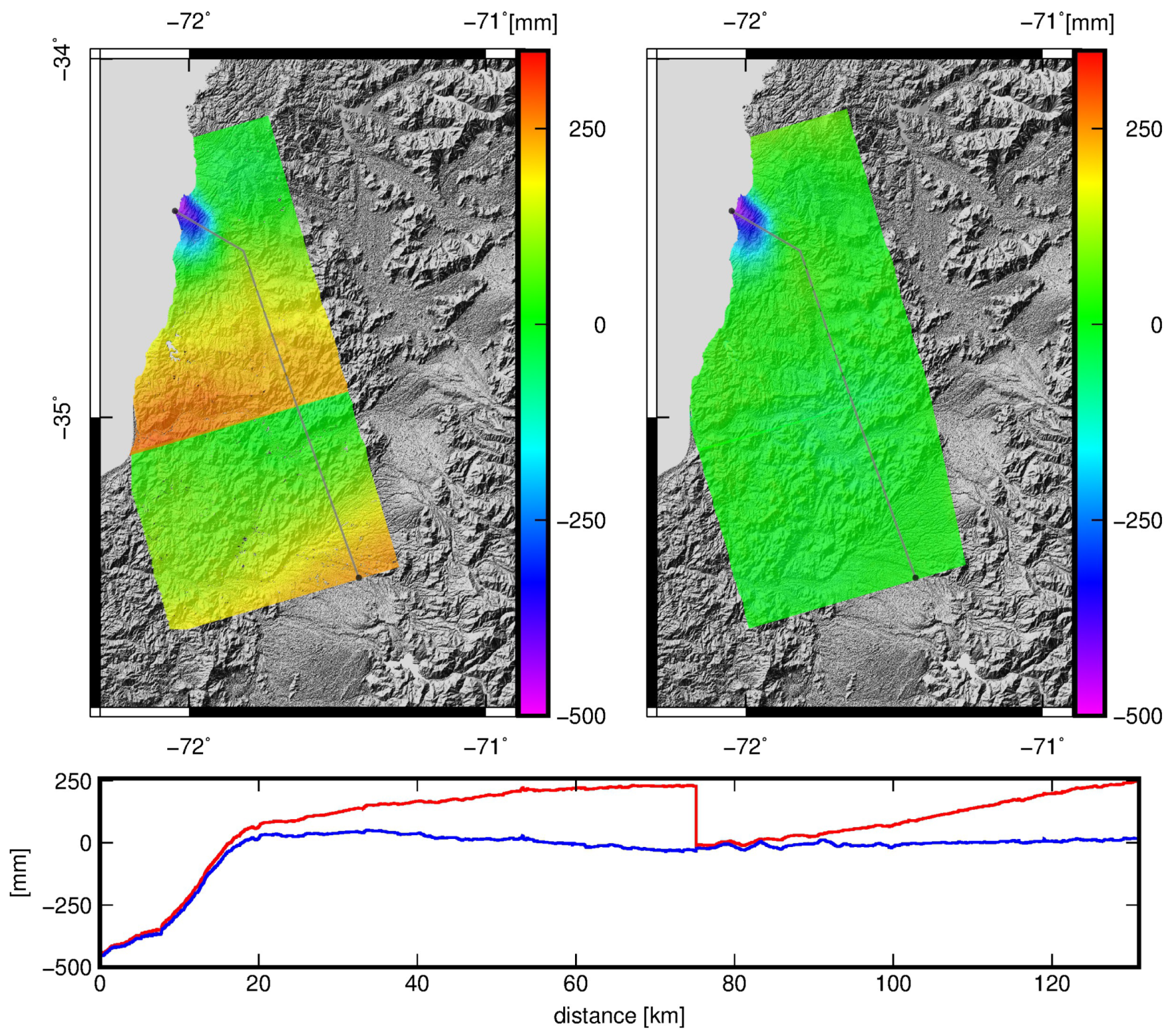
3.5. Chile—Natural Earthquake on 11 March 2010
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Albano, M.; Polcari, M.; Bignami, C.; Moro, M.; Saroli, M.; Stramondo, S. Did anthropogenic activities trigger the 3 April 2017 Mw 6.5 Botswana earthquake? Remote Sens. 2017, 9, 1028. [Google Scholar] [CrossRef]
- Krawczyk, A.; Grzybek, R. An evaluation of processing InSAR Sentinel-1A/B data for correlation of mining subsidence with mining induced tremors in the Upper Silesian Coal Basin (Poland). E3S Web Conf. 2018, 26, 1–5. [Google Scholar] [CrossRef]
- Malinowska, A.A.; Witkowski, W.T.; Guzy, A.; Hejmanowski, R. Mapping ground movements caused by mining-induced earthquakes applying satellite radar interferometry. Eng. Geol. 2018, 246, 402–411. [Google Scholar] [CrossRef]
- Keranen, K.M.; Weingarten, M. Induced Seismicity. Ann. Rev. Earth Planet. Sci. 2018, 46, 149–174. [Google Scholar] [CrossRef]
- Simons, M.; Fialko, Y.; Rivera, L. Earthquake as Inferred from InSAR and GPS Observations. Bull. Seismol. Soc. Am. 2002, 92, 1390–1402. [Google Scholar] [CrossRef]
- Baer, G.; Magen, Y.; Nof, R.N.; Raz, E.; Lyakhovsky, V.; Shalev, E. InSAR Measurements and Viscoelastic Modeling of Sinkhole Precursory Subsidence: Implications for Sinkhole Formation, Early Warning, and Sediment Properties. J. Geophys. Res. Earth Surf. 2018, 123, 678–693. [Google Scholar] [CrossRef]
- Xu, X.; Sandwell, D.T.; Tymofyeyeva, E.; González-Ortega, A.; Tong, X. Tectonic and Anthropogenic Deformation at the Cerro Prieto Geothermal Step-Over Revealed by Sentinel-1A InSAR. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5284–5292. [Google Scholar] [CrossRef]
- Tong, X.; Sandwell, D.T.; Smith-Konter, B. High-resolution interseismic velocity data along the San Andreas Fault from GPS and InSAR. J. Geophys. Res. Solid Earth 2013, 118, 369–389. [Google Scholar] [CrossRef]
- Pagli, C.; Wang, H.; Wright, T.J.; Calais, E.; Lewi, E. Current plate boundary deformation of the Afar rift from a 3-D velocity field inversion of InSAR and GPS. J. Geophys. Res. Solid Earth 2014, 8562–8575. [Google Scholar] [CrossRef]
- Tong, X.; Sandwell, D.T.; Schmidt, D.A. Surface Creep Rate and Moment Accumulation Rate Along the Aceh Segment of the Sumatran Fault from L-band ALOS-1/PALSAR-1 Observations. Geophys. Res. Lett. 2018, 45, 3404–3412. [Google Scholar] [CrossRef]
- Bürgmann, R.; Rosen, P.A.; Fielding, E.J. Synthetic Aperture Radar Interferometry to Measure Earth’s Surface Topography and Its Deformation. Ann. Rev. Earth Planet. Sci. 2000, 28, 169–209. [Google Scholar] [CrossRef]
- Yu, C.; Penna, N.T.; Li, Z. Generation of real-time mode high-resolution water vapor fields from GPS observations. J. Geophys. Res. 2017, 122, 2008–2025. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Penna, N.T.; Crippa, P. Generic Atmospheric Correction Model for Interferometric Synthetic Aperture Radar Observations. J. Geophys. Res. Solid Earth 2018, 9202–9222. [Google Scholar] [CrossRef]
- Brcic, R.; Parizzi, A.; Eineder, M.; Bamler, R.; Meyer, F. Estimation and compensation of ionospheric delay for SAR interferometry. Int. Geosci. Remote Sens. Symp. 2010, 2908–2911. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Chen, C. Measurement and mitigation of the ionosphere in L-band Interferometric SAR data. IEEE Natl. Radar Conf. Proc. 2010, 1459–1463. [Google Scholar] [CrossRef]
- Gomba, G.; Parizzi, A.; Zan, F.D.; Eineder, M.; Member, S.; Bamler, R. Toward Operational Compensation of Ionospheric Effects in SAR Interferograms: The Split-Spectrum Method. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1446–1461. [Google Scholar] [CrossRef]
- Böhm, J.; Schuh, H. (Eds.) Atmospheric Effects in Space Geodesy; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Shim, J.A.S. Analysis of Total Electron Content (TEC) Variations in the Low- and Middle-Latitude Ionosphere. Ph.D. Thesis, Utah State University, Logan, UT, USA, 2009. [Google Scholar]
- Fattahi, H.; Simons, M.; Agram, P. InSAR Time-Series Estimation of the Ionospheric Phase Delay: An Extension of the Split Range-Spectrum Technique. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5984–5996. [Google Scholar] [CrossRef]
- Gomba, G.; Rodriguez Gonzalez, F.; De Zan, F. Ionospheric phase screen compensation for the Sentinel-1 TOPS and ALOS-2 ScanSAR modes. IEEE Trans. Geosci. Remote Sens. 2017, 55, 223–235. [Google Scholar] [CrossRef]
- Rignot, E.J.M. Effect of Faraday rotation on L-band interferometric and polarimetric synthetic-aperture radar data. IEEE Trans. Geosci. Remote Sens. 2000, 38, 383–390. [Google Scholar] [CrossRef]
- Wright, P.A.; Quegan, S.; Wheadon, N.S.; Hall, C.D. Faraday rotation effects on L-band spaceborne SAR data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2735–2744. [Google Scholar] [CrossRef]
- Meyer, F.; Bamler, R.; Jakowski, N.; Fritz, T. The Potential of Low-Frequency SAR Systems for Mapping Ionospheric TEC Distributions. IEEE Geosci. Remote Sens. Lett. 2006, 3, 560–564. [Google Scholar] [CrossRef]
- Jung, H.; Lee, D.; Lu, Z.; Won, J. Ionospheric Correction of SAR Interferograms by Multiple-Aperture Interferometry. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3191–3199. [Google Scholar] [CrossRef]
- Baby, H.B.; Golé, P.; Lavergnat, J. A model for the tropospheric excess path length of radio waves from surface meteorological measurements. Radio Sci. 1988, 23, 1023–1038. [Google Scholar] [CrossRef]
- Ernest, K.; Smith, J.; Weintraub, S. The Constants in the Equation for Atmospheric Refractive Index at Radio Frequencies. Proc. IRE 1953, 50, 1035–1037. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Kluwer Academic: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Wicks, C.W.; Dzurisin, D.; Ingebritsen, S.; Thatcher, W.; Lu, Z.; Iverson, J. Magmatic activity beneath the quiescent Three Sisters volcanic center, central Oregon Cascade Range, USA. Geophys. Res. Lett. 2002, 29, 24–26. [Google Scholar] [CrossRef]
- Lin, Y.N.; Simons, M.; Hetland, E.A.; Muse, P.; DiCaprio, C. A multiscale approach to estimating topographically correlated propagation delays in radar interferograms. Geochem. Geophys. Geosyst. 2010, 11. [Google Scholar] [CrossRef]
- Bekaert, D.P.S.; Walters, R.J.; Wright, T.J.; Hooper, A.J.; Parker, D.J. Statistical comparison of InSAR tropospheric correction techniques. Remote Sens. Environ. 2015, 170, 40–47. [Google Scholar] [CrossRef]
- Bekaert, D.P.S.; Hooper, A.; Wright, T.J. A spatially variable power law tropospheric correction technique for InSAR data. J. Geophys. Res. Solid Earth 2015, 120, 1345–1356. [Google Scholar] [CrossRef]
- Tymofyeyeva, E.; Fialko, Y. Mitigation of atmospheric phase delays in InSAR data, with application to the eastern California shear zone. J. Geophys. Res. Solid Earth 2015, 120, 5952–5963. [Google Scholar] [CrossRef]
- Doin, M.P.; Lasserre, C.; Peltzer, G.; Cavalié, O.; Doubre, C. Corrections of stratified tropospheric delays in SAR interferometry: Validation with global atmospheric models. J. Appl. Geophys. 2009, 69, 35–50. [Google Scholar] [CrossRef]
- Löfgren, J.S.; Björndahl, F.; Moore, A.W.; Webb, F.H.; Fielding, E.J.; Fishbein, E.F. Tropospheric correction for InSAR using interpolated ECMWF data and GPS Zenith Total Delay from the Southern California Integrated GPS Network. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 4503–4506. [Google Scholar] [CrossRef]
- Jolivet, R.; Grandin, R.; Lasserre, C.; Doin, M.P.; Peltzer, G. Systematic InSAR tropospheric phase delay corrections from global meteorological reanalysis data. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Gong, W.; Meyer, F.; Webley, P.W.; Morton, D.; Liu, S. Performance analysis of atmospheric correction in InSAR data based on the Weather Research and Forecasting Model (WRF). In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 2900–2903. [Google Scholar] [CrossRef]
- Li, Z.; Muller, J.P.; Cross, P.; Albert, P.; Hewison, T.; Watson, R.; Fisher, J.; Bennartz, R. Validation of MERIS Near IR Water Vapour Retrievals Using MWR and GPS Measurements. In Proceedings of the MERIS User Workshop, Frascati, Italy, 10–13 November 2003. [Google Scholar]
- Li, Z.; Muller, J.P.; Cross, P.; Albert, P.; Fischer, J.; Bennartz, R. Assessment of the potential of MERIS near-infrared water vapour products to correct ASAR interferometric measurements. Int. J. Remote Sens. 2006, 27, 349–365. [Google Scholar] [CrossRef]
- Li, Z.; Fielding, E.J.; Cross, P.; Preusker, R. Advanced InSAR atmospheric correction: MERIS/MODIS combination and stacked water vapour models. Int. J. Remote Sens. 2009, 30, 3343–3363. [Google Scholar] [CrossRef]
- Cheng, S.; Perissin, D.; Lin, H.; Chen, F. Atmospheric delay analysis from GPS meteorology and InSAR APS. J. Atmos. Sol. Terr. Phys. 2012, 86, 71–82. [Google Scholar] [CrossRef]
- Zhu, W.; Ding, X.L.; Jung, H.S.; Zhang, Q.; Zhang, B.C.; Qu, W. Investigation of ionospheric effects on SAR Interferometry (InSAR): A case study of Hong Kong. Adv. Space Res. 2016, 58, 564–576. [Google Scholar] [CrossRef]
- Wessel, P.; Smith, W.H.F.; Scharroo, R.; Luis, J.; Wobbe, F. Generic Mapping Tools: Improved Version Released. Eos Trans. Am. Geophys. Union 2013, 94, 409–410. [Google Scholar] [CrossRef]
- Sandwell, D.; Mellors, R.; Tong, X.; Wei, M.; Wessel, P. Open Radar Interferometry Software for Mapping Surface Deformation. Eos Trans. Am. Geophys. Union 2011, 92, 234. [Google Scholar] [CrossRef]
- Farr, T.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45, 1–33. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Hayes, G.P.; Meyers, E.K.; Dewey, J.W.; Briggs, R.W.; Earle, P.S.; Benz, H.M.; Smoczyk, G.M.; Flamme, H.E.; Barnhart, W.D.; Gold, R.D.; et al. USGS Open-File Report 2016–1192. Tectonic Summaries of Magnitude 7 and Greater Earthquakes from 2000 to 2015. Tech. Rep. 2016. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J.; Orus, R.; Garcia-Rigo, A.; Feltens, J.; Komjathy, A.; Schaer, S.C.; Krankowski, A. The IGS VTEC maps: A reliable source of ionospheric information since 1998. J. Geod. 2009, 83, 263–275. [Google Scholar] [CrossRef]


| Techniques | Delay | Equation | Selected References | |
|---|---|---|---|---|
| Linear | Both-combined | [28,29,30] | ||
| (without turbulence) | ||||
| Power-law | [31] | |||
| Empirical | ANC | Tropospheric, ionospheric | [7,32] | |
| and orbital artifacts | ||||
| Split-spectrum | Ionospheric | [14,15,16] | ||
| Era-Interim ECMWF | [30,33,34,35] | |||
| HRES ECMWF | Dry | |||
| Weather | ||||
| models | WRF | Wet | [30,36] | |
| MERRA | [35] | |||
| MERIS | [30,37,38,39] | |||
| Spectrometer | Wet only | Same as for weather models | ||
| MODIS | [30,37,39] | |||
| Wet and dry | Same as for weather models | [38,40] | ||
| GNSS | ||||
| Ionospheric | [41] | |||
| Date and Time of Event (UTC) (Day/Month/Year) | Type | Strength [] | Event Location | Satellite | Master Date and Time (UTC) (Day/Month/Year) | Slave Date and Time (UTC) (Day/Month/Year) | Path |
|---|---|---|---|---|---|---|---|
| 29/11/2016 8:09:39 P.M. | Induced tremor | 4.2 | Sentinel 1A | 28/11/2016 4:43:20 P.M. | 10/12/2016 4:43:20 P.M. | 73 | |
| 7/12/2017 5:42:50 P.M. | Induced tremor | 4.5 | Poland, the LGCB region | Sentinel 1A/1B | 5/12/2017 4:43:33 P.M. | 11/12/2017 4:42:51 P.M. | |
| 29/1/2019 12:53:45 P.M. | Induced tremor | 4.1 | Sentinel 1A/1B | 26/1/2019 5:09:03 A.M. | 1/2/2019 5:08:27 A.M. | 22 | |
| 11/3/2010 2:55:27 P.M. | Natural earthquake | 7.0 | Chile, Cardenal Caro province | ALOS 1 | 9/3/2010 4:03:29 A.M. | 24/4/2010 4:03:06 A.M. | 114 |
| 9/3/2010 4:03:03 A.M. | 24/4/2010 4:03:15 A.M. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Milczarek, W.; Kopeć, A.; Głąbicki, D. Estimation of Tropospheric and Ionospheric Delay in DInSAR Calculations: Case Study of Areas Showing (Natural and Induced) Seismic Activity. Remote Sens. 2019, 11, 621. https://doi.org/10.3390/rs11060621
Milczarek W, Kopeć A, Głąbicki D. Estimation of Tropospheric and Ionospheric Delay in DInSAR Calculations: Case Study of Areas Showing (Natural and Induced) Seismic Activity. Remote Sensing. 2019; 11(6):621. https://doi.org/10.3390/rs11060621
Chicago/Turabian StyleMilczarek, Wojciech, Anna Kopeć, and Dariusz Głąbicki. 2019. "Estimation of Tropospheric and Ionospheric Delay in DInSAR Calculations: Case Study of Areas Showing (Natural and Induced) Seismic Activity" Remote Sensing 11, no. 6: 621. https://doi.org/10.3390/rs11060621
APA StyleMilczarek, W., Kopeć, A., & Głąbicki, D. (2019). Estimation of Tropospheric and Ionospheric Delay in DInSAR Calculations: Case Study of Areas Showing (Natural and Induced) Seismic Activity. Remote Sensing, 11(6), 621. https://doi.org/10.3390/rs11060621