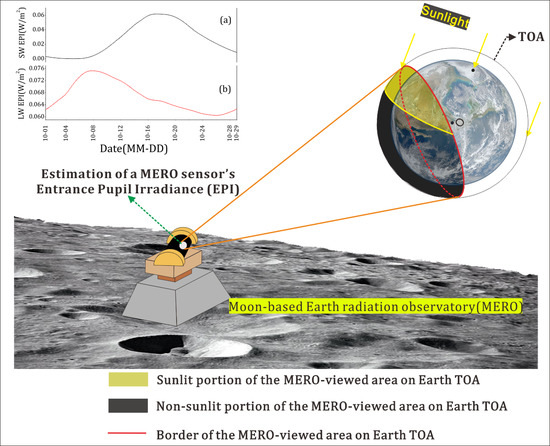
Entrance Pupil Irradiance Estimating Model for a Moon-Based Earth Radiation Observatory Instrument
Abstract
1. Introduction
2. Model
2.1. General Features
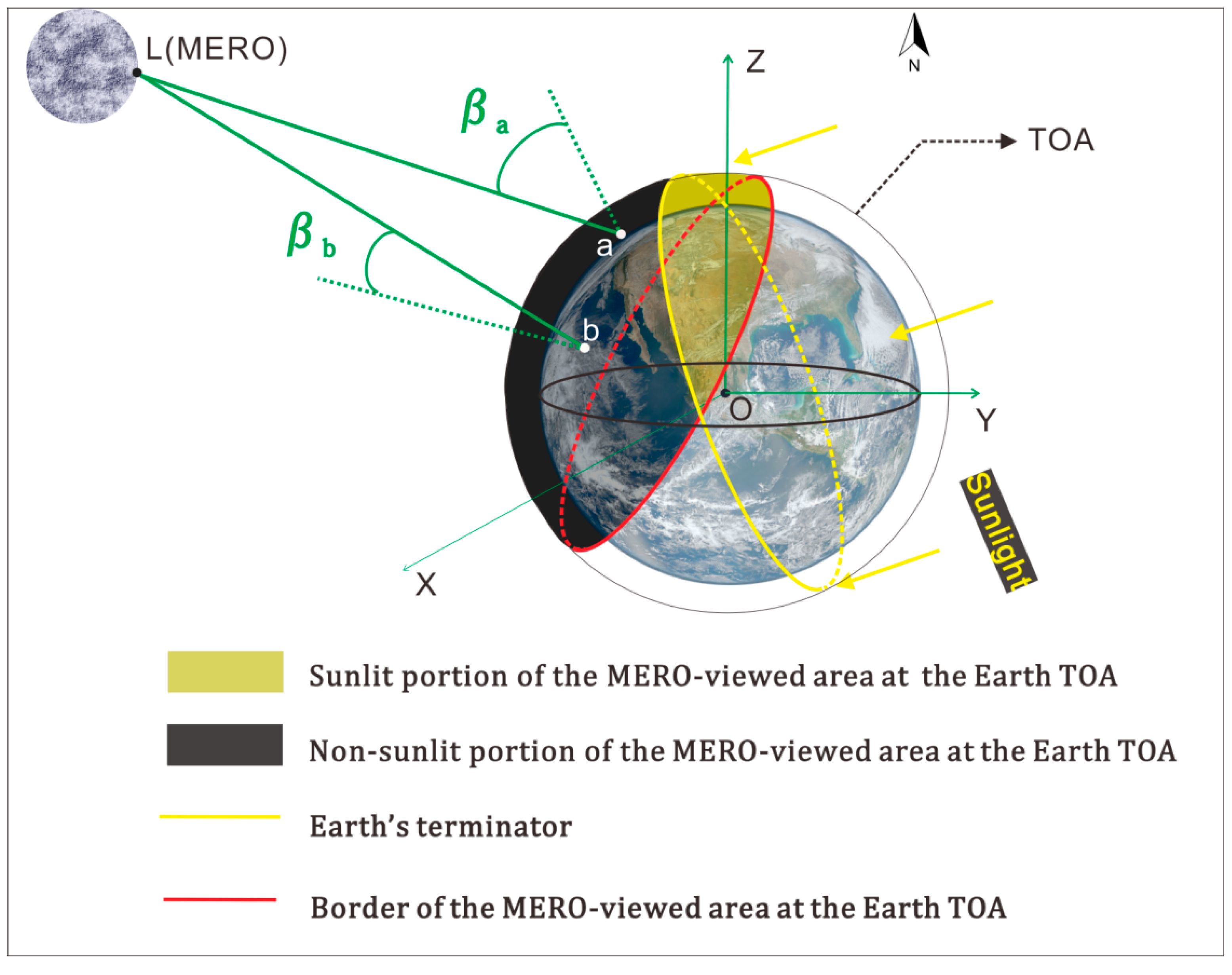
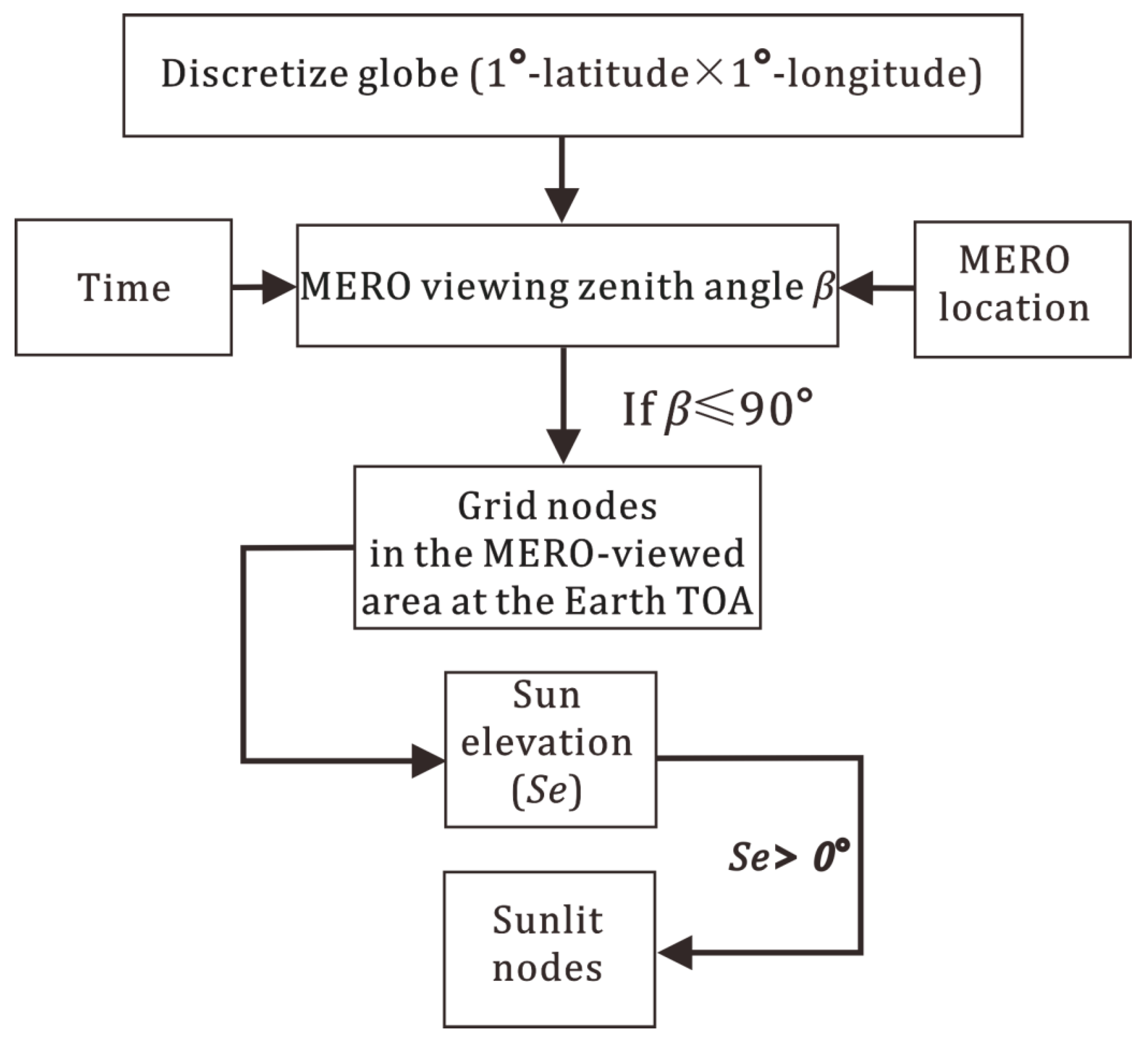
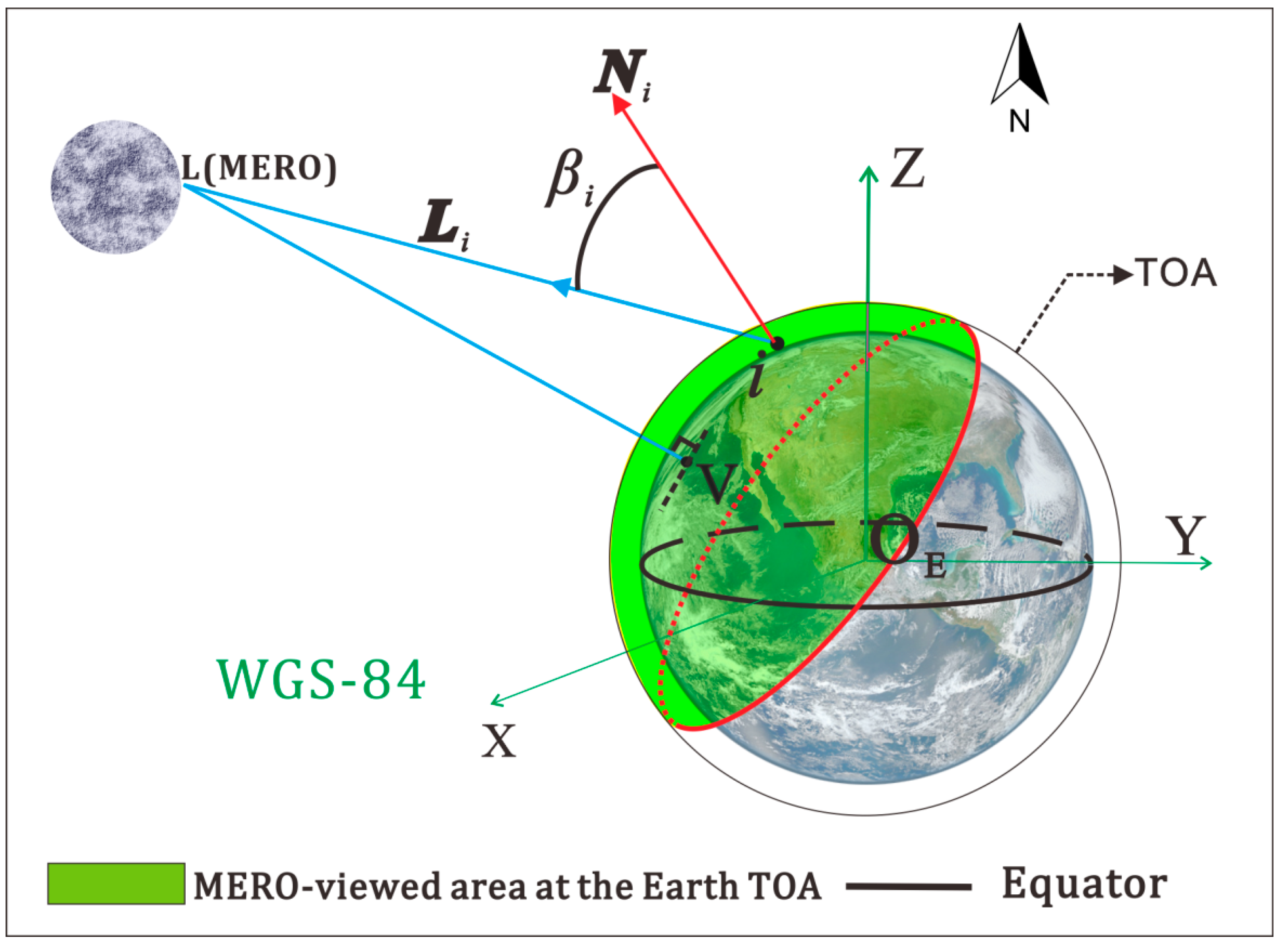
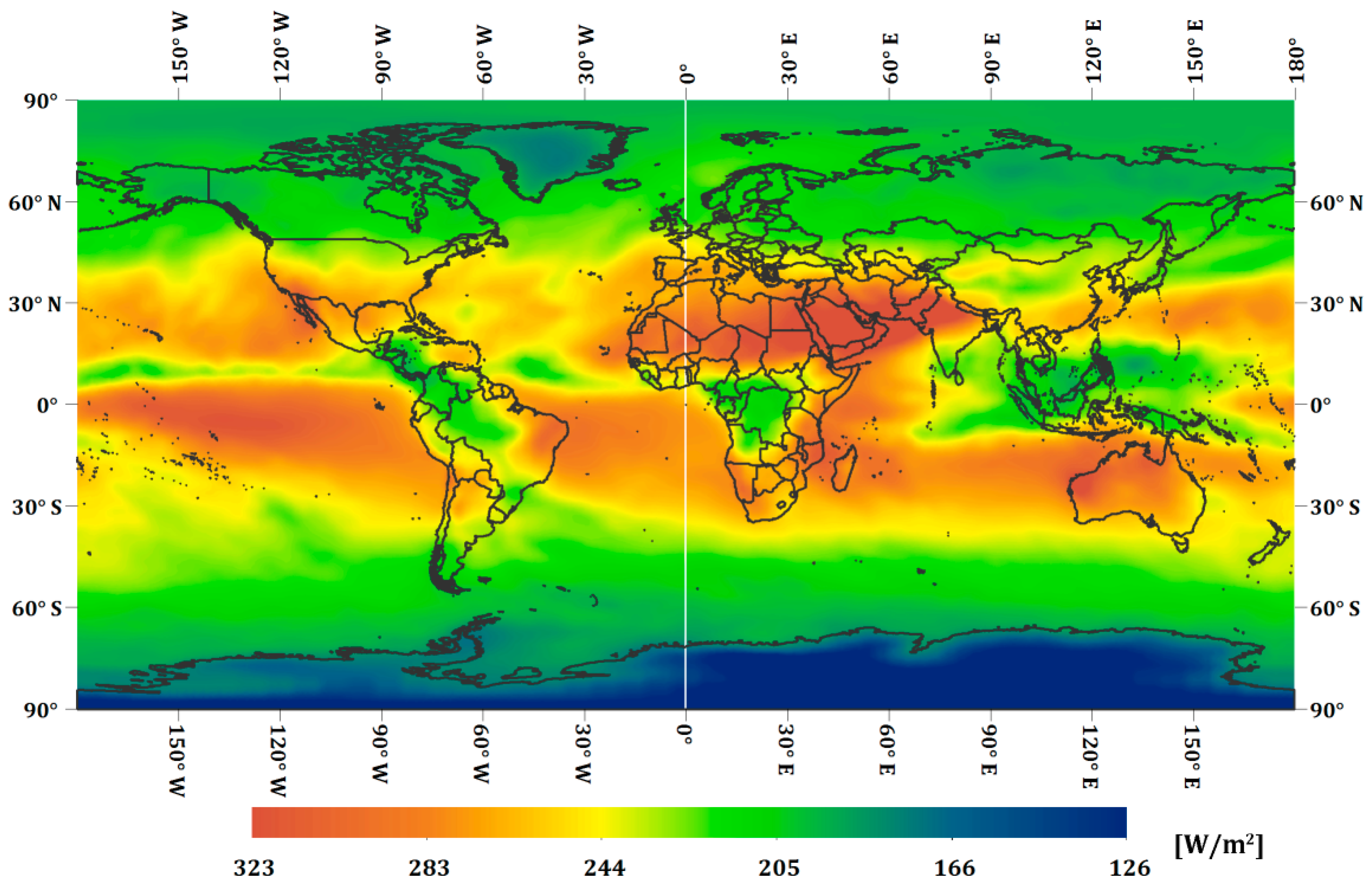
2.2. Temporal–Spatial Distribution of MERO-Viewed Area at the Earth TOA
2.3. Radiation Transfer Function
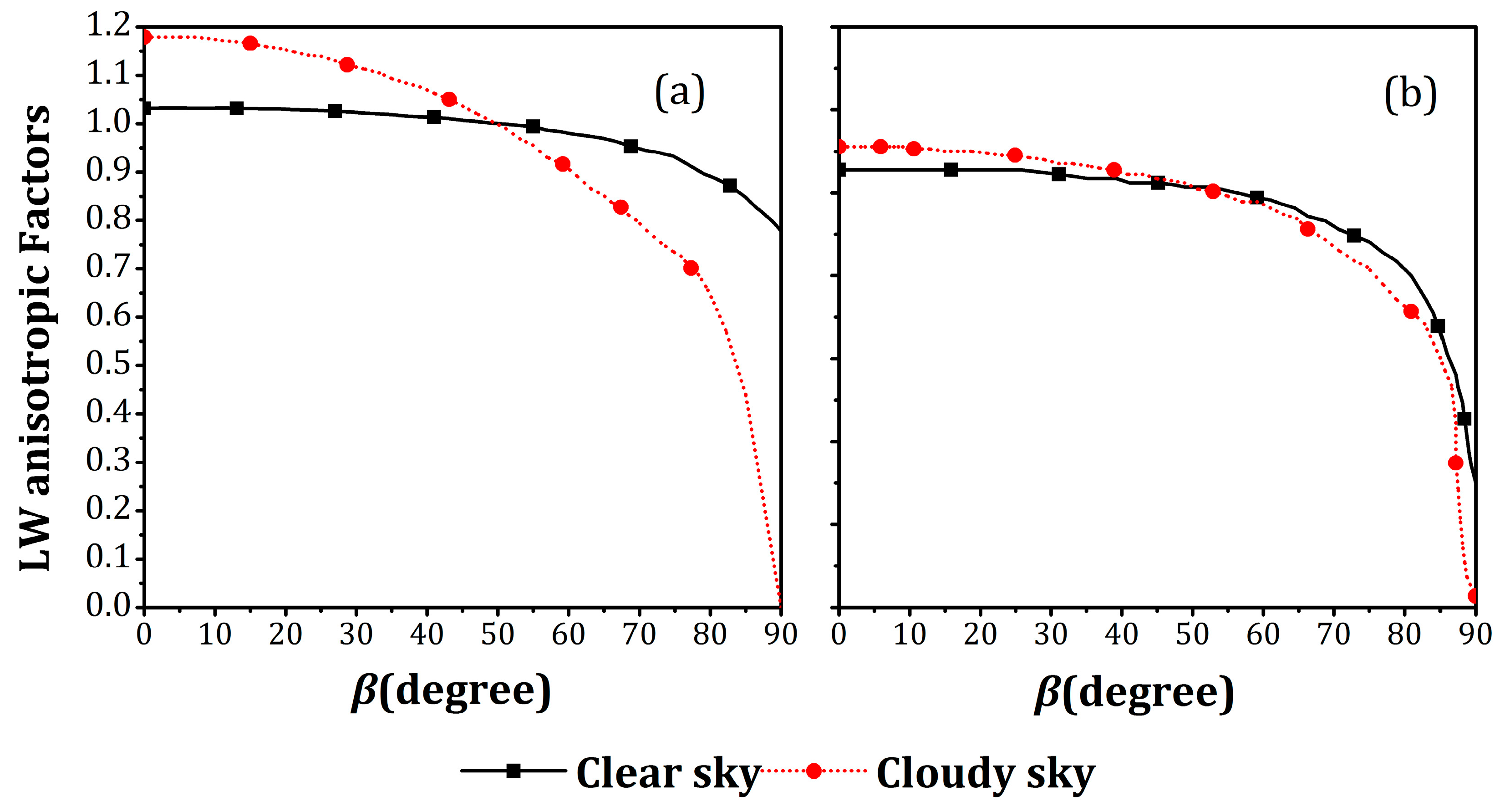
2.4. Earth TOA Anisotropic Factors
- According to the CERES LW ADMs [25], the TOA LW anisotropic factor is determined by a set of viewing-zenith-angle-dependent functions under several scene types. We simplified these scene types as a combination of surface types (ocean, land, desert, and snow) with two cloud conditions (clear sky and cloudy sky), and the surface of a TOA node is defined as the 1° latitude × 1° longitude area at the Earth’s surface directly beneath this node. The clear condition is defined by cloud coverage f ≤ 0.1%. f could be derived from the CERES SYN1deg Ed4A dataset.
3. Application Results and Discussion
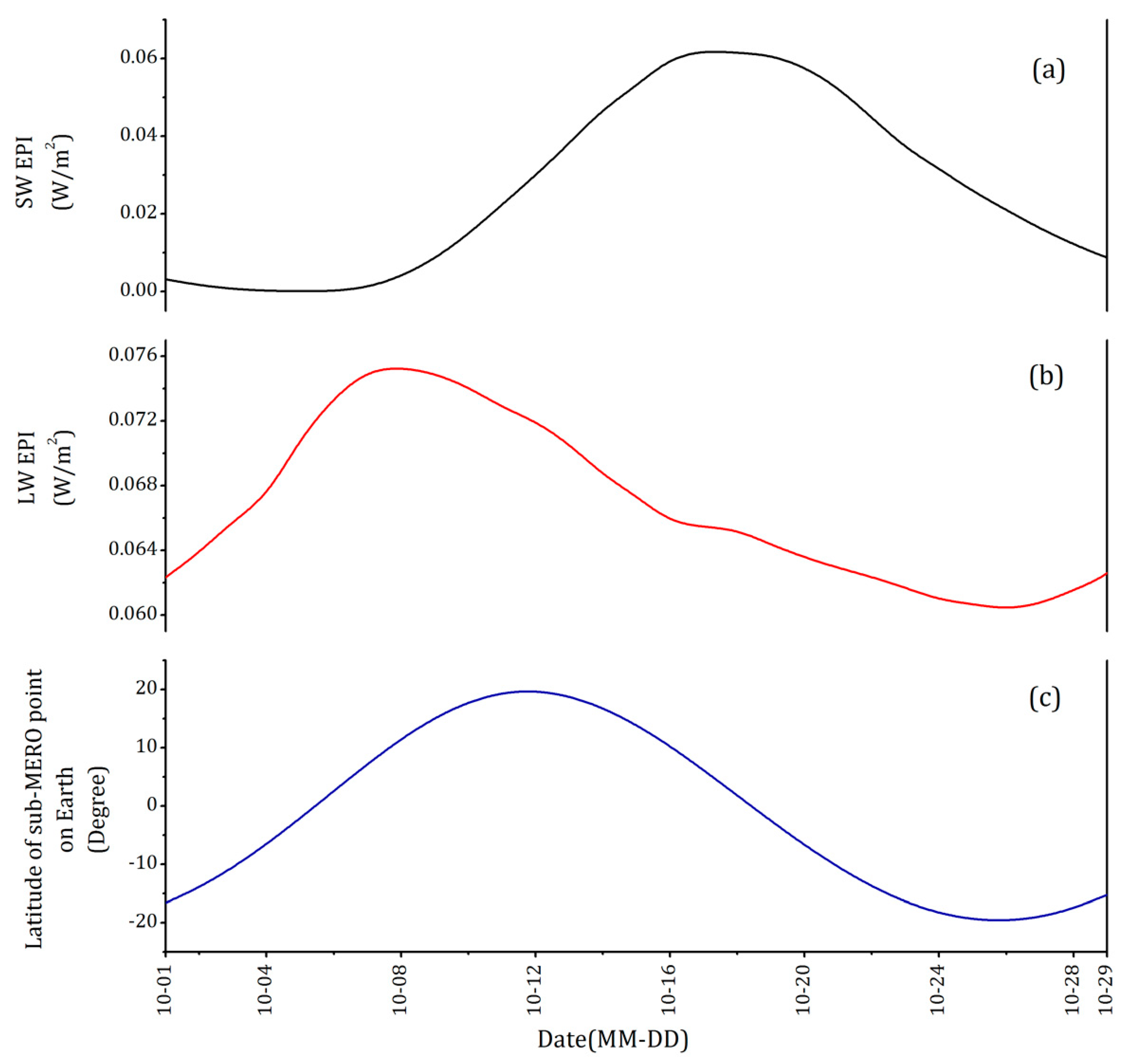
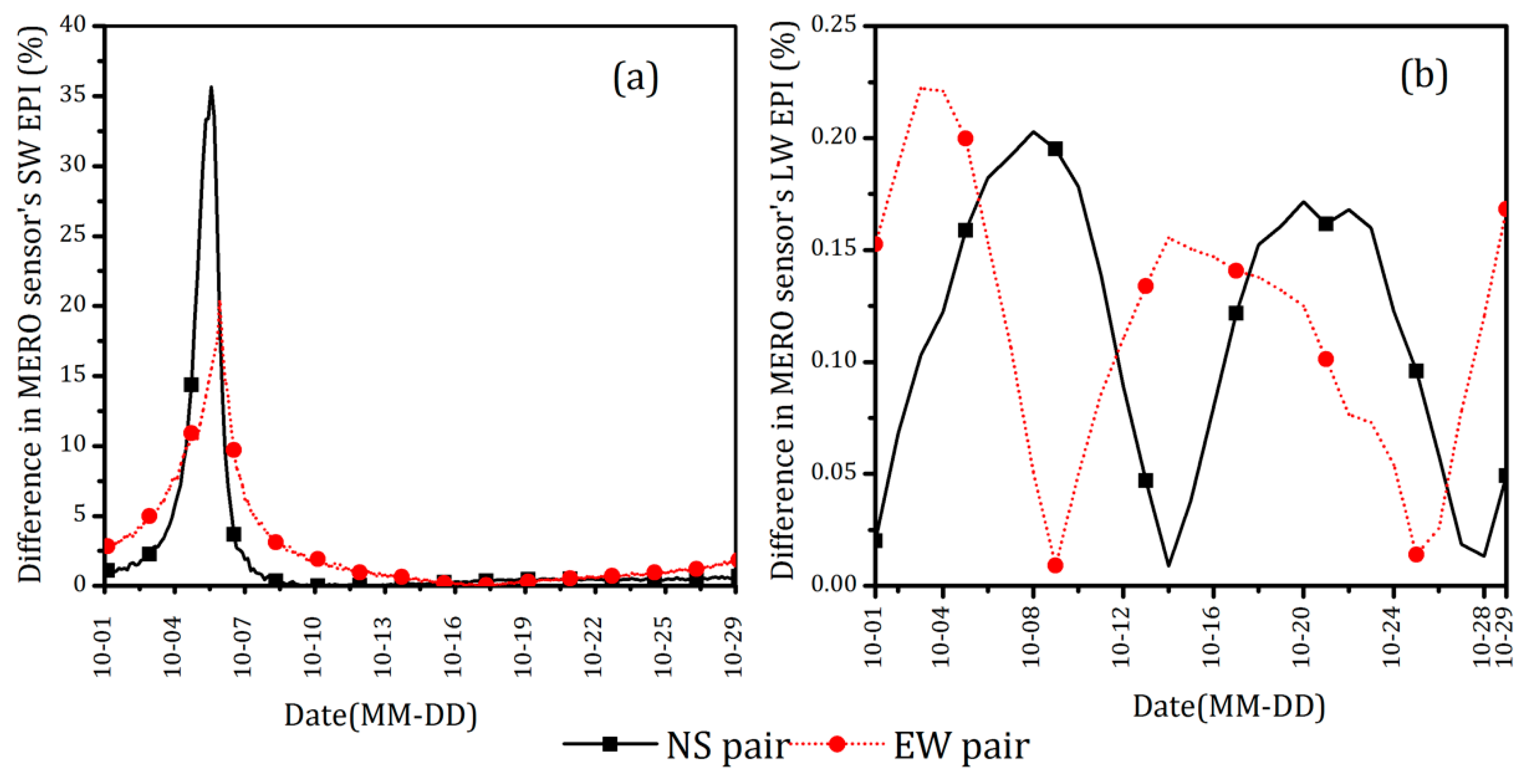
3.1. EPIs over the Moon’s Orbital Period
3.2. EPIs over the Future 18.6 Years
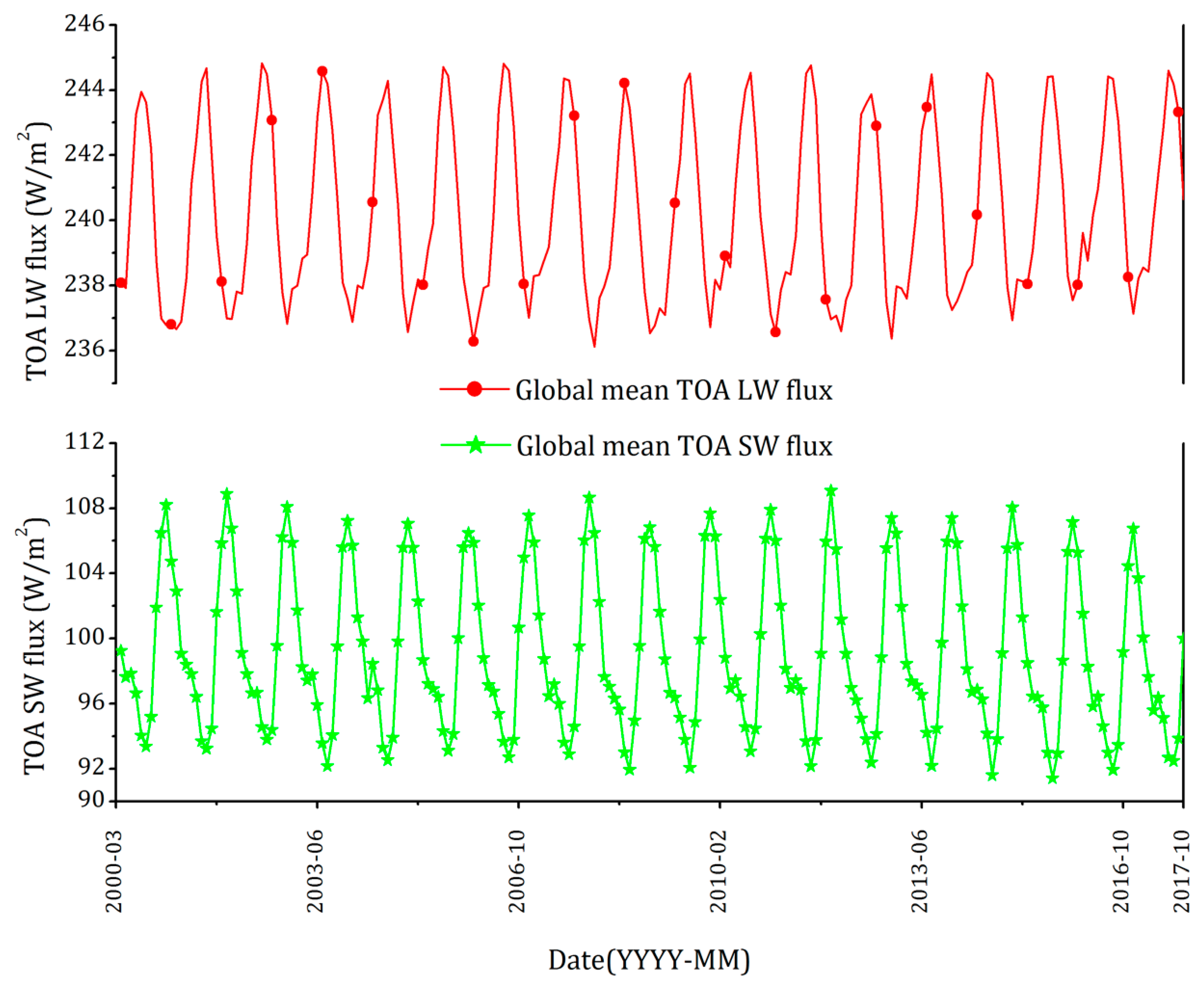
3.2.1. Earth TOA Flux
3.2.2. The Moon–Earth Orbit
3.2.3. Selenographic Location
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wielicki, B.A.; Wong, T.; Allan, R.P.; Slingo, A.; Kiehl, J.T.; Soden, B.J.; Gordon, C.T.; Miller, A.J.; Yang, S.K.; Randall, D.A.; et al. Evidence for large decadal variability in the tropical mean radiative energy budget. Science 2002, 295, 841–844. [Google Scholar] [CrossRef] [PubMed]
- Pinker, R.T.; Zhang, B.; Dutton, E.G. Do satellites detect trends in surface solar radiation? Science 2005, 308, 850–854. [Google Scholar] [CrossRef] [PubMed]
- Luther, M.R.; Cooper, J.E.; Taylor, G.R. The Earth Radiation Budget Experiment Nonscanner Instrument. Rev. Geophys. 1986, 24, 391–399. [Google Scholar] [CrossRef]
- Barkstrom, B.R.; Smith, G.L. The Earth Radiation Budget Experiment: Science and implementation. Rev. Geophys. 1986, 24, 379–390. [Google Scholar] [CrossRef]
- Kopia, L.P. Earth Radiation Budget Experiment Scanner Instrument. Rev. Geophys. 1986, 24, 400–406. [Google Scholar] [CrossRef]
- Wielicki, B.A.; Barkstrom, B.R.; Baum, B.A.; Charlock, T.P.; Green, R.N.; Kratz, D.P.; Lee, R.B.; Minnis, P.; Smith, G.L.; Wong, T. Clouds and the Earth’s Radiant Energy System (CERES): Algorithm overview. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1127–1141. [Google Scholar] [CrossRef]
- Wielicki, B.A.; Barkstrom, B.R.; Harrison, E.F.; Lee, R.B., III; Smith, G.L.; Cooper, J.E. Clouds and the Earth’s Radiant Energy System (CERES): An Earth Observing System Experiment. Bull. Am. Meteorol. Soc. 1996, 77, 853–868. [Google Scholar] [CrossRef]
- Loeb, N.G.; Manalo-Smith, N.; Su, W.; Shankar, M.; Thomas, S. CERES top-of-atmosphere earth radiation budget climate data record: Accounting for in-orbit changes in instrument calibration. Remote Sens. 2016, 8, 182. [Google Scholar] [CrossRef]
- Harries, J.; Crommelynck, D. The geostationary earth radiation budget experiment on MSG-1 and its potential applications. Adv. Space Res. 1999, 24, 915–919. [Google Scholar] [CrossRef]
- Harries, J.E.; Russell, J.; Hanafin, J.; Brindley, H.; Futyan, J.; Rufus, J.; Kellock, S.; Matthews, G.; Wrigley, R.; Last, A. The geostationary earth radiation budget project. Bull. Am. Meteorol. Soc. 2005, 86, 945–960. [Google Scholar] [CrossRef]
- De Paepe, B.; Ignatov, A.; Dewitte, S.; Ipe, A. Aerosol retrieval over ocean from SEVIRI for the use in GERB Earth’s radiation budget analyses. Remote Sens. Environ. 2008, 112, 2455–2468. [Google Scholar] [CrossRef]
- Mantziaras, D. EOS Terra Mission Status. In Proceedings of the Earth Science Constellation MOWG Meeting, Goddard Space Flight Center, Greenbelt, MD, USA, 13–15 June 2017. [Google Scholar]
- Smith, G.L.; Wong, T.; Bush, K.A. Time-Sampling Errors of Earth Radiation From Satellites: Theory for Outgoing Longwave Radiation. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1656–1665. [Google Scholar] [CrossRef]
- Smith, G.L.; Wong, T. Time-Sampling Errors of Earth Radiation from Satellites: Theory for Monthly Mean Albedo. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3107–3115. [Google Scholar] [CrossRef]
- Doelling, D.R.; Loeb, N.G.; Keyes, D.F.; Nordeen, M.L.; Morstad, D.; Nguyen, C.; Wielicki, B.A.; Young, D.F.; Sun, M. Geostationary enhanced temporal interpolation for CERES flux products. J. Atmos. Ocean. Technol. 2013, 30, 1072–1090. [Google Scholar] [CrossRef]
- Huang, S. Surface temperatures at the nearside of the Moon as a record of the radiation budget of Earth’s climate system. Adv. Space Res. 2008, 41, 1853–1860. [Google Scholar] [CrossRef]
- Pallé, E.; Goode, P.R. The Lunar Terrestrial Observatory: Observing the Earth using photometers on the Moon’s surface. Adv. Space Res. 2009, 43, 1083–1089. [Google Scholar] [CrossRef]
- Rogalski, A. Next decade in infrared detectors. In Proceedings of the Electro-Optical and Infrared Systems: Technology and Applications XIV, Warsaw, Poland, 9 October 2017. [Google Scholar]
- Lohmeyer, W.Q.; Cahoy, K. Space weather radiation effects on geostationary satellite solid-state power amplifiers. Space Weather 2013, 11, 476–488. [Google Scholar] [CrossRef]
- Durante, M.; Cucinotta, F.A. Physical basis of radiation protection in space travel. Rev. Modern Phys. 2011, 83, 1245–1281. [Google Scholar] [CrossRef]
- Cressler, J.D.; Mantooth, H.A. Extreme Environment Electronics, 1st ed.; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Chen, T. Digital Camera System Simulator and Applications; Stanford University: Stanford, CA, USA, 2003. [Google Scholar]
- Loeb, N.G.; Kato, S.; Loukachine, K.; Manalo-Smith, N. Angular Distribution Models for Top-of-Atmosphere Radiative Flux Estimation from the Clouds and the Earth‘s Radiant Energy System Instrument on the Terra Satellite. Part I: Methodology. J. Atmos. Ocean. Technol. 2005, 22, 338–351. [Google Scholar] [CrossRef]
- Loeb, N.G.; Kato, S.; Loukachine, K.; Manalo-Smith, N.; Doelling, D.R. Angular distribution models for top-of-atmosphere radiative flux estimation from the Clouds and the Earth’s Radiant Energy System instrument on the Terra satellite. Part II: Validation. J. Atmos. Ocean. Technol. 2007, 24, 564–584. [Google Scholar] [CrossRef]
- Su, W.; Corbett, J.; Eitzen, Z.; Liang, L. Next-generation angular distribution models for top-of-atmosphere radiative flux calculation from CERES instruments: Methodology. Atmos. Meas. Tech. 2015, 7, 8817–8880. [Google Scholar] [CrossRef]
- Giorgini, J.D. Status of the JPL horizons ephemeris system. In Proceedings of the IAU General Assembly, Honolulu, HI, USA, 3–14 August 2015. [Google Scholar]
- CERES_SYN1deg_Ed4A Data Quality Summary. Available online: https://ceres.larc.nasa.gov/documents/DQ_summaries/CERES_SYN1deg_Ed4A_DQS.pdf (accessed on 10 January 2018).
- Smith, G.; Priestley, K.; Loeb, N.; Wielicki, B.; Charlock, T.; Minnis, P.; Doelling, D.; Rutan, D. Clouds and Earth Radiant Energy System (CERES), a review: Past, present and future. Adv. Space Res. 2011, 48, 254–263. [Google Scholar] [CrossRef]
- Doelling, D.R.; Sun, M.; Nguyen, L.T.; Nordeen, M.L.; Haney, C.O.; Keyes, D.F.; Mlynczak, P.E. Advances in geostationary-derived longwave fluxes for the CERES synoptic (SYN1deg) product. J. Atmos. Ocean. Technol. 2016, 33, 503–521. [Google Scholar] [CrossRef]
- CERES Surface Type ID. Available online: https://ceres.larc.nasa.gov/science_information.php?page=CeresSurfID# (accessed on 20 September 2017).
- CERES EBAF TOA Ed4.0 Data Ordering. Available online: https://ceres-tool.larc.nasa.gov/ord-tool/jsp/EBAF4Selection.jsp (accessed on 15 February 2018).
- Duan, W.; Huang, S.; Nie, C. Conceptual design of a Moon-based Earth radiation observatory. Int. J. Remote Sens. 2018, 39, 5834–5849. [Google Scholar] [CrossRef]
- CERES Algorithm Theoretical Basis Document. Available online: https://ceres.larc.nasa.gov/documents/ATBD/pdf/r2_2/ceres-atbd2.2-s4.4.pdf (accessed on 10 November 2017).



| Parameter | Depiction | Unit |
|---|---|---|
| Time | UTC time | |
| 399_ins_LT_LE () | Instantaneous light-time of MERO location with respect to the Earth center at the set-time | Minutes |
| Sub-MERO latitude () | WGS-84 latitude of the sub-MERO point V | Degree |
| Sub-MERO longitude () | WGS-84 longitude of the sub-MERO point V | Degree |
| Sub-solar latitude () | WGS-84 latitude of the sub-solar point S | Degree |
| Sub-solar longitude () | WGS-84 longitude of the sub-solar point S | Degree |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, W.; Huang, S.; Nie, C. Entrance Pupil Irradiance Estimating Model for a Moon-Based Earth Radiation Observatory Instrument. Remote Sens. 2019, 11, 583. https://doi.org/10.3390/rs11050583
Duan W, Huang S, Nie C. Entrance Pupil Irradiance Estimating Model for a Moon-Based Earth Radiation Observatory Instrument. Remote Sensing. 2019; 11(5):583. https://doi.org/10.3390/rs11050583
Chicago/Turabian StyleDuan, Wentao, Shaopeng Huang, and Chenwei Nie. 2019. "Entrance Pupil Irradiance Estimating Model for a Moon-Based Earth Radiation Observatory Instrument" Remote Sensing 11, no. 5: 583. https://doi.org/10.3390/rs11050583
APA StyleDuan, W., Huang, S., & Nie, C. (2019). Entrance Pupil Irradiance Estimating Model for a Moon-Based Earth Radiation Observatory Instrument. Remote Sensing, 11(5), 583. https://doi.org/10.3390/rs11050583