Estimation of Surface Air Specific Humidity and Air–Sea Latent Heat Flux Using FY-3C Microwave Observations
Abstract
:1. Introduction
2. Data Descriptions
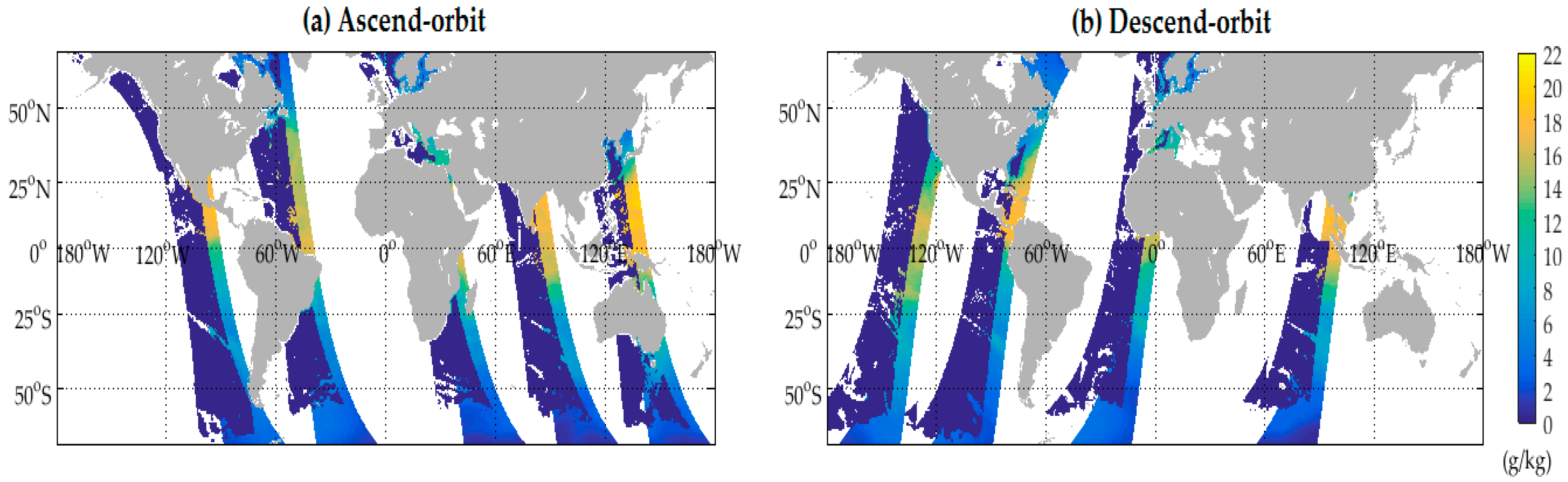
2.1. Satellite Observations
2.2. In Situ Measurements
2.3. NOAA CIRES
2.4. ERA-Interim Reanalysis Data
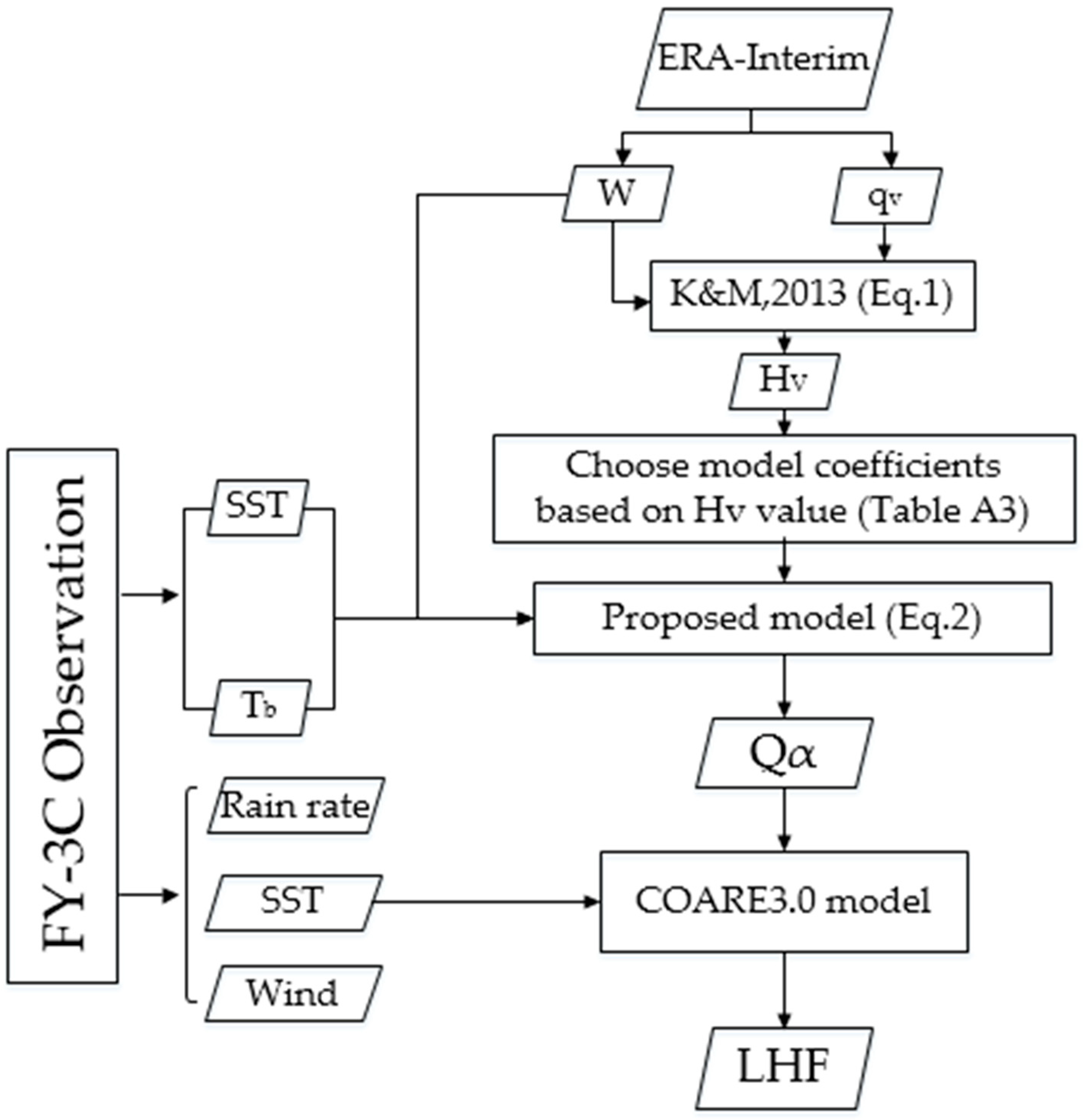
3. Methodology
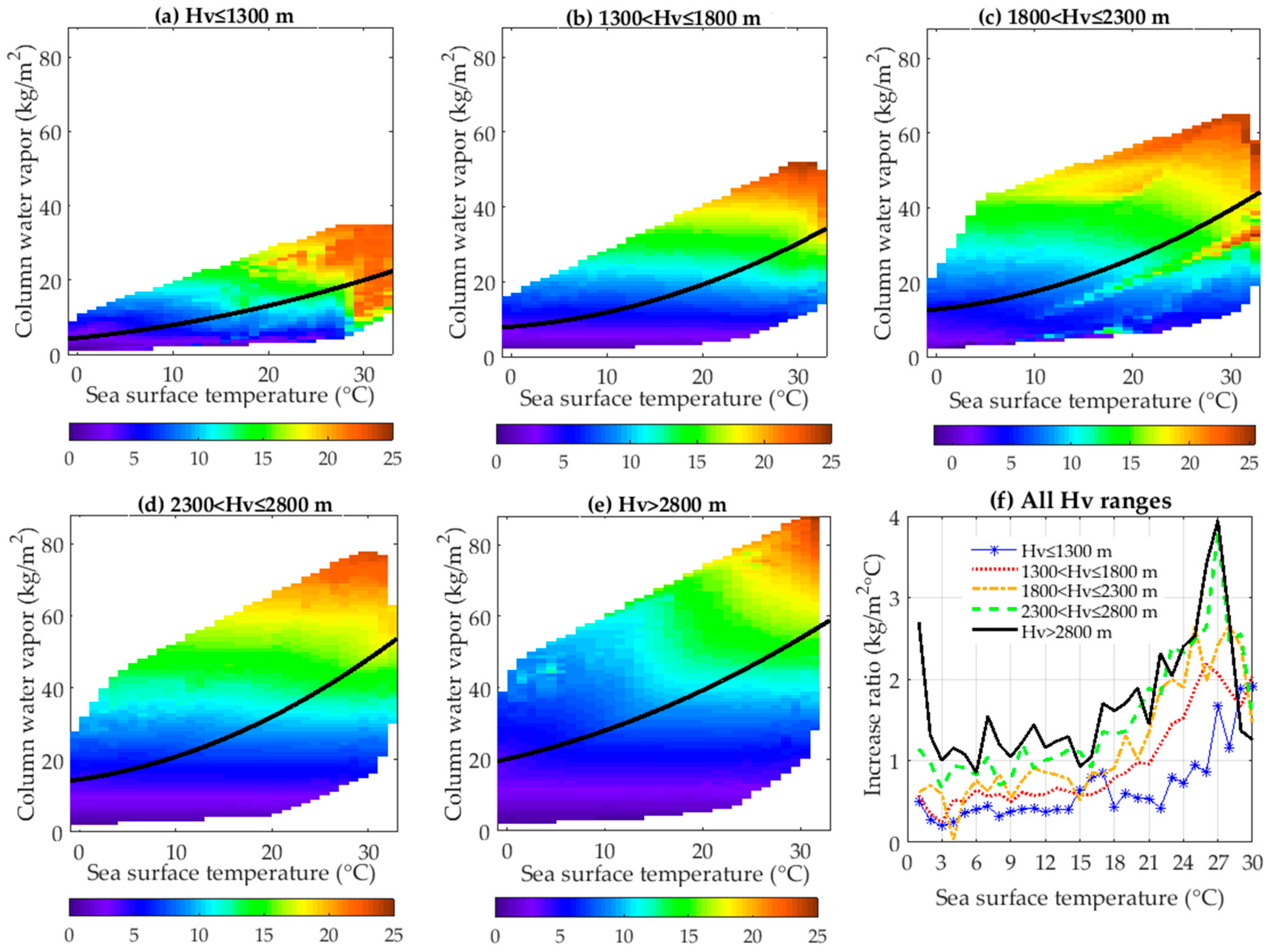
3.1. Relationship between SST and W
3.2. Channel Sensitivity
3.3. Developed Algorithm
4. Experimental Results
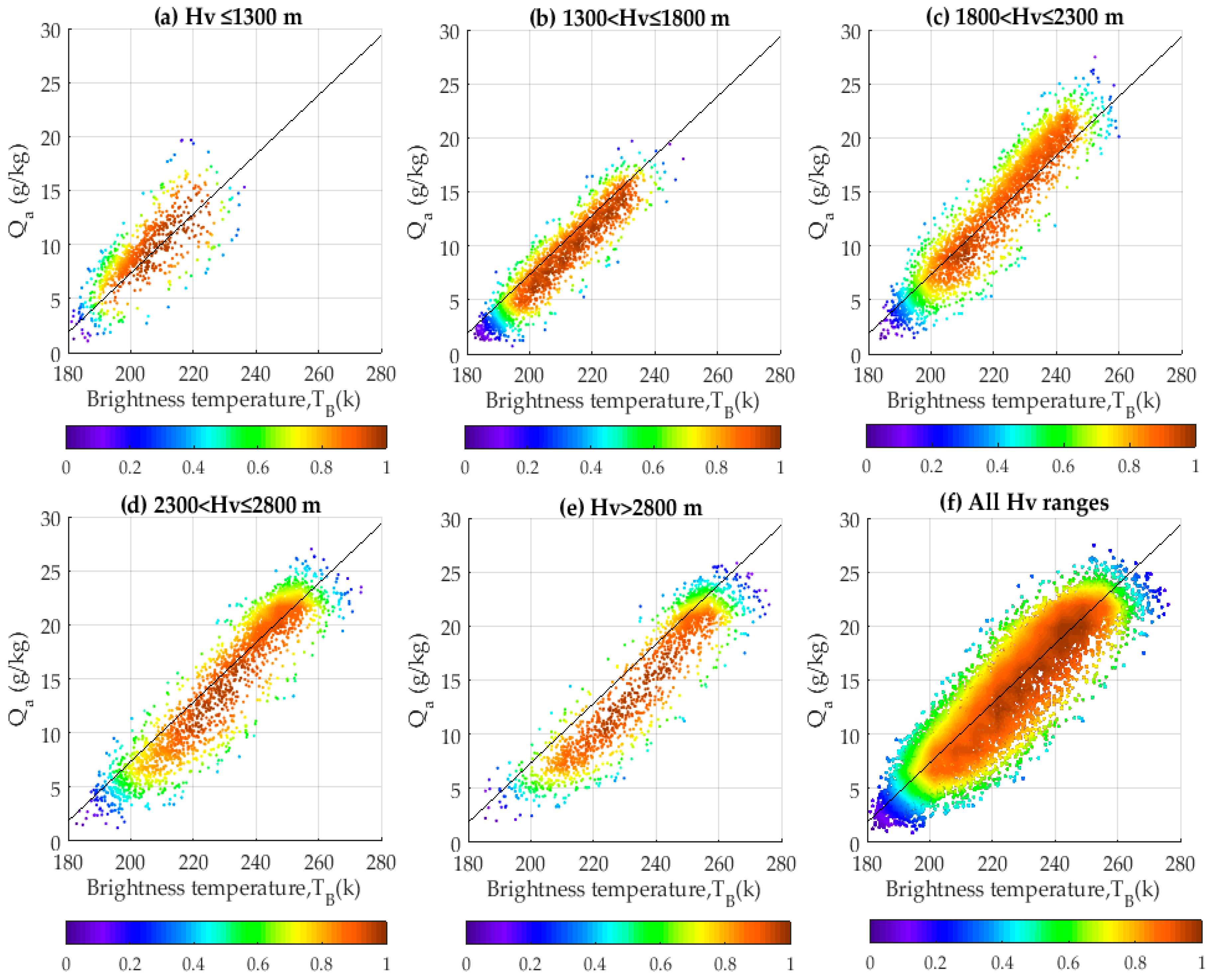
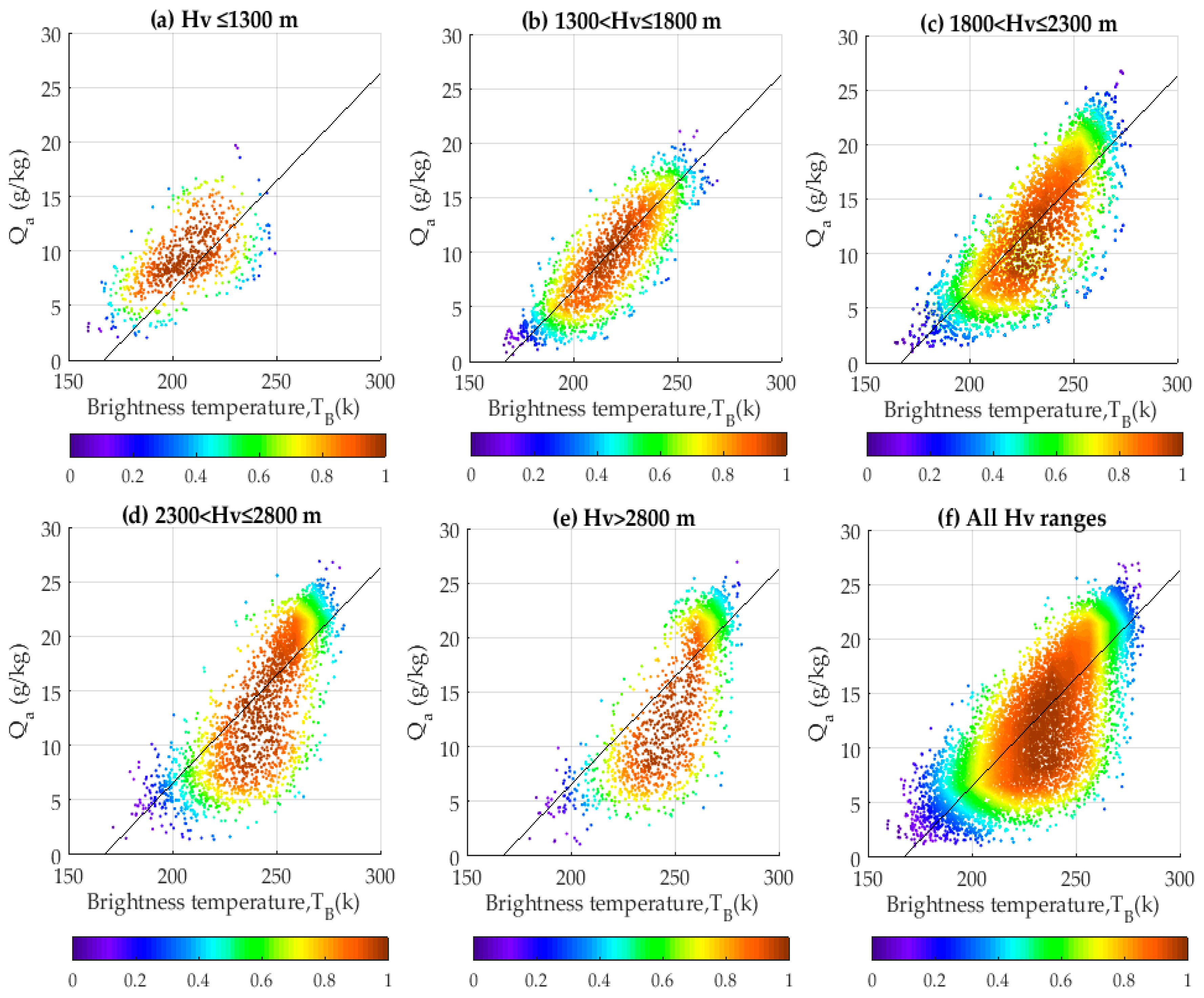
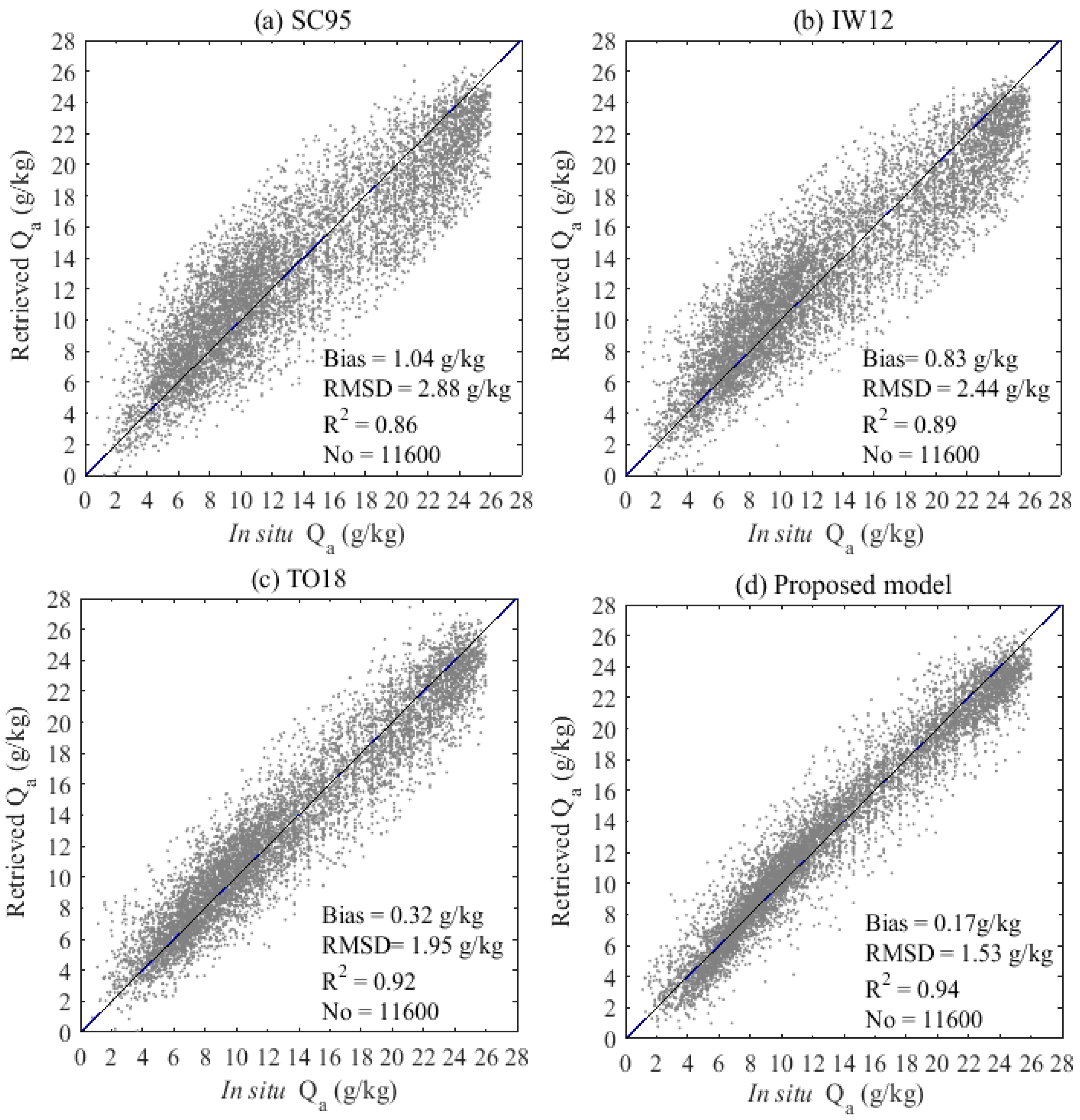
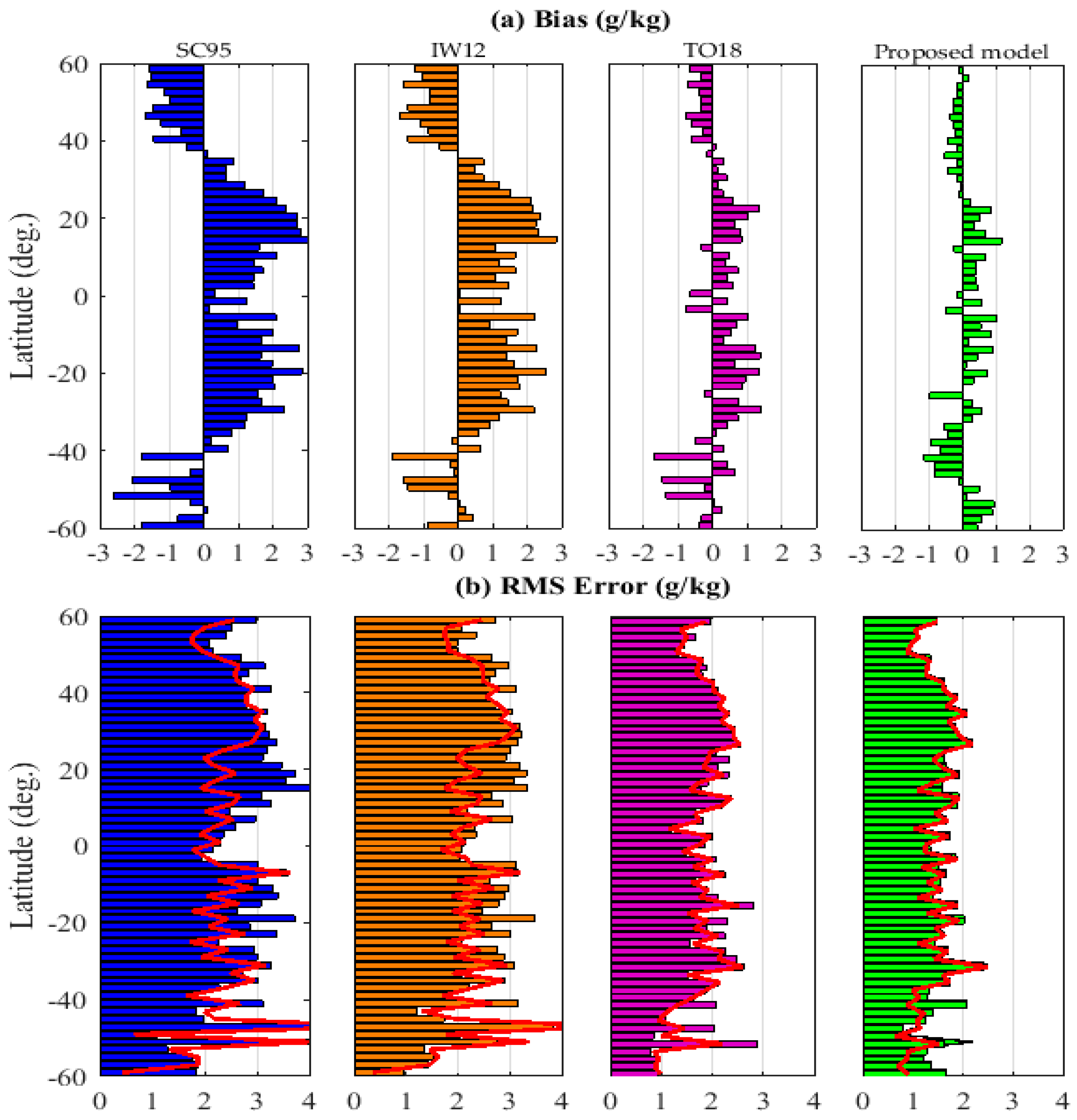
4.1. Evaluation with In Situ Data
4.1.1. Air Specific Humidity
4.1.2. Latent Heat Flux
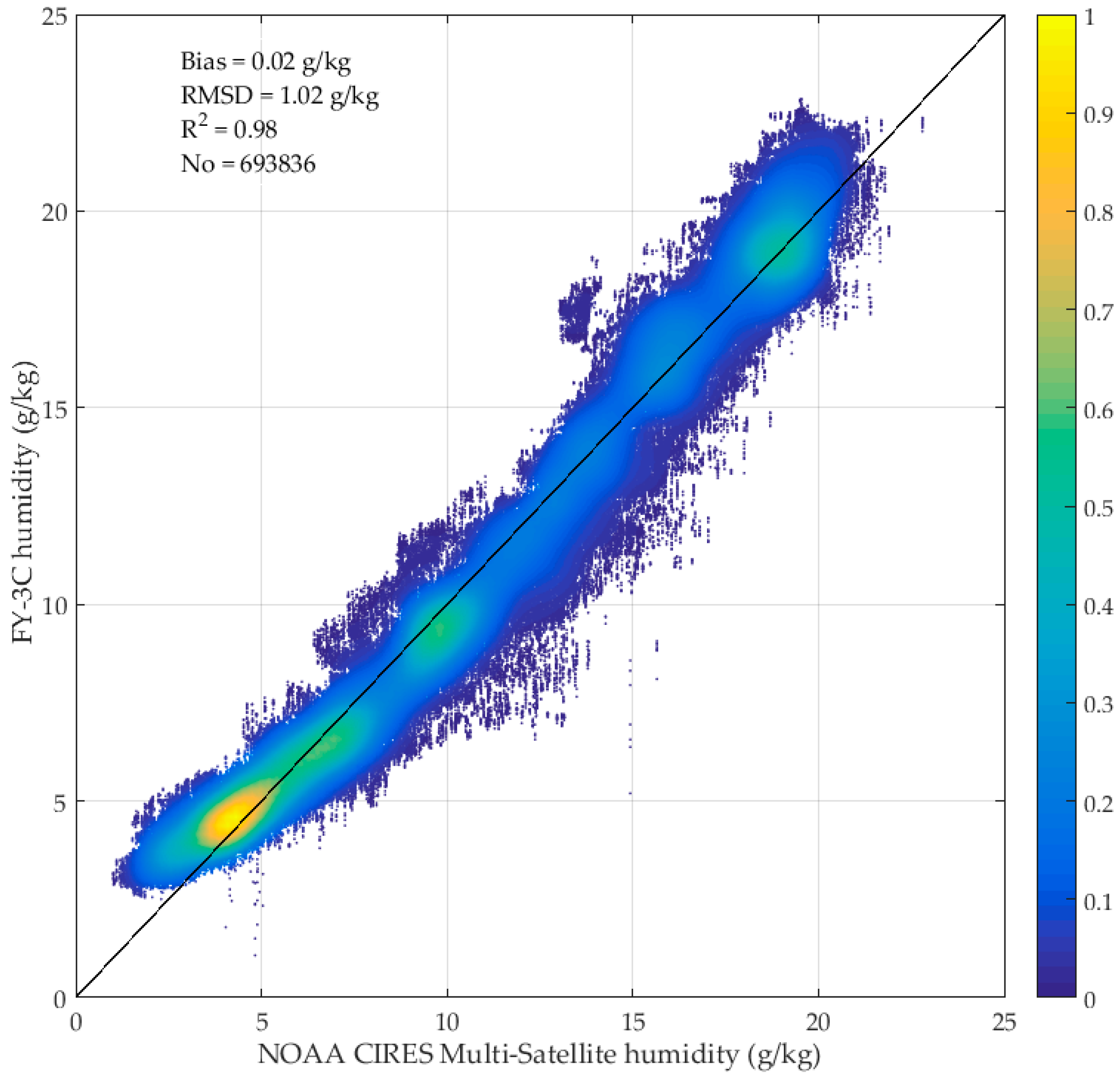
4.2. Comparison with NOAA CIRES Datasets
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| B1 | B2 | B3 | B4 | B5 | B6 | B7 | B8 | B9 | B10 | W·SST | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.000 | ||||||||||||
| B1 * | 0.459 | 1.000 | ||||||||||
| B2 | 0.220 | 0.916 | 1.000 | |||||||||
| B3 | 0.744 | 0.805 | 0.683 | 1.000 | ||||||||
| B4 | 0.670 | 0.822 | 0.740 | 0.961 | 1.000 | |||||||
| B5 | 0.901 | 0.624 | 0.437 | 0.910 | 0.880 | 1.000 | ||||||
| B6 | 0.871 | 0.627 | 0.458 | 0.916 | 0.901 | 0.993 | 1.000 | |||||
| B7 | 0.676 | 0.667 | 0.567 | 0.912 | 0.935 | 0.892 | 0.910 | 1.000 | ||||
| B8 | 0.543 | 0.629 | 0.581 | 0.855 | 0.913 | 0.797 | 0.835 | 0.971 | 1.000 | |||
| B9 | 0.869 | 0.403 | 0.185 | 0.695 | 0.625 | 0.874 | 0.850 | 0.695 | 0.567 | 1.000 | ||
| B10 | 0.818 | 0.439 | 0.263 | 0.761 | 0.734 | 0.908 | 0.908 | 0.818 | 0.742 | 0.949 | 1.000 | |
| W·SST | 0.947 | 0.460 | 0.242 | 0.774 | 0.718 | 0.910 | 0.890 | 0.726 | 0.612 | 0.821 | 0.805 | 1.000 |
| Model | Adjusted R Square | Residual Mean Square | F-Test | |||
|---|---|---|---|---|---|---|
| F | df1 | df2 | Sig. F Change | |||
| 1 * | 0.897 | 2.544367 | 104,793.588 | 1 | 11,598 | 0.000 |
| 2 | 0.922 | 1.933543 | 708,22.499 | 1 | 11,597 | 0.000 |
| 3 | 0.928 | 1.774980 | 51,823.867 | 1 | 11,596 | 0.000 |
| 4 | 0.930 | 1.636417 | 42,380.563 | 1 | 11,595 | 0.000 |
| 5 | 0.935 | 1.488377 | 37,518.207 | 1 | 11,594 | 0.000 |
| 6 | 0.940 | 1.428013 | 32,669.545 | 1 | 11,593 | 0.000 |
| 7 | 0.942 | 1.399309 | 28,620.837 | 1 | 11,592 | 0.000 |
| 8 | 0.943 | 1.394626 | 25,140.234 | 1 | 11,591 | 0.000 |
| 9 | 0.944 | 1.382297 | 22,546.893 | 1 | 11,590 | 0.000 |
| 10 | 0.944 | 1.378660 | 20,621.421 | 1 | 11,589 | 0.000 |
| 11 | 0.945 | 1.361343 | 19,567.475 | 1 | 11,588 | 0.000 |
| Coefficients | ||||||
|---|---|---|---|---|---|---|
| C0 | −101.7520 | −74.1441 | −56.4953 | −46.2155 | −61.2600 | −86.3314 |
| C1 | 0.0252 | −0.0103 | −0.0149 | −0.0089 | −0.0725 | −0.0519 |
| C2 | −0.0125 | 0.0093 | 0.0043 | 0.0021 | 0.0325 | 0.0183 |
| C3 | 0.0000 | −0.0110 | −0.0404 | −0.0725 | −0.1106 | −0.0247 |
| C4 | −0.0358 | −0.0138 | 0.0105 | 0.0163 | 0.0418 | 0.0000 |
| C5 | −0.2015 | 0.1604 | 0.3649 | 0.6717 | 0.9174 | 1.1411 |
| C6 | 0.0005 | −0.0003 | −0.0009 | −0.0013 | −0.0019 | −0.0024 |
| C7 | 0.1012 | 0.0548 | 0.0359 | −0.1322 | −0.2903 | −0.3309 |
| C8 | −0.0002 | −2.40 × 10−5 | 7.54 × 10−5 | 0.0004 | 0.0008 | 0.0010 |
| C9 | −0.0902 | −0.0450 | −0.0123 | −0.0097 | 0.0684 | 0.0000 |
| C10 | 0.0235 | −0.0264 | −0.0228 | −0.0029 | −0.0442 | −0.0223 |
| C11 | 0.9919 | 0.5658 | 0.2115 | −0.1695 | −0.2098 | 0.0000 |
| C12 | −0.0016 | −0.0010 | −0.0003 | 0.0005 | 0.0005 | 8.82 × 10−5 |
| C13 | −0.0743 | −0.0805 | −0.0282 | 0.1024 | 0.1952 | −0.0173 |
| C14 | 0.0000 | 0.0001 | 1.12 × 10−5 | −0.0003 | −0.0005 | 0.0000 |
| C15 | 0.0180 | 0.0121 | 0.0097 | 0.0074 | 0.0071 | 0.0061 |
References
- Gulev, S.K.; Latif, M.; Keenlyside, N.; Park, W.; Koltermann, K.P. North atlantic ocean control on surface heat flux on multidecadal timescales. Nature 2013, 499, 464–467. [Google Scholar] [CrossRef] [PubMed]
- Dutra, E.; Stepanenko, V.M.; Balsamo, G.; Viterbo, P.; Miranda, P.M.A.; Mironov, D.; Schar, C. An offline study of the impact of lakes on the performance of the ecmwf surface scheme. Boreal Environ. Res. 2010, 15, 100–112. [Google Scholar]
- Woolway, R.I.; Verburg, P.; Lenters, J.D.; Merchant, C.J.; Hamilton, D.P.; Brookes, J.; de Eyto, E.; Kelly, S.; Healey, N.C.; Hook, S.; et al. Geographic and temporal variations in turbulent heat loss from lakes: A global analysis across 45 lakes. Limnol. Oceanogr. 2018, 63, 2436–2449. [Google Scholar] [CrossRef]
- Bourassa, M.A.; Gille, S.T.; Bitz, C.; Carlson, D.; Cerovecki, I.; Clayson, C.A.; Cronin, M.F.; Drennan, W.M.; Fairall, C.W.; Hoffman, R.N.; et al. High-latitude ocean and sea ice surface fluxes: Challenges for climate research. Bull. Am. Meteorol. Soc. 2013, 94, 403–423. [Google Scholar] [CrossRef]
- Bunker, A.F. Computations of surface-energy flux and annual air-sea interaction cycles of north-atlantic ocean. Mon. Weather Rev. 1976, 104, 1122–1140. [Google Scholar] [CrossRef]
- Hasse, L.; Smith, S.D. Local sea surface wind, wind stress, and sensible and latent heat fluxes. J. Clim. 1997, 10, 2711–2724. [Google Scholar] [CrossRef]
- Bentamy, A.; Piolle, J.F.; Grouazel, A.; Danielson, R.; Gulev, S.; Paul, F.; Azelmat, H.; Mathieu, P.P.; von Schuckmann, K.; Sathyendranath, S.; et al. Review and assessment of latent and sensible heat flux accuracy over the global oceans. Remote Sens. Environ. 2017, 201, 196–218. [Google Scholar] [CrossRef]
- Andersson, A.; Fennig, K.; Klepp, C.; Bakan, S.; Grassl, H.; Schulz, J. The hamburg ocean atmosphere parameters and fluxes from satellite data—Hoaps-3. Earth Syst. Sci. Data 2010, 3, 143–194. [Google Scholar] [CrossRef]
- Andersson, A.; Klepp, C.; Fennig, K.; Bakan, S.; Grassl, H.; Schulz, J. Evaluation of hoaps-3 ocean surface freshwater flux components. J. Appl. Meteorol. Climatol. 2011, 50, 379–398. [Google Scholar] [CrossRef]
- Kubota, M.; Iwasaka, N.; Kizu, S.; Kondo, M.; Kutsuwada, K. Japanese ocean flux data sets with use of remote sensing observations (j-ofuro). J. Oceanogr. 2002, 58, 213–225. [Google Scholar] [CrossRef]
- Shie, C.L.; Chiu, L.S.; Adler, R.; Nelkin, E.; Lin, I.I.; Xie, P.P.; Wang, F.C.; Chokngamwong, R.; Olson, W.; Chu, D.A. A note on reviving the goddard satellite-based surface turbulent fluxes (gsstf) dataset. Adv. Atmos. Sci. 2009, 26, 1071–1080. [Google Scholar] [CrossRef]
- Bentamy, A.; Grodsky, S.A.; Katsaros, K.; Mestas-Nunez, A.M.; Blanke, B.; Desbiolles, F. Improvement in airsea flux estimates derived from satellite observations. Int. J. Remote Sens. 2013, 34, 5243–5261. [Google Scholar] [CrossRef]
- Tomita, H.; Kubota, M.; Cronin, M.F.; Iwasaki, S.; Konda, M.; Ichikawa, H. An assessment of surface heat fluxes from j-ofuro2 at the keo and jkeo sites. J. Geophys. Res. Oceans 2010, 115. [Google Scholar] [CrossRef]
- Liu, W.T.; Niiler, P.P. Determination of monthly mean humidity in the atmospheric surface-layer over oceans from satellite data. J. Phys. Oceanogr. 1984, 14, 1451–1457. [Google Scholar] [CrossRef]
- Liu, W.T. Statistical relation between monthly mean precipitable water and surface-level humidity over global oceans. Mon. Weather Rev. 1986, 114, 1591–1602. [Google Scholar] [CrossRef]
- Schulz, J.; Schluessel, P.; Grassl, H. Water-vapor in the atmospheric boundary layer over oceans from ssm/i measurements. Int. J. Remote Sens. 1993, 14, 2773–2789. [Google Scholar] [CrossRef]
- Schlussel, P.; Schanz, L.; Englisch, G. Retrieval of latent-heat flux and longwave irradiance at the sea-surface from ssm/i and avhrr measurements. In Satellite Monitoring of the Earth’s Surface and Atmosphere; Arnault, S., Ed.; Pergamon Press Ltd: Oxford, UK, 1995; Volume 16, pp. 107–116. [Google Scholar]
- Bentamy, A.; Katsaros, K.B.; Mestas-Nunez, A.M.; Drennan, W.M.; Forde, E.B.; Roquet, H. Satellite estimates of wind speed and latent heat flux over the global oceans. J. Clim. 2003, 16, 637–656. [Google Scholar] [CrossRef]
- Iwasaki, S.; Kubota, M. Algorithms for estimation of air-specific humidity using tmi data. Int. J. Remote Sens. 2012, 33, 7413–7430. [Google Scholar] [CrossRef]
- Jackson, D.L.; Wick, G.A.; Bates, J.J. Near-surface retrieval of air temperature and specific humidity using multisensor microwave satellite observations. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Jackson, D.L.; Wick, G.A.; Robertson, F.R. Improved multisensor approach to satellite-retrieved near-surface specific humidity observations. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Jones, C.; Peterson, P.; Gautier, C. A new method for deriving ocean surface specific humidity and air temperature: An artificial neural network approach. J. Appl. Meteorol. 1999, 38, 1229–1245. [Google Scholar] [CrossRef]
- Singh, R.; Joshi, P.C.; Kishtawal, C.M. A new technique for estimation of surface latent heat fluxes using satellite-based observations. Mon. Weather Rev. 2005, 133, 2692–2710. [Google Scholar] [CrossRef]
- Roberts, J.B.; Clayson, C.A.; Robertson, F.R.; Jackson, D.L. Predicting near-surface atmospheric variables from special sensor microwave/imager using neural networks with a first-guess approach. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Tomita, H.; Hihara, T.; Kubota, M. Improved satellite estimation of near-surface humidity using vertical water vapor profile information. Geophys. Res. Lett. 2018, 45, 899–906. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, P.; Lu, N.M.; Yang, Z.D.; Shi, J.M.; Dong, C.H. Improvements on global meteorological observations from the current fengyun 3 satellites and beyond. Int. J. Digit. Earth 2012, 5, 251–265. [Google Scholar] [CrossRef]
- Freeman, E.; Woodruff, S.D.; Worley, S.J.; Lubker, S.J.; Kent, E.C.; Angel, W.E.; Berry, D.I.; Brohan, P.; Eastman, R.; Gates, L.; et al. Icoads release 3.0: A major update to the historical marine climate record. Int. J. Climatol. 2017, 37, 2211–2232. [Google Scholar] [CrossRef]
- Buck, A.L. New equations for computing vapor-pressure and enhancement factor. J. Appl. Meteorol. 1981, 20, 1527–1532. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 2nd ed.; Academic Press: San Diego, CA, USA, 2006; 627p. [Google Scholar]
- Fairall, C.W.; Bradley, E.F.; Hare, J.E.; Grachev, A.A.; Edson, J.B. Bulk parameterization of air-sea fluxes: Updates and verification for the coare algorithm. J. Clim. 2003, 16, 571–591. [Google Scholar] [CrossRef]
- Jackson, D.L.; Wick, G.A. Near-surface air temperature retrieval derived from amsu-a and sea surface temperature observations. J. Atmos. Ocean. Technol. 2010, 27, 1769–1776. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The era-interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Kanemaru, K.; Masunaga, H. A satellite study of the relationship between sea surface temperature and column water vapor over tropical and subtropical oceans. J. Clim. 2013, 26, 4204–4218. [Google Scholar] [CrossRef]
- Stephens, G.L. On the relationship between water-vapor over the oceans and sea-surface temperature. J. Clim. 1990, 3, 634–645. [Google Scholar] [CrossRef]
- Jackson, D.L.; Stephens, G.L. A study of ssm/i-derived columnar water-vapor over the global oceans. J. Clim. 1995, 8, 2025–2038. [Google Scholar] [CrossRef]
- Grody, N.C. Remote-sensing of atmospheric water-content from satellites using microwave radiometry. IEEE Trans. Antennas Propag. 1976, 24, 155–162. [Google Scholar] [CrossRef]
- Singh, R.; Joshi, P.C.; Kishtawal, C.M.; Pal, P.K. A new method for estimation of near surface specific humidity over global oceans. Meteorol. Atmos. Phys. 2006, 94, 1–10. [Google Scholar] [CrossRef]
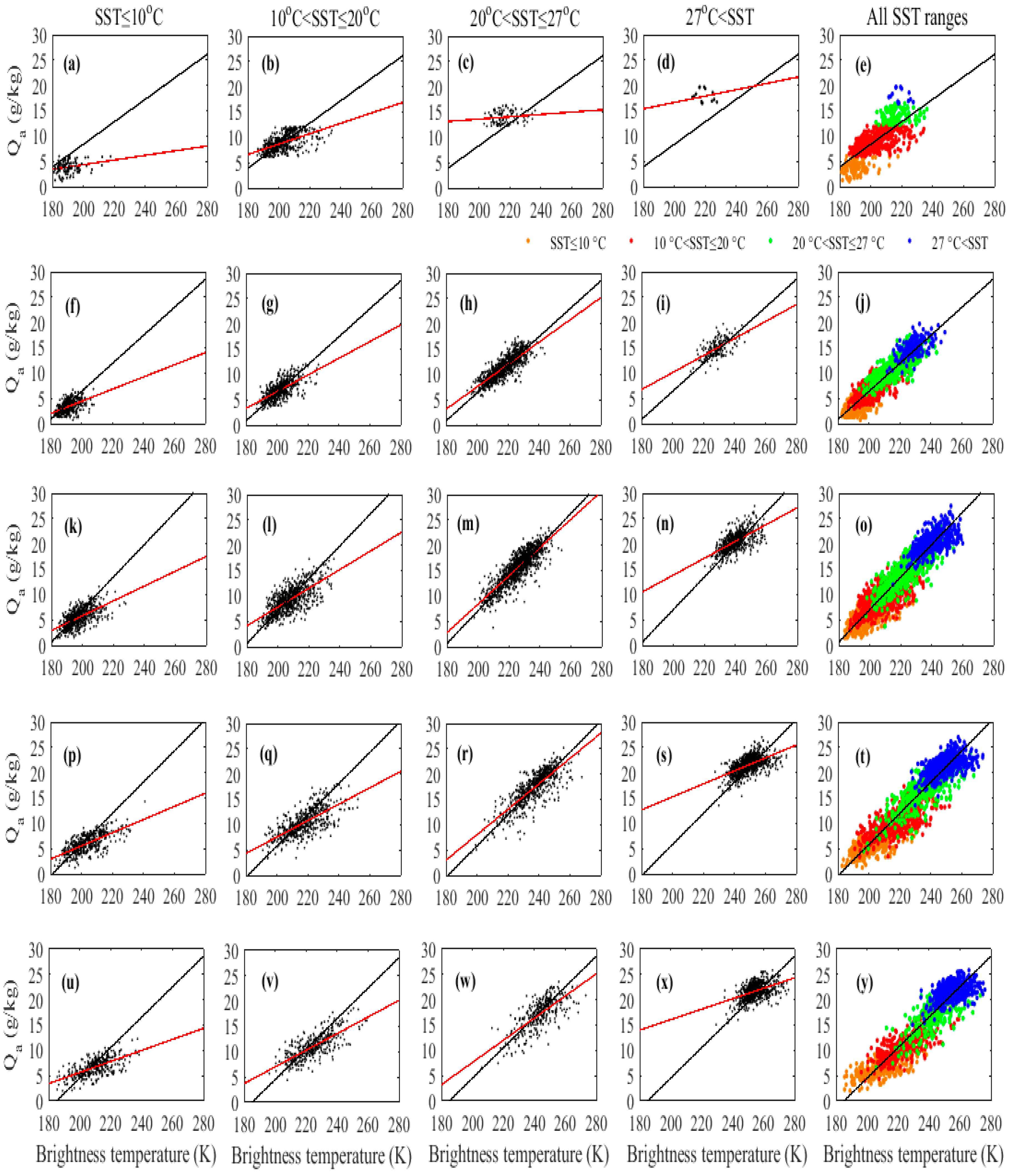
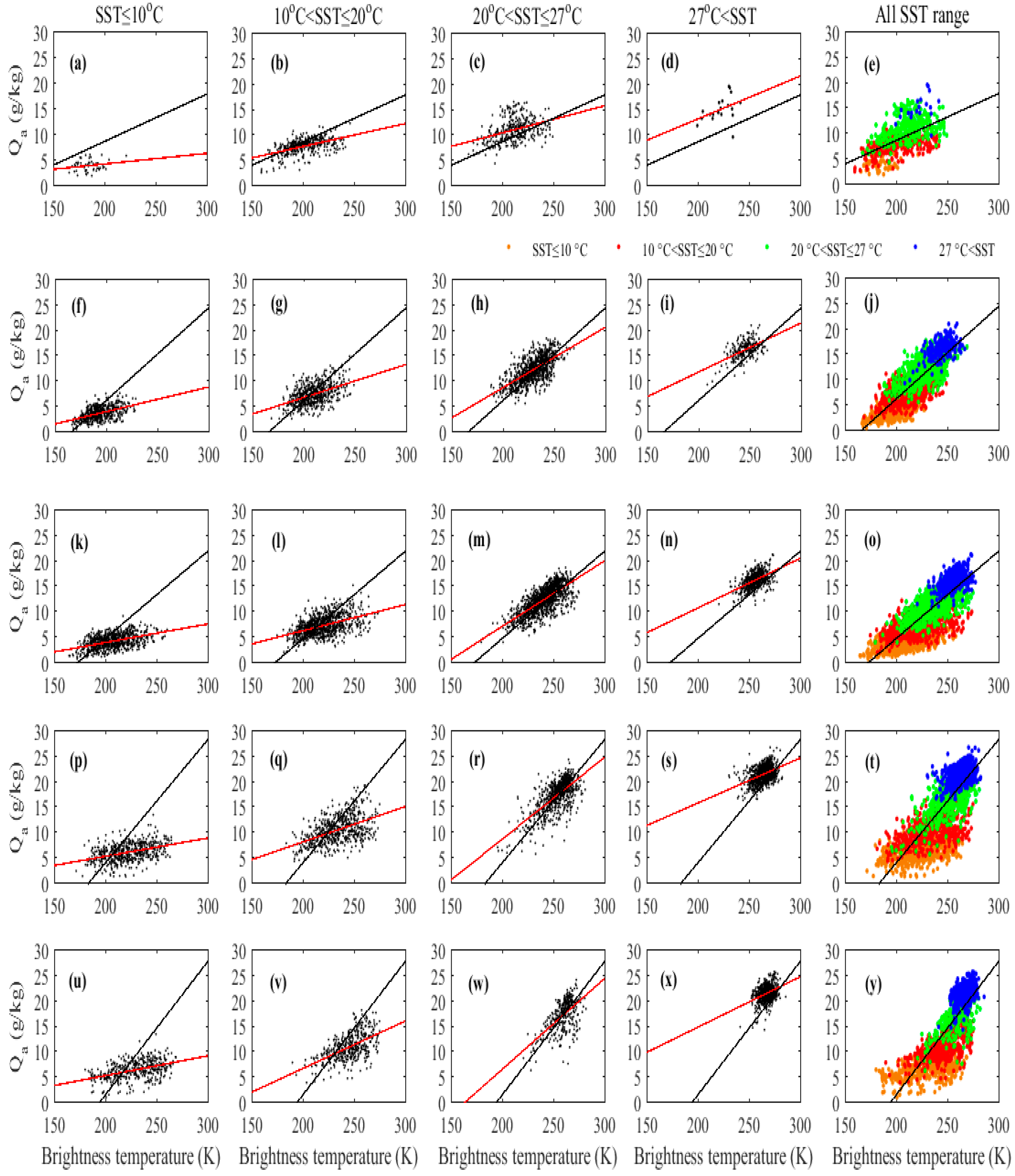
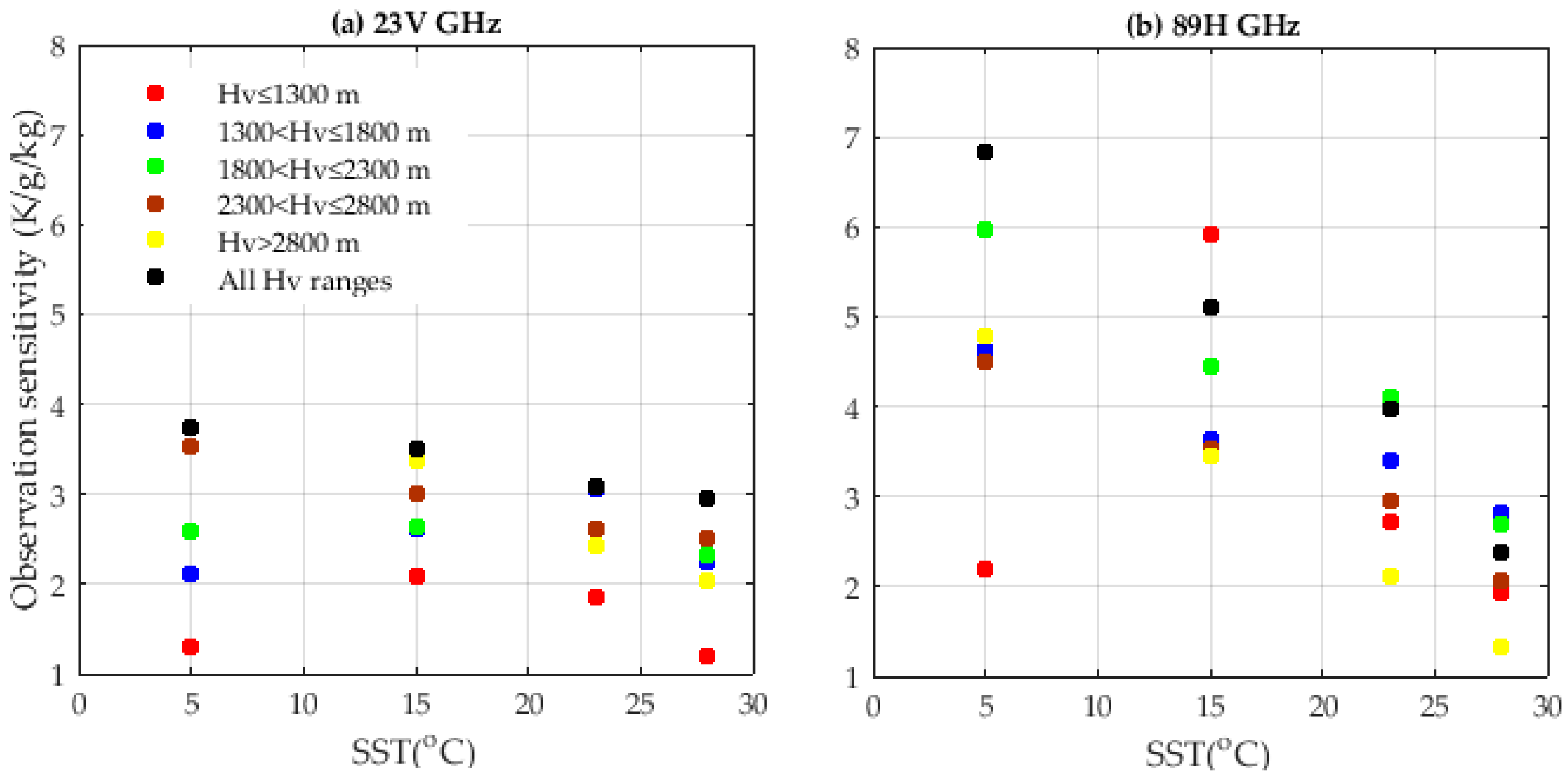
| Channel Name | Central Frequency (GHz) | Bandwidth (MHz) | IFOVResolution |
|---|---|---|---|
| 10 V/H * | 10.65 | 180 | 51 × 85 km |
| 19 V/H | 18.7 | 200 | 30 × 50 km |
| 23 V/H | 23.8 | 400 | 27 × 45 km |
| 37 V/H | 36.5 | 900 | 18 × 30 km |
| 89 V/H | 89.0 | 4600 | 9 × 15 km |
| p-Values | ||||||
|---|---|---|---|---|---|---|
| C0 | 1.51 × 10−63 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 6.60 × 10−77 |
| C1 | 3.27 × 10−15 | 4.71 × 10−69 | 6.58 × 10−94 | 5.12 × 10−141 | 0.0000 | 3.33 × 10−76 |
| C2 | 2.41 × 10−06 | 8.39 × 10−227 | 2.40 × 10−59 | 4.94 × 10−152 | 0.0000 | 3.77 × 10−37 |
| C3 | 0.532 | 9.67 × 10−125 | 0.0000 | 0.0000 | 0.0000 | 6.14 × 10−08 |
| C4 | 4.02 × 10−11 | 1.68 × 10−363 | 0.0272 | 0.0010 | 8.81 × 10−22 | 0.2000 |
| C5 | 1.04 × 10−06 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 5.22 × 10−132 |
| C6 | 4.71 × 10−08 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 3.25 × 10−124 |
| C7 | 1.17 × 10−13 | 0.0000 | 2.71 × 10−05 | 0.0000 | 0.0000 | 3.60 × 10−107 |
| C8 | 3.86 × 10−05 | 0.0000 | 5.87 × 10−156 | 0.0000 | 0.0000 | 6.83 × 10−145 |
| C9 | 1.53 × 10−42 | 3.38 × 10−56 | 6.78 × 10−15 | 8.98 × 10−06 | 6.73 × 10−17 | 0.0640 |
| C10 | 1.10 × 10−09 | 0.0000 | 0.0000 | 3.65 × 10−45 | 4.90 × 10−88 | 9.94 × 10−19 |
| C11 | 6.15 × 10−59 | 0.0000 | 0.0000 | 5.15 × 10−223 | 8.84 × 10−90 | 0.4254 |
| C12 | 3.89 × 10−37 | 0.0000 | 1.10 × 10−226 | 0.0000 | 4.14 × 10−118 | 0.0214 |
| C13 | 3.09 × 10−10 | 0.0000 | 0.0000 | 2.01 × 10−215 | 1.02 × 10−150 | 0.0070 |
| C14 | 0.647 | 0.0000 | 2.93 × 10−141 | 0.0000 | 1.19 × 10−188 | 0.6800 |
| C15 | 1.51 × 10−63 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 6.62 × 10−77 |
| Algorithm | 10 GHz | 19 GHz | 23 GHz | 37 GHz | 89 GHz | Parameters |
|---|---|---|---|---|---|---|
| SC95 | 19 V/H | 23 V | 37 V/H | |||
| IW12 | 19 V/H | 23 V | 37 V/H | 89 V/H | ||
| TO18 | 10 V/H | 19 V/H | 23 V/H | 37 V/H | 89 V/H | W |
| Proposed model | 10 V/H | 19 V/H | 23 V/H | 37 V/H | 89 V/H | W and SST |
| Statistics | Specific Air Humidity | Latent Heat Flux | ||||
|---|---|---|---|---|---|---|
| Bias (g/kg) | RMSD (g/kg) | Correlation (R2) | Bias (W/m2) | RMSD (W/m2) | Correlation (R2) | |
| SC95 | ||||||
| 45°–60° N 45°–60° S | −1.34 | 2.46 | 0.85 | −26.50 | 39.24 | 0.48 |
| 15°–45° N 15°– 45° S | 0.66 | 3.16 | 0.81 | 14.10 | 51.96 | 0.51 |
| 15° S–15° N | 1.72 | 2.96 | 0.70 | 34.98 | 48.14 | 0.49 |
| IW12 | ||||||
| 45°–60° N 45°– 60° S | −1.16 | 2.29 | 0.86 | −22.76 | 36.54 | 0.49 |
| 15°–45° N 15°–45° S | 0.53 | 2.98 | 0.84 | 11.89 | 48.84 | 0.55 |
| 15° S–15° N | 1.41 | 2.41 | 0.74 | 28.74 | 42.61 | 0.54 |
| TO18 | ||||||
| 45°– 60° N 45°– 60° S | −0.48 | 1.57 | 0.93 | −16.18 | 31.87 | 0.63 |
| 15°– 45° N 15°–45° S | 0.15 | 2.20 | 0.90 | 10.98 | 44.14 | 0.75 |
| 15° S–15° N | 0.44 | 1.83 | 0.82 | 8.45 | 35.50 | 0.70 |
| Proposed model | ||||||
| 45°–60° N 45°–60° S | −0.14 | 1.11 | 0.95 | −12.89 | 23.44 | 0.72 |
| 15°–45° N 15°–45° S | 0.08 | 1.76 | 0.92 | 2.40 | 34.24 | 0.87 |
| 15° S–15° N | 0.24 | 1.51 | 0.86 | 4.87 | 29.05 | 0.82 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Q.; Wang, S.; Yang, X. Estimation of Surface Air Specific Humidity and Air–Sea Latent Heat Flux Using FY-3C Microwave Observations. Remote Sens. 2019, 11, 466. https://doi.org/10.3390/rs11040466
Gao Q, Wang S, Yang X. Estimation of Surface Air Specific Humidity and Air–Sea Latent Heat Flux Using FY-3C Microwave Observations. Remote Sensing. 2019; 11(4):466. https://doi.org/10.3390/rs11040466
Chicago/Turabian StyleGao, Qidong, Sheng Wang, and Xiaofeng Yang. 2019. "Estimation of Surface Air Specific Humidity and Air–Sea Latent Heat Flux Using FY-3C Microwave Observations" Remote Sensing 11, no. 4: 466. https://doi.org/10.3390/rs11040466
APA StyleGao, Q., Wang, S., & Yang, X. (2019). Estimation of Surface Air Specific Humidity and Air–Sea Latent Heat Flux Using FY-3C Microwave Observations. Remote Sensing, 11(4), 466. https://doi.org/10.3390/rs11040466







