Integrating Temporal Evolution with Cellular Automata for Simulating Land Cover Change
Abstract
:1. Introduction
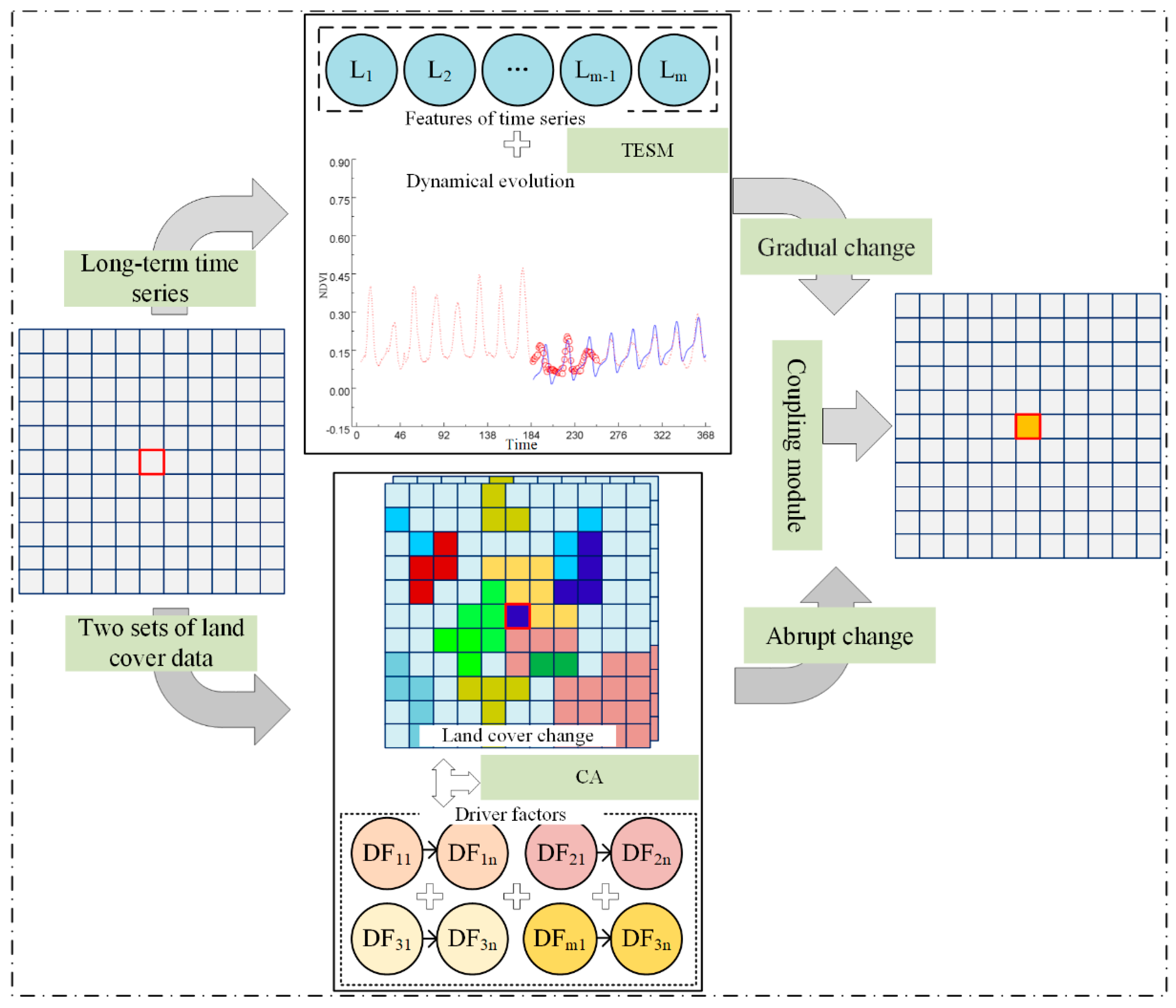
2. Methodology
2.1. The Temporal Evolution Simulation Module
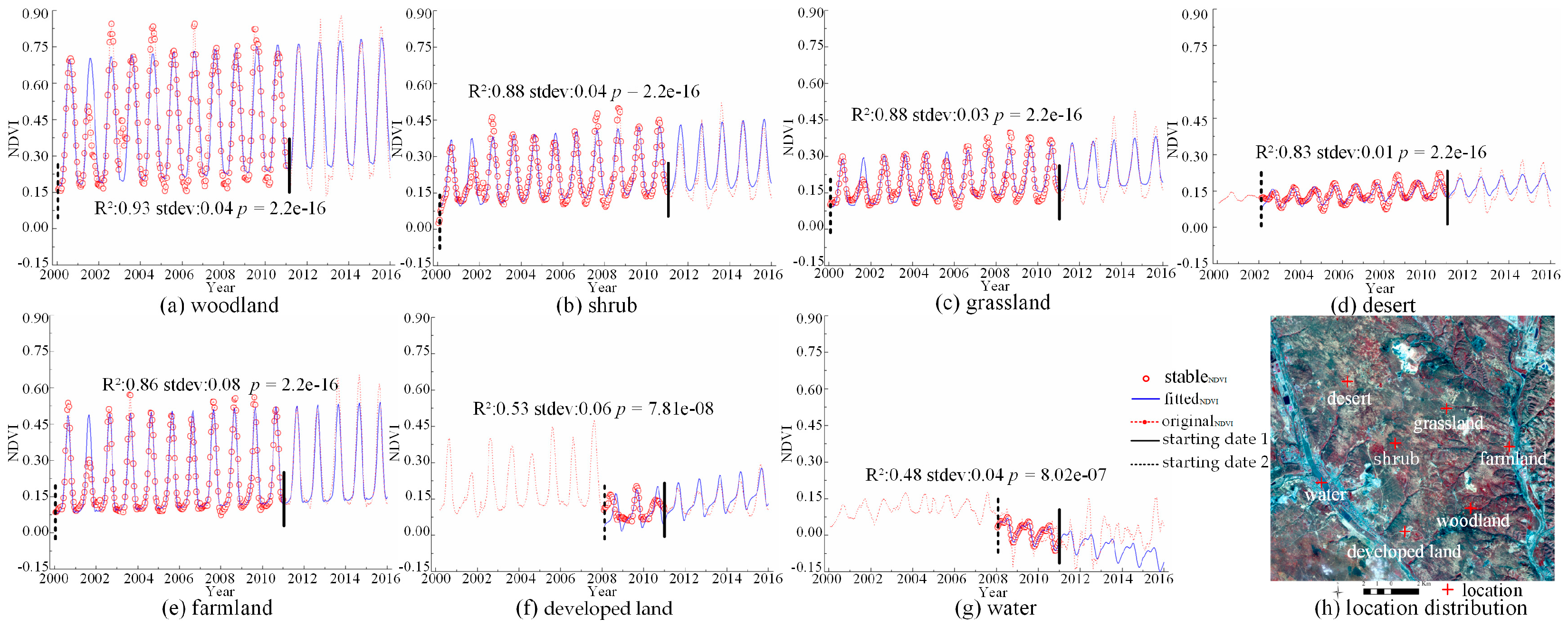
2.1.1. The BFAST-Monitor
2.1.2. Classification
2.2. The CA-Based Spatial Self-Organizing Simulation Module
2.2.1. The Traditional RF-CA
2.2.2. Optimization of RF-CA
2.3. Integrating Temporal Evolution Simulation Module with the Optimized RF-CA
2.4. Accuracy Assesment
3. Study Area and Data Processing
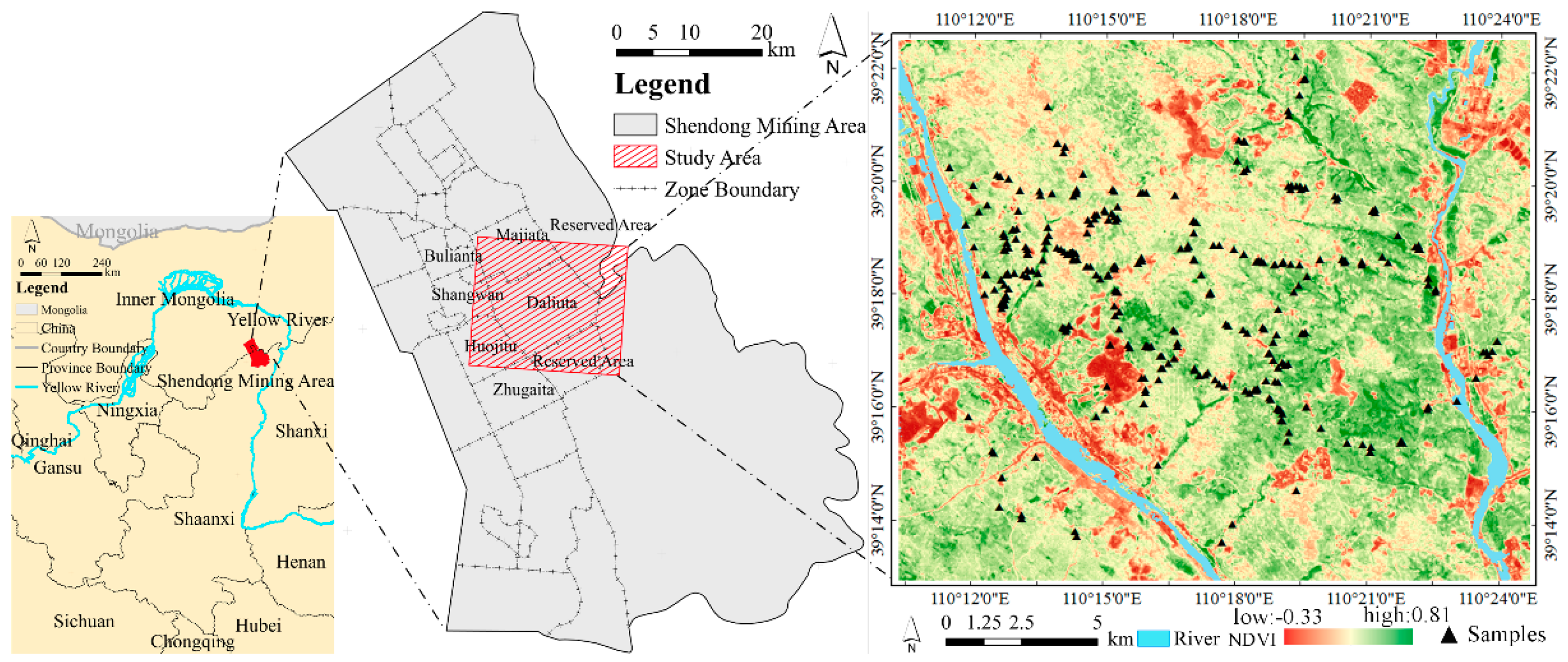
3.1. Study Area
3.2. Data and Its Preprocessing
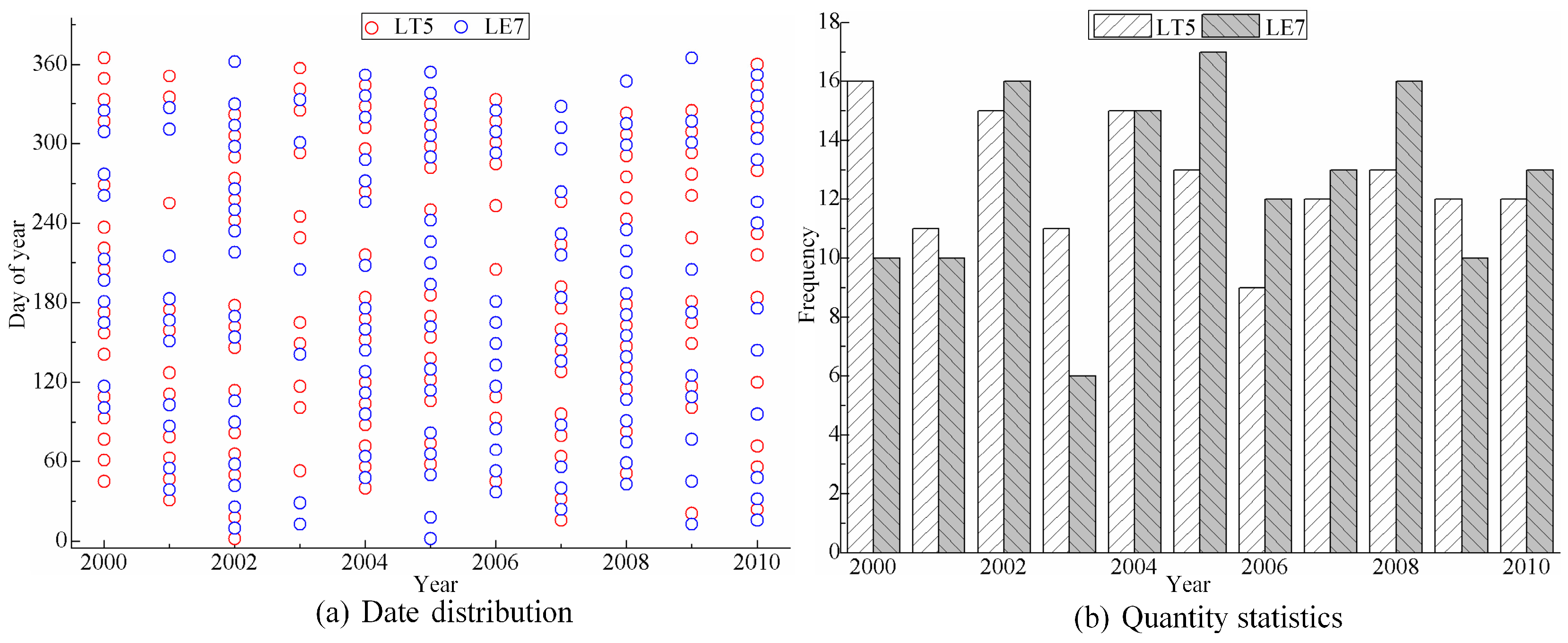
3.2.1. Remote Sensing Data for the Temporal Evolution Simulation Module
3.2.2. Driving Factors for the CA-Based Spatial Self-Organizing Simulation Module
4. Results
4.1. Model Initialization and Parameter Setteing
4.2. Comparison of the TDE-CA and a Null Model
4.3. Comparison of the TDE-CA and its Sub-Models
4.3.1. Comparison of the TDE-CA and its Sub-Models in Accuracy
4.3.2. Comparison of the TDE-CA and Sub-Models in Spatial Pattern
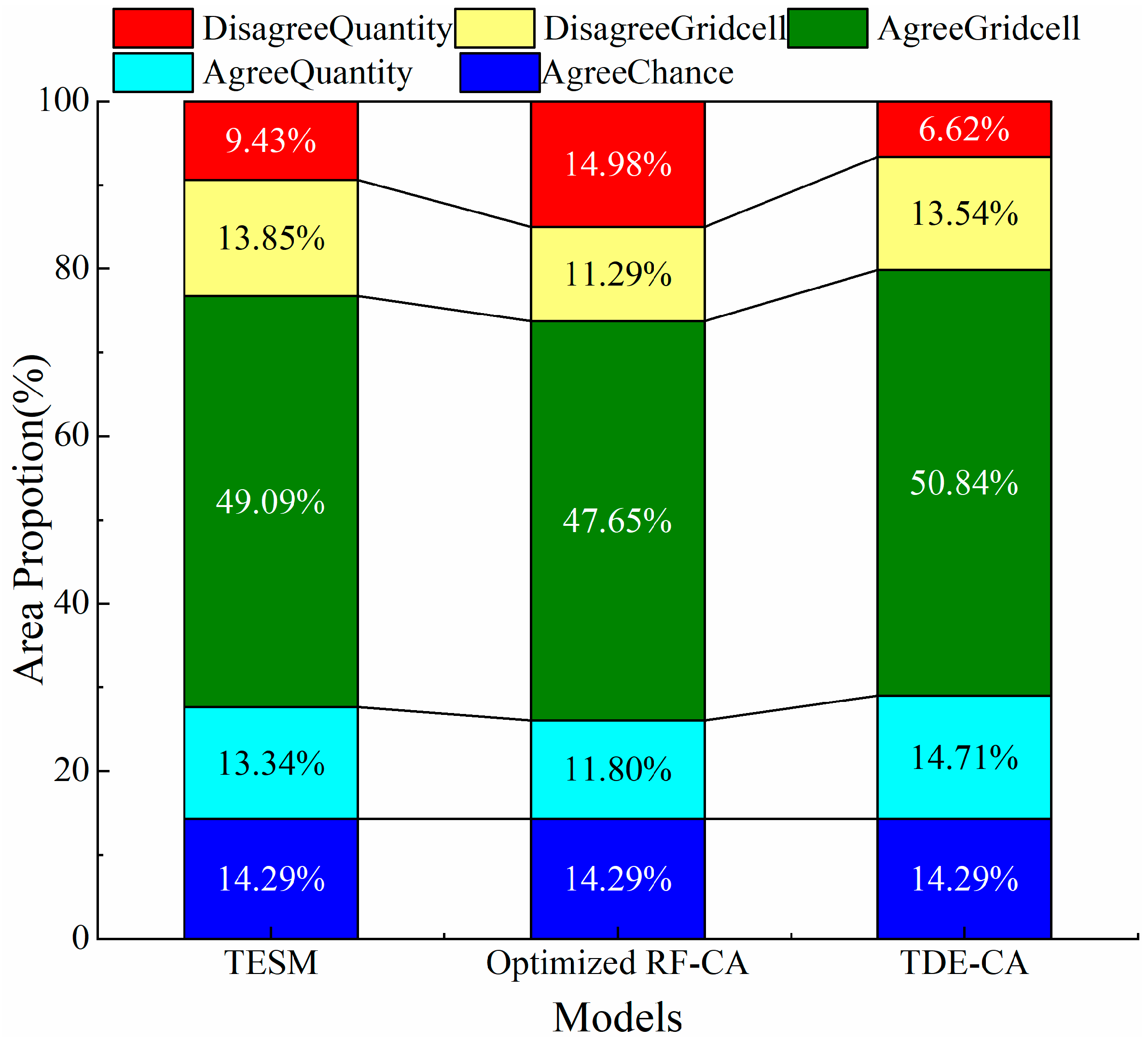
4.3.3. Comparison of the TDE-CA and Sub-Models in Agreements and Disagreements
4.4. Comparison of the TDE-CA and Other Simulation Models
4.4.1. Comparison of the TDE-CA and Other Models in Accuracy
4.4.2. Comparison of the TDE-CA and Other Models in Spatial Pattern
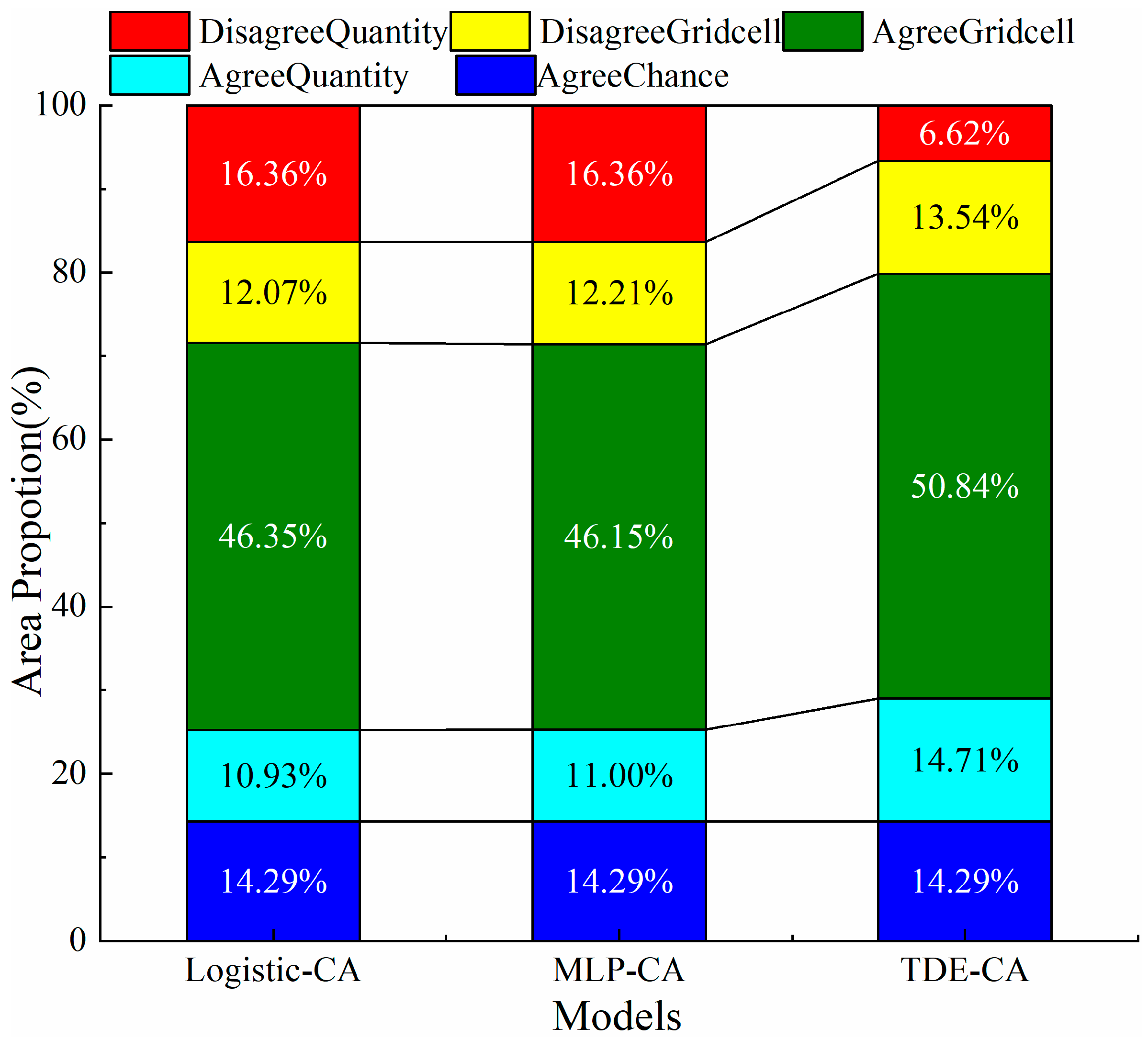
4.4.3. Comparison of the TDE-CA and Other Models in Agreements and Disagreements
5. Discussion
5.1. Parameter Sensitivity Analysis
5.2. Advantages and Adaptability of the TDE-CA
5.3. Limitations and Future Work
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, X.; Liang, X.; Li, X.; Xu, X.; Ou, J.; Chen, Y.; Li, S.; Wang, S.; Pei, F. A future land use simulation model (FLUS) for simulating multiple land use scenarios by coupling human and natural effects. Landsc. Urban Plan. 2017, 168, 94–116. [Google Scholar] [CrossRef]
- Luo, B.; Li, J.B.; Huang, G.H.; Li, H.L. A simulation-based interval two-stage stochastic model for agricultural non-point source pollution control through land retirement. Sci. Total Environ. 2006, 361, 38–56. [Google Scholar] [CrossRef] [PubMed]
- Vogelmann, J.E.; Gallant, A.L.; Shi, H.; Zhu, Z. Perspectives on monitoring gradual change across the continuity of Landsat sensors using time-series data. Remote Sens. Environ. 2016, 185, 258–270. [Google Scholar] [CrossRef]
- Arsanjani, J.J. Characterizing, monitoring, and simulating land cover dynamics using GlobeLand30: A case study from 2000 to 2030. J. Environ. Manag. 2018, 214, 66–75. [Google Scholar] [CrossRef] [PubMed]
- Brown, D.; Band, L.E.; Green, K.O.; Irwin, E.G.; Jain, A.; Lambin, E.F.; Pontius, R.G.; Seto, K.C.; Turner, B.L., II; Verburg, P.H. Advancing Land Change Modeling: Opportunities and Research Requirements; The National Research Council Press: Washington, DC, USA, 2013; ISBN 9780309288330. [Google Scholar]
- Wolfram, S. Cellular automata as models of complexity. Nature 1984, 311, 419–424. [Google Scholar] [CrossRef]
- Salhab, R.; Malhamé, R.P.; Ny, J.L. A Dynamic Game Model of Collective Choice in Multiagent Systems. In Proceedings of the IEEE Conference on Decision and Control, Osaka, Japan, 15–18 December 2015; pp. 4444–4449. [Google Scholar]
- Shang, C.; Fang, H.; Chen, J.; Zhang, J. Interacting with multi-agent systems through intention field based shared control methods. In Proceedings of the Asian Control Conference, Gold Coast, QLD, Australia, 17–20 December 2017; pp. 150–155. [Google Scholar]
- Parker, D.C.; Manson, S.M.; Janssen, M.A.; Hoffmann, M.J.; Deadman, P. Multi-Agent Systems for the Simulation of Land-Use and Land-Cover Change: A review. Ann. Assoc. Am. Geogr. 2015, 93, 314–337. [Google Scholar] [CrossRef]
- Zhang, P.; Gong, M.; Su, L.; Liu, J.; Li, Z. Change detection based on deep feature representation and mapping transformation for multi-spatial-resolution remote sensing images. ISPRS J. Photogramm. Remote Sens. 2016, 116, 24–41. [Google Scholar] [CrossRef]
- Jiang, X.; Lin, M.; Zhao, J. Woodland Cover Change Assessment Using Decision Trees, Support Vector Machines and Artificial Neural Networks Classification Algorithms. In Proceedings of the 4th International Conference on Intelligent Computation Technology and Automation, Shenzhen, China, 28–29 March 2011; pp. 312–315. [Google Scholar]
- Basse, R.M.; Charif, O.; Bódis, K. Spatial and temporal dimensions of land use change in cross border region of Luxembourg. Development of a hybrid approach integrating GIS, cellular automata and decision learning tree models. Appl. Geogr. 2016, 67, 94–108. [Google Scholar]
- Samardzic-Petrovic, M.; Kovačević, M.; Bajat, B.; Dragicevic, S. Machine Learning Techniques for Modelling Short Term Land-Use Change. ISPRS Int. J. Geo-Inf. 2017, 6, 387. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; Liu, X.; Chen, Y. Assimilating process context information of cellular automata into change detection for monitoring land use changes. Int. J. Geogr. Inf. Sci. 2012, 26, 1667–1687. [Google Scholar] [CrossRef]
- Lauf, S.; Haase, D.; Hostert, P.; Lakes, T.; Kleinschmit, B. Uncovering land-use dynamics driven by human decision-making—A combined model approach using cellular automata and system dynamics. Environ. Model. Softw. 2012, 27–28, 71–82. [Google Scholar] [CrossRef]
- Moreno, N.; Wang, F.; Marceau, D.J. Implementation of a dynamic neighborhood in a land-use vector-based cellular automata model. Comput. Environ. Urban Syst. 2009, 33, 44–54. [Google Scholar] [CrossRef]
- Li, X.; Liu, X.; Yu, L. A systematic sensitivity analysis of constrained cellular automata model for urban growth simulation based on different transition rules. Int. J. Geogr. Inf. Sci. 2014, 28, 1317–1335. [Google Scholar] [CrossRef]
- Liang, X.; Liu, X.; Li, X.; Chen, Y.; Tian, H.; Yao, Y. Delineating multi-scenario urban growth boundaries with a CA-based FLUS model and morphological method. Landsc. Urban Plan. 2018, 177, 47–63. [Google Scholar] [CrossRef]
- Li, X.; Chen, Y.; Liu, X.; Li, D.; He, J. Concepts, methodologies, and tools of an integrated geographical simulation and optimization system. Int. J. Geogr. Inf. Sci. 2011, 25, 633–655. [Google Scholar] [CrossRef]
- Li, X.; Yeh, G.O. Calibration of Cellular Automata by Using Neural Networks for the Simulation of Complex Urban Systems. Environ. Plan. A 2001, 33, 1445–1462. [Google Scholar] [CrossRef]
- Liu, X.; Ma, L.; Li, X.; Ai, B.; Li, S.; He, Z. Simulating urban growth by integrating landscape expansion index (LEI) and cellular automata. Int. J. Geogr. Inf. Sci. 2014, 28, 148–163. [Google Scholar] [CrossRef]
- Fulong, W. Calibration of stochastic cellular automata: the application to rural-urban land conversions. Int. J. Geogr. Inf. Syst. 2002, 16, 795–818. [Google Scholar]
- Ozturk, D. Urban Growth Simulation of Atakum (Samsun, Turkey) Using Cellular Automata-Markov Chain and Multi-Layer Perceptron-Markov Chain Models. Remote Sens. 2015, 7, 5918–5950. [Google Scholar] [CrossRef]
- Yang, Q.; Li, X.; Shi, X. Cellular automata for simulating land use changes based on support vector machines. Comput. Geosci. 2006, 34, 592–602. [Google Scholar] [CrossRef]
- Kamusoko, C.; Gamba, J. Simulating Urban Growth Using a Random Forest-Cellular Automata (RF-CA) Model. ISPRS Int. J. Geo-Inform. 2015, 4, 447–470. [Google Scholar] [CrossRef]
- Chen, Y.; Li, X.; Liu, X.; Ai, B.; Li, S. Capturing the varying effects of driving forces over time for the simulation of urban growth by using survival analysis and cellular automata. Landsc. Urban Plan. 2016, 152, 59–71. [Google Scholar] [CrossRef]
- Feng, Y.; Liu, Y.; Tong, X.; Liu, M.; Deng, S. Modeling dynamic urban growth using cellular automata and particle swarm optimization rules. Landsc. Urban Plan. 2011, 102, 188–196. [Google Scholar] [CrossRef]
- Aburas, M.M.; Ho, Y.M.; Ramli, M.F.; Ash’Aari, Z.H. The simulation and prediction of spatio-temporal urban growth trends using cellular automata models: A review. Int. J. Appl. Earth. Obs. Geoinf. 2016, 52, 380–389. [Google Scholar] [CrossRef]
- Rienow, A.; Goetzke, R. Supporting SLEUTH—Enhancing a cellular automaton with support vector machines for urban growth modeling. Comput. Environ. Urban Syst. 2015, 49, 66–81. [Google Scholar] [CrossRef]
- Xu, Z.; Coors, V. Combining system dynamics model, GIS and 3D visualization in sustainability assessment of urban residential development. Build. Environ. 2012, 47, 272–287. [Google Scholar] [CrossRef]
- Moghadam, H.S.; Helbich, M. Spatiotemporal urbanization processes in the megacity of Mumbai, India: A Markov chains-cellular automata urban growth model. Appl. Geogr. 2013, 40, 140–149. [Google Scholar]
- Candau, J.; Rasmussen, S.; Clarke, K.C. A coupled cellular automaton model for land use/land cover dynamics. In Proceedings of the 4th International Conference on Integrating GIS and Environmental Modeling (GIS/EM4): Problems, Prospects and Research Needs, Banff, AB, Canada, 2–8 September 2000; pp. 2–8. [Google Scholar]
- Xu, X.; Du, Z.; Zhang, H. Integrating the system dynamic and cellular automata models to predict land use and land cover change. Int. J. Appl. Earth. Obs. Geoinf. 2016, 52, 568–579. [Google Scholar] [CrossRef]
- Li, W.; Wu, C.; Zang, S. Modeling urban land use conversion of Daqing City, China: a comparative analysis of “top-down” and “bottom-up” approaches. Stoch. Environ. Res. Risk Assess. 2014, 28, 817–828. [Google Scholar] [CrossRef]
- Herold, M. Spatio-temporal dynamics in California’s Central Valley: Empirical links to urban theory. Int. J. Geogr. Inf. Sci. 2005, 19, 175–195. [Google Scholar]
- Gómez, C.; White, J.C.; Wulder, M.A. Optical remotely sensed time series data for land cover classification: A review. ISPRS J. Photogramm. Remote Sens. 2016, 116, 55–72. [Google Scholar] [CrossRef]
- Zhu, Z.; Fu, Y.; Woodcock, C.E.; Olofsson, P.; Vogelmann, J.E.; Holden, C.; Wang, M.; Dai, S.; Yu, Y. Including land cover change in analysis of greenness trends using all available Landsat 5, 7, and 8 images: A case study from Guangzhou, China (2000–2014). Remote Sens. Environ. 2016, 185, 243–257. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E.; Olofsson, P. Continuous monitoring of forest disturbance using all available Landsat imagery. Remote Sens. Environ. 2012, 122, 75–91. [Google Scholar] [CrossRef]
- Kennedy, R.E.; Yang, Z.; Cohen, W.B. Detecting trends in forest disturbance and recovery using yearly Landsat time series: 1. LandTrendr—Temporal segmentation algorithms. Remote Sens. Environ. 2010, 114, 2897–2910. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Continuous change detection and classification of land cover using all available Landsat data. Remote Sens. Environ. 2014, 144, 152–171. [Google Scholar] [CrossRef]
- Verbesselt, J.; Zeileis, A.; Herold, M. Near real-time disturbance detection using satellite image time series. Remote Sens. Environ. 2012, 123, 98–108. [Google Scholar] [CrossRef]
- Ding, J.; Zhou, J.; Tarokh, V. Optimal prediction of data with unknown abrupt change points. In Proceedings of the IEEE Global Conference on Signal and Information Processing (GlobalSIP), Montreal, QC, Canada, 14–16 November 2017; pp. 928–932. [Google Scholar]
- Chang, C.C.; Lin, C.J. LIBSVM:a library for support vector machines. ACM TIST 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Jonsson, P.; Eklundh, L. Seasonality extraction by function fitting to time-series of satellite sensor data. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1824–1832. [Google Scholar] [CrossRef]
- Jia, D.; Wang, C.; Lei, S. Semisupervised GDTW kernel-based fuzzy c-means algorithm for mapping vegetation dynamics in mining region using normalized difference vegetation index time series. J. Appl. Remote Sens. 2018, 12, 1. [Google Scholar] [CrossRef]
- Chen, C.; Wang, J.; Qin, W.; Dong, X. A new adaptive weight algorithm for salt and pepper noise removal. In Proceedings of the 2011 International Conference on Consumer Electronics, Communications and Networks (CECNet), Xianning, China, 16–18 April 2011; pp. 26–29. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Erna, L.; Gerardo, B.; Manuel, M.; Emilio, D. Predicting land-cover and land-use change in the urban fringe: A case in Morelia city, Mexico. Landsc. Urban Plan. 2001, 55, 271–285. [Google Scholar]
- Evensen, G. The Ensemble Kalman Filter: theoretical formulation and practical implementation. Ocean Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- Pontius, R.G.P.J.; Millones, M. Death to Kappa: birth of quantity disagreement and allocation disagreement for accuracy assessment. Int. J. Remote Sens. 2011, 32, 4407–4429. [Google Scholar] [CrossRef]
- Pontius, R.G.P.J.; Boersma, W.; Castella, J.-C.; Clarke, K.; de Nijs, T.; Dietzel, C.; Duan, Z.; Fotsing, E.; Goldstein, N.; Kok, K.; et al. Comparing the input, output, and validation maps for several models of land change. Ann. Reg. Sci. 2008, 42, 11–37. [Google Scholar] [CrossRef]
- Pontius, R.G.P.J.; Huffaker, D.; Denman, K. Useful techniques of validation for spatially explicit land-change models. Ecol. Model. 2004, 179, 445–461. [Google Scholar] [CrossRef]
- Emelyanova, I.V.; Mcvicar, T.R.; Niel, T.G.V.; Li, L.T.; Dijk, A.I.J.M.V. Assessing the accuracy of blending Landsat–MODIS surface reflectances in two landscapes with contrasting spatial and temporal dynamics: A framework for algorithm selection. Remote Sens. Environ. 2013, 133, 193–209. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar]
- Zhu, X.L.; Jin, C.; Feng, G.; Chen, X.H.; Masek, J.G. An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions. Remote Sens. Environ. 2010, 114, 2610–2623. [Google Scholar] [CrossRef]
- Chen, J.; Jönsson, P.; Tamura, M.; Gu, Z.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky–Golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, G.; Huang, C.; Liu, S.; Zhao, J. A tasseled cap transformation for Landsat 8 OLI TOA reflectance images. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 541–544. [Google Scholar]
- Hepinstall, J.A.; Alberti, M.; Marzluff, J.M. Predicting land cover change and avian community responses in rapidly urbanizing environments. Landsc. Ecol. 2008, 23, 1257–1276. [Google Scholar] [CrossRef]
- Schröder, B.; Seppelt, R. Analysis of pattern–process interactions based on landscape models—Overview, general concepts, and methodological issues. Ecol. Model. 2006, 199, 505–516. [Google Scholar] [CrossRef]
- Liu, X.; Ou, J.; Li, X.; Ai, B. Combining system dynamics and hybrid particle swarm optimization for land use allocation. Ecol. Model. 2013, 257, 11–24. [Google Scholar] [CrossRef]
- Lei, S.; Ren, L.; Bian, Z. Time–space characterization of vegetation in a semiarid mining area using empirical orthogonal function decomposition of MODIS NDVI time series. Environ. Earth Sci. 2016, 75, 516. [Google Scholar] [CrossRef]
- Tattoni, C.; Ciolli, M.; Ferretti, F. The Fate of Priority Areas for Conservation in Protected Areas: A Fine-Scale Markov Chain Approach. Environ. Manag. 2011, 47, 263–278. [Google Scholar] [CrossRef] [PubMed]
- Meentemeyer, R.K.; Shoemaker, D.A. FUTURES: Multilevel Simulations of Emerging Urban–Rural Landscape Structure Using a Stochastic Patch-Growing Algorithm. Ann. Assoc. Am. Geogr. 2013, 103, 785–807. [Google Scholar] [CrossRef]
- Castagnetti, C.; Bertacchini, E.; Corsini, A.; Rivola, R. A reliable methodology for monitoring unstable slopes: the multi-platform and multi-sensor approach. In Proceedings of the SPIE Remote Sensing, Earth Resources and Environmental Remote Sensing/GIS Applications, Amsterdam, The Netherlands, 22–25 September 2014; pp. 1–10. [Google Scholar]
- Li, X.; Lu, H.; Zhou, Y.; Hu, T.; Liang, L.; Liu, X.; Hu, G.; Yu, L. Exploring the performance of spatio-temporal assimilation in an urban cellular automata model. Int. J. Geogr. Inf. Sci. 2017, 2195–2215. [Google Scholar] [CrossRef]


| Type | Woodland | Shrub | Grassland | Desert | Farmland | Developed Land | Water |
|---|---|---|---|---|---|---|---|
| pseudo-invariant samples | 249 | 540 | 336 | 198 | 294 | 300 | 300 |
| cross-validation samples | 2811 | 6172 | 3649 | 1075 | 1079 | 17102 | 1925 |
| Category | Factor | Data sources |
|---|---|---|
| MD | Width-depth ratio | Extracted by distance analysis module in ArcGIS® according to contradistinguish map of mine well |
| Depth-thickness ratio | ||
| Underground gob distribution | ||
| Distance from exploit place | ||
| Distance from goaf | ||
| Distribution of groundwater | ||
| LSH | Distance from the river | Extracted by distance analysis module in ArcGIS® based on distribution map of river system |
| Wetness | Extracted from Landsat image with tasseled cap transformation [57] | |
| Brightness | ||
| Greenness | ||
| Elevation | Calculated from DEM using ArcGIS® | |
| Slope | ||
| AFLU | Excavation and occupation area | Extracted from contradistinguish map of mine well |
| Resource processing factory distance | ||
| Industrial square distance | ||
| Reclamation area | ||
| Main road distance | Calculated using distance analysis in ArcGIS® based on vector features layer drawn by hand with the Google maps as reference map | |
| Railway distance | ||
| Secondary road distance | ||
| Town center distance |
| Module | Parameters |
|---|---|
| TESM | ·Starting date of prediction period = 2011.01; ·Pseudo-samples. |
| CA Module | ·Transformation rule: random forest (RF); ·Neighborhood windows: 3×3; ·Random variable control parameter: λ= 5; ·Threshold value: K = 0.75; ·Iterative decrease rate: rate = 0.0008; ·Number of iterations = 100 times/year; ·Probability update condition: R2 ≥ 0.6 and p ≤ 0.05; ·Area control coefficient r = [1.01 1.03 1.05 0.5 0.7 1.07 1]. |
| CM | ·Time interval of assimilation = 1 year; ·Observation operator: H = 1 × 1; ·Window size: W = 30 × 30; ·The size of state variables ensemble: Num = 50. |
| AgreeChance a | AgreeQuantity a | AgreeGridcell a | Kno b | Klocation b | Kstandard b | |
|---|---|---|---|---|---|---|
| Null Model | 0.1429 | 0.0981 | 0.4172 | 0.6012 | 0.7171 | 0.5497 |
| TDE-CA | 0.1604 | 0.1095 | 0.5315 | 0.7648 | 0.7897 | 0.7161 |
| TESM | Optimized RF-CA | TDE-CA | ||||
|---|---|---|---|---|---|---|
| UA (%) | PA (%) | UA (%) | PA (%) | UA (%) | PA (%) | |
| woodland | 64.17 | 64.67 | 54.55 | 81.22 | 67.86 | 79.33 |
| shrub | 46.39 | 44.60 | 59.25 | 81.84 | 68.02 | 78.50 |
| grassland | 18.95 | 25.46 | 57.45 | 57.71 | 57.28 | 53.49 |
| desert | 62.91 | 65.25 | 70.89 | 77.49 | 56.78 | 77.86 |
| farmland | 33.61 | 96.65 | 56.52 | 82.39 | 75.26 | 73.86 |
| developed land | 94.99 | 70.90 | 98.16 | 73.22 | 95.4 | 84.38 |
| water | 57.81 | 95.12 | 93.01 | 93.35 | 81.56 | 99.01 |
| OA (%) | 62.70 | 75.36 | 79.84 | |||
| Kappa | 0.4994 | 0.6649 | 0.7161 | |||
| Logistic-CA | MLP-CA | TDE-CA | ||||
|---|---|---|---|---|---|---|
| UA (%) | PA (%) | UA (%) | PA (%) | UA (%) | PA (%) | |
| woodland | 55.15 | 81.15 | 52.42 | 82.78 | 67.86 | 79.33 |
| shrub | 58.88 | 88.22 | 59.2 | 87.38 | 68.02 | 78.50 |
| grassland | 54.56 | 61.47 | 56.28 | 54.75 | 57.28 | 53.49 |
| desert | 63.61 | 70.88 | 48.85 | 65.12 | 56.78 | 77.86 |
| farmland | 41.86 | 63.11 | 45.96 | 70.06 | 75.26 | 73.86 |
| developed land | 96.7 | 65.71 | 97.57 | 66.57 | 95.4 | 84.38 |
| water | 80.25 | 78.08 | 83.33 | 85.19 | 81.56 | 99.01 |
| OA (%) | 71.43 | 71.56 | 79.84 | |||
| Kappa | 0.6176 | 0.6198 | 0.7161 | |||
| Neighborhood Window Size | Number of Iterations | ||||||
|---|---|---|---|---|---|---|---|
| 3 × 3 | 5 × 5 | 7 × 7 | 9 × 9 | 50 | 100 | 150 | |
| OA (%) | 69.64 | 66.63 | 63.93 | 61.53 | 69.91 | 69.64 | 69.55 |
| Kappa | 0.5971 | 0.5604 | 0.5288 | 0.4972 | 0.5993 | 0.5971 | 0.5945 |
| Feature Update | Non-Feature Update | Area Control | Non-Area Control | RF-CA | Optimized RF-CA | |
|---|---|---|---|---|---|---|
| OA (%) | 69.64 | 71.49 | 72.37 | 67.60 | 69.64 | 75.36 |
| Kappa | 0.5971 | 0.6119 | 0.6267 | 0.5783 | 0.5971 | 0.6649 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Lei, S.; Elmore, A.J.; Jia, D.; Mu, S. Integrating Temporal Evolution with Cellular Automata for Simulating Land Cover Change. Remote Sens. 2019, 11, 301. https://doi.org/10.3390/rs11030301
Wang C, Lei S, Elmore AJ, Jia D, Mu S. Integrating Temporal Evolution with Cellular Automata for Simulating Land Cover Change. Remote Sensing. 2019; 11(3):301. https://doi.org/10.3390/rs11030301
Chicago/Turabian StyleWang, Cangjiao, Shaogang Lei, Andrew J. Elmore, Duo Jia, and Shouguo Mu. 2019. "Integrating Temporal Evolution with Cellular Automata for Simulating Land Cover Change" Remote Sensing 11, no. 3: 301. https://doi.org/10.3390/rs11030301
APA StyleWang, C., Lei, S., Elmore, A. J., Jia, D., & Mu, S. (2019). Integrating Temporal Evolution with Cellular Automata for Simulating Land Cover Change. Remote Sensing, 11(3), 301. https://doi.org/10.3390/rs11030301





