Estimating the Height and Basal Area at Individual Tree and Plot Levels in Canadian Subarctic Lichen Woodlands Using Stereo WorldView-3 Images
Abstract
1. Introduction
2. Materials and Methods
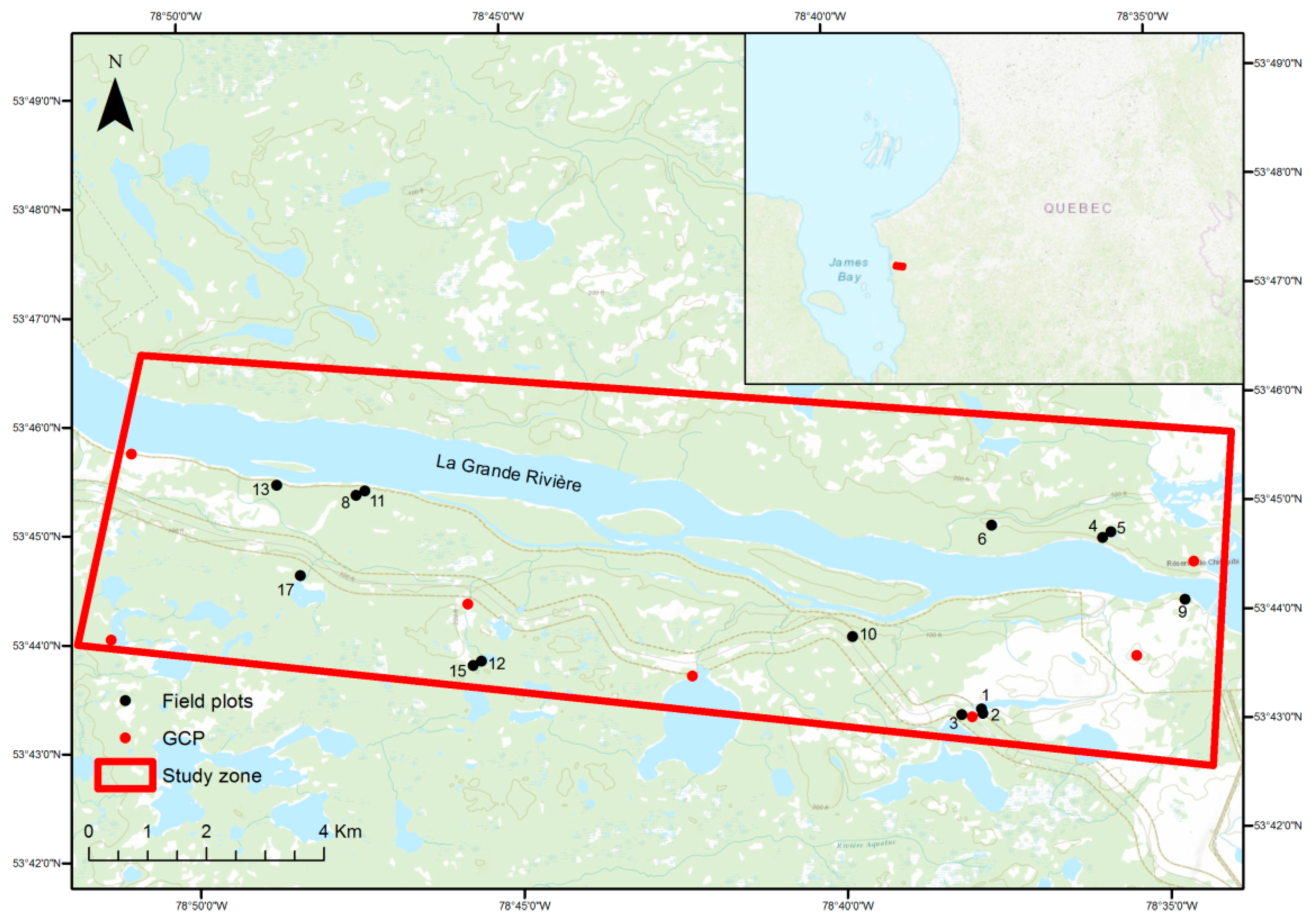
2.1. Study Area
2.2. Field Data
2.3. Remote Sensing Imagery
2.4. Image Georeferencing
2.5. Tree Height Measurements and Stem Counts from the WV3 Images
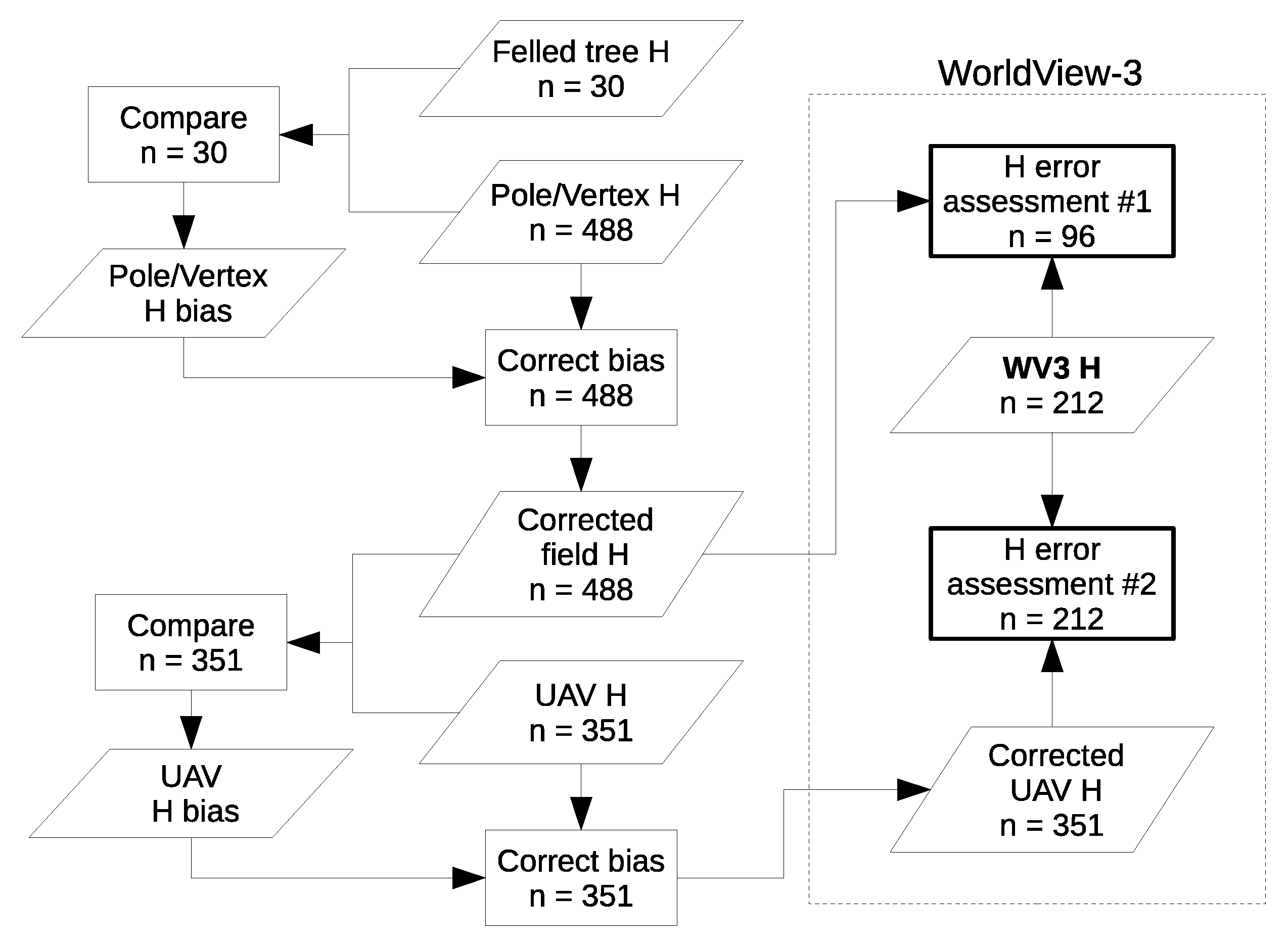
- Estimated the bias between the pole/Vertex heights and the true height measured on the corresponding felled trees (n = 30), and then corrected all the non-destructive height measurements accordingly;
- estimated the bias between the bias-corrected field heights and the corresponding heights extracted from the UAV 3D point clouds, and then corrected all the UAV heights accordingly.
2.6. Estimating Basal Area at Tree and Plot Level
3. Results
3.1. Georeferencing and Measurement Error in Reference Data
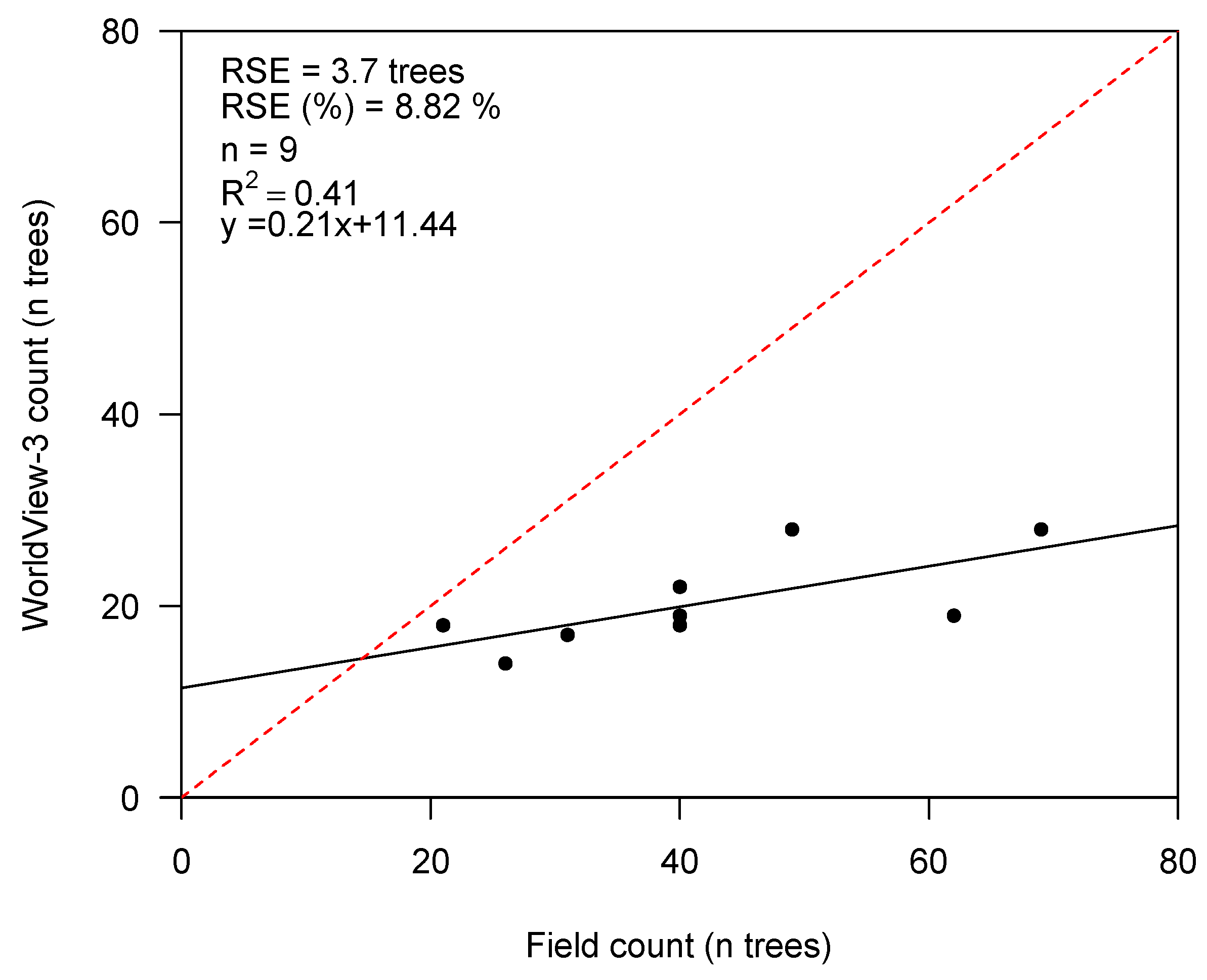
3.2. Detection Rates and Stem Density
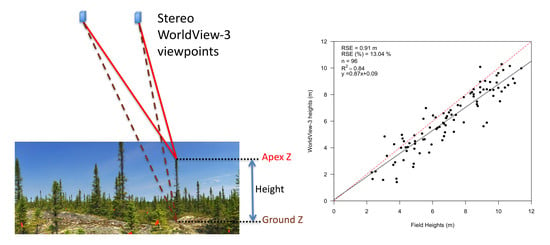
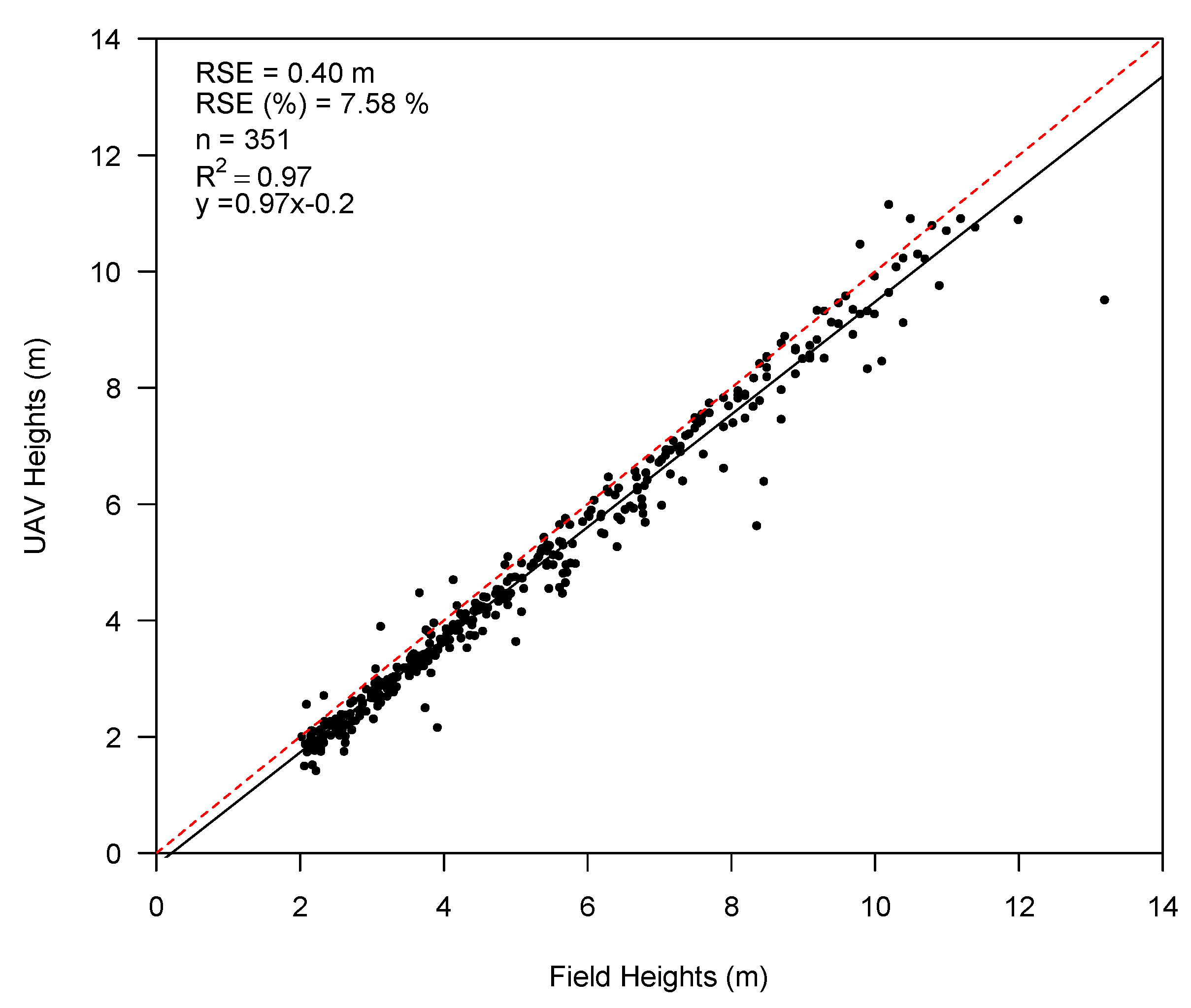
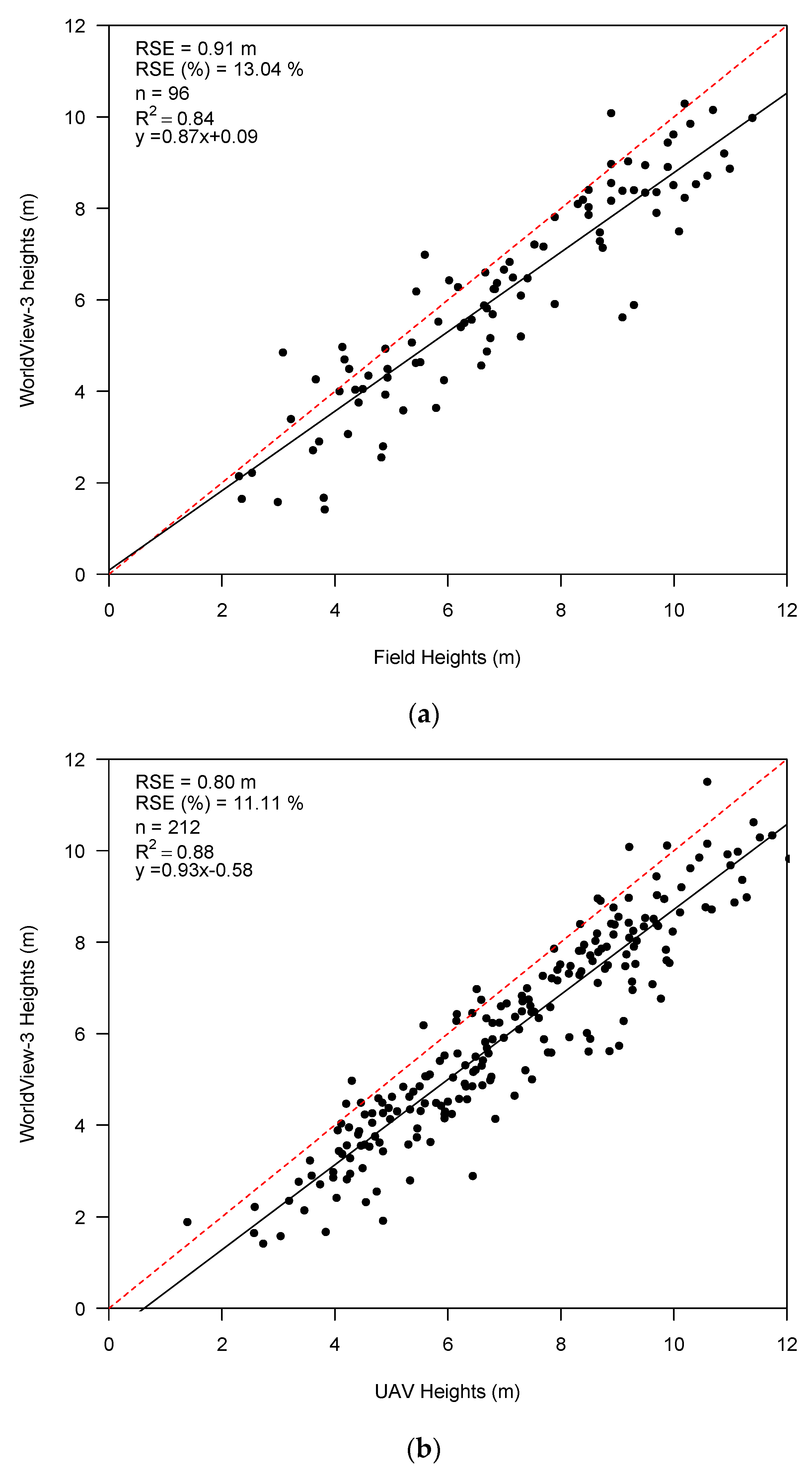
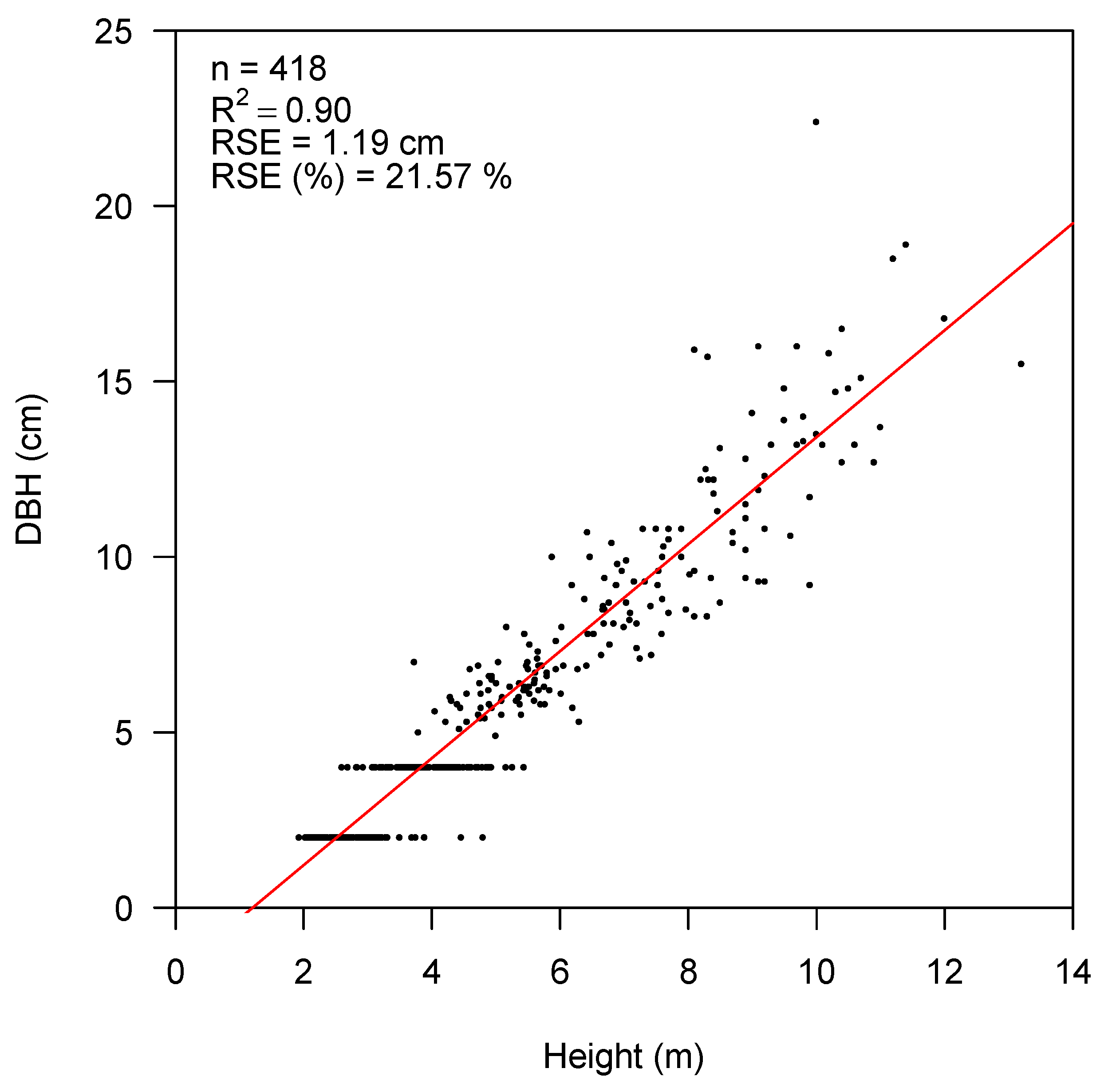
3.3. Tree Height Measurements from the Imagery
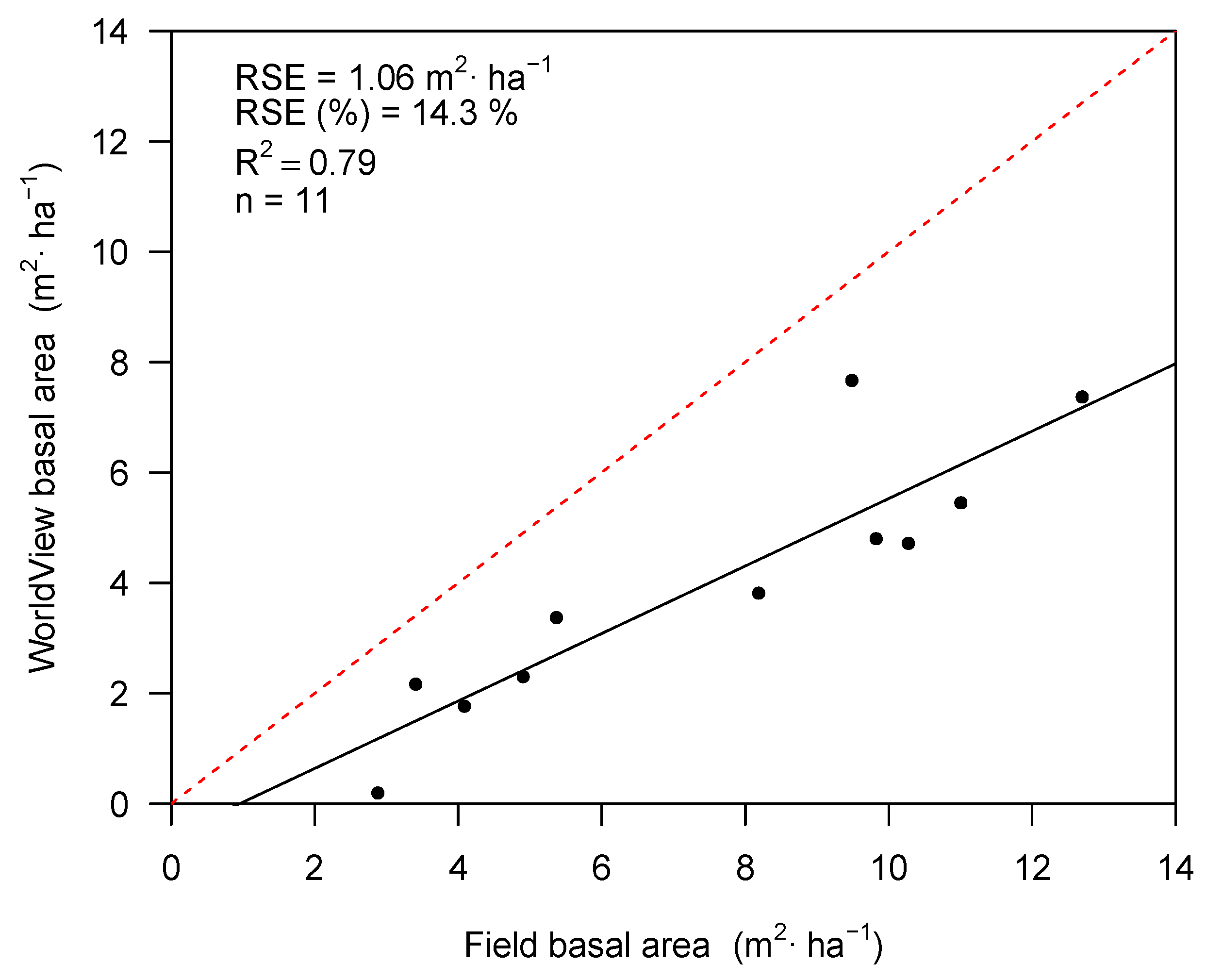
3.4. Tree and Plot Level Basal Area
4. Discussion
4.1. Detection Rates and Stem Density
4.2. Height Measurement Accuracy
4.3. Basal Area and Biomass
4.4. Limitations, Usefulness and Implications
5. Conclusions
- It is possible to accurately measure (residual standard error of 0.80–0.91 m) the height of individual conifer trees from space in sparse woodlands;
- the underestimation of heights (bias of −0.83 to −1.07 m) was mainly caused by that of the elevation of the tree top (−1.27 m), while the bias of ground elevations was much smaller (−0.44 m);
- it is difficult to measure a large proportion of trees because many of the smaller ones are occluded by taller trees on at least one of the images, precluding stereo measurements;
- tree top discernibility is higher when the background (ground cover type) is bright because it increases the contrast with the relatively dark crowns.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Callaghan, T.V.; Crawford, R.M.M.; Eronen, M.; Hofgaard, A.; Payette, S.; Rees, W.G.; Skre, O.; Sveinbjörnsson, B.; Vlassova, T.K.; Werkman, B.R. The dynamics of the tundra-taiga boundary: An overview and suggested coordinated and integrated approach to research. AMBIO Spec. Rep. 2002, 12, 3–5. [Google Scholar] [CrossRef]
- Rowe, J.S. Forest Regions of Canada; Fisheries and Environment Canada: Ottawa, ON, Canada, 1972.
- Hare, F.K.; Ritchie, J.C. The Boreal Bioclimates. Geogr. Rev. 1972, 62, 333–365. [Google Scholar] [CrossRef]
- Payette, S.; Fortin, M.-J.; Gamache, I. The Subarctic Forest–Tundra: The Structure of a Biome in a Changing Climate. Bioscience 2001, 51, 709. [Google Scholar] [CrossRef]
- Payette, S.; Delwaide, A. Tamm review: The North-American lichen woodland. For. Ecol. Manag. 2018, 417, 167–183. [Google Scholar] [CrossRef]
- Montesano, P.M.; Neigh, C.; Sun, G.; Duncanson, L.; Van Den Hoek, J.; Ranson, K.J. Remote Sensing of Environment The use of sun elevation angle for stereogrammetric boreal forest height in open canopies. Remote Sens. Environ. 2017, 196, 76–88. [Google Scholar] [CrossRef]
- Hauglin, M.; Næsset, E. Detection and segmentation of small trees in the forest-tundra ecotone using airborne laser scanning. Remote Sens. 2016, 8, 407. [Google Scholar] [CrossRef]
- Ropars, P.; Boudreau, S. Shrub expansion at the foresttundra ecotone: Spatial heterogeneity linked to local topography. Environ. Res. Lett. 2012, 7, 015501. [Google Scholar] [CrossRef]
- Ouranos. Vers l’Adaptation. Synthèse des Connaissances sur les Changements Climatiques au Québec. Partie 2: Vulnérabilités, Impacts et Adaptation aux Changements Climatiques. 2015. Available online: https://www.ouranos.ca/publication-scientifique/SyntheseRapportfinal.pdf. (accessed on 15 November 2018).
- Kirdyanov, A.V.; Hagedorn, F.; Knorre, A.A.; Fedotova, E.V.; Vaganov, E.A.; Naurzbaev, M.M.; Moiseev, P.A.; Rigling, A. 20th century tree-line advance and vegetation changes along an altitudinal transect in the Putorana Mountains, northern Siberia. Boreas 2012, 41, 56–67. [Google Scholar] [CrossRef]
- Ranson, K.J.; Montesano, P.M.; Nelson, R. Object-based mapping of the circumpolar taiga-tundra ecotone with MODIS tree cover. Remote Sens. Environ. 2011, 115, 3670–3680. [Google Scholar] [CrossRef]
- Montesano, P.M.; Sun, G.; Dubayah, R.; Ranson, K.J. The Uncertainty of Plot-Scale Forest Height Estimates from Complementary Spaceborne Observations in the taiga-tundra ecotone. Remote Sens. 2014, 6, 10070–10088. [Google Scholar] [CrossRef]
- Peng, C.; Zhang, L.; Zhou, X.; Dang, Q.; Huang, S. Developing and evaluating tree height-diameter models at three geographic scales for black spruce in Ontario. North. J. Appl. For. 2004, 21, 83–92. [Google Scholar]
- Korpela, I. Individual tree measurements by means of digital aerial photogrammetry. Silva Fenn. 2004, Monographs 3, 1–93. [Google Scholar]
- Spurr, S.H. Photogrammetry and Photo-Interpretation, 2nd ed.; The Ronald Press Company: New York, NY, USA, 1960. [Google Scholar]
- St-Onge, B.; Jumelet, J.; Cobello, M.; Véga, C. Measuring individual tree height using a combination of stereophotogrammetry and lidar. Can. J. For. Res. 2004, 34, 2122–2130. [Google Scholar] [CrossRef]
- Sawaya, K.E.; Olmanson, L.G.; Heinert, N.J.; Brezonik, P.L.; Bauer, M.E. Extending satellite remote sensing to local scales: Land and water resource monitoring using high-resolution imagery. Remote Sens. Environ. 2003, 88, 144–156. [Google Scholar] [CrossRef]
- Leboeuf, A.; Beaudoin, A.; Fournier, R.A.; Guindon, L.; Luther, J.E.; Lambert, M.C. A shadow fraction method for mapping biomass of northern boreal black spruce forests using QuickBird imagery. Remote Sens. Environ. 2007, 110, 488–500. [Google Scholar] [CrossRef]
- Leboeuf, A.; Fournier, R.A.; Luther, J.E.; Beaudoin, A.; Guindon, L. Forest attribute estimation of northeastern Canadian forests using QuickBird imagery and a shadow fraction method. For. Ecol. Manag. 2012, 266, 66–74. [Google Scholar] [CrossRef]
- Ozdemir, I. Estimating stem volume by tree crown area and tree shadow area extracted from pan—Sharpened Quickbird imagery in open Crimean juniper forests. Int. J. Remote Sens. 2008, 29, 5643–5655. [Google Scholar] [CrossRef]
- St-Onge, B.; Vega, C.; Fournier, R.A.; Hu, Y. Mapping canopy height using a combination of digital stereo-photogrammetry and lidar. Int. J. Remote Sens. 2008, 29, 3343–3364. [Google Scholar] [CrossRef]
- Abshire, J.B.; Sun, X.; Riris, H.; Sirota, J.M.; McGarry, J.F.; Palm, S.; Yi, D.; Liiva, P. Geoscience Laser Altimeter System (GLAS) on the ICESat mission: On-orbit measurement performance. Geophys. Res. Lett. 2005, 32, 1–4. [Google Scholar] [CrossRef]
- Shean, D.E.; Alexandrov, O.; Moratto, Z.M.; Smith, B.E.; Joughin, I.R.; Porter, C.; Morin, P. An automated, open-source pipeline for mass production of digital elevation models (DEMs) from very-high-resolution commercial stereo satellite imagery. ISPRS J. Photogramm. Remote Sens. 2016, 116, 101–117. [Google Scholar] [CrossRef]
- Meddens, A.J.H.; Vierling, L.A.; Eitel, J.U.H.; Jennewein, J.S.; White, J.C.; Wulder, M.A. Developing 5m resolution canopy height and digital terrain models from WorldView and ArcticDEM data. Remote Sens. Environ. 2018, 218, 174–188. [Google Scholar] [CrossRef]
- Center, P.G. ArcticDEM. Available online: https://www.pgc.umn.edu/data/arcticdem/ (accessed on 15 November 2018).
- Immitzer, M.; Stepper, C.; Böck, S.; Straub, C.; Atzberger, C. Use of WorldView-2 stereo imagery and National Forest Inventory data for wall-to-wall mapping of growing stock. For. Ecol. Manag. 2016, 359, 232–246. [Google Scholar] [CrossRef]
- Pearse, G.D.; Dash, J.P.; Persson, H.J.; Watt, M.S. Comparison of high-density LiDAR and satellite photogrammetry for forest inventory. ISPRS J. Photogramm. Remote Sens. 2018, 142, 257–267. [Google Scholar] [CrossRef]
- Thomas, V.; Treitz, P.; Jelinski, D.; Miller, J.; Lafleur, P.; McCaughey, J.H. Image classificaiton of a northern peatland complex using spectral and plant community data. Remote Sens. Environ. 2002, 84, 83–99. [Google Scholar] [CrossRef]
- Vastaranta, M.; Yu, X.; Luoma, V.; Karjalainen, M.; Saarinen, N.; Wulder, M.A.; White, J.C.; Persson, H.J.; Hollaus, M.; Yrttimaa, T.; et al. Aboveground forest biomass derived using multiple dates of WorldView-2 stereo-imagery: Quantifying the improvement in estimation accuracy. Int. J. Remote Sens. 2018, 39, 1–18. [Google Scholar] [CrossRef]
- Longbotham, N.; Pacifici, F.; Malitz, S.; Baugh, W.; Camps-valls, G. Measuring the Spatial and Spectral Performance of WorldView-3. In Hyperspectral Imaging and Sounding of the Environment; Optical Society of America: Lake Arrowhead, CA, USA, 2015; p. 2703. [Google Scholar]
- Airbus. Pléiades Neo. Available online: https://www.intelligence-airbusds.com/files/pmedia/public/r51130_9_leaflet-pleiadesneov2.pdf (accessed on 15 November 2017).
- Aguilar, M.A.; Nemmaoui, A.; Aguilar, F.J.; Qin, R. Quality assessment of digital surface models extracted from WorldView-2 and WorldView-3 stereo pairs over different land covers. GISci. Remote Sens. 2018, 56, 109–129. [Google Scholar] [CrossRef]
- Qin, R. RPC stereo processor (RSP)—A software package for digital surface model and orthophoto generation from satellite stereo imagery. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 3, 77–82. [Google Scholar] [CrossRef]
- Goldbergs, G.; Maier, S.W.; Levick, S.R.; Edwards, A. Limitations of high resolution satellite stereo imagery for estimating canopy height in Australian tropical savannas. Int. J. Appl. Earth Obs. Geoinf. 2019, 75, 83–95. [Google Scholar] [CrossRef]
- Jeong, J.; Kim, T. Analysis of Dual-Sensor Stereo Geometry and Its Positioning Accuracy. Photogramm. Eng. Remote Sens. 2014, 80, 653–661. [Google Scholar] [CrossRef]
- Jeong, J.; Kim, T. Quantitative Estimation and Validation of the Effects of the Convergence, Bisector Elevation, and Asymmetry Angles on the Positioning Accuracies of Satellite Stereo Pairs. Photogramm. Eng. Remote Sens. 2016, 82, 625–633. [Google Scholar] [CrossRef]
- Gobakken, T.; Næsset, E.; Thieme, N.; Bollandsa, O.M. Detection of small single trees in the forest tundra ecotone using height values from airborne laser scanning. Can. J. Remote Sens. 2011, 37, 264–274. [Google Scholar] [CrossRef]
- Margolis, H.A.; Nelson, R.F.; Montesano, P.M.; Beaudoin, A.; Sun, G.; Andersen, H.-E.; Wulder, M.A. Combining satellite lidar, airborne lidar, and ground plots to estimate the amount and distribution of aboveground biomass in the boreal forest of North America. Can. J. For. Res. 2015, 45, 838–855. [Google Scholar] [CrossRef]
- Hopkinson, M.A.; Wulder, N.C.; Coops, T.; Milne, A.; Fox, C.W.B. Airborne lidar sampling of the Canadian boreal forest: Planning, execution, and initial processing. In Proceedings of the SilviLaser 2011 Conference, Hobart, Australia, 16–20 October 2011. [Google Scholar]
- Anonymous. GEDI Ecosystem Lidar. Available online: https://gedi.umd.edu/ (accessed on 15 November 2018).
- Popescu, S.C.; Zhou, T.; Nelson, R.; Neuenschwander, A.; Sheridan, R.; Narine, L.; Walsh, K.M. Photon counting LiDAR: An adaptive ground and canopy height retrieval algorithm for ICESat-2 data. Remote Sens. Environ. 2018, 208, 154–170. [Google Scholar] [CrossRef]
- Gerardin, V.; McKenney, D. Une Classification Climatique du Québec à Partir de Modèles de Distribution Spatiale de Données Climatiques Mensuelles: vers une Définition des Bioclimats du Québec; Contribution du Service de la Cartographie éCologique, no 60; Ministère de l’Environnement: Québec, QC, Canada, 2001.
- DigitalGlobe. WorldView-3 Above and Beyond. Available online: http://worldview3.digitalglobe.com/ (accessed on 16 November 2018).
- Chen, S.; Mcdermid, G.J. Measuring Vegetation Height in Linear Disturbances in the Boreal Forest with UAV Photogrammetry. Remote Sens. 2017, 9, 1257. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Korpela, I.; Dahlin, B.; Schäfer, H.; Bruun, E.; Haapaniemi, F.; Honkasalo, J.; Ilvesniemi, S.; Kuutti, V.; Linkosalmi, M.; Mustonen, J.; et al. Single-tree forest inventory using lidar and aerial images for 3D treetop positioning, species recognition, height and crown width estimation. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2007, 36, 227–233. [Google Scholar] [CrossRef]
- Kwak, D.A.; Lee, W.K.; Lee, J.H.; Biging, G.S.; Gong, P. Detection of individual trees and estimation of tree height using LiDAR data. J. For. Res. 2007, 12, 425–434. [Google Scholar] [CrossRef]
- Chiba, Y. Architectural analysis of relationship between biomass and basal area based on pipe model theory. Ecol. Model. 1998, 108, 219–225. [Google Scholar] [CrossRef]

| Plot | Cover Type | Density * (stems ha−1) | Type | Avg DBH in cm (SD) | Avg H in m (SD) |
|---|---|---|---|---|---|
| 1 | Rocky | 1320 | Standard | 5.4 (2.7) | 4.63 (1.61) |
| 2 | Rocky | 1417 | Standard | 5.6 (2.7) | 4.73 (1.61) |
| 3 | Lichen | 2627 | Standard | 6.3 (3.6) | 5.29 (2.10) |
| 4 | Lichen | 1467 | Intensive | 9.8 (4.0) | 8.05 (2.52) |
| 5 | Peatland | 1467 | Intensive | 3.9 (1.8) | 3.5 (1.24) |
| 6 | Lichen | 720 | Standard | 8.0 (5.9) | 6.3 (3.47) |
| 7 | Lichen | 1151 | Intensive | 6.2 (4.5) | 4.74 (2.11) |
| 8 | Lichen | 3335 | Standard | 5.2 (3.7) | 4.54 (2.20) |
| 9 | Lichen | 1559 | Standard | 7.6 (5.0) | 5.98 (2.93) |
| 10 | Lichen | 3368 | Intensive | 4.7 (3.9) | 4.15 (2.09) |
| 11 | Peatland | 3338 | Standard | 4.9 (2.6) | 4.47 (1.53) |
| 12 | Lichen | 4168 | Intensive | 5.3 (3.4) | 4.45 (2.13) |
| 13 | Lichen | 1659 | Standard | 5.3 (3.6) | 4.57 (2.12) |
| 14 | Peatland | 2768 | Intensive | 5.3 (2.8) | 4.6 (1.85) |
| Parameter | Image 1 | Image 2 |
|---|---|---|
| Time of acquisition (UTC) | 16 h 47 min 02 s | 16 h 47 min 55 s |
| Solar azimuth | 165.5° | 165.8° |
| Solar elevation | 58.4° | 58.4° |
| Satellite azimuth | 24.1° | 186.5° |
| Satellite elevation | 71.5° | 71.0° |
| Cover Type | n | R2 | Bias (m) | RMSE (m) |
|---|---|---|---|---|
| Lichen | 170 | 0.87 | 1.06 | 1.33 |
| Rocky | 27 | 0.80 | 0.95 | 1.16 |
| Peatland | 15 | 0.53 | 1.62 | 1.84 |
| Comparison | RMSE (m) | Bias (m) |
|---|---|---|
| UAV ground point—GNSS | 1.40 | 0.15 |
| WorldView-3—UAV ground point | 1.08 | −0.44 |
| Cover Type | n | Trees with H ≥ 2 m | Trees with H ≥ 4 m | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RSE (m2 ha−1) | % RSE | R2 | p-Value | RSE (m2 ha−1) | % RSE | R2 | p-Value | ||
| All cover types | 14 | 1.57 | 20.2 | 0.62 | <0.001 | 1.47 | 21.3 | 0.67 | <0.001 |
| Lichen and rocky | 11 | 1.11 | 13.5 | 0.77 | <0.001 | 1.06 | 14.3 | 0.79 | <0.001 |
| Lichen | 9 | 1.19 | 12.8 | 0.66 | 0.005 | 1.11 | 13.3 | 0.70 | 0.003 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
St-Onge, B.; Grandin, S. Estimating the Height and Basal Area at Individual Tree and Plot Levels in Canadian Subarctic Lichen Woodlands Using Stereo WorldView-3 Images. Remote Sens. 2019, 11, 248. https://doi.org/10.3390/rs11030248
St-Onge B, Grandin S. Estimating the Height and Basal Area at Individual Tree and Plot Levels in Canadian Subarctic Lichen Woodlands Using Stereo WorldView-3 Images. Remote Sensing. 2019; 11(3):248. https://doi.org/10.3390/rs11030248
Chicago/Turabian StyleSt-Onge, Benoît, and Simon Grandin. 2019. "Estimating the Height and Basal Area at Individual Tree and Plot Levels in Canadian Subarctic Lichen Woodlands Using Stereo WorldView-3 Images" Remote Sensing 11, no. 3: 248. https://doi.org/10.3390/rs11030248
APA StyleSt-Onge, B., & Grandin, S. (2019). Estimating the Height and Basal Area at Individual Tree and Plot Levels in Canadian Subarctic Lichen Woodlands Using Stereo WorldView-3 Images. Remote Sensing, 11(3), 248. https://doi.org/10.3390/rs11030248