1. Introduction
Extracting plastic greenhouse (PG) segments from well-segmented high-resolution imagery is a basic goal for many applications, such as area monitoring, production forecast, and the accurate inversion of land surface temperature; and it is more effective than traditional manual drawing when many samples have to be selected as the reference polygons in large-scale research.
Segmentation, its evaluation, and texture analysis are crucial steps in geographic object-based image analysis (GEOBIA). According to 254 case studies in Ma et al. [
1], 80.9% used eCognition (Trimble, Munich, Germany) for segmentation, whereas the remaining segmentation software mainly includes ENVI (Harris Geospatial Solutions, Inc., Broomfield, USA), SPRING (National Institute for Space Research, São José dos Campos, Brazil) and ERDAS (Hexagon Geospatial, Madison, USA). Generally, objects can be obtained via chessboard, quadtree-based, contrast split, contrast filter, multi-threshold, superpixel [
2,
3,
4,
5], watershed [
6,
7], and multi-resolution segmentation (MRS) [
8,
9] in eCognition software [
10], or the active contours (snakes) [
11,
12,
13] method in MATLAB (MathWorks, Natick, USA). MRS is most widely and successfully employed method under the context of remote sensing GEOBIA applications [
14,
15,
16,
17,
18]. Even though thematic vector data can improve the quality of the segmentation [
19], the decision of the optimal value of scale parameter (SP), shape, and compactness in MRS is not easy, since the conventional try-and-evaluate method [
19,
20] is too complicated, time consuming, and provides incomplete results. Therefore, Estimation of Scale Parameter (ESP) and ESP 2 are methods that have been introduced to calculate variance among segmentation results that are produced by the given shape, compactness, and step-changing scale levels. ESP estimates the SP for MRS on single-layer image data or other continuous data (e.g., digital surface models) semi-automatically [
21], and ESP 2 can automatically obtain optimal scale parameter (OSP) on multiple layers [
22]. As an updated version, ESP 2 has been adopted to find the specific scale levels for specific target objects [
23], and is also employed to determine the optimal parameters for extracting greenhouses from WorldView-2 and WorldView-3 multispectral imagery [
17,
18]. The segmentation results of GaoFen-2 (GF-2) multispectral and panchromatic fusion imagery based on the ESP 2 tool still do not meet the requirements for the degree of over-segmentation and struggle to delineate the natural boundary of PGs, which is an obstacle to fully using the panchromatic band. Namely, over-segmentation and under-segmentation [
14,
24] are still two critical issues for PG segments, which is called problem I.
The pixels of one class display some texture features that differ from other categories in satellite imagery. To illustrate, textural information can be used as an additional band to improve the object-oriented classification of urban areas in Quickbird imagery [
25]; however, a similar pixel-based maximum likelihood PG classification in Agüera et al.’s research [
26] showed that the inclusion of a band with texture information did not significantly improve the overwhelming majority quality index values compared to those found when only multi-spectral bands were considered. Another object-based work conducted by Hasituya et al. [
27] showed that adding textural features from medium-resolution imagery provides only limited improvement in accuracy, whereas spectral features more significantly contribute to monitoring plastic-mulched farmland. Some researchers treated the grey-level co-occurrence matrix (GLCM) [
28] parameter values as available features of separated objects for sample training [
20,
29]. However, these schemes were executed in a so-called “black box” without a practical physical mechanism, so they are not easily reproducible for another similar task. The recognition and use of texture information in eCognition is another formidable time-consuming task [
10], even if optimal SP, shape, and compactness are derived from ESP or ESP 2 based on initial fusion imagery. As an ancillary feature for mapping greenhouses, texture should be further studied both in pixel-based and object-based extraction, which can be called problem II.
Purposive preprocessing operations based on pixel-level imagery are important prior to MRS. Apart from frequently-used orthorectification, radiometric and atmospheric correction [
18], and pan sharpening, texture analysis of these images can also generate derivative input data, and then influence the results of MRS. Thus, our first process involved compressing the heterogeneity of the fusion image by different texture analysis to produce some derivative images, and then exploring what effects image texture analysis would exert on PG segments. This led to our second idea that, in order to compare the accuracy of different PG segments, a reliable evaluation system is indispensable, which can be called problem III.
Many evaluation methods have been proposed. Depending on whether a human evaluator examines the segmented image visually or not, Zhang et al. [
30] introduced a hierarchy of segmentation evaluation methods and a survey of unsupervised methods. Zhang et al. [
31], Gao et al. [
32], and Wang et al. [
33] each proposed novel unsupervised methods respectively to evaluate the segmentation quality; however, these methods still need supervised evaluation for verification. Supervised evaluation [
34,
35,
36], also known as relative evaluation [
37], is a method used for comparing the resulting segments against a manually-delineated reference polygons. For instance, Lucieer et al. [
38] quantified the uncertainty of segments by those with the largest overlapping area with corresponding reference polygons. Möller et al. [
39] and Clinton et al. [
40] used the area of each overlapping polygon partitioned by segments and reference polygons. Persello et al. [
41] and Marpu et al. [
24] used the largest area of overlapping polygons. Clinton et al. [
40] also summarized goodness, area-based, location-based, and combined measures that facilitate the identification of optimal segmentation results relative to a training set. Marpu et al. [
24] provided a detailed view of the segmentation quality in respect to over- and under-segmentation compared with reference polygons, which proved that MRS performs well under a reasonable SP. Liu et al. [
42] proposed three discrepancy indices—Potential Segmentation Error (PSE), Number-of-Segments Ratio (NSR), and Euclidean Distance 2 (ED2)—to measure the discrepancy between the reference polygons and the corresponding image segments. PSE, NSR and ED2 were used [
43] and adopted by Aguilar et al. [
17] and Gao et al. [
44] to evaluate the effects of different segmentation parameters on MRS, and modified by Novelli et al. [
45] to the evaluation of object-based greenhouse detection. Cai et al. [
46] presented four kinds of supervised measurement methods based on area, object number, feature similarity, and distance to study the influence of different object characteristics on extraction accuracy. With defined variables, the pros and cons of these supervised evaluation methods are discussed in
Section 3.4. of this paper, and more detailed reviews of accuracy assessment for object-based image analysis can be found in Ye et al. [
47] and Chen et al. [
48].
The three main contributions of this study were: (1) to improve the PG segments derived from eCognition, we tried a two texture analysis method that involved increasing AOS or decreasing GQL prior to MRS; (2) to evaluate the quality of PG segments generated from different derivative images, we designed a supervised evaluation pattern named the Over-Segmentation Index (OSI)-Under-Segmentation Index (USI)-Error Index of Total Area (ETA)-Composite Error Index (CEI) based on pixel level and independent from the number of manual delineated reference polygons; and (3) to prove the availability of the proposed pattern, we compared it with several supervised evaluation methods theoretically, and contrasted it with the PSE-NSR-ED2 method by numerical and visualized analysis.
The remainder of this paper is organized as follows:
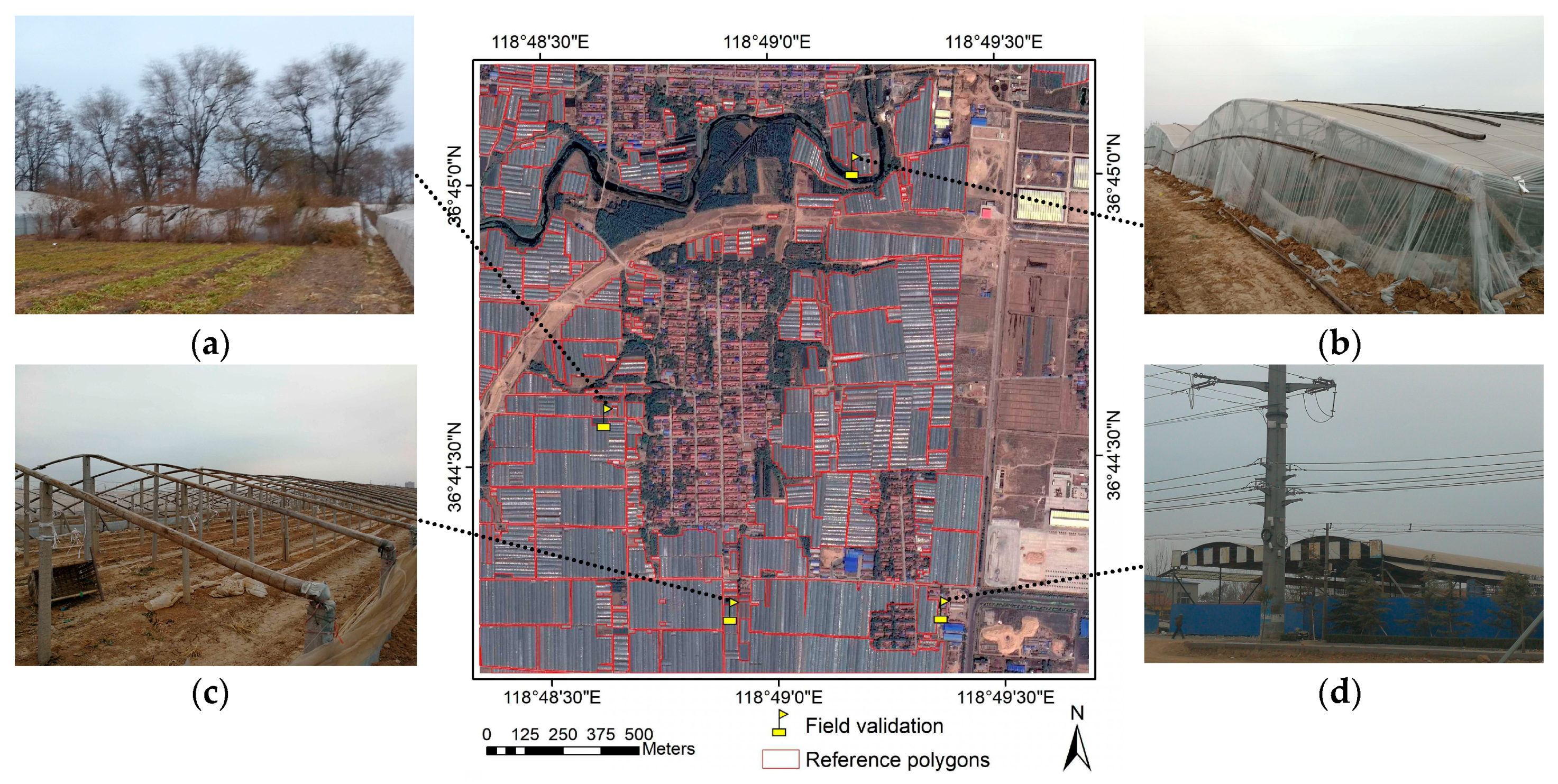
Section 2 introduces the study area and data source,
Section 3 explains the methodologies applied in the analysis,
Section 4 outlines the effects of image texture analysis on PG segments via recognition of the OSI-USI-ETA-CEI pattern and explains our hypothesis,
Section 5 discusses several key points and provides a comparison of our method with some related methods, and
Section 6 summarizes the conclusions.
3. Methodology
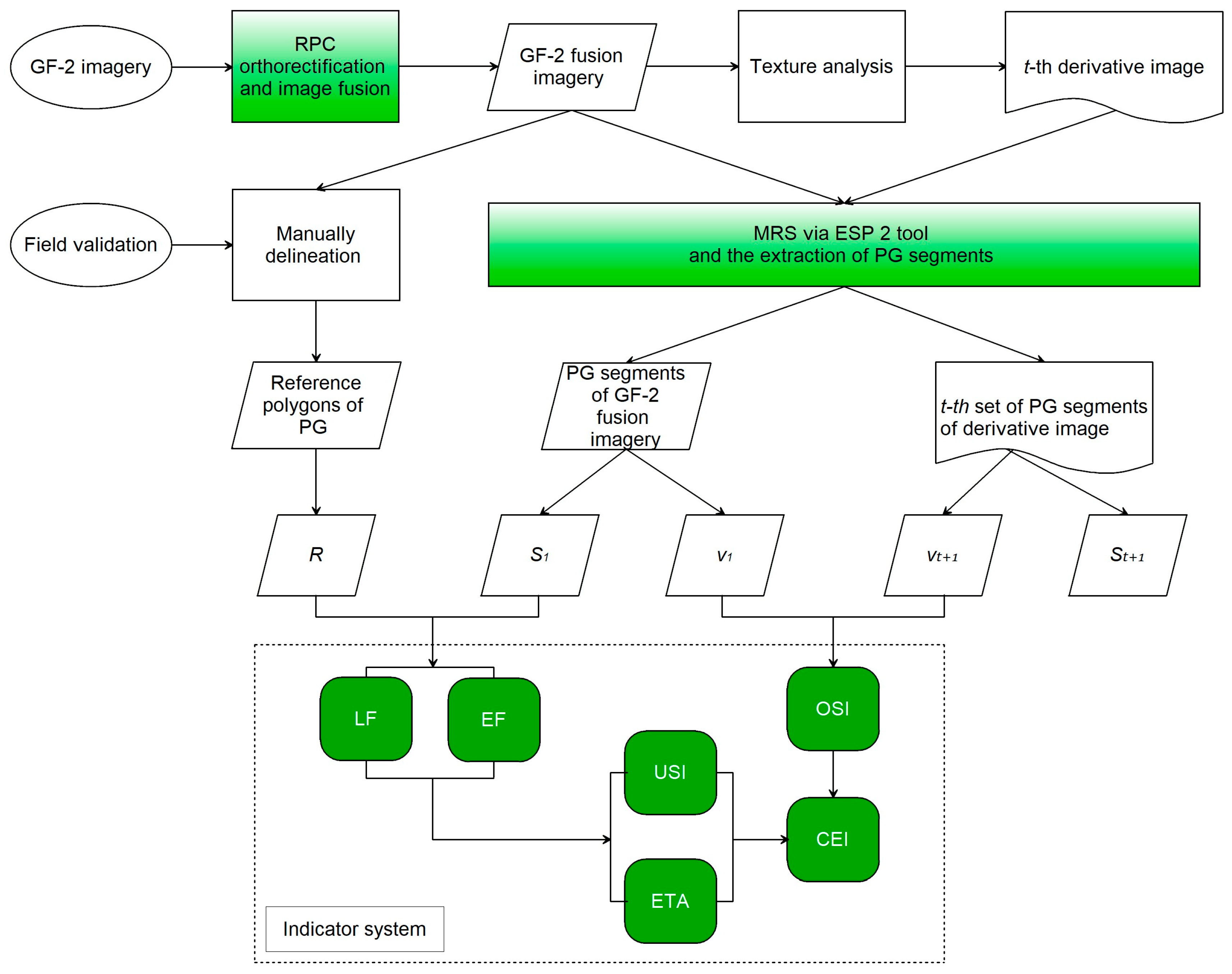
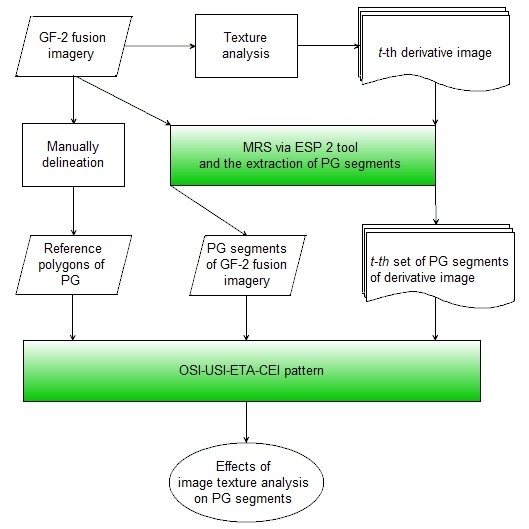
A flowchart of experiment design, methods, variables, and indicator system for the evaluation of the effects of texture analysis on PG segments is shown in
Figure 3.
3.1. Texture Analysis
Texture is the visual effect caused by spatial variation in tonal quantity over relatively small areas [
51], among which the homogeneity and heterogeneity are a pair of coupled features. Even though homogeneity is more frequently employed in texture analysis, we choses the concept of heterogeneity to explain our method and enable understanding. The definition of heterogeneity refers to the distinctly nonuniformity in composition or character (i.e. color, shape, size, texture, etc.)
PG can be more discernible in very high resolution satellite imageries such as Quickbird, Worldview, and GF-2, whereas the heterogeneity is a nonnegligible obstacle when segmenting these images based on GEOBIA. If the heterogeneity of a PG surface can be compressed, a better segmentation result might be derived from the processed image. Considering the nature of heterogeneity in a digital number image, image preprocessing that increases the average operator size (AOS) or decrease the greyscale quantization level (GQL) is the method used to produce derivative images with different heterogeneities in this study.
For an averaging operator [
11], the template weighting functions are unity (such as 1/9 in AOS 3 × 3). The goal of averaging is to reduce noise, which is its foundation for compressing the heterogeneity. Averaging is a low-pass filter, since it allows low spatial frequencies to be retained and to suppress high frequency components. The size of an averaging operator is then equivalent to the reciprocal of the bandwidth of the low-pass filter it implements. A larger template, say 11 × 11 or 13 × 13, will remove more noise (high frequencies) but reduce the level of detail.
The GQL size is dependent on the maximum quantization level in a monochromatic image or a single channel of a multichannel image. It can be decreased according to the assigned maximum quantization level and a particular weighted combination of frequencies, which is a redistribution of the greyscale value at each pixel, so that the values can be clustered in a certain range if they are spread over a broad range. As long as GQL decreases, the heterogeneity of each band is compressed.
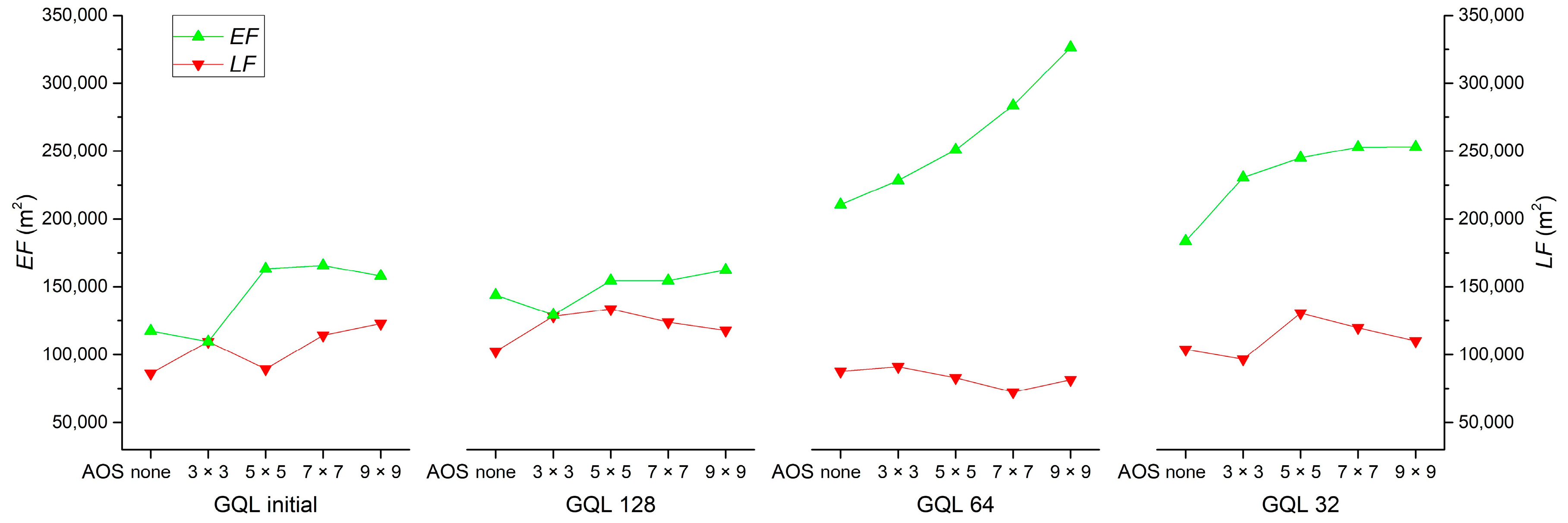
By increasing AOS or decreasing GQL, information of the pixel’s neighborhood can be effectively used, preceding the MRS. To evaluate the effects of AOS and GQL on MRS segmentation, four increased AOSs (3 × 3, 5 × 5, 7 × 7, and 9 × 9) and three decreased GQLs (128, 64, and 32) were adopted to produce another 19 images based on the initial fusion imagery (GQL initial). Hence, there were 20 input data that were used for segmentation, rather than merely evaluating the segmentation results from the sole data source.
The 19 derivative images were also produced in ENVI 5.3, in which the co-occurrence measures tool can simultaneously change the AOS and GQL of multi-bands among GQL initial, 64, and 32. The derivative images of GQL 128 were produced using the stretch tool, and averaging operations on GQL 128 were conducted using low pass convolution filters, since the co-occurrence measures tool does not support the conversion between GQL initial and GQL 128.
3.2. MRS via ESP 2 Tool
MRS in eCognition is based on the Fractal Net Evolution Approach (FNEA) principle and is widely used for segmentation. It is a region-growing process, and the optimization procedure starts with single-image objects of one pixel and repeatedly merges them in pairs to larger units until an upper threshold is not exceeded locally [
8,
17,
18]. For this purpose, a scale parameter (SP) is proposed to adjust the threshold calculation. Higher values of the scale parameter would result in larger image objects, and smaller values result in smaller image objects. The basic goal of an optimization procedure is to minimize the incorporated heterogeneity at each single merge [
8]. If the resulting increase in heterogeneity when fusing two adjacent objects exceeds a threshold determined by the SP, then no further fusion occurs, and the segmentation stops [
33]. The SP criteria are defined as a combination of shape and color criteria (color = 1 − shape), whereas shape is interiorly divided as compactness and smoothness criteria; thus, the three parameter values that must be set are SP, shape, and compactness.
ESP 2 is a generic tool for eCognition software that employs local variance (
LV) to measure the difference in the MRS under increment scales [
22]. When the
LV value at a given level (
LVe) is equal to or lower than the value recorded at the previous level (
LVe−1). The level
e − 1 is then selected as the OSP for segmentation. Based on this concept, ESP 2 can help derive the dependent SP, whereas shape and compactness can be deduced from the try-and-error experiment within different assessment systems [
17,
18], which recommend obtaining the SP parameter by fixing the compactness at 0.5 and the testing shape values around 0.3.
Since this study focused on the effect of texture analysis on MRS, the uniform shape and compactness were set to 0.3 and 0.5, respectively. Thus, the OSP was automatically calculated by the ESP 2 tool with the algorithm parameters set as shown in
Table 2. The Level 1 and its segments in the exported results were adopted for the next step of analysis.
3.3. Extraction of PG Segments
As different derivative images required different samples, features, parameters, or threshold values in automatic extraction, and ensuring good quality is difficult, the greenhouse objects in this study were manually selected by artificial visual interpretation using the single select button on the manual editing toolbar in eCognition 9.0, so that each segmentation object can be as precisely evaluated as possible. Theoretically, manual extraction would have a maximum precision on the criterion of geometric accuracy, but this is only credible for the criterion of the area, since, in other methods, the commission area also has a probability of offsetting the omissions while the geometric error can only be accumulated.
The principle used to assign an object as a greenhouse is when the proportion of greenhouse area is more than 60% [
24] and the feature of other categories is negligible from visual analysis. Otherwise, the object’s feature is deemed to be unusable to extract the greenhouse contained within, which would be evaluated as omission error in follow-up work.
After exporting from eCognition 9.0, two statistical parameters of the extracted PG segments were obtained in ArcGIS 10.3: number of PG segments and summation area.
3.4. Establishment of OSI-USI-ETA-CEI Pattern
3.4.1. Case Study and Variable Definition
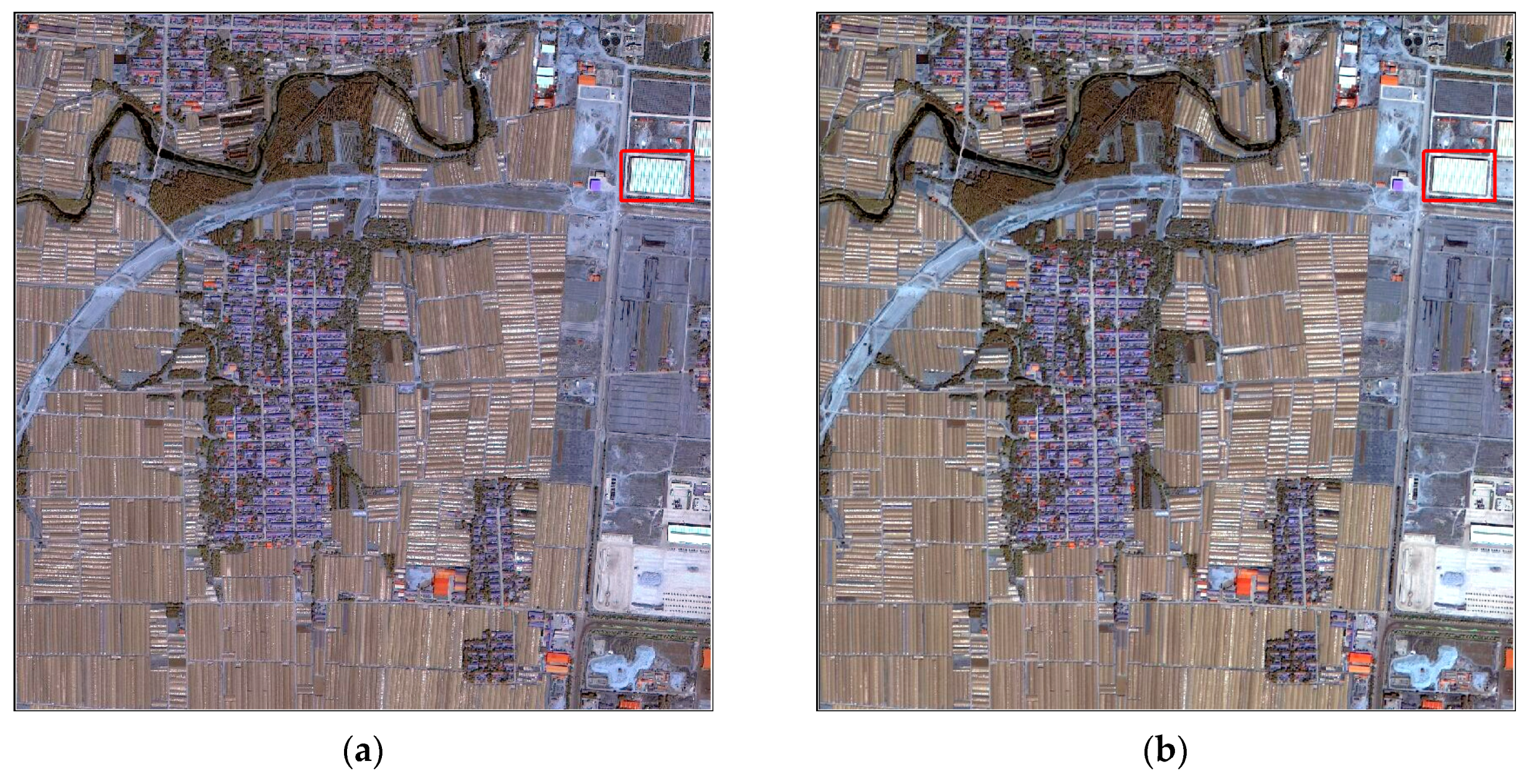
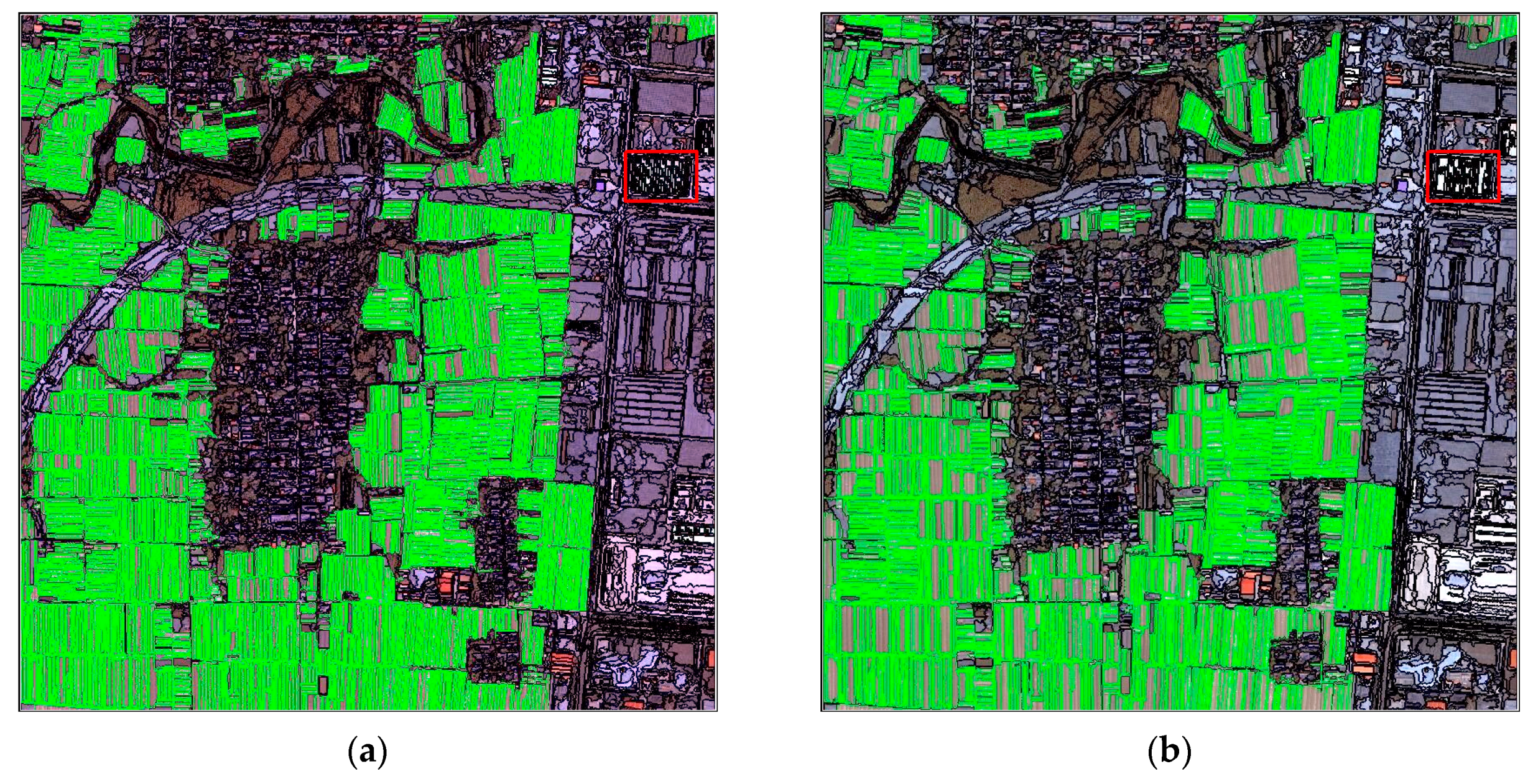
To better understand the problems in PG segmentation, the definitions of variables, and the establishment of OSI-USI-ETA-CEI pattern, five cases of PG segments that were extracted from initial GF-2 fusion imagery and four derivative images are demonstrated in
Figure 4, and all images were segmented under their optimal scale parameter provided by the ESP 2 tool. Notably, these cases cannot represent the segmentation quality of a whole image.
Without decreasing the GQL, the degree of over-segmentation of the PG segments that were extracted from the initial GF-2 fusion imagery (
Figure 4a) or images derived from the treatment of AOS 3 × 3 (
Figure 4b) are much worse than those extracted from other derivative images (
Figure 4c–e), since the dark and the sunny sides of the PG in the two images are segmented as different parts, making it hard to delineate the PGs’ boundaries, which is not convenient for subsequent feature recognition and extraction.
Apart from the number of PG segments, the number and area of the fragments (the smaller polygons that are partitioned jointly by reference polygons and PG segments) are also need to be explored in depth.
To parameterize the relationship between the reference polygons and PG segments, four quantity-based variables, seven area-based variables and their assemblies were defined in
Table 3:
It is generally thought that a high-quality image segmentation should result in a minimum amount of over- and under-segmentation, and different area-based or number-based indicators have been designed based on selected samples and their corresponding reference polygons [
14,
24,
39,
41,
42,
43,
45,
52], which we rewrote using variables defined above for comparison, as shown in
Table 4.
Some feature similarity-based, location-based or distance-based [
41,
46] methods are available for measuring the quality of segmentation, but these methods only work when segments have an approximately one-to-one relationship with the reference polygons, whereas the segmentation results of continuous greenhouses always have the relationship with the reference of poly-to-one.
The OSI-USI-ETA-CEI pattern is based on the reference polygons that were manually delineated in
Section 2.3. and the PG segments extracted in
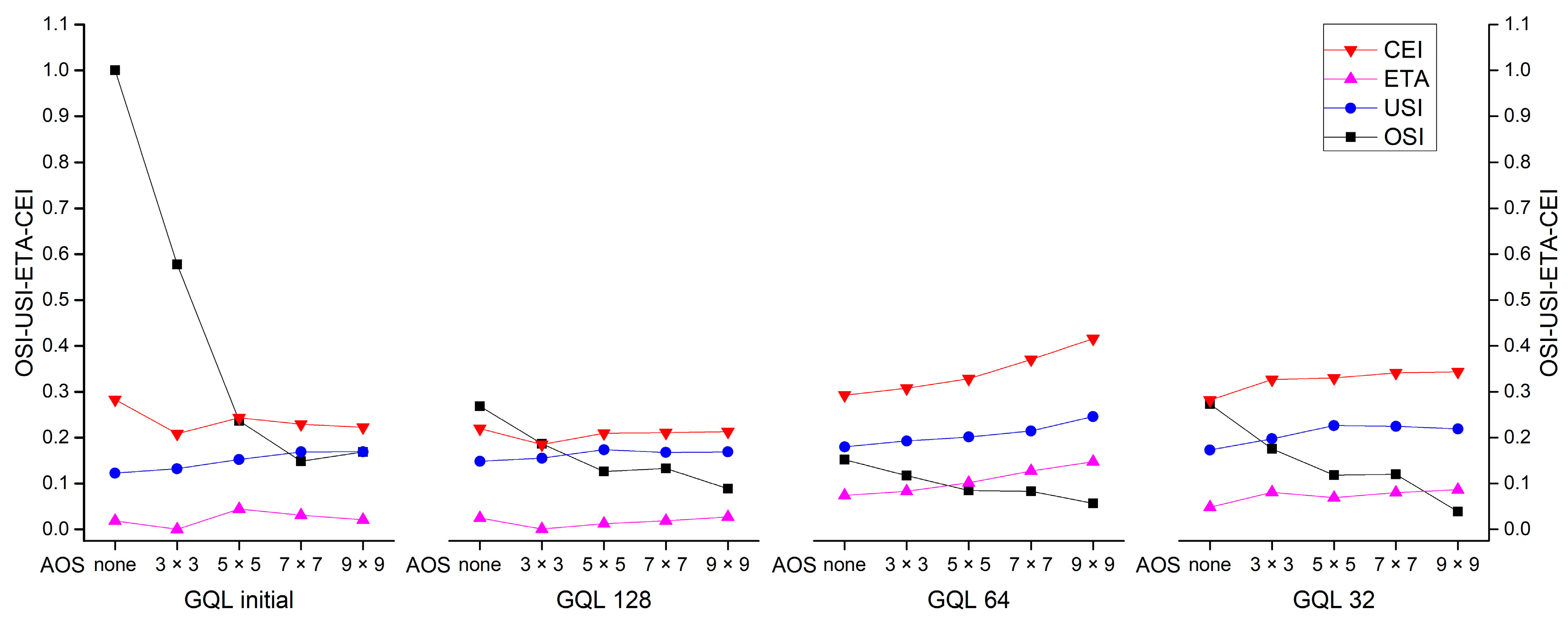
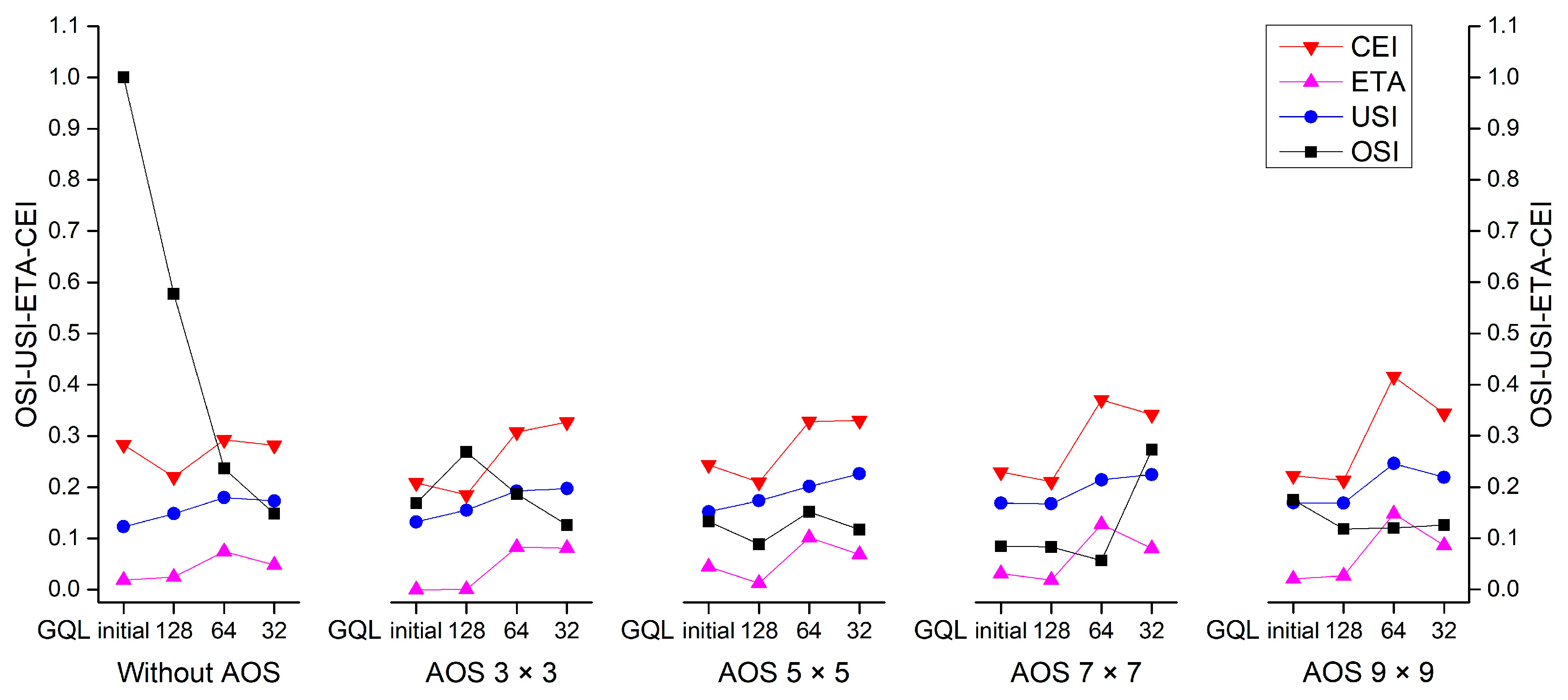
Section 3.3. The method is designed for evaluating the segmentation quality of PG segments from images with different heterogeneities. In short, OSI denotes the extent to which the number of PG segments may affect the USI and ETA, USI indicates the absolute geometric error of PG segments, ETA indicates the discrepancy in the total area between PG segments and reference polygons, and CEI indicates the composite error.
3.4.2. Over-Segmentation Index (OSI)
Segmentation results that are over-segmented are more likely to cause omission and commission errors in follow-up classification because the number and some feature values (like mean value) of both the interested and non-interested objects that are over-segmented would range widely compared with those that are not over-segmented. An extreme example of this is when an image is segmented on the pixel level. Even though it is much easier to compare the number rather than other feature values for two assemblies of polygons, indicators that compare the number of reference polygons with segments [
17,
18,
42,
43,
44,
45] and that compare the area of a reference polygon with its biggest corresponding segment [
24,
38,
53] were both designed or applied in over-segmentation analysis. However, these criteria are designed for pursuing perfect segmentation that is similar to manually delineated reference polygons, which is not suitable for evaluating the segments of continuous PGs since drawing those reference polygons is different from segmenting an image. Reference polygons prefer to draw the outline of a single or continuous greenhouse rather than divide pixels with different grey levels, whereas segmentation prefers the latter, especially when some pixels’ material or Bidirectional Reflectance Distribution Function (BRDF) varies significantly from their surrounding pixels. To manually draw the outline of continuous greenhouses is so subjective that it is hard to determine the size of a reference polygon as well as the total number of reference polygons, i.e., no wonderful polygons can be used to define whether a segmentation is over-segmented or not. A similar view was reported by Zhang et al. [
30]. Thus, continuous greenhouse extraction in high-resolution imagery does not require a similar segment number compared to the manual reference polygons, nor accordant outlines or even skeletons (
Figure 4). However, we should consider counting the segment numbers in the initial fusion imagery as an effective reference to assess over-segmentation instead, since the high heterogeneity among greenhouse pixels in an initial fusion image tends to lead to the worst over-segmenting result compared with derivative images with lower heterogeneity. Therefore, the segment numbers of the initial fusion imagery under its OSP using ESP 2 can be regarded as ancillary data of reference polygons in
Section 2.3. The ancillary data provides a numerical reference and the manually delineated polygons provides a geometric reference.
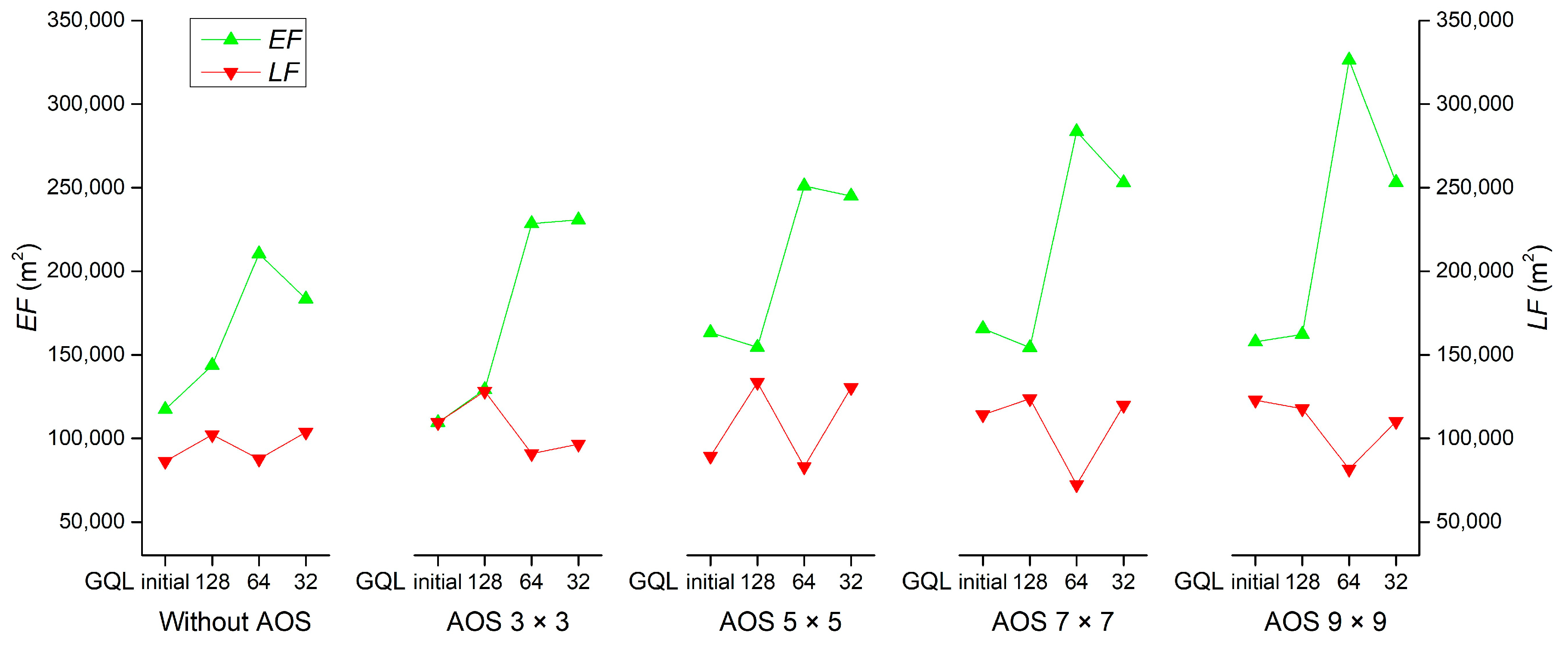
Synthesizing the situation stated above, over-segmentation of PG segments is indicated by a new OSI in this study, which is a relative value calculated by Equation (1):
where
v denotes the number of extracted PG segments when the corresponding image is under the optimal segmentation using ESP 2 tool,
v1 denotes the number of PG segments extracted from the initial GF-2 fusion image, and
vt+1 denotes the number of PG segments extracted from the
t-th derivative image. A higher OSI indicates a larger error of over-segmentation.
3.4.3. Under-Segmentation Index (USI)
When an image is over-segmented, it is still possible to construct the object, but when an image is under-segmented, the object may not be recovered [
24]. Under-segmentation is more worthwhile to be exactly evaluated.
From
Figure 4, both lost and extra fragments are shown to have many members with very tiny areas, and the boundaries of the reference polygons usually have fewer polylines than that of PG segments. The number of lost and extra fragments are not only caused by geometric errors but also changed by how we draw the outline of single or continuous greenhouses, so it is not appropriate to neither count the number nor calculate the mean value of those fragments [
24] when evaluating the geometric errors of continuous greenhouses.
In general, the area of extra-segments are parts of under-segmentation error according to some studies (
Table 4), as the PG segments should slice those pixels that are not representing a PG. However, lost fragments can be considered as a result of under-segmentation of those segments that do not contain enough PG pixels, i.e., the lost fragments can be regarded as the extra fragments of another category (
Figure 4). Therefore, it is necessary to adequately evaluate both the
LF and
EF error rather than to consider only one and then combine the two errors into a single index (USI) to indicate the intension of under-segmentation of PG segments. The theoretical value should range between zero and one. The index can be calculated as:
where
LF,
EF, and
R are the total area of lost fragments, extra fragments, and the real area of PG, respectively. A higher USI indicates a larger under-segmentation error.
3.4.4. Error Index of Total Area (ETA)
Lost and extra fragments have an opposite influence on the final area of extraction even though both directly contribute to the under-segmentation. Although area-based measures were discussed in Clinton et al. [
40] and some new measures based on area were designed after that [
24,
42,
46], these sample-based studies only focused on the proportion of the omission or commission area in a segmentation, but the percentage of the difference in the total area between segmentation results and corresponding reference polygons seems to be ignored, which should be fully considered when evaluating the precision of the total area of extraction and the consequence of under-segmentation. Thus, the Error Index of Total Area (ETA) can be used to indicate the discrepancy, which can be calculated by:
where
S denotes the summation area of extracted PG segments when corresponding image is under the optimal segmentation using the ESP 2 tool,
S1 denotes the summation area of PG segments extracted from the initial GF-2 fusion image, and
St+1 denotes the summation area of PG segments extracted from the
t-th derivative image. A higher ETA value indicates a larger total area error.
3.4.5. Composite Error Index (CEI)
In general, the more the PG segments are over-segmented, the larger the omission and commission error produced indirectly in automatic classification or extraction. Under-segmentation causes geometric errors and directly leads to an area difference from the reference. Given this consideration, a new CEI is presented in Equation (4) to consider the composite error of segmentation results when comparing to a set of reference polygons:
where
λ is a possible weight used to rescale the value of quantity-based OSI so that the indicator will not overwhelm the value of area-based USI and ETA; thus, the OSI multiplied by
λ denotes the indirect influence of the number of PG segments on extraction in CEI.
When omission or commission segments in an extraction are generated due to over-segmenting, their geometric error and area difference from the real value (indicated by USI and ETA, respectively) couple on the extraction. Thus, the value of λ in this study is defined as the sum of USI and ETA as: