Abstract
The mangrove ecosystem plays a vital role in the global carbon cycle, by reducing greenhouse gas emissions and mitigating the impacts of climate change. However, mangroves have been lost worldwide, resulting in substantial carbon stock losses. Additionally, some aspects of the mangrove ecosystem remain poorly characterized compared to other forest ecosystems due to practical difficulties in measuring and monitoring mangrove biomass and their carbon stocks. Without a quantitative method for effectively monitoring biophysical parameters and carbon stocks in mangroves, robust policies and actions for sustainably conserving mangroves in the context of climate change mitigation and adaptation are more difficult. In this context, remote sensing provides an important tool for monitoring mangroves and identifying attributes such as species, biomass, and carbon stocks. A wide range of studies is based on optical imagery (aerial photography, multispectral, and hyperspectral) and synthetic aperture radar (SAR) data. Remote sensing approaches have been proven effective for mapping mangrove species, estimating their biomass, and assessing changes in their extent. This review provides an overview of the techniques that are currently being used to map various attributes of mangroves, summarizes the studies that have been undertaken since 2010 on a variety of remote sensing applications for monitoring mangroves, and addresses the limitations of these studies. We see several key future directions for the potential use of remote sensing techniques combined with machine learning techniques for mapping mangrove areas and species, and evaluating their biomass and carbon stocks.
1. Introduction
Mangrove forests are found in the intertidal zone along tropical and subtropical coasts, and play a vital role in the coastal zone by providing a range of different ecosystem services to coastal populations [1]. For example, mangrove forests are important in global carbon cycling and the reduction of atmospheric greenhouse gas (GHG) concentrations [2,3]. Mangroves are efficient carbon sinks [4] by sequestering carbon in their above-ground [5,6] and below-ground biomass and sediments [7]. Mangroves are also able to stabilize coastlines and protect the land from erosion. Mangrove forests also contribute significantly to the livelihoods of coastal dwellers through fisheries, sources of timber and firewood, and non-timber forest products [8,9].
Despite their benefits and services, mangroves continue to be threatened by high population growth and migration into coastal areas, leading to coastal development and increased demand for aquaculture and agriculture products. The situation is further exacerbated by poor land-use planning, weak governance, and uncoordinated economic development in the coastal zone. Up to 3.6 million hectares of mangrove forests may have been lost worldwide between 1980 and 2005 [10], although rates of loss regionally and globally have reduced in the first decade of the 21st century [11,12,13]. Mangrove loss releases a substantial proportion of their stored carbon into the atmosphere (Figure 1), with mangrove deforestation in Indonesia contributing 10–31% of the country’s land-use sector-linked carbon emissions [14,15].
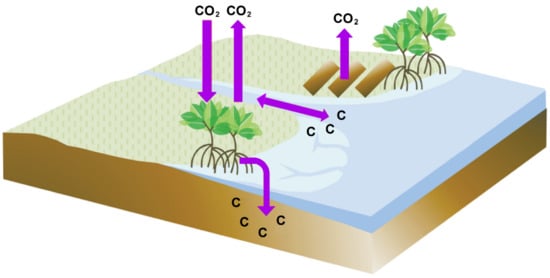
Figure 1.
Major carbon flux pathways in mangrove forests. Modified from http://thebluecarboninitiative.org/.
Drivers of mangrove deforestation vary regionally, but include conversion to aquaculture, agriculture (particularly rice and oil palm in West Africa and Southeast Asia), urban development, salt pond construction, and overexploitation [12,16,17]. Importantly, drivers of deforestation operate at large spatial scales, and in the past, we have had a poor idea of exactly how much mangrove forest is being lost and by what driver [18]. We also have little knowledge of the impact of deforestation on ecosystem services such as carbon at large spatial scales. Standardized remote sensing techniques offer a way to reduce uncertainty in estimates of mangrove ecosystem service loss, and are needed for the monitoring, reporting, and verification (MRV) of international conservation programs that protect carbon, such as Reducing Emissions from Deforestation and forest Degradation (REDD+).
Remote sensing offers opportunities for mapping the biophysical and structural parameters of mangroves (including biomass and carbon stocks) with lower cost, faster speed, and at a wider scale than field measurements. The recent application of machine learning algorithms and data integration to mangrove mapping has contributed to a number of new publications that shed light on various aspects of the mangrove ecosystem, especially those that have data with high dimensionality [19]. As this is an emerging field, machine learning techniques for discriminating mangrove species, monitoring mangrove structures, and estimating mangrove biomass are not well documented, and the current literature does not critically analyze the advantages and disadvantages of these approaches.
This review provides a critical overview of the key studies that have been undertaken after the year 2010 on a variety of remote sensing applications for monitoring mangrove forests, highlighting the limitations of current studies and future directions for the use of remote sensing techniques combined with state-of-the-art machine learning algorithms. This review updates previous reviews of mangrove remote sensing by Heumann [20], Kuenzer et al. [21], and Lucas et al. [22], but importantly, it focuses on the methodologies that discriminate mangrove species, quantify biophysical parameters and structure, and estimate mangrove biomass.
2. Remote Sensing of Mangrove Species
The identification of mangrove species is important for management, as understanding the characteristics of each species can provide necessary information on geomorphic and environmental conditions and changes [23]. However, mapping mangrove species still remains a challenge [20,21], as it is difficult to map individual trees that may be smaller than the resolution of the imagery, and mangrove tree species are often found in mixed communities with closely related species and genera that exhibit a similar spectral reflectance. We review the current approaches used for identifying and mapping the spatial distribution of mangrove species using traditional and machine learning methods based on various optical, synthetic aperture radar (SAR), and hyperspectral sensors, and a fusion of optical and SAR data.
2.1. Traditional Approaches to Discriminate Mangrove Species
While traditional image classification approaches have struggled to discriminate mangrove species due to spatial and spectral constraints, very high spatial resolution data and novel techniques have shown success in mapping mangrove species (Table 1). High spatial resolution images can be space-borne, i.e., IKONOS, Quick Bird, GeoEye, and WorldView, all of which feature spatial resolution of less than five m. The spatial resolution of the panchromatic data of WorldView, Quick Bird, IKONOS, and GeoEye are 0.50 m, 0.61 m, 0.83 m, and two meters, respectively. Visual interpretation can be used for both aerial photographs and high spatial resolution satellite images, i.e., WorldView-2. However, the overall accuracy employed by these techniques is traditionally quite low, ranging from 42% to 68% [24]. Pixel-based image classification approaches are often utilized for identifying mangrove species’ distribution, especially for very high spatial resolution sensors such as QuickBird and IKONOS data. Using pixel-based maximum likelihood classification (MLC) on these data can produce products with an accuracy ranging from 63% to 82% [25]. Pixel-based fuzzy classification approaches can achieve an overall accuracy of 72% for discriminating several mangrove species using pan-sharpened QuickBird data, or less than 60% using hyperspectral CASI-2 data [26].

Table 1.
Traditional remote sensing approaches to discriminate mangrove species.
Recently, object-based image classification approaches using image segmentation such as object-based image analysis (OBIA) have been frequently employed for mapping mangrove species. Several studies have concluded that OBIA approaches can provide higher overall accuracy than pixel-based approaches for detecting mangrove species communities [26,27,28]. Hyperspectral datasets such as the EO-1 Hyperion and the CASI-2 play an important role in discriminating mangrove species [27,29]. In most cases, OBIA approaches outperformed traditional pixel-based methods for mapping mangrove species using high spatial resolution and hyperspectral data (see Table 1). A hybrid method based on OBIA with a lacunarity spatial measure or machine learning algorithm can improve accuracy assessment when mapping mangrove species to >80% for medium spatial resolution imagery i.e., Landsat, and >94% for higher resolution Pléiades-1 imagery [30]. Feature extraction from very high spatial resolution imagery also improves image classification for discriminating mangrove species and communities; grey-level co-occurrence matrix (GLCM) is increasingly used for classifying mangrove species, showing the promising accuracies of >81% using IKONOS and ~89% using WorldView-2 imagery [24].
Remote sensing products beyond optical imagery have also been used to discriminate mangrove species. A recent study by Pham et al. [31] showed that the Advanced Land Observing Satellite Phased Array type L-band Synthetic Aperture Radar (ALOS PALSAR) data can be employed for classifying mangrove species in Vietnam using an object-based logistic model tree (LMT) algorithm with an accuracy of >80%. A more recent study conducted by Valderrama-Landeros et al. [32] showed the potential use of normalized difference vegetation index (NDVI) pixel-based classifier for mapping mangrove species in Mexico using different remote sensing data sources from medium to very high spatial resolution (i.e., Landsat-8 OLI, SPOT-5, Sentinel-2A, and WorldView-2) and concluded that the higher spatial resolutions produce higher accuracy (Table 1).
2.2. Machine Learning Approaches for Mapping Mangrove Species
Recent advances in computer vision, pattern recognition, and artificial intelligence (AI) technologies have resulted in the development of new machine learning techniques, allowing the discrimination of mangrove species with higher accuracy than traditional classification techniques (Table 2). Machine learning techniques can be employed for classifying mangrove species using both optical [24,30,39,40] and hyperspectral imagery [41,42], as well as SAR data [31,39]. Several classic machine learning algorithms such as decision trees (DT), i.e., CART (classification and regression tree), and C4.5 algorithms, which are used in other ecosystems, are rarely used for classifying mangrove species [30,39]. Instead, mangrove researchers tend to use support vector machine (SVM), artificial neural network (ANN), and random forests (RF) for classifying mangrove communities, as these techniques are able to construct non-parametric classification models that do not rely on any assumption about data distribution [30,39,40,43,44]. For instance, Wang et al. [30] compared the performance of selected machine learning algorithms for mapping artificial mangrove species using Pléiades-1 data. This study showed that among the common machine learning algorithms, SVM produced higher overall accuracy for pixel-based image analysis, while RF yielded the highest performance for object-based image classification (see Table 2). Algorithms such as SVM can classify mangrove species using pan-sharpened WorldView-2, producing accuracies over 87% [24] and using Satellite Pour l’Observation de la Terre (SPOT) and Gaofen-1 (GF-1) time-series data with overall accuracies ranging from 67% to 92% [40].

Table 2.
Machine learning approaches to discriminate mangrove species.
Machine learning techniques are particularly promising for discriminating mangrove species when they use a combination of textural and differential spectral features [45]. For example, clustering-based neural networks can discriminate certain mangrove species to an overall accuracy of >90% using high-resolution multispectral imagery combined with textural information from the panchromatic band. Wong and Fung [42] compared selected machine learning algorithms for mangrove species classification at the Mai Po Ramsar site (Hong Kong) and suggested that a combination of optical and radar can improve the classification accuracy. A more recent study by Zhang et al. [39] reported that a combination of optical and SAR data can improve the overall accuracy and Kappa coefficient for discriminating mangrove species using rotation forest (RoF). This study also compared several machine learning algorithms for classifying mangrove species, showing that RoF performs well (85.23%) and outperforms SVM and RF algorithms (Table 2).
3. Modeling Mangrove Characteristics and Structure
Various remotely sensed data have been used to better understand the spatial ecology and characterize the biophysical parameters of mangroves [22], such as tree and canopy heights, basal area (BA), crown diameter, tree density, leaf area index (LAI), and leaf pigments of mangrove ecosystems i.e., nitrogen and chlorophyll concentrations. Mangrove biophysical parameters have been mapped using passive spectral data, and active remote sensing technologies such as light detection and ranging (LiDAR) and synthetic aperture radar (SAR) have been widely used to map and estimate these structural parameters of mangrove ecosystems from various satellite, airborne, and unmanned aerial vehicle (UAV) platforms. Multispectral data can determine parameters such as LAI and leaf pigments (chlorophyll and nitrogen concentrations), whereas SAR and LiDAR data can estimate tree and canopy height, basal area, and crown diameter. Table 3 summarizes recent studies from 2010 to 2018 that employed spectral, optical, LiDAR, and SAR data to characterize, measure, and map the biophysical parameters of the mangrove ecosystem.

Table 3.
Examples of recent studies that examined mangrove biophysical parameters using remote sensing.
3.1. Relationships between Biophysical Parameters of Mangroves and Spectral Remotely Sensed Data
The key issue for the use of multispectral remotely-sensed data is to understand the correlation between the spectral reflectance of mangrove forests and their biophysical parameters. Spectral data ranging from low resolution (i.e., MODIS, 250 m), medium resolution (i.e., Landsat TM, Landsat OLI, 30 m), and high resolution (ALOS AVNIR-2, Sentinel-2, SPOT, ~10 m) to very high spatial (Rapid Eye, QuickBird, IKONOS, WorldView-2, ~2 m) resolutions have been used to map the various biophysical parameters of mangrove forests. In most cases, higher spatial resolution spectral data often produces a higher accuracy when modeling parameters such as LAI [56,57] and leaf chlorophyll [56]. Spectral remote sensing is effective at retrieving the leaf pigments such as chlorophyll a, b, and nitrogen concentrations [49,50,51,52,53]. Recently, Kamal, Phinn, and Johansen [59] investigated the ability of different optical sensors such as WorldView-2, ALOS AVNIR-2, and Landsat TM for measuring and monitoring mangrove LAI, and showed that ALOS AVNIR-2 data yields the highest accuracy for the LAI estimation of mangrove ecosystems in Karimunjawa Island, Indonesia. More recently, Sentinel-2A data have been employed to retrieve and model mangrove biophysical parameters such as LAI, leaf chlorophyll, and tree density [66,84]. Mangrove canopy heights can also be estimated using the high-resolution stereo-photogrammetry of WorldView-1 data in the Mozambique [58,61].
A wide range of studies have been conducted using different remote sensing approaches to estimate the biophysical parameters of mangroves, which can be grouped into two main categories: radiative transfer models and empirical–statistical regression models [85]. The former are developed to inverse forest biophysical parameters [86,87], while the latter are commonly utilized to retrieve these parameters based on parametric statistical and non-parametric machine learning algorithms [53,56,60,63]. Among the various biophysical parameters, leaf area index (LAI) is considered an important biophysical parameter for understanding mangrove forest conditions. Our review of the current literature shows that the methods that have been used for estimating the biophysical parameters of mangrove ecosystems using remotely sensed data are diversified from multilinear regression models to machine learning approaches such as: artificial neural networks (ANN), support vector machines (SVM), and random forests (RF) [56,63]. In most cases, machine learning techniques i.e., ANN, SVM, and RF outperform parametric regression models in estimating the leaf pigments of mangrove forests. For instance, Zhang, et al. [51] reported that the ANN model produced better performance (R2 = 0.91) for the N concentration estimations of black mangrove (A. germinans) than the stepwise multiple linear regression model (SMLR) (R2 = 0.71). Zhu et al. [63] suggested that machine learning can be used to accurately estimate the LAI of mangrove forests and RF algorithms, outperforming other algorithms in estimating LAI across a mangrove forest.
3.2. Relationships between Biophysical Parameters of Mangroves and SAR and LiDAR Data
Active remote sensing techniques such as SAR and LiDAR have distinct advantages over spectral data when mapping the biophysical parameters of mangroves. Firstly, SAR sensors can remotely sense the land surface through clouds, which is a perennial problem when mapping mangroves in the tropics. Secondly, they can effectively measure forest structure such as biomass and canopy crowns, where passive data must indirectly infer these attributes from their spectral response. The recent launch of the Sentinel-1 (SAR) missions offers a new opportunity to estimate the biophysical structure parameters of mangrove ecosystems [65,66].
Wavelength and Polarization of SAR Data
SAR data can be acquired at different wavelengths, including X, C, L, and P bands with different polarizations, which have a wide range of azimuth resolutions (Figure 2). Each band has its own characteristics and capability related to forest stand parameters [88]. Short wavelengths such as the X-band (3.75–2.5 cm) and C-band (7.5–3.75 cm) strongly interact with the surface of the canopy, whilst long wavelengths such as the L-band (30–15 cm) and P-band (68 cm) penetrate into the canopy and reflect information on branches and stems [89,90,91,92,93,94]. The longer wavelengths are more strongly correlated with forest biomass and other biophysical parameters than short wavelengths [95].
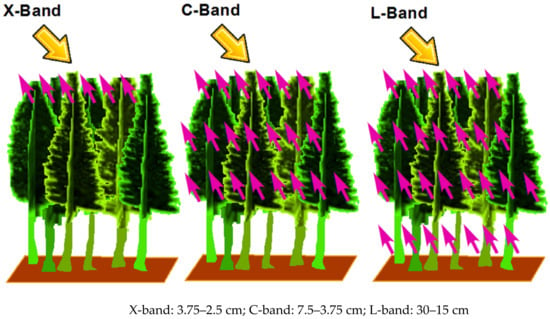
Figure 2.
Wavelength illustration of multi-frequency radar system through vegetation. Source: modified from the European Space Agency (ESA ).
The polarization of SAR plays an important role in understanding the interactions between electromagnetic waves and reflectors. There are two ways of emitted a signal in horizontal (H) or vertical (V) polarizations [96].
Different frequencies (C/X/L/P bands) of microwave radar have been employed to examine the biophysical parameters of mangrove ecosystems using airborne multi-polarimetric SAR (PolSAR) and polarimetric SAR interferometry (Pol-InSAR) data. Several studies have shown relationships between the backscatter coefficients of the ALOS PALSAR L-band and Radarsat-2 C-band and mangrove structural parameters such as tree height, diameter at breast height (DBH), basal area (BA), LAI, and stem density. For instance, significant negative correlation coefficients were observed between the HH backscatters of Avicennia germinans and biophysical parameters such as tree stand height, BA, and mean DBH [70]. In contrast, strong positive significant correlation coefficients were observed between the cross-polarization HV backscatter and LAI of mangrove forest stands. Pereira, Kampel, and Cunha-Lignon [76] showed that ALOS PALSAR L-band imagery can be used to characterize tree and canopy height, as well as the DBH of mangrove forests with satisfactory results. Kovacs et al. [71] and Cougo et al. [75] concluded that Radarsat-2 C-band at VH and VV polarizations can be used to estimate the LAI, stem density, BA, and DBH of several mangrove species with differing structures, such as Rhizophora mangle, Avicennia germinans, Avicennia schaueriana, and Laguncularia racemosa in the Amazon River, Brazil. Recent studies indicated that a strong correlation was observed between biophysical parameters such as the tree height, DBH, biomass, crown diameter, and crown area of several mangrove species and backscatters at dual HH and HV polarizations of ALOS-2 PALSAR-2 L-band data [5]. The stepwise multiple regression models were commonly used to estimate LAI based on quad polarization texture parameters derived from the grey-level co-occurrence matrix (GLCM) of the Radarsat-2 C-band data [71].
Active remote sensing techniques can also be used to estimate tree height compared to ground elevations. For example, Pol-InSAR has been used to estimate forest height through the inversion of a scattering model of the forest canopy [61,97]. Mangrove tree height also shows a strong correlation with interferometric coherence using TanDEM-X InSAR data. These results show the sensitivity of the InSAR inversion to mangrove canopy heights, and choosing an appropriate baseline elevation is required for the estimation of mangrove forest canopies. Additionally, multi-baseline InSAR inversion models can produce accurate estimates of mangrove heights [81].
LiDAR has been increasingly used to estimate mangrove tree stand diameters (Table 3), and can be combined with TanDEM-X to estimate mangrove canopy height [61] and tree height [73,81,98]. Full waveform LiDAR is able to map three-dimensional (3-D) vegetation structures because it can penetrate the forest canopy [78], unlike passive optical sensors. Thus, LiDAR is effective when combined with optical data—i.e., Landsat 8 OLI [99], Rapid Eye [36], and SAR data—to map the canopy height and biomass of mangrove forests [79,100]. Several studies found the potential use of LiDAR and the Shuttle Radar Topography Mission (SRTM) global digital elevation model (DEM) for estimating the canopy height of mangrove forests [83,100] and tree height using calibration equations [101].
4. Estimating Mangrove Biomass Using Remote Sensing
Mangrove structure influences other vegetation characteristics such as above-ground biomass (AGB). Understanding the distribution of mangrove AGB is important in order to estimate the above-ground carbon pool [102]. Globally, mangroves store 1.23 Pg of carbon in their biomass [15], and the ‘blue carbon’ sequestered and stored by such coastal ecosystems has become an important part of the international climate change agenda as a potential method of mitigating anthropogenic climate change emissions [103,104]. Therefore, information on AGB and carbon is required in national carbon accounting (e.g., nationally determined contributions linked to the Paris Climate Agreement) and for carbon credit schemes that pay for forest carbon stocks in order to incentivize their conservation [105].
Numerous studies have developed methods to estimate mangrove AGB based on the relationship between the biophysical parameters of forests or plantations such as DBH, BA, tree height, crown cover, and age [105,106,107,108]. Field-based biomass surveys have been conducted in mangrove forests for decades [109,110,111,112], and various studies have established allometric equations to estimate mangrove AGB from in situ measurements [113] and inventory data on stem weights, trees height, and DBH [111,114]. However, these studies are based on small-scale, plot-based research, and can be influenced by site selection biases. Additionally, other factors such as tidal inundation and time and labor constraints may lead to difficulty in estimating mangrove structure and biomass on a large scale in the field [2,115]. Remote sensing approaches have shown their effectiveness for assessing mangrove AGB at large scales. These methods are becoming popular for estimating forest AGB due to their ability to capture spatial variation in biomass and allow repeatable monitoring in remote regions [116,117,118]. Remote sensing techniques have numerous advantages in estimating above-ground biomass (AGB) over traditional field-survey measurement approaches, as they can estimate forest AGB at different scales [119].
Methods used to estimate mangrove AGB include parametric regression models [113,120] and non-parametric machine learning approaches [5,6,121]. Recently, machine learning approaches have been proven to be effective for modeling mangrove AGB biomass using multispectral imagery [121] and SAR data [6,122,123], as they often outperform the parametric regression models.
4.1. Mangrove Biomass Estimation Using Optical Data
Optical remotely sensed data especially high spatial resolution (HR) and very high spatial resolution (VHR) data may play a crucial role in assessing the AGB of mangroves. Recent studies have used HR and VHR optical data such as LISS IV, SPOT 5, IKONOS, RapidEye, WorldView-2, and Quick-Bird for AGB estimation in mangrove forests [67,106,123,124,125]. Optical remote sensing data can be used to estimate AGB with different parametric approaches, including multiple regression models and non-parametric sophisticated machine learning approaches such as support vector machines and neural networks [121,126], and can also be estimated from canopy parameters such as crown diameter [127,128]. For instance, Jachowski et al. [121] used machine learning trained on Geoeye-1 and Landsat data to estimate the AGB and the below-ground biomass (BGB) of a mangrove in Southwest Thailand with a promising R2 result of 0.66. Friess et al. [129] employed generalized linear models (GLMs) to predict AGB and BGB biomass in mangroves across the entire nation of Singapore using two-meter Pleiades data and associated field measurements. This method was more accurate than using field data alone, because Singapore’s mangroves show substantial variation in the geomorphic setting and the degree of degradation experienced, which significantly influences the spatial distribution of AGB across the country.
Hirata et al. [106] showed the use of Quick-Bird and multispectral data to estimate the AGB of four mangrove species in the coastal zone of Southern Ranong province (Thailand). The regression analysis results showed that the biomass derived from the field survey and estimated biomass from Quick-Bird data reached R2 = 0.65. A recent study reported by Pham and Brabyn [123] in Vietnam combined spectral, vegetation association type, texture, and vegetation indices to model AGB. Nevertheless, stand AGB estimates based on Quick-Bird data can be underestimated due to a lack of data availability on individual mangrove species biomass and the crowns of large trees [106]. Additionally, there are several drawbacks of using high spatial resolution data. The first drawback is that forest canopy complexity can affect the generation of predicted AGB models. Secondly, high spectral resolution data often lack shortwave infrared data. This is a useful wavelength for estimating forest AGB, as shortwave-infrared wavelengths are sensitive to forest biomass [130,131,132]. However, high-resolution data can also be more expensive and require more resources to process, which are two important factors that limit the application of high spatial resolution data for AGB retrieval at large scales [119].
Recent launches of Sentinel-2A, 2B optical sensors have provided more opportunities for estimating mangrove AGB in the tropics. For instance, Castillo et al. [65] and Baloloy et al. [66] compared the performance of different optical sensors and concluded that Sentinel-2A data showed a promising result (R2= 0.92) for the estimation of mangrove forest AGB in the Philippines. To date, a few studies have employed these new satellite sensors for estimating mangrove AGB at the species level. Thus, more research needs to be undertaken to clarify the potential and limitations of the new optical sensors for the AGB estimation of mangrove species derived from high to very high spatial resolution data in the future.
4.2. Biomass Estimation for Mangrove Forests Using SAR Data
Active sensors such as SAR offer unique benefits that have several advantages over optical sensors [95], including day and nighttime capability (SAR is independent of intensity and sun illumination angle); data acquisition in all weather conditions (including cloud cover; penetration capability through vegetation); sensitivity to surface roughness, dielectric properties and moisture; and sensitivity to wave polarization and frequency.
While SAR data is useful for modeling structure and biomass, it suffers from saturation. The level of saturation depends on the wavelength (C, L, or P bands), polarizations (HH, HV, VH, and VV), and the characteristics of ground conditions. Shugart et al. [133] showed that the L-band saturates at around 100–150 Mg ha−1, whilst the P-band could be sensitive for biomass estimation at a saturation level of 100–300 Mg ha−1 [134]. The saturation level of the AGB estimation in a mangrove ecosystem using L-band SAR data was at over 100–150 Mg ha−1 depending on the tidal inundation level of different mangrove species in tropical and subtropical climates [6,135].
Previous studies indicated that SAR data plays a crucial role in AGB retrieval, especially in the tropics where cloud conditions occur frequently. Nevertheless, SAR image processing requires more skills, specific software, and scientific knowledge, and is time consuming due to the many steps involved, such as pre-processing and noise removal. In addition, the long wavelengths, i.e., ALOS-2 PALSAR-2 L-band SAR data, may be costlier than the short wavelengths i.e., RADARSAT C-band.
There are two main approaches to estimate mangrove AGB using SAR—backscatter coefficient extraction and polarimetric SAR interferometry (Pol-InSAR)--with the latter based on the coherent combination of both polarimetric and interferometric observables.
4.2.1. Backscatter Coefficient Extraction for Mangrove Biomass Estimation
The most common method for biomass estimation uses regression based on extracted backscatter coefficients and field survey biomass measurements (Table 4).

Table 4.
Methods used for above-ground biomass (AGB) estimation using backscatters.
Regression analysis is the most common method used to estimate the AGB of mangrove forests. This method was investigated by several authors in different case studies in French Guiana, Malaysia [107], and Vietnam [5,138,140]. More recently, machine learning techniques have been used for mangrove AGB estimation. For instance, the AGB of Sonneratia caseolaris was estimated by the multilayer perceptron neural networks (MLPNN) model with leave-one-out cross-validation technique, showing a promising result with R2 = 0.78 and the model-estimated AGB ranging between 2.78–298.95 Mg ha−1 [122]. A recent study used the Sentinel-1A imagery in the retrieval and mapping of mangrove biomass in Honada Bay in the Philippines [66]. Recent research using L-band ALOS PALSAR to estimate the AGB of the Matang mangrove in Malaysia found that HV backscatter gave the best correlation coefficient between polarimetric ALOS PALSAR backscatter and AGB for three dominant species: Rhizophora apiculata, Avicennia alba, and Bruguiera parviflora. HV backscatter coefficients became saturated at AGB estimates exceeding 100 Mg ha-1, and the error of the estimation increased when the AGB exceeded 150 Mg ha−1 [107]. This can limit the utility of SAR for quantifying mangrove biomass, because the average AGB may exceed this [4] for many mangrove types.
4.2.2. Biomass Estimation using Interferometry (InSAR) and Pol-InSAR Techniques
Interferometry is a technique based on interference, where two waves superimposed lead to a wave of greater or lower amplitude, and is used in remote sensing through. Interferometric synthetic aperture radar (InSAR) and polarimetric interferometric SAR (Pol-InSAR) techniques use at least two SAR images in the phase and the coherence of the waves [95]. InSAR and Pol-InSAR techniques can overcome the saturation problem of backscatter approaches [94,141] and provide more accurate results than using a single SAR image [142]. These techniques can be used to estimate tree height by subtracting a digital terrain model (DTM) from an InSAR height, or by dual Pol-InSAR data generated from TanDEM-X and TerraSAR-X, or at low frequencies (L and P-bands) [143,144,145]; then, forest AGB can be estimated based on regression analyses [146,147]. Several models have been developed using InSAR and Pol-InSAR to estimate forest AGB such as the interferometric water cloud model (IWCM), random volume over ground (RVoG) model, motion-over-ground (RMoG), random-motion-over-ground-legendre (RMoGL), and a simple model based on penetration depth (PD) [143,145,148,149]. The RVoG model does not take into consideration the temporal decorrelation, whereas the RMoG and RMoGL models consider this issue, resulting in better results for biomass estimation [145,148].
4.3. Mangrove Biomass Estimation Using LiDAR and Data Fusion
LiDAR is an active sensor that utilizes a pulsed laser to measure ranges and examine the surface of the Earth [150,151]. The LiDAR data have important roles in estimating AGB, since LiDAR pulses can penetrate vegetation canopies. LiDAR can estimate vegetation biomass, as various LiDAR-derived metrics can correlate with AGB [152,153].
Biomass estimation using airborne LiDAR can offer higher accuracy in tree extraction [154], tree height estimation [155], and AGB estimation [156] than those from radar and optical data [157], since LiDAR can characterize both horizontal and vertical canopy structures [130]. A recent study by Feliciano et al. [99] used a terrestrial laser scanner (TLS) and a tripod mounted LiDAR to estimate the mangrove AGB in the western Everglades National Park in the United States (USA). A more recent study by Fatoyinbo et al. [153] used airborne LiDAR to estimate mangrove AGB in the Zambezi Delta, Mozambique with R2 values between 0.80–0.88 with a mean AGB value of 203 Mg ha−1. However, the coverage and availability of LiDAR data are generally limited to small areas, and may be more costly than data obtained from space-borne sensors over a large area [119]. In addition, LiDAR has limited spectral information, in most cases, having only one wavelength of laser point intensity [130].
Several studies have demonstrated the potential use of data fusion or multisource data for mangrove AGB estimation [6,77]. Table 5 shows recent studies that employed multisensor data for the estimation of mangrove AGB and carbon stocks. For instance, Aslan et al. [77] used quantile regression models with an integration of Landsat 8 OLI and ALOS PALSAR to estimate a mean standing biomass of 237.52 ± 98.2 Mg ha−1 for Avicennia and Sonneratia species to 353.52 ± 98.43 Mg ha−1 in Rhizophora stands. A recent study by Pham et al. [6] estimated the biomass of a mangrove plantation in North Vietnam based on the incorporation of ALOS-2 PALSAR-2 and Sentinel-2A data and SVR models, with mean AGB values ranging from 36.22 to 230.14 Mg ha−1. Navarro et al. [139] estimated mangrove AGB in deltaic settings in Senegal by a combination of Sentinel-1A C-band and Sentinel-2A data using SVR models, with mean AGB values ranging between 6.04–9.12 Mg ha−1. A more recent work reported by Simard et al. [83] showed that the SRTM and the GLAS (Geoscience Laser Altimeter System) GLAS LiDAR data can be accurately used for a large-scale mangrove AGB estimation with an accuracy of 84.2 Mg ha−1 (Table 5).

Table 5.
Examples of multisensor data used for mangrove AGB estimation.
4.4. Biomass Estimation Using Hyperspectral Data
Hyperspectral sensors can acquire rich spectral information of the surface with a large number of spectral bands from visible to near infrared (NIR) or shortwave infrared (SWIR) range. Hyperspectral imaging has potential for classifying vegetation cover and estimating vegetation biomass compared with other multispectral sensors. For instance, Sibanda et al. [158] reported that hyperspectral data can provide slightly higher accuracies in estimating grass biomass than the Sentinel-2A multispectral images (MSI). However, Vaglio Laurin et al. [159] claimed that hyperspectral data had limited predictive ability using the partial least square (PLS) regression models (R2 = 0.36, RMSE = 91.1 Mg ha−1), even when vegetation indices (VIs) were entered into the models. However, combining the hyperspectral bands to LiDAR metrics using the PLS model increased the accuracy moderately (R2 = 0.70, RMSE = 61.7 Mg ha−1), whilst replacing the hyperspectral bands with the VIs led to a smaller increment (R2 = 0. 67, RMSE = 64.3 Mg ha−1) due to limited information from the vertical structure i.e., tree height and canopy height. The integration of LiDAR and hyperspectral or multisource data improved biomass estimation significantly with a relative high accuracy [160]. The hyperspectral data used in the literature were mainly airborne and captured in small and limited areas [119]. Space-borne hyperspectral satellites are anticipated to offer a large coverage and further promote the research of biomass estimation in mangroves.
5. Limitations and Uncertainties in Mangrove Remote Sensing
The classification of tree species and estimation of AGB are limited by the different spatial, spectral, and radiometric resolutions of remote sensing data. Medium to low spatial resolution data, i.e., Landsat 5 TM, Landsat 7 ETM+, and Landsat 8 OLI with 30-m spatial resolution contain many mixed pixels that have information for different tree species in a single pixel. Thus, medium spatial resolution data may have difficulties in classifying mangrove species due to the complexity of mangrove communities. Additionally, spectral resolution is also needed to be taken into consideration when choosing an appropriate satellite sensor for different tasks. For instance, Landsat sensors have six multispectral bands ranging from visible, near infrared, and shortwave infrared, as well as one thermal band, which could limit distinguishing certain mangrove species, whereas Sentinel-2 provides better spatial and spectral resolutions, and thus can play an important role for tree species classification and AGB retrieval. Wang et al. [44] pointed out that the red-edge band derived from the Sentinel-2 imagery is the most important feature for mangrove discrimination. Meanwhile, Zhu et al. [125] found that the red-edge band derived from the WorldView-2 is more sensitive than vegetation indices and other multispectral bands to mangrove AGB. In addition to spectral resolution, radiometric resolution also needs to be taken into consideration, such as eight-bit of the Landsat 5 TM and 12-bit of the Landsat 8 OLI data, because the digital number (DN) value saturates the AGB estimation due to similarities between mangrove stand structures and their biomass. Hyperspectral imagery could improve these limitations due to a larger number of bands with narrow wavelengths [119].
Optical imagery often requires radiometric and atmospheric correction to reduce topographic effects and minimize atmospheric conditions such as water vapor content and aerosols, particularly in forested areas [125,161]. The accuracy of mangrove AGB remote sensing may be influenced by radiometric and atmospheric corrections. Different approaches for radiometric and atmospheric correction have been developed and proposed for specific case studies to overcome this issue [162,163,164,165]. For instance, Xu et al. [163] used multivariate alteration detection (MAD) transformation-based normalization and principal component analysis (PCA)-based correction to retrieve forest attributes. Pons et al. [164] developed an automatic and improved radiometric correction of Landsat imagery based on the reference values from MODIS surface reflectance images. The most common methods for atmospheric correction are the fast line-of-sight atmospheric analysis of the spectral hypercubes (FLAASH), the dark-object subtraction (DOS), the ATmospheric CORection (ATCOR), and the Second Simulation of Satellite Signal in the Solar Spectrum models (6S) for multispectral sensors i.e., Landsat TM, SPOT 5, and WorldView-2 [161,165,166], and the Sen2Cor available in the Sentionel-2 toolbox used for Sentinel-2 data [167]. Nguyen et al. [161] and López et al. [165] suggested that the 6S model is optimal for AGB estimation based on optical remote sensing data.
For SAR data, speckling is a common problem that influences the accuracy of SAR image classification and AGB retrieval. Despeckling SAR data by applying a filter can remove noise and retain image features, although it may also result in blurring or filtered images, which affects the accuracy of AGB retrieval and image classification. Nonlocal filters for reducing noise in SAR images [168,169,170,171] should be performed cautiously in order to solve the limitations of speckles in future studies.
As optical or SAR sensors have their own characteristics in reflecting land surfaces and forest structures, we recommend the integration of different and complementary satellite remotely sensed data to enhance the information extracted for mangrove species, structure, and AGB. Data fusion of multi-sensors or multi-resolution data can offer a variety of advances for the improvement of AGB estimation. Several research studies have attempted data fusion for AGB estimation based on the integration of different optical sensors, such as SPOT HRV and Landsat TM [172], or SPOT multispectral and panchromatic bands [173,174]. In addition, the integration of SAR and optical data, such as Landsat TM and ALOS PALSAR, or Sentinel-2A [175] and ALOS-2 PALSAL-2 [6,176], can provide higher accuracies in quantifying biophysical parameters such as LAI, leaf pigments, and canopy height, and assessing tropical forest biomass. Despite the advantages of using data fusion, the time and labor constraints involved in image processing should be taken into consideration, especially over large areas [77,119]. More research on data fusion is needed for exploring the improvement of AGB estimation for mangrove forests.
6. Conclusions
Mangrove forests are important to coastal populations, but continue to be threatened throughout their range. Since they cover large areas and are often inaccessible for field research, remote sensing is a key tool with which to characterize mangroves and their structure, and quantify the benefits (such as carbon) that they provide. This review highlighted the recent trends for the use of remote sensing approaches for the analysis of mangroves, and showed the advantages of using machine learning techniques for discriminating mangrove species, characterizing biophysical parameters, and estimating mangrove biomass. Machine learning approaches have generally been proved to be effective for estimating mangrove biophysical parameters, i.e., LAI, tree height and leaf pigments, classifying mangrove communities, and provide a better overall accuracy in estimating mangrove biomass using various remotely sensed data in comparison to parametric approaches.
Very high spatial resolution data can contribute to higher accuracies in classifying mangrove species and AGB at a range of spatial scales. Nevertheless, the cost of data acquisition, the effects of shadows, and huge data storage requirements are important drawbacks of very high spatial resolution data, limiting their application at large scales. Medium to high spatial resolution data such as Sentinel-2A and Landsat imagery can be used to classify mangrove species and assess AGB at a regional scale; however, the mixed pixel and data saturation associated with optical imagery are the primary problems for classification of species. Low spatial resolution data such as MODIS would be used at a national or global scale, but have not yet been utilized extensively due to difficulties in accurately linking low spatial resolution data to field survey measurements. Combining multi-resolution and multisource data may improve the accuracy of mangrove species classification, structure, and AGB retrieval at the continental and global scale.
Active remote sensing data such as SAR and LiDAR may offer other approaches for tree and canopy height retrieval and AGB estimation, and can overcome the disadvantages of optical remotely sensed data. The COSMO-SkyMed (Constellation Of small Satellites for Mediterranean basin Observation) system, which consists of four satellites with a high-resolution SAR at the X-band, plays an important role in monitoring forest dynamics, thus providing an alternative SAR data source to monitor mangrove structures. The cross-polarization of long wavelengths such as L and P-bands in SAR would be more sensitive to the biomass and structure of mangrove forests. A combination of texture SAR image analysis, backscattering coefficients, interferometry analysis, and polarimetric analysis of SAR data is useful for improving mangrove height and AGB estimations. Using multiple independent measurements derived from LiDAR, InSAR, Pol-InSAR, or very high resolution stereophotogrammetry techniques are the most appropriate approaches for estimating mangrove canopy height. The integration of multi-temporal optical, microwave (SAR/InSAR/Pol-InSAR), and LiDAR would be the best choice for estimating mangrove biophysical parameters and AGB.
Several future directions exist for mangrove remote sensing, including the choice of remote sensing data and the variety of machine learning approaches available for the monitoring of mangrove species, structure, and biomass (Table 6). Machine learning approaches are likely to become more attractive in mangrove remote sensing. Recent developments of deep learning for texture information in classification can provide further directions for mangrove remote sensing. Deep learning plays an important role in identifying appropriate window sizes and spectral bands; thus, it may provide potential directions for tree species classification using very high spatial resolution imagery. Additionally, novel machine learning algorithms should be also taken into consideration to develop a guideline on how to select suitable image textures for monitoring mangrove ecosystems in future research. Further studies should focus on the development and the choices of novel machine learning algorithms for monitoring mangrove ecosystems in the context of REDD+ and blue carbon programs.

Table 6.
Recommendations for monitoring mangrove areas and structures. InSAR: interferometric synthetic aperture radar, Pol-InSAR: polarimetric SAR interferometry.
Author Contributions
T.D.P., N.Y., D.T.B., and D.A.F. wrote the draft of the manuscript. K.Y. and D.A.F. gave comments, suggestions and edits for the revision of the manuscript. All the authors have read and approved the final manuscript.
Funding
This research received no external funding. The APC was funded by the RIKEN Center for Advanced Intelligent Project (AIP), Japan.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Brander, L.M.; Wagtendonk, A.J.; Hussain, S.S.; McVittie, A.; Verburg, P.H.; de Groot, R.S.; van der Ploeg, S. Ecosystem service values for mangroves in southeast asia: A meta-analysis and value transfer application. Ecosyst. Serv. 2012, 1, 62–69. [Google Scholar] [CrossRef]
- Alongi, D.M. Present state and future of the world’s mangrove forests. Environ. Conserv. 2002, 29, 331–349. [Google Scholar] [CrossRef]
- Barbier, E.B.; Cox, M. An economic analysis of shrimp farm expansion and mangrove conversion in thailand. Land Econ. 2004, 80, 391–407. [Google Scholar] [CrossRef]
- Donato, D.C.; Kauffman, J.B.; Murdiyarso, D.; Kurnianto, S.; Stidham, M.; Kanninen, M. Mangroves among the most carbon-rich forests in the tropics. Nat. Geosci. 2011, 4, 293–297. [Google Scholar] [CrossRef]
- Pham, T.D.; Yoshino, K. Aboveground biomass estimation of mangrove species using alos-2 palsar imagery in hai phong city, vietnam. J. Appl. Remote Sens. 2017, 11, 026010. [Google Scholar] [CrossRef]
- Pham, T.D.; Yoshino, K.; Le, N.; Bui, D. Estimating aboveground biomass of a mangrove plantation on the northern coast of vietnam using machine learning techniques with an integration of alos-2 palsar-2 and sentinel-2a data. Int. J. Remote Sens. 2018, 39, 7761–7788. [Google Scholar] [CrossRef]
- Kauffman, J.B.; Heider, C.; Norfolk, J.; Payton, F. Carbon stocks of intact mangroves and carbon emissions arising from their conversion in the dominican republic. Ecol. Appl. 2013, 24, 518–527. [Google Scholar] [CrossRef]
- Hong, P.N.; San, H.T. Mangroves of Vietnam; IUCN: Bangkok, Thailand, 1993; p. 173. [Google Scholar]
- Tuan, L.D.; Oanh, T.T.K.; Thanh, C.V.; Quy, N.D. Can Gio Mangrove Biosphere Reserve; Agricultural Publishing House: Ho Chi Minh City, Vietnam, 2002; 311p. [Google Scholar]
- FAO. The World’s Mangroves 1980–2005. A Thematic Study Prepared in the Framework of the Global Forest Resources Assessment 2005; ISSN 0258-6150. Food and Agriculture Organization of the United Nations: Rome, Italy, 2007; p. 89. [Google Scholar]
- Hamilton, S.E.; Casey, D. Creation of a high spatio-temporal resolution global database of continuous mangrove forest cover for the 21st century (cgmfc-21). Glob. Ecol. Biogeogr. 2016, 25, 729–738. [Google Scholar] [CrossRef]
- Richards, D.R.; Friess, D.A. Rates and drivers of mangrove deforestation in southeast asia, 2000–2012. Proc. Natl. Acad. Sci. USA 2016, 113, 344–349. [Google Scholar] [CrossRef]
- Feller, I.C.; Friess, D.A.; Krauss, K.W.; Lewis, R.R. The state of the world’s mangroves in the 21st century under climate change. Hydrobiologia 2017, 803, 1–12. [Google Scholar] [CrossRef]
- Murdiyarso, D.; Purbopuspito, J.; Kauffman, J.B.; Warren, M.W.; Sasmito, S.D.; Donato, D.C.; Manuri, S.; Krisnawati, H.; Taberima, S.; Kurnianto, S. The potential of indonesian mangrove forests for global climate change mitigation. Nat. Clim. Chang. 2015, 5, 1089. [Google Scholar] [CrossRef]
- Hamilton, S.E.; Friess, D.A. Global carbon stocks and potential emissions due to mangrove deforestation from 2000 to 2012. Nat. Clim. Chang. 2018, 8, 240–244. [Google Scholar] [CrossRef]
- Duke, N.; Nagelkerken, I.; Agardy, T.; Wells, S.; Van Lavieren, H. The Importance of Mangroves to People: A Call to Action; United Nations Environment Programme World Conservation Monitoring Centre (UNEP-WCMC): Cambridge, UK, 2014. [Google Scholar]
- Pham, T.D.; Yoshino, K. Impacts of mangrove management systems on mangrove changes in the northern coast of vietnam. Tropics 2016, 24, 141–151. [Google Scholar] [CrossRef]
- Friess, D.A.; Webb, E.L. Variability in mangrove change estimates and implications for the assessment of ecosystem service provision. Glob. Ecol. Biogeogr. 2014, 23, 715–725. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of machine-learning classification in remote sensing: An applied review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef]
- Heumann, B.W. Satellite remote sensing of mangrove forests: Recent advances and future opportunities. Prog. Phys. Geogr. 2011, 35, 87–108. [Google Scholar] [CrossRef]
- Kuenzer, C.; Bluemel, A.; Gebhardt, S.; Quoc, T.V.; Dech, S. Remote sensing of mangrove ecosystems: A review. Remote Sens. 2011, 3, 878–928. [Google Scholar] [CrossRef]
- Lucas, R.; Lule, A.V.; Rodríguez, M.T.; Kamal, M.; Thomas, N.; Asbridge, E.; Kuenzer, C. Spatial ecology of mangrove forests: A remote sensing perspective. In Mangrove Ecosystems: A Global Biogeographic Perspective: Structure, Function, and Services; Rivera-Monroy, V.H., Lee, S.Y., Kristensen, E., Twilley, R.R., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 87–112. [Google Scholar]
- Lewis, R.R. Ecological engineering for successful management and restoration of mangrove forests. Ecol. Eng. 2005, 24, 403–418. [Google Scholar] [CrossRef]
- Heenkenda, M.; Joyce, K.; Maier, S.; Bartolo, R. Mangrove species identification: Comparing worldview-2 with aerial photographs. Remote Sens. 2014, 6, 6064–6088. [Google Scholar] [CrossRef]
- Viennois, G.; Proisy, C.; Féret, J.B.; Prosperi, J.; Sidik, F.; Suhardjono; Rahmania, R.; Longépé, N.; Germain, O.; Gaspar, P. Multitemporal analysis of high-spatial-resolution optical satellite imagery for mangrove species mapping in Bali, Indonesia. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3680–3686. [Google Scholar] [CrossRef]
- Kamal, M.; Phinn, S. Hyperspectral data for mangrove species mapping: A comparison of pixel-based and object-based approach. Remote Sens. 2011, 3, 2222–2242. [Google Scholar] [CrossRef]
- Jia, M.; Zhang, Y.; Wang, Z.; Song, K.; Ren, C. Mapping the distribution of mangrove species in the core zone of mai po marshes nature reserve, hong kong, using hyperspectral data and high-resolution data. Int. J. Appl. Earth Obs. Geoinf. 2014, 33, 226–231. [Google Scholar] [CrossRef]
- Kamal, M.; Phinn, S.; Johansen, K. Object-based approach for multi-scale mangrove composition mapping using multi-resolution image datasets. Remote Sens. 2015, 7, 4753–4783. [Google Scholar] [CrossRef]
- Chakravortty, S.; Ghosh, D.; Sinha, D. A Dynamic Model to Recognize Changes in Mangrove Species in Sunderban Delta Using Hyperspectral Image Analysis; Springer: Singapore, 2018; pp. 59–67. [Google Scholar]
- Wang, D.; Wan, B.; Qiu, P.; Su, Y.; Guo, Q.; Wu, X. Artificial mangrove species mapping using pléiades-1: An evaluation of pixel-based and object-based classifications with selected machine learning algorithms. Remote Sens. 2018, 10, 294. [Google Scholar] [CrossRef]
- Pham, T.D.; Bui, D.T.; Yoshino, K.; Le, N.N. Optimized rule-based logistic model tree algorithm for mapping mangrove species using alos palsar imagery and gis in the tropical region. Environ. Earth Sci. 2018, 77, 159. [Google Scholar] [CrossRef]
- Valderrama-Landeros, L.; Flores-de-Santiago, F.; Kovacs, J.M.; Flores-Verdugo, F. An assessment of commonly employed satellite-based remote sensors for mapping mangrove species in mexico using an ndvi-based classification scheme. Environ. Monit. Assess. 2017, 190, 23. [Google Scholar] [CrossRef] [PubMed]
- Kovacs, J.; de Santiago, F.; Bastien, J.; Lafrance, P. An assessment of mangroves in guinea, west africa, using a field and remote sensing based approach. Wetlands 2010, 30, 773–782. [Google Scholar] [CrossRef]
- Manjunath, K.R.; Kumar, T.; Kundu, N.; Panigrahy, S. Discrimination of mangrove species and mudflat classes using in situ hyperspectral data: A case study of Indian Sundarbans. Gisci. Remote Sens. 2013, 50, 400–417. [Google Scholar] [CrossRef]
- Chakravortty, S. Analysis of end member detection and subpixel classification algorithms on hyperspectral imagery for tropical mangrove species discrimination in the Sunderbans Delta, India. J. Appl. Remote Sens. 2013, 7, 073523. [Google Scholar] [CrossRef]
- Maeda, Y.; Fukushima, A.; Imai, Y.; Tanahashi, Y.; Nakama, E.; Ohta, S.; Kawazoe, K.; Akune, N. Estimating carbon stock changes of mangrove forests using satellite imagery and airborne lidar data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 705–709. [Google Scholar] [CrossRef]
- Giardino, C.; Bresciani, M.; Fava, F.; Matta, E.; Brando, V.; Colombo, R. Mapping submerged habitats and mangroves of lampi island marine national park (myanmar) from in situ and satellite observations. Remote Sens. 2016, 8, 2. [Google Scholar] [CrossRef]
- Satyanarayana, B.; Muslim, A.M.; Izzaty Horsali, N.A.; Mat Zauki, N.A.; Otero, V.; Nadzri, M.I.; Ibrahim, S.; Husain, M.-L.; Dahdouh-Guebas, F. Status of the undisturbed mangroves at Brunei bay, east Malaysia: A preliminary assessment based on remote sensing and ground-truth observations. PeerJ 2018, 6, e4397. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Wang, T.; Liu, M.; Jia, M.; Lin, H.; Chu, L.; Devlin, A. Potential of combining optical and dual polarimetric sar data for improving mangrove species discrimination using rotation forest. Remote Sens. 2018, 10, 467. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, H.; Lin, G.; Lin, H.; Tang, D. Zonation and directional dynamics of mangrove forests derived from time-series satellite imagery in Mai Po, Hong Kong. Sustainability 2018, 10, 1913. [Google Scholar] [CrossRef]
- Koedsin, W.; Vaiphasa, C. Discrimination of tropical mangroves at the species level with eo-1 hyperion data. Remote Sens. 2013, 5, 3562–3582. [Google Scholar] [CrossRef]
- Wong, F.K.K.; Fung, T. Combining eo-1 hyperion and envisat asar data for mangrove species classification in Mai Po Ramsar Site, Hong Kong. Int. J. Remote Sens. 2014, 35, 7828–7856. [Google Scholar] [CrossRef]
- Rogers, K.; Lymburner, L.; Salum, R.; Brooke, B.P.; Woodroffe, C.D. Mapping of mangrove extent and zonation using high and low tide composites of landsat data. Hydrobiologia 2017, 803, 49–68. [Google Scholar] [CrossRef]
- Wang, D.; Wan, B.; Qiu, P.; Su, Y.; Guo, Q.; Wang, R.; Sun, F.; Wu, X. Evaluating the performance of sentinel-2, landsat 8 and pléiades-1 in mapping mangrove extent and species. Remote Sens. 2018, 10, 1468. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, H.; Lin, H.; Fang, C. Textural–spectral feature-based species classification of mangroves in mai po nature reserve from worldview-3 imagery. Remote Sens. 2016, 8, 24. [Google Scholar] [CrossRef]
- Cao, J.; Leng, W.; Liu, K.; Liu, L.; He, Z.; Zhu, Y. Object-based mangrove species classification using unmanned aerial vehicle hyperspectral images and digital surface models. Remote Sens. 2018, 10, 89. [Google Scholar] [CrossRef]
- Ruwaimana, M.; Satyanarayana, B.; Otero, V.; Muslim, A.M.; Syafiq, A.M.; Ibrahim, S.; Raymaekers, D.; Koedam, N.; Dahdouh-Guebas, F. The advantages of using drones over space-borne imagery in the mapping of mangrove forests. PLoS ONE 2018, 13, e0200288. [Google Scholar] [CrossRef] [PubMed]
- Kovacs, J.M.; Liu, Y.; Zhang, C.; Flores-Verdugo, F.; de Santiago, F.F. A field based statistical approach for validating a remotely sensed mangrove forest classification scheme. Wetl. Ecol. Manag. 2011, 19, 409. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, K.; Liu, Y.; Kovacs, J.M.; Flores-Verdugo, F.; Santiago, F.J.F. Spectral response to varying levels of leaf pigments collected from a degraded mangrove forest. J. Appl. Remote Sens. 2012, 6, 063501. [Google Scholar]
- Flores-de-Santiago, F.; Kovacs, J.M.; Flores-Verdugo, F. The influence of seasonality in estimating mangrove leaf chlorophyll-a content from hyperspectral data. Wetl. Ecol. Manag. 2013, 21, 193–207. [Google Scholar] [CrossRef]
- Zhang, C.; Kovacs, J.; Wachowiak, M.; Flores-Verdugo, F. Relationship between hyperspectral measurements and mangrove leaf nitrogen concentrations. Remote Sens. 2013, 5, 891–908. [Google Scholar] [CrossRef]
- Fauzi, A.; Skidmore, A.K.; Gils, H.V.; Schlerf, M.; Heitkönig, I.M.A. Shrimp pond effluent dominates foliar nitrogen in disturbed mangroves as mapped using hyperspectral imagery. Mar. Pollut. Bull. 2013, 76, 42–51. [Google Scholar] [CrossRef]
- Axelsson, C.; Skidmore, A.K.; Schlerf, M.; Fauzi, A.; Verhoef, W. Hyperspectral analysis of mangrove foliar chemistry using plsr and support vector regression. Int. J. Remote Sens. 2013, 34, 1724–1743. [Google Scholar] [CrossRef]
- Kamal, M.; Phinn, S.; Johansen, K. Characterizing the spatial structure of mangrove features for optimizing image-based mangrove mapping. Remote Sens. 2014, 6, 984–1006. [Google Scholar] [CrossRef]
- Pastor-Guzman, J.; Atkinson, P.; Dash, J.; Rioja-Nieto, R. Spatiotemporal variation in mangrove chlorophyll concentration using landsat 8. Remote Sens. 2015, 7, 14530–14558. [Google Scholar] [CrossRef]
- Heenkenda, M.K.; Joyce, K.E.; Maier, S.W.; de Bruin, S. Quantifying mangrove chlorophyll from high spatial resolution imagery. ISPRS J. Photogramm. Remote Sens. 2015, 108, 234–244. [Google Scholar] [CrossRef]
- Pu, R.; Cheng, J. Mapping forest leaf area index using reflectance and textural information derived from worldview-2 imagery in a mixed natural forest area in Florida, US. Int. J. Appl. Earth Obs. Geoinf. 2015, 42, 11–23. [Google Scholar] [CrossRef]
- Lagomasino, D.; Fatoyinbo, T.; Lee, S.-K.; Simard, M. High-resolution forest canopy height estimation in an African blue carbon ecosystem. Remote Sens. Ecol. Conserv. 2015, 1, 51–60. [Google Scholar] [CrossRef] [PubMed]
- Kamal, M.; Phinn, S.; Johansen, K. Assessment of multi-resolution image data for mangrove leaf area index mapping. Remote Sens. Environ. 2016, 176, 242–254. [Google Scholar] [CrossRef]
- Heenkenda, M.; Maier, S.; Joyce, K. Estimating mangrove biophysical variables using worldview-2 satellite data: Rapid creek, northern territory, Australia. J. Imaging 2016, 2, 24. [Google Scholar] [CrossRef]
- Lagomasino, D.; Fatoyinbo, T.; Lee, S.; Feliciano, E.; Trettin, C.; Simard, M. A comparison of mangrove canopy height using multiple independent measurements from land, air, and space. Remote Sens. 2016, 8, 327. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Stupp, P.; Dahal, S.; Remillard, C.; Bledsoe, R.; Stone, A.; Cameron, C.; Rastogi, G.; Samal, R.; Mishra, D.R. A multi-sensor approach for assessing mangrove biophysical characteristics in coastal Odisha, India. Proc. Natl. Acad. Sci. India Sect. A Phys. Sci. 2017, 87, 679–700. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, K.; Liu, L.; Myint, S.; Wang, S.; Liu, H.; He, Z. Exploring the potential of worldview-2 red-edge band-based vegetation indices for estimation of mangrove leaf area index with machine learning algorithms. Remote Sens. 2017, 9, 1060. [Google Scholar] [CrossRef]
- Tian, J.; Wang, L.; Li, X.; Gong, H.; Shi, C.; Zhong, R.; Liu, X. Comparison of uav and worldview-2 imagery for mapping leaf area index of mangrove forest. Int. J. Appl. Earth Obs. Geoinf. 2017, 61, 22–31. [Google Scholar] [CrossRef]
- Castillo, J.A.A.; Apan, A.A.; Maraseni, T.N.; Salmo, S.G. Estimation and mapping of above-ground biomass of mangrove forests and their replacement land uses in the Philippines using sentinel imagery. ISPRS J. Photogramm. Remote Sens. 2017, 134, 70–85. [Google Scholar] [CrossRef]
- Baloloy, A.B.; Blanco, A.C.; Candido, C.G.; Argamosa, R.J.L.; Dumalag, J.B.L.C.; Dimapilis, L.L.C.; Paringit, E.C. Estimation of mangrove forest aboveground biomass using multispectral bands, vegetation indices and biophysical variables derived from optical satellite imageries: Rapideye, planetscope and sentinel-2. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, IV-3, 29–36. [Google Scholar] [CrossRef]
- Dou, Z.; Cui, L.; Li, J.; Zhu, Y.; Gao, C.; Pan, X.; Lei, Y.; Zhang, M.; Zhao, X.; Li, W. Hyperspectral estimation of the chlorophyll content in short-term and long-term restorations of mangrove in Quanzhou bay estuary, China. Sustainability 2018, 10, 1127. [Google Scholar] [CrossRef]
- Pastor-Guzman, J.; Dash, J.; Atkinson, P.M. Remote sensing of mangrove forest phenology and its environmental drivers. Remote Sens. Environ. 2018, 205, 71–84. [Google Scholar] [CrossRef]
- Fatoyinbo, T.E.; Simard, M. Height and biomass of mangroves in africa from icesat/glas and srtm. Int. J. Remote Sens. 2013, 34, 668–681. [Google Scholar] [CrossRef]
- Kovacs, J.M.; Lu, X.X.; Flores-Verdugo, F.; Zhang, C.; Flores de Santiago, F.; Jiao, X. Applications of alos palsar for monitoring biophysical parameters of a degraded black mangrove (avicennia germinans) forest. ISPRS J. Photogramm. Remote Sens. 2013, 82, 102–111. [Google Scholar] [CrossRef]
- Kovacs, J.M.; Jiao, X.; Flores-de-Santiago, F.; Zhang, C.; Flores-Verdugo, F. Assessing relationships between radarsat-2 c-band and structural parameters of a degraded mangrove forest. Int. J. Remote Sens. 2013, 34, 7002–7019. [Google Scholar] [CrossRef]
- Wong, F.K.K.; Fung, T. Combining hyperspectral and radar imagery for mangrove leaf area index modeling. Photogramm. Eng. Remote Sens. 2013, 79, 479–490. [Google Scholar] [CrossRef]
- Wannasiri, W.; Nagai, M.; Honda, K.; Santitamnont, P.; Miphokasap, P. Extraction of mangrove biophysical parameters using airborne lidar. Remote Sens. 2013, 5, 1787–1808. [Google Scholar] [CrossRef]
- Lee, S.K.; Fatoyinbo, T.E. Tandem-x pol-insar inversion for mangrove canopy height estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3608–3618. [Google Scholar] [CrossRef]
- Cougo, M.; Souza-Filho, P.; Silva, A.; Fernandes, M.; Santos, J.; Abreu, M.; Nascimento, W.; Simard, M. Radarsat-2 backscattering for the modeling of biophysical parameters of regenerating mangrove forests. Remote Sens. 2015, 7, 17097–17112. [Google Scholar] [CrossRef]
- Pereira, F.R.D.S.; Kampel, M.; Cunha-Lignon, M. Mangrove vegetation structure in southeast brazil from phased array l-band synthetic aperture radar data. J. Appl. Remote Sens. 2016, 10, 036021. [Google Scholar] [CrossRef]
- Aslan, A.; Rahman, A.F.; Warren, M.W.; Robeson, S.M. Mapping spatial distribution and biomass of coastal wetland vegetation in Indonesian Papua by combining active and passive remotely sensed data. Remote Sens. Environ. 2016, 183, 65–81. [Google Scholar] [CrossRef]
- Guo, Q.; Su, Y.; Hu, T.; Zhao, X.; Wu, F.; Li, Y.; Liu, J.; Chen, L.; Xu, G.; Lin, G.; et al. An integrated uav-borne lidar system for 3d habitat mapping in three forest ecosystems across china. Int. J. Remote Sens. 2017, 38, 2954–2972. [Google Scholar] [CrossRef]
- Feliciano, E.A.; Wdowinski, S.; Potts, M.D.; Lee, S.-K.; Fatoyinbo, T.E. Estimating mangrove canopy height and above-ground biomass in the everglades national park with airborne lidar and tandem-x data. Remote Sens. 2017, 9, 702. [Google Scholar] [CrossRef]
- Tien Dat, P.; Kunihiko, Y. Characterization of mangrove species using alos-2 palsar in Hai Phong city, Vietnam. IOP Conf. Ser. Earth Environ. Sci. 2016, 37, 012036. [Google Scholar]
- Lee, S.K.; Fatoyinbo, T.E.; Lagomasino, D.; Feliciano, E.; Trettin, C. Multibaseline tandem-x mangrove height estimation: The selection of the vertical wavenumber. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 99, 1–9. [Google Scholar] [CrossRef]
- Aslan, A.; Rahman, A.F.; Robeson, S.M. Investigating the use of alos prism data in detecting mangrove succession through canopy height estimation. Ecol. Indic. 2018, 87, 136–143. [Google Scholar] [CrossRef]
- Simard, M.; Fatoyinbo, L.; Smetanka, C.; Rivera-Monroy, V.H.; Castañeda-Moya, E.; Thomas, N.; Van der Stocken, T. Mangrove canopy height globally related to precipitation, temperature and cyclone frequency. Nat. Geosci. 2019, 12, 40–45. [Google Scholar] [CrossRef]
- Muhsoni, F.F.; Sambah34, A.; Mahmudi, M.; Wiadnya, D. Comparison of different vegetation indices for assessing mangrove density using sentinel-2 imagery. Int. J. Geomate 2018, 14, 42–51. [Google Scholar]
- Siegmann, B.; Jarmer, T. Comparison of different regression models and validation techniques for the assessment of wheat leaf area index from hyperspectral data. Int. J. Remote Sens. 2015, 36, 4519–4534. [Google Scholar] [CrossRef]
- Schlerf, M.; Atzberger, C. Inversion of a forest reflectance model to estimate structural canopy variables from hyperspectral remote sensing data. Remote Sens. Environ. 2006, 100, 281–294. [Google Scholar] [CrossRef]
- Houborg, R.; Boegh, E. Mapping leaf chlorophyll and leaf area index using inverse and forward canopy reflectance modeling and spot reflectance data. Remote Sens. Environ. 2008, 112, 186–202. [Google Scholar] [CrossRef]
- Henderson, F.M.; Lewis, A.J. Principles and Applications of Imaging Radar. Manual of Remote Sensing, 3rd ed.; Wiley: Hoboken, NJ, USA, 1998; Volume 2, p. 896. [Google Scholar]
- Le Toan, T.; Quegan, S.; Woodward, I.; Lomas, M.; Delbart, N.; Picard, G. Relating radar remote sensing of biomass to modelling of forest carbon budgets. Clim. Chang. 2004, 67, 379–402. [Google Scholar] [CrossRef]
- Englhart, S.; Keuck, V.; Siegert, F. Aboveground biomass retrieval in tropical forests—The potential of combined x- and l-band sar data use. Remote Sens. Environ. 2011, 115, 1260–1271. [Google Scholar] [CrossRef]
- Sarker, L.; Nichol, J.; Mubin, A. Potential of multiscale texture polarization ratio of c-band sar for forest biomass estimation. In Developments in Multidimensional Spatial Data Models; Abdul Rahman, A., Boguslawski, P., Gold, C., Said, M.N., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 69–83. [Google Scholar]
- Thumaty, K.; Fararoda, R.; Middinti, S.; Gopalakrishnan, R.; Jha, C.S.; Dadhwal, V.K. Estimation of above ground biomass for central indian deciduous forests using alos palsar l-band data. J. Indian Soc. Remote Sens. 2016, 44, 31–39. [Google Scholar] [CrossRef]
- Sandberg, G.; Ulander, L.M.H.; Fransson, J.E.S.; Holmgren, J.; Le Toan, T. L- and p-band backscatter intensity for biomass retrieval in hemiboreal forest. Remote Sens. Environ. 2011, 115, 2874–2886. [Google Scholar] [CrossRef]
- Kubota, V.R.; Yoneda, T.; Okuda, T.; Kadir, W.R. Suitability of interferometric synthetic aperture radar (ifsar) for biomass estimation in a selectively logged tropical rainforest in peninsular malaysia. Tropics 2015, 24, 101–111. [Google Scholar] [CrossRef]
- Sinha, S.; Jeganathan, C.; Sharma, L.K.; Nathawat, M.S. A review of radar remote sensing for biomass estimation. Int. J. Environ. Sci. Technol. 2015, 12, 1779–1792. [Google Scholar] [CrossRef]
- Ghasemi, N.; Sahebi, M.R.; Mohammadzadeh, A. A review on biomass estimation methods using synthetic aperture radar data. Int. J. Geomat. Geosci. 2011, 1, 776–788. [Google Scholar]
- Lee, S.; Kugler, F.; Papathanassiou, K.P.; Hajnsek, I. Quantification of temporal decorrelation effects at l-band for polarimetric sar interferometry applications. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1351–1367. [Google Scholar] [CrossRef]
- Feliciano, E.A.; Wdowinski, S.; Potts, M.D. Assessing mangrove above-ground biomass and structure using terrestrial laser scanning: A case study in the Everglades National Park. Wetlands 2014, 34, 955–968. [Google Scholar] [CrossRef]
- Hickey, S.M.; Callow, N.J.; Phinn, S.; Lovelock, C.E.; Duarte, C.M. Spatial complexities in aboveground carbon stocks of a semi-arid mangrove community: A remote sensing height-biomass-carbon approach. Estuar. Coast. Shelf Sci. 2018, 200, 194–201. [Google Scholar] [CrossRef]
- Simard, M.; Zhang, K.; Rivera-Monroy, V.H.; Ross, M.S.; Ruiz, P.L.; Castañeda-Moya, E.; Twilley, R.R.; Rodriguez, E. Mapping height and biomass of mangrove forests in everglades national park with srtm elevation data. Photogramm. Eng. Remote Sens. 2006, 72, 299–311. [Google Scholar] [CrossRef]
- Fatoyinbo, T.E.; Simard, M.; Washington-Allen, R.A.; Shugart, H.H. Landscape-scale extent, height, biomass, and carbon estimation of mozambique’s mangrove forests with landsat etm+ and shuttle radar topography mission elevation data. J. Geophys. Res. Biogeosci. 2008, 113. [Google Scholar] [CrossRef]
- Clark, D.B.; Clark, D.A. Landscape-scale variation in forest structure and biomass in a tropical rain forest. For. Ecol. Manag. 2000, 137, 185–198. [Google Scholar] [CrossRef]
- Grimsditch, G.; Alder, J.; Nakamura, T.; Kenchington, R.; Tamelander, J. The blue carbon special edition—Introduction and overview. Ocean Coast. Manag. 2013, 83, 1–4. [Google Scholar] [CrossRef]
- Howard, J.; Hoyt, S.; Isensee, K.; Pidgeon, E.; Telszewski, M. Coastal Blue Carbon: Methods for Assessing Carbon Stocks and Emissions Factors in Mangroves, Tidal Salt Marshes, and Seagrass Meadows; Conservation International, Intergovernmental Oceanographic Commission of UNESCO, International Union for Conservation of Nature: Arlington, VA, USA, 2014. [Google Scholar]
- Locatelli, T.; Binet, T.; Kairo, J.G.; King, L.; Madden, S.; Patenaude, G.; Upton, C.; Huxham, M. Turning the tide: How blue carbon and payments for ecosystem services (pes) might help save mangrove forests. AMBIO 2014, 43, 981–995. [Google Scholar] [CrossRef]
- Hirata, Y.; Tabuchi, R.; Patanaponpaiboon, P.; Poungparn, S.; Yoneda, R.; Fujioka, Y. Estimation of aboveground biomass in mangrove forests using high-resolution satellite data. J. Res. 2014, 19, 34–41. [Google Scholar] [CrossRef]
- Hamdan, O.; Khali Aziz, H.; Mohd Hasmadi, I. L-band alos palsar for biomass estimation of matang mangroves, malaysia. Remote Sens. Environ. 2014, 155, 69–78. [Google Scholar] [CrossRef]
- Latifi, H.; Fassnacht, F.E.; Hartig, F.; Berger, C.; Hernández, J.; Corvalán, P.; Koch, B. Stratified aboveground forest biomass estimation by remote sensing data. Int. J. Appl. Earth Obs. Geoinf. 2015, 38, 229–241. [Google Scholar] [CrossRef]
- Jin-Eong, O.; Khoon, G.W.; Clough, B.F. Structure and productivity of a 20-year-old stand of rhizophora apiculata bl. Mangrove forest. J. Biogeogr. 1995, 22, 417–424. [Google Scholar] [CrossRef]
- Clough, B.F.; Dixon, P.; Dalhaus, O. Allometric relationships for estimating biomass in multi-stemmed mangrove trees. Aust. J. Bot. 1997, 45, 1023–1031. [Google Scholar] [CrossRef]
- Komiyama, A.; Jintana, V.; Sangtiean, T.; Kato, S. A common allometric equation for predicting stem weight of mangroves growing in secondary forests. Ecol. Res. 2002, 17, 415–418. [Google Scholar] [CrossRef]
- Komiyama, A.; Ong, J.E.; Poungparn, S. Allometry, biomass, and productivity of mangrove forests: A review. Aquat. Bot. 2008, 89, 128–137. [Google Scholar] [CrossRef]
- Chave, J.; Andalo, C.; Brown, S.; Cairns, M.A.; Chambers, J.Q.; Eamus, D.; Fölster, H.; Fromard, F.; Higuchi, N.; Kira, T.; et al. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 2005, 145, 87–99. [Google Scholar] [CrossRef] [PubMed]
- Komiyama, A.; Poungparn, S.; Kato, S. Common allometric equations for estimating the tree weight of mangroves. J. Trop. Ecol. 2005, 21, 471–477. [Google Scholar] [CrossRef]
- Ellison, A. Macroecology of mangroves: Large-scale patterns and processes in tropical coastal forests. Trees 2002, 16, 181–194. [Google Scholar] [CrossRef]
- Rosillo-Calle, F.; Groot, P.; Hemstock, S.L.; Woods, J. The Biomass Assessment Handbook: Bioenergy for a Sustainable Environment; Earthscan: London, UK, 2007; p. 294. [Google Scholar]
- Avtar, R.; Kumar, P.; Oono, A.; Saraswat, C.; Dorji, S.; Hlaing, Z. Potential application of remote sensing in monitoring ecosystem services of forests, mangroves and urban areas. Geocarto Int. 2017, 32, 874–885. [Google Scholar] [CrossRef]
- Pham, T.D.; Yoshino, K.; Kaida, N. Monitoring mangrove forest changes in cat ba biosphere reserve using alos palsar imagery and a gis-based support vector machine algorithm. In Advances and Applications in Geospatial Technology and Earth Resources: Proceedings of the International Conference on Geo-Spatial Technologies and Earth Resources 2017; Tien Bui, D., Ngoc Do, A., Bui, H.-B., Hoang, N.-D., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 103–118. [Google Scholar]
- Lu, D. The potential and challenge of remote sensing-based biomass estimation. Int. J. Remote Sens. 2006, 27, 1297–1328. [Google Scholar] [CrossRef]
- Ross, M.; Ruiz, P.; Telesnicki, G.; Meeder, J. Estimating above-ground biomass and production in mangrove communities of Biscayne National park, Florida (U.S.A.). Wetl. Ecol. Manag. 2001, 9, 27–37. [Google Scholar] [CrossRef]
- Jachowski, N.R.A.; Quak, M.S.Y.; Friess, D.A.; Duangnamon, D.; Webb, E.L.; Ziegler, A.D. Mangrove biomass estimation in southwest Thailand using machine learning. Appl. Geogr. 2013, 45, 311–321. [Google Scholar] [CrossRef]
- Pham, T.D.; Yoshino, K.; Bui, D.T. Biomass estimation of sonneratia caseolaris (l.) engler at a coastal area of Hai Phong City (Vietnam) using alos-2 palsar imagery and gis-based multi-layer perceptron neural networks. GISci. Remote Sens. 2017, 54, 329–353. [Google Scholar] [CrossRef]
- Pham, L.T.H.; Brabyn, L. Monitoring mangrove biomass change in Vietnam using spot images and an object-based approach combined with machine learning algorithms. ISPRS J. Photogramm. Remote Sens. 2017, 128, 86–97. [Google Scholar] [CrossRef]
- Manna, S.; Nandy, S.; Chanda, A.; Akhand, A.; Hazra, S.; Dadhwal, V.K. Estimating aboveground biomass in Avicennia marina plantation in Indian Sundarbans using high-resolution satellite data. J. Appl. Remote Sens. 2014, 8, 083638. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, K.; Liu, L.; Wang, S.; Liu, H. Retrieval of mangrove aboveground biomass at the individual species level with worldview-2 images. Remote Sens. 2015, 7, 12192–12214. [Google Scholar] [CrossRef]
- Mutanga, O.; Skidmore, A.K. Narrow band vegetation indices overcome the saturation problem in biomass estimation. Int. J. Remote Sens. 2004, 25, 3999–4014. [Google Scholar] [CrossRef]
- Phua, M.-H.; Saito, H. Estimation of biomass of a mountainous tropical forest using landsat tm data. Can. J. Remote Sens. 2003, 29, 429–440. [Google Scholar] [CrossRef]
- Popescu, S.C.; Wynne, R.H.; Nelson, R.F. Measuring individual tree crown diameter with lidar and assessing its influence on estimating forest volume and biomass. Can. J. Remote Sens. 2003, 29, 564–577. [Google Scholar] [CrossRef]
- Friess, D.A.; Richards, D.R.; Phang, V.X.H. Mangrove forests store high densities of carbon across the tropical urban landscape of singapore. Urban Ecosyst. 2016, 19, 795–810. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Liu, L.; Li, G.; Moran, E. A survey of remote sensing-based aboveground biomass estimation methods in forest ecosystems. Int. J. Digit. Earth 2016, 9, 63–105. [Google Scholar] [CrossRef]
- Kumar, L.; Sinha, P.; Taylor, S.; Alqurashi, A.F. Review of the use of remote sensing for biomass estimation to support renewable energy generation. J. Appl. Remote Sens. 2015, 9, 097696. [Google Scholar] [CrossRef]
- Gleason, C.J.; Im, J. A review of remote sensing of forest biomass and biofuel: Options for small-area applications. Gisci. Remote Sens. 2011, 48, 141–170. [Google Scholar] [CrossRef]
- Shugart, H.H.; Saatchi, S.; Hall, F.G. Importance of structure and its measurement in quantifying function of forest ecosystems. J. Geophys. Res. Biogeosci. 2010, 115. [Google Scholar] [CrossRef]
- FAO. Gtos: Biomass Assessment of the Status of the Development of the Standards for the Terrestrial Essential Climate Variables; FAO: Rome, Italy, 2009; p. 18. [Google Scholar]
- Lucas, R.M.; Mitchell, A.L.; Rosenqvist, A.; Proisy, C.; Melius, A.; Ticehurst, C. The potential of l-band sar for quantifying mangrove characteristics and change: Case studies from the tropics. Aquat. Conserv. Mar. Freshw. Ecosyst. 2007, 17, 245–264. [Google Scholar] [CrossRef]
- Carreiras, J.M.B.; Vasconcelos, M.J.; Lucas, R.M. Understanding the relationship between aboveground biomass and alos palsar data in the forests of guinea-bissau (west africa). Remote Sens. Environ. 2012, 121, 426–442. [Google Scholar] [CrossRef]
- Peregon, A.; Yamagata, Y. The use of alos/palsar backscatter to estimate above-ground forest biomass: A case study in western siberia. Remote Sens. Environ. 2013, 137, 139–146. [Google Scholar] [CrossRef]
- Vu, T.D.; Takeuchi, W.; Van, N.A. Carbon stock calculating and forest change assessment toward redd+ activities for the mangrove forest in vietnam. Trans. Jpn. Soc. Aeronaut. Space Sci. Aerosp. Technol. Jpn. 2014, 12, Pn_23–Pn_31. [Google Scholar] [CrossRef]
- Navarro, J.A.; Algeet, N.; Fernández-Landa, A.; Esteban, J.; Rodríguez-Noriega, P.; Guillén-Climent, M.L. Integration of uav, sentinel-1, and sentinel-2 data for mangrove plantation aboveground biomass monitoring in senegal. Remote Sens. 2019, 11, 77. [Google Scholar] [CrossRef]
- Takeuchi, W.; Tien, D.V.; Phuong, V.T.; Van, A.N.; Oo, K.S. Above ground biomass mapping of mangrove forest in vietnam by alos palsar. In Proceedings of the 2011 3rd International Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Seoul, Korea, 26–30 September 2011; pp. 1–3. [Google Scholar]
- Fransson, J.E.S.; Smith, G.; Askne, J.; Olsson, H. Stem volume estimation in boreal forests using ers-1/2 coherence and spot xs optical data. Int. J. Remote Sens. 2001, 22, 2777–2791. [Google Scholar] [CrossRef]
- Pulliainen, J.; Engdahl, M.; Hallikainen, M. Feasibility of multi-temporal interferometric sar data for stand-level estimation of boreal forest stem volume. Remote Sens. Environ. 2003, 85, 397–409. [Google Scholar] [CrossRef]
- Askne, J.; Fransson, J.; Santoro, M.; Soja, M.; Ulander, L. Model-based biomass estimation of a hemi-boreal forest from multitemporal tandem-x acquisitions. Remote Sens. 2013, 5, 5574–5597. [Google Scholar] [CrossRef]
- Kugler, F.; Schulze, D.; Hajnsek, I.; Pretzsch, H.; Papathanassiou, K.P. Tandem-x pol-insar performance for forest height estimation. Ieee Trans. Geosci. Remote Sens. 2014, 52, 6404–6422. [Google Scholar] [CrossRef]
- Ghasemi, N.; Tolpekin, V.; Stein, A. Assessment of forest above-ground biomass estimation from polinsar in the presence of temporal decorrelation. Remote Sens. 2018, 10, 815. [Google Scholar] [CrossRef]
- Solberg, S.; Astrup, R.; Gobakken, T.; Næsset, E.; Weydahl, D.J. Estimating spruce and pine biomass with interferometric x-band sar. Remote Sens. Environ. 2010, 114, 2353–2360. [Google Scholar] [CrossRef]
- Neumann, M.; Saatchi, S.S.; Ulander, L.M.H.; Fransson, J.E.S. Assessing performance of l- and p-band polarimetric interferometric sar data in estimating boreal forest above-ground biomass. IEEE Trans. Geosci. Remote Sens. 2012, 50, 714–726. [Google Scholar] [CrossRef]
- Lavalle, M.; Hensley, S. Extraction of structural and dynamic properties of forests from polarimetric-interferometric sar data affected by temporal decorrelation. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4752–4767. [Google Scholar] [CrossRef]
- Askne, J.I.H.; Soja, M.J.; Ulander, L.M.H. Biomass estimation in a boreal forest from tandem-x data, lidar dtm, and the interferometric water cloud model. Remote Sens. Environ. 2017, 196, 265–278. [Google Scholar] [CrossRef]
- NOAA. Lidar—Light Detection and Ranging—Is a Remote Sensing Method Used to Examine the Surface of the Earth. Available online: http://oceanservice.noaa.gov/facts/lidar.html (accessed on 4 December 2017).
- Lefsky, M.A.; Cohen, W.B.; Parker, G.G.; Harding, D.J. Lidar remote sensing for ecosystem studies: Lidar, an emerging remote sensing technology that directly measures the three-dimensional distribution of plant canopies, can accurately estimate vegetation structural attributes and should be of particular interest to forest, landscape, and global ecologists. BioScience 2002, 52, 19–30. [Google Scholar]
- Ahmed, R.; Siqueira, P.; Hensley, S. A study of forest biomass estimates from lidar in the northern temperate forests of new england. Remote Sens. Environ. 2013, 130, 121–135. [Google Scholar] [CrossRef]
- Fatoyinbo, T.; Feliciano, A.E.; Lagomasino, D.; Lee, S.K.; Trettin, C. Estimating mangrove aboveground biomass from airborne lidar data: A case study from the zambezi river delta. Environ. Res. Lett. 2018, 13, 025012. [Google Scholar] [CrossRef]
- Lee, S.J.; Kim, J.R.; Choi, Y.S. The extraction of forest co2 storage capacity using high-resolution airborne lidar data. GISci. Remote Sens. 2013, 50, 154–171. [Google Scholar] [CrossRef]
- Unger, D.R.; Hung, I.K.; Brooks, R.; Williams, H. Estimating number of trees, tree height and crown width using lidar data. GISci. Remote Sens. 2014, 51, 227–238. [Google Scholar] [CrossRef]
- Rocha de Souza Pereira, F.; Kampel, M.; Gomes Soares, M.; Estrada, G.; Bentz, C.; Vincent, G. Reducing uncertainty in mapping of mangrove aboveground biomass using airborne discrete return lidar data. Remote Sens. 2018, 10, 637. [Google Scholar] [CrossRef]
- Zolkos, S.G.; Goetz, S.J.; Dubayah, R. A meta-analysis of terrestrial aboveground biomass estimation using lidar remote sensing. Remote Sens. Environ. 2013, 128, 289–298. [Google Scholar] [CrossRef]
- Sibanda, M.; Mutanga, O.; Rouget, M. Comparing the spectral settings of the new generation broad and narrow band sensors in estimating biomass of native grasses grown under different management practices. Giscience Remote Sens. 2016, 53, 614–633. [Google Scholar] [CrossRef]
- Vaglio Laurin, G.; Chen, Q.; Lindsell, J.A.; Coomes, D.A.; Frate, F.D.; Guerriero, L.; Pirotti, F.; Valentini, R. Above ground biomass estimation in an african tropical forest with lidar and hyperspectral data. ISPRS J. Photogramm. Remote Sens. 2014, 89, 49–58. [Google Scholar] [CrossRef]
- Luo, S.; Wang, C.; Xi, X.; Pan, F.; Peng, D.; Zou, J.; Nie, S.; Qin, H. Fusion of airborne lidar data and hyperspectral imagery for aboveground and belowground forest biomass estimation. Ecol. Indic. 2017, 73, 378–387. [Google Scholar] [CrossRef]
- Nguyen, H.; Jung, J.; Lee, J.; Choi, S.-U.; Hong, S.-Y.; Heo, J. Optimal atmospheric correction for above-ground forest biomass estimation with the etm+ remote sensor. Sensors 2015, 15, 18865. [Google Scholar] [CrossRef]
- Lam-Dao, N.; Pham-Bach, V.; Nguyen-Thanh, M.; Pham-Thi, M.-T.; Hoang-Phi, P. Change detection of land use and riverbank in mekong delta, vietnam using time series remotely sensed data. J. Resour. Ecol. 2011, 2, 370–374. [Google Scholar]
- Xu, Q.; Hou, Z.; Tokola, T. Relative radiometric correction of multi-temporal alos avnir-2 data for the estimation of forest attributes. ISPRS J. Photogramm. Remote Sens. 2012, 68, 69–78. [Google Scholar] [CrossRef]
- Pons, X.; Pesquer, L.; Cristóbal, J.; González-Guerrero, O. Automatic and improved radiometric correction of landsat imagery using reference values from modis surface reflectance images. Int. J. Appl. Earth Obs. Geoinf. 2014, 33, 243–254. [Google Scholar] [CrossRef]
- López-Serrano, P.; Corral-Rivas, J.; Díaz-Varela, R.; Álvarez-González, J.; López-Sánchez, C. Evaluation of radiometric and atmospheric correction algorithms for aboveground forest biomass estimation using landsat 5 tm data. Remote Sens. 2016, 8, 369. [Google Scholar]
- Balthazar, V.; Vanacker, V.; Lambin, E.F. Evaluation and parameterization of atcor3 topographic correction method for forest cover mapping in mountain areas. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 436–450. [Google Scholar] [CrossRef]
- Martins, V.; Barbosa, C.; de Carvalho, L.; Jorge, D.; Lobo, F.; Novo, E. Assessment of atmospheric correction methods for sentinel-2 msi images applied to amazon floodplain lakes. Remote Sens. 2017, 9, 322. [Google Scholar] [CrossRef]
- Qiu, F.; Berglund, J.; Jensen, J.R.; Thakkar, P.; Ren, D. Speckle noise reduction in sar imagery using a local adaptive median filter. GISci. Remote Sens. 2004, 41, 244–266. [Google Scholar] [CrossRef]
- Zhong, H.; Li, Y.; Jiao, L. Sar image despeckling using bayesian nonlocal means filter with sigma preselection. IEEE Geosci. Remote Sens. Lett. 2011, 8, 809–813. [Google Scholar] [CrossRef]
- Zhu, H.M.; Zhong, W.Q.; Jiao, L.C. Combination of target detection and block-matching 3d filter for despeckling sar images. Electron. Lett. 2013, 49, 495–497. [Google Scholar] [CrossRef]
- Baier, G.; Rossi, C.; Lachaise, M.; Zhu, X.X.; Bamler, R. Nonlocal insar filtering for high resolution dem generation from tandem-x interferograms. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 103–106. [Google Scholar]
- Yocky, D.A. Multiresolution wavelet decomposition i me merger of landsat thematic mapper and spot panchromatic data. Photogramm. Eng. Remote Sens. 1996, 62, 1067–1074. [Google Scholar]
- Garguet-Duport, B.; Girel, J.; Chassery, J.-M.; Patou, G. The use of multiresolution analysis and wavelets transform for merging spot panchromatic and multispectral image data. Photogramm. Eng. Remote Sens. 1996, 62, 1057–1066. [Google Scholar]
- Shaban, M.; Dikshit, O. Evaluation of the merging of spot multispectral and panchromatic data for classification of an urban environment. Int. J. Remote Sens. 2002, 23, 249–262. [Google Scholar] [CrossRef]
- Basuki, T.M.; Skidmore, A.K.; Hussin, Y.A.; Van Duren, I. Estimating tropical forest biomass more accurately by integrating alos palsar and landsat-7 etm+ data. Int. J. Remote Sens. 2013, 34, 4871–4888. [Google Scholar] [CrossRef]
- Vafaei, S.; Soosani, J.; Adeli, K.; Fadaei, H.; Naghavi, H.; Pham, T.D.; Tien Bui, D. Improving accuracy estimation of forest aboveground biomass based on incorporation of alos-2 palsar-2 and sentinel-2a imagery and machine learning: A case study of the hyrcanian forest area (iran). Remote Sens. 2018, 10, 172. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).