3.1. Excess Emissivity Due to Wind
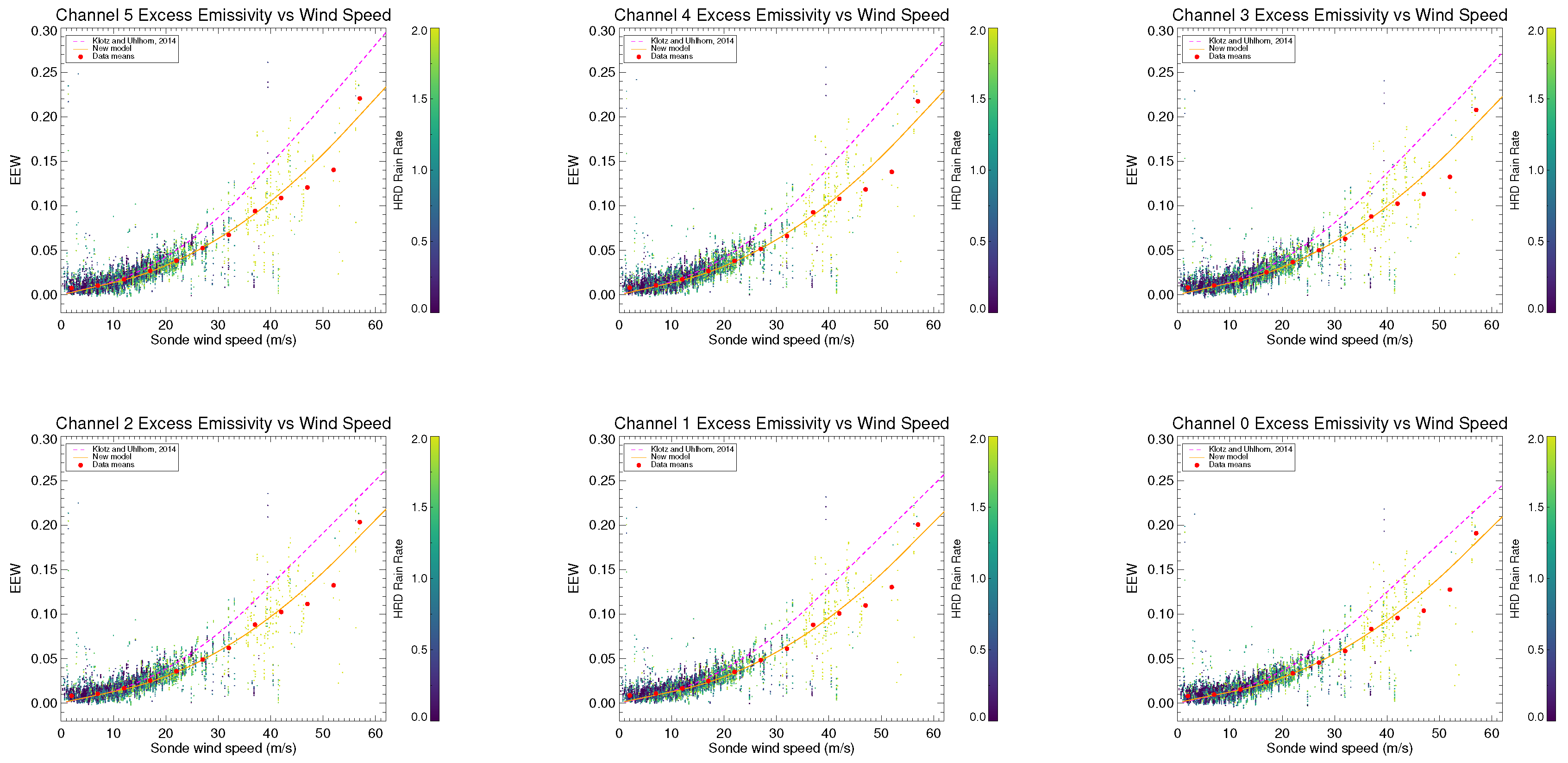
Figure 3 shows a scatter plot of SFMR channel 5 (highest frequency) EEW (
) as a function of dropsonde wind speed. Each point is colored according to its corresponding HRD rain rate. The solid line is the model developed from a straightforward application of the above methodology from the wind-speed-binned averages, and the dashed line is the current operational model from [
8]. Since different dropsondes and slightly different filtering criteria are used, some small differences between the two can be expected. However, the new model shown is not sufficient to correct the observed wind-speed bias shown later in Figure 5.
The EEW estimates show a small trend with HRD-retrieved rain rate. EEW was estimated assuming no atmospheric effects and total ocean emissivity was assumed to only be affected by SST, salinity, and wind speed (e.g., not affected by rain) for the SFMR polarization, frequencies, and low incidence angles. This effect is therefore an unaccounted source of Tb that remains in the estimate.
The most likely source is in the atmosphere: either the rain-free assumption does not apply, or the simple atmospheric models are not sufficiently detailed or capable of resolving minute T
b changes. Though it has long been understood that the low SFMR rain-rate retrievals (
mm
−1 [
16] or, more recently,
mm
−1 [
8]) are nearing the low end of the sensitivity capabilities of the SFMR, the SFMR retrieval algorithm still reports them. This suggests that there is some information contained in the low rain rate retrievals, but it may not be rain rate. Regardless, if this excess T
b is not removed then it is included in the EEW estimate, inflating what is assumed to be emissivity solely from wind effects.
It could be argued that the observed trend is in reality a wind-speed dependence that was erroneously retrieved as rain rate. If that were the case, we would expect to see a trend with dropsonde wind speed introduced into the retrievals using the EEW model developed from this methodology. As we show later in Figure 5, there are no systematic biases introduced by this revision. In fact, the existing trend with wind speed is eliminated and errors present in rain are largely reduced.
The resulting EEW GMFs as functions of 10
equivalent-neutral wind speed are shown as the solid lines passing through the filled circles (means) in
Figure 4. To obtain the GMFs, EEW data is grouped into 5
−1-wide bins. The channel 5 means are fit to the coefficients in (
5) using a Levenberg-Marquardt least-squares technique. Since there are few samples at high winds, the slope for channel 5 at 37
−1 (the previous
from (
5)) is retained from the current model. The 2014 SFMR GMFs are also shown for reference. At the lower end of the wind-speed range, the dropsonde error is close to the measured wind speed and SFMR is not capable of reliably sensing these wind speeds. As a result, we only use data above 10
−1 that have a significant number of points to generate the GMFs for (
6) and the quadratic and high-wind linear portions of (
5).
The wind-generated foam to which the SFMR is primarily sensitive does not exist below approximately 7
−1, the traditional transition point of the SFMR GMF from a linear function to a quadratic. In this manuscript the transition point was chosen such that the slope of the frequency-independent quadratic function matches a line that intercepts the origin. As a result, the slope of the linear portion was also allowed to vary. Referring to (
5), this condition requires
The
coefficient is derived from
,
,
, and
to make a line from the origin meet the quadratic at
. The values for
–
are given in
Table 3.
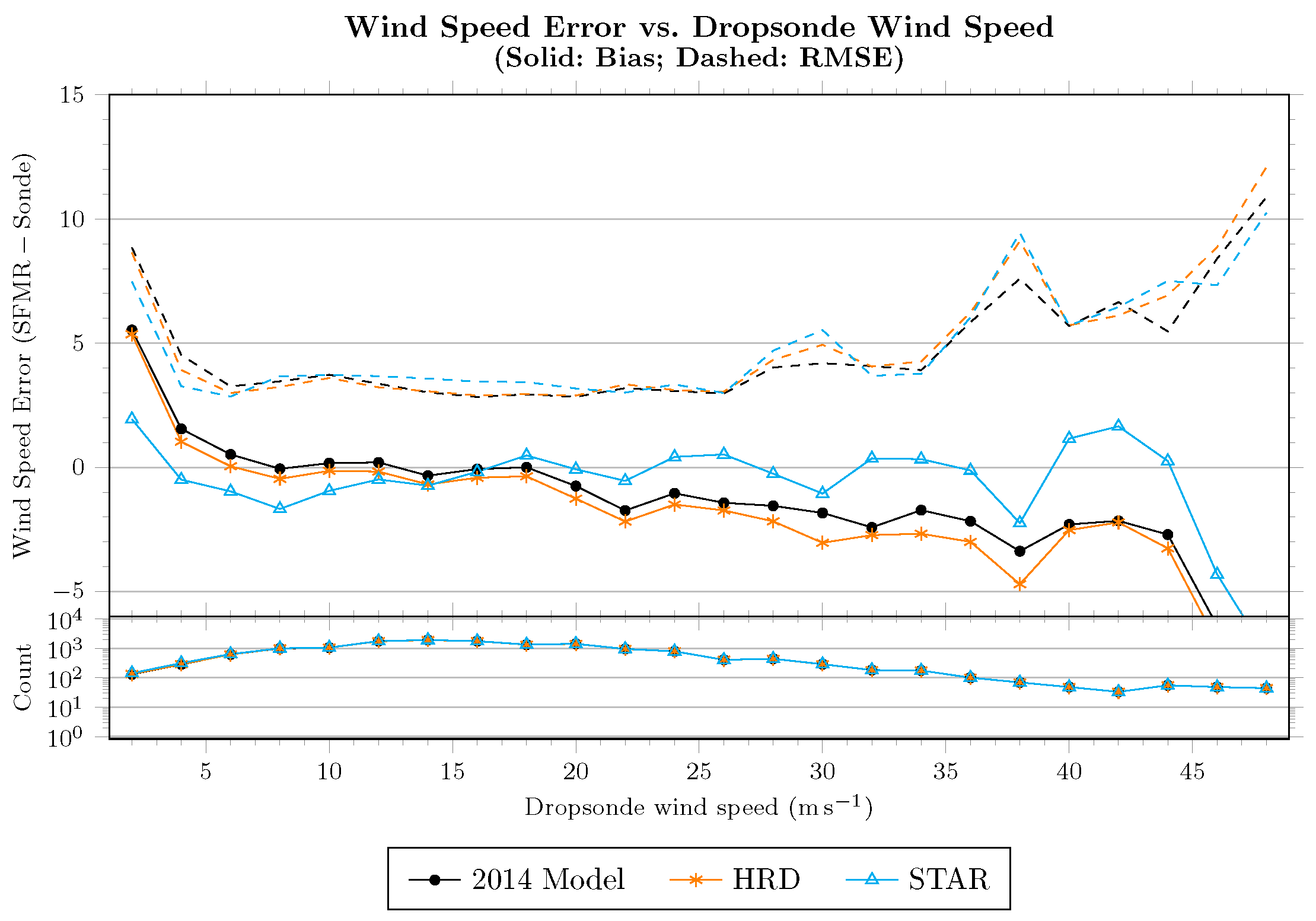
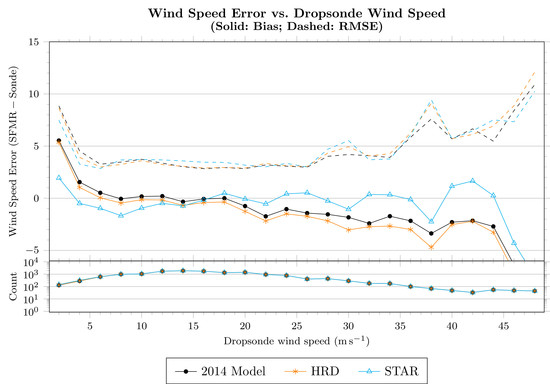
Figure 5 shows the wind-speed error as a function of dropsonde surface wind speed estimate, where error is defined as the SFMR retrieval less the dropsonde-estimated
. Retrievals using the model developed in this section (and, necessarily, the model from
Section 2.4) are shown as empty blue triangles. Compared to both the retrievals performed by the authors with the 2014 models and the HRD retrievals (both of which have nearly the same characteristics), the mean error above 20
−1 is reduced while maintaining or improving the RMS error.
Figure 6 shows these HRD (left panel) and STAR (right panel) retrievals versus dropsonde surface wind speed as two-dimensional histograms. The number of points within each 1 by 1
−1 bin is averaged and shown as a color. Histograms for each axis are shown on the outside of the corresponding axis. The mean value of each ordinate is calculated from the points within each 1
−1 dropsonde bin and is shown as a solid orange line. Both show a general trend of the 2014 model (implemented by HRD here) to underestimate the dropsonde surface wind speed and that the STAR model better matches the dropsondes.
3.2. Rain
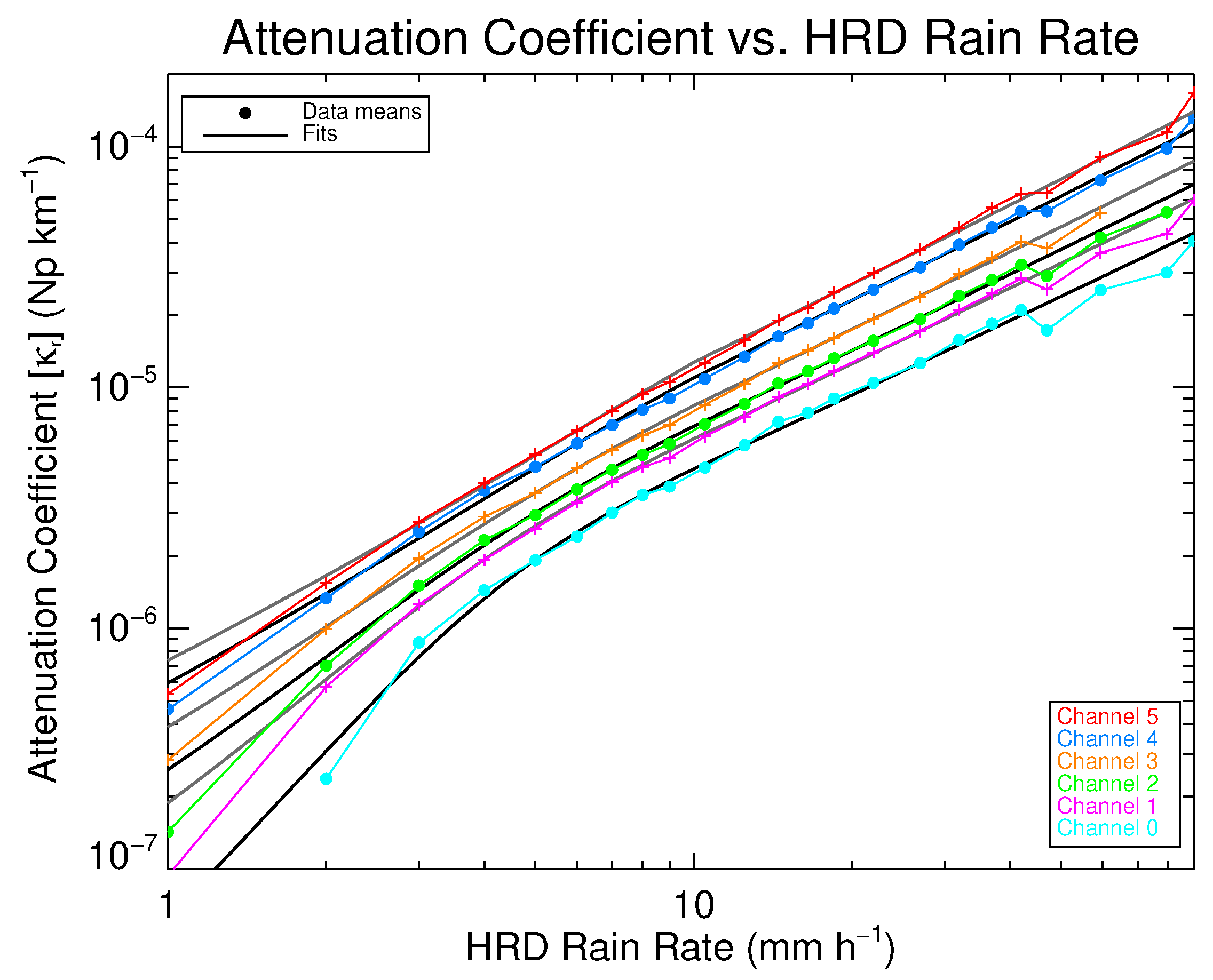
Figure 7 shows the estimated
from SFMR data as a function of the HRD rain-rate retrieval on a log-log plot. The solid lines are the fits to the data for each frequency (increasing in value with frequency) and the filled circles are the binned
averages. Immediately noticeable is the downward curve below 3 mm
−1, due to a lower sensitivity of the lower channels to rain at low rain rates and thus a higher variance of
. Though [
8] provided a significant validation of higher rain-rate retrievals, the precision of rain-rate retrievals from SFMR at and below 3 mm
−1 should not be relied upon. The values of the absorption coefficients given in (
8) are listed in
Table 4.
Even though the precision may be lacking, a separate curve was fitted below 10 mm
−1 to avoid overestimating and to improve matching of STAR retrievals to those from HRD at low rain rates. The rain-absorption model used for rain rates below 10 mm
−1 in the STAR retrievals (
) is
where
is from (
8) and the coefficients are listed in
Table 4 and
Table 5.
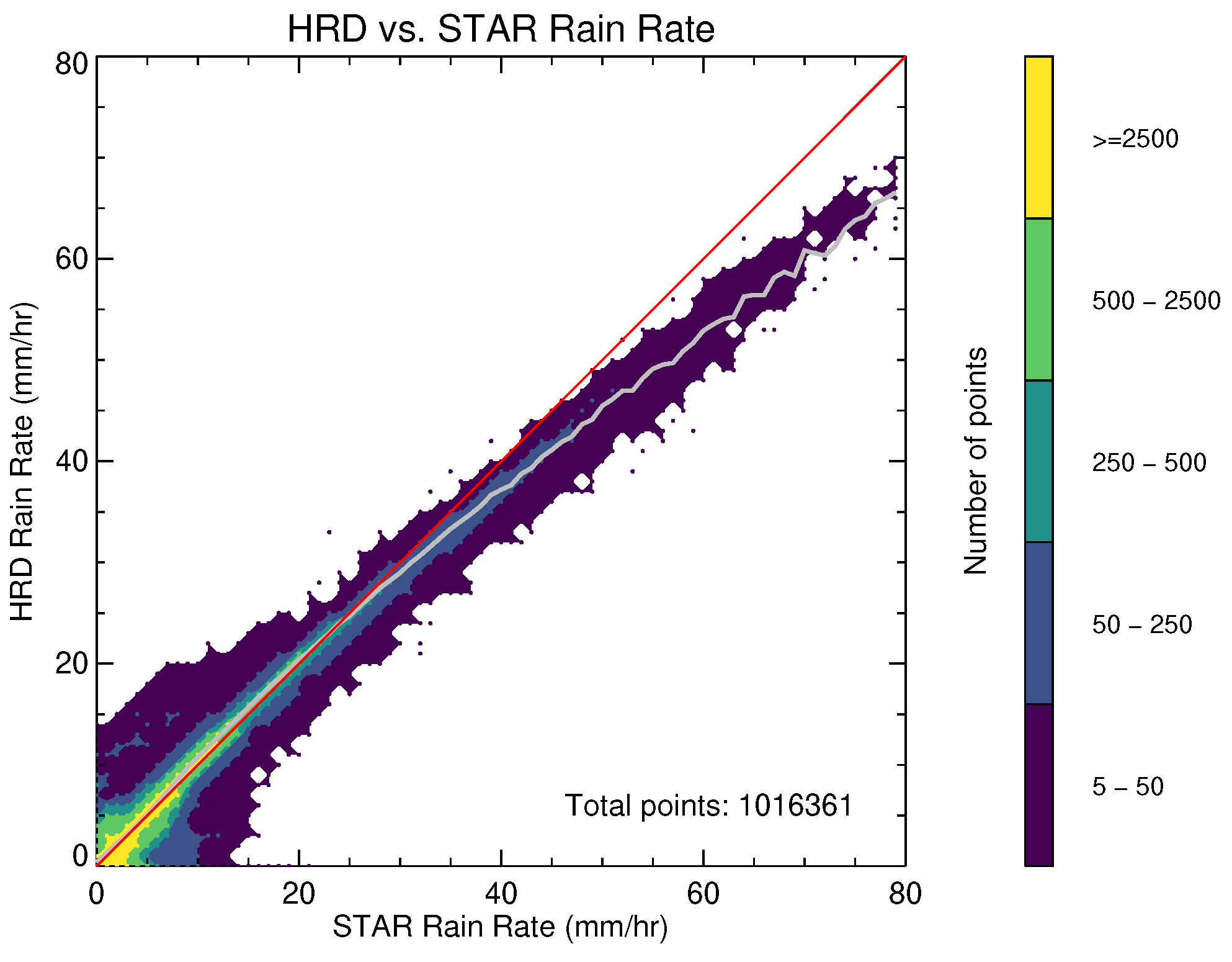
One method of verifying that the newly retrieved rain rates are comparable to the HRD-retrieved rain rates is to use a two-dimensional histogram, shown in
Figure 8. The data is colored by number of points in each 1 mm
−1 square, and most of the data is in the low rain rate bins. The new model generally produces the same results. Below 25 mm
−1, the STAR retrieval algorithm produces slightly lower rain rates than the HRD retrieval algorithm, and above 25 mm
−1 STAR produces higher rain rates. The largest discrepancies are at rain rates above 40 mm
−1, where there were few validation data used during development of the 2014 model (less than 10% of the data shown in g 8 of [
8]).
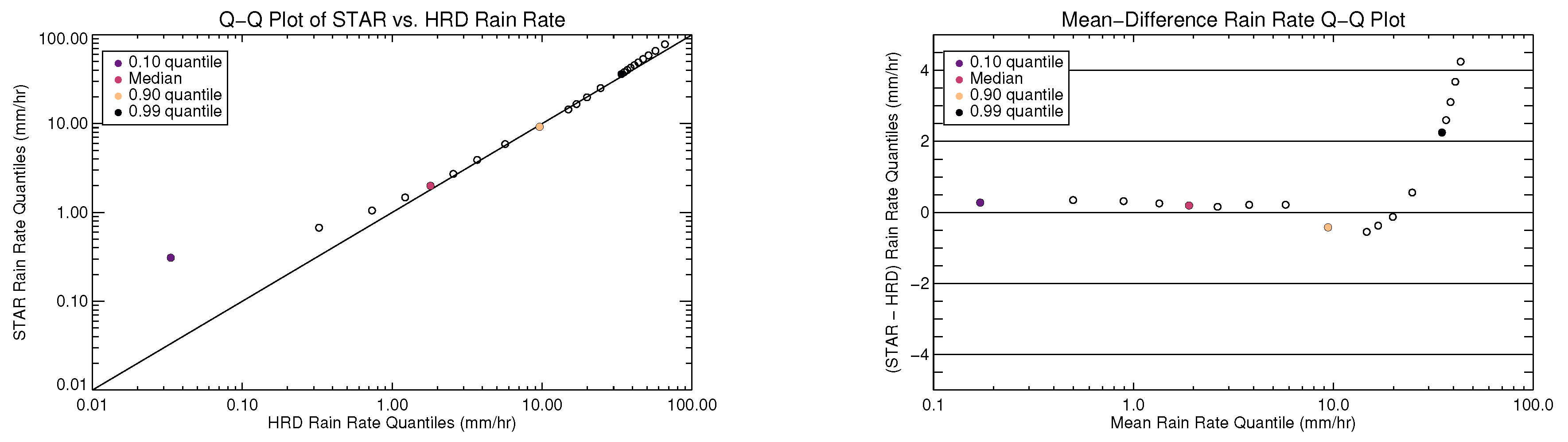
Two other methods of confirming the validity of the new model are shown in
Figure 9: a quantile-quantile plot and a mean-difference plot of the quantiles. This is a way of evaluating the overall statistics rather than comparing retrievals from the same scene. All collocated scenes presented in
Figure 8 were used to generate quantiles for each data set. The deciles are shown starting at 10%, as well as quantiles from 95 to 99% in 1% steps and 99 to 99.9% in 0.1% steps. The mean-difference plot shows the difference between the quantiles of the two datasets as a function of the means of each quantile pair. For example, the 10% quantile is plotted between 0.1 and 0.2 mm
−1 on the horizontal axis because the HRD value is approximately 0.03 and the value for the STAR retrievals is approximately 0.3.
These plots show that for the lowest 80% of the data (
mm
−1), the new retrievals are higher than the HRD retrievals by less than
mm
−1. This is the same behavior as when the model from [
8] is implemented and compared against the HRD retrievals in the same way (e.g., the “2014 model” shown in
Figure 5). For the lowest 98% of the data (
mm
−1), the new retrievals are different from the HRD retrievals by at most 2 mm
−1. Up to 40 mm
−1, the STAR retrievals are up to 4 mm
−1 (< 10%) higher than HRD. Though there are some differences in the output of the two retrieval algorithms, the differences are small (
mm
−1) in the regime where there are the most data. The rain rates output by the new model still represent the physical scene as well as SFMR can measure given its spatial and temporal footprint.
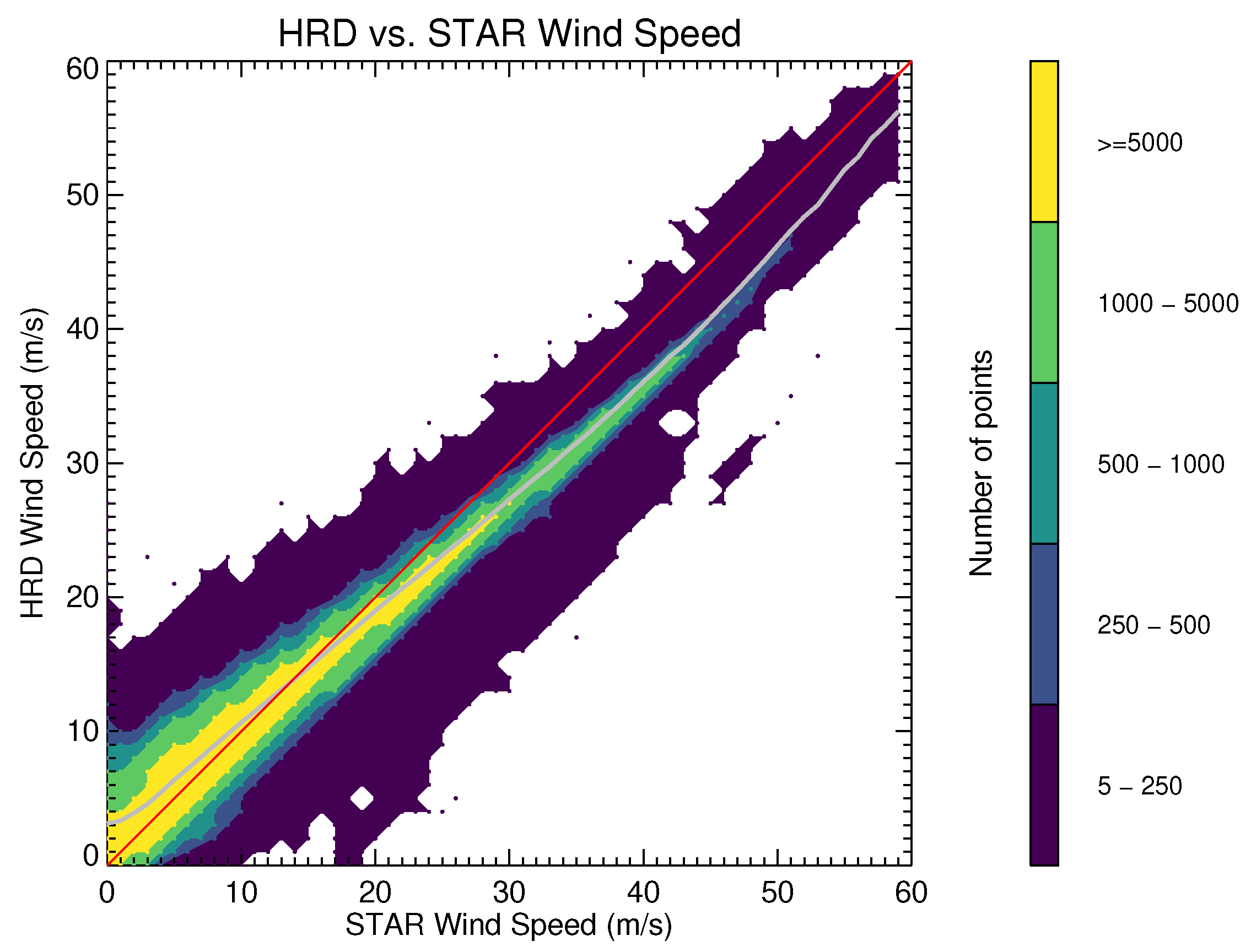
Figure 10 shows a comparison two-dimensional histogram between all collocated HRD and STAR wind-speed retrievals. A solid gray line shows the mean HRD wind speed for each wind speed retrieved by the new model. Above 15
−1 the STAR-model-retrieved wind speeds tend to exceed those retrieved by HRD. The maximum difference in the mean between the two is approximately 5
−1, which occurs at the highest wind speeds shown.
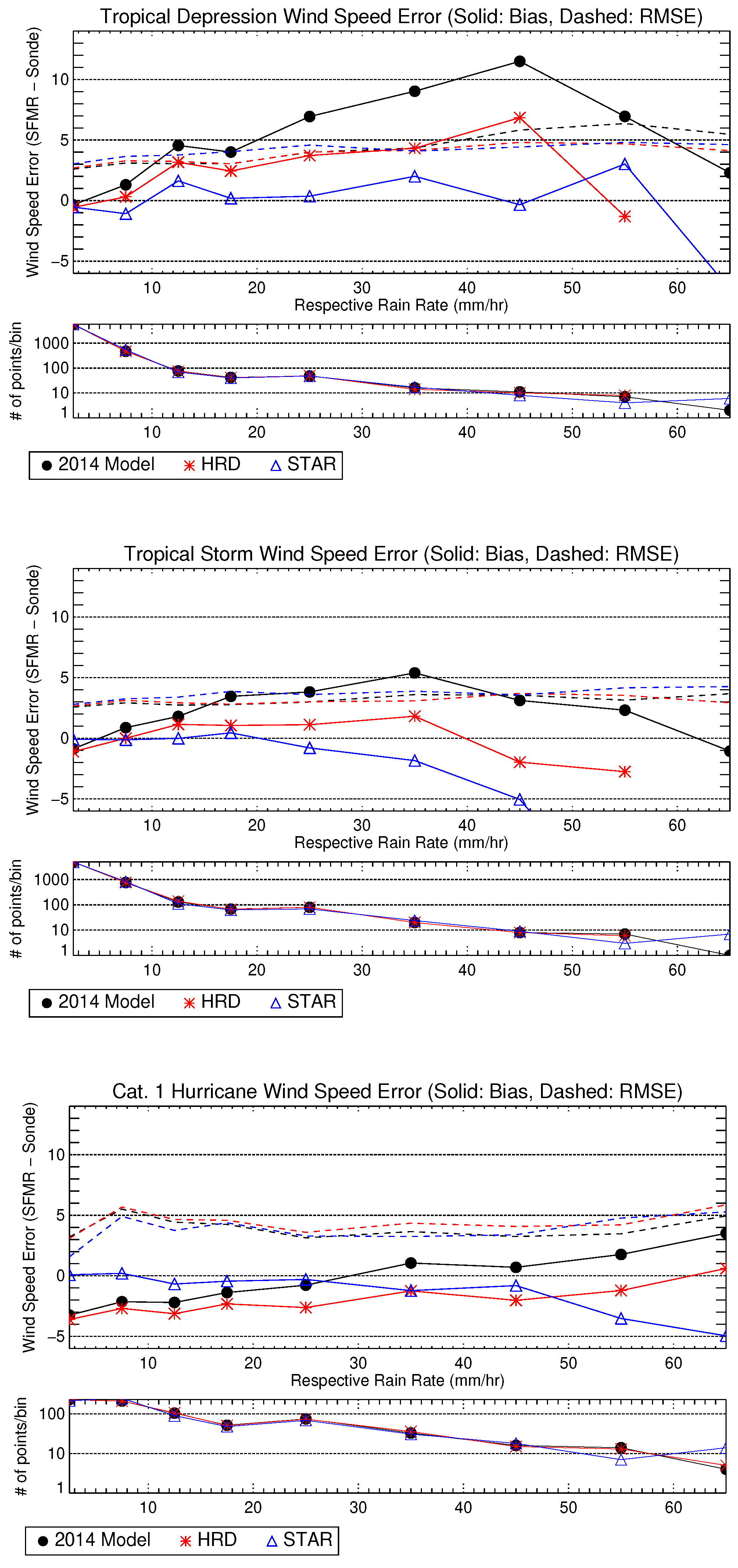
Figure 11 shows a comparison similar to the one at the end of [
8] (i.e., Figure 14). There is a different selection of data used here, so some differences can be expected. The plots show wind-speed error (SFMR minus dropsonde
) versus the rain rate retrieved by each of three algorithms: the “2014 model” described in [
8], HRD, and STAR. The latter two have some additional filtering implemented beyond what is described in [
8].
These figures suggest that rain above 10 mm
−1 do not necessarily indicate a high bias, sometimes called “rain contamination”, in the wind-speed retrievals. However, unlike [
8], very little bias in the mean is found below approximately 45 mm
−1 in tropical storm conditions for either the HRD or STAR retrievals—though the retrievals performed by the authors just using the 2014 model more closely resemble their results. This suggests a rain-rate-dependent wind-speed correction is being applied to the HRD retrievals.
In “Category 1” hurricane conditions the HRD algorithm is generally biased low compared to dropsondes, but the STAR algorithm shows no wind-speed bias for rain rates up to at least 45 mm −1. An important feature of the STAR retrievals is the lack of bias at rain rates below this threshold, which shows that rain does not necessarily contaminate SFMR wind-speed retrievals. Additionally, the RMS error for the STAR retrievals is lower than that of HRD up to 45 mm −1, which is a reversal from the lower-wind observations. As a result of these data, we consider wind-speed retrievals questionable where the rain rate is at least 45 mm −1.
In tropical storm conditions, there is no mean bias in the STAR algorithm below 45 mm −1. Surprisingly, there is not as significant rain influence on wind-speed retrievals in low-wind (“Tropical Depression”) scenarios, though we would caution against using any SFMR wind-speed retrievals in this wind-speed regime. As a general rule, we suggest that the precision of wind-speed retrievals below 15 −1 should not be relied upon.
There is slightly more spread in the STAR retrievals (RMS errors) in the two lower-wind regimes compared to those from HRD. This is likely due to the differences in smoothing or filtering of the retrieval algorithms. The STAR filtering criteria were chosen to retain high-wind gradients while reducing geophysical and system noise and thus can be expected to exhibit more scatter at all wind speeds.
Table 6,
Table 7 and
Table 8 show means, standard deviations, and number of samples of SFMR errors (versus dropsondes) within selected wind-speed and rain-rate bins. As shown on the above plots, the STAR mean errors are generally closer to 0 than those from HRD except in the highest rain-rate group (
mm
−1). The increased spread of the STAR retrievals is evident in that the standard deviations are slightly higher in all regimes.