Comparison of Two Synergy Approaches for Hybrid Cropland Mapping
Abstract
1. Introduction
2. Principles of the two synergy methods
2.1. Geographical Weighted Regression
2.2. Modified Fuzzy Agreement Scoring
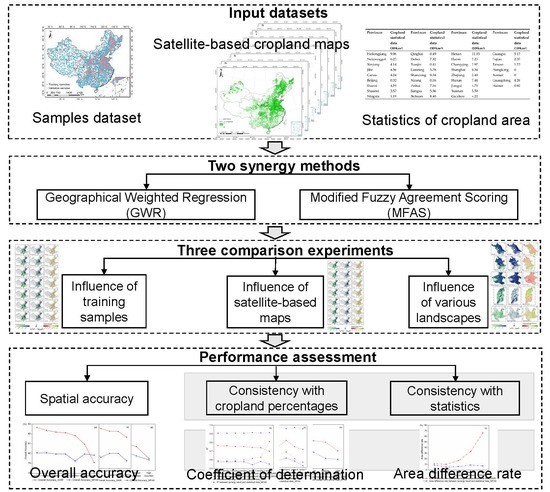
3. Data and Experiment Design
3.1. Data and processing
3.2. Experiment Description
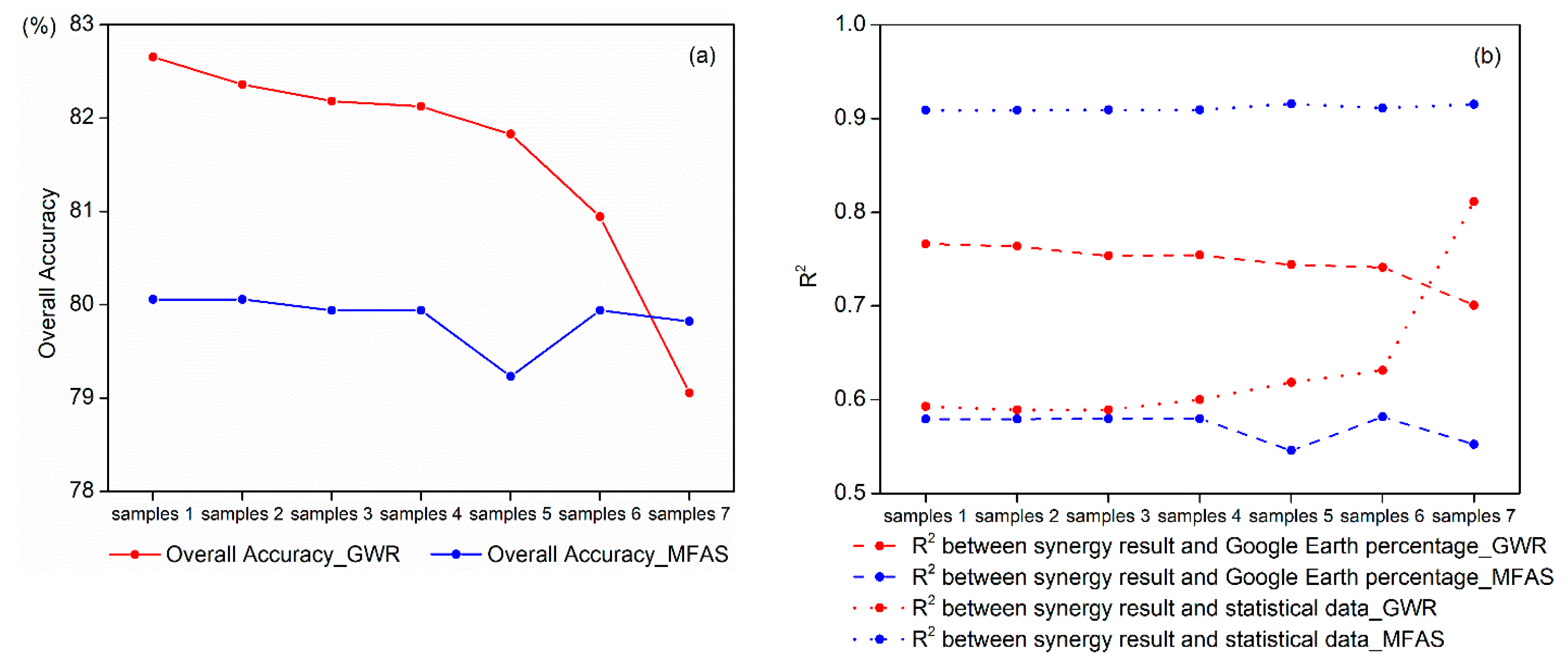
3.2.1. Synergy Cropland Mapping with Various Training Sample Sizes
3.2.2. Synergy Cropland Mapping with Different Satellite-Based Maps
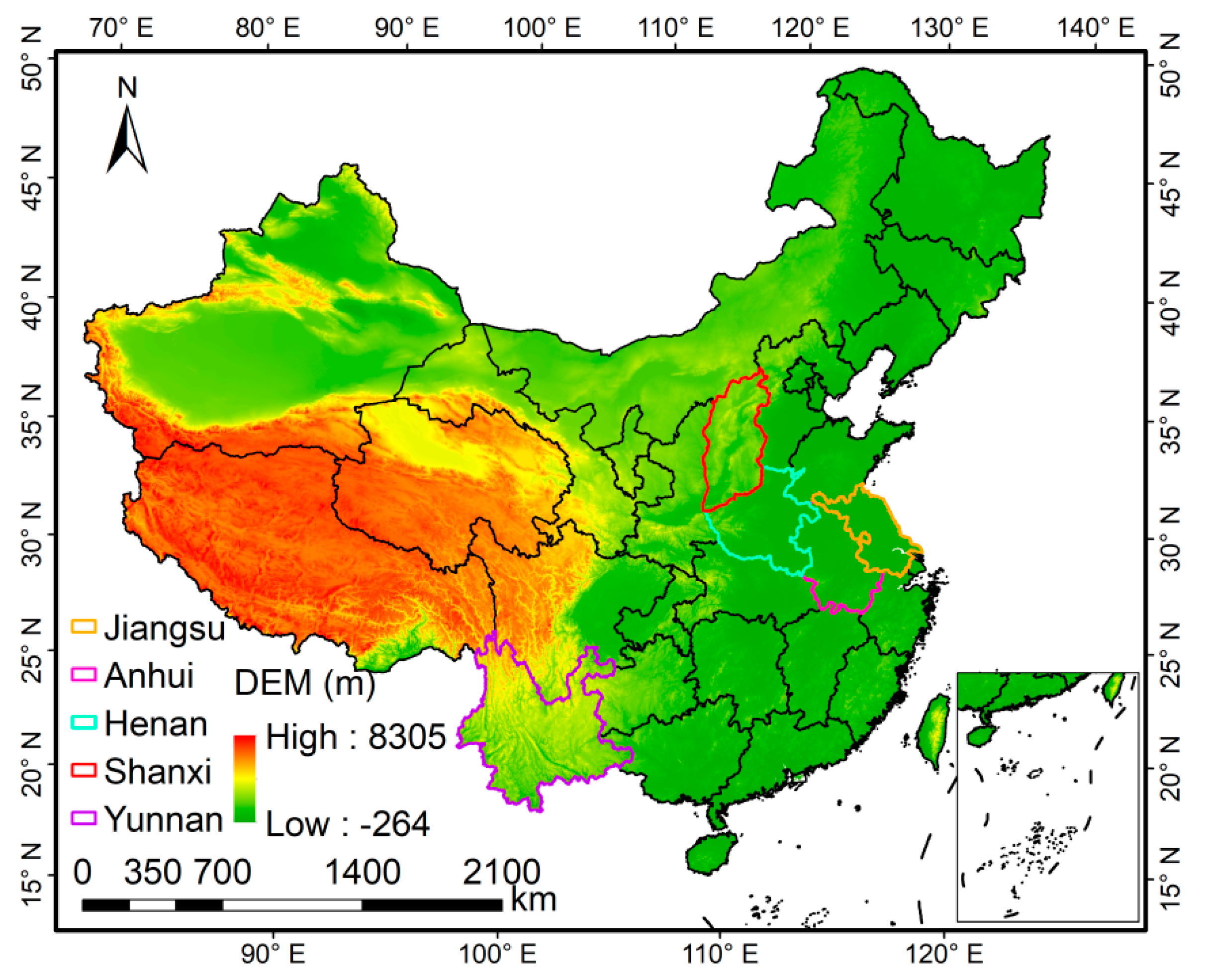
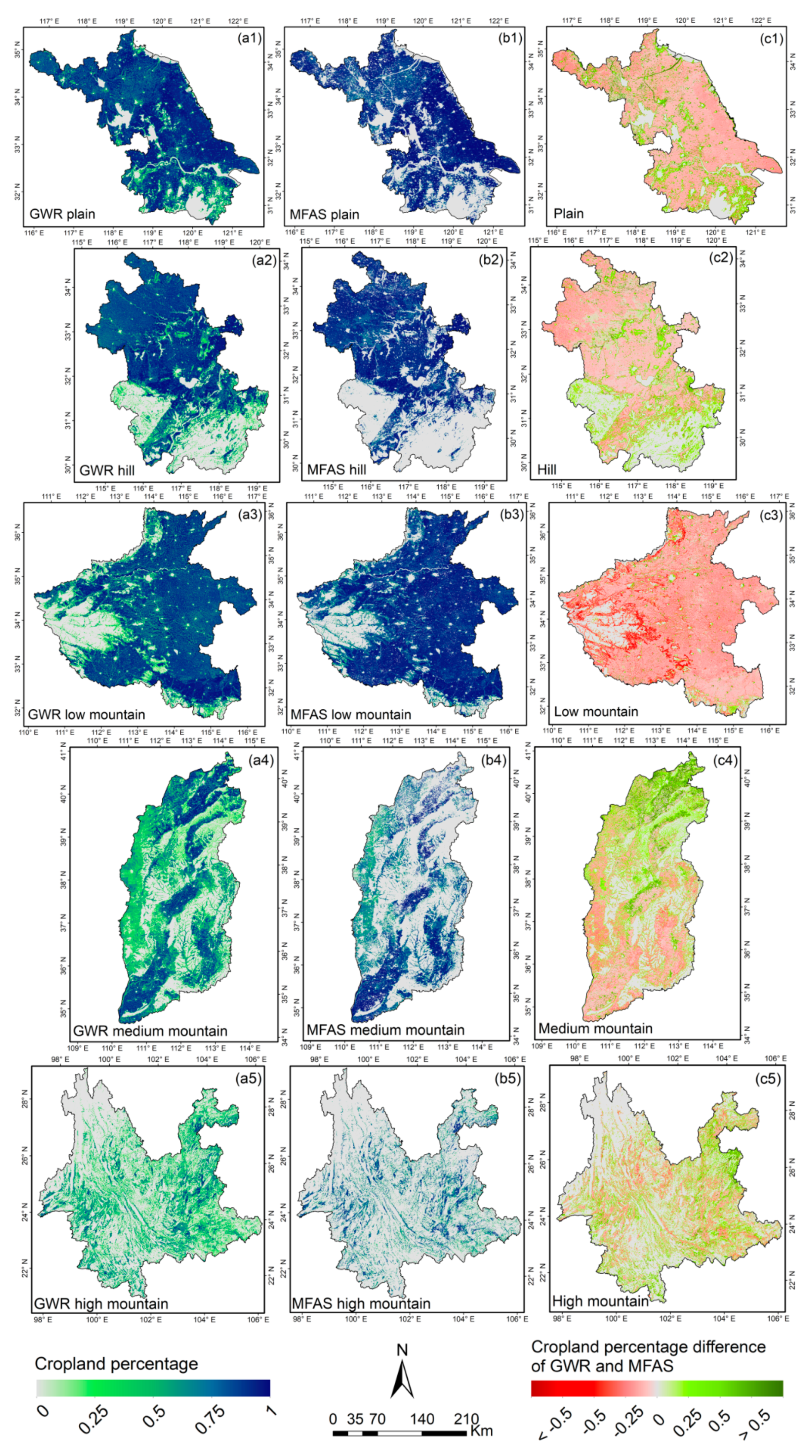
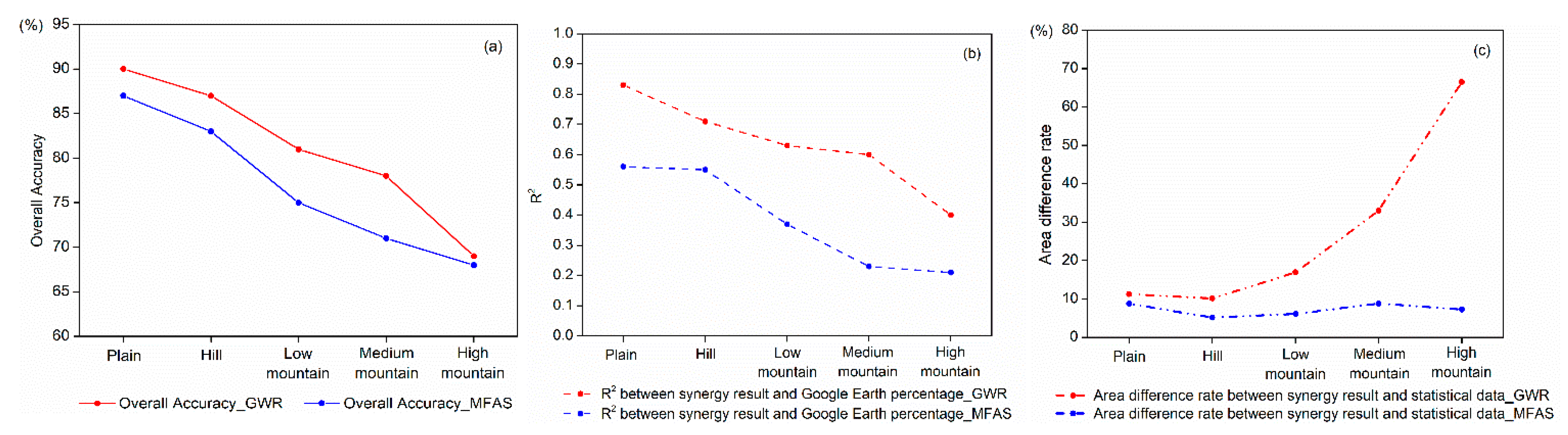
3.2.3. Synergy Cropland Mapping with Various Landscapes
3.3. Performance Assessment
4. Results
4.1. Influence of Training Samples
4.2. Influence of Satellite-Based Maps
4.3. Influence of Various Landscapes
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Foley, J.A.; Ramankutty, N.; Brauman, K.A.; Cassidy, E.S.; Gerber, J.S.; Johnston, M.; Mueller, N.D.; O’Connell, C.; Ray, D.K.; West, P.C.; et al. Solutions for a cultivated planet. Nature 2011, 478, 337–342. [Google Scholar] [CrossRef] [PubMed]
- Kearney, J. Food consumption trends and drivers. Philos. Trans. R. Soc. B 2010, 365, 2793–2807. [Google Scholar] [CrossRef] [PubMed]
- Godfray, H.; Beddington, J.; Crute, I.; Haddad, L.; Lawrence, D.; Muir, J.; Pretty, J.; Robinson, S.; Thomas, S.; Toulmin, C. Food security: The challenge of feeding 9 billion people. Science 2010, 327, 812–818. [Google Scholar] [CrossRef] [PubMed]
- Fritz, S.; See, L.; Mccallum, I.; You, L.; Bun, A.; Moltchanova, E.; Duerauer, M.; Albrecht, F.; Schill, C.; Perger, C.; et al. Mapping global cropland and field size. Glob. Chang. Biol. 2015, 21, 1980–1992. [Google Scholar] [CrossRef]
- Lu, M.; Wu, W.; You, L.; Chen, D.; Zhang, L.; Yang, P.; Tang, H. A synergy cropland of china by fusing multiple existing maps and statistics. Sensors 2017, 17, 1613. [Google Scholar] [CrossRef] [PubMed]
- Stansfield, J. The United Nations sustainable development goals (SDGs): A framework for intersectoral collaboration. Whanake Pac. J. Community Dev. 2017, 3, 38–49. [Google Scholar]
- Bartholome, E.; Belward, A.S. GLC2000: A new approach to global land cover mapping from earth observation data. Int. J. Remote Sens. 2005, 26, 1959–1977. [Google Scholar] [CrossRef]
- Hansen, M.; Defries, R.; Townshend, J.; Sohlberg, R. Global land cover classification at 1 km spatial resolution using a classification tree approach. Int. J. Remote Sens. 2000, 21, 1331–1364. [Google Scholar] [CrossRef]
- Friedl, M.; Sulla-Menashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.; Huang, X. MODIS collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ. 2010, 114, 168–182. [Google Scholar] [CrossRef]
- Pittman, K.; Hansen, M.; Beckerreshef, I.; Potapov, P.; Justice, C. Estimating global cropland extent with multi-year MODIS data. Remote Sens. 2010, 2, 1844–1863. [Google Scholar] [CrossRef]
- Chen, J.; Chen, J.; Liao, A.; Cao, X.; Chen, L.; Chen, X.; Peng, S.; Han, G.; Zhang, H.; He, C.; et al. Concepts and key techniques for 30 m global land cover mapping. Acta Geod. Cartogr. Sinica 2014, 43, 551–557. (In Chinese) [Google Scholar]
- Wu, W.; Shibasaki, R.; Yang, P.; Zhou, Q.; Tang, H. Remotely sensed estimation of cropland in China: A comparison of the maps derived from four global land cover datasets. Can. J. Remote Sens. 2008, 34, 467–479. [Google Scholar] [CrossRef]
- Lu, M.; Wu, W.; Zhang, L.; Liao, A.; Peng, S.; Tang, H. A comparative analysis of five global cropland datasets in China. Sci. China Earth Sci. 2016, 59, 2307–2317. [Google Scholar] [CrossRef]
- Congalton, R.; Gu, J.; Yadav, K.; Ozdogan, M. Global land cover mapping: A review and uncertainty analysis. Remote Sens. 2014, 6, 12070–12093. [Google Scholar] [CrossRef]
- Yu, L.; Wang, J.; Clinton, N.; Xin, Q.; Zhong, L.; Chen, Y.; Gong, P. FROM-GC: 30 m global cropland extent derived through multisource data integration. Int. J. Digit. Earth 2013, 6, 521–533. [Google Scholar] [CrossRef]
- Liang, L.; Gong, P. Evaluation of global land cover maps for cropland area estimation in the conterminous United States. Int. J. Digit. Earth 2015, 8, 102–117. [Google Scholar] [CrossRef]
- Castanedo, F. A review of data fusion techniques. Sci. World J. 2013, 2013, 704504. [Google Scholar] [CrossRef]
- See, L.; Schepaschenko, D.; Lesiv, M.; McCallum, I.; Fritz, S.; Comber, A.; Perger, C.; Schill, C.; Zhao, Y.; Maus, V.; et al. Building a hybrid land cover map with crowdsourcing and geographically weighted regression. ISPRS J. Photogramm. Remote Sens. 2015, 103, 48–56. [Google Scholar] [CrossRef]
- Verburg, P.; Neumann, K.; Nol, L. Challenges in using land use and land cover data for global change studies. Glob. Chang. Biol. 2011, 17, 974–989. [Google Scholar] [CrossRef]
- Schepaschenko, D.; See, L.; Lesiv, M.; Mccallum, I.; Fritz, S.; Salk, C.; Moltchanova, E.; Perger, C.; Shchepashchenko, M.; Shvidenko, A.; et al. Development of a global hybrid forest mask through the synergy of remote sensing, crowdsourcing and FAO statistics. Remote Sens. Environ. 2015, 162, 208–220. [Google Scholar] [CrossRef]
- Chen, D.; WU, W.; Lu, M.; Hu, Q.; Zhou, Q. Progresses in land cover data reconstruction method based on multi-source data fusion. Chin. J. Agric. Resour. Reg. Plan. 2016, 37, 62–70. (In Chinese) [Google Scholar]
- Kinoshita, T.; Iwao, K.; Yamagata, Y. Creation of a global land cover and a probability map through a new map integration method. Int. J. Appl. Earth Obs. Geoinf. 2014, 28, 70–77. [Google Scholar] [CrossRef]
- Jung, M.; Henkel, K.; Herold, M.; Churkina, G. Exploiting synergies of global land cover products for carbon cycle modeling. Remote Sens. Environ. 2006, 101, 534–553. [Google Scholar] [CrossRef]
- Clinton, N.; Yu, L.; Gong, P. Geographic stacking: Decision fusion to increase global land cover map accuracy. Glob. Land Cover Mapp. Monit. 2015, 103, 57–65. [Google Scholar] [CrossRef]
- Lesiv, M.; Moltchanova, E.; Schepaschenko, D.; See, L.; Shvidenko, A.; Comber, A.; Fritz, S. Comparison of data fusion methods using crowdsourced data in creating a hybrid forest cover map. Remote Sens. 2016, 8, 261. [Google Scholar] [CrossRef]
- Fritz, S.; McCallum, I.; Schill, C.; Perger, C.; Grillmayer, R.; Achard, F.; Kraxner, F.; Obersteiner, M. Geo-wiki.org: The use of crowdsourcing to improve global land cover. Remote Sens. 2009, 1, 345–354. [Google Scholar] [CrossRef]
- Fritz, S.; McCallum, I.; Schill, C.; Perger, C.; See, L.; Schepaschenko, D.; van der Velde, M.; Kraxner, F.; Obersteiner, M. Geo-wiki: An online platform for improving global land cover. Environ. Model. Softw. 2012, 31, 110–123. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Charlton, M.E.; Brunsdon, C. Geographically weighted regression: A natural evolution of the expansion method for spatial data analysis. Environ. Plan. A 1998, 30, 1905–1927. [Google Scholar] [CrossRef]
- Fritz, S.; You, L.; Bun, A.; See, L.; Mccallum, I.; Schill, C.; Perger, C.; Liu, J.; Hansen, M.; Obersteiner, M. Cropland for sub-saharan Africa: A synergistic approach using five land cover data sets. Geophys. Res. Lett. 2011, 38, 155–170. [Google Scholar] [CrossRef]
- Chen, J.; Chen, J.; Liao, A.; Cao, X.; Chen, L.; Chen, X.; He, C.; Han, G.; Peng, S.; Lu, M.; et al. Global land cover mapping at 30 m resolution: A POK-based operational approach. ISPRS J. Photogramm. Remote Sens. 2015, 103, 7–27. [Google Scholar] [CrossRef]
- Defourny, P.; Kirches, G.; Brockmann, C.; Boettcher, M.; Peters, M.; Bontemps, S.; Lamarche, C.; Schlerf, M.; Santoro, M. Land Cover CCI: Product User Guide Version 2. Available online: http://maps.elie.ucl.ac.be/CCI/viewer/download/ESACCI-LC-PUG-v2.5.pdf (accessed on 8 February 2018).
- Bontemps, S.; Defourny, P.; Bogaert, E.; Arino, O.; Kalogirou, V.; Perez, J. GLOBCOVER 2009. Products Description and Validation Report. Available online: https://core.ac.uk/download/pdf/11773712.pdf (accessed on 8 February 2018).
- Waldner, F.; Fritz, S.; Di Gregorio, A.; Defourny, P. Mapping priorities to focus cropland mapping activities: Fitness assessment of existing global, regional and national cropland maps. Remote Sens. 2015, 7, 7959–7986. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, X.; Zhao, X.; Liu, B.; Yi, L.; Zuo, L.; Wen, Q.; Liu, F.; Xu, J.; Hu, S. A 2010 update of National land use/cover database of China at 1: 100000 scale using medium spatial resolution satellite images. Remote Sens. Environ. 2014, 149, 142–154. [Google Scholar] [CrossRef]
- Ning, J.; Liu, J.; Kuang, W.; Xu, X.; Zhang, S.; Yan, C.; Li, R.; Wu, S.; Hu, Y.; Du, G.; et al. Spatiotemporal patterns and characteristics of land-use change in China during 2010–2015. J. Geogr. Sci. 2018, 28, 547–562. [Google Scholar] [CrossRef]
- Gong, P.; Wang, J.; Yu, L.; Zhao, Y.; Zhao, Y.; Liang, L.; Niu, Z.; Huang, X.; Fu, H.; Liu, S.; et al. Finer resolution observation and monitoring of GLC: First mapping results with Landsat TM and ETM+ data. Int. J. Remote Sens. 2013, 34, 2607–2654. [Google Scholar] [CrossRef]
- Xiong, J.; Thenkabail, P.; Gumma, M.; Teluguntla, P.; Poehnelt, J.; Congalton, R.; Yadav, K.; Thau, D. Automated cropland mapping of continental Africa using Google Earth engine cloud computing. ISPRS. J. Photogramm. 2017, 126, 225–244. [Google Scholar] [CrossRef]
- Chai, Z. The Suggestion of Using Relative Altitude to Divide the Geomorphologic Forms. In Geographical Society of China. Theses of Geomorphology; Science Press: Beijing, China, 1983; pp. 90–97. (In Chinese) [Google Scholar]
- Pontius, R.G.; Millones, M. Death to Kappa: Birth of quantity disagreement and allocation disagreement for accuracy assessment. Int. J. Remote Sens. 2011, 32, 4407–4429. [Google Scholar] [CrossRef]
- Schepaschenko, D.; Shvidenko, A.; Lesiv, M.; Ontikov, P.; Shchepashchenko, M.V.; Kraxner, F. Estimation of forest area and its dynamics in Russia based on synthesis of remote sensing products. Contemp. Probl. Ecol. 2015, 8, 811–817. [Google Scholar] [CrossRef]
- Zhong, L.; Gong, P.; Biging, G.S. Efficient corn and soybean mapping with temporal extendability: A multi-year experiment using Landsat imagery. Remote Sens. Environ. 2014, 140, 1–13. [Google Scholar] [CrossRef]
- Hu, Q.; Ma, Y.; Xu, B.; Song, Q.; Tang, H.; Wu, W. Estimating sub-pixel soybean fraction from time-series modis data using an optimized geographically weighted regression model. Remote Sens. 2018, 10, 491. [Google Scholar] [CrossRef]
- Pérez-Hoyos, A.; García-Haro, F.; San-Miguel-Ayanz, J. A methodology to generate a synergetic land-cover map by fusion of different land-cover products. Int. J. Appl. Earth Obs. Geoinf. 2012, 19, 72–87. [Google Scholar] [CrossRef]
- Chen, D.; Yu, Q.; Hu, Q.; Xiang, M.; Zhou, Q.; Wu, W. Cultivated land change in the Belt and Road Initiative region. J. Geogr. Sci. 2018, 28, 1580–1594. [Google Scholar] [CrossRef]
- Monfreda, C.; Ramankutty, N.; Foley, J.A. Farming the planet: 2. Geographic distribution of crop areas, yields, physiological types, and net primary production in the year 2000. Global Biogeochem. Cycles 2008, 22, GB1022. [Google Scholar] [CrossRef]
- You, L.; Wood, S.; Wood-Sichra, U.; Wu, W. Generating global crop distribution maps: From census to grid. Agr. Syst. 2014, 127, 53–60. [Google Scholar] [CrossRef]
- Yu, Q.; Hu, Q.; Vliet, J.; Verburg, P.; Wu, W. GlobeLand30 shows little cropland area loss but greater fragmentation in China. Int. J. Appl. Earth. Obs. 2018, 66, 37–45. [Google Scholar] [CrossRef]


| Cropland Maps | Overall Accuracy (%) | R2 between Maps and the Cropland Percentage | R2 between Maps and the Cropland Area Statistics |
|---|---|---|---|
| Unified Cropland | 81.18 | 0.68 | 0.79 |
| GlobeLand30 | 77.76 | 0.60 | 0.80 |
| NLUD-C | 76.76 | 0.55 | 0.83 |
| MODIS Collection5 | 76.58 | 0.38 | 0.74 |
| CCI-LC | 75.69 | 0.36 | 0.58 |
| MODIS Cropland | 71.86 | 0.27 | 0.44 |
| GlobCover 2009 | 69.50 | 0.23 | 0.38 |
| Samples 1 | Samples 2 | Samples 3 | Samples 4 | Samples 5 | Samples 6 | Samples 7 | |
|---|---|---|---|---|---|---|---|
| Proportion of total training sample | 90% | 70% | 50% | 30% | 10% | 5% | 1% |
| Cropland training samples | 1777 | 1383 | 969 | 574 | 176 | 92 | 15 |
| Noncropland training samples | 1783 | 1386 | 1009 | 613 | 220 | 106 | 25 |
| Validation samples | Cropland: 847 Noncropland: 848 | ||||||
| Input datasets combination | #1, #2, #3 | ||||||
| Group 1 | Group 2 | Group 3 | Group 4 | Group 5 | Group 6 | Group 7 | |
|---|---|---|---|---|---|---|---|
| Input map combination | #1, #2, #3 | #1, #4, #5 | #1, #4, #6 | #2, #5, #6 | #2, #3, #7 | #3, #5, #7 | #5, #6, #7 |
| Average accuracy (%) | 78.57 | 77.82 | 76.54 | 75.10 | 74.67 | 73.98 | 72.35 |
| Training samples | Cropland: 1953 Noncropland: 2003 Total: 3956 | ||||||
| Validation samples | Cropland: 847 Noncropland: 848 | ||||||
| Test 1 | Test 2 | Test 3 | Test 4 | Test 5 | ||
|---|---|---|---|---|---|---|
| Province | Jiangsu | Anhui | Henan | Shanxi | Yunnan | |
| Landscape | Plain | Hill | Low mountain | Medium mountain | High mountain | |
| Average DEM (m) | 13.26 | 119.01 | 247.59 | 1160.68 | 1889.64 | |
| Validation samples | Cropland | 74 | 70 | 70 | 60 | 35 |
| Noncropland | 26 | 30 | 30 | 40 | 65 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, D.; Lu, M.; Zhou, Q.; Xiao, J.; Ru, Y.; Wei, Y.; Wu, W. Comparison of Two Synergy Approaches for Hybrid Cropland Mapping. Remote Sens. 2019, 11, 213. https://doi.org/10.3390/rs11030213
Chen D, Lu M, Zhou Q, Xiao J, Ru Y, Wei Y, Wu W. Comparison of Two Synergy Approaches for Hybrid Cropland Mapping. Remote Sensing. 2019; 11(3):213. https://doi.org/10.3390/rs11030213
Chicago/Turabian StyleChen, Di, Miao Lu, Qingbo Zhou, Jingfeng Xiao, Yating Ru, Yanbing Wei, and Wenbin Wu. 2019. "Comparison of Two Synergy Approaches for Hybrid Cropland Mapping" Remote Sensing 11, no. 3: 213. https://doi.org/10.3390/rs11030213
APA StyleChen, D., Lu, M., Zhou, Q., Xiao, J., Ru, Y., Wei, Y., & Wu, W. (2019). Comparison of Two Synergy Approaches for Hybrid Cropland Mapping. Remote Sensing, 11(3), 213. https://doi.org/10.3390/rs11030213