Cloud Detection from FY-4A’s Geostationary Interferometric Infrared Sounder Using Machine Learning Approaches
Abstract
1. Introduction
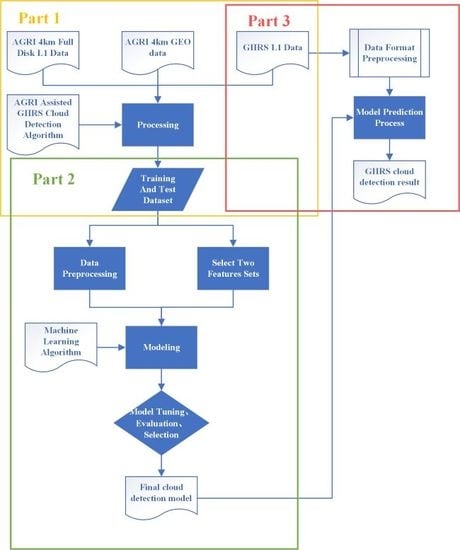
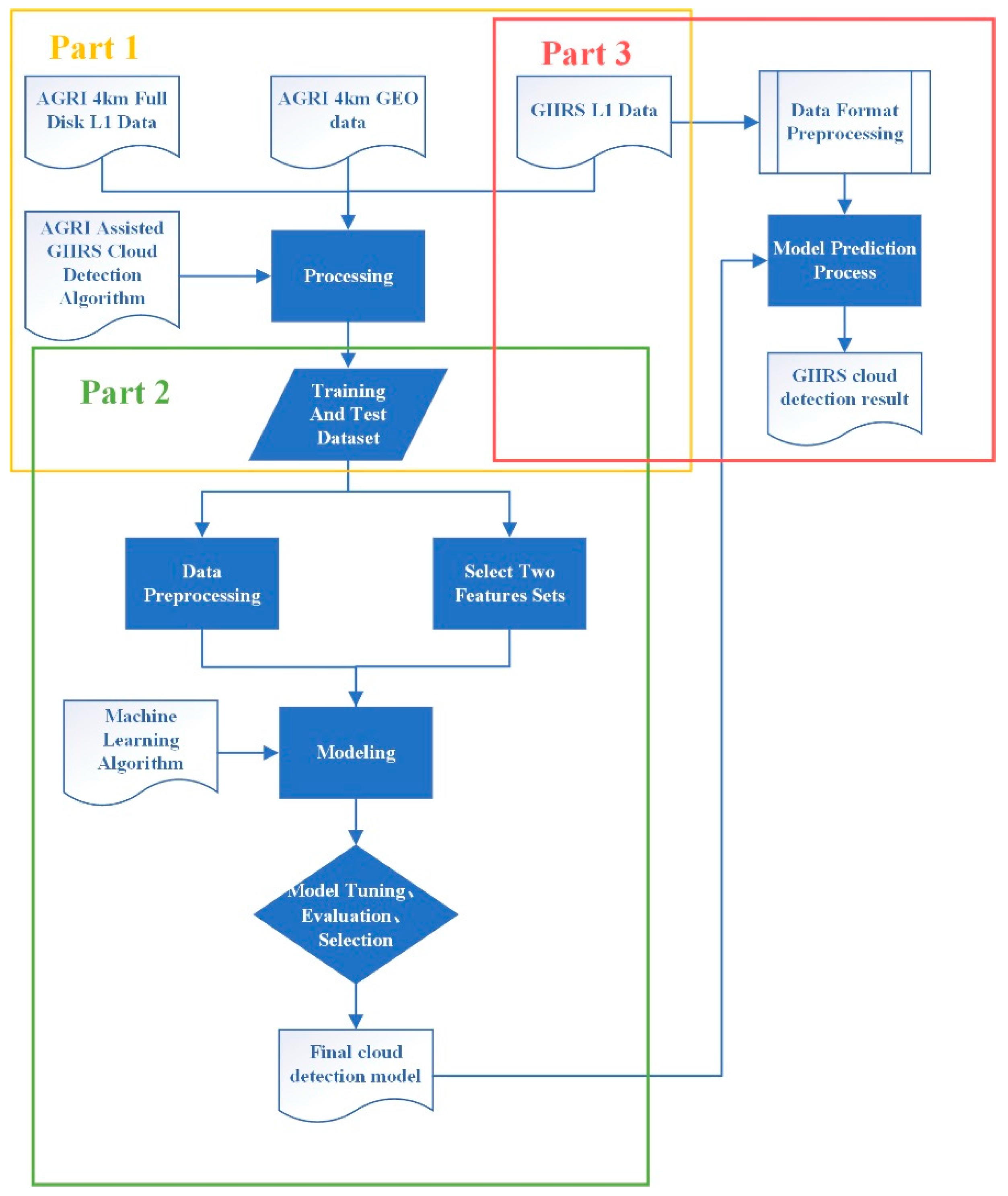
2. Methods and Materials
2.1. Methods
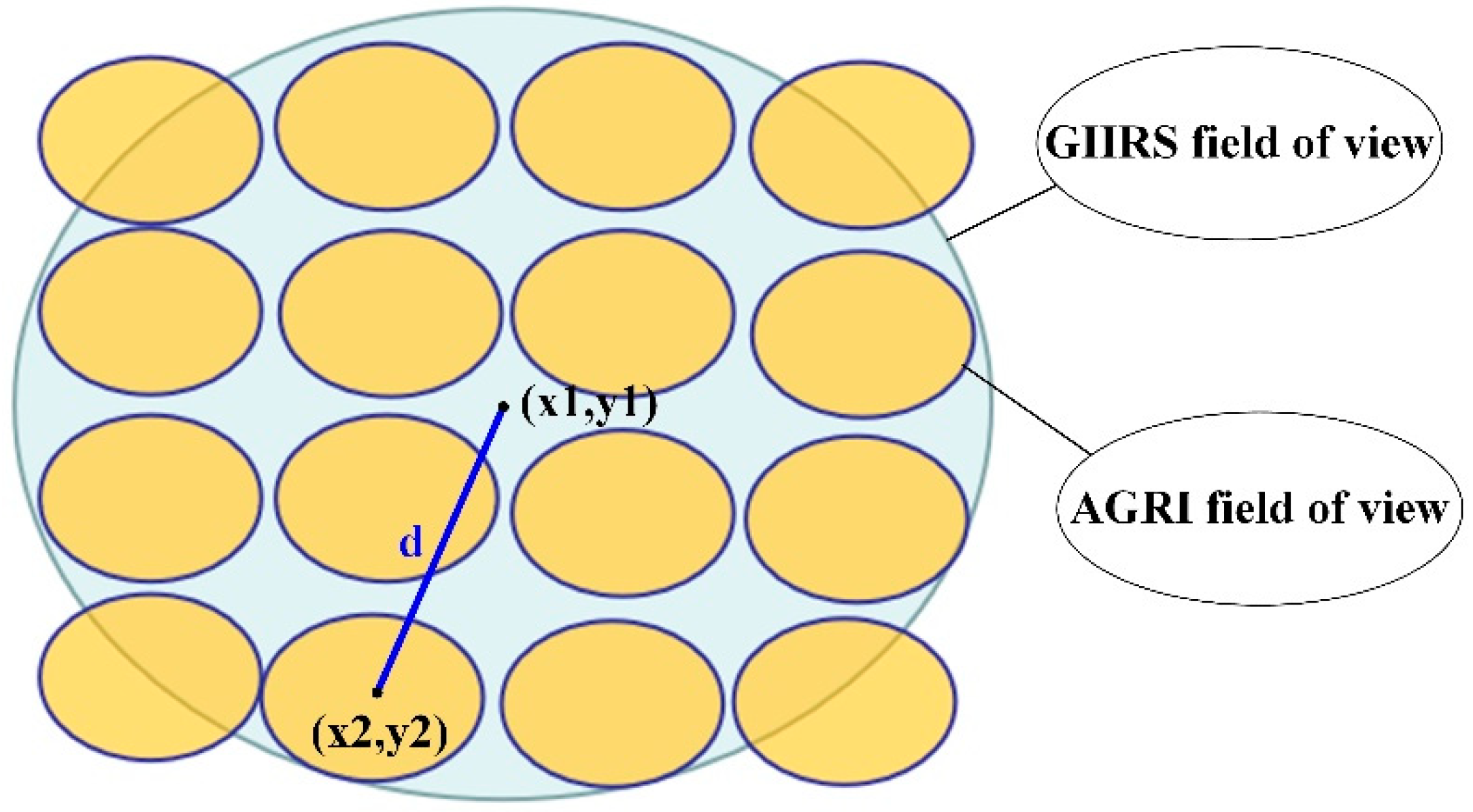
2.1.1. AGRI-GIIRS Cloud Detection Method
- (1)
- all AGRI FOVs were probably clear or probably cloud.
- (2)
- some AGRI FOVs were probably cloud or probably clear, while others were clear or cloud.
2.1.2. Machine Learning Cloud Detection Method
2.2. Data and Materials
2.2.1. Input Data of the AGRI-GIIRS Cloud Detection Method
2.2.2. Input Data for the Machine Learning Cloud Detection Algorithm
- When training machine learning cloud used the detection model, the real cloud label of GIIRS FOV was obtained using the AGRI-GIIRS cloud detection algorithm (0 for cloud GIIRS FOVs and 1 for clear GIIRS FOVs) and the GIIRS channels observation data were used as input features.
- When using the established machine learning cloud detection model, GIIRS data were processed into the file which conformed to the model input format through the preprocessing program as the input.
2.2.3. Auxiliary Validation Data
3. Machine Learning Cloud Detection Experiment
3.1. Training Data and Test Data
3.2. Machine Learning Cloud Detection Model
3.3. Model Parameter Tuning and Performance Evaluation
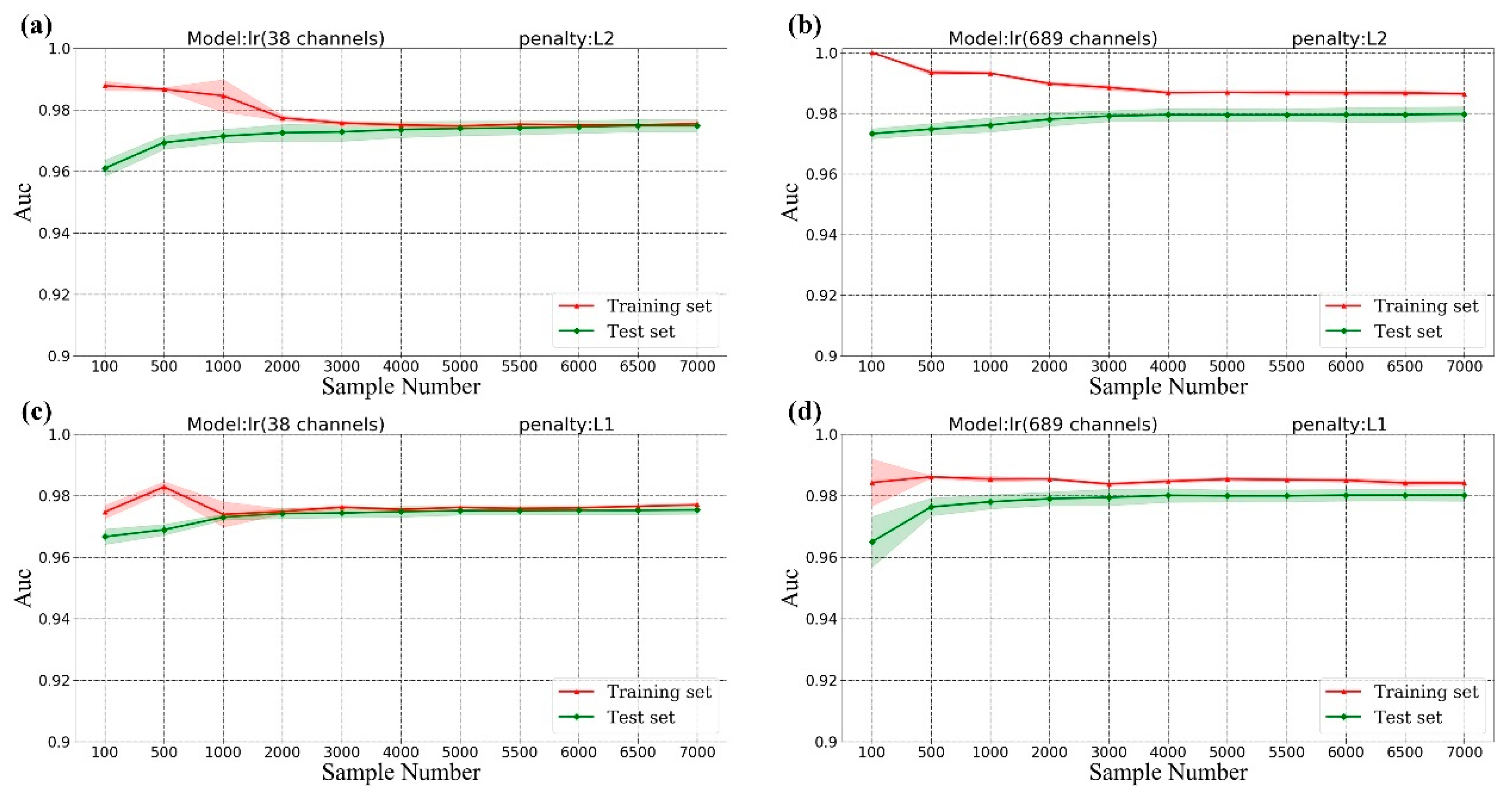
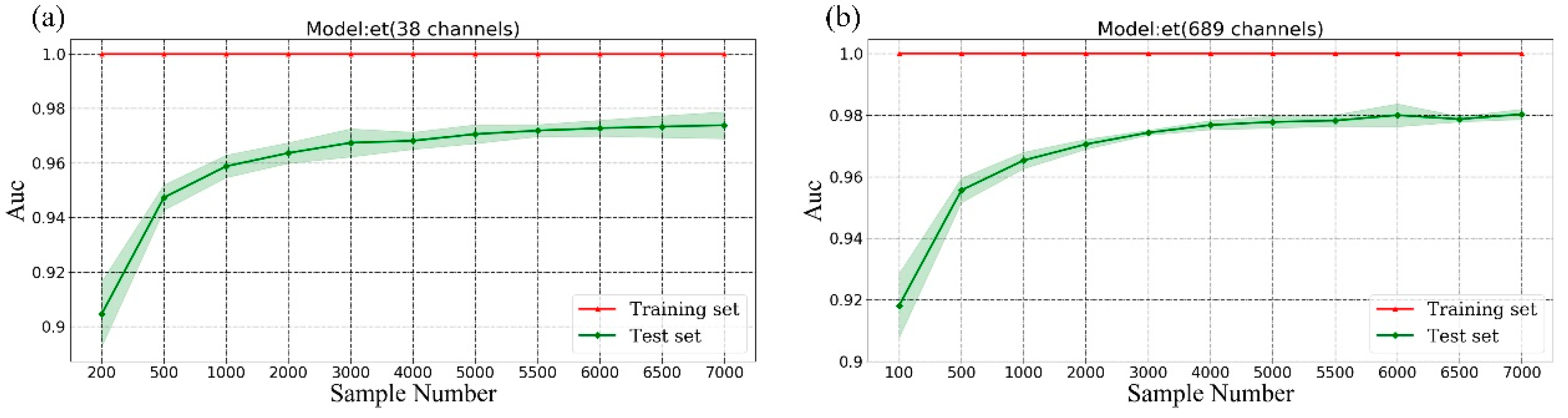
3.3.1. Sample Size
- The AUC score for the test data in this section was derived using a 5-fold cross-validation method;
- The default value was used for hyperparameters (e.g., C = 1).
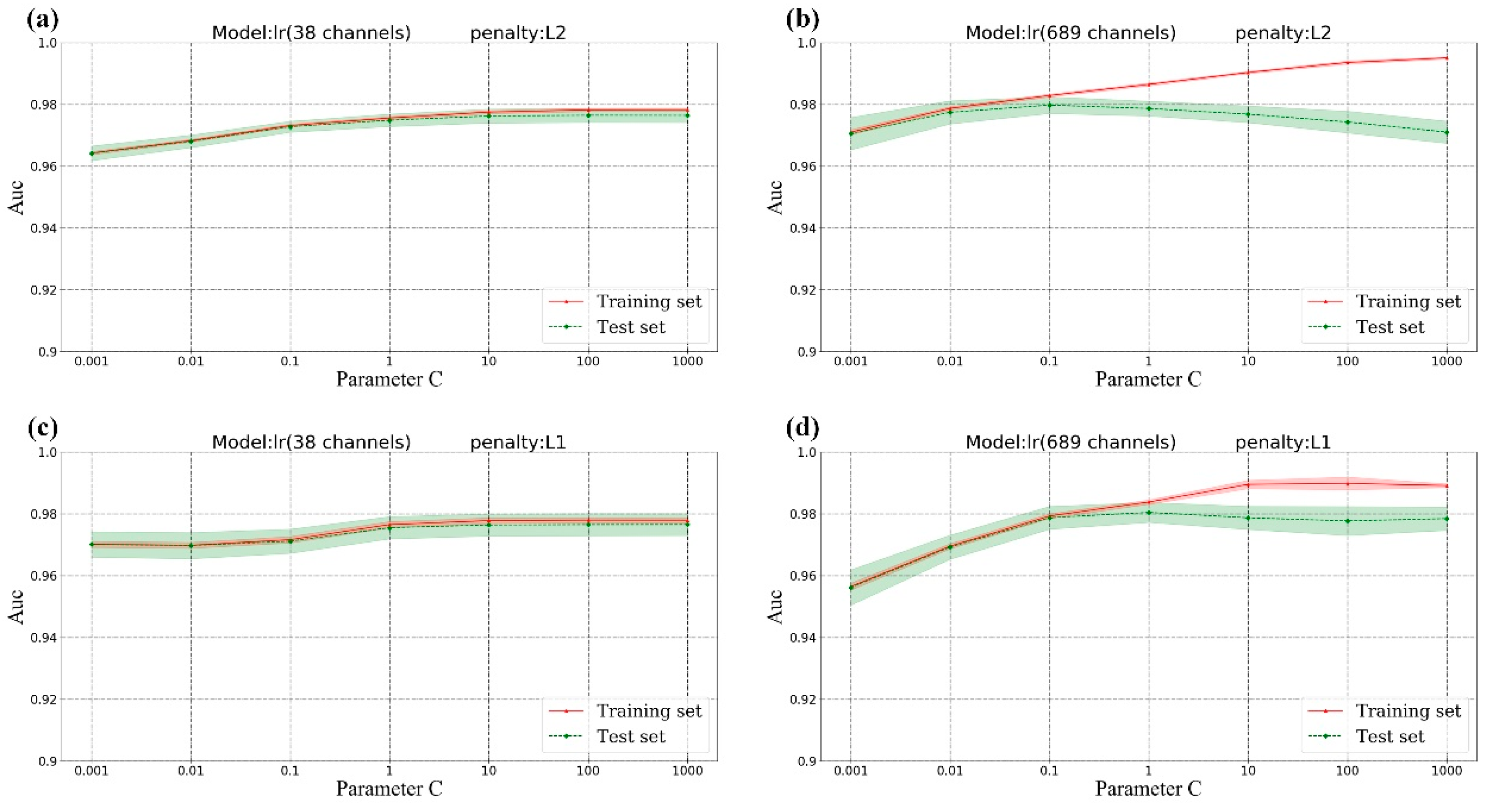
- All AUC scores in the four models (training and test data) tended to be stable when the sample number was greater than or equal to 4000, indicting that at least 4000 samples are required for 4 cloud detection models.
- The AUC score of lr (689 channels) (Figure 6b,d) on the training set was always higher than that of on the test set, indicating that the model was over-fitted. Generally speaking, over-fitting can be improved by increasing the amount of data, reducing the complexity of the model (stronger regularization) or reducing the number of model features. Compared with lr (689 channels) models, the score of lr (38 channels) models (Figure 6a,c) on the training set was the same as that on the test set when the number of training samples is more than 4000, which indicated that over-fitting phenomenon did disappear after reducing some features. Additionally, when the number of training samples increased from 4000 to 7000, the over-fitting phenomenon of the lr (689 channels) models still existed. Thus, increasing the number of training samples could not improve the over-fitting in this problem. In Section 3.3.2, hyperparameter ‘C’ was tuned to improve the over-fitting issue.
- For models with the same input features, L1 and L2 regularization almost scored the same when the AUC of the training set and test set were not changed with sample size.
3.3.2. Hyperparameters Tuning
3.3.3. Probability Threshold Tuning
4. Results
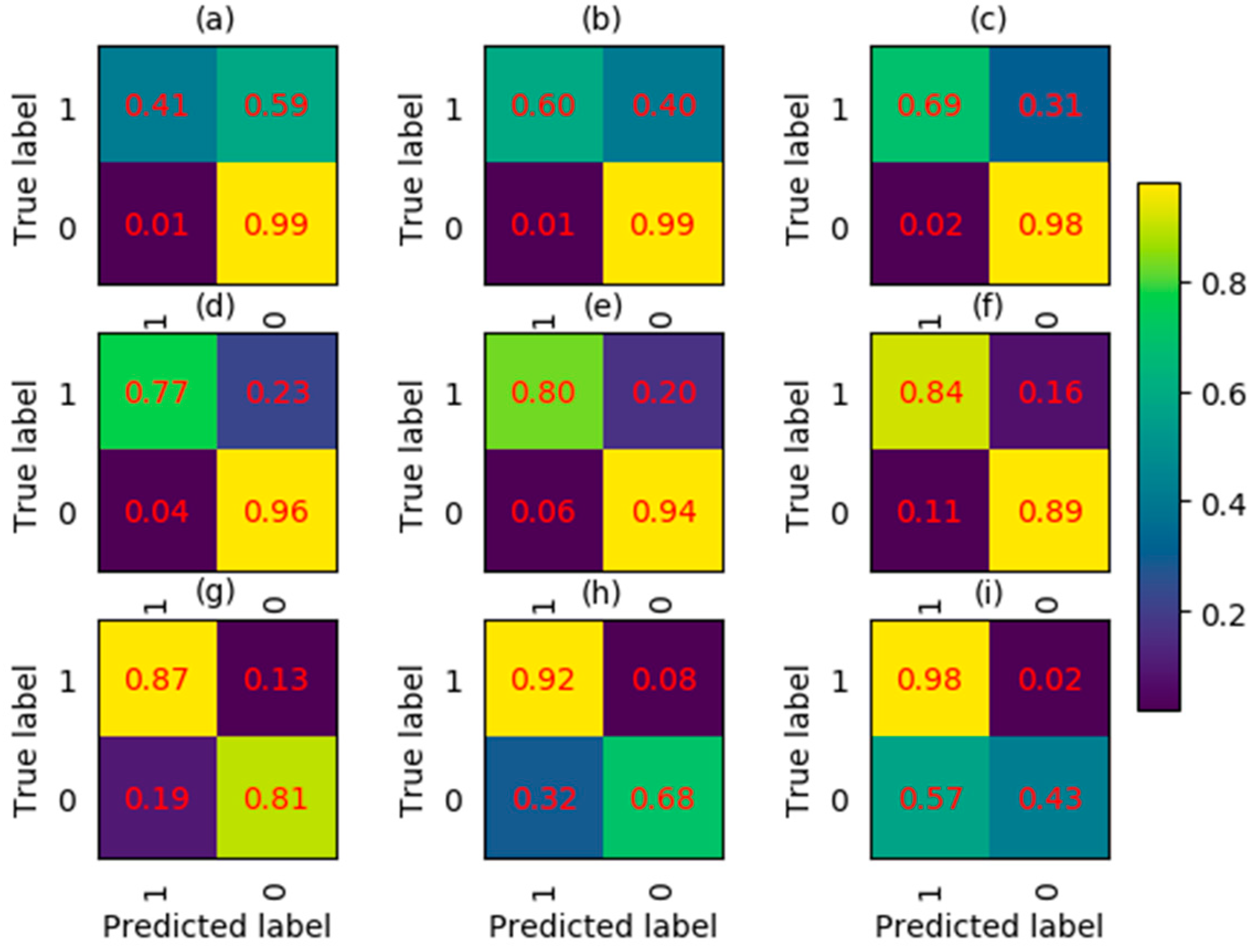
4.1. Statistics of Four Cloud Detection Models on Test Data
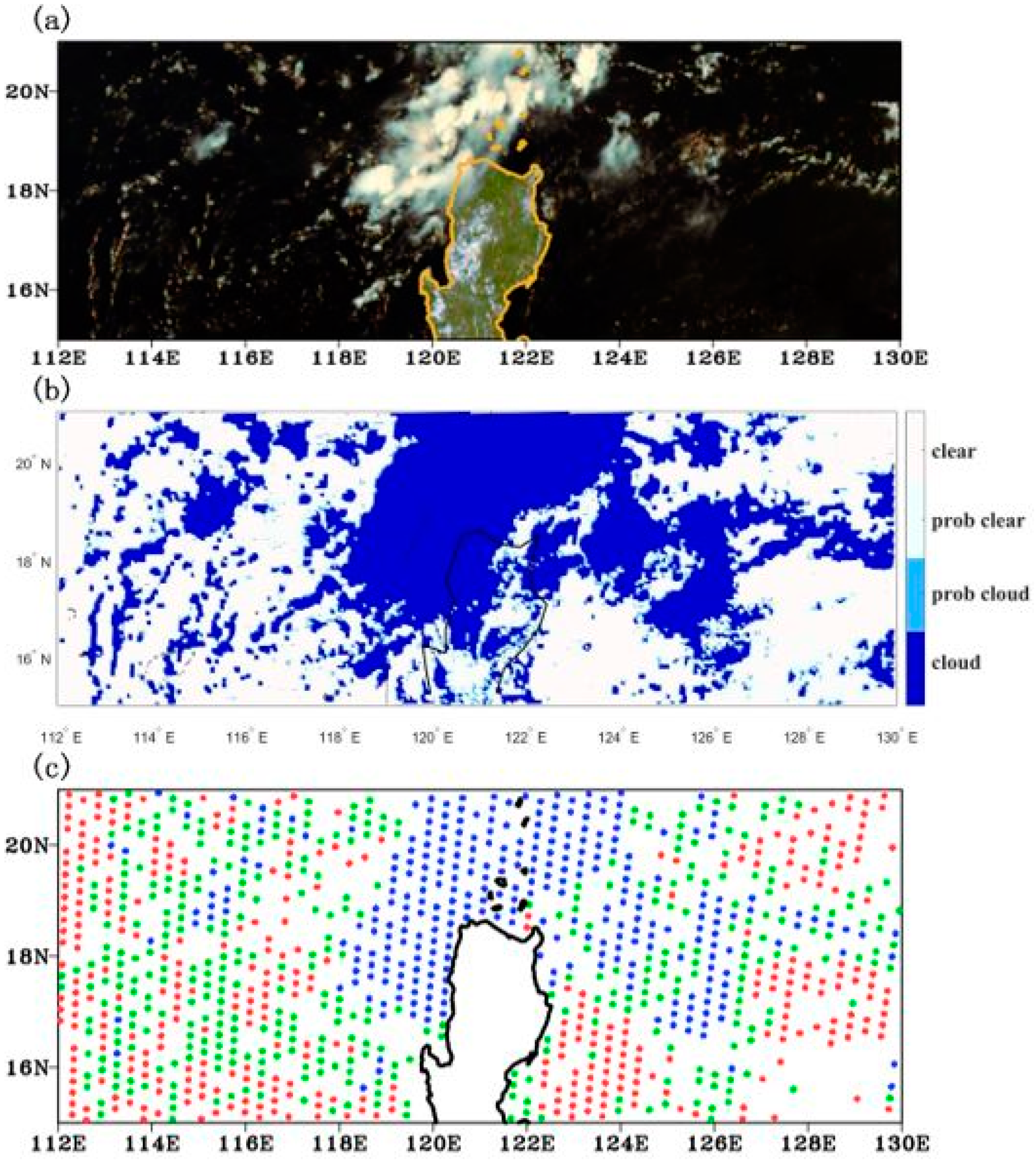
4.2. Visualization Verification of The Model Classification Effect
5. Discussion
5.1. Time Complexity of AGRI-GIIRS Cloud Detection and Machine learning Cloud Detection
Time Complexity
5.2. Applicability of The Machine Learning Cloud Detection Algorithm
5.2.1. Applicability of Time
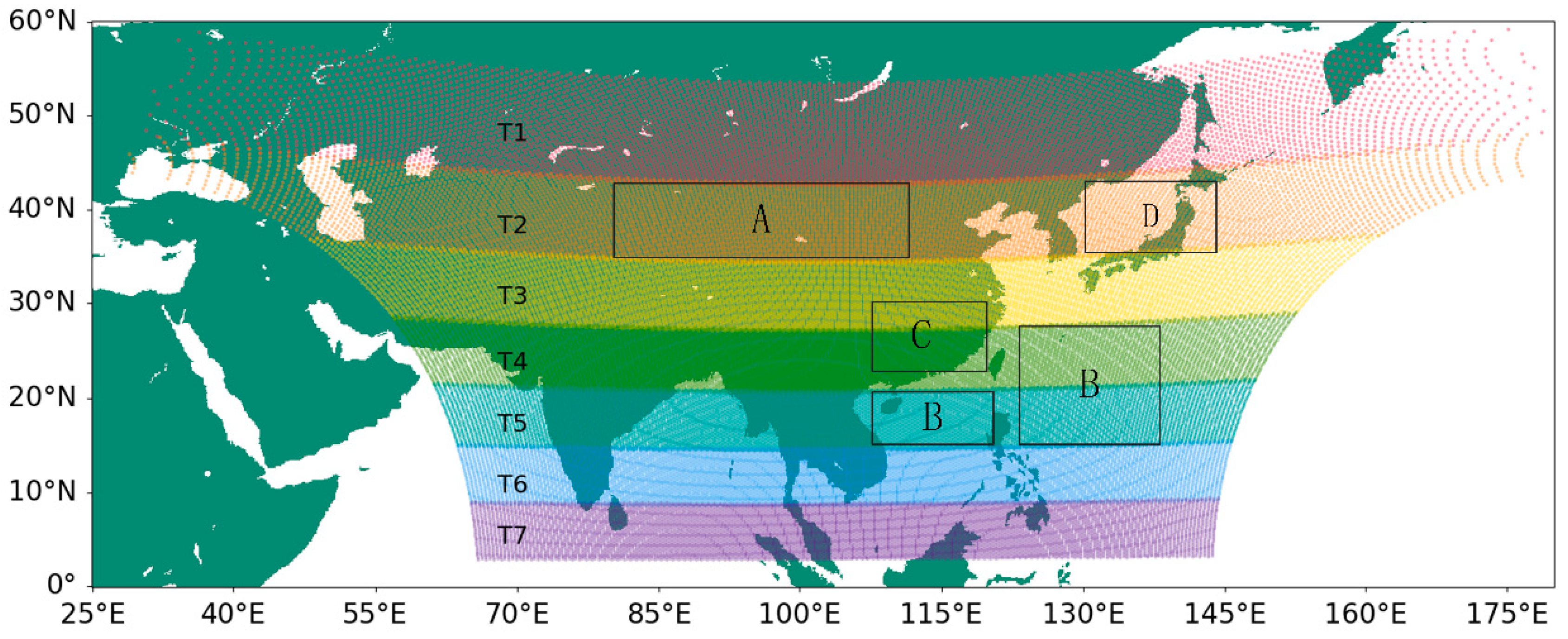
5.2.2. Spatial Applicability
5.3. Comparison of Cloud Detection Methods Between Machine Learning Cloud Detection and Weather Research and Forecasting Model Data Assimilation System(WRFDA)
- model cloud water path detection;
- 956 cm−1 long wave window channel brightness temperature detection;
- sea surface temperature deviation detection;
- cloud cover area detection.
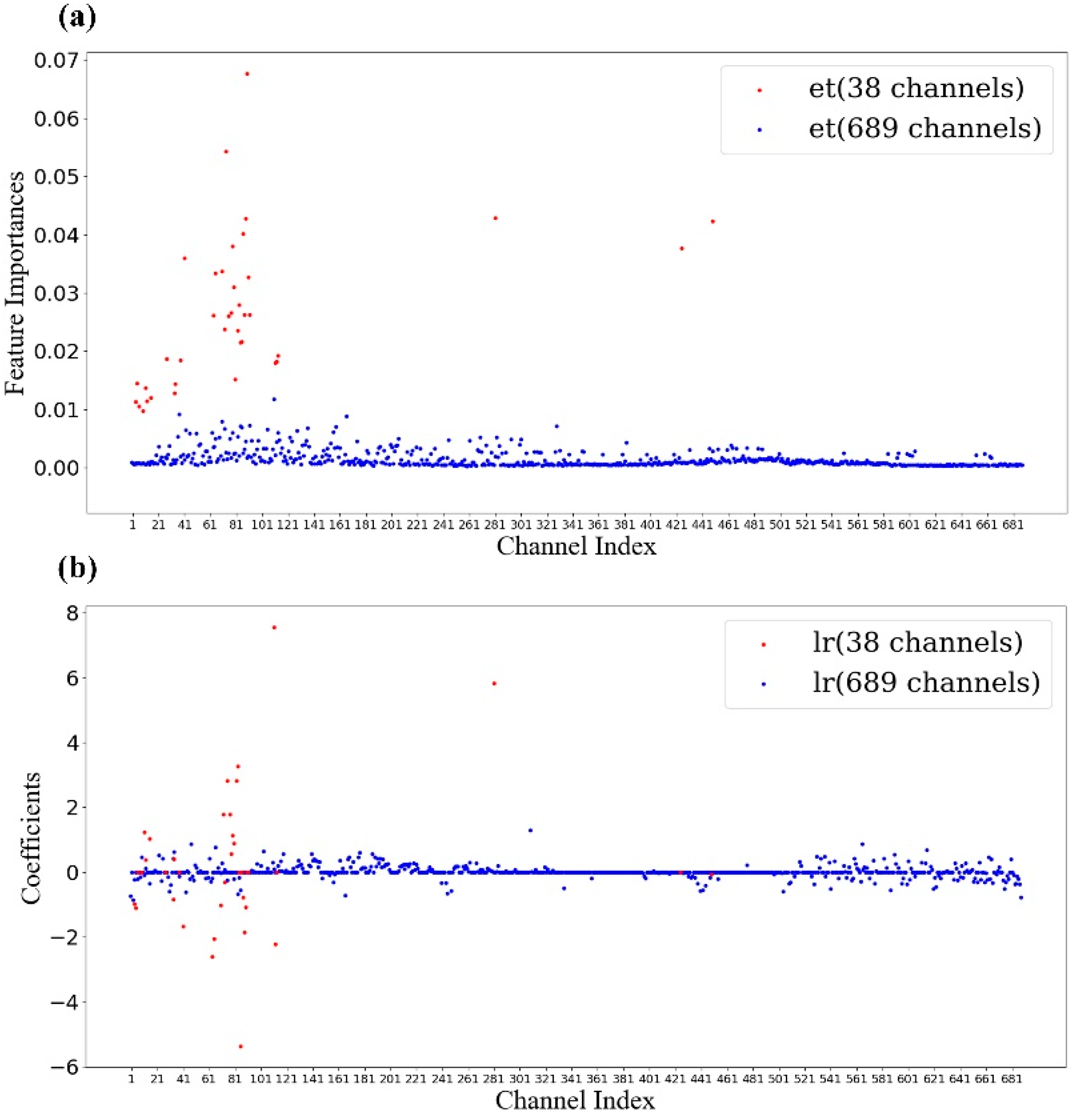
5.4. Channel Contribution
5.5. Limitations and some Exploration of Machine Learning Cloud Detection Method
5.5.1. Model Applicable Scenario
- Can the model established above separate partially cloudy GIIRS FOVs from the totally clear GIIRS FOVs?
- Can adding some cloud pixels to the training set improve the effect of the model recognition part with cloud pixels?
5.1.2. The Reliability of Training Set and Test Set
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Aumann, H.H.; Miller, C.R. Atmospheric infrared sounder (AIRS) on the earth observing system. Proc. SPIE, Int. Soc. Opt. Eng. 1995, 2583, 332–343. [Google Scholar]
- Smith, N.; Smith, W.L.; Weisz, E.; Revercomb, H.E. AIRS, IASI and CrIS retrieval records at climate scales: An investigation into the propagation systematic uncertainty. J. Appl. Meteorol. Climatol. 2015, 54, 1465–1481. [Google Scholar] [CrossRef]
- Clerbaux, C.; Hadji-Lazaro, J.; Turquety, S.; George, M.; Coheur, P.F.; Hurtmans, D.; Wespes, C.; Herbin, H.; Blumstein, D.; Tourniers, B.; et al. The IASI/MetOp 1 mission: First observations and highlights of its potential contribution to GMES 2. Space Res. Today 2007, 168, 19–24. [Google Scholar] [CrossRef]
- Smith, A.; Atkinson, N.; Bell, W.; Doherty, A. An initial assessment of observations from the Suomi-NPP satellite: Data from the Cross-track Infrared Sounder (CrIS). Atmos. Sci. Lett. 2015, 16, 260–266. [Google Scholar] [CrossRef]
- Li, Z.; Li, J.; Wang, P.; Lim, A.; Li, J.; Schmit, T.J.; Atlas, R.; Boukabara, S.A.; Hoffman, R. Value-added impact of geostationary hyperspectral infrared sounders on local severe storm forecasts—Via a quick regional OSSE. Adv. Atmos. Sci. 2018, 35, 1217–1230. [Google Scholar] [CrossRef]
- Lu, F.; Zhang, X.; Chen, B.; Liu, H.; Wu, R.; Han, Q.; Feng, X.; Li, J.; Zhan, Z. FY-4 geostationary meteorological satellite imaging characteristic and its application prospects. J. Mar. Meteorol. 2017, 37, 1–12. [Google Scholar]
- Yang, J.; Zhang, Z.; Wei, C.; Lu, F.; Guo, Q. Introducing the new generation of Chinese geostationary weather satellites, Fengyun-4(FY-4). Bull. Am. Meteorol. Soc. 2016, 98, 1637–1658. [Google Scholar] [CrossRef]
- Chen, W. Satellite Meteorology; China Meteorological Press: Beijing, China, 2003. [Google Scholar]
- Dong, C.; Li, J.; Zhang, P. The Principle and Application of Satellite Hyperspectral Infrared Atmospheric Remote Sensing; Science Press: Beijing, China, 2013. [Google Scholar]
- Wylie, D.P.; Menzel, W.P.; Woolf, H.M.; Strabala, K.I. Four years of global cirrus cloud statistics using HIRS. J. Clim. 1994, 7, 1972–1986. [Google Scholar] [CrossRef]
- Li, J.; Liu, C.; Huang, H.; Schmit, T.J.; Wu, X.; Menzel, W.P.; Gurka, J.J. Optimal cloud-clearing for AIRS radiances using MODIS. IEEE Trans. Geosci. Electron. 2005, 43, 1266–1278. [Google Scholar]
- McNally, A.P.; Watts, P.D. A cloud detection algorithm for high-spectral-resolution infrared sounders. Q. J. R. Meteorol. Soc. 2003, 129, 3411–3423. [Google Scholar] [CrossRef]
- Rossow, W.B.; Garder, L.C. Cloud detection using satellite measurements of infrared and visible radiances for ISCCP. J. Clim. 1993, 12, 2341–2369. [Google Scholar] [CrossRef]
- Rossow, W.; Mosher, F.; Kinsella, E.; Arking, A.; Desbois, M.; Harrison, E.; Minnis, P.; Ruprecht, E.; Seze, G.; Simmer, C.; et al. ISCCP cloud algorithm intercomparison. J. Appl. Meteorol. 1985, 24, 184–192. [Google Scholar] [CrossRef]
- Kriebel, K.T.; Gesell, G.; Kastner, M.; Mannstein, H. The cloud analysis tool APOLLO: Improvements and validations. Int. J. Remote Sens. 2003, 24, 2389–2408. [Google Scholar] [CrossRef]
- Stowe, L.L.; Davis, P.A.; Mcclain, E.P. Scientific basis and initial evaluation of the CLAVR-1 global clear/cloud classification algorithm for the advanced very high resolution radiometer. J. Atmos. Ocean. Technol. 1999, 16, 656–681. [Google Scholar] [CrossRef]
- Baum, B.A.; Arduini, R.F.; Wielicki, B.A.; Minns, P.; Tsay, S.C. Multilevel cloud retrieval using multispectral HIRS and AVHRR data: Nighttime oceanic analysis. J. Geophys. Res. Atmos. 1994, 99, 5499–5514. [Google Scholar] [CrossRef]
- Ackerman, S.A.; Strabala, K.I.; Menzel, W.P.; Frey, R.A.; Moeller, C.C. Discriminating clear sky from clouds with MODIS. J. Geophys. Res. 1998, 103, 32141. [Google Scholar] [CrossRef]
- Ackerman, S.A.; Holz, R.E.; Frey, R.; Eloranta, E.W.; Maddux, B.C.; McGill, M.R. Cloud detection with MODIS. Part II: Validation. J. Atmos. Ocean. Technol. 2010, 25, 1073–1086. [Google Scholar] [CrossRef]
- Li, J.; Menzel, P.W.; Sun, F.; Schmit, T.J.; Gurka, J.J. AIRS subpixel cloud characterization using MODIS cloud products. J. Appl. Meteorol. 2004, 43, 1083–1094. [Google Scholar] [CrossRef]
- Eresmaa, R. Imager-assisted cloud detection for assimilation of infrared atmospheric sounding interferometer radiances. Q. J. R. Meteorol. Soc. 2014, 140, 2342–2352. [Google Scholar] [CrossRef]
- Ma, Y.; Wu, H.; Wang, L.; Huang, B.; Ranjan, R.; Zomaya, A.; Jie, W. Remote sensing big data computing: Challenges and opportunities. Future Gener. Comput. Syst. 2014, 51, 47–60. [Google Scholar] [CrossRef]
- Qiu, J.; Wu, Q.; Ding, G.; Xu, Y.; Feng, S. A survey of machine learning for big data processing. EURASIP J. Adv. Signal Process. 2016, 2016, 67. [Google Scholar] [CrossRef]
- Li, P.; Dong, L.; Xiao, H.; Xu, M. A cloud image detection method based on SVM vector machine. Neurocomputing 2015, 169, 34–42. [Google Scholar] [CrossRef]
- Bai, T.; Li, D.; Sun, K.; Chen, Y.; Li, W. Cloud detection for high-resolution satellite imagery using machine learning and multi-feature fusion. Remote Sens. 2016, 8, 715. [Google Scholar] [CrossRef]
- Luo, T.; Zhang, W.; Yu, Y.; Feng, M.; Duan, B.; Xing, D. Cloud detection using infrared atmospheric sounding interferometer observations by logistic regression. Int. J. Remote Sens. 2019, 40, 1–12. [Google Scholar] [CrossRef]
- Han, B.; Kang, L.; Song, H. A fast cloud detection approach by integration of image segmentation and support vector machine. In Proceedings of the International Symposium on Neural Networks, Chengdu, China, 28 May–1 June 2006. [Google Scholar]
- Latry, C.; Panem, C.; Dejean, P. Cloud detection with SVM technique. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007. [Google Scholar]
- Xu, L.; Wong, A.; Clausi, D.A. A novel Bayesian spatial-temporal random field model applied to cloud detection from remotely sensed imagery. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4913–4924. [Google Scholar] [CrossRef]
- Li, Q.; Lu, W.; Yang, J.; Wang, J.Z. Thin cloud detection of all-sky images using Markov random fields. IEEE Geosci. Remote Sens. Lett. 2012, 9, 417–421. [Google Scholar] [CrossRef]
- Yang, J.; Guo, J.; Yue, H.; Liu, Z.; Hu, H.; Li, K. CDnet: CNN-based cloud detection for remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2019, 99, 1–17. [Google Scholar] [CrossRef]
- Mohajerani, S.; Saeedi, P. Cloud-net: An end-to-end cloud detection algorithm for Landsat 8 imagery. arXiv 2019, arXiv:1901.10077. [Google Scholar]
- Xie, F.; Shi, M.; Shi, Z.; Yin, J.; Zhao, D. Multilevel cloud detection in remote sensing images based on deep learning. IEEE J. Sel. Topics Appl. Earth Obs. Remote Sens. 2017, 10, 3631–3640. [Google Scholar] [CrossRef]
- Mohajerani, S.; Krammer, T.A.; Saeedi, P. A cloud detection algorithm for remote sensing images using fully convolutional neural networks. In Proceedings of the 20th IEEE International Workshop on Multimedia Signal Processing, Cape Town, South Africa, 21–24 October 2018. [Google Scholar]
- Zhang, Z.; Iwasaki, A.; Song, J. Small satellite cloud detection based on deep learning and image compression. Preprints 2018. [Google Scholar] [CrossRef]
- Sim, S.; Im, J.; Park, S.; Park, H.; Ahn, M.W.; Chan, P. Icing detection over East Asia from geostationary satellite data using machine learning approaches. Remote Sens. 2018, 4, 631. [Google Scholar] [CrossRef]
- Han, D.; Lee, J.; Im, J.; Sim, S.; Lee, S.; Han, H. A novel framework of detecting convective initiation combining automated sampling, machine learning, and repeated model tuning from geostationary satellite data. Remote Sens. 2019, 12, 1454. [Google Scholar] [CrossRef]
- Han, H.; Lee, S.; Im, J.; Kim, M.; Lee, M.; Ahn, M.; Chung, S. Detection of convective initiation using meteorological imager onboard communication, ocean, and meteorological satellite based on machine learning approaches. Remote Sens. 2015, 7, 9184–9204. [Google Scholar] [CrossRef]
- Kim, M.; Im, J.; Park, H.; Park, S.; Lee, M.; Ahn, M. Detection of tropical overshooting cloud tops using Himawari-8 imagery. Remote Sens. 2017, 7, 685. [Google Scholar] [CrossRef]
- Kleinbaum, D.G.; Klein, M. Logistic Regression (A Self-Learning Text); Springer: Berlin/Heidelberg, German, 2002. [Google Scholar]
- Liao, J.G.; Chin, K.V. Logistic Regression for Disease Classification Using Microarray Data; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Komarek, P. Logistic Regression for Data Mining and High Dimensional Classification. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 2004. [Google Scholar]
- Koh, K.; Kim, S.J.; Boyd, S.P. A method for large-scale L1-regularized logistic regression. In Proceedings of the Twenty-Second AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 22–26 July 2007. [Google Scholar]
- Andrew, Y.N. Feature selection, L1 vs. L2 regularization, and rotational invariance. In Proceedings of the International Conference on Machine learning, Louisville, KY, USA, 16–18 December 2004. [Google Scholar]
- Fan, R.E.; Chang, K.W.; Hsieh, C.J.; Wang, X.R.; Lin, C.J. Liblinear: A library for large linear classification. J. Mach. Learn. Res. 2008, 9, 1871–1874. [Google Scholar]
- Gill, P.E.; Murray, W. Quasi-Newton methods for unconstrained optimization. IMA J. Appl. Math. 1972, 9, 91–108. [Google Scholar] [CrossRef]
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Schapire, R.E. Explaining AdaBoost. In Empirical Inference; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Collins, M.; Schapire, R.E.; Singer, Y. Logistic regression, AdaBoost and Bregman distances. Mach. Learn. 2001, 48, 253–285. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Jerome, H.F. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar]
- Goetz, M.; Weber, C.; Bloecher, J.; Stieltjes, B.; Meinzer, H.P.; Maier-Hein, K. Extremely randomized trees based brain tumor segmentation. In Proceedings of the MICCAI BraTS (Brain Tumor Segmentation Challenge), Boston, MA, USA, 14–18 September 2014. [Google Scholar]
- Guan, L.; Xiao, W. Retrieval of cloud parameters using infrared hyperspectral observations. Chin. J. Atmos. Sci. 2007, 31, 1123–1128. (In Chinese) [Google Scholar]
- Han, W. Assimilation of GIIRS radiances in GRAPES. In Proceedings of the 35th Chinese Meteorological Society Conference, Hefei, Anhui, China, 23–26 October 2019. [Google Scholar]
- Bradley, P. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recogn. 1996, 30, 1145–1159. [Google Scholar] [CrossRef]
- Nurmi, P. Recommendations on the Verification of Local Weather Forecasts; ECMWF Technical Memoranda 430 European Centre for Medium-Range Weather Forecasts (ECMWF): Reading, UK, 2003. [Google Scholar]
- Alberto, J.V. Insights into the area under the receiver operating characteristic curve (AUC) as a discrimination measure in species distribution modelling. Glob. Ecol. Biogeogr. 2011, 21, 498–507. [Google Scholar]
- Cortes, C.; Jackel, L.; Solla, S.A.; Vapnik, V.; Denker, J. Learning curves: Asymptotic values and rate of convergence. In Proceedings of the 7th Advances in Neural Information Processing Systems 6, Denver, CO, USA, 1993. [Google Scholar]
- Wang, B.; Gong, N.Z. Stealing hyperparameters in machine learning. In Proceedings of the 39th IEEE Symposium on Security and Privacy, San Francisco, CA, USA, 21–23 May 2018. [Google Scholar]
- Sun, Y.; Wang, Y.; Guo, L.; Ma, Z.; Jin, S. The comparison of optimizing SVM by GA and grid search. In Proceedings of the 13th IEEE International Conference on Electronic Measurement & Instruments, Yangzhou, China, 20–23 October 2017. [Google Scholar]
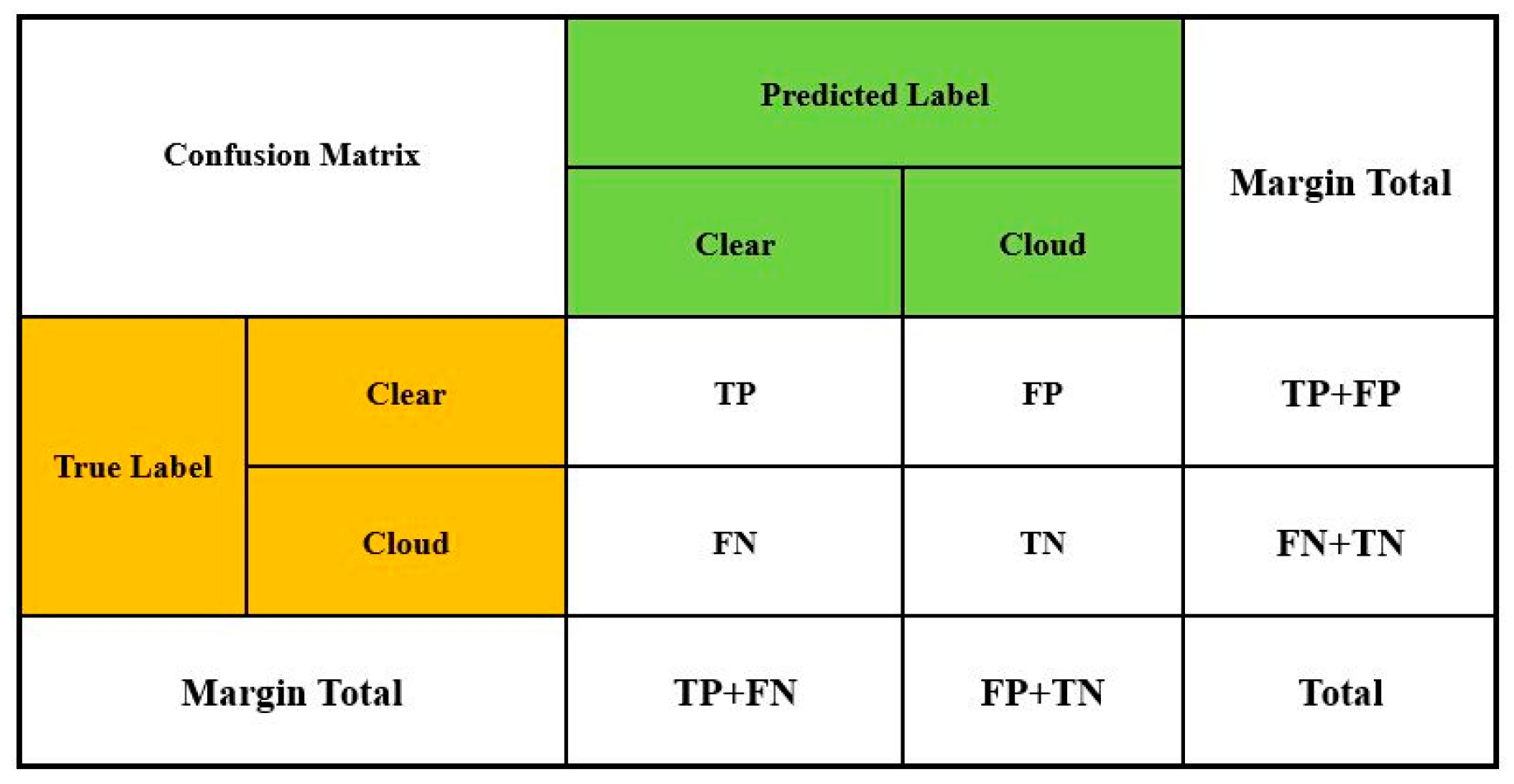
- Ting, K.M. Confusion matrix. In Encyclopedia of Machine Learning and Data Mining; Springer: Boston, MA, USA, 2016. [Google Scholar]
- Min, M.; Wu, C.; Li, C.; Xu, N.; Wu, X.; Chen, L.; Wang, F.; Sun, F.; Qin, D.; Wang, X.; et al. Developing the science product algorithm testbed for Chinese next-generation geostationary meteorological satellites: Fengyun-4 series. J. Meteorol. Res. 2017, 31, 708–719. [Google Scholar] [CrossRef]
- Hong, G.; Yang, P.; Gao, B.C.; Baum, B.A.; Hu, Y.X.; King, M.D.; Platnick, S. High cloud properties from three years of MODIS Terra and Aqua collection-4 Data over the tropics. J. Appl. Meteorol. Clim. 2007, 46, 1840–1856. [Google Scholar] [CrossRef]
- Yang, P.; Zhang, L.; Hong, G.; Nasiri, S.L.; Baum, B.A.; Huang, H.L.; King, M.D.; Platnick, S. Differences between collection 4 and 5 MODIS ice cloud optical/microphysical products and their impact on radiative forcing simulations. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2886–2899. [Google Scholar] [CrossRef]
- King, M.D.; Kaufman, Y.J.; Menzel, W.P.; Tanre, D. Remote sensing of cloud, aerosol, and water vapor properties from the Moderate Resolution Imaging Spectrometer (MODIS). IEEE Trans. Geosci. Remote Sens. 1992, 30, 2–27. [Google Scholar] [CrossRef]
- Zhuge, X.; Zou, X. Test of a modified infrared-only ABI cloud mask algorithm for AHI radiance observations. J. Appl. Meteorol. Climatol. 2016, 55, 2529–2546. [Google Scholar] [CrossRef]
- Wang, X.; Guo, Z.; Huang, Y.; Fan, H.; Li, W. A cloud detection scheme for the Chinese carbon dioxide observation satellite (TANSAT). Adv. Atmos. Sci. 2017, 34, 16–25. [Google Scholar] [CrossRef]
- Lai, R.; Teng, B.; Yi, B.; Letu, H.; Min, M.; Tang, S.; Liu, C. Comparison of cloud properties from Himawari-8 and FengYun-4A geostationary satellite radiometers with MODIS cloud retrieval. Remote Sens. 2019, 11, 1703. [Google Scholar] [CrossRef]
- Bessho, K.; Date, K.; Hayashi, M.; Ikeda, A.; Imai, T.; Inoue, H.; Kumagai, Y.; Miyakawa, T.; Murata, H.; Ohno, T.; et al. An introduction to Himawari-8/9—Japan’s new-generation geostationary meteorological satellites. J. Meteorol. Soc. Jpn. Ser. II 2016, 94, 151–183. [Google Scholar] [CrossRef]
- Wang, Y.; Han, Y.; Ma, G.; Liu, H.; Wang, Y. Influential experiments of AIRS data quality control method on hurricane track simulation. J. Meteorol. Sci. 2014, 34, 383–389. [Google Scholar]

| Model | C | n_estimators | max_depth | max_features | min_samples_leaf | Min_samples_split |
|---|---|---|---|---|---|---|
| lr | ✓ | - | - | - | - | - |
| et | - | ✓ | ✓ | ✓ | ✓ | ✓ |
| Type | Training Data | Test Data |
|---|---|---|
| sea_cloud | 4254 | 1986 |
| sea_clear | 4855 | 1885 |
| land_cloud | 4301 | 2068 |
| land_clear | 4486 | 2081 |
| Date(YYYY-MM-DD-HH:MM) | Land/Sea Flag | Day/Night Flag |
|---|---|---|
| 2019-01-24-00:15 | Land | Day |
| 2019-05-14-12:15 | Land | Night |
| 2019-05-15-03:00 | Land | Day |
| 2019-06-15-12:15 | Land | Night |
| 2019-02-11-19:00 | Sea | Night |
| 2019-05-15-03:00 | Sea | Day |
| 2019-05-15-20:45 | Sea | Night |
| 2019-08-15-15:00 | Sea | Night |
| Model | Area | Input Features | Abbreviation | Data Solution |
|---|---|---|---|---|
| et | Land | 689 channels | et(689 channels) | - |
| et | Land | 38 channels | et(38 channels) | - |
| lr | Sea | 689 channels | lr(689 channels) | Standardization |
| lr | Sea | 38 channels | lr(38 channels) | Standardization |
| Model | n estimators | max features | max depth | n samples split | min samples leaf | AUC (origin) | AUC (tuned) |
|---|---|---|---|---|---|---|---|
| et (38channels) | 100 | 20 | 5 | 2 | 1 | 0.975 | 0.980 |
| et (689channels) | 130 | 30 | 10 | 2 | 1 | 0.980 | 0.984 |
| et (38 channels) | et (689 channels) | lr (38 channels) | lr (689 channels) |
|---|---|---|---|
| 0.55 | 0.6 | 0.98 | 0.98 |
| Model | POD | FAR | ACC | HSS |
|---|---|---|---|---|
| et(38 channels) | 0.914 | 0.177 | 0.872 | 0.741 |
| et(689 channels) | 0.916 | 0.166 | 0.891 | 0.780 |
| lr(38 channels) | 0.986 | 0.071 | 0.956 | 0.912 |
| lr(689 channels) | 0.993 | 0.047 | 0.973 | 0.945 |
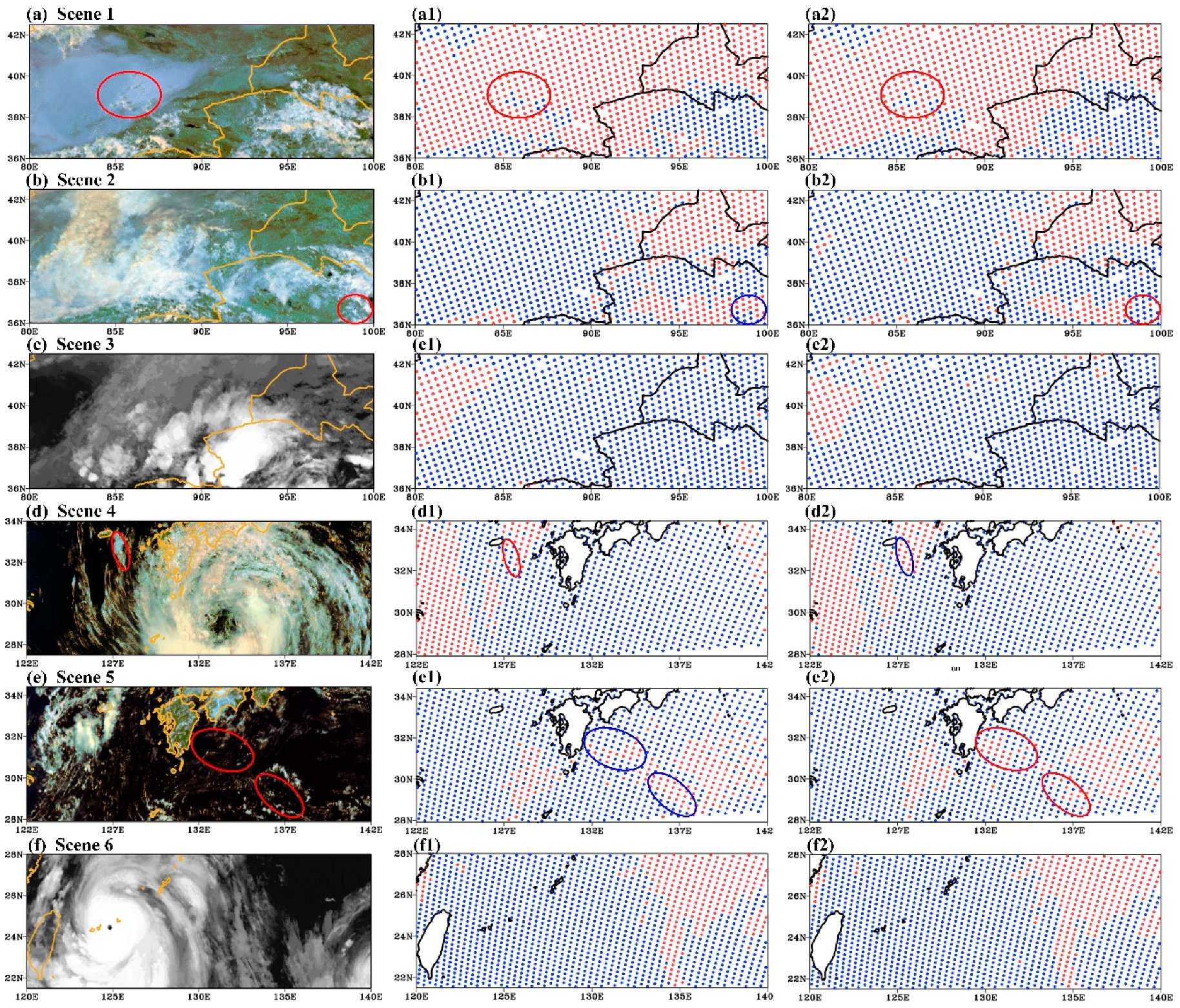
| Scene Number | Date (YYYY-MM-DD-HH:MM) | Day/Night Flag | Region | Land/Sea Flag | Characteristics |
|---|---|---|---|---|---|
| 1 | 2019-08-16-08:15 | Day | Land | Snow, Cloud Shadow | |
| 2 | 2019-08-20-04:15 | Day | Land | Multi-layer Cloud | |
| 3 | 2019-08-18-12:15 | Night | Land | - | |
| 4 | 2019-08-14-02:30 | Day | Sea | Typhoon KROSA | |
| 5 | 2019-08-21-04:30 | Day | Sea | Thin Cirrus, Broken Cloud | |
| 6 | 2019-08-08-12:45 | Night | Sea | Typhoon LEKIMA |
| Model | GIIRS FOV Number | Runtime |
|---|---|---|
| AGRI-GIIRS Cloud Detection | 1280 | 265 |
| 1920 | 600 | |
| 2560 | 885 | |
| et (38 channels) | 1280 | within 1.5 s |
| 1920 | ||
| 2560 | ||
| et (689 channels) | 1280 | within 1.5 s |
| 1920 | ||
| 2560 | ||
| lr (38 channels) | 1280 | within 0.15 s |
| 1920 | ||
| 2560 | ||
| lr (689 channels) | 1280 | within 0.2 s |
| 1920 | ||
| 2560 |
| Model | POD | FAR | ACC | HSS |
|---|---|---|---|---|
| et (38 channels) | 0.902 | 0.460 | 0.749 | 0.432 |
| et (689 channels) | 0.912 | 0.431 | 0.775 | 0.501 |
| lr (38 channels) | 0.873 | 0.376 | 0.766 | 0.527 |
| lr (689 channels) | 0.929 | 0.36 | 0.787 | 0.504 |
| Cloud | Clear | Partial Cloud | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Label | Training Samples | Label | Training Samples | Label | Training Samples | ||||
| Sea | Land | Sea | Land | Sea | Land | ||||
| Model_1 | 0 | 7000 | 9300 | 1 | 7000 | 9300 | 2 | 6830 | 9202 |
| Model_2 | 0 | 7000 | 9300 | 1 | 14,500 | 16,595 | 0 | 6830 | 9202 |
| Type | model | region | input features | ACC | HSS |
|---|---|---|---|---|---|
| Three-Class Classification | Model_1 | Land | 38 channels | 0.562 | 0.334 |
| Model_1 | Land | 689 channels | 0.571 | 0.351 | |
| Model_1 | Sea | 38 channels | 0.644 | 0.438 | |
| Model_1 | sea | 689 channels | 0.736 | 0.604 | |
| Binary Classification | Mdoel_2 | Land | 38 channels | 0.783 | 0.401 |
| Model_2 | Land | 689 channels | 0.797 | 0.511 | |
| Model_2 | Sea | 38 channels | 0.762 | 0.467 | |
| Model_2 | sea | 689 channels | 0.769 | 0.545 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Yu, Y.; Zhang, W.; Luo, T.; Wang, X. Cloud Detection from FY-4A’s Geostationary Interferometric Infrared Sounder Using Machine Learning Approaches. Remote Sens. 2019, 11, 3035. https://doi.org/10.3390/rs11243035
Zhang Q, Yu Y, Zhang W, Luo T, Wang X. Cloud Detection from FY-4A’s Geostationary Interferometric Infrared Sounder Using Machine Learning Approaches. Remote Sensing. 2019; 11(24):3035. https://doi.org/10.3390/rs11243035
Chicago/Turabian StyleZhang, Qi, Yi Yu, Weimin Zhang, Tengling Luo, and Xiang Wang. 2019. "Cloud Detection from FY-4A’s Geostationary Interferometric Infrared Sounder Using Machine Learning Approaches" Remote Sensing 11, no. 24: 3035. https://doi.org/10.3390/rs11243035
APA StyleZhang, Q., Yu, Y., Zhang, W., Luo, T., & Wang, X. (2019). Cloud Detection from FY-4A’s Geostationary Interferometric Infrared Sounder Using Machine Learning Approaches. Remote Sensing, 11(24), 3035. https://doi.org/10.3390/rs11243035