Influence of Tropical Cyclone Intensity and Size on Storm Surge in the Northern East China Sea
Abstract
1. Introduction
1.1. Background
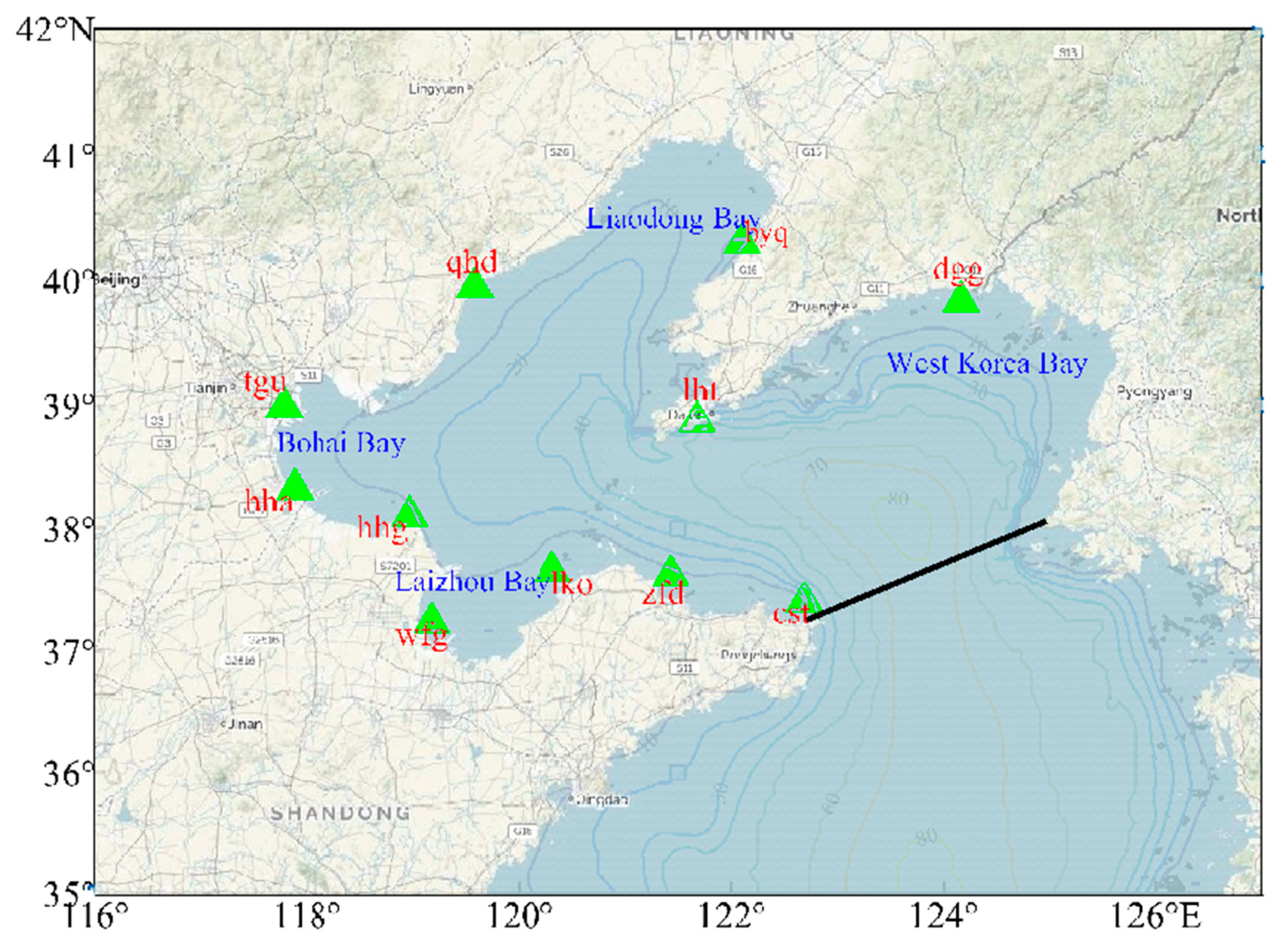
1.2. Study Area
2. Data and Methods
2.1. Typhoon Information and Data Processing
2.1.1. Typhoon Information
2.1.2. Satellite Data
2.1.3. Tide Station Data Processing
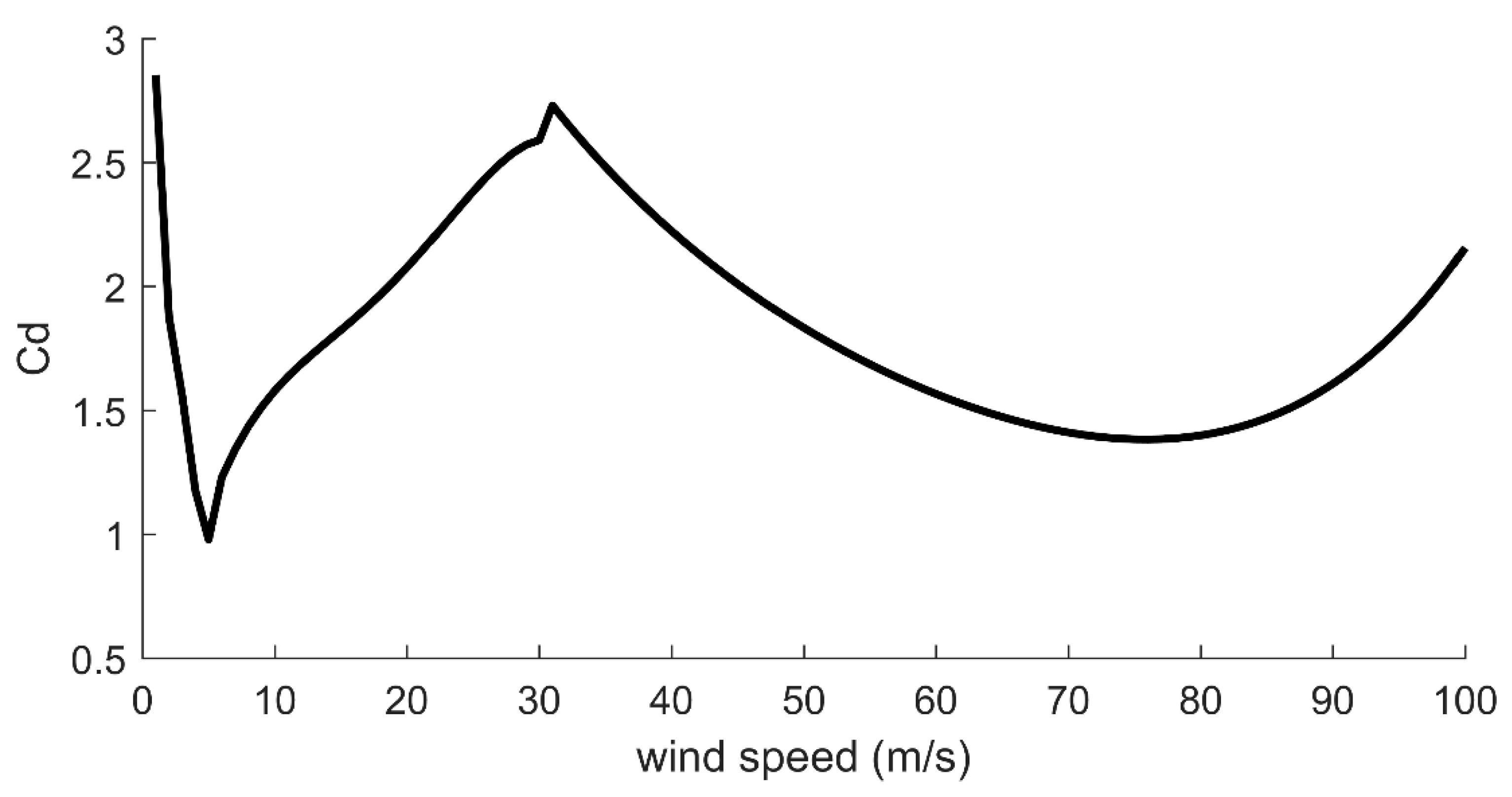
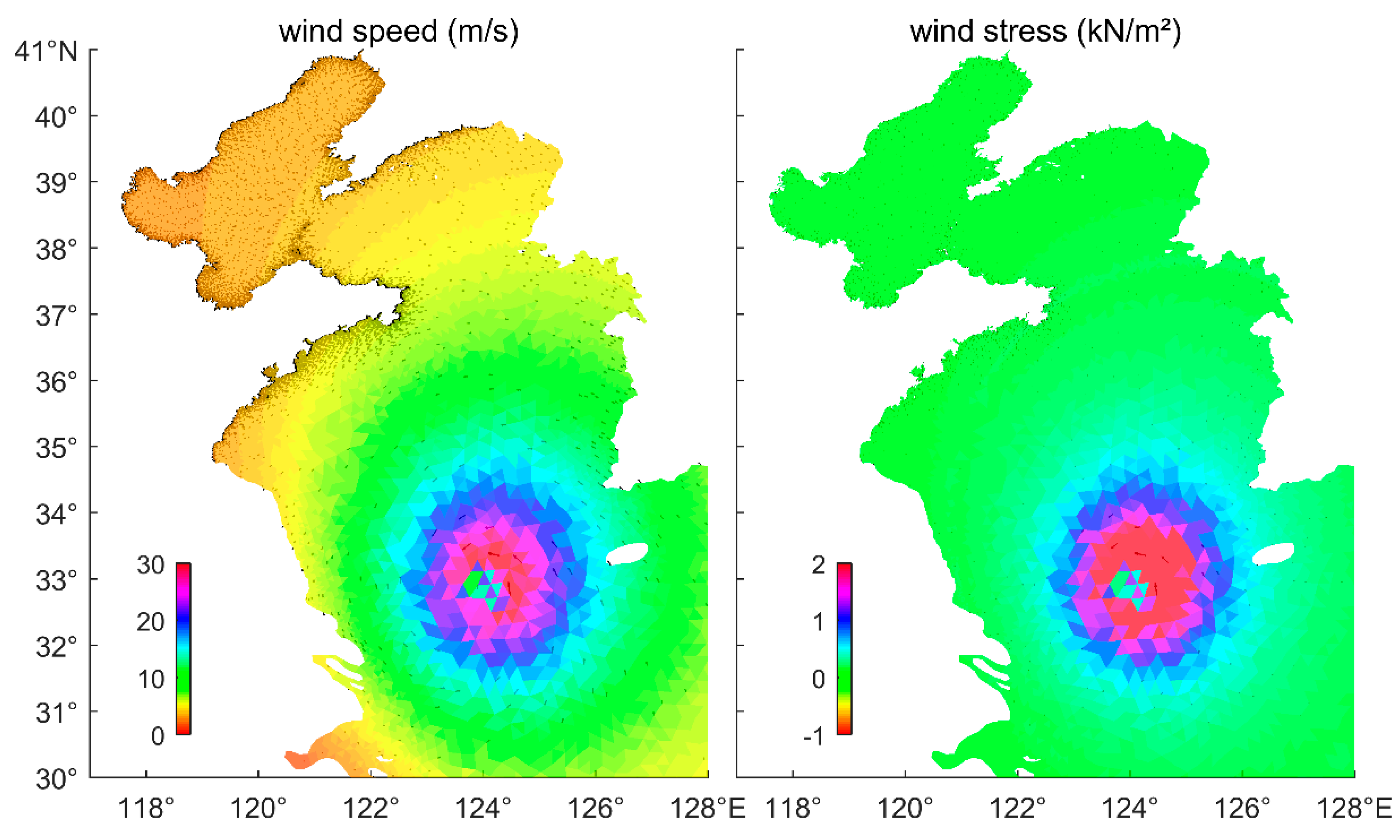
2.2. Wind Formula
3. Model and Validation
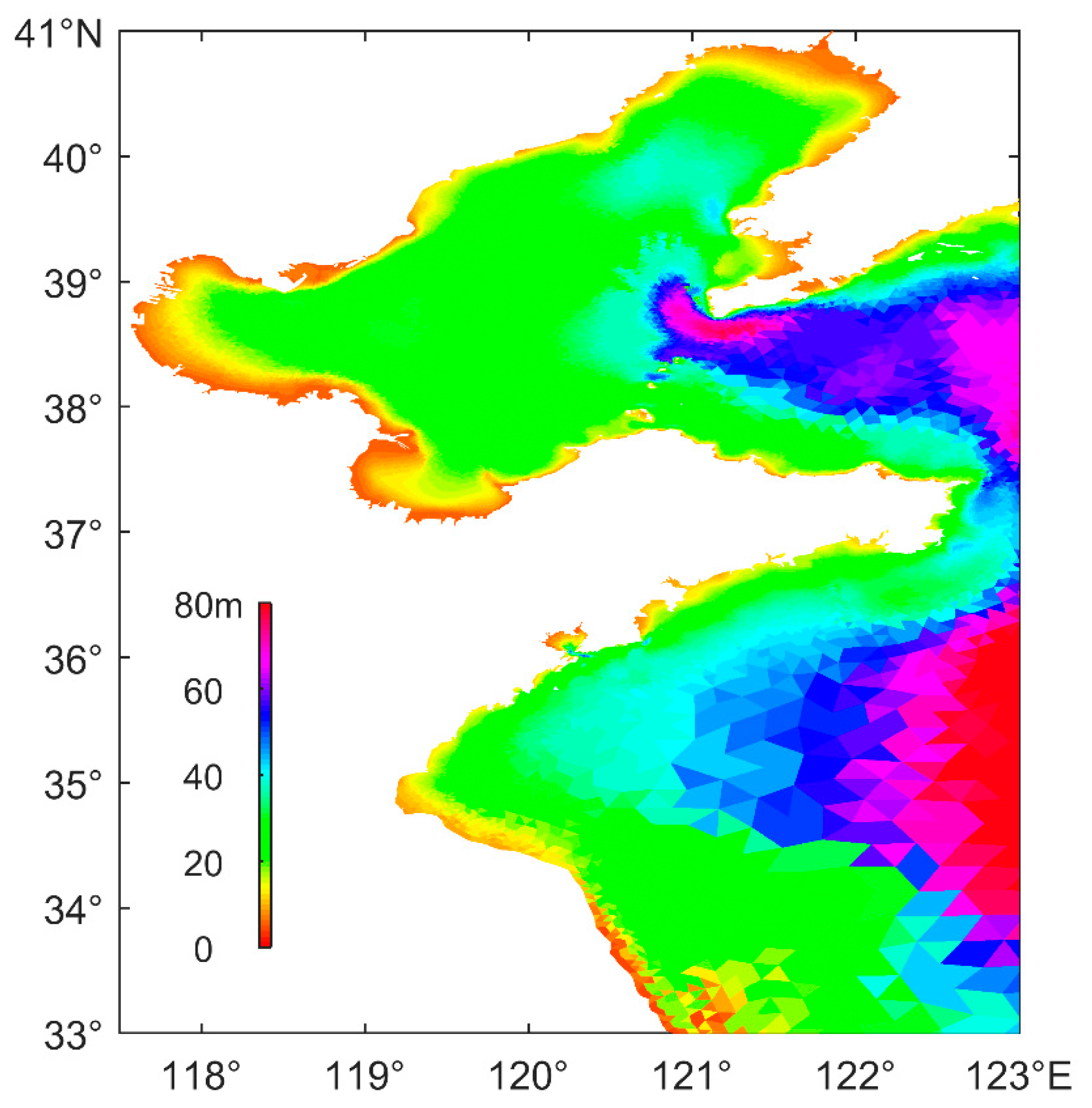
3.1. Model Description and Configuration
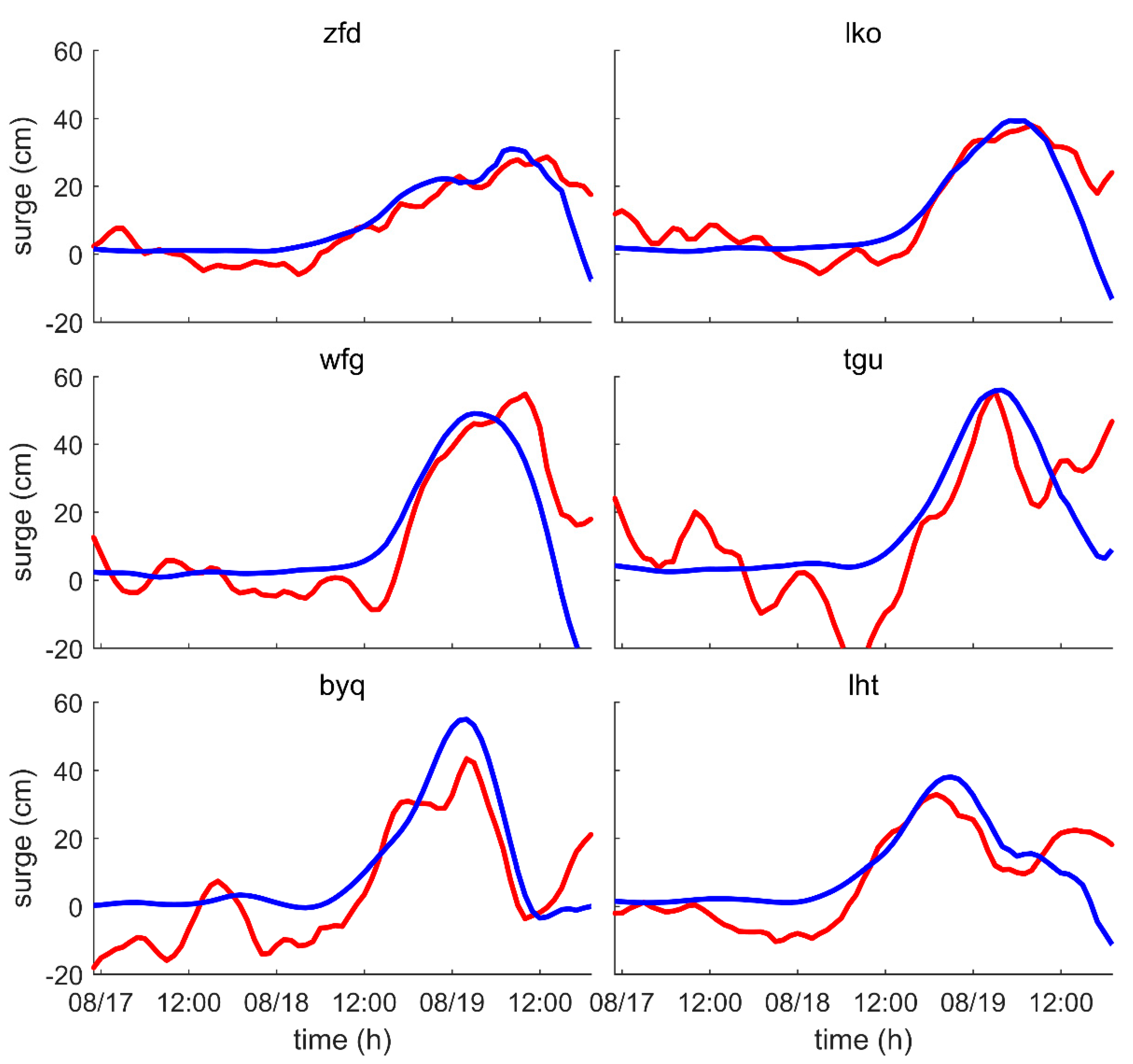
3.2. Model Validation
4. Results
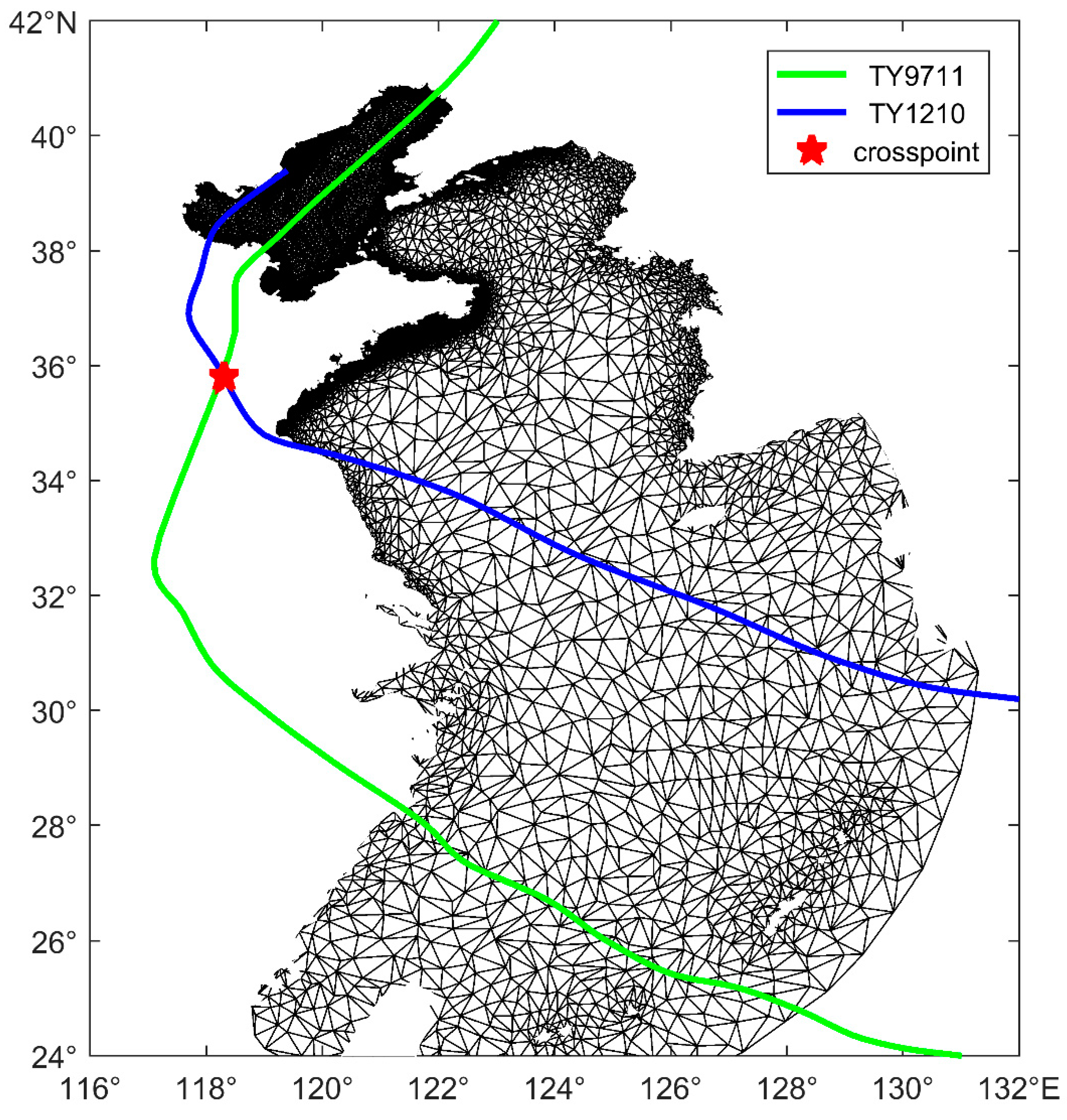
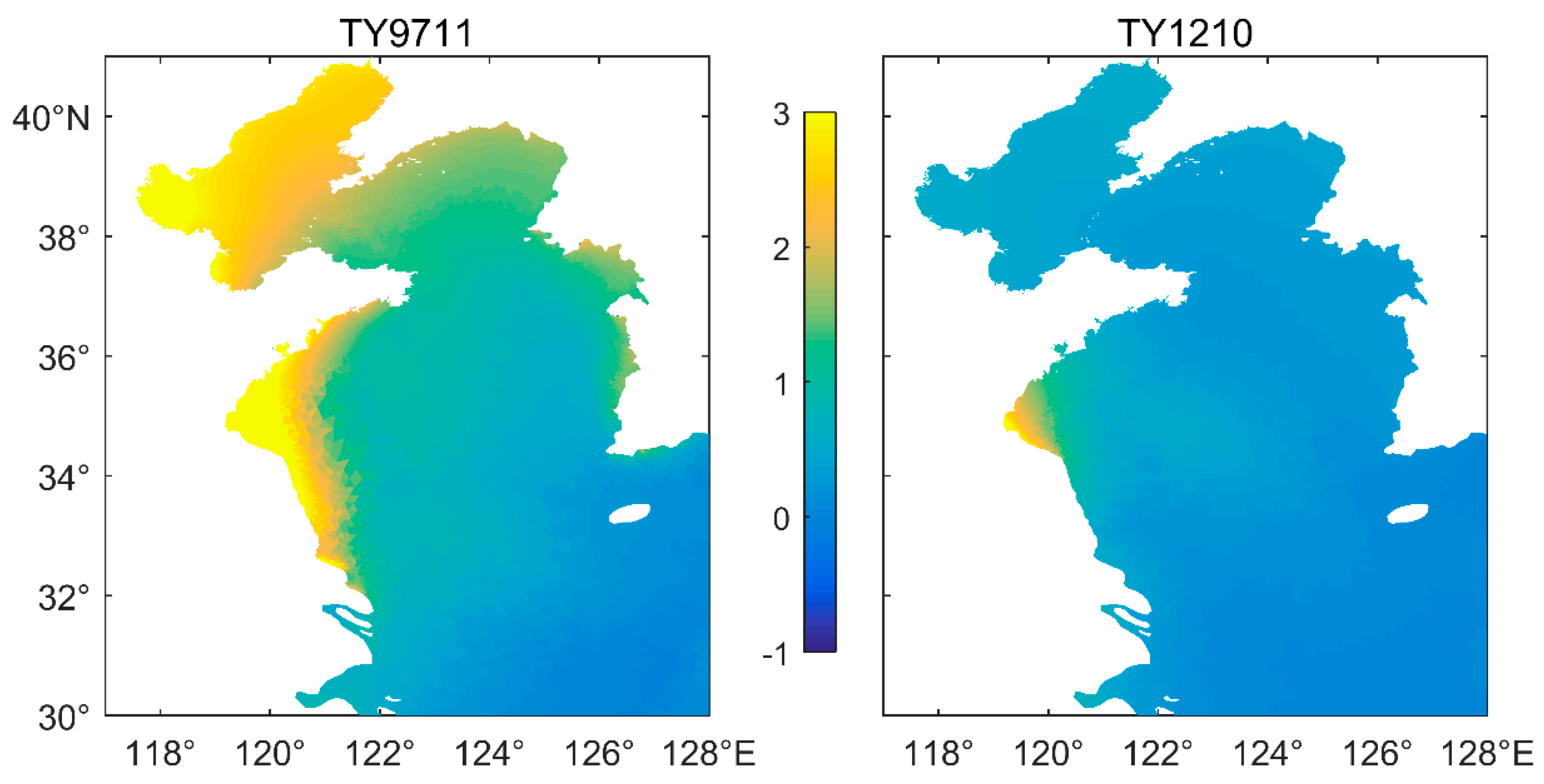
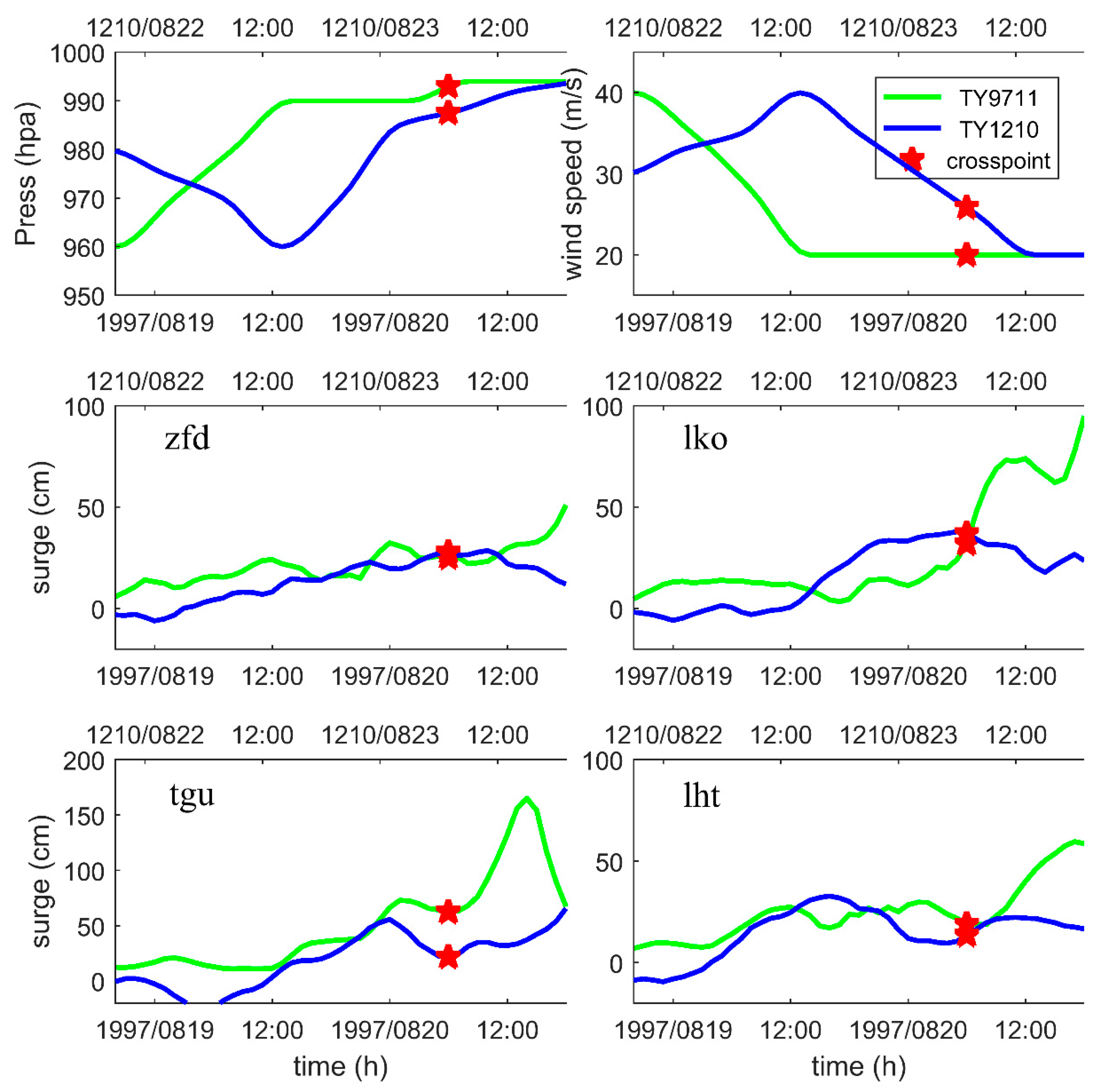
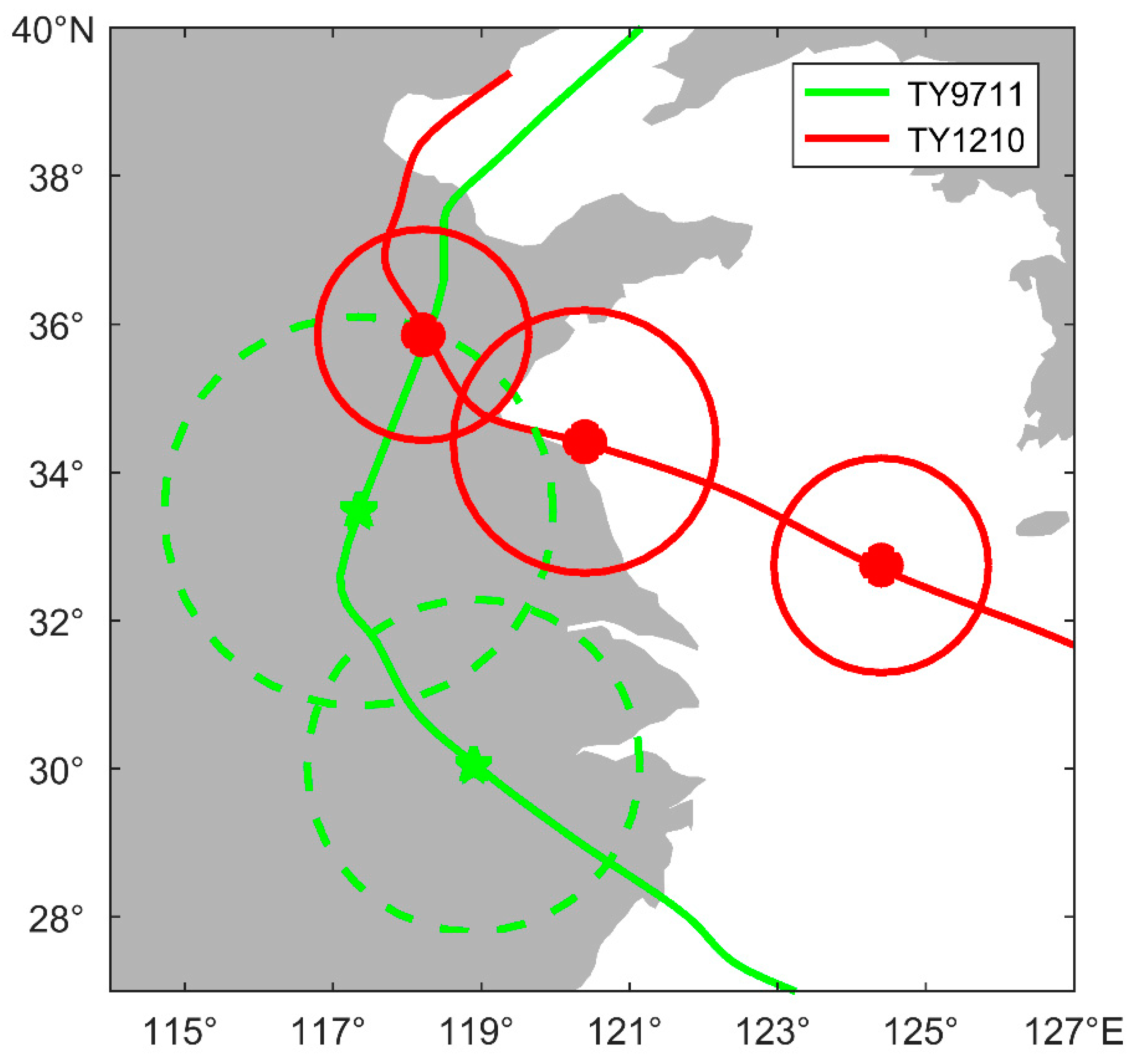
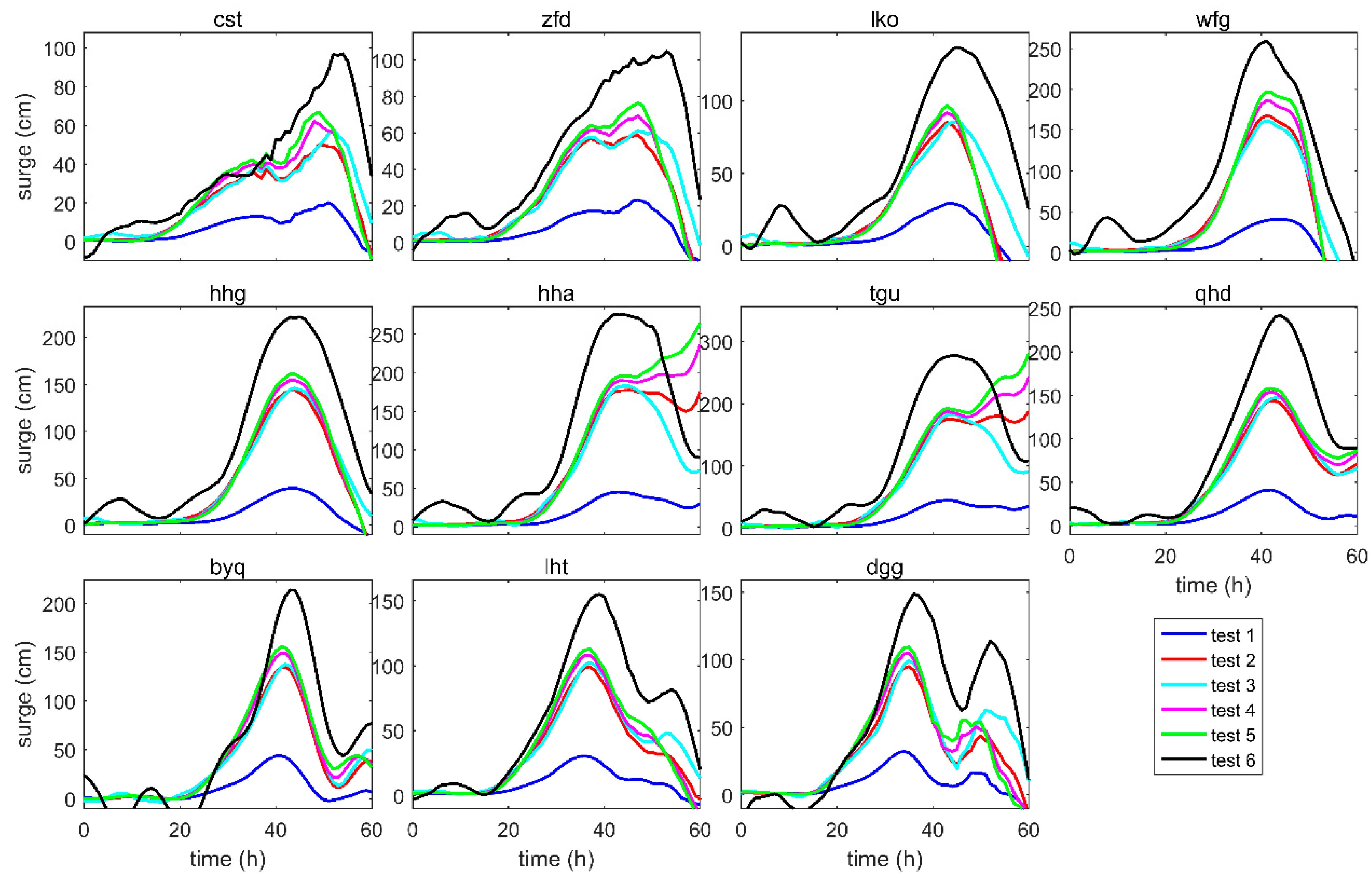
4.1. Comparison of Similar Typhoon Storm Surges
4.2. Ideal Tests
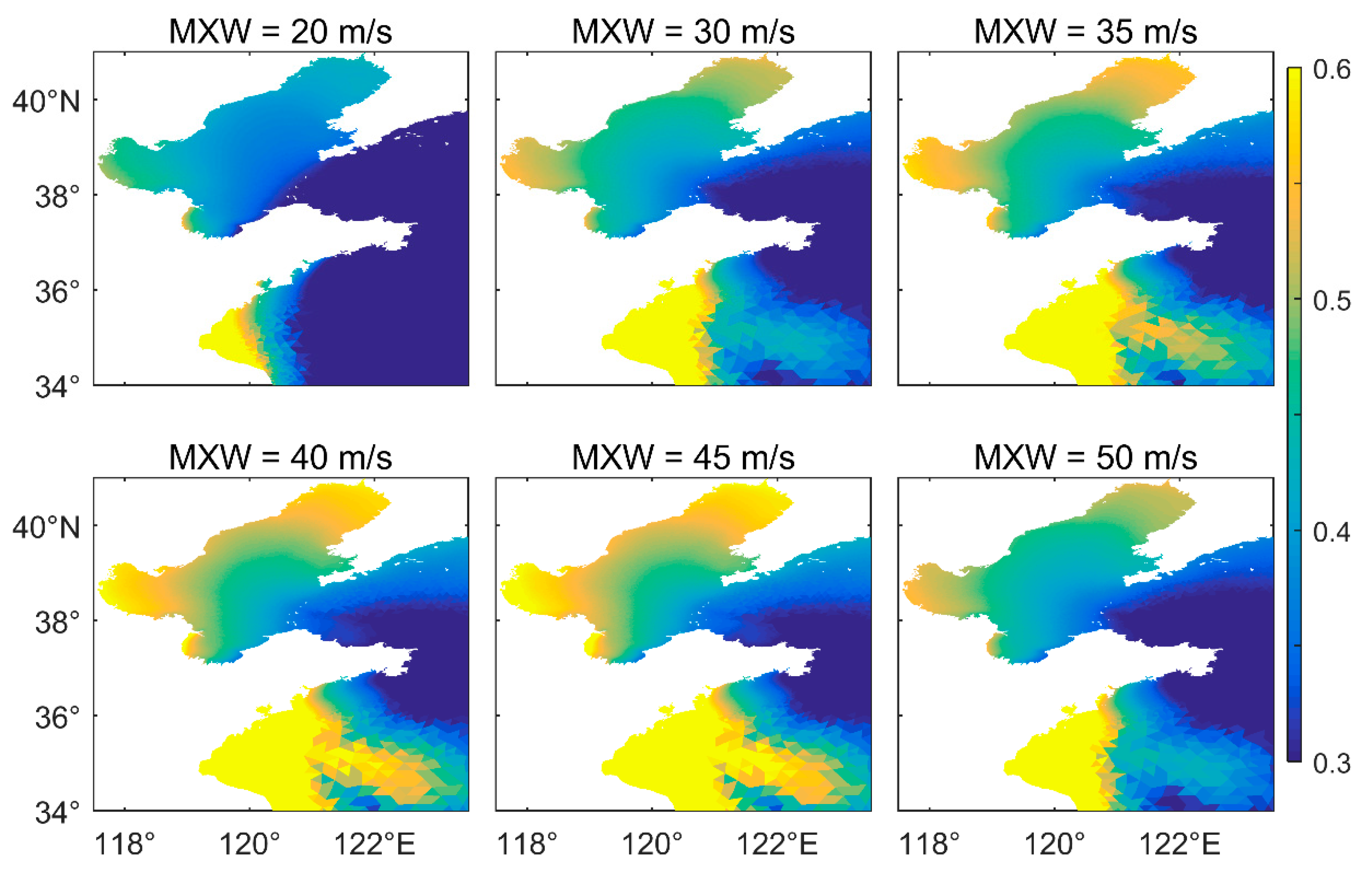
4.2.1. Maximum Wind Speed
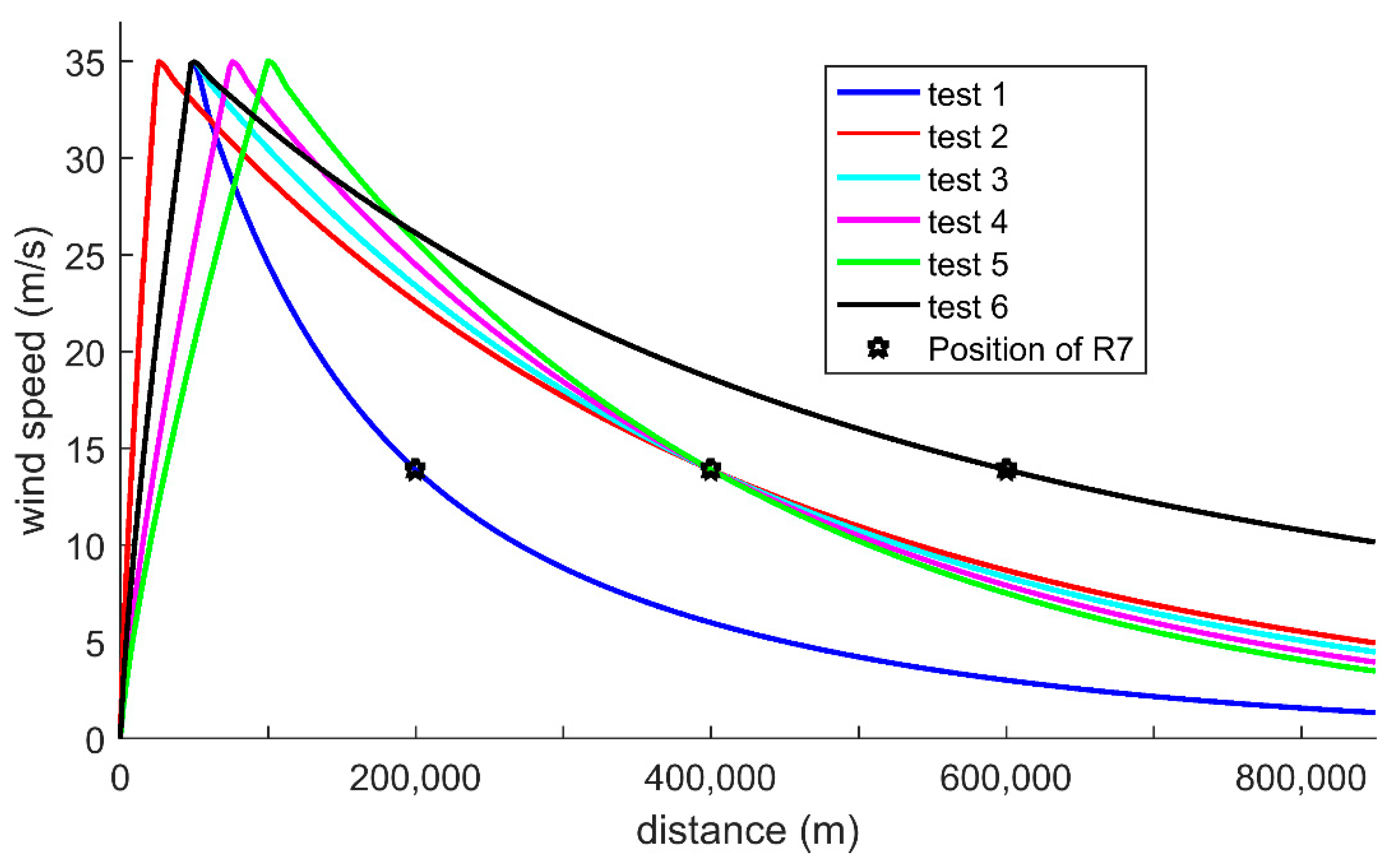
4.2.2. TC Size and RMW
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- You, S.H.; Seo, J.W. Storm surge prediction using an artificial neural network model and cluster analysis. Nat. Hazards 2009, 51, 97–114. [Google Scholar] [CrossRef]
- Yang, Z.Q.; Wang, T.P.; Leung, R.; Hibbard, K.; Janetos, T.; Kraucunas, I.; Rice, J.; Preston, B.; Wilbanks, T. A modeling study of coastal inundation induced by storm surge, sea-level rise, and subsidence in the Gulf of Mexico. Nat. Hazards 2014, 71, 1771–1794. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, Y.; Cao, A.; Liu, Q.; Lv, X. Effects of tide-surge interactions on storm surges along the coast of the Bohai Sea, Yellow Sea, and East China Sea. Sci. China Earth Sci. 2016, 59, 1308–1316. [Google Scholar] [CrossRef]
- Rey, W.; Mendoza, E.T.; Salles, P.; Zhang, K.; Teng, Y.C.; Trejo-Rangel, M.A.; Franklin, G.L. Hurricane flood risk assessment for the Yucatan and Campeche State Coastal Area. Nat. Hazards 2019, 96, 1041–1065. [Google Scholar] [CrossRef]
- Lin, N.; Emanuel, K.; Oppenheimer, M.; Vanmarcke, E. Physically based assessment of hurricane surge threat under climate change. Nat. Clim. Chang. 2012, 2, 462–467. [Google Scholar] [CrossRef]
- Andrade, C.A.; Thomas, Y.F.; Lerma, A.N.; Durand, P.; Anselme, B. Coastal flooding hazard related to swell events in Cartagena de Indias, Colombia. J. Coast. Res. 2013, 29, 1126–1136. [Google Scholar] [CrossRef]
- Olbert, A.; Nash, S.; Cunnane, C.; Hartnett, M. Tide-surge interactions and their effects on total sea levels in Irish coastal waters. Ocean Dyn. 2013, 63, 599–614. [Google Scholar] [CrossRef]
- Haigh, I.D.; Macpherson, L.R.; Mason, M.S.; Wijeratne, E.M.; Pattiaratchi, C.B.; Crompton, R.P. Estimating present day extreme water level exceedance probabilities around the coastline of Australia: Tropical cyclone-induced storm surges. Clim. Dyn. 2014, 42, 139–157. [Google Scholar] [CrossRef]
- Bonaldo, D.; Antonioli, F.; Archetti, R.; Bezzi, A.; Correggiari, A.; Davolio, S.; Falco, D.G.; Fantini, M.; Fontolan, G.; Furlani, S.; et al. Integrating multidisciplinary instruments for assessing coastal vulnerability to erosion and sea level rise: Lessons and challenges from the Adriatic Sea, Italy. J. Coast. Conserv. 2019, 23, 19–37. [Google Scholar] [CrossRef]
- Weisberg, R.H.; Zheng, L. Hurricane storm surge simulation for Tampa Bay. Estuar. Coasts 2006, 29, 899–913. [Google Scholar] [CrossRef]
- Orton, P.; Georgas, N.; Blumberg, A.; Pullen, J. Detailed modeling of recent severe storm tides in estuaries of the New York City region. J. Geophys. Res. Oceans 2012, 117. [Google Scholar] [CrossRef]
- Condon, A.J.; Sheng, Y.P. Optimal storm generation for evaluation of the storm surge inundation threat. Ocean Eng. 2012, 43, 13–22. [Google Scholar] [CrossRef]
- Iish, J.L.; Resio, D.T.; Ratcliff, J.J. The influence of storm size on hurricane surge. J. Phys. Oceanogr. 2008, 38, 2003–2013. [Google Scholar] [CrossRef]
- Sun, Y.; Zhong, Z.; Li, T.; Yi, L.; Hu, Y.; Wan, H.; Chen, H.; Liao, Q.; Ma, C.; Li, Q. Impact of ocean warming on tropical cyclone size and its destructiveness. Sci. Rep. 2017, 7, 8154. [Google Scholar] [CrossRef] [PubMed]
- Brand, S. Very large and very small typhoon of the Western North Pacific Ocean. J. Meteorol. Soc. Jpn. Ser. II 1972, 50, 332–341. [Google Scholar] [CrossRef]
- Merrill, R.T. A comparison of large and small tropical cyclones. Mon. Weather Rev. 1984, 112, 1408–1418. [Google Scholar] [CrossRef]
- Cocks, S.B.; Gray, W.M. Variability of the outer wind profiles of western North Pacific typhoons: Classifications and techniques for analysis and forecasting. Mon. Weather Rev. 2002, 130, 1989–2005. [Google Scholar] [CrossRef]
- Knaff, J.A.; Longmore, S.P.; Molenar, D.A. An objective satellite-based tropical cyclone size climatology. J. Clim. 2014, 27, 455–476. [Google Scholar] [CrossRef]
- Knaff, J.A.; Slocum, C.J.; Musgrave, K.D.; Sampson, C.R.; Strahl, B.R. Using Routinely Available Information to Estimate Tropical Cyclone Wind Structure. Mon. Weather Rev. 2016, 144, 1233–1247. [Google Scholar] [CrossRef]
- Holmlund, K.; Velden, C.S.; Rohn, M. Enhanced automated quality control applied to high-density satellite-derived winds. Mon. Weather Rev. 2016, 129, 517–529. [Google Scholar] [CrossRef]
- Velden, C.; Daniels, J.; Stettner, D.; Santek, D.; Key, J.; Dunion, J.; Holmlund, K.; Dengel, G.; Bresky, W.; Menzel, P. Recent innovations in deriving tropospheric winds from meteorological satellites. Bull. Am. Meteorol. Soc. 2005, 86, 205–223. [Google Scholar] [CrossRef]
- Jones, W.L.; Grantham, W.L.; Schroeder, L.C.; Johnson, J.W. Microwave scattering from the ocean surface (short papers). Microw. Theory Tech. IEEE Trans. 1975, 23, 1053–1058. [Google Scholar] [CrossRef]
- Lu, X.; Yu, H.; Yang, X.; Li, X. Estimating tropical cyclone size in the northwestern pacific from geostationary satellite infrared images. Remote Sens. 2017, 9, 728. [Google Scholar] [CrossRef]
- Lee, C.S.; Cheung, K.K.W.; Fang, W.T.; Elsberry, R.L. Initial maintenance of tropical cyclone size in the western North Pacific. Mon. Weather Rev. 2010, 138, 3207–3223. [Google Scholar] [CrossRef]
- Chan, K.T.F.; Chan, J.C.L. Size and strength of tropical cyclones as inferred from QuikSCAT data. Mon. Weather Rev. 2012, 140, 811–824. [Google Scholar] [CrossRef]
- Liu, K.S.; Chan, J.C.L. Size of Tropical cyclone as inferred from ERS-1 and ERS-2 Data. Mon. Weather Rev. 1999, 127, 2992–3001. [Google Scholar] [CrossRef]
- Holland, G. An analytic model of the wind and pressure profiles in Hurricanes. Mon. Weather Rev. 1980, 108, 1212–1218. [Google Scholar] [CrossRef]
- Zou, X.L.; Xiao, Q.N. Studies on the initialization and simulation of a mature hurricane using a variational bogus data assimilation scheme. J. Atmos. Sci. 1999, 57, 836–860. [Google Scholar] [CrossRef]
- Knaff, J.A.; DeMaria, M.; Molenar, D.A.; Sampson, C.R.; Seybold, M.G. An automated, objective, multi-satellite platform tropical cyclone surface wind analysis. J. Appl. Meteorol. Climatol. 2011, 50, 2149–2166. [Google Scholar] [CrossRef]
- Ricchi, A.; Miglietta, M.M.; Bonaldo, D.; Cioni, G.; Rizza, U.; Carniel, S. Multi-physics ensemble versus Atmosphere–Ocean coupled model simulations for a tropical-like cyclone in the Mediterranean Sea. Atmosphere 2019, 10, 202. [Google Scholar] [CrossRef]
- Benetazzo, A.; Barbariol, F.; Bergamasco, F.; Torsello, A.; Carniel, S.; Sclavo, M. Observation of extreme sea waves in a space-time ensemble. J. Phys. Oceanogr. 2015, 45, 2261–2275. [Google Scholar] [CrossRef]
- Needham, H.F.; Keim, B.D. An empirical analysis on the relationship between tropical cyclone size and storm surge heights along the US. Gulf Coast. Earth Interact. 2014, 18, 1–15. [Google Scholar] [CrossRef]
- Mo, D.; Hou, Y.; Li, J.; Liu, Y. Study on the storm surges induced by cold waves in the northern east China Sea. J. Mar. Syst. 2016, 160, 26–39. [Google Scholar] [CrossRef]
- Liu, F.; Su, J.; Moll, A.; Krasemann, H.; Chen, X.; Pohlmann, T.; Wirtz, K. Assessment of the summer–autumn bloom in the bohai sea using satellite images to identify the roles of wind mixing and light conditions. J. Mar. Syst. 2014, 129, 303–317. [Google Scholar] [CrossRef]
- Hu, L.; Shi, X.; Bai, Y.; Qiao, S.; Li, L.; Yu, Y.; Yang, G.; Ma, D.; Guo, Z. Recent organic carbon sequestration in the shelf sediments of the Bohai Sea and Yellow Sea, China. J. Mar. Syst. 2015, 155, 50–58. [Google Scholar] [CrossRef]
- Bao, X.; Na, L.; Yao, Z.; Wu, D. Seasonal variation characteristics of temperature and salinity of the North Yellow Sea. Period. Ocean. Univ. China 2009, 39, 553–562. [Google Scholar]
- Hyangsun, H.; Sanggyun, L.; Jungho, I.; Miae, K.; Myong-In, L.; Myoung, A.; Sung, C. Detection of convective initiation using meteorological imager onboard communication, ocean, and meteorological satellite based on machine learning approaches. Remote Sens. 2015, 7, 9184–9204. [Google Scholar] [CrossRef]
- Broomhall, M.; Grant, I.; Majewski, L.; Willmott, M.; Jones, D.; Kuleshov, Y. Improving the Australian tropical cyclone database: Extension of the GMS satellite digital image archive. In Indian Ocean Tropical Cyclones and Climate Change; Springer: Haarlem, The Netherlands, 2010; pp. 199–206. [Google Scholar] [CrossRef]
- Yi, L.; Zhang, S.P.; Thies, B.; Shi, X.M.; Trachte, K.; Bendix, J. Spatio-temporal detection of fog and low stratus top heights over the yellow sea with geostationary satellite data as a precondition for ground fog detection—A feasibility study. Atmos. Res. 2015, 151, 212–223. [Google Scholar] [CrossRef]
- Willoughby, H.E.; Darling, R.W.; Rahn, M.E. Parametric representation of the primary hurricane vortex. Part II: A new family of sectionally continuous profiles. Mon. Weather Rev. 2006, 134, 1102–1120. [Google Scholar] [CrossRef]
- Jelesnianski, C.; Chen, J.; Shaffer, W. SLOSH: Sea, Lake, and Overland Surges from Hurricanes; NOAA Tech. Rep. NWS 48; United States Department of Commerce, NOAA/AOML Library: Miami, FL, USA, 1992; p. 71.
- Holland, G.J.; Belanger, J.I.; Fritz, A. A revised model for radial profiles of hurricane winds. Mon. Weather Rev. 2010, 138, 4393–4401. [Google Scholar] [CrossRef]
- Moon, I.J.; Ginis, I.; Hara, T. Impact of the reduced drag coefficient on ocean wave modeling under hurricane conditions. Mon. Weather Rev. 2018, 136, 1217–1223. [Google Scholar] [CrossRef]
- Powell, M.D.; Vickery, P.J.; Reinhold, T.A. Reduced drag coefficient for high wind speeds in tropical cyclones. Nature 2003, 422, 279–283. [Google Scholar] [CrossRef] [PubMed]
- Oey, L.Y.; Ezer, T.; Wang, D.P.; Fan, S.J.; Yin, X.Q. Loop current warming by Hurricane Wilma. Geophys. Res. Lett. 2006, 33, 153–172. [Google Scholar] [CrossRef]
- Chen, C.; Liu, H.; Beardsley, R.C. An unstructured grid, finite-volume, three-dimensional, primitive equations ocean model: Application to coastal ocean and estuaries. J. Atmos. Ocean. Technol. 2003, 20, 159–186. [Google Scholar] [CrossRef]
- Benassai, G.; Migliaccio, M.; Montuori, A. Sea wave numerical simulations with COSMO-SkyMed? SAR data. J. Coast. Res. 2013, 65, 660–665. [Google Scholar] [CrossRef]
- Zachry, B.C.; Booth, W.J.; Rhome, J.R.; Sharon, T.M. A national view of storm surge risk and inundation. Weather Clim. Soc. 2015, 7, 109–117. [Google Scholar] [CrossRef]
- Lin, Y.; Zhao, M.; Zhang, M. Tropical cyclone rainfall area controlled by relative sea surface temperature. Nat. Commun. 2015, 6, 6591. [Google Scholar] [CrossRef]
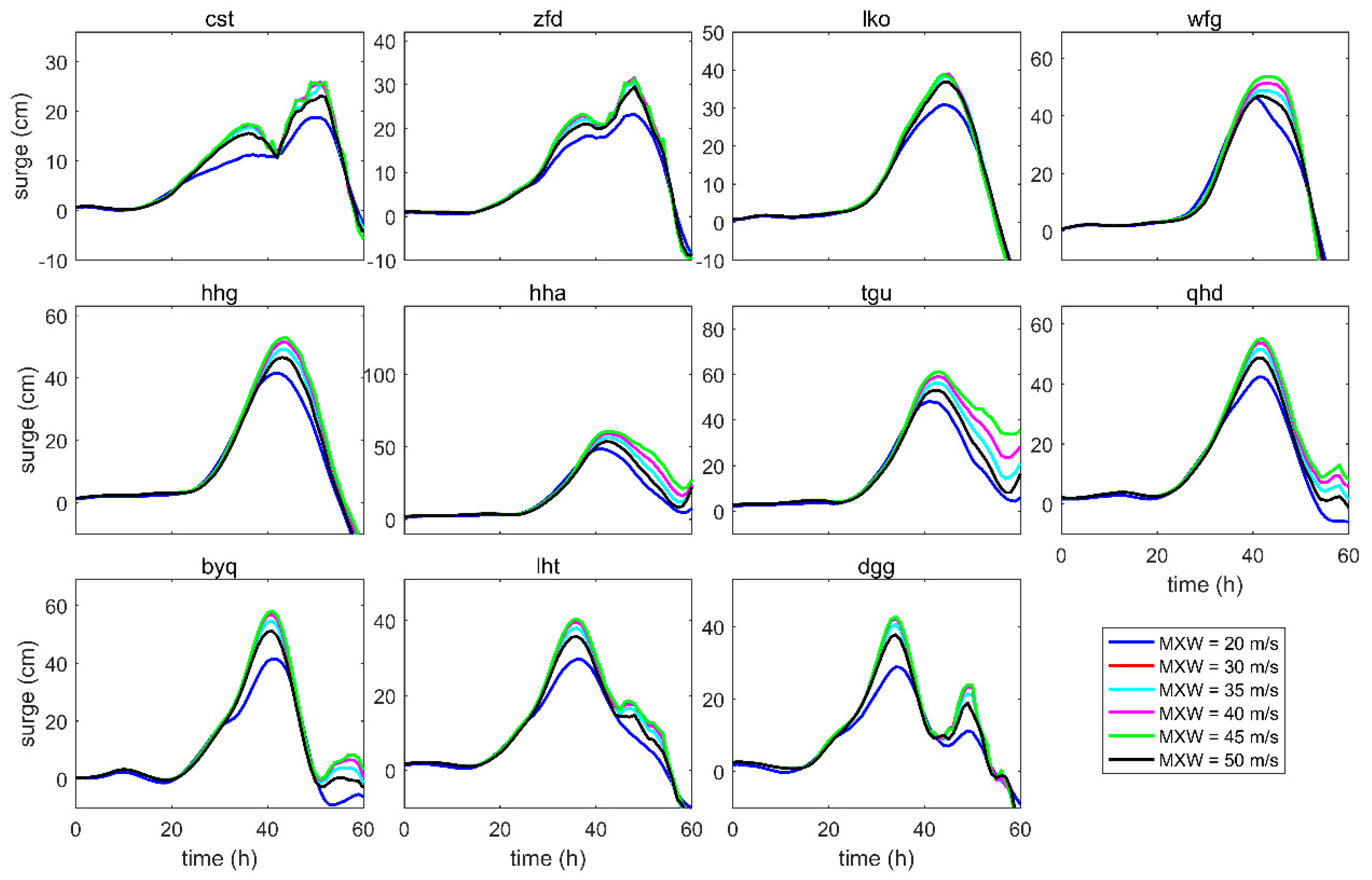
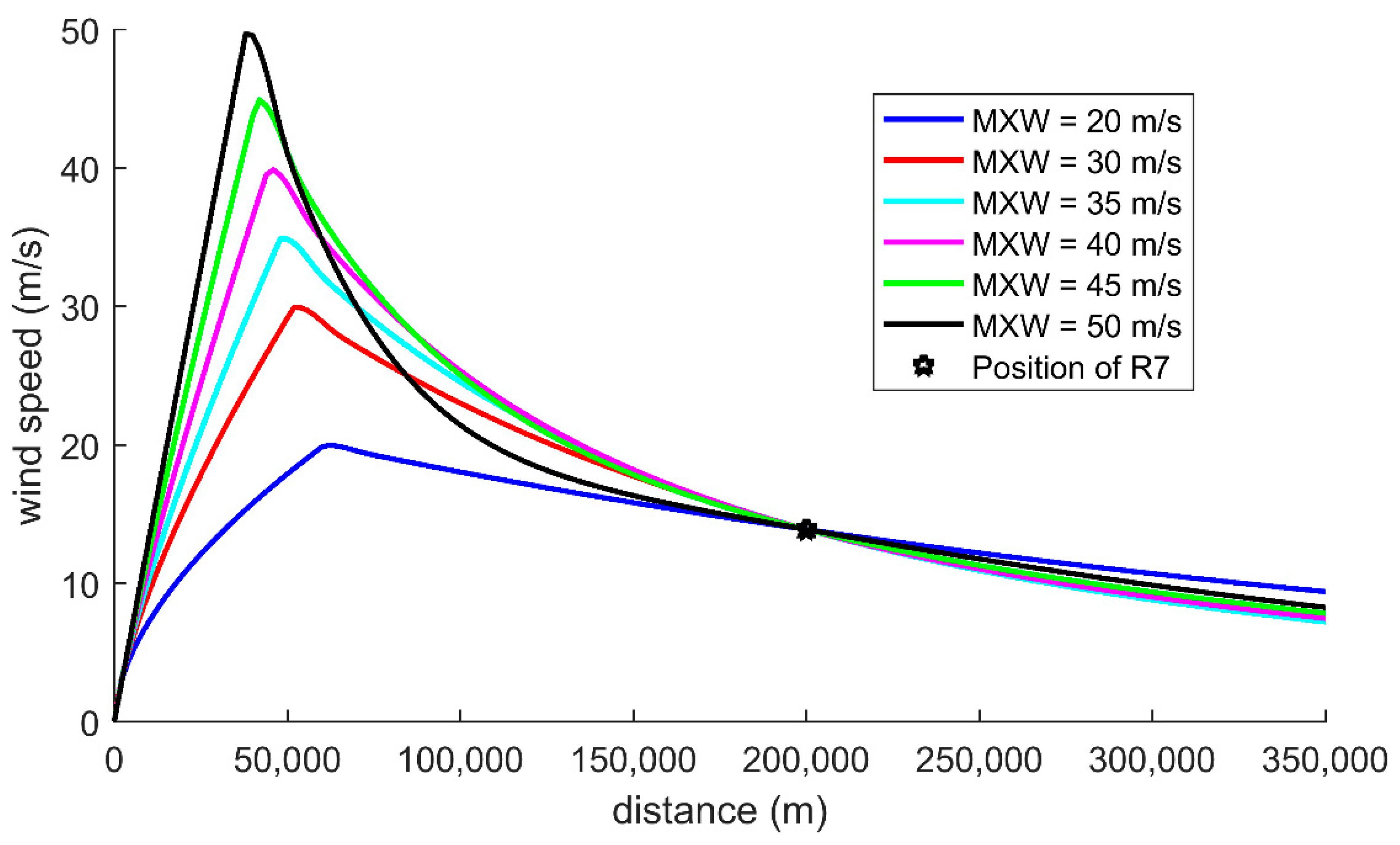
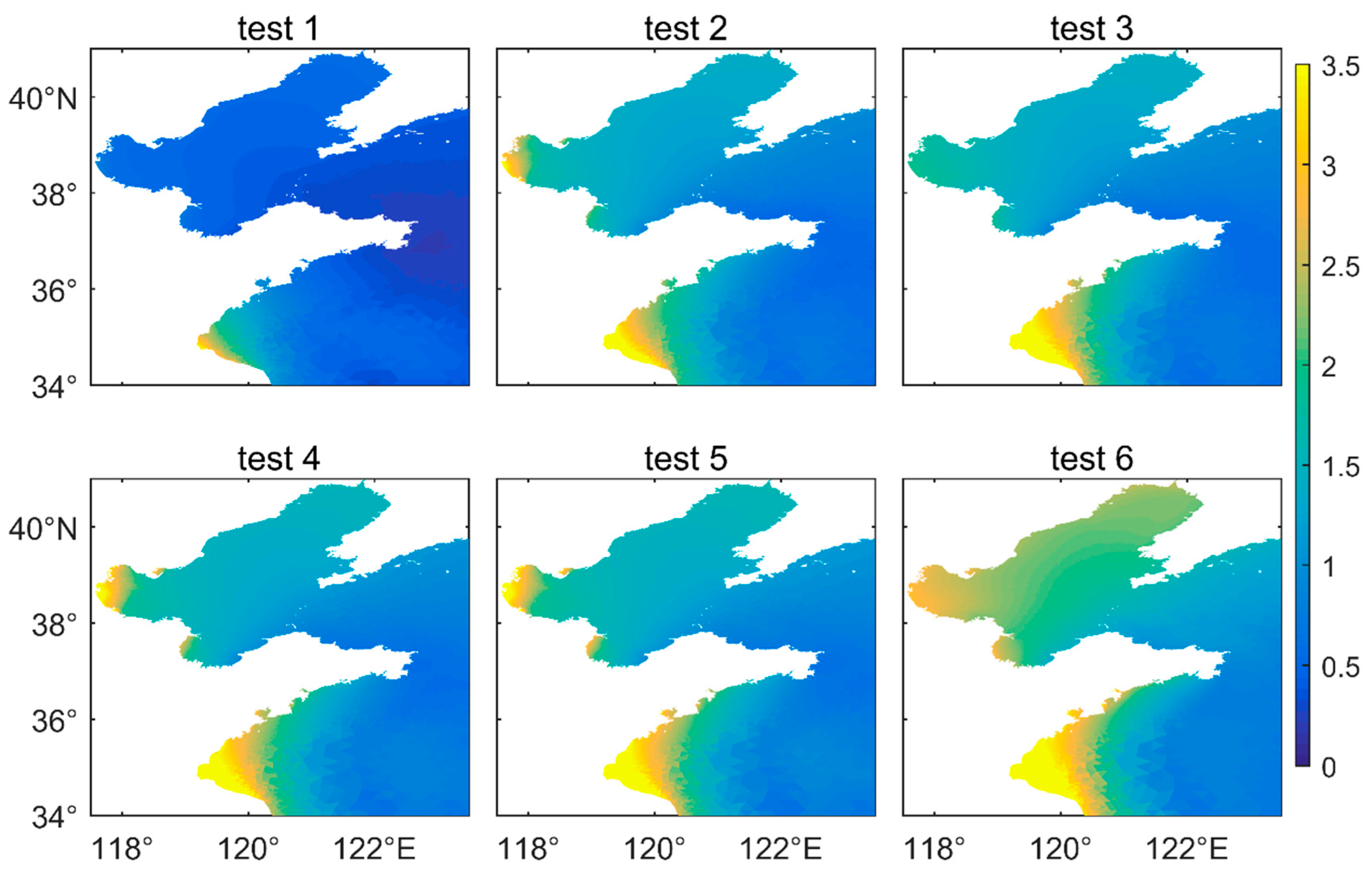
| MXW (m/s) | RMW (m, Latitude = 36°N) | R7 (m) | |
|---|---|---|---|
| test 1 | 20 | 62,533 | 200,000 |
| test 2 | 30 | 53,555 | 200,000 |
| test 3 | 35 | 49,561 | 200,000 |
| test 4 | 40 | 45,865 | 200,000 |
| test 5 | 45 | 42,445 | 200,000 |
| test 6 | 50 | 39,279 | 200,000 |
| MXW (m/s) | RMW (m, Latitude = 36°N) | R7 (m) | |
|---|---|---|---|
| test 1 | 35 m/s | 49,561 | 200,000 |
| test 2 | 35 m/s | 25,000 | 400,000 |
| test 3 | 35 m/s | 49,561 | 400,000 |
| test 4 | 35 m/s | 75,000 | 400,000 |
| test 5 | 35 m/s | 100,000 | 400,000 |
| test 6 | 35 m/s | 49,561 | 600,000 |
| Jiangsu | Shandong | Hebei | Tianjin | Total | |
|---|---|---|---|---|---|
| TY9711 (million yuan) | 3000 | 4500 | 200 | 600 | 8300 |
| TY1210 (million yuan) | 537 | 1599 | 2044 | 4 | 4184 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Hou, Y.; Mo, D.; Liu, Q.; Zhang, Y. Influence of Tropical Cyclone Intensity and Size on Storm Surge in the Northern East China Sea. Remote Sens. 2019, 11, 3033. https://doi.org/10.3390/rs11243033
Li J, Hou Y, Mo D, Liu Q, Zhang Y. Influence of Tropical Cyclone Intensity and Size on Storm Surge in the Northern East China Sea. Remote Sensing. 2019; 11(24):3033. https://doi.org/10.3390/rs11243033
Chicago/Turabian StyleLi, Jian, Yijun Hou, Dongxue Mo, Qingrong Liu, and Yuanzhi Zhang. 2019. "Influence of Tropical Cyclone Intensity and Size on Storm Surge in the Northern East China Sea" Remote Sensing 11, no. 24: 3033. https://doi.org/10.3390/rs11243033
APA StyleLi, J., Hou, Y., Mo, D., Liu, Q., & Zhang, Y. (2019). Influence of Tropical Cyclone Intensity and Size on Storm Surge in the Northern East China Sea. Remote Sensing, 11(24), 3033. https://doi.org/10.3390/rs11243033





