1. Introduction
The rapid and accurate acquisition of disaster losses can provide great help for disaster emergency response and decision-making. Remote sensing (RS) and Geographic Information System (GIS) can help assess earthquake damage within a short period of time after the event.
Many studies have presented assessment techniques for earthquake building damage by using aerial or satellite images [
1,
2,
3,
4,
5]. Booth et al. [
6] used vertical aerial images, Pictometry images, and ground observations to assess building damage in the 2011 Haitian earthquake. Building by building visual damage interpretation [
7] based on the European Macroseismic Scale (EMS-98) [
8] was carried out in a case study of the Bam earthquake. Huyck et al. [
9] used multisensor optical satellite imagery to map citywide damage with neighborhood edge dissimilarities. Many different features have been introduced to determine building damage from remote sensing images [
10]. Anniballe et al. [
11] investigated the capability of earthquake damage mapping at the scale of individual buildings with a set of 13 change detention features and support vector machine (SVM). Simon Plank [
12] reviewed the methods of rapid damage assessment using multitemporal Synthetic Aperture Radar(SAR) data. Gupta et al. [
13] present a satellite imagery dataset for building damage assessment with over 700,000 labeled building instances covering over 5000 km
2 of imagery.
Recent studies show that the machine learning algorithm performs well in earthquake damage assessment. Li [
14] assessed building damage with one-class SVM using pre- and post-earthquake QuickBird imagery and assessed the discrimination power of different level (pixel-level, texture, and object-based) features. Haiyang et al. [
15] combined SVM and the image segmentation method to detect building damage. Cooner et al. [
16] evaluate the effectiveness of machine learning algorithms in detecting earthquake damage. A series of textural and structural features were used in this study. A SVM and feature selection approach was carried out for damage mapping with post-event very high spatial resolution(VHR) image and obtained overall accuracy (OA) of 96.8% and Kappa of 0.5240 [
11]. Convolutional neural networks (CNN) was utilized to identify collapsed buildings from post-event satellite imagery and obtained an OA of 80.1% and Kappa of 0.46 [
17]. Multiresolution feature maps were derived and fused with CNN for the image classification of building damages in [
18], and an OA of 88.7% was obtained.
Most of the above-mentioned damage information extraction studies classified damaged buildings into two classes: damaged and intact. However, these two classes are not enough to meet actual needs.
Recently, deep learning (DL) methods have provided new ideas for remote sensing image recognition technology. An end-to-end framework with CNN for satellite image classification was proposed in [
19]. Scott et al. [
20] used transfer learning and data augmentation to demonstrate the performance of CNNs for remote sensing land-cover classification. Zou et al. [
21] proposed a DL method for remote sensing scene classification. A DL-based image classification framework was introduced in [
22]. Xie et al. [
23] designed a deep CNN model that can achieve a multilevel detection of clouds. Chen et al. [
24] combined a pretrained CNN feature extractor and the k-Nearest Neighbor(KNN) method to improve the performance of ship classification from remote sensing images.
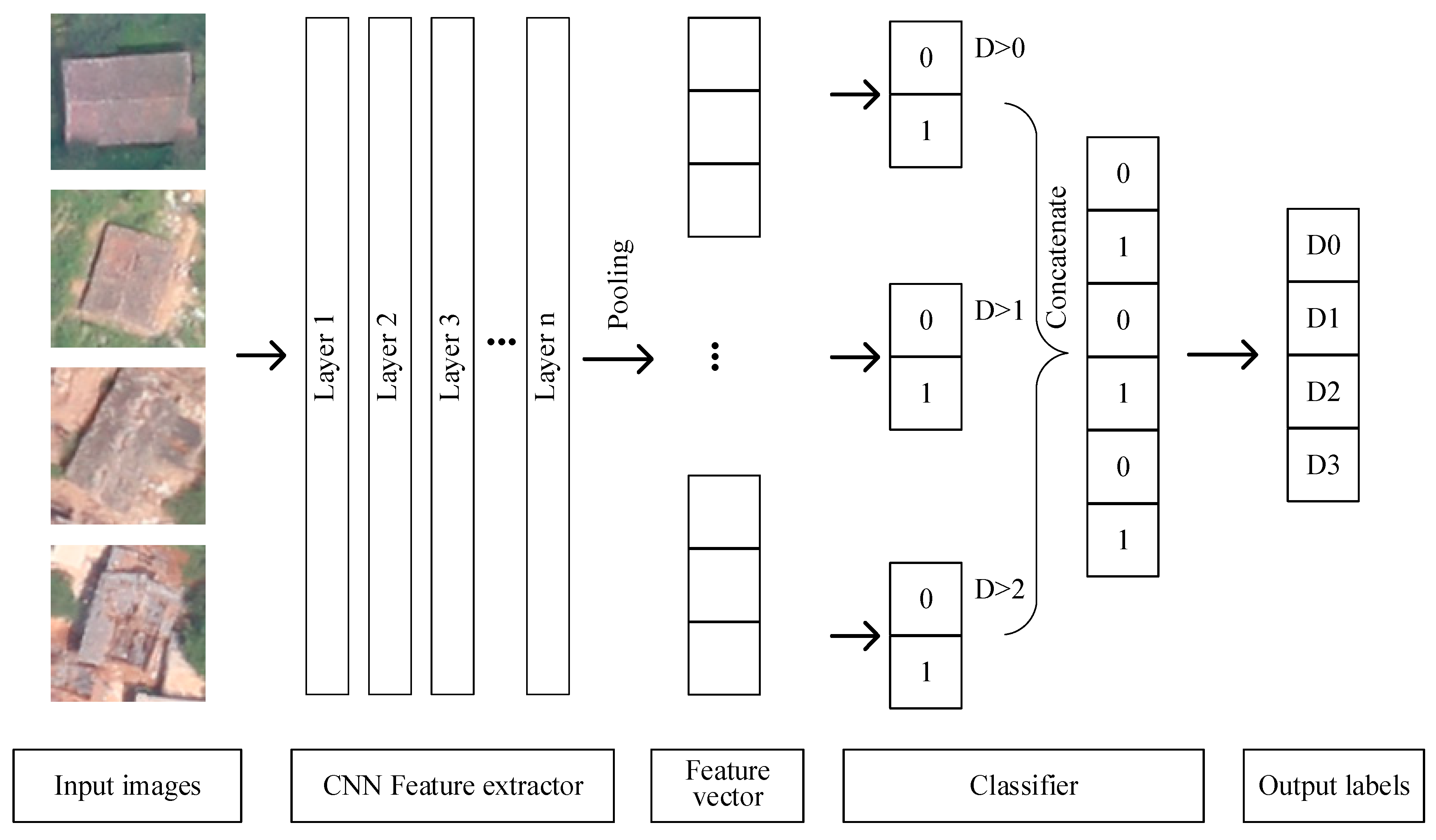
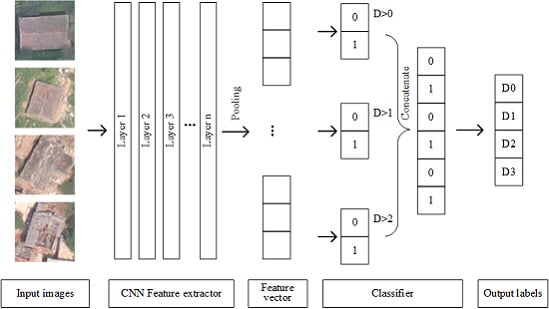
In this paper, we propose a new approach based on CNNs and ordinal regression (OR) aiming at assessing the degree of building damage caused by earthquakes with aerial imagery. CNNs hierarchically extract useful high-level features from input building images, and then OR is used to classify the features into four different damage grades. Then, we can get the degree of damaged buildings. The manually labeled damaged building dataset in this paper was obtained from aerial images after several historical earthquakes. The proposed mothed was evaluated with different network architecture and classifiers. We also compared the method with several state-of-the-art methods including hand-engineered features such as edge, texture, spectra, and morphology feature and machine learning methods.
This is the first attempt to apply OR to assess the degree of building damage from aerial imagery. OR (also called ”ordinal classification”) is used to predict an ordinal variable. In this paper, the building damage degree, on a scale from “no observable damage” to “collapse”, is just an ordinal variable. However, typical multiclass classification ignores the ordered information between the damage degree, while damage degrees have a strong ordinal correlation. Thus, we cast the assessment problem of the degree building damage as an OR problem and develop an ordinal classifier and corresponding loss function to learn our network parameters. Information utilization was improved by OR, so we can achieve a better accuracy with the same or a lesser amount of data. When categorizing the damage to buildings into four types, we apply the method proposed in this paper to aerial images acquired from the 2014 Ludian earthquake and achieve an overall accuracy of 77.49%; when categorizing the damage to buildings into two types, the overall accuracy of the model is 93.95%, exceeding such values in similar types of theories and methods.
Another contribution of this work is a dataset of labeled building damage including 13,780 individual buildings from aerial data by visual interpretation that is classified into four damage degrees building by building.
The main contributions of this paper are summarized as follows:
(1) A deep ordinal regression network for assessing the degree of building damage caused by an earthquake. The proposed network uses a CNN for extracting features and an OR loss for optimizing classification results. Different CNNs’ architecture has also been evaluated.
(2) A dataset with more than 13,000 optical aerial images of labeled damage buildings can be download freely.
The rest of the paper is organized as follows:
Section 2 presents an introduction to the dataset used in this research.
Section 3 has a brief introduction to CNN and OR.
Section 4 describes the proposed method and the different CNN architectures that we evaluated. We present the results of the experiments in
Section 5. Finally, conclusions are drawn in
Section 6.
6. Discussion
The proposed method is an "end-to-end" solution. The input to this method is the sample image data, and the output is the damage level label. The method can directly obtain the available results without worrying about intermediate products. Considering the damage level of a building as an OR problem with ordered labels, it can make more effective use of model input information, which can improve the accuracy of the model and reduce the MSE of the prediction results. The deep learning-based algorithm model applied in this paper can also be regarded as a data-driven method. This means that the larger the dataset, the better the model performance.
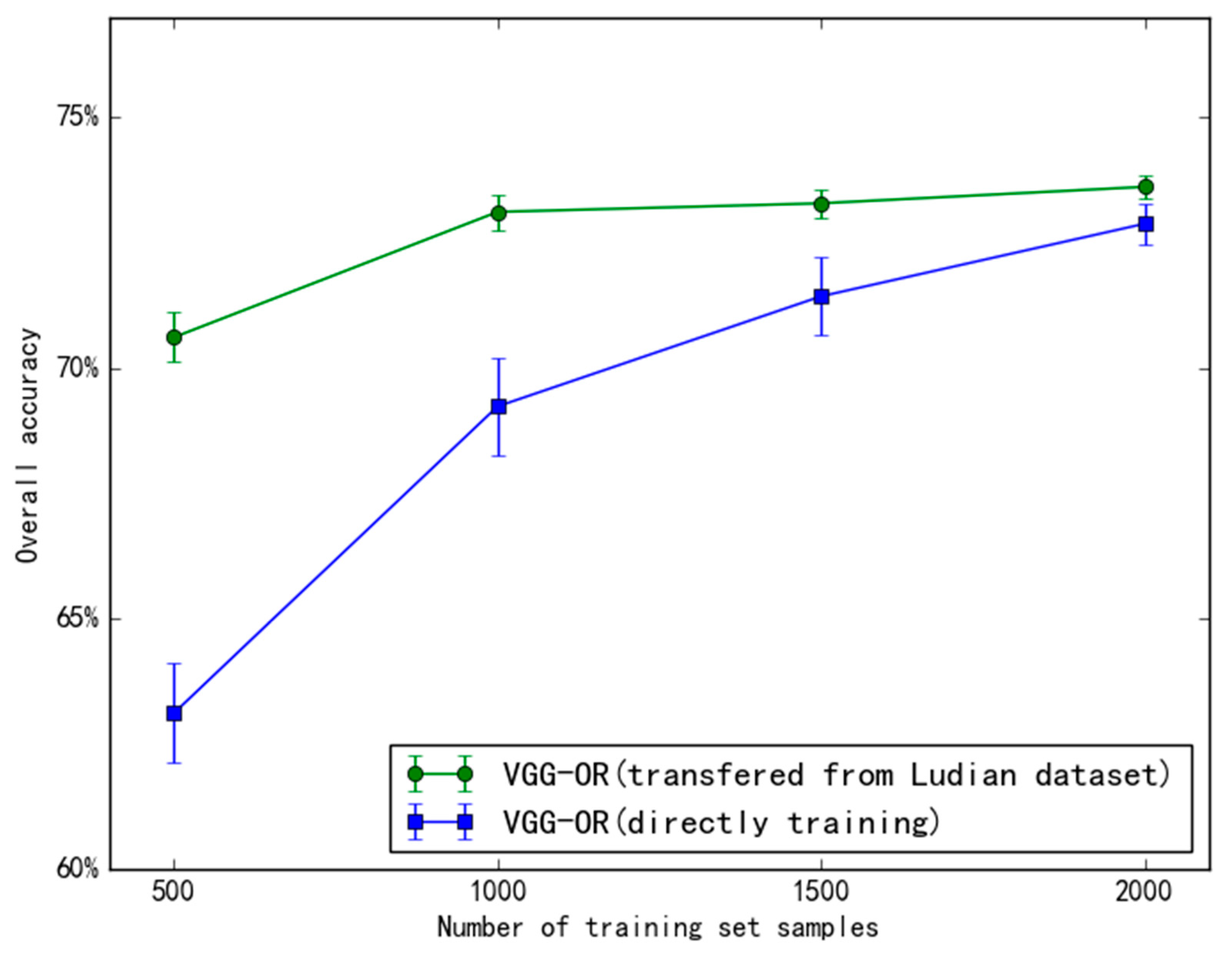
In this study, we try to transfer the model between datasets of labeled damage buildings acquired from different earthquake locations. The datasets share the same damage levels but have different data characteristics. They are similar but not the same, so a model trained with one cannot be used for the other. The transfer learning experiment not only verified a method to solve the problem of a lack of data, but also proved the stability of the model in different regions.
In the study of machine learning, it is commonly accepted that the more samples for the training model there are, the better, but it does not mean that increasing the data of one model will definitely lead to an obvious performance improvement. When there are few samples, the performance of the algorithm based on DL may not be good because the algorithm needs a large amount of parameters in many data-training models. Correspondingly, if there is less data, the performance of the machine learning algorithm based on manual characteristic selection may be better with customized rules and the help of professionals. With a huge amount of data, the performance of the DL algorithm will increase with the increasing data scale.
CNN models are developed by training the network to represent the relationships and processes that are inherent within the datasets. They perform an input–output mapping using a set of interconnected simple processing features. We should realize that such models typically do not really represent the physics of a modeled process; they are just devices used to capture relationships between the relevant input and output variables [
61]. These models can also be considered as data-driven models. So, the amount and quality of an input dataset may influence the upper limit of the model performance.
A critical factor for the use of proposed model is data availability. The amount of well-labeled samples should be enough. In the case study of the Yushu dataset, 1500 or more images are needed in the training set, and the validation and testing sets also need some data. This number can go down significantly if a pretrained model is used.
In this study, four damage grades were adopted. However, the visual interpretation of aerial images includes uncertainty or mis-classification especially for light and heavy damage levels [
6]. The damage degree will be underestimated by aerial images (
Figure 6). A Bayesian updating process is discussed in [
6] to reduce uncertainties with ground truth data.
7. Conclusions
The study was carried out on the high-precision and automated assessment method of damage to buildings; the entire process, including experimental data preparation, dataset construction, detailed model implementation, verification by experiment, and assessment and verification, was systematically conducted; and the performance of the model in practical applications was predicted through independent and disparate datasets, applying and validating the strengths and potential of the proposed assessment method.
We propose a new approach based on CNNs and OR aiming at assessing the degree of building damage caused by earthquakes with aerial imagery. The network consists of a CNN feature extractor and an OR classifier. This is the first attempt to apply OR to assess the degree of building damage from aerial imagery. Information utilization was improved by OR, so we can achieve a better accuracy with the same or a lesser amount of data. As the buildings to be evaluated are classified as damaged or not damaged in most current studies, we recalculate the evaluation indicators in the case of two classes and three classes. The proposed method significantly outperforms previous approaches.
In this study, we produced a new dataset that consisted of labeled images of damaged buildings. More than 13,000 optical aerial images were classified into four damage degrees based on the damage scale in
Table 3. The dataset and code are freely available online and can be found at [
62].
In the future, we will attempt to expand the training data on more sensors and types of buildings. A transfer learning algorithm will also be considered when lacking training data. Based on the existing classification model, combined with the object detection algorithm, such as RetinaNet [
63], the end-to-end automatic extraction of damaged building locations and corresponding damage levels within the image range can be achieved, further reducing the intermediate process. We would apply our method to more extensive and diverse types of remote sensing data. OR method has great potential to be widely used in other ordinal-scale signals, such as sea ice concentration.